Isomorphism

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Isomorphism 

The group of fifth roots of unity under multiplication is isomorphic to the group of rotations of the regular pentagon under composition.

In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσος isos "equal", and μορφή morphe "form" or "shape".

The interest in isomorphisms lies in the fact that two isomorphic objects have the same properties (excluding further information such as additional structure or names of objects). Thus isomorphic structures cannot be distinguished from the point of view of structure only, and may be identified. In mathematical jargon, one says that two objects are the same up to an isomorphism.

An automorphism is an isomorphism from a structure to itself. An isomorphism between two structures is a canonical isomorphism (a canonical map that is an isomorphism) if there is only one isomorphism between the two structures (as it is the case for solutions of a universal property), or if the isomorphism is much more natural (in some sense) than other isomorphisms. For example, for every prime number p, all fields with p elements are canonically isomorphic, with a unique isomorphism. The isomorphism theorems provide canonical isomorphisms that are not unique.

The term isomorphism is mainly used for algebraic structures. In this case, mappings are called homomorphisms, and a homomorphism is an isomorphism if and only if it is bijective.

In various areas of mathematics, isomorphisms have received specialized names, depending on the type of structure under consideration. For example:

• An isometry is an isomorphism of metric spaces.
• A homeomorphism is an isomorphism of topological spaces.
• A diffeomorphism is an isomorphism of spaces equipped with a differential structure, typically differentiable manifolds.
• A permutation is an automorphism of a set.
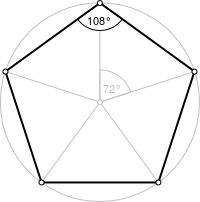
• In geometry, isomorphisms and automorphisms are often called transformations, for example rigid transformations, affine transformations, projective transformations.

Category theory, which can be viewed as a formalization of the concept of mapping between structures, provides a language that may be used to unify the approach to these different aspects of the basic idea.

Examples

Logarithm and exponential

Let ${\displaystyle \mathbb {R} ^{+}}$ be the multiplicative group of positive real numbers, and let ${\displaystyle \mathbb {R} }$ be the additive group of real numbers.

The logarithm function ${\displaystyle \log :\mathbb {R} ^{+}\to \mathbb {R} }$ satisfies ${\displaystyle \log(xy)=\log x+\log y}$ for all ${\displaystyle x,y\in \mathbb {R} ^{+},}$ so it is a group homomorphism. The exponential function ${\displaystyle \exp :\mathbb {R} \to \mathbb {R} ^{+}}$ satisfies for all ${\displaystyle x,y\in \mathbb {R} ,}$ so it too is a homomorphism.

The identities ${\displaystyle \log \exp x=x}$ and ${\displaystyle \exp \log y=y}$ show that ${\displaystyle \log }$ and ${\displaystyle \exp }$ are inverses of each other. Since ${\displaystyle \log }$ is a homomorphism that has an inverse that is also a homomorphism, ${\displaystyle \log }$ is an isomorphism of groups.

The ${\displaystyle \log }$ function is an isomorphism which translates multiplication of positive real numbers into addition of real numbers. This facility makes it possible to multiply real numbers using a ruler and a table of logarithms, or using a slide rule with a logarithmic scale.

Integers modulo 6

Consider the group ${\displaystyle (\mathbb {Z} _{6},+),}$ the integers from 0 to 5 with addition modulo 6. Also consider the group ${\displaystyle \left(\mathbb {Z} _{2}\times \mathbb {Z} _{3},+\right),}$ the ordered pairs where the x coordinates can be 0 or 1, and the y coordinates can be 0, 1, or 2, where addition in the x-coordinate is modulo 2 and addition in the y-coordinate is modulo 3.

These structures are isomorphic under addition, under the following scheme:

$${\displaystyle {\begin{alignedat}{4}(0,0)&\mapsto 0\\(1,1)&\mapsto 1\\(0,2)&\mapsto 2\\(1,0)&\mapsto 3\\(0,1)&\mapsto 4\\(1,2)&\mapsto 5\\\end{alignedat}}}$$

or in general ${\displaystyle (a,b)\mapsto (3a+4b)\mod 6.}$

For example, ${\displaystyle (1,1)+(1,0)=(0,1),}$ which translates in the other system as ${\displaystyle 1+3=4.}$

Even though these two groups "look" different in that the sets contain different elements, they are indeed isomorphic: their structures are exactly the same. More generally, the direct product of two cyclic groups ${\displaystyle \mathbb {Z} _{m}}$ and ${\displaystyle \mathbb {Z} _{n}}$ is isomorphic to ${\displaystyle (\mathbb {Z} _{mn},+)}$ if and only if m and n are coprime, per the Chinese remainder theorem.

Relation-preserving isomorphism

If one object consists of a set X with a binary relation R and the other object consists of a set Y with a binary relation S then an isomorphism from X to Y is a bijective function ${\displaystyle f:X\to Y}$ such that:

$${\displaystyle \operatorname {S} (f(u),f(v))\quad {\text{ if and only if }}\quad \operatorname {R} (u,v)}$$

S is reflexive, irreflexive, symmetric, antisymmetric, asymmetric, transitive, total, trichotomous, a partial order, total order, well-order, strict weak order, total preorder (weak order), an equivalence relation, or a relation with any other special properties, if and only if R is.

For example, R is an ordering ≤ and S an ordering ${\displaystyle \scriptstyle \sqsubseteq ,}$ then an isomorphism from X to Y is a bijective function ${\displaystyle f:X\to Y}$ such that

$${\displaystyle f(u)\sqsubseteq f(v)\quad {\text{ if and only if }}\quad u\leq v.}$$

Such an isomorphism is called an order isomorphism or (less commonly) an isotone isomorphism.

If ${\displaystyle X=Y,}$ then this is a relation-preserving automorphism.

Applications

In algebra, isomorphisms are defined for all algebraic structures. Some are more specifically studied; for example:

• Linear isomorphisms between vector spaces; they are specified by invertible matrices.
• Group isomorphisms between groups; the classification of isomorphism classes of finite groups is an open problem.
• Ring isomorphism between rings.
• Field isomorphisms are the same as ring isomorphism between fields; their study, and more specifically the study of field automorphisms is an important part of Galois theory.

Just as the automorphisms of an algebraic structure form a group, the isomorphisms between two algebras sharing a common structure form a heap. Letting a particular isomorphism identify the two structures turns this heap into a group.

In mathematical analysis, the Laplace transform is an isomorphism mapping hard differential equations into easier algebraic equations.

In graph theory, an isomorphism between two graphs G and H is a bijective map f from the vertices of G to the vertices of H that preserves the "edge structure" in the sense that there is an edge from vertex u to vertex v in G if and only if there is an edge from ${\displaystyle f(u)}$ to ${\displaystyle f(v)}$ in H. See graph isomorphism.

In mathematical analysis, an isomorphism between two Hilbert spaces is a bijection preserving addition, scalar multiplication, and inner product.

In early theories of logical atomism, the formal relationship between facts and true propositions was theorized by Bertrand Russell and Ludwig Wittgenstein to be isomorphic. An example of this line of thinking can be found in Russell's Introduction to Mathematical Philosophy.

In cybernetics, the good regulator or Conant–Ashby theorem is stated "Every good regulator of a system must be a model of that system". Whether regulated or self-regulating, an isomorphism is required between the regulator and processing parts of the system.

Category theoretic view

In category theory, given a category C, an isomorphism is a morphism ${\displaystyle f:a\to b}$ that has an inverse morphism ${\displaystyle g:b\to a,}$ that is, ${\displaystyle fg=1_{b}}$ and ${\displaystyle gf=1_{a}.}$ For example, a bijective linear map is an isomorphism between vector spaces, and a bijective continuous function whose inverse is also continuous is an isomorphism between topological spaces, called a homeomorphism.

Two categories C and D are isomorphic if there exist functors ${\displaystyle F:C\to D}$ and ${\displaystyle G:D\to C}$ which are mutually inverse to each other, that is, ${\displaystyle FG=1_{D}}$ (the identity functor on D) and ${\displaystyle GF=1_{C}}$ (the identity functor on C).

Isomorphism vs. bijective morphism

In a concrete category (roughly, a category whose objects are sets (perhaps with extra structure) and whose morphisms are structure-preserving functions), such as the category of topological spaces or categories of algebraic objects (like the category of groups, the category of rings, and the category of modules), an isomorphism must be bijective on the underlying sets. In algebraic categories (specifically, categories of varieties in the sense of universal algebra), an isomorphism is the same as a homomorphism which is bijective on underlying sets. However, there are concrete categories in which bijective morphisms are not necessarily isomorphisms (such as the category of topological spaces).

Relation with equality

See also: Equality (mathematics)

In certain areas of mathematics, notably category theory, it is valuable to distinguish between equality on the one hand and isomorphism on the other. Equality is when two objects are exactly the same, and everything that is true about one object is true about the other, while an isomorphism implies everything that is true about a designated part of one object's structure is true about the other's. For example, the sets

are equal; they are merely different representations—the first an intensional one (in set builder notation), and the second extensional (by explicit enumeration)—of the same subset of the integers. By contrast, the sets ${\displaystyle \{A,B,C\}}$ and ${\displaystyle \{1,2,3\}}$ are not equal—the first has elements that are letters, while the second has elements that are numbers. These are isomorphic as sets, since finite sets are determined up to isomorphism by their cardinality (number of elements) and these both have three elements, but there are many choices of isomorphism—one isomorphism is

${\displaystyle {\text{A}}\mapsto 1,{\text{B}}\mapsto 2,{\text{C}}\mapsto 3,}$ while another is ${\displaystyle {\text{A}}\mapsto 3,{\text{B}}\mapsto 2,{\text{C}}\mapsto 1,}$

and no one isomorphism is intrinsically better than any other.^{[note 1][note 2]} On this view and in this sense, these two sets are not equal because one cannot consider them identical: one can choose an isomorphism between them, but that is a weaker claim than identity—and valid only in the context of the chosen isomorphism.

Sometimes the isomorphisms can seem obvious and compelling, but are still not equalities. As a simple example, the genealogical relationships among Joe, John, and Bobby Kennedy are, in a real sense, the same as those among the American football quarterbacks in the Manning family: Archie, Peyton, and Eli. The father-son pairings and the elder-brother-younger-brother pairings correspond perfectly. That similarity between the two family structures illustrates the origin of the word isomorphism (Greek iso-, "same", and -morph, "form" or "shape"). But because the Kennedys are not the same people as the Mannings, the two genealogical structures are merely isomorphic and not equal.

Another example is more formal and more directly illustrates the motivation for distinguishing equality from isomorphism: the distinction between a finite-dimensional vector space V and its dual space ${\displaystyle V^{*}=\left\{\varphi :V\to \mathbf {K} \right\}}$ of linear maps from V to its field of scalars ${\displaystyle \mathbf {K} .}$ These spaces have the same dimension, and thus are isomorphic as abstract vector spaces (since algebraically, vector spaces are classified by dimension, just as sets are classified by cardinality), but there is no "natural" choice of isomorphism ${\displaystyle \scriptstyle V\mathrel {\overset {\sim }{\to }} V^{*}.}$ If one chooses a basis for V, then this yields an isomorphism: For all ${\displaystyle u,v\in V,}$

$${\displaystyle v\mathrel {\overset {\sim }{\mapsto }} \phi _{v}\in V^{*}\quad {\text{ such that }}\quad \phi _{v}(u)=v^{\mathrm {T} }u.}$$

This corresponds to transforming a column vector (element of V) to a row vector (element of V*) by transpose, but a different choice of basis gives a different isomorphism: the isomorphism "depends on the choice of basis". More subtly, there is a map from a vector space V to its double dual ${\displaystyle V^{**}=\left\{x:V^{*}\to \mathbf {K} \right\}}$ that does not depend on the choice of basis: For all ${\displaystyle v\in V{\text{ and }}\varphi \in V^{*},}$

$${\displaystyle v\mathrel {\overset {\sim }{\mapsto }} x_{v}\in V^{**}\quad {\text{ such that }}\quad x_{v}(\phi )=\phi (v).}$$

This leads to a third notion, that of a natural isomorphism: while ${\displaystyle V}$ and ${\displaystyle V^{**}}$ are different sets, there is a "natural" choice of isomorphism between them. This intuitive notion of "an isomorphism that does not depend on an arbitrary choice" is formalized in the notion of a natural transformation; briefly, that one may consistently identify, or more generally map from, a finite-dimensional vector space to its double dual, ${\displaystyle \scriptstyle V\mathrel {\overset {\sim }{\to }} V^{**},}$ for any vector space in a consistent way. Formalizing this intuition is a motivation for the development of category theory.

However, there is a case where the distinction between natural isomorphism and equality is usually not made. That is for the objects that may be characterized by a universal property. In fact, there is a unique isomorphism, necessarily natural, between two objects sharing the same universal property. A typical example is the set of real numbers, which may be defined through infinite decimal expansion, infinite binary expansion, Cauchy sequences, Dedekind cuts and many other ways. Formally, these constructions define different objects which are all solutions with the same universal property. As these objects have exactly the same properties, one may forget the method of construction and consider them as equal. This is what everybody does when referring to "the set of the real numbers". The same occurs with quotient spaces: they are commonly constructed as sets of equivalence classes. However, referring to a set of sets may be counterintuitive, and so quotient spaces are commonly considered as a pair of a set of undetermined objects, often called "points", and a surjective map onto this set.

If one wishes to distinguish between an arbitrary isomorphism (one that depends on a choice) and a natural isomorphism (one that can be done consistently), one may write ${\displaystyle \,\approx \,}$ for an unnatural isomorphism and ≅ for a natural isomorphism, as in ${\displaystyle V\approx V^{*}}$ and ${\displaystyle V\cong V^{**}.}$ This convention is not universally followed, and authors who wish to distinguish between unnatural isomorphisms and natural isomorphisms will generally explicitly state the distinction.

Generally, saying that two objects are equal is reserved for when there is a notion of a larger (ambient) space that these objects live in. Most often, one speaks of equality of two subsets of a given set (as in the integer set example above), but not of two objects abstractly presented. For example, the 2-dimensional unit sphere in 3-dimensional space and the Riemann sphere ${\displaystyle {\widehat {\mathbb {C} }}}$ which can be presented as the one-point compactification of the complex plane ${\displaystyle \mathbb {C} \cup \{\infty \}}$ or as the complex projective line (a quotient space) are three different descriptions for a mathematical object, all of which are isomorphic, but not equal because they are not all subsets of a single space: the first is a subset of ${\displaystyle \mathbb {R} ^{3},}$ the second is ${\displaystyle \mathbb {C} \cong \mathbb {R} ^{2}}$ plus an additional point, and the third is a subquotient of ${\displaystyle \mathbb {C} ^{2}.}$

In the context of category theory, objects are usually at most isomorphic—indeed, a motivation for the development of category theory was showing that different constructions in homology theory yielded equivalent (isomorphic) groups. Given maps between two objects X and Y, however, one asks if they are equal or not (they are both elements of the set ${\displaystyle \hom(X,Y),}$ hence equality is the proper relationship), particularly in commutative diagrams.

Kirchhoff's circuit laws

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws 

Kirchhoff's circuit laws are two equalities that deal with the current and potential difference (commonly known as voltage) in the lumped element model of electrical circuits. They were first described in 1845 by German physicist Gustav Kirchhoff. This generalized the work of Georg Ohm and preceded the work of James Clerk Maxwell. Widely used in electrical engineering, they are also called Kirchhoff's rules or simply Kirchhoff's laws. These laws can be applied in time and frequency domains and form the basis for network analysis.

Both of Kirchhoff's laws can be understood as corollaries of Maxwell's equations in the low-frequency limit. They are accurate for DC circuits, and for AC circuits at frequencies where the wavelengths of electromagnetic radiation are very large compared to the circuits.

Kirchhoff's current law

The current entering any junction is equal to the current leaving that junction. i₂ + i₃ = i₁ + i₄

This law, also called Kirchhoff's first law, Kirchhoff's point rule, or Kirchhoff's junction rule (or nodal rule), states that, for any node (junction) in an electrical circuit, the sum of currents flowing into that node is equal to the sum of currents flowing out of that node; or equivalently:

The algebraic sum of currents in a network of conductors meeting at a point is zero.

Recalling that current is a signed (positive or negative) quantity reflecting direction towards or away from a node, this principle can be succinctly stated as:  ,

where n is the total number of branches with currents flowing towards or away from the node.

Kirchhoff's circuit laws were originally obtained from experimental results. However, the current law can be viewed as an extension of the conservation of charge, since charge is the product of current and the time the current has been flowing. If the net charge in a region is constant, the current law will hold on the boundaries of the region. This means that the current law relies on the fact that the net charge in the wires and components is constant.

Uses

A matrix version of Kirchhoff's current law is the basis of most circuit simulation software, such as SPICE. The current law is used with Ohm's law to perform nodal analysis.

The current law is applicable to any lumped network irrespective of the nature of the network; whether unilateral or bilateral, active or passive, linear or non-linear.

Kirchhoff's voltage law

The sum of all the voltages around a loop is equal to zero:  v₁ + v₂ + v₃ + v₄ = 0

This law, also called Kirchhoff's second law, Kirchhoff's loop (or mesh) rule, or Kirchhoff's second rule, states the following:

The directed sum of the potential differences (voltages) around any closed loop is zero.

Similarly to Kirchhoff's current law, the voltage law can be stated as: ,

where n is the total number of voltages measured.

Derivation of Kirchhoff's voltage law

A similar derivation can be found in The Feynman Lectures on Physics, Volume II, Chapter 22: AC Circuits.

Consider some arbitrary circuit. Approximate the circuit with lumped elements, so that (time-varying) magnetic fields are contained to each component and the field in the region exterior to the circuit is negligible. Based on this assumption, the Maxwell–Faraday equation reveals that

in the exterior region. If each of the components has a finite volume, then the exterior region is simply connected, and thus the electric field is conservative in that region. Therefore, for any loop in the circuit, we find that , where ${\textstyle {\mathcal {P}}_{i}}$ are paths around the exterior of each of the components, from one terminal to another.

Note that this derivation uses the following definition for the voltage rise from ${\displaystyle a}$ to ${\displaystyle b}$:  .

However, the electric potential (and thus voltage) can be defined in other ways, such as via the Helmholtz decomposition.

Generalization

In the low-frequency limit, the voltage drop around any loop is zero. This includes imaginary loops arranged arbitrarily in space – not limited to the loops delineated by the circuit elements and conductors. In the low-frequency limit, this is a corollary of Faraday's law of induction (which is one of Maxwell's equations).

This has practical application in situations involving "static electricity".

Limitations

Kirchhoff's circuit laws are the result of the lumped-element model and both depend on the model being applicable to the circuit in question. When the model is not applicable, the laws do not apply.

The current law is dependent on the assumption that the net charge in any wire, junction or lumped component is constant. Whenever the electric field between parts of the circuit is non-negligible, such as when two wires are capacitively coupled, this may not be the case. This occurs in high-frequency AC circuits, where the lumped element model is no longer applicable. For example, in a transmission line, the charge density in the conductor may be constantly changing.

In a transmission line, the net charge in different parts of the conductor changes with time. In the direct physical sense, this violates KCL.

On the other hand, the voltage law relies on the fact that the action of time-varying magnetic fields are confined to individual components, such as inductors. In reality, the induced electric field produced by an inductor is not confined, but the leaked fields are often negligible.

Modelling real circuits with lumped elements

The lumped element approximation for a circuit is accurate at low frequencies. At higher frequencies, leaked fluxes and varying charge densities in conductors become significant. To an extent, it is possible to still model such circuits using parasitic components. If frequencies are too high, it may be more appropriate to simulate the fields directly using finite element modelling or other techniques.

To model circuits so that both laws can still be used, it is important to understand the distinction between physical circuit elements and the ideal lumped elements. For example, a wire is not an ideal conductor. Unlike an ideal conductor, wires can inductively and capacitively couple to each other (and to themselves), and have a finite propagation delay. Real conductors can be modeled in terms of lumped elements by considering parasitic capacitances distributed between the conductors to model capacitive coupling, or parasitic (mutual) inductances to model inductive coupling. Wires also have some self-inductance.

Example

Assume an electric network consisting of two voltage sources and three resistors.

According to the first law:

$${\displaystyle i_{1}-i_{2}-i_{3}=0}$$

Applying the second law to the closed circuit s₁, and substituting for voltage using Ohm's law gives:

$${\displaystyle -R_{2}i_{2}+{\mathcal {E}}_{1}-R_{1}i_{1}=0}$$

The second law, again combined with Ohm's law, applied to the closed circuit s₂ gives:

$${\displaystyle -R_{3}i_{3}-{\mathcal {E}}_{2}-{\mathcal {E}}_{1}+R_{2}i_{2}=0}$$

This yields a system of linear equations in i₁, i₂, i₃:

$${\displaystyle {\begin{cases}i_{1}-i_{2}-i_{3}&=0\\-R_{2}i_{2}+{\mathcal {E}}_{1}-R_{1}i_{1}&=0\\-R_{3}i_{3}-{\mathcal {E}}_{2}-{\mathcal {E}}_{1}+R_{2}i_{2}&=0\end{cases}}}$$

 which is equivalent to

$${\displaystyle {\begin{cases}i_{1}+(-i_{2})+(-i_{3})&=0\\R_{1}i_{1}+R_{2}i_{2}+0i_{3}&={\mathcal {E}}_{1}\\0i_{1}+R_{2}i_{2}-R_{3}i_{3}&={\mathcal {E}}_{1}+{\mathcal {E}}_{2}\end{cases}}}$$

 Assuming

$${\displaystyle {\begin{aligned}R_{1}&=100\Omega ,&R_{2}&=200\Omega ,&R_{3}&=300\Omega ,\\{\mathcal {E}}_{1}&=3{\text{V}},&{\mathcal {E}}_{2}&=4{\text{V}}\end{aligned}}}$$

the solution is

$${\displaystyle {\begin{cases}i_{1}={\frac {1}{1100}}{\text{A}}\\[6pt]i_{2}={\frac {4}{275}}{\text{A}}\\[6pt]i_{3}=-{\frac {3}{220}}{\text{A}}\end{cases}}}$$

The current i₃ has a negative sign which means the assumed direction of i₃ was incorrect and i₃ is actually flowing in the direction opposite to the red arrow labeled i₃. The current in R₃ flows from left to right.