Maxwell–Boltzmann statistics

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Maxwell%E2%80%93Boltzmann_statistics

Maxwell–Boltzmann statistics can be used to derive the Maxwell–Boltzmann distribution of particle speeds in an ideal gas. Shown: distribution of particle speed for 10⁶ oxygen particles at -100, 20 and 600 °C.

In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density is low enough to render quantum effects negligible.

The expected number of particles with energy ${\displaystyle {\epsilon }_i}$ for Maxwell–Boltzmann statistics is

${\displaystyle ⟨N_i⟩=\frac{g_i}{e^{({\epsilon }_i-\mu )/kT}}=\frac{N}{Z}{g}_i{e}^{-{\epsilon }_i/kT},}$

where:

• ${\displaystyle {\epsilon }_i}$ is the energy of the i-th energy level,
• ${\displaystyle ⟨N_i⟩}$ is the average number of particles in the set of states with energy ${\displaystyle {\epsilon }_i}$,
• ${\displaystyle g_i}$ is the degeneracy of energy level i, that is, the number of states with energy ${\displaystyle {\epsilon }_i}$ which may nevertheless be distinguished from each other by some other means,
• μ is the chemical potential,
• k is the Boltzmann constant,
• T is absolute temperature,
• N is the total number of particles:
  $${\displaystyle N=\sum _i{N}_i,}$$

  
• Z is the partition function:
  $${\displaystyle Z=\sum _i{g}_i{e}^{-{\epsilon }_i/kT},}$$

  
• e is Euler's number

Equivalently, the number of particles is sometimes expressed as

${\displaystyle ⟨N_i⟩=\frac{1}{e^{({\epsilon }_i-\mu )/kT}}=\frac{N}{Z}{e}^{-{\epsilon }_i/kT},}$

where the index i now specifies a particular state rather than the set of all states with energy ${\displaystyle {\epsilon }_i}$, and $Z=\sum _i{e}^{-{\epsilon }_i/kT}$.

History

Further information: Maxwell–Boltzmann distribution

Maxwell–Boltzmann statistics grew out of the Maxwell–Boltzmann distribution, most likely as a distillation of the underlying technique. The distribution was first derived by Maxwell in 1860 on heuristic grounds. Boltzmann later, in the 1870s, carried out significant investigations into the physical origins of this distribution. The distribution can be derived on the ground that it maximizes the entropy of the system.

Applicability

Comparison of average occupancy of the ground state for three statistics

Maxwell–Boltzmann statistics is used to derive the Maxwell–Boltzmann distribution of an ideal gas. However, it can also be used to extend that distribution to particles with a different energy–momentum relation, such as relativistic particles (resulting in Maxwell–Jüttner distribution), and to other than three-dimensional spaces.

Maxwell–Boltzmann statistics is often described as the statistics of "distinguishable" classical particles. In other words, the configuration of particle A in state 1 and particle B in state 2 is different from the case in which particle B is in state 1 and particle A is in state 2. This assumption leads to the proper (Boltzmann) statistics of particles in the energy states, but yields non-physical results for the entropy, as embodied in the Gibbs paradox.

At the same time, there are no real particles that have the characteristics required by Maxwell–Boltzmann statistics. Indeed, the Gibbs paradox is resolved if we treat all particles of a certain type (e.g., electrons, protons, etc.) as principally indistinguishable. Once this assumption is made, the particle statistics change. The change in entropy in the entropy of mixing example may be viewed as an example of a non-extensive entropy resulting from the distinguishability of the two types of particles being mixed.

Quantum particles are either bosons (following instead Bose–Einstein statistics) or fermions (subject to the Pauli exclusion principle, following instead Fermi–Dirac statistics). Both of these quantum statistics approach the Maxwell–Boltzmann statistics in the limit of high temperature and low particle density.

Derivations

Maxwell–Boltzmann statistics can be derived in various statistical mechanical thermodynamic ensembles:

• The grand canonical ensemble, exactly.
• The canonical ensemble, exactly.
• The microcanonical ensemble, but only in the thermodynamic limit.

In each case it is necessary to assume that the particles are non-interacting, and that multiple particles can occupy the same state and do so independently.

Derivation from microcanonical ensemble

Suppose we have a container with a huge number of very small particles all with identical physical characteristics (such as mass, charge, etc.). Let's refer to this as the system. Assume that though the particles have identical properties, they are distinguishable. For example, we might identify each particle by continually observing their trajectories, or by placing a marking on each one, e.g., drawing a different number on each one as is done with lottery balls.

The particles are moving inside that container in all directions with great speed. Because the particles are speeding around, they possess some energy. The Maxwell–Boltzmann distribution is a mathematical function that describes about how many particles in the container have a certain energy. More precisely, the Maxwell–Boltzmann distribution gives the non-normalized probability (this means that the probabilities do not add up to 1) that the state corresponding to a particular energy is occupied.

In general, there may be many particles with the same amount of energy ${\displaystyle \epsilon }$. Let the number of particles with the same energy ${\displaystyle {\epsilon }_1}$ be ${\displaystyle N_1}$, the number of particles possessing another energy ${\displaystyle {\epsilon }_2}$ be ${\displaystyle N_2}$, and so forth for all the possible energies ${\displaystyle \{{\epsilon }_i\mid i=1,2,3,\dots \}.}$ To describe this situation, we say that ${\displaystyle N_i}$ is the occupation number of the energy level ${\displaystyle i.}$ If we know all the occupation numbers ${\displaystyle \{N_i\mid i=1,2,3,\dots \},}$ then we know the total energy of the system. However, because we can distinguish between which particles are occupying each energy level, the set of occupation numbers ${\displaystyle \{N_i\mid i=1,2,3,\dots \}}$ does not completely describe the state of the system. To completely describe the state of the system, or the microstate, we must specify exactly which particles are in each energy level. Thus when we count the number of possible states of the system, we must count each and every microstate, and not just the possible sets of occupation numbers.

To begin with, assume that there is only one way to put ${\displaystyle N_i}$ particles into the energy level ${\displaystyle i}$ (there is no degeneracy). What follows next is a bit of combinatorial thinking which has little to do in accurately describing the reservoir of particles. For instance, let's say there is a total of ${\displaystyle k}$ boxes labelled ${\displaystyle a,b,\dots ,k}$. With the concept of combination, we could calculate how many ways to arrange ${\displaystyle N}$ balls into respective l-th box in which there would be ${\displaystyle N_l}$ balls without an order. To begin with, we select ${\displaystyle N_a}$ balls from a total of ${\displaystyle N}$ balls, placing them in box ${\displaystyle a}$, and continuing on selection from the remaining until no ball is left outside. The total number of ways that the balls can be arranged is

${\displaystyle \begin{array}{rl}W& =\frac{N!}{N_a!\cancel{(N-N_a)!}}\times \frac{\cancel{(N-N_a)!}}{N_b!\cancel{(N-N_a-N_b)!}}\times \frac{\cancel{(N-N_a-N_b)!}}{N_c!\cancel{(N-N_a-N_b-N_c)!}}\times \cdots \times \frac{\cancel{(N-\cdots -N_{\ell })!}}{N_k!(N-\cdots -N_{\ell }-N_k)!}\\ & =\frac{N!}{N_a!N_b!N_c!\cdots N_k!(N-N_a-\cdots -N_{\ell }-N_k)!}\end{array}}$

and because not even a single ball is to be left outside the boxes (all balls should be put in boxes), which implies that the sum made of the terms ${\displaystyle N_a,N_b,\dots ,N_k}$ must equal to ${\displaystyle N}$; thus the term ${\displaystyle (N-N_a-N_b-\cdots -N_k)!}$ in the relation above evaluates to 0! (0! = 1), and we simplify the relation as

${\displaystyle W=N!\prod _{\ell =a,b,\dots }^k\frac{1}{N_{\ell }!}}$

This is just the multinomial coefficient, the number of ways of arranging N items into k boxes, the l-th box holding N_l items, ignoring the permutation of items in each box.

Now, consider the case where there is more than one way to put ${\displaystyle N_i}$ particles in the box ${\displaystyle i}$ (i.e. taking the degeneracy problem into consideration). If the ${\displaystyle i}$-th box has a "degeneracy" of ${\displaystyle g_i}$, that is, it has ${\displaystyle g_i}$ "sub-boxes" (${\displaystyle g_i}$ boxes with the same energy ${\displaystyle {\epsilon }_i}$. These states/boxes with the same energy are called degenerate states.), such that any way of filling the ${\displaystyle i}$-th box where the number in the sub-boxes is changed is a distinct way of filling the box, then the number of ways of filling the i-th box must be increased by the number of ways of distributing the ${\displaystyle N_i}$ objects in the ${\displaystyle g_i}$ "sub-boxes". The number of ways of placing ${\displaystyle N_i}$ distinguishable objects in ${\displaystyle g_i}$ "sub-boxes" is ${\displaystyle g_i^{N_i}}$ (the first object can go into any of the ${\displaystyle g_i}$ boxes, the second object can also go into any of the ${\displaystyle g_i}$ boxes, and so on). Thus the number of ways ${\displaystyle W}$ that a total of ${\displaystyle N}$ particles can be classified into energy levels according to their energies, while each level ${\displaystyle i}$ having ${\displaystyle g_i}$ distinct states such that the i-th level accommodates ${\displaystyle N_i}$ particles is:

${\displaystyle W=N!\prod _i\frac{g_i^{N_i}}{N_i!}}$

This is the form for W first derived by Boltzmann. Boltzmann's fundamental equation ${\displaystyle S=k\ln W}$ relates the thermodynamic entropy S to the number of microstates W, where k is the Boltzmann constant. It was pointed out by Gibbs however, that the above expression for W does not yield an extensive entropy, and is therefore faulty. This problem is known as the Gibbs paradox. The problem is that the particles considered by the above equation are not indistinguishable. In other words, for two particles (A and B) in two energy sublevels the population represented by [A,B] is considered distinct from the population [B,A] while for indistinguishable particles, they are not. If we carry out the argument for indistinguishable particles, we are led to the Bose–Einstein expression for W:

${\displaystyle W=\prod _i\frac{(N_i+g_i-1)!}{N_i!(g_i-1)!}}$

The Maxwell–Boltzmann distribution follows from this Bose–Einstein distribution for temperatures well above absolute zero, implying that ${\displaystyle g_i\gg 1}$. The Maxwell–Boltzmann distribution also requires low density, implying that ${\displaystyle g_i\gg N_i}$. Under these conditions, we may use Stirling's approximation for the factorial:

${\displaystyle N!\approx N^N{e}^{-N},}$

to write:

${\displaystyle W\approx \prod _i\frac{(N_i+g_i{)}^{N_i+g_i}}{N_i^{N_i}{g}_i^{g_i}}\approx \prod _i\frac{g_i^{N_i}(1+N_i/g_i{)}^{g_i}}{N_i^{N_i}}}$

Using the fact that ${\displaystyle (1+N_i/g_i{)}^{g_i}\approx e^{N_i}}$ for ${\displaystyle g_i\gg N_i}$ we can again use Stirling's approximation to write:

${\displaystyle W\approx \prod _i\frac{g_i^{N_i}}{N_i!}}$

This is essentially a division by N! of Boltzmann's original expression for W, and this correction is referred to as correct Boltzmann counting.

We wish to find the ${\displaystyle N_i}$ for which the function ${\displaystyle W}$ is maximized, while considering the constraint that there is a fixed number of particles $\left(N=\sum N_i\right)$ and a fixed energy $\left(E=\sum N_i{\epsilon }_i\right)$ in the container. The maxima of ${\displaystyle W}$ and ${\displaystyle \ln (W)}$ are achieved by the same values of ${\displaystyle N_i}$ and, since it is easier to accomplish mathematically, we will maximize the latter function instead. We constrain our solution using Lagrange multipliers forming the function:

${\displaystyle f(N_1,N_2,\dots ,N_n)=\ln (W)+\alpha (N-\sum N_i)+\beta (E-\sum N_i{\epsilon }_i)}$

${\displaystyle \ln W=\ln \left[\prod _{i=1}^n\frac{g_i^{N_i}}{N_i!}\right]\approx \sum _{i=1}^n\left(N_i\ln g_i-N_i\ln N_i+N_i\right)}$

Finally

${\displaystyle f(N_1,N_2,\dots ,N_n)=\alpha N+\beta E+\sum _{i=1}^n\left(N_i\ln g_i-N_i\ln N_i+N_i-(\alpha +\beta {\epsilon }_i)N_i\right)}$

In order to maximize the expression above we apply Fermat's theorem (stationary points), according to which local extrema, if exist, must be at critical points (partial derivatives vanish):

${\displaystyle \frac{\mathrm{\partial }f}{\mathrm{\partial }{N}_i}=\ln g_i-\ln N_i-(\alpha +\beta {\epsilon }_i)=0}$

By solving the equations above (${\displaystyle i=1\dots n}$) we arrive to an expression for ${\displaystyle N_i}$:

${\displaystyle N_i=\frac{g_i}{e^{\alpha +\beta {\epsilon }_i}}}$

Substituting this expression for ${\displaystyle N_i}$ into the equation for ${\displaystyle \ln W}$ and assuming that ${\displaystyle N\gg 1}$ yields:

${\displaystyle \ln W=(\alpha +1)N+\beta E}$

or, rearranging:

${\displaystyle E=\frac{\ln W}{\beta }-\frac{N}{\beta }-\frac{\alpha N}{\beta }}$

Boltzmann realized that this is just an expression of the Euler-integrated fundamental equation of thermodynamics. Identifying E as the internal energy, the Euler-integrated fundamental equation states that :

${\displaystyle E=TS-PV+\mu N}$

where T is the temperature, P is pressure, V is volume, and μ is the chemical potential. Boltzmann's famous equation ${\displaystyle S=k\ln W}$ is the realization that the entropy is proportional to ${\displaystyle \ln W}$ with the constant of proportionality being the Boltzmann constant. Using the ideal gas equation of state (PV = NkT), It follows immediately that ${\displaystyle \beta =1/kT}$ and ${\displaystyle \alpha =-\mu /kT}$ so that the populations may now be written:

${\displaystyle N_i=\frac{g_i}{e^{({\epsilon }_i-\mu )/(kT)}}}$

Note that the above formula is sometimes written:

${\displaystyle N_i=\frac{g_i}{e^{{\epsilon }_i/kT}/z}}$

where ${\displaystyle z=\exp (\mu /kT)}$ is the absolute activity.

Alternatively, we may use the fact that

${\displaystyle \sum _i{N}_i=N}$

to obtain the population numbers as

${\displaystyle N_i=N\frac{g_i{e}^{-{\epsilon }_i/kT}}{Z}}$

where Z is the partition function defined by:

${\displaystyle Z=\sum _i{g}_i{e}^{-{\epsilon }_i/kT}}$

In an approximation where ε_i is considered to be a continuous variable, the Thomas–Fermi approximation yields a continuous degeneracy g proportional to ${\displaystyle \sqrt{\epsilon }}$ so that:

${\displaystyle \frac{\sqrt{\epsilon }{e}^{-\epsilon /kT}}{{\int }_0^{\mathrm{\infty }}\sqrt{\epsilon }{e}^{-\epsilon /kT}}=\frac{\sqrt{\epsilon }{e}^{-\epsilon /kT}}{\frac{\sqrt{\pi }}{2}(kT{)}^{3/2}}=\frac{2\sqrt{\epsilon }{e}^{-\epsilon /kT}}{\sqrt{\pi (kT{)}^3}}}$

which is just the Maxwell–Boltzmann distribution for the energy.

Derivation from canonical ensemble

In the above discussion, the Boltzmann distribution function was obtained via directly analysing the multiplicities of a system. Alternatively, one can make use of the canonical ensemble. In a canonical ensemble, a system is in thermal contact with a reservoir. While energy is free to flow between the system and the reservoir, the reservoir is thought to have infinitely large heat capacity as to maintain constant temperature, T, for the combined system.

In the present context, our system is assumed to have the energy levels ${\displaystyle {\epsilon }_i}$ with degeneracies ${\displaystyle g_i}$. As before, we would like to calculate the probability that our system has energy ${\displaystyle {\epsilon }_i}$.

If our system is in state ${\displaystyle s_1}$, then there would be a corresponding number of microstates available to the reservoir. Call this number ${\displaystyle {\mathrm{\Omega }}_R(s_1)}$. By assumption, the combined system (of the system we are interested in and the reservoir) is isolated, so all microstates are equally probable. Therefore, for instance, if ${\displaystyle {\mathrm{\Omega }}_R(s_1)=2{\mathrm{\Omega }}_R(s_2)}$, we can conclude that our system is twice as likely to be in state ${\displaystyle s_1}$ than ${\displaystyle s_2}$. In general, if ${\displaystyle P(s_i)}$ is the probability that our system is in state ${\displaystyle s_i}$,

${\displaystyle \frac{P(s_1)}{P(s_2)}=\frac{{\mathrm{\Omega }}_R(s_1)}{{\mathrm{\Omega }}_R(s_2)}.}$

Since the entropy of the reservoir ${\displaystyle S_R=k\ln {\mathrm{\Omega }}_R}$, the above becomes

${\displaystyle \frac{P(s_1)}{P(s_2)}=\frac{e^{S_R(s_1)/k}}{e^{S_R(s_2)/k}}=e^{(S_R(s_1)-S_R(s_2))/k}.}$

Next we recall the thermodynamic identity (from the first law of thermodynamics):

${\displaystyle d{S}_R=\frac{1}{T}(d{U}_R+Pd{V}_R-\mu d{N}_R).}$

In a canonical ensemble, there is no exchange of particles, so the ${\displaystyle d{N}_R}$ term is zero. Similarly, ${\displaystyle d{V}_R=0.}$ This gives

${\displaystyle S_R(s_1)-S_R(s_2)=\frac{1}{T}(U_R(s_1)-U_R(s_2))=-\frac{1}{T}(E(s_1)-E(s_2)),}$

where ${\displaystyle U_R(s_i)}$ and ${\displaystyle E(s_i)}$ denote the energies of the reservoir and the system at ${\displaystyle s_i}$, respectively. For the second equality we have used the conservation of energy. Substituting into the first equation relating ${\displaystyle P(s_1),P(s_2)}$:

${\displaystyle \frac{P(s_1)}{P(s_2)}=\frac{e^{-E(s_1)/kT}}{e^{-E(s_2)/kT}},}$

which implies, for any state s of the system

${\displaystyle P(s)=\frac{1}{Z}{e}^{-E(s)/kT},}$

where Z is an appropriately chosen "constant" to make total probability 1. (Z is constant provided that the temperature T is invariant.)

${\displaystyle Z=\sum _s{e}^{-E(s)/kT},}$

where the index s runs through all microstates of the system. Z is sometimes called the Boltzmann sum over states (or "Zustandssumme" in the original German). If we index the summation via the energy eigenvalues instead of all possible states, degeneracy must be taken into account. The probability of our system having energy ${\displaystyle {\epsilon }_i}$ is simply the sum of the probabilities of all corresponding microstates:

${\displaystyle P({\epsilon }_i)=\frac{1}{Z}{g}_i{e}^{-{\epsilon }_i/kT}}$

where, with obvious modification,

${\displaystyle Z=\sum _j{g}_j{e}^{-{\epsilon }_j/kT},}$

this is the same result as before.

Comments on this derivation:

• Notice that in this formulation, the initial assumption "... suppose the system has total N particles..." is dispensed with. Indeed, the number of particles possessed by the system plays no role in arriving at the distribution. Rather, how many particles would occupy states with energy ${\displaystyle {\epsilon }_i}$ follows as an easy consequence.
• What has been presented above is essentially a derivation of the canonical partition function. As one can see by comparing the definitions, the Boltzmann sum over states is equal to the canonical partition function.
• Exactly the same approach can be used to derive Fermi–Dirac and Bose–Einstein statistics. However, there one would replace the canonical ensemble with the grand canonical ensemble, since there is exchange of particles between the system and the reservoir. Also, the system one considers in those cases is a single particle state, not a particle. (In the above discussion, we could have assumed our system to be a single atom.)

High-voltage direct current

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/High-voltage_direct_current 

 

Long distance HVDC lines carrying hydroelectricity from Canada's Nelson River to this converter station where it is converted to AC for use in southern Manitoba's grid

A high-voltage direct current (HVDC) electric power transmission system (also called a power superhighway or an electrical superhighway) uses direct current (DC) for electric power transmission, in contrast with the more common alternating current (AC) transmission systems.

Most HVDC links use voltages between 100 kV and 800 kV. However, a 1,100 kV link in China was completed in 2019 over a distance of 3,300 km (2,100 mi) with a power capacity of 12 GW. With this dimension, intercontinental connections become possible which could help to deal with the fluctuations of wind power and photovoltaics.

HVDC allows power transmission between AC transmission systems that are not synchronized. Since the power flow through an HVDC link can be controlled independently of the phase angle between source and load, it can stabilize a network against disturbances due to rapid changes in power. HVDC also allows the transfer of power between grid systems running at different frequencies, such as 50 and 60 Hz. This improves the stability and economy of each grid, by allowing the exchange of power between previously incompatible networks.

The modern form of HVDC transmission uses technology developed extensively in the 1930s in Sweden (ASEA) and in Germany. Early commercial installations included one in the Soviet Union in 1951 between Moscow and Kashira, and a 100 kV, 20 MW system between Gotland and mainland Sweden in 1954. Before the Chinese project of 2019, the longest HVDC link in the world was the Rio Madeira link in Brazil, which consists of two bipoles of ±600 kV, 3150 MW each, connecting Porto Velho in the state of Rondônia to the São Paulo area with a length of more than 2,500 km (1,600 mi).

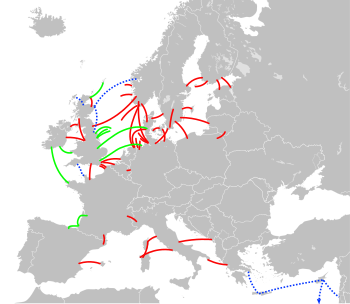
HVDC links in Europe

  Existing links

  Under construction

  Proposed

 

Many of these HVDC lines transfer power from renewable sources such as hydro and wind. For names, see also the annotated version.

High voltage transmission

High voltage is used for electric power transmission to reduce the energy lost in the resistance of the wires. For a given quantity of power transmitted, doubling the voltage will deliver the same power at only half the current:

$${\displaystyle \text{power}=(\text{voltage})\cdot (\text{current})=(2\cdot \text{voltage})\cdot (\frac{1}{2}\cdot \text{current})}$$

Since the power lost as heat in the wires is directly proportional to the square of the current $(\text{heat}={\text{current}}^2\cdot \text{resistance}),$ using half the current at double the voltage reduces the line losses by a factor of 4. While power lost in transmission can also be reduced by decreasing the resistance by increasing the conductor size, larger conductors are heavier and more expensive.

High voltage cannot readily be used for lighting or motors, so transmission-level voltages must be reduced for end-use equipment. Transformers are used to change the voltage levels in alternating current (AC) transmission circuits, but can't pass DC current. Transformers made AC voltage changes practical, and AC generators were more efficient than those using DC. These advantages led to early low-voltage DC transmission systems being supplanted by AC systems around the turn of the 20th century.

Practical conversion of power between AC and DC became possible with the development of power electronics devices such as mercury-arc valves and, starting in the 1970s, power semiconductor devices including thyristors, integrated gate-commutated thyristors (IGCTs), MOS-controlled thyristors (MCTs) and insulated-gate bipolar transistors (IGBT).

History

Electromechanical systems

Schematic diagram of a Thury HVDC transmission system

 

HVDC in 1971: this 150 kV mercury-arc valve converted AC hydropower voltage for transmission to distant cities from Manitoba Hydro generators.

 

Pylons of the Baltic Cable HVDC in Sweden

The first long-distance transmission of electric power was demonstrated using direct current in 1882 at Miesbach-Munich Power Transmission, but only 1.5 kW was transmitted. An early method of HVDC transmission was developed by the Swiss engineer René Thury and his method, the Thury system, was put into practice by 1889 in Italy by the Acquedotto De Ferrari-Galliera company. This system used series-connected motor-generator sets to increase the voltage. Each set was insulated from electrical ground and driven by insulated shafts from a prime mover. The transmission line was operated in a constant-current mode, with up to 5,000 volts across each machine, some machines having double commutators to reduce the voltage on each commutator. This system transmitted 630 kW at 14 kV DC over a distance of 120 kilometres (75 mi). The Moutiers–Lyon system transmitted 8,600 kW of hydroelectric power a distance of 200 kilometres (120 mi), including 10 kilometres (6.2 mi) of underground cable. This system used eight series-connected generators with dual commutators for a total voltage of 150 kV between the positive and negative poles, and operated from c.1906 until 1936. Fifteen Thury systems were in operation by 1913. Other Thury systems operating at up to 100 kV DC worked into the 1930s, but the rotating machinery required high maintenance and had high energy loss.

Various other electromechanical devices were tested during the first half of the 20th century with little commercial success. One technique attempted for conversion of direct current from a high transmission voltage to lower utilization voltage was to charge series-connected batteries, then reconnect the batteries in parallel to serve distribution loads. While at least two commercial installations were tried around the turn of the 20th century, the technique was not generally useful owing to the limited capacity of batteries, difficulties in switching between series and parallel configurations, and the inherent energy inefficiency of a battery charge/discharge cycle.

Mercury arc valves

First proposed in 1914, the grid controlled mercury-arc valve became available during the period 1920 to 1940 for the rectifier and inverter functions associated with DC transmission. Starting in 1932, General Electric tested mercury-vapor valves and a 12 kV DC transmission line, which also served to convert 40 Hz generation to serve 60 Hz loads, at Mechanicville, New York. In 1941, a 60 MW, ±200 kV, 115 km (71 mi) buried cable link, known as the Elbe-Project, was designed for the city of Berlin using mercury arc valves but, owing to the collapse of the German government in 1945, the project was never completed. The nominal justification for the project was that, during wartime, a buried cable would be less conspicuous as a bombing target. The equipment was moved to the Soviet Union and was put into service there as the Moscow–Kashira HVDC system. The Moscow–Kashira system and the 1954 connection by Uno Lamm's group at ASEA between the mainland of Sweden and the island of Gotland marked the beginning of the modern era of HVDC transmission.

Mercury arc valves require an external circuit to force the current to zero and thus turn off the valve. In HVDC applications, the AC power system itself provides the means of commutating the current to another valve in the converter. Consequently, converters built with mercury arc valves are known as line-commutated converters (LCC). LCCs require rotating synchronous machines in the AC systems to which they are connected, making power transmission into a passive load impossible.

Mercury arc valves were common in systems designed up to 1972, the last mercury arc HVDC system (the Nelson River Bipole 1 system in Manitoba, Canada) having been put into service in stages between 1972 and 1977. Since then, all mercury arc systems have been either shut down or converted to use solid state devices. The last HVDC system to use mercury arc valves was the Inter-Island HVDC link between the North and South Islands of New Zealand, which used them on one of its two poles. The mercury arc valves were decommissioned on 1 August 2012, ahead of commissioning of replacement thyristor converters.

Thyristor valves

Since 1977, new HVDC systems have used only solid-state devices, in most cases thyristors. Like mercury arc valves, thyristors require connection to an external AC circuit in HVDC applications to turn them on and off. HVDC using thyristors is also known as Line-Commutated Converter (LCC) HVDC.

Development of thyristor valves for HVDC began in the late 1960s. The first complete HVDC scheme based on thyristor was the Eel River scheme in Canada, which was built by General Electric and went into service in 1972.

On March 15, 1979, a 1920 MW thyristor based direct current connection between Cabora Bassa and Johannesburg (1,410 km; 880 mi) was energized. The conversion equipment was built in 1974 by Allgemeine Elektricitäts-Gesellschaft AG (AEG), and Brown, Boveri & Cie (BBC) and Siemens were partners in the project. Service interruptions of several years were a result of a civil war in Mozambique.^[] The transmission voltage of ±533 kV was the highest in the world at the time.

Capacitor-commutated converters (CCC)

Line-commutated converters have some limitations in their use for HVDC systems. This results from requiring the AC circuit to turn off the thyristor current and the need for a short period of 'reverse' voltage to effect the turn-off (turn-off time). An attempt to address these limitations is the capacitor-commutated converter (CCC) which has been used in a small number of HVDC systems. The CCC differs from a conventional HVDC system in that it has series capacitors inserted into the AC line connections, either on the primary or secondary side of the converter transformer. The series capacitors partially offset the commutating inductance of the converter and help to reduce fault currents. This also allows a smaller extinction angle to be used with a converter/inverter, reducing the need for reactive power support.

However, CCC has remained only a niche application because of the advent of voltage-source converters (VSC) which eliminate the need for an extinction (turn-off) time.

Voltage-source converters (VSC)

See also: HVDC converter § Voltage-source converters

Widely used in motor drives since the 1980s, voltage-source converters started to appear in HVDC in 1997 with the experimental Hellsjön–Grängesberg project in Sweden. By the end of 2011, this technology had captured a significant proportion of the HVDC market.

The development of higher rated insulated-gate bipolar transistors (IGBTs), gate turn-off thyristors (GTOs) and integrated gate-commutated thyristors (IGCTs), has made smaller HVDC systems economical. The manufacturer ABB Group calls this concept HVDC Light, while Siemens calls a similar concept HVDC PLUS (Power Link Universal System) and Alstom call their product based upon this technology HVDC MaxSine. They have extended the use of HVDC down to blocks as small as a few tens of megawatts and overhead lines as short as a few dozen kilometers. There are several different variants of VSC technology: most installations built until 2012 use pulse-width modulation in a circuit that is effectively an ultrahigh-voltage motor drive. Current installations, including HVDC PLUS and HVDC MaxSine, are based on variants of a converter called a Modular Multilevel Converter (MMC).

Multilevel converters have the advantage that they allow harmonic filtering equipment to be reduced or eliminated altogether. By way of comparison, AC harmonic filters of typical line-commutated converter stations cover nearly half of the converter station area.

With time, voltage-source converter systems will probably replace all installed simple thyristor-based systems, including the highest DC power transmission applications.

Comparison with AC

Advantages

A long-distance, point-to-point HVDC transmission scheme generally has lower overall investment cost and lower losses than an equivalent AC transmission scheme. HVDC conversion equipment at the terminal stations is costly, but the total DC transmission-line costs over long distances are lower than for an AC line of the same distance. HVDC requires less conductor per unit distance than an AC line, as there is no need to support three phases and there is no skin effect.

Depending on voltage level and construction details, HVDC transmission losses are quoted at 3.5% per 1,000 km (620 mi), about 50% less than AC (6.7%) lines at the same voltage. This is because direct current transfers only active power and thus causes lower losses than alternating current, which transfers both active and reactive power.

HVDC transmission may also be selected for other technical benefits. HVDC can transfer power between separate AC networks. HVDC powerflow between separate AC systems can be automatically controlled to support either network during transient conditions, but without the risk that a major power-system collapse in one network will lead to a collapse in the second. HVDC improves on system controllability, with at least one HVDC link embedded in an AC grid—in the deregulated environment, the controllability feature is particularly useful where control of energy trading is needed.

The combined economic and technical benefits of HVDC transmission can make it a suitable choice for connecting electricity sources that are located far away from the main users.

Specific applications where HVDC transmission technology provides benefits include:

• Undersea-cable transmission schemes (e.g. the 720 km (450 mi)North Sea Link, the 580 km (360 mi) NorNed cable between Norway and the Netherlands, Italy's 420 km (260 mi) SAPEI cable between Sardinia and the mainland, the 290 km (180 mi) Basslink between the Australian mainland and Tasmania, and the 250 km (160 mi) Baltic Cable between Sweden and Germany).
• Endpoint-to-endpoint long-haul bulk power transmission without intermediate 'taps,' usually to connect a remote generating plant to the main grid, for example the Nelson River DC Transmission System in Canada.
• Increasing the capacity of an existing power grid in situations where additional wires are difficult or expensive to install.
• Power transmission and stabilization between unsynchronized AC networks, with the extreme example being an ability to transfer power between countries that use AC at different frequencies. Since such transfer can occur in either direction, it increases the stability of both networks by allowing them to draw on each other in emergencies and failures.
• Stabilizing a predominantly AC power grid, without increasing fault levels (prospective short-circuit current).
• Integration of renewable resources such as wind into the main transmission grid. HVDC overhead lines for onshore wind integration projects and HVDC cables for offshore projects have been proposed in North America and Europe for both technical and economic reasons. DC grids with multiple voltage-source converters (VSCs) are one of the technical solutions for pooling offshore wind energy and transmitting it to load centers located far away onshore.

Cable systems

Long undersea or underground high-voltage cables have a high electrical capacitance compared with overhead transmission lines, since the live conductors within the cable are surrounded by a relatively thin layer of insulation (the dielectric), and a metal sheath. The geometry is that of a long coaxial capacitor. The total capacitance increases with the length of the cable. This capacitance is in a parallel circuit with the load. Where alternating current is used for cable transmission, additional current must flow in the cable to charge this cable capacitance. This extra current flow causes added energy loss via dissipation of heat in the conductors of the cable, raising its temperature. Additional energy losses also occur as a result of dielectric losses in the cable insulation.

However, if direct current is used, the cable capacitance is charged only when the cable is first energized or if the voltage level changes; there is no additional current required. For a sufficiently long AC cable, the entire current-carrying ability of the conductor would be needed to supply the charging current alone. This cable capacitance issue limits the length and power-carrying ability of AC power cables. DC powered cables are limited only by their temperature rise and Ohm's law. Although some leakage current flows through the dielectric insulator, this is small compared to the cable's rated current.

Overhead line systems

Three-phase high voltage transmission lines use alternating currents to distribute power over long distances between electric generation plants and consumers. The lines in the picture are located in eastern Utah.

The capacitive effect of long underground or undersea cables in AC transmission applications also applies to AC overhead lines, although to a much lesser extent. Nevertheless, for a long AC overhead transmission line, the current flowing just to charge the line capacitance can be significant, and this reduces the capability of the line to carry useful current to the load at the remote end. Another factor that reduces the useful current-carrying ability of AC lines is the skin effect, which causes a nonuniform distribution of current over the cross-sectional area of the conductor. Transmission line conductors operating with direct current suffer from neither constraint. Therefore, for the same conductor losses (or heating effect), a given conductor can carry more power to the load when operating with HVDC than AC.

Finally, depending upon the environmental conditions and the performance of overhead line insulation operating with HVDC, it may be possible for a given transmission line to operate with a constant HVDC voltage that is approximately the same as the peak AC voltage for which it is designed and insulated. The power delivered in an AC system is defined by the root mean square (RMS) of an AC voltage, but RMS is only about 71% of the peak voltage. Therefore, if the HVDC line can operate continuously with an HVDC voltage that is the same as the peak voltage of the AC equivalent line, then for a given current (where HVDC current is the same as the RMS current in the AC line), the power transmission capability when operating with HVDC is approximately 40% higher than the capability when operating with AC.

Asynchronous connections

Valve hall at Henday converter station, part of the Nelson River DC Transmission System in Canada.

Because HVDC allows power transmission between unsynchronized AC distribution systems, it can help increase system stability, by preventing cascading failures from propagating from one part of a wider power transmission grid to another. Changes in load that would cause portions of an AC network to become unsynchronized and to separate, would not similarly affect a DC link, and the power flow through the DC link would tend to stabilize the AC network. The magnitude and direction of power flow through a DC link can be directly controlled, and changed as needed to support the AC networks at either end of the DC link. This has caused many power system operators to contemplate wider use of HVDC technology for its stability benefits alone.

Disadvantages

The disadvantages of HVDC are in conversion, switching, control, availability, and maintenance.

HVDC is less reliable and has lower availability than alternating current (AC) systems, mainly due to the extra conversion equipment. Single-pole systems have availability of about 98.5%, with about a third of the downtime unscheduled due to faults. Fault-tolerant bipole systems provide high availability for 50% of the link capacity, but availability of the full capacity is about 97% to 98%.

The required converter stations are expensive and have limited overload capacity. At smaller transmission distances, the losses in the converter stations may be bigger than in an AC transmission line for the same distance. The cost of the converters may not be offset by reductions in line construction cost and power line loss.

Operating an HVDC scheme requires many spare parts to be kept, often exclusively for one system, as HVDC systems are less standardized than AC systems and technology changes more quickly.

In contrast to AC systems, realizing multi-terminal systems is complex (especially with line commutated converters), as is expanding existing schemes to multi-terminal systems. Controlling power flow in a multi-terminal DC system requires good communication between all the terminals; power flow must be actively regulated by the converter control system instead of relying on the inherent impedance and phase angle properties of an AC transmission line. Multi-terminal systems are rare. As of 2012 only two are in service: the Hydro Québec – New England transmission between Radisson, Sandy Pond, and Nicolet and the Sardinia–mainland Italy link which was modified in 1989 to also provide power to the island of Corsica.

High-voltage DC circuit breaker

HVDC circuit breakers are difficult to build because of arcing: under AC the voltage inverts, and in doing so crosses zero volts, dozens of times a second. An AC arc will "self-extinguish" at one of these zero-crossing points, because there cannot be an arc where there is no potential difference. DC will never cross zero volts and never self-extinguish, so arc distance and duration is far greater with DC than the same voltage AC. This means some mechanism must be included in the circuit breaker to force current to zero and extinguish the arc, otherwise arcing and contact wear would be too great to allow reliable switching.

In November 2012, ABB announced development of the world's first ultrafast HVDC circuit breaker. Mechanical circuit breakers are too slow for use in HVDC grids, although they have been used for years in other applications. Conversely, semiconductor breakers are fast enough but have a high resistance when conducting, wasting energy and generating heat in normal operation. The ABB breaker combines semiconductor and mechanical breakers to produce a "hybrid breaker" with both a fast break time and a low resistance in normal operation.

Costs

Generally, providers of HVDC systems, such as GE Vernova, Siemens and ABB, do not specify cost details of particular projects. Such costs are treated as Confidential Business Matters between the supplier and the client.

Costs vary widely depending on the specifics of the project (such as power rating, circuit length, overhead vs. cabled route, land costs, site seismology, and AC network improvements required at either terminal). A detailed comparison of DC vs. AC transmission costs may be required in situations where there is no clear technical advantage to DC, and economical reasoning alone drives the selection.

However, some practitioners have provided some information:

For an 8 GW 40 km (25 mi) link laid under the English Channel, the following are approximate primary equipment costs for a 2000 MW 500 kV bipolar conventional HVDC link (exclude way-leaving, on-shore reinforcement works, consenting, engineering, insurance, etc.)

• Converter stations ~£110M (~€120M or $173.7M)
• Subsea cable + installation ~£1M/km (£1.6m/mile) (~€1.2M or ~$1.6M/km; €2m or $2.5m/mile)

So for an 8 GW capacity between Britain and France in four links, little is left over from £750M for the installed works. Add another £200–300M for the other works depending on additional onshore works required.

An April 2010 announcement for a 2,000 MW, 64 km (40 mi) line between Spain and France is estimated at €700 million. This includes the cost of a tunnel through the Pyrenees.

Conversion process

Converter

Main article: HVDC converter

At the heart of an HVDC converter station, the equipment which performs the conversion between AC and DC is referred to as the converter. Almost all HVDC converters are inherently capable of converting from AC to DC (rectification) and from DC to AC (inversion), although in many HVDC systems, the system as a whole is optimized for power flow in only one direction. Irrespective of how the converter itself is designed, the station that is operating (at a given time) with power flow from AC to DC is referred to as the rectifier and the station that is operating with power flow from DC to AC is referred to as the inverter.

Early HVDC systems used electromechanical conversion (the Thury system) but all HVDC systems built since the 1940s have used electronic (static) converters. Electronic converters for HVDC are divided into two main categories:

• Line-commutated converters (LCC)
• Voltage-sourced converters, or current-source converters.

Line-commutated converters

Most of the HVDC systems in operation today are based on line-commutated converters.

The basic LCC configuration uses a three-phase bridge rectifier or six-pulse bridge, containing six electronic switches, each connecting one of the three phases to one of the two DC rails. A complete switching element is usually referred to as a valve, irrespective of its construction. However, with a phase change only every 60°, considerable harmonic distortion is produced at both the DC and AC terminals when this arrangement is used.

A twelve-pulse bridge rectifier

An enhancement of this arrangement uses 12 valves in a twelve-pulse bridge. The AC is split into two separate three phase supplies before transformation. One of the sets of supplies is then configured to have a star (wye) secondary, the other a delta secondary, establishing a 30° phase difference between the two sets of three phases. With twelve valves connecting each of the two sets of three phases to the two DC rails, there is a phase change every 30°, and harmonics are considerably reduced. For this reason the twelve-pulse system has become standard on most line-commutated converter HVDC systems built since the 1970s.

With line commutated converters, the converter has only one degree of freedom – the firing angle, which represents the time delay between the voltage across a valve becoming positive (at which point the valve would start to conduct if it were made from diodes) and the thyristors being turned on. The DC output voltage of the converter steadily becomes less positive as the firing angle is increased: firing angles of up to 90° correspond to rectification and result in positive DC voltages, while firing angles above 90° correspond to inversion and result in negative DC voltages. The practical upper limit for the firing angle is about 150–160° because above this, the valve would have insufficient turnoff time.

Early LCC systems used mercury-arc valves, which were rugged but required high maintenance. Because of this, many mercury-arc HVDC systems were built with bypass switchgear across each six-pulse bridge so that the HVDC scheme could be operated in six-pulse mode for short periods of maintenance. The last mercury arc system was shut down in 2012.

The thyristor valve was first used in HVDC systems in 1972. The thyristor is a solid-state semiconductor device similar to the diode, but with an extra control terminal that is used to switch the device on at a particular instant during the AC cycle. Because the voltages in HVDC systems, up to 800 kV in some cases, far exceed the breakdown voltages of the thyristors used, HVDC thyristor valves are built using large numbers of thyristors in series. Additional passive components such as grading capacitors and resistors need to be connected in parallel with each thyristor in order to ensure that the voltage across the valve is evenly shared between the thyristors. The thyristor plus its grading circuits and other auxiliary equipment is known as a thyristor level.

Thyristor valve stacks for Pole 2 of the HVDC Inter-Island between the North and South Islands of New Zealand. The man at the bottom gives scale to the size of the valves.

Each thyristor valve will typically contain tens or hundreds of thyristor levels, each operating at a different (high) potential with respect to earth. The command information to turn on the thyristors therefore cannot simply be sent using a wire connection – it needs to be isolated. The isolation method can be magnetic but is usually optical. Two optical methods are used: indirect and direct optical triggering. In the indirect optical triggering method, low-voltage control electronics send light pulses along optical fibres to the high-side control electronics, which derives its power from the voltage across each thyristor. The alternative direct optical triggering method dispenses with most of the high-side electronics, instead using light pulses from the control electronics to switch light-triggered thyristors (LTTs), although a small monitoring electronics unit may still be required for protection of the valve.

In a line-commutated converter, the DC current (usually) cannot change direction; it flows through a large inductance and can be considered almost constant. On the AC side, the converter behaves approximately as a current source, injecting both grid-frequency and harmonic currents into the AC network. For this reason, a line commutated converter for HVDC is also considered as a current-source inverter.

Voltage-sourced converters

Because thyristors can only be turned on (not off) by control action, the control system has only one degree of freedom – when to turn on the thyristor. This is an important limitation in some circumstances.

With some other types of semiconductor device such as the insulated-gate bipolar transistor (IGBT), both turn-on and turn-off can be controlled, giving a second degree of freedom. As a result, they can be used to make self-commutated converters. In such converters, the electric polarity of DC voltage is usually fixed and the DC voltage, being smoothed by a large capacitance, can be considered constant. For this reason, an HVDC converter using IGBTs is usually referred to as a voltage sourced converter. The additional controllability gives many advantages, notably the ability to switch the IGBTs on and off many times per cycle in order to improve the harmonic performance. Being self-commutated, the converter no longer relies on synchronous machines in the AC system for its operation. A voltage sourced converter can therefore feed power to an AC network consisting only of passive loads, something which is impossible with LCC HVDC.

HVDC systems based on voltage sourced converters normally use the six-pulse connection because the converter produces much less harmonic distortion than a comparable LCC and the twelve-pulse connection is unnecessary.

Most of the VSC HVDC systems built until 2012 were based on the two level converter, which can be thought of as a six pulse bridge in which the thyristors have been replaced by IGBTs with inverse-parallel diodes, and the DC smoothing reactors have been replaced by DC smoothing capacitors. Such converters derive their name from the discrete, two voltage levels at the AC output of each phase that correspond to the electrical potentials of the positive and negative DC terminals. Pulse-width modulation (PWM) is usually used to improve the harmonic distortion of the converter.

Some HVDC systems have been built with three level converters, but today most new VSC HVDC systems are being built with some form of multilevel converter, most commonly the modular multilevel converter (MMC), in which each valve consists of a number of independent converter submodules, each containing its own storage capacitor. The IGBTs in each submodule either bypass the capacitor or connect it into the circuit, allowing the valve to synthesize a stepped voltage with very low levels of harmonic distortion.

Converter transformers

A single-phase, three-winding converter transformer. The long valve-winding bushings, which project through the wall of the valve hall, are shown on the left. The line-winding bushing projects vertically upwards at center-right

At the AC side of each converter, a bank of transformers, often three physically separated single-phase transformers, isolate the station from the AC supply, to provide a local earth, and to ensure the correct eventual DC voltage. The output of these transformers is then connected to the converter.

Converter transformers for LCC HVDC schemes are quite specialized because of the high levels of harmonic currents which flow through them, and because the secondary winding insulation experiences a permanent DC voltage, which affects the design of the insulating structure (valve side requires more solid insulation) inside the tank. In LCC systems, the transformers also need to provide the 30° phase shift needed for harmonic cancellation.

Converter transformers for VSC HVDC systems are usually simpler and more conventional in design than those for LCC HVDC systems.

Reactive power

A major drawback of HVDC systems using line-commutated converters is that the converters inherently consume reactive power. The AC current flowing into the converter from the AC system lags behind the AC voltage so that, irrespective of the direction of active power flow, the converter always absorbs reactive power, behaving in the same way as a shunt reactor. The reactive power absorbed is at least 0.5 Mvar/MW under ideal conditions and can be higher than this when the converter is operating at higher than usual firing or extinction angle, or reduced DC voltage.

Although at HVDC converter stations connected directly to power stations some of the reactive power may be provided by the generators themselves, in most cases the reactive power consumed by the converter must be provided by banks of shunt capacitors connected at the AC terminals of the converter. The shunt capacitors are usually connected directly to the grid voltage but in some cases may be connected to a lower voltage via a tertiary winding on the converter transformer.

Since the reactive power consumed depends on the active power being transmitted, the shunt capacitors usually need to be subdivided into a number of switchable banks (typically four per converter) in order to prevent a surplus of reactive power being generated at low transmitted power.

The shunt capacitors are almost always provided with tuning reactors and, where necessary, damping resistors so that they can perform a dual role as harmonic filters.

Voltage-source converters, on the other hand, can either produce or consume reactive power on demand, with the result that usually no separate shunt capacitors are needed (other than those required purely for filtering).

Harmonics and filtering

All power electronic converters generate some degree of harmonic distortion on the AC and DC systems to which they are connected, and HVDC converters are no exception.

With the recently developed modular multilevel converter (MMC), levels of harmonic distortion may be practically negligible, but with line-commutated converters and simpler types of voltage-source converters, considerable harmonic distortion may be produced on both the AC and DC sides of the converter. As a result, harmonic filters are nearly always required at the AC terminals of such converters, and in HVDC transmission schemes using overhead lines, may also be required on the DC side.

Filters for line-commutated converters

The basic building-block of a line-commutated HVDC converter is the six-pulse bridge. This arrangement produces very high levels of harmonic distortion by acting as a current source injecting harmonic currents of order 6n±1 into the AC system and generating harmonic voltages of order 6n superimposed on the DC voltage.

It is very costly to provide harmonic filters capable of suppressing such harmonics, so a variant known as the twelve-pulse bridge (consisting of two six-pulse bridges in series with a 30° phase shift between them) is nearly always used. With the twelve-pulse arrangement, harmonics are still produced but only at orders 12n±1 on the AC side and 12n on the DC side. The task of suppressing such harmonics is still challenging, but manageable.

Line-commutated converters for HVDC are usually provided with combinations of harmonic filters designed to deal with the 11th and 13th harmonics on the AC side, and 12th harmonic on the DC side. Sometimes, high-pass filters may be provided to deal with 23rd, 25th, 35th, 37th... on the AC side and 24th, 36th... on the DC side. Sometimes, the AC filters may also need to provide damping at lower-order, noncharacteristic harmonics such as 3rd or 5th harmonics.

The task of designing AC harmonic filters for HVDC converter stations is complex and computationally intensive, since in addition to ensuring that the converter does not produce an unacceptable level of voltage distortion on the AC system, it must be ensured that the harmonic filters do not resonate with some component elsewhere in the AC system. A detailed knowledge of the harmonic impedance of the AC system, at a wide range of frequencies, is needed in order to design the AC filters.

DC filters are required only for HVDC transmission systems involving overhead lines. Voltage distortion is not a problem in its own right, since consumers do not connect directly to the DC terminals of the system, so the main design criterion for the DC filters is to ensure that the harmonic currents flowing in the DC lines do not induce interference in nearby open-wire telephone lines. With the rise in digital mobile telecommunication systems, which are much less susceptible to interference, DC filters are becoming less important for HVDC systems.

Filters for voltage-sourced converters

Some types of voltage-sourced converters may produce such low levels of harmonic distortion that no filters are required at all. However, converter types such as the two-level converter, used with pulse-width modulation (PWM), still require some filtering, albeit less than on line-commutated converter systems.

With such converters, the harmonic spectrum is generally shifted to higher frequencies than with line-commutated converters. This usually allows the filter equipment to be smaller. The dominant harmonic frequencies are sidebands of the PWM frequency and multiples thereof. In HVDC applications, the PWM frequency is typically around 1 to 2 kHz.

Configurations

Monopole

Block diagram of a monopole system with earth return

In a monopole configuration one of the terminals of the rectifier is connected to earth ground. The other terminal, at high voltage relative to ground, is connected to a transmission line. The earthed terminal may be connected to the corresponding connection at the inverting station by means of a second conductor.

If no metallic return conductor is installed, current flows in the earth (or water) between two electrodes. This arrangement is a type of single-wire earth return system.

The electrodes are usually located some tens of kilometers from the stations and are connected to the stations via a medium-voltage electrode line. The design of the electrodes themselves depends on whether they are located on land, on the shore or at sea. For the monopolar configuration with earth return, the earth current flow is unidirectional, which means that the design of one of the electrodes (the cathode) can be relatively simple, although the design of anode electrode is quite complex.

For long-distance transmission, earth return can be considerably cheaper than alternatives using a dedicated neutral conductor, but it can lead to problems such as:

• Electrochemical corrosion of long buried metal objects such as pipelines
• Underwater earth-return electrodes in seawater may produce chlorine or otherwise affect water chemistry.
• An unbalanced current path may result in a net magnetic field, which can affect magnetic navigational compasses for ships passing over an underwater cable.

These effects can be eliminated with installation of a metallic return conductor between the two ends of the monopolar transmission line. Since one terminal of the converters is connected to earth, the return conductor need not be insulated for the full transmission voltage which makes it less costly than the high-voltage conductor. The decision of whether or not to use a metallic return conductor is based upon economic, technical and environmental factors.

Modern monopolar systems for pure overhead lines carry typically 1.5 GW. If underground or underwater cables are used, the typical value is 600 MW.

Most monopolar systems are designed for future bipolar expansion. Transmission line towers may be designed to carry two conductors, even if only one is used initially for the monopole transmission system. The second conductor is either unused, used as electrode line or connected in parallel with the other (as in case of Baltic Cable).

Symmetrical monopole

An alternative is to use two high-voltage conductors, operating at about half of the DC voltage, with only a single converter at each end. In this arrangement, known as the symmetrical monopole, the converters are earthed only via a high impedance and there is no earth current. The symmetrical monopole arrangement is uncommon with line-commutated converters (the NorNed interconnector being a rare example) but is very common with Voltage Sourced Converters when cables are used.

Bipolar

Block diagram of a bipolar system that also has an earth return

In bipolar transmission a pair of conductors is used, each at a high potential with respect to ground, in opposite polarity. Since these conductors must be insulated for the full voltage, transmission line cost is higher than a monopole with a return conductor. However, there are a number of advantages to bipolar transmission which can make it an attractive option.

• Under normal load, negligible earth-current flows, as in the case of monopolar transmission with a metallic earth-return. This reduces earth return loss and environmental effects.
• When a fault develops in a line, with earth return electrodes installed at each end of the line, approximately half the rated power can continue to flow using the earth as a return path, operating in monopolar mode.
• Since for a given total power rating each conductor of a bipolar line carries only half the current of monopolar lines, the cost of the second conductor is reduced compared to a monopolar line of the same rating.
• In very adverse terrain, the second conductor may be carried on an independent set of transmission towers, so that some power may continue to be transmitted even if one line is damaged.

A bipolar system may also be installed with a metallic earth return conductor.

Bipolar systems may carry as much as 4 GW at voltages of ±660 kV with a single converter per pole, as on the Ningdong–Shandong project in China. With a power rating of 2,000 MW per twelve-pulse converter, the converters for that project were (as of 2010) the most powerful HVDC converters ever built. Even higher powers can be achieved by connecting two or more twelve-pulse converters in series in each pole, as is used in the ±800 kV Xiangjiaba–Shanghai project in China, which uses two twelve-pulse converter bridges in each pole, each rated at 400 kV DC and 1,600 MW.

Submarine cable installations initially commissioned as a monopole may be upgraded with additional cables and operated as a bipole.

A block diagram of a bipolar HVDC transmission system, between two stations designated A and B. AC – represents an alternating current network CON – represents a converter valve, either rectifier or inverter, TR represents a power transformer, DCTL is the direct-current transmission line conductor, DCL is a direct-current filter inductor, BS represents a bypass switch, and PM represent power factor correction and harmonic filter networks required at both ends of the link. The DC transmission line may be very short in a back-to-back link, or extend hundreds of miles (km) overhead, underground or underwater. One conductor of the DC line may be replaced by connections to earth ground.

A bipolar scheme can be implemented so that the polarity of one or both poles can be changed. This allows the operation as two parallel monopoles. If one conductor fails, transmission can still continue at reduced capacity. Losses may increase if ground electrodes and lines are not designed for the extra current in this mode. To reduce losses in this case, intermediate switching stations may be installed, at which line segments can be switched off or parallelized. This was done at Inga–Shaba HVDC.

Back to back

A back-to-back station (or B2B for short) is a plant in which both converters are in the same area, usually in the same building. The length of the direct current line is kept as short as possible. HVDC back-to-back stations are used for

• coupling of electricity grids of different frequencies (as in Japan and South America; and the GCC interconnector between UAE and Saudi Arabia (50 Hz) completed in 2009)
• coupling two networks of the same nominal frequency but no fixed phase relationship (as until 1995/96 in Etzenricht, Dürnrohr, Vienna, and the Vyborg HVDC scheme).
• different frequency and phase number (for example, as a replacement for traction current converter plants)

The DC voltage in the intermediate circuit can be selected freely at HVDC back-to-back stations because of the short conductor length. The DC voltage is usually selected to be as low as possible, in order to build a small valve hall and to reduce the number of thyristors connected in series in each valve. For this reason, at HVDC back-to-back stations, valves with the highest available current rating (in some cases, up to 4,500 A) are used.

Multi-terminal systems

The most common configuration of an HVDC link consists of two converter stations connected by an overhead power line or undersea cable.

Multi-terminal HVDC links, connecting more than two points, are rare. The configuration of multiple terminals can be series, parallel, or hybrid (a mixture of series and parallel). Parallel configuration tends to be used for large capacity stations, and series for lower capacity stations. An example is the 2,000 MW Quebec - New England Transmission system opened in 1992, which is currently the largest multi-terminal HVDC system in the world.

Multi-terminal systems are difficult to realize using line commutated converters because reversals of power are effected by reversing the polarity of DC voltage, which affects all converters connected to the system. With Voltage Sourced Converters, power reversal is achieved instead by reversing the direction of current, making parallel-connected multi-terminals systems much easier to control. For this reason, multi-terminal systems are expected to become much more common in the near future.

China is expanding its grid to keep up with increased power demand, while addressing environmental targets. China Southern Power Grid started a three terminals VSC HVDC pilot project in 2011. The project has designed ratings of ±160 kV/200 MW-100 MW-50 MW and will be used to bring wind power generated on Nanao island into the mainland Guangdong power grid through 32 km (20 mi) of combination of HVDC land cables, sea cables and overhead lines. This project was put into operation on December 19, 2013.

In India, the multi-terminal North-East Agra project is planned for commissioning in 2015–2017. It is rated 6,000 MW, and it transmits power on a ±800 kV bipolar line from two converter stations, at Biswanath Chariali and Alipurduar, in the east to a converter at Agra, a distance of 1,728 km (1,074 mi).

Other arrangements

Cross-Skagerrak consisted since 1993 of 3 poles, from which 2 were switched in parallel and the third used an opposite polarity with a higher transmission voltage. This configuration ended in 2014 when poles 1 and 2 again were rebuilt to work in bipole and pole 3 (LCC) works in bipole with a new pole 4 (VSC). This is the first HVDC transmission where LCC and VSC poles cooperate in a bipole.

A similar arrangement was the HVDC Inter-Island in New Zealand after a capacity upgrade in 1992, in which the two original converters (using mercury-arc valves) were parallel-switched feeding the same pole and a new third (thyristor) converter installed with opposite polarity and higher operation voltage. This configuration ended in 2012 when the two old converters were replaced with a single, new, thyristor converter.

A scheme patented in 2004 is intended for conversion of existing AC transmission lines to HVDC. Two of the three circuit conductors are operated as a bipole. The third conductor is used as a parallel monopole, equipped with reversing valves (or parallel valves connected in reverse polarity). This allows heavier currents to be carried by the bipole conductors, and full use of the installed third conductor for energy transmission. High currents can be circulated through the line conductors even when load demand is low, for removal of ice. As of 2012, no tripole conversions are in operation, although a transmission line in India has been converted to bipole HVDC (HVDC Sileru-Barsoor).

Corona discharge

Corona discharge is the creation of ions in a fluid (such as air) by the presence of a strong electric field. Electrons are torn from neutral air, and either the positive ions or the electrons are attracted to the conductor, while the charged particles drift. This effect can cause considerable power loss, create audible and radio-frequency interference, generate toxic compounds such as oxides of nitrogen and ozone, and bring forth arcing.

Both AC and DC transmission lines can generate coronas, in the former case in the form of oscillating particles, in the latter a constant wind. Due to the space charge formed around the conductors, an HVDC system may have about half the loss per unit length of a high voltage AC system carrying the same amount of power. With monopolar transmission the choice of polarity of the energized conductor leads to a degree of control over the corona discharge. In particular, the polarity of the ions emitted can be controlled, which may have an environmental impact on ozone creation. Negative coronas generate considerably more ozone than positive coronas, and generate it further downwind of the power line, creating the potential for health effects. The use of a positive voltage will reduce the ozone impacts of monopole HVDC power lines.

Applications

Overview

The controllability of a current-flow through HVDC rectifiers and inverters, their application in connecting unsynchronized networks, and their applications in efficient submarine cables mean that HVDC interconnectors are often used at national or regional boundaries for the exchange of power (in North America, HVDC connections divide much of Canada and the United States into several electrical regions that cross national borders, although the purpose of these connections is still to connect unsynchronized AC grids to each other). Offshore windfarms also require undersea cables, and their turbines are unsynchronized. In very long-distance connections between two locations, such as power transmission from a large hydroelectric power plant at a remote site to an urban area, HVDC transmission systems may appropriately be used; several schemes of these kind have been built. For interconnectors to Siberia, Canada, India, and the Scandinavian North, the decreased line-costs of HVDC also make it applicable, see List of HVDC projects. Other applications are noted throughout this article.

AC network interconnectors

AC transmission lines can interconnect only synchronized AC networks with the same frequency with limits on the allowable phase difference between the two ends of the line. Many areas that wish to share power have unsynchronized networks. The power grids of the UK, Northern Europe and continental Europe are not united into a single synchronized network. Japan has 50 Hz and 60 Hz networks. Continental North America, while operating at 60 Hz throughout, is divided into regions which are unsynchronized: East, West, Texas, Quebec, and Alaska. Brazil and Paraguay, which share the enormous Itaipu Dam hydroelectric plant, operate on 60 Hz and 50 Hz respectively. However, HVDC systems make it possible to interconnect unsynchronized AC networks, and also add the possibility of controlling AC voltage and reactive power flow.

A generator connected to a long AC transmission line may become unstable and fall out of synchronization with a distant AC power system. An HVDC transmission link may make it economically feasible to use remote generation sites. Wind farms located off-shore may use HVDC systems to collect power from multiple unsynchronized generators for transmission to the shore by an underwater cable.

In general, however, an HVDC power line will interconnect two AC regions of the power-distribution grid. Machinery to convert between AC and DC power adds a considerable cost in power transmission. The conversion from AC to DC is known as rectification, and from DC to AC as inversion. Above a certain break-even distance (about 50 km; 31 mi for submarine cables, and perhaps 600–800 km; 370–500 mi for overhead cables), the lower cost of the HVDC electrical conductors outweighs the cost of the electronics.

The conversion electronics also present an opportunity to effectively manage the power grid by means of controlling the magnitude and direction of power flow. An additional advantage of the existence of HVDC links, therefore, is potential increased stability in the transmission grid.

Renewable electricity superhighways

Two HVDC lines cross near Wing, North Dakota.

A number of studies have highlighted the potential benefits of very wide area super grids based on HVDC since they can mitigate the effects of intermittency by averaging and smoothing the outputs of large numbers of geographically dispersed wind farms or solar farms. Czisch's study concludes that a grid covering the fringes of Europe could bring 100% renewable power (70% wind, 30% biomass) at close to today's prices. There has been debate over the technical feasibility of this proposal and the political risks involved in energy transmission across a large number of international borders.

The construction of such green power superhighways is advocated in a white paper that was released by the American Wind Energy Association and the Solar Energy Industries Association in 2009. Clean Line Energy Partners is developing four HVDC lines in the U.S. for long-distance electric power transmission.

In January 2009, the European Commission proposed €300 million to subsidize the development of HVDC links between Ireland, Britain, the Netherlands, Germany, Denmark, and Sweden, as part of a wider €1.2 billion package supporting links to offshore wind farms and cross-border interconnectors throughout Europe. Meanwhile, the recently founded Union of the Mediterranean has embraced a Mediterranean Solar Plan to import large amounts of concentrated solar power into Europe from North Africa and the Middle East. Japan-Taiwan-Philippines HVDC interconnector was proposed in 2020. The purpose of this interconnector is to facilitate cross-border renewable power trading with Indonesia and Australia, in preparation for the future Asian Pacific Super Grid.

Advancements in UHVDC

UHVDC (ultrahigh-voltage direct-current) is shaping up to be the latest technological front in high voltage DC transmission technology. UHVDC is defined as DC voltage transmission of above 800 kV (HVDC is generally just 100 to 800 kV).

One of the problems with current UHVDC supergrids is that – although less than AC transmission or DC transmission at lower voltages – they still suffer from power loss as the length is extended. A typical loss for 800 kV lines is 2.6% over 800 km (500 mi). Increasing the transmission voltage on such lines reduces the power loss, but until recently, the interconnectors required to bridge the segments were prohibitively expensive. However, with advances in manufacturing, it is becoming more and more feasible to build UHVDC lines.

In 2010, ABB Group built the world's first 800 kV UHVDC in China. The Zhundong–Wannan UHVDC line with 1100 kV, 3,400 km (2,100 mi) length and 12 GW capacity was completed in 2018. As of 2020, at least thirteen UHVDC transmission lines in China have been completed.

While the majority of recent UHVDC technology deployment is in China, it has also been deployed in South America as well as other parts of Asia. In India, a 1,830 km (1,140 mi), 800 kV, 6 GW line between Raigarh and Pugalur is expected to be completed in 2019. In Brazil, the Xingu-Estreito line over 2,076 km (1,290 mi) with 800 kV and 4 GW was completed in 2017, and the Xingu-Rio line over 2,543 km (1,580 mi) with 800 kV and 4 GW was completed in 2019, both to transmit the energy from Belo Monte Dam. As of 2020, no UHVDC line (≥ 800 kV) exists in Europe or North America.