Cubic equation

From Wikipedia, the free encyclopedia

Graph of a cubic function with 3 real roots (where the curve crosses the horizontal axis at y = 0). The case shown has two critical points. Here the function is ${\displaystyle f(x)=\frac{1}{4}\left(x^3+3x^2-6x-8\right)}$.

In algebra, a cubic equation in one variable is an equation of the form

${\displaystyle a{x}^3+b{x}^2+cx+d=0}$

in which a is nonzero.

The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the coefficients a, b, c, and d of the cubic equation are real numbers, then it has at least one real root (this is true for all odd-degree polynomial functions). All of the roots of the cubic equation can be found by the following means:

• algebraically: more precisely, they can be expressed by a cubic formula involving the four coefficients, the four basic arithmetic operations, square roots and cube roots. (This is also true of quadratic (second-degree) and quartic (fourth-degree) equations, but not for higher-degree equations, by the Abel–Ruffini theorem.)
• trigonometrically
• numerical approximations of the roots can be found using root-finding algorithms such as Newton's method.

The coefficients do not need to be real numbers. Much of what is covered below is valid for coefficients in any field with characteristic other than 2 and 3. The solutions of the cubic equation do not necessarily belong to the same field as the coefficients. For example, some cubic equations with rational coefficients have roots that are irrational (and even non-real) complex numbers.

History

Cubic equations were known to the ancient Babylonians, Greeks, Chinese, Indians, and Egyptians. Babylonian (20th to 16th centuries BC) cuneiform tablets have been found with tables for calculating cubes and cube roots. The Babylonians could have used the tables to solve cubic equations, but no evidence exists to confirm that they did. The problem of doubling the cube involves the simplest and oldest studied cubic equation, and one for which the ancient Egyptians did not believe a solution existed. In the 5th century BC, Hippocrates reduced this problem to that of finding two mean proportionals between one line and another of twice its length, but could not solve this with a compass and straightedge construction, a task which is now known to be impossible. Methods for solving cubic equations appear in The Nine Chapters on the Mathematical Art, a Chinese mathematical text compiled around the 2nd century BC and commented on by Liu Hui in the 3rd century. In the 3rd century AD, the Greek mathematician Diophantus found integer or rational solutions for some bivariate cubic equations (Diophantine equations). Hippocrates, Menaechmus and Archimedes are believed to have come close to solving the problem of doubling the cube using intersecting conic sections, though historians such as Reviel Netz dispute whether the Greeks were thinking about cubic equations or just problems that can lead to cubic equations. Some others like T. L. Heath, who translated all of Archimedes' works, disagree, putting forward evidence that Archimedes really solved cubic equations using intersections of two conics, but also discussed the conditions where the roots are 0, 1 or 2.

Graph of the cubic function f(x) = 2x³ − 3x² − 3x + 2 = (x + 1) (2x − 1) (x − 2)

In the 7th century, the Tang dynasty astronomer mathematician Wang Xiaotong in his mathematical treatise titled Jigu Suanjing systematically established and solved numerically 25 cubic equations of the form x³ + px² + qx = N, 23 of them with p, q ≠ 0, and two of them with q = 0.

In the 11th century, the Persian poet-mathematician, Omar Khayyam (1048–1131), made significant progress in the theory of cubic equations. In an early paper, he discovered that a cubic equation can have more than one solution and stated that it cannot be solved using compass and straightedge constructions. He also found a geometric solution. In his later work, the Treatise on Demonstration of Problems of Algebra, he wrote a complete classification of cubic equations with general geometric solutions found by means of intersecting conic sections. Khayyam made an attempt to come up with an algebraic formula for extracting cubic roots. He wrote:

“We have tried to express these roots by algebra but have failed. It may be, however, that men who come after us will succeed.”

In the 12th century, the Indian mathematician Bhaskara II attempted the solution of cubic equations without general success. However, he gave one example of a cubic equation: x³ + 12x = 6x² + 35. In the 12th century, another Persian mathematician, Sharaf al-Dīn al-Tūsī (1135–1213), wrote the Al-Muʿādalāt (Treatise on Equations), which dealt with eight types of cubic equations with positive solutions and five types of cubic equations which may not have positive solutions. He used what would later be known as the "Ruffini-Horner method" to numerically approximate the root of a cubic equation. He also used the concepts of maxima and minima of curves in order to solve cubic equations which may not have positive solutions. He understood the importance of the discriminant of the cubic equation to find algebraic solutions to certain types of cubic equations.

In his book Flos, Leonardo de Pisa, also known as Fibonacci (1170–1250), was able to closely approximate the positive solution to the cubic equation x³ + 2x² + 10x = 20. Writing in Babylonian numerals he gave the result as 1,22,7,42,33,4,40 (equivalent to 1 + 22/60 + 7/60² + 42/60³ + 33/60⁴ + 4/60⁵ + 40/60⁶), which has a relative error of about 10⁻⁹.

In the early 16th century, the Italian mathematician Scipione del Ferro (1465–1526) found a method for solving a class of cubic equations, namely those of the form x³ + mx = n. In fact, all cubic equations can be reduced to this form if one allows m and n to be negative, but negative numbers were not known to him at that time. Del Ferro kept his achievement secret until just before his death, when he told his student Antonio Fior about it.

Niccolò Fontana Tartaglia

In 1535, Niccolò Tartaglia (1500–1557) received two problems in cubic equations from Zuanne da Coi and announced that he could solve them. He was soon challenged by Fior, which led to a famous contest between the two. Each contestant had to put up a certain amount of money and to propose a number of problems for his rival to solve. Whoever solved more problems within 30 days would get all the money. Tartaglia received questions in the form x³ + mx = n, for which he had worked out a general method. Fior received questions in the form x³ + mx² = n, which proved to be too difficult for him to solve, and Tartaglia won the contest.

Later, Tartaglia was persuaded by Gerolamo Cardano (1501–1576) to reveal his secret for solving cubic equations. In 1539, Tartaglia did so only on the condition that Cardano would never reveal it and that if he did write a book about cubics, he would give Tartaglia time to publish. Some years later, Cardano learned about del Ferro's prior work and published del Ferro's method in his book Ars Magna in 1545, meaning Cardano gave Tartaglia six years to publish his results (with credit given to Tartaglia for an independent solution). Cardano's promise to Tartaglia said that he would not publish Tartaglia's work, and Cardano felt he was publishing del Ferro's, so as to get around the promise. Nevertheless, this led to a challenge to Cardano from Tartaglia, which Cardano denied. The challenge was eventually accepted by Cardano's student Lodovico Ferrari (1522–1565). Ferrari did better than Tartaglia in the competition, and Tartaglia lost both his prestige and his income.

Cardano noticed that Tartaglia's method sometimes required him to extract the square root of a negative number. He even included a calculation with these complex numbers in Ars Magna, but he did not really understand it. Rafael Bombelli studied this issue in detail and is therefore often considered as the discoverer of complex numbers.

François Viète (1540–1603) independently derived the trigonometric solution for the cubic with three real roots, and René Descartes (1596–1650) extended the work of Viète.

Factorization

If the coefficients of a cubic equation are rational numbers, one can obtain an equivalent equation with integer coefficients, by multiplying all coefficients by a common multiple of their denominators. Such an equation

${\displaystyle a{x}^3+b{x}^2+cx+d=0,}$

with integer coefficients, is said to be reducible if the polynomial on the left-hand side is the product of polynomials of lower degrees. By Gauss's lemma, if the equation is reducible, one can suppose that the factors have integer coefficients.

Finding the roots of a reducible cubic equation is easier than solving the general case. In fact, if the equation is reducible, one of the factors must have degree one, and thus have the form

${\displaystyle qx-p}$

with q and p being coprime integers. The rational root test allows finding q and p by examining a finite number of cases (because q must be a divisor of a, and p must be a divisor of d).

Thus, one root is ${\displaystyle x_1=\frac{p}{q},}$ and the other roots are the roots of the other factor, which can be found by polynomial long division. This other factor is

${\displaystyle \frac{a}{q}{x}^2+\frac{bq+ap}{q^2}x+\frac{c{q}^2+bpq+a{p}^2}{q^3}}$

(The coefficients seem not to be integers, but must be integers if p / q is a root.)

Then, the other roots are the roots of this quadratic polynomial and can be found by using the quadratic formula.

Depressed cubic

Cubics of the form

${\displaystyle t^3+pt+q}$

are said to be depressed. They are much simpler than general cubics, but are fundamental, because the study of any cubic may be reduced by a simple change of variable to that of a depressed cubic.

Let

${\displaystyle a{x}^3+b{x}^2+cx+d=0}$

be a cubic equation. The change of variable

${\displaystyle x=t-\frac{b}{3a}}$

gives a cubic (in t) that has no term in t².

After dividing by a one gets the depressed cubic equation

${\displaystyle t^3+pt+q=0,}$

with

${\displaystyle \begin{array}{rl}t=& x+\frac{b}{3a}\\ p=& \frac{3ac-b^2}{3a^2}\\ q=& \frac{2b^3-9abc+27a^{2}d}{27a^3}.\end{array}}$

The roots ${\displaystyle x_1,x_2,x_3}$ of the original equation are related to the roots ${\displaystyle t_1,t_2,t_3}$ of the depressed equation by the relations

$${\displaystyle x_i=t_i-\frac{b}{3a},}$$

for ${\displaystyle i=1,2,3}$.

Discriminant and nature of the roots

The nature (real or not, distinct or not) of the roots of a cubic can be determined without computing them explicitly, by using the discriminant.

Discriminant

The discriminant of a polynomial is a function of its coefficients that is zero if and only if the polynomial has a multiple root, or, if it is divisible by the square of a non-constant polynomial. In other words, the discriminant is nonzero if and only if the polynomial is square-free.

If r₁, r₂, r₃ are the three roots (not necessarily distinct nor real) of the cubic ${\displaystyle a{x}^3+b{x}^2+cx+d,}$ then the discriminant is

${\displaystyle a^4(r_1-r_2{)}^2(r_1-r_3{)}^2(r_2-r_3{)}^2.}$

The discriminant of the depressed cubic ${\displaystyle t^3+pt+q}$ is

${\displaystyle -\left(4p^3+27q^2\right).}$

The discriminant of the general cubic ${\displaystyle a{x}^3+b{x}^2+cx+d}$ is

${\displaystyle 18abcd-4b^{3}d+b^2{c}^2-4a{c}^3-27a^2{d}^2.}$

It is the product of ${\displaystyle a^4}$ and the discriminant of the corresponding depressed cubic. Using the formula relating the general cubic and the associated depressed cubic, this implies that the discriminant of the general cubic can be written as

${\displaystyle \frac{4(b^2-3ac{)}^3-(2b^3-9abc+27a^{2}d{)}^2}{27a^2}.}$

It follows that one of these two discriminants is zero if and only if the other is also zero, and, if the coefficients are real, the two discriminants have the same sign. In summary, the same information can be deduced from either one of these two discriminants.

To prove the preceding formulas, one can use Vieta's formulas to express everything as polynomials in r₁, r₂, r₃, and a. The proof then results in the verification of the equality of two polynomials.

Nature of the roots

If the coefficients of a polynomial are real numbers, and its discriminant ${\displaystyle \mathrm{\Delta }}$ is not zero, there are two cases:

• If ${\displaystyle \mathrm{\Delta }>0,}$ the cubic has three distinct real roots
• If ${\displaystyle \mathrm{\Delta }<0,}$ the cubic has one real root and two non-real complex conjugate roots.

This can be proved as follows. First, if r is a root of a polynomial with real coefficients, then its complex conjugate is also a root. So the non-real roots, if any, occur as pairs of complex conjugate roots. As a cubic polynomial has three roots (not necessarily distinct) by the fundamental theorem of algebra, at least one root must be real.

As stated above, if r₁, r₂, r₃ are the three roots of the cubic ${\displaystyle a{x}^3+b{x}^2+cx+d}$, then the discriminant is

${\displaystyle \mathrm{\Delta }=a^4(r_1-r_2{)}^2(r_1-r_3{)}^2(r_2-r_3{)}^2}$

If the three roots are real and distinct, the discriminant is a product of positive reals, that is ${\displaystyle \mathrm{\Delta }>0.}$

If only one root, say r₁, is real, then r₂ and r₃ are complex conjugates, which implies that r₂ – r₃ is a purely imaginary number, and thus that (r₂ – r₃)² is real and negative. On the other hand, r₁ – r₂ and r₁ – r₃ are complex conjugates, and their product is real and positive. Thus the discriminant is the product of a single negative number and several positive ones. That is ${\displaystyle \mathrm{\Delta }<0.}$

Multiple root

If the discriminant of a cubic is zero, the cubic has a multiple root. If furthermore its coefficients are real, then all of its roots are real.

The discriminant of the depressed cubic ${\displaystyle t^3+pt+q}$ is zero if ${\displaystyle 4p^3+27q^2=0.}$ If p is also zero, then p = q = 0 , and 0 is a triple root of the cubic. If ${\displaystyle 4p^3+27q^2=0,}$ and p ≠ 0 , then the cubic has a simple root

${\displaystyle t_1=\frac{3q}{p}}$

and a double root

${\displaystyle t_2=t_3=-\frac{3q}{2p}.}$

In other words,

${\displaystyle t^3+pt+q=\left(t-\frac{3q}{p}\right){\left(t+\frac{3q}{2p}\right)}^2.}$

This result can be proved by expanding the latter product or retrieved by solving the rather simple system of equations resulting from Vieta's formulas.

By using the reduction of a depressed cubic, these results can be extended to the general cubic. This gives: If the discriminant of the cubic ${\displaystyle a{x}^3+b{x}^2+cx+d}$ is zero, then

• either, if ${\displaystyle b^2=3ac,}$ the cubic has a triple root

${\displaystyle x_1=x_2=x_3=-\frac{b}{3a},}$

and

${\displaystyle a{x}^3+b{x}^2+cx+d=a{\left(x+\frac{b}{3a}\right)}^3}$

• or, if ${\displaystyle b^2\ne 3ac,}$ the cubic has a double root

${\displaystyle x_2=x_3=\frac{9ad-bc}{2(b^2-3ac)},}$

and a simple root,

${\displaystyle x_1=\frac{4abc-9a^{2}d-b^3}{a(b^2-3ac)}.}$

and thus

${\displaystyle a{x}^3+b{x}^2+cx+d=a(x-x_1)(x-x_2{)}^2.}$

Characteristic 2 and 3

The above results are valid when the coefficients belong to a field of characteristic other than 2 or 3, but must be modified for characteristic 2 or 3, because of the involved divisions by 2 and 3.

The reduction to a depressed cubic works for characteristic 2, but not for characteristic 3. However, in both cases, it is simpler to establish and state the results for the general cubic. The main tool for that is the fact that a multiple root is a common root of the polynomial and its formal derivative. In these characteristics, if the derivative is not a constant, it is a linear polynomial in characteristic 3, and is the square of a linear polynomial in characteristic 2. Therefore, for either characteristic 2 or 3, the derivative has only one root. This allows computing the multiple root, and the third root can be deduced from the sum of the roots, which is provided by Vieta's formulas.

A difference with other characteristics is that, in characteristic 2, the formula for a double root involves a square root, and, in characteristic 3, the formula for a triple root involves a cube root.

Cardano's formula

Gerolamo Cardano is credited with publishing the first formula for solving cubic equations, attributing it to Scipione del Ferro and Niccolo Fontana Tartaglia. The formula applies to depressed cubics, but, as shown in § Depressed cubic, it allows solving all cubic equations.

Cardano's result is that, if

${\displaystyle t^3+pt+q=0}$

is a cubic equation such that p and q are real numbers such that ${\displaystyle \mathrm{\Delta }=\frac{q^2}{4}+\frac{p^3}{27}}$ is positive, then the equation has the real root

${\displaystyle \sqrt[3]{u_1}+\sqrt[3]{u_2},}$

where ${\displaystyle u_1}$ and ${\displaystyle u_2}$ are the two numbers ${\displaystyle -\frac{q}{2}+\sqrt{\mathrm{\Delta }}}$ and ${\displaystyle -\frac{q}{2}-\sqrt{\mathrm{\Delta }}.}$

See § Derivation of the roots, below, for several methods for getting this result.

As shown in § Nature of the roots, the two other roots are non-real complex conjugate numbers, in this case. It was later shown (Cardano did not know complex numbers) that the two other roots are obtained by multiplying one of the cube roots by the primitive cube root of unity ${\displaystyle {\epsilon }_1=\frac{-1+i\sqrt{3}}{2},}$ and the other cube root by the other primitive cube root of the unity ${\displaystyle {\epsilon }_2={\epsilon }_1^2=\frac{-1-i\sqrt{3}}{2}.}$ That is, the other roots of the equation are ${\displaystyle {\epsilon }_1\sqrt[3]{u_1}+{\epsilon }_2\sqrt[3]{u_2}}$ and ${\displaystyle {\epsilon }_2\sqrt[3]{u_1}+{\epsilon }_1\sqrt[3]{u_2}.}$

If ${\displaystyle 4p^3+27q^2<0,}$ there are three real roots, but Galois theory allows proving that, if there is no rational root, the roots cannot be expressed by an algebraic expression involving only real numbers. Therefore, the equation cannot be solved in this case with the knowledge of Cardano's time. This case has thus been called casus irreducibilis, meaning irreducible case in Latin.

In casus irreducibilis, Cardano's formula can still be used, but some care is needed in the use of cube roots. A first method is to define the symbols ${\displaystyle \sqrt{{}^{}}}$ and ${\displaystyle \sqrt[3]{{}^{}}}$ as representing the principal values of the root function (that is the root that has the largest real part). With this convention Cardano's formula for the three roots remains valid, but is not purely algebraic, as the definition of a principal part is not purely algebraic, since it involves inequalities for comparing real parts. Also, the use of principal cube root may give a wrong result if the coefficients are non-real complex numbers. Moreover, if the coefficients belong to another field, the principal cube root is not defined in general.

The second way for making Cardano's formula always correct, is to remark that the product of the two cube roots must be –p / 3. It results that a root of the equation is

${\displaystyle C-\frac{p}{3C}\text{with}C=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}.}$

In this formula, the symbols ${\displaystyle \sqrt{{}^{}}}$ and ${\displaystyle \sqrt[3]{{}^{}}}$ denote any square root and any cube root. The other roots of the equation are obtained either by changing of cube root or, equivalently, by multiplying the cube root by a primitive cube root of unity, that is ${\displaystyle \frac{-1\pm \sqrt{-3}}{2}.}$

This formula for the roots is always correct except when p = q = 0, with the proviso that if p = 0, the square root is chosen so that C ≠ 0. However, the formula is useless in these cases as the roots can be expressed without any cube root. Similarly, the formula is also useless in the other cases where no cube root is needed, that is when ${\displaystyle 4p^3+27q^2=0}$ and when the cubic polynomial is not irreducible.

This formula is also correct when p and q belong to any field of characteristic other than 2 or 3.

General cubic formula

A cubic formula for the roots of the general cubic equation (with a ≠ 0)

${\displaystyle a{x}^3+b{x}^2+cx+d=0}$

can be deduced from every variant of Cardano's formula by reduction to a depressed cubic. The variant that is presented here is valid not only for real coefficients, but also for coefficients a, b, c, d belonging to any field of characteristic different of 2 and 3.

The formula being rather complicated, it is worth splitting it in smaller formulas.

Let

${\displaystyle \begin{array}{rl}{\mathrm{\Delta }}_0& =b^2-3ac,\\ {\mathrm{\Delta }}_1& =2b^3-9abc+27a^{2}d.\end{array}}$

(Both ${\displaystyle {\mathrm{\Delta }}_0}$ and ${\displaystyle {\mathrm{\Delta }}_1}$ can be expressed as resultants of the cubic and its derivatives: ${\displaystyle {\mathrm{\Delta }}_1}$ is −1/8a times the resultant of the cubic and its second derivative, and ${\displaystyle {\mathrm{\Delta }}_0}$ is −1/12a times the resultant of the first and second derivatives of the cubic polynomial.)

Then let

${\displaystyle C=\sqrt[3]{\frac{{\mathrm{\Delta }}_1\pm \sqrt{{\mathrm{\Delta }}_1^2-4{\mathrm{\Delta }}_0^3}}{2}},}$

where the symbols ${\displaystyle \sqrt{{}^{}}}$ and ${\displaystyle \sqrt[3]{{}^{}}}$ are interpreted as any square root and any cube root, respectively (every nonzero complex number has two square roots and three cubic roots). The sign "±" before the square root is either "+" or "–"; the choice is almost arbitrary, and changing it amounts to choosing a different square root. However, if a choice yields C = 0 (this occurs if ${\displaystyle {\mathrm{\Delta }}_0=0}$), then the other sign must be selected instead. If both choices yield C = 0, that is, if ${\displaystyle {\mathrm{\Delta }}_0={\mathrm{\Delta }}_1=0,}$ a fraction 0/0 occurs in following formulas; this fraction must be interpreted as equal to zero (see the end of this section). With these conventions, one of the roots is

${\displaystyle x=-\frac{1}{3a}\left(b+C+\frac{{\mathrm{\Delta }}_0}{C}\right)\text{.}}$

The other two roots can be obtained by changing the choice of the cube root in the definition of C, or, equivalently by multiplying C by a primitive cube root of unity, that is –1 ± √–3/2. In other words, the three roots are

${\displaystyle x_k=-\frac{1}{3a}\left(b+{\xi }^{k}C+\frac{{\mathrm{\Delta }}_0}{{\xi }^{k}C}\right),k\in \{0,1,2\}\text{,}}$

where ξ = –1 + √–3/2.

As for the special case of a depressed cubic, this formula applies but is useless when the roots can be expressed without cube roots. In particular, if ${\displaystyle {\mathrm{\Delta }}_0={\mathrm{\Delta }}_1=0,}$ the formula gives that the three roots equal ${\displaystyle \frac{-b}{3a},}$ which means that the cubic polynomial can be factored as ${\displaystyle a(x+\frac{b}{3a}{)}^3.}$ A straightforward computation allows verifying that the existence of this factorization is equivalent with ${\displaystyle {\mathrm{\Delta }}_0={\mathrm{\Delta }}_1=0.}$

Trigonometric and hyperbolic solutions

Trigonometric solution for three real roots

When a cubic equation with real coefficients has three real roots, the formulas expressing these roots in terms of radicals involve complex numbers. Galois theory allows proving that when the three roots are real, and none is rational (casus irreducibilis), one cannot express the roots in terms of real radicals. Nevertheless, purely real expressions of the solutions may be obtained using trigonometric functions, specifically in terms of cosines and arccosines. More precisely, the roots of the depressed cubic

${\displaystyle t^3+pt+q=0}$

are

${\displaystyle t_k=2\sqrt{-\frac{p}{3}}\cos \left[\frac{1}{3}\arccos \left(\frac{3q}{2p}\sqrt{\frac{-3}{p}}\right)-\frac{2\pi k}{3}\right]\text{for }k=0,1,2.}$

This formula is due to François Viète. It is purely real when the equation has three real roots (that is ${\displaystyle 4p^3+27q^2<0}$). Otherwise, it is still correct but involves complex cosines and arccosines when there is only one real root, and it is nonsensical (division by zero) when p = 0.

This formula can be straightforwardly transformed into a formula for the roots of a general cubic equation, using the back-substitution described in § Depressed cubic.

The formula can be proved as follows: Starting from the equation t³ + pt + q = 0, let us set  t = u cos θ. The idea is to choose u to make the equation coincide with the identity

${\displaystyle 4{\cos }^3\theta -3\cos \theta -\cos (3\theta )=0.}$

For this, choose ${\displaystyle u=2\sqrt{-\frac{p}{3}},}$ and divide the equation by ${\displaystyle \frac{u^3}{4}.}$ This gives

${\displaystyle 4{\cos }^3\theta -3\cos \theta -\frac{3q}{2p}\sqrt{\frac{-3}{p}}=0.}$

Combining with the above identity, one gets

${\displaystyle \cos (3\theta )=\frac{3q}{2p}\sqrt{\frac{-3}{p}},}$

and the roots are thus

${\displaystyle t_k=2\sqrt{-\frac{p}{3}}\cos \left[\frac{1}{3}\arccos \left(\frac{3q}{2p}\sqrt{\frac{-3}{p}}\right)-\frac{2\pi k}{3}\right]\text{for }k=0,1,2.}$

Hyperbolic solution for one real root

When there is only one real root (and p ≠ 0), this root can be similarly represented using hyperbolic functions, as

${\displaystyle \begin{array}{rl}{t}_0& =-2\frac{|q|}{q}\sqrt{-\frac{p}{3}}\cosh \left[\frac{1}{3}\mathrm{arcosh}\left(\frac{-3|q|}{2p}\sqrt{\frac{-3}{p}}\right)\right]\text{if }4p^3+27q^2>0\text{ and }p<0,\\ t_0& =-2\sqrt{\frac{p}{3}}\sinh \left[\frac{1}{3}\mathrm{arsinh}\left(\frac{3q}{2p}\sqrt{\frac{3}{p}}\right)\right]\text{if }p>0.\end{array}}$

If p ≠ 0 and the inequalities on the right are not satisfied (the case of three real roots), the formulas remain valid but involve complex quantities.

When p = ±3, the above values of t₀ are sometimes called the Chebyshev cube root. More precisely, the values involving cosines and hyperbolic cosines define, when p = −3, the same analytic function denoted C_1/3(q), which is the proper Chebyshev cube root. The value involving hyperbolic sines is similarly denoted S_1/3(q), when p = 3.

Geometric solutions

Omar Khayyám's solution

Omar Khayyám's geometric solution of a cubic equation, for the case m = 2, n = 16, giving the root 2. The intersection of the vertical line on the x-axis at the center of the circle is happenstance of the example illustrated.

For solving the cubic equation x³ + m²x = n where n > 0, Omar Khayyám constructed the parabola y = x²/m, the circle that has as a diameter the line segment [0, n/m²] on the positive x-axis, and a vertical line through the point where the circle and the parabola intersect above the x-axis. The solution is given by the length of the horizontal line segment from the origin to the intersection of the vertical line and the x-axis (see the figure).

A simple modern proof is as follows. Multiplying the equation by x/m² and regrouping the terms gives

${\displaystyle \frac{x^4}{m^2}=x\left(\frac{n}{m^2}-x\right).}$

The left-hand side is the value of y² on the parabola. The equation of the circle being y² + x(x − n/m²) = 0, the right hand side is the value of y² on the circle.

Solution with angle trisector

A cubic equation with real coefficients can be solved geometrically using compass, straightedge, and an angle trisector if and only if it has three real roots.

A cubic equation can be solved by compass-and-straightedge construction (without trisector) if and only if it has a rational root. This implies that the old problems of angle trisection and doubling the cube, set by ancient Greek mathematicians, cannot be solved by compass-and-straightedge construction.

Geometric interpretation of the roots

Three real roots

For the cubic (1) with three real roots, the roots are the projection on the x-axis of the vertices A, B, and C of an equilateral triangle. The center of the triangle has the same x-coordinate as the inflection point.

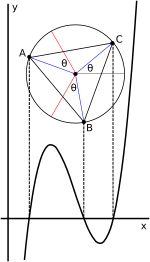
Viète's trigonometric expression of the roots in the three-real-roots case lends itself to a geometric interpretation in terms of a circle. When the cubic is written in depressed form (2), t³ + pt + q = 0, as shown above, the solution can be expressed as

${\displaystyle t_k=2\sqrt{-\frac{p}{3}}\cos \left(\frac{1}{3}\arccos \left(\frac{3q}{2p}\sqrt{\frac{-3}{p}}\right)-k\frac{2\pi }{3}\right)\text{for}k=0,1,2.}$

Here ${\displaystyle \arccos \left(\frac{3q}{2p}\sqrt{\frac{-3}{p}}\right)}$ is an angle in the unit circle; taking 1/3 of that angle corresponds to taking a cube root of a complex number; adding −k2π/3 for k = 1, 2 finds the other cube roots; and multiplying the cosines of these resulting angles by ${\displaystyle 2\sqrt{-\frac{p}{3}}}$ corrects for scale.

For the non-depressed case (1) (shown in the accompanying graph), the depressed case as indicated previously is obtained by defining t such that x = t − b/3a so t = x + b/3a. Graphically this corresponds to simply shifting the graph horizontally when changing between the variables t and x, without changing the angle relationships. This shift moves the point of inflection and the centre of the circle onto the y-axis. Consequently, the roots of the equation in t sum to zero.

One real root

In the Cartesian plane

The slope of line RA is twice that of RH. Denoting the complex roots of the cubic as g ± hi, g = OM (negative here) and h = √tan ORH = √slope of line RH = BE = DA.

When the graph of a cubic function is plotted in the Cartesian plane, if there is only one real root, it is the abscissa (x-coordinate) of the horizontal intercept of the curve (point R on the figure). Further, if the complex conjugate roots are written as g ± hi, then the real part g is the abscissa of the tangency point H of the tangent line to cubic that passes through x-intercept R of the cubic (that is the signed length OM, negative on the figure). The imaginary parts ±h are the square roots of the tangent of the angle between this tangent line and the horizontal axis.

In the complex plane

With one real and two complex roots, the three roots can be represented as points in the complex plane, as can the two roots of the cubic's derivative. There is an interesting geometrical relationship among all these roots.

The points in the complex plane representing the three roots serve as the vertices of an isosceles triangle. (The triangle is isosceles because one root is on the horizontal (real) axis and the other two roots, being complex conjugates, appear symmetrically above and below the real axis.) Marden's theorem says that the points representing the roots of the derivative of the cubic are the foci of the Steiner inellipse of the triangle—the unique ellipse that is tangent to the triangle at the midpoints of its sides. If the angle at the vertex on the real axis is less than π/3 then the major axis of the ellipse lies on the real axis, as do its foci and hence the roots of the derivative. If that angle is greater than π/3, the major axis is vertical and its foci, the roots of the derivative, are complex conjugates. And if that angle is π/3, the triangle is equilateral, the Steiner inellipse is simply the triangle's incircle, its foci coincide with each other at the incenter, which lies on the real axis, and hence the derivative has duplicate real roots.

Galois group

Given a cubic irreducible polynomial over a field K of characteristic different from 2 and 3, the Galois group over K is the group of the field automorphisms that fix K of the smallest extension of K (splitting field). As these automorphisms must permute the roots of the polynomials, this group is either the group S₃ of all six permutations of the three roots, or the group A₃ of the three circular permutations.

The discriminant Δ of the cubic is the square of

${\displaystyle \sqrt{\mathrm{\Delta }}=a^2(r_1-r_2)(r_1-r_3)(r_2-r_3),}$

where a is the leading coefficient of the cubic, and r₁, r₂ and r₃ are the three roots of the cubic. As ${\displaystyle \sqrt{\mathrm{\Delta }}}$ changes of sign if two roots are exchanged, ${\displaystyle \sqrt{\mathrm{\Delta }}}$ is fixed by the Galois group only if the Galois group is A₃. In other words, the Galois group is A₃ if and only if the discriminant is the square of an element of K.

As most integers are not squares, when working over the field Q of the rational numbers, the Galois group of most irreducible cubic polynomials is the group S₃ with six elements. An example of a Galois group A₃ with three elements is given by p(x) = x³ − 3x − 1, whose discriminant is 81 = 9².

Derivation of the roots

This section regroups several methods for deriving Cardano's formula.

Cardano's method

This method is due to Scipione del Ferro and Tartaglia, but is named after Gerolamo Cardano who first published it in his book Ars Magna (1545).

This method applies to a depressed cubic t³ + pt + q = 0. The idea is to introduce two variables u and v such that u + v = t and to substitute this in the depressed cubic, giving

${\displaystyle u^3+v^3+(3uv+p)(u+v)+q=0.}$

At this point Cardano imposed the condition 3uv + p = 0. This removes the third term in previous equality, leading to the system of equations

${\displaystyle \begin{array}{rl}{u}^3+v^3& =-q\\ uv& =-\frac{p}{3}.\end{array}}$

Knowing the sum and the product of u³ and v³, one deduces that they are the two solutions of the quadratic equation

${\displaystyle (x-u^3)(x-v^3)=x^2-(u^3+v^3)x+u^3{v}^3=x^2-(u^3+v^3)x+(uv{)}^3=0,}$

so

${\displaystyle x^2+qx-\frac{p^3}{27}=0,}$

The discriminant of this equation is ${\displaystyle \mathrm{\Delta }=q^2+\frac{4p^3}{27}}$, and assuming it is positive, real solutions to this equation are (after folding division by 4 under the square root):

${\displaystyle -\frac{q}{2}\pm \sqrt{\frac{q^2}{4}+\frac{p^3}{27}}.}$

So (without loss of generality in choosing u or v):

${\displaystyle u=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}.}$

${\displaystyle v=\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}.}$

As u + v = t, the sum of the cube roots of these solutions is a root of the equation. That is

${\displaystyle t=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}}$

is a root of the equation; this is Cardano's formula.

This works well when ${\displaystyle 4p^3+27q^2>0,}$ but, if ${\displaystyle 4p^3+27q^2<0,}$ the square root appearing in the formula is not real. As a complex number has three cube roots, using Cardano's formula without care would provide nine roots, while a cubic equation cannot have more than three roots. This was clarified first by Rafael Bombelli in his book L'Algebra (1572). The solution is to use the fact that uv = –p/3, that is v = –p/3u. This means that only one cube root needs to be computed, and leads to the second formula given in § Cardano's formula.

The other roots of the equation can be obtained by changing of cube root, or, equivalently, by multiplying the cube root by each of the two primitive cube roots of unity, which are ${\displaystyle \frac{-1\pm \sqrt{-3}}{2}.}$

Vieta's substitution

Vieta's substitution is a method introduced by François Viète (Vieta is his Latin name) in a text published posthumously in 1615, which provides directly the second formula of § Cardano's method, and avoids the problem of computing two different cube roots.

Starting from the depressed cubic t³ + pt + q = 0, Vieta's substitution is t = w – p/3w.

The substitution t = w – p/3w transforms the depressed cubic into

${\displaystyle w^3+q-\frac{p^3}{27w^3}=0.}$

Multiplying by w³, one gets a quadratic equation in w³:

${\displaystyle (w^3{)}^2+q(w^3)-\frac{p^3}{27}=0.}$

Let

${\displaystyle W=-\frac{q}{2}\pm \sqrt{\frac{p^3}{27}+\frac{q^2}{4}}}$

be any nonzero root of this quadratic equation. If w₁, w₂ and w₃ are the three cube roots of W, then the roots of the original depressed cubic are w₁ − p/3w₁, w₂ − p/3w₂, and w₃ − p/3w₃. The other root of the quadratic equation is ${\displaystyle -\frac{p^3}{27W}.}$ This implies that changing the sign of the square root exchanges w_i and − p/3w_i for i = 1, 2, 3, and therefore does not change the roots. This method only fails when both roots of the quadratic equation are zero, that is when p = q = 0, in which case the only root of the depressed cubic is 0.

Lagrange's method

In his paper Réflexions sur la résolution algébrique des équations ("Thoughts on the algebraic solving of equations"), Joseph Louis Lagrange introduced a new method to solve equations of low degree in a uniform way, with the hope that he could generalize it for higher degrees. This method works well for cubic and quartic equations, but Lagrange did not succeed in applying it to a quintic equation, because it requires solving a resolvent polynomial of degree at least six. Apart from the fact that nobody had previously succeeded, this was the first indication of the non-existence of an algebraic formula for degrees 5 and higher; as was later proved by the Abel–Ruffini theorem. Nevertheless, modern methods for solving solvable quintic equations are mainly based on Lagrange's method.

In the case of cubic equations, Lagrange's method gives the same solution as Cardano's. Lagrange's method can be applied directly to the general cubic equation ax³ + bx² + cx + d = 0, but the computation is simpler with the depressed cubic equation, t³ + pt + q = 0.

Lagrange's main idea was to work with the discrete Fourier transform of the roots instead of with the roots themselves. More precisely, let ξ be a primitive third root of unity, that is a number such that ξ³ = 1 and ξ² + ξ + 1 = 0 (when working in the space of complex numbers, one has ${\displaystyle \xi =\frac{-1\pm i\sqrt{3}}{2}=e^{2i\pi /3},}$ but this complex interpretation is not used here). Denoting x₀, x₁ and x₂ the three roots of the cubic equation to be solved, let

${\displaystyle \begin{array}{rl}{s}_0& =x_0+x_1+x_2,\\ s_1& =x_0+\xi x_1+{\xi }^2{x}_2,\\ s_2& =x_0+{\xi }^2{x}_1+\xi x_2,\end{array}}$

be the discrete Fourier transform of the roots. If s₀, s₁ and s₂ are known, the roots may be recovered from them with the inverse Fourier transform consisting of inverting this linear transformation; that is,

${\displaystyle \begin{array}{rl}{x}_0& =\frac{1}{3}(s_0+s_1+s_2),\\ x_1& =\frac{1}{3}(s_0+{\xi }^2{s}_1+\xi s_2),\\ x_2& =\frac{1}{3}(s_0+\xi s_1+{\xi }^2{s}_2).\end{array}}$

By Vieta's formulas, s₀ is known to be zero in the case of a depressed cubic, and −b/a for the general cubic. So, only s₁ and s₂ need to be computed. They are not symmetric functions of the roots (exchanging x₁ and x₂ exchanges also s₁ and s₂), but some simple symmetric functions of s₁ and s₂ are also symmetric in the roots of the cubic equation to be solved. Thus these symmetric functions can be expressed in terms of the (known) coefficients of the original cubic, and this allows eventually expressing the s_i as roots of a polynomial with known coefficients. This works well for every degree, but, in degrees higher than four, the resulting polynomial that has the s_i as roots has a degree higher than that of the initial polynomial, and is therefore unhelpful for solving. This is the reason for which Lagrange's method fails in degrees five and higher.

In the case of a cubic equation, ${\displaystyle P=s_1{s}_2,}$ and ${\displaystyle S=s_1^3+s_2^3}$ are such symmetric polynomials (see below). It follows that ${\displaystyle s_1^3}$ and ${\displaystyle s_2^3}$ are the two roots of the quadratic equation ${\displaystyle z^2-Sz+P^3=0.}$ Thus the resolution of the equation may be finished exactly as with Cardano's method, with ${\displaystyle s_1}$ and ${\displaystyle s_2}$ in place of u and v.

In the case of the depressed cubic, one has ${\displaystyle x_0=\frac{1}{3}(s_1+s_2)}$ and ${\displaystyle s_1{s}_2=-3p,}$ while in Cardano's method we have set ${\displaystyle x_0=u+v}$ and ${\displaystyle uv=\frac{1}{3}p.}$ Thus, up to the exchange of u and v, we have ${\displaystyle s_1=3u}$ and ${\displaystyle s_2=3v.}$ In other words, in this case, Cardano's method and Lagrange's method compute exactly the same things, up to a factor of three in the auxiliary variables, the main difference being that Lagrange's method explains why these auxiliary variables appear in the problem.

Computation of S and P

A straightforward computation using the relations ξ³ = 1 and ξ² + ξ + 1 = 0 gives

${\displaystyle \begin{array}{rl}P& =s_1{s}_2=x_0^2+x_1^2+x_2^2-(x_0{x}_1+x_1{x}_2+x_2{x}_0),\\ S& =s_1^3+s_2^3=2(x_0^3+x_1^3+x_2^3)-3(x_0^2{x}_1+x_1^2{x}_2+x_2^2{x}_0+x_0{x}_1^2+x_1{x}_2^2+x_2{x}_0^2)+12x_0{x}_1{x}_2.\end{array}}$

This shows that P and S are symmetric functions of the roots. Using Newton's identities, it is straightforward to express them in terms of the elementary symmetric functions of the roots, giving

${\displaystyle \begin{array}{rl}P& =e_1^2-3e_2,\\ S& =2e_1^3-9e_1{e}_2+27e_3,\end{array}}$

with e₁ = 0, e₂ = p and e₃ = −q in the case of a depressed cubic, and e₁ = −b/a, e₂ = c/a and e₃ = −d/a, in the general case.

Applications

Cubic equations arise in various other contexts.

In mathematics

• Angle trisection and doubling the cube are two ancient problems of geometry that have been proved to not be solvable by straightedge and compass construction, because they are equivalent to solving a cubic equation.
• Marden's theorem states that the foci of the Steiner inellipse of any triangle can be found by using the cubic function whose roots are the coordinates in the complex plane of the triangle's three vertices. The roots of the first derivative of this cubic are the complex coordinates of those foci.
• The area of a regular heptagon can be expressed in terms of the roots of a cubic. Further, the ratios of the long diagonal to the side, the side to the short diagonal, and the negative of the short diagonal to the long diagonal all satisfy a particular cubic equation. In addition, the ratio of the inradius to the circumradius of a heptagonal triangle is one of the solutions of a cubic equation. The values of trigonometric functions of angles related to ${\displaystyle 2\pi /7}$ satisfy cubic equations.
• Given the cosine (or other trigonometric function) of an arbitrary angle, the cosine of one-third of that angle is one of the roots of a cubic.
• The solution of the general quartic equation relies on the solution of its resolvent cubic.
• The eigenvalues of a 3×3 matrix are the roots of a cubic polynomial which is the characteristic polynomial of the matrix.
• The characteristic equation of a third-order constant coefficients or Cauchy–Euler (equidimensional variable coefficients) linear differential equation or difference equation is a cubic equation.
• Intersection points of cubic Bézier curve and straight line can be computed using direct cubic equation representing Bézier curve.
• Critical points of a quartic function are found by solving a cubic equation (the derivative set equal to zero).
• Inflection points of a quintic function are the solution of a cubic equation (the second derivative set equal to zero).

In other sciences

• In analytical chemistry, the Charlot equation, which can be used to find the pH of buffer solutions, can be solved using a cubic equation.
• In thermodynamics, equations of state (which relate pressure, volume, and temperature of a substances), e.g. the Van der Waals equation of state, are cubic in the volume.
• Kinematic equations involving linear rates of acceleration are cubic.
• The speed of seismic Rayleigh waves is a solution of the Rayleigh wave cubic equation.
• The steady state speed of a vehicle moving on a slope with air friction for a given input power is solved by a depressed cubic equation.
• Kepler's third law of planetary motion is cubic in the semi-major axis.

Free content

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Free_content

Logo of the Definition of Free Cultural Works project

Free content, libre content, libre information, or free information, is any kind of functional work, work of art, or other creative content that meets the definition of a free cultural work, meaning "works or expressions which can be freely studied, applied, copied and/or modified, by anyone, for any purpose."

Definition

A free cultural work is, according to the definition of Free Cultural Works, one that has no significant legal restriction on people's freedom to:

• use the content and benefit from using it,
• study the content and apply what is learned,
• make and distribute copies of the content,
• change and improve the content and distribute these derivative works.

Free content encompasses all works in the public domain and also those copyrighted works whose licenses honor and uphold the freedoms mentioned above. Because the Berne Convention in most countries by default grants copyright holders monopolistic control over their creations, copyright content must be explicitly declared free, usually by the referencing or inclusion of licensing statements from within the work.

Although there are a great many different definitions in regular everyday use, free content is legally very similar, if not like an identical twin, to open content. An analogy is a use of the rival terms free software and open-source, which describe ideological differences rather than legal ones. For instance, the Open Knowledge Foundation's Open Definition describes "open" as synonymous to the definition of free in the "Definition of Free Cultural Works" (as also in the Open Source Definition and Free Software Definition). For such free/open content both movements recommend the same three Creative Commons licenses, the CC BY, CC BY-SA, and CC0.

Legal matters

Copyright

Main article: Copyright

Copyright symbol

Copyright is a legal concept, which gives the author or creator of a work legal control over the duplication and public performance of their work. In many jurisdictions, this is limited by a time period after which the works then enter the public domain. Copyright laws are a balance between the rights of creators of intellectual and artistic works and the rights of others to build upon those works. During the time period of copyright the author's work may only be copied, modified, or publicly performed with the consent of the author, unless the use is a fair use. Traditional copyright control limits the use of the work of the author to those who either pay royalties to the author for usage of the author's content or limit their use to fair use. Secondly, it limits the use of content whose author cannot be found. Finally, it creates a perceived barrier between authors by limiting derivative works, such as mashups and collaborative content.

Public domain

Main article: Public domain

Public domain logo

The public domain is a range of creative works whose copyright has expired or was never established, as well as ideas and facts which are ineligible for copyright. A public domain work is a work whose author has either relinquished to the public or no longer can claim control over, the distribution and usage of the work. As such, any person may manipulate, distribute, or otherwise use the work, without legal ramifications. A work in the public domain or released under a permissive license may be referred to as "copycenter".

Copyleft

Main article: Copyleft

Copyleft symbol

Copyleft is a play on the word copyright and describes the practice of using copyright law to remove restrictions on distributing copies and modified versions of a work. The aim of copyleft is to use the legal framework of copyright to enable non-author parties to be able to reuse and, in many licensing schemes, modify content that is created by an author. Unlike works in the public domain, the author still maintains copyright over the material, however, the author has granted a non-exclusive license to any person to distribute, and often modify, the work. Copyleft licenses require that any derivative works be distributed under the same terms and that the original copyright notices be maintained. A symbol commonly associated with copyleft is a reversal of the copyright symbol, facing the other way; the opening of the C points left rather than right. Unlike the copyright symbol, the copyleft symbol does not have a codified meaning.

Usage

Projects that provide free content exist in several areas of interest, such as software, academic literature, general literature, music, images, video, and engineering. Technology has reduced the cost of publication and reduced the entry barrier sufficiently to allow for the production of widely disseminated materials by individuals or small groups. Projects to provide free literature and multimedia content have become increasingly prominent owing to the ease of dissemination of materials that are associated with the development of computer technology. Such dissemination may have been too costly prior to these technological developments.

Media

Creative Commons logo

In media, which includes textual, audio, and visual content, free licensing schemes such as some of the licenses made by Creative Commons have allowed for the dissemination of works under a clear set of legal permissions. Not all Creative Commons licenses are entirely free; their permissions may range from very liberal general redistribution and modification of the work to a more restrictive redistribution-only licensing. Since February 2008, Creative Commons licenses which are entirely free carry a badge indicating that they are "approved for free cultural works". Repositories exist which exclusively feature free material and provide content such as photographs, clip art, music, and literature. While extensive reuse of free content from one website in another website is legal, it is usually not sensible because of the duplicate content problem. Wikipedia is amongst the most well-known databases of user-uploaded free content on the web. While the vast majority of content on Wikipedia is free content, some copyrighted material is hosted under fair-use criteria.

Software

Main article: Free and open-source software

OSI logo

Free Software Foundation logo

Free and open-source software, which is also often referred to as open source software and free software, is a maturing technology with major companies using free software to provide both services and technology to both end-users and technical consumers. The ease of dissemination has allowed for increased modularity, which allows for smaller groups to contribute to projects as well as simplifying collaboration. Open source development models have been classified as having a similar peer-recognition and collaborative benefit incentives that are typified by more classical fields such as scientific research, with the social structures that result from this incentive model decreasing production cost. Given sufficient interest in a software component, by using peer-to-peer distribution methods, distribution costs of software may be reduced, removing the burden of infrastructure maintenance from developers. As distribution resources are simultaneously provided by consumers, these software distribution models are scalable, that is the method is feasible regardless of the number of consumers. In some cases, free software vendors may use peer-to-peer technology as a method of dissemination. In general, project hosting and code distribution is not a problem for the most of free projects as a number of providers offer them these services free.

Engineering and technology

Main articles: Open-source hardware and Open-design movement

Logo of the Open Source Hardware Association

Free content principles have been translated into fields such as engineering, where designs and engineering knowledge can be readily shared and duplicated, in order to reduce overheads associated with project development. Open design principles can be applied in engineering and technological applications, with projects in mobile telephony, small-scale manufacture, the automotive industry, and even agricultural areas. Technologies such as distributed manufacturing can allow computer-aided manufacturing and computer-aided design techniques to be able to develop small-scale production of components for the development of new, or repair of existing, devices. Rapid fabrication technologies underpin these developments, which allow end-users of technology to be able to construct devices from pre-existing blueprints, using software and manufacturing hardware to convert information into physical objects.

Academia

Main article: Open access

In academic work, the majority of works are not free, although the percentage of works that are open access is growing rapidly. Open access refers to online research outputs that are free of all restrictions on access (e.g. access tolls) and free of many restrictions on use (e.g. certain copyright and license restrictions). Authors may see open access publishing as a method of expanding the audience that is able to access their work to allow for greater impact of the publication, or may support it for ideological reasons. Open access publishers such as PLOS and BioMed Central provide capacity for review and publishing of free works; though such publications are currently more common in science than humanities. Various funding institutions and governing research bodies have mandated that academics must produce their works to be open-access, in order to qualify for funding, such as the US National Institutes of Health, Research Councils UK (effective 2016) and the European Union (effective 2020). At an institutional level some universities, such as the Massachusetts Institute of Technology, have adopted open access publishing by default by introducing their own mandates. Some mandates may permit delayed publication and may charge researchers for open access publishing.

Open content publication has been seen as a method of reducing costs associated with information retrieval in research, as universities typically pay to subscribe for access to content that is published through traditional means whilst improving journal quality by discouraging the submission of research articles of reduced quality. Subscriptions for non-free content journals may be expensive for universities to purchase, though the article are written and peer-reviewed by academics themselves at no cost to the publisher. This has led to disputes between publishers and some universities over subscription costs, such as the one which occurred between the University of California and the Nature Publishing Group. For teaching purposes, some universities, including MIT, provide freely available course content, such as lecture notes, video resources and tutorials. This content is distributed via Internet resources to the general public. Publication of such resources may be either by a formal institution-wide program, or alternately via informal content provided by individual academics or departments.

Legislation

Any country has its own law and legal system, sustained by its legislation, a set of law-documents—documents containing statutory obligation rules, usually law and created by legislatures. In a democratic country, each law-document is published as open media content, is in principle free content; but in general, there are no explicit licenses attributed for each law-document, so the license must be interpreted, an implied license. Only a few countries have explicit licenses in their law-documents, as the UK's Open Government Licence (a CC BY compatible license). In the other countries, the implied license comes from its proper rules (general laws and rules about copyright in government works). The automatic protection provided by Berne Convention not apply to law-documents: Article 2.4 excludes the official texts from the automatic protection. It is also possible to "inherit" the license from context. The set of country's law-documents is made available through national repositories. Examples of law-document open repositories: LexML Brazil, Legislation.gov.uk, N-Lex. In general, a law-document is offered in more than one (open) official version, but the main one is that published by a government gazette. So, law-documents can eventually inherit license expressed by the repository or by the gazette that contains it.

Open content

Open Content Project logo, 1998

The logo on the screen in the subject's left hand is a Creative Commons license, while the paper in his right hand explains, in Khmer, that the image is open content.

Open content describes any work that others can copy or modify freely by attributing to the original creator, but without needing to ask for permission. This has been applied to a range of formats, including textbooks, academic journals, films and music. The term was an expansion of the related concept of open-source software. Such content is said to be under an open license.

History

The concept of applying free software licenses to content was introduced by Michael Stutz, who in 1997 wrote the paper "Applying Copyleft to Non-Software Information" for the GNU Project. The term "open content" was coined by David A. Wiley in 1998 and evangelized via the Open Content Project, describing works licensed under the Open Content License (a non-free share-alike license, see 'Free content' below) and other works licensed under similar terms.

It has since come to describe a broader class of content without conventional copyright restrictions. The openness of content can be assessed under the '5Rs Framework' based on the extent to which it can be reused, revised, remixed and redistributed by members of the public without violating copyright law. Unlike free content and content under open-source licenses, there is no clear threshold that a work must reach to qualify as 'open content'.

Although open content has been described as a counterbalance to copyright, open content licenses rely on a copyright holder's power to license their work, as copyleft which also utilizes copyright for such a purpose.

In 2003 Wiley announced that the Open Content Project has been succeeded by Creative Commons and their licenses, where he joined as "Director of Educational Licenses".

In 2005, the Open Icecat project was launched, in which product information for e-commerce applications was created and published under the Open Content License. It was embraced by the tech sector, which was already quite open source minded.

Open Knowledge Foundation

In 2006 the Creative Commons' successor project was the Definition of Free Cultural Works for free content, put forth by Erik Möller, Richard Stallman, Lawrence Lessig, Benjamin Mako Hill, Angela Beesley, and others. The Definition of Free Cultural Works is used by the Wikimedia Foundation. In 2008, the Attribution and Attribution-ShareAlike Creative Commons licenses were marked as "Approved for Free Cultural Works" among other licenses.

Another successor project is the Open Knowledge Foundation, founded by Rufus Pollock in Cambridge, in 2004 as a global non-profit network to promote and share open content and data. In 2007 the OKF gave an Open Knowledge Definition for "content such as music, films, books; data be it scientific, historical, geographic or otherwise; government and other administrative information". In October 2014 with version 2.0 Open Works and Open Licenses were defined and "open" is described as synonymous to the definitions of open/free in the Open Source Definition, the Free Software Definition and the Definition of Free Cultural Works. A distinct difference is the focus given to the public domain and that it focuses also on the accessibility (open access) and the readability (open formats). Among several conformant licenses, six are recommended, three own (Open Data Commons Public Domain Dedication and Licence, Open Data Commons Attribution License, Open Data Commons Open Database License) and the CC BY, CC BY-SA, and CC0 Creative Commons licenses.

"Open content" definition

The website of the Open Content Project once defined open content as 'freely available for modification, use and redistribution under a license similar to those used by the open-source / free software community'. However, such a definition would exclude the Open Content License because that license forbids charging for content; a right required by free and open-source software licenses.

The term since shifted in meaning. Open content is "licensed in a manner that provides users with free and perpetual permission to engage in the 5R activities."

The 5Rs are put forward on the Open Content Project website as a framework for assessing the extent to which content is open:

1. Retain – the right to make, own, and control copies of the content (e.g., download, duplicate, store, and manage)
2. Reuse – the right to use the content in a wide range of ways (e.g., in a class, in a study group, on a website, in a video)
3. Revise – the right to adapt, adjust, modify, or alter the content itself (e.g., translate the content into another language)
4. Remix – the right to combine the original or revised content with other open content to create something new (e.g., incorporate the content into a mashup)
5. Redistribute – the right to share copies of the original content, your revisions, or your remixes with others (e.g., give a copy of the content to a friend)

This broader definition distinguishes open content from open-source software, since the latter must be available for commercial use by the public. However, it is similar to several definitions for open educational resources, which include resources under noncommercial and verbatim licenses.

The later Open Definition by the Open Knowledge Foundation define open knowledge with open content and open data as sub-elements and draws heavily on the Open Source Definition; it preserves the limited sense of open content as free content, unifying both.

Open access

Open access symbol, originally designed by PLOS

"Open access" refers to toll-free or gratis access to content, mainly published originally peer-reviewed scholarly journals. Some open access works are also licensed for reuse and redistribution (libre open access), which would qualify them as open content.

Open content and education

Further information: Open educational resources

Unesco's Open Educational Resources logo

 

Open Content Alliance logo

Over the past decade, open content has been used to develop alternative routes towards higher education. Traditional universities are expensive, and their tuition rates are increasing. Open content allows a free way of obtaining higher education that is "focused on collective knowledge and the sharing and reuse of learning and scholarly content." There are multiple projects and organizations that promote learning through open content, including OpenCourseWare, Khan Academy and the Saylor Academy. Some universities, like MIT, Yale, and Tufts are making their courses freely available on the internet.

Textbooks

Main article: Open textbook

The textbook industry is one of the educational industries in which open content can make the biggest impact. Traditional textbooks, aside from being expensive, can also be inconvenient and out of date, because of publishers' tendency to constantly print new editions. Open textbooks help to eliminate this problem, because they are online and thus easily updatable. Being openly licensed and online can be helpful to teachers, because it allows the textbook to be modified according to the teacher's unique curriculum. There are multiple organizations promoting the creation of openly licensed textbooks. Some of these organizations and projects include the University of Minnesota's Open Textbook Library, Connexions, OpenStax College, the Saylor Academy, Open Textbook Challenge and Wikibooks.

Licenses

According to the current definition of open content on the OpenContent website, any general, royalty-free copyright license would qualify as an open license because it 'provides users with the right to make more kinds of uses than those normally permitted under the law. These permissions are granted to users free of charge.'

However, the narrower definition used in the Open Definition effectively limits open content to libre content, any free content license, defined by the Definition of Free Cultural Works, would qualify as an open content license. According to this narrower criteria, the following still-maintained licenses qualify:

• Creative Commons licenses (only Creative Commons Attribution, Attribution-Share Alike and Zero)
• Open Publication License (the original license of the Open Content Project, the Open Content License, did not permit for-profit copying of the licensed work and therefore does not qualify)
• Against DRM license
• GNU Free Documentation License (without invariant sections)
• Open Game License (designed for role-playing games by Wizards of the Coast)
• Free Art License

Further information: Open Knowledge Foundation, Free content, and Definition of Free Cultural Works