Dynamo theory

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Dynamo_theory

Illustration of the dynamo mechanism that generates the Earth's magnetic field: convection currents of fluid metal in the Earth's outer core, driven by heat flow from the inner core, organized into rolls by the Coriolis force, generate circulating electric currents, which supports the magnetic field.^[1]

In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.

History of theory

When William Gilbert published de Magnete in 1600, he concluded that the Earth is magnetic and proposed the first hypothesis for the origin of this magnetism: permanent magnetism such as that found in lodestone. In 1822, André-Marie Ampère proposed that internal currents are responsible of Earth Magnetism. In 1919, Joseph Larmor proposed that a dynamo might be generating the field. However, even after he advanced his hypothesis, some prominent scientists advanced alternative explanations. The Nobel Prize winner Patrick Blackett did a series of experiments looking for a fundamental relation between angular momentum and magnetic moment, but found none.

Walter M. Elsasser, considered a "father" of the presently accepted dynamo theory as an explanation of the Earth's magnetism, proposed that this magnetic field resulted from electric currents induced in the fluid outer core of the Earth. He revealed the history of the Earth's magnetic field through pioneering the study of the magnetic orientation of minerals in rocks.

In order to maintain the magnetic field against ohmic decay (which would occur for the dipole field in 20,000 years), the outer core must be convecting. The convection is likely some combination of thermal and compositional convection. The mantle controls the rate at which heat is extracted from the core. Heat sources include gravitational energy released by the compression of the core, gravitational energy released by the rejection of light elements (probably sulfur, oxygen, or silicon) at the inner core boundary as it grows, latent heat of crystallization at the inner core boundary, and radioactivity of potassium, uranium and thorium.

At the dawn of the 21st century, numerical modeling of the Earth's magnetic field has not been successfully demonstrated. Initial models are focused on field generation by convection in the planet's fluid outer core. It was possible to show the generation of a strong, Earth-like field when the model assumed a uniform core-surface temperature and exceptionally high viscosities for the core fluid. Computations which incorporated more realistic parameter values yielded magnetic fields that were less Earth-like, but indicated that model refinements may ultimately lead to an accurate analytic model. Slight variations in the core-surface temperature, in the range of a few millikelvins, result in significant increases in convective flow and produce more realistic magnetic fields.

Formal definition

Dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid acts to maintain a magnetic field. This theory is used to explain the presence of anomalously long-lived magnetic fields in astrophysical bodies. The conductive fluid in the geodynamo is liquid iron in the outer core, and in the solar dynamo is ionized gas at the tachocline. Dynamo theory of astrophysical bodies uses magnetohydrodynamic equations to investigate how the fluid can continuously regenerate the magnetic field.

It was once believed that the dipole, which comprises much of the Earth's magnetic field and is misaligned along the rotation axis by 11.3 degrees, was caused by permanent magnetization of the materials in the earth. This means that dynamo theory was originally used to explain the Sun's magnetic field in its relationship with that of the Earth. However, this hypothesis, which was initially proposed by Joseph Larmor in 1919, has been modified due to extensive studies of magnetic secular variation, paleomagnetism (including polarity reversals), seismology, and the solar system's abundance of elements. Also, the application of the theories of Carl Friedrich Gauss to magnetic observations showed that Earth's magnetic field had an internal, rather than external, origin.

There are three requisites for a dynamo to operate:

• An electrically conductive fluid medium
• Kinetic energy provided by planetary rotation
• An internal energy source to drive convective motions within the fluid.

In the case of the Earth, the magnetic field is induced and constantly maintained by the convection of liquid iron in the outer core. A requirement for the induction of field is a rotating fluid. Rotation in the outer core is supplied by the Coriolis effect caused by the rotation of the Earth. The Coriolis force tends to organize fluid motions and electric currents into columns (also see Taylor columns) aligned with the rotation axis. Induction or generation of magnetic field is described by the induction equation:

$${\displaystyle \frac{\mathrm{\partial }\mathbf{B}}{\mathrm{\partial }t}=\eta {\mathrm{\nabla }}^2\mathbf{B}+\mathrm{\nabla }\times (\mathbf{u}\times \mathbf{B})}$$

where u is velocity, B is magnetic field, t is time, and ${\displaystyle \eta =1/(\sigma \mu )}$ is the magnetic diffusivity with ${\displaystyle \sigma }$ electrical conductivity and ${\displaystyle \mu }$ permeability. The ratio of the second term on the right hand side to the first term gives the magnetic Reynolds number, a dimensionless ratio of advection of magnetic field to diffusion.

Tidal heating supporting a dynamo

Tidal forces between celestial orbiting bodies cause friction that heats up their interiors. This is known as tidal heating, and it helps keep the interior in a liquid state. A liquid interior that can conduct electricity is required to produce a dynamo. Saturn's Enceladus and Jupiter's Io have enough tidal heating to liquify their inner cores, but they may not create a dynamo because they cannot conduct electricity. Mercury, despite its small size, has a magnetic field, because it has a conductive liquid core created by its iron composition and friction resulting from its highly elliptical orbit. It is theorized that the Moon once had a magnetic field, based on evidence from magnetized lunar rocks, due to its short-lived closer distance to Earth creating tidal heating. An orbit and rotation of a planet helps provide a liquid core, and supplements kinetic energy that supports a dynamo action.

Kinematic dynamo theory

In kinematic dynamo theory the velocity field is prescribed, instead of being a dynamic variable: The model makes no provision for the flow distorting in response to the magnetic field. This method cannot provide the time variable behaviour of a fully nonlinear chaotic dynamo, but can be used to study how magnetic field strength varies with the flow structure and speed.

Using Maxwell's equations simultaneously with the curl of Ohm's law, one can derive what is basically a linear eigenvalue equation for magnetic fields (B), which can be done when assuming that the magnetic field is independent from the velocity field. One arrives at a critical magnetic Reynolds number, above which the flow strength is sufficient to amplify the imposed magnetic field, and below which the magnetic field dissipates.

Practical measure of possible dynamos

The most functional feature of kinematic dynamo theory is that it can be used to test whether a velocity field is or is not capable of dynamo action. By experimentally applying a certain velocity field to a small magnetic field, one can observe whether the magnetic field tends to grow (or not) in response to the applied flow. If the magnetic field does grow, then the system is either capable of dynamo action or is a dynamo, but if the magnetic field does not grow, then it is simply referred to as “not a dynamo”.

An analogous method called the membrane paradigm is a way of looking at black holes that allows for the material near their surfaces to be expressed in the language of dynamo theory.

Spontaneous breakdown of a topological supersymmetry

Kinematic dynamo can be also viewed as the phenomenon of the spontaneous breakdown of the topological supersymmetry of the associated stochastic differential equation related to the flow of the background matter. Within stochastic supersymmetric theory, this supersymmetry is an intrinsic property of all stochastic differential equations, its interpretation is that the model’s phase space preserves continuity via continuous time flows. When the continuity of that flow spontaneously breaks down, the system is in the stochastic state of deterministic chaos. In other words, kinematic dynamo arises because of chaotic flow in the underlying background matter.

Nonlinear dynamo theory

The kinematic approximation becomes invalid when the magnetic field becomes strong enough to affect the fluid motions. In that case the velocity field becomes affected by the Lorentz force, and so the induction equation is no longer linear in the magnetic field. In most cases this leads to a quenching of the amplitude of the dynamo. Such dynamos are sometimes also referred to as hydromagnetic dynamos. Virtually all dynamos in astrophysics and geophysics are hydromagnetic dynamos.

The main idea of the theory is that any small magnetic field existing in the outer core creates currents in the moving fluid there due to Lorentz force. These currents create further magnetic field due to Ampere's law. With the fluid motion, the currents are carried in a way that the magnetic field gets stronger (as long as ${\displaystyle \mathbf{u}\cdot (\mathbf{J}\times \mathbf{B})}$ is negative). Thus a "seed" magnetic field can get stronger and stronger until it reaches some value that is related to existing non-magnetic forces.

Numerical models are used to simulate fully nonlinear dynamos. The following equations are used:

• The induction equation, presented above.
• Maxwell's equations for negligible electric field:
  $${\displaystyle \begin{array}{rl}& \mathrm{\nabla }\cdot \mathbf{B}=0\\ & \mathrm{\nabla }\times \mathbf{B}={\mu }_0\mathbf{J}\end{array}}$$

  
• The continuity equation for conservation of mass, for which the Boussinesq approximation is often used:
  $${\displaystyle \mathrm{\nabla }\cdot \mathbf{u}=0,}$$

  
• The Navier-Stokes equation for conservation of momentum, again in the same approximation, with the magnetic force and gravitation force as the external forces:
  $${\displaystyle \frac{D\mathbf{u}}{Dt}=-\frac{1}{{\rho }_0}\mathrm{\nabla }p+\nu {\mathrm{\nabla }}^2\mathbf{u}+{\rho }^{\prime }\mathbf{g}+2\mathbf{\Omega }\times \mathbf{u}+\mathbf{\Omega }\times \mathbf{\Omega }\times \mathbf{R}+\frac{1}{{\rho }_0}\mathbf{J}\times \mathbf{B},}$$

  
  where ${\displaystyle \nu }$ is the kinematic viscosity, ${\displaystyle {\rho }_0}$is the mean density and ${\displaystyle {\rho }^{\prime }}$ is the relative density perturbation that provides buoyancy (for thermal convection ${\displaystyle {\rho }^{\prime }=\alpha \mathrm{\Delta }T}$ where ${\displaystyle \alpha }$ is coefficient of thermal expansion), ${\displaystyle \mathrm{\Omega }}$ is the rotation rate of the Earth, and ${\displaystyle \mathbf{J}}$ is the electric current density.
• A transport equation, usually of heat (sometimes of light element concentration):
  $${\displaystyle \frac{\mathrm{\partial }T}{\mathrm{\partial }t}=\kappa {\mathrm{\nabla }}^{2}T+\epsilon }$$

  
  where T is temperature, ${\displaystyle \kappa =k/\rho c_p}$ is the thermal diffusivity with k thermal conductivity, ${\displaystyle c_p}$ heat capacity, and ${\displaystyle \rho }$ density, and ${\displaystyle \epsilon }$ is an optional heat source. Often the pressure is the dynamic pressure, with the hydrostatic pressure and centripetal potential removed.

These equations are then non-dimensionalized, introducing the non-dimensional parameters,

$${\displaystyle R_{\mathsf{a}}=\frac{g\alpha T{D}^3}{\nu \kappa },E=\frac{\nu }{\mathrm{\Omega }{D}^2},P_{\mathsf{r}}=\frac{\nu }{\kappa },P_{\mathsf{m}}=\frac{\nu }{\eta }}$$

where R_a is the Rayleigh number, E the Ekman number, P_r and P_m the Prandtl and magnetic Prandtl number. Magnetic field scaling is often in Elsasser number units ${\displaystyle B=(\rho \mathrm{\Omega }/\sigma {)}^{1/2}.}$

Energy conversion between magnetic and kinematic energy

The scalar product of the above form of Navier-Stokes equation with ${\displaystyle {\rho }_0\mathbf{u}}$ gives the rate of increase of kinetic energy density, ${\displaystyle \frac{1}{2}{\rho }_0{u}^{2}c}$, on the left-hand side. The last term on the right-hand side is then ${\displaystyle \mathbf{u}\cdot (\mathbf{J}\times \mathbf{B})}$, the local contribution to the kinetic energy due to Lorentz force.

The scalar product of the induction equation with $\frac{1}{{\mu }_0}\mathbf{B}$ gives the rate of increase of the magnetic energy density, ${\displaystyle \frac{1}{2}{\mu }_0{B}^2}$, on the left-hand side. The last term on the right-hand side is then $\frac{1}{{\mu }_0}\mathbf{B}\cdot \left(\mathrm{\nabla }\times \left(\mathbf{u}\times \mathbf{B}\right)\right).$ Since the equation is volume-integrated, this term is equivalent up to a boundary term (and with the double use of the scalar triple product identity) to $-\mathbf{u}\cdot \left(\frac{1}{{\mu }_0}\left(\mathrm{\nabla }\times \mathbf{B}\right)\times \mathbf{B}\right)=-\mathbf{u}\cdot \left(\mathbf{J}\times \mathbf{B}\right)$ (where one of Maxwell's equations was used). This is the local contribution to the magnetic energy due to fluid motion.

Thus the term ${\displaystyle -\mathbf{u}\cdot (\mathbf{J}\times \mathbf{B})}$ is the rate of transformation of kinetic energy to magnetic energy. This has to be non-negative at least in part of the volume, for the dynamo to produce magnetic field.^[19]

From the diagram above, it is not clear why this term should be positive. A simple argument can be based on consideration of net effects. To create the magnetic field, the net electric current must wrap around the axis of rotation of the planet. In that case, for the term to be positive, the net flow of conducting matter must be towards the axis of rotation. The diagram only shows a net flow from the poles to the equator. However mass conservation requires an additional flow from the equator toward the poles. If that flow was along the axis of rotation, that implies the circulation would be completed by a flow from the ones shown towards the axis of rotation, producing the desired effect.

Order of magnitude of the magnetic field created by Earth's dynamo

The above formula for the rate of conversion of kinetic energy to magnetic energy, is equivalent to a rate of work done by a force of ${\displaystyle \mathbf{J}\times \mathbf{B}}$ on the outer core matter, whose velocity is ${\displaystyle \mathbf{u}}$. This work is the result of non-magnetic forces acting on the fluid.

Of those, the gravitational force and the centrifugal force are conservative and therefore have no overall contribution to fluid moving in closed loops. Ekman number (defined above), which is the ratio between the two remaining forces, namely the viscosity and Coriolis force, is very low inside Earth's outer core, because its viscosity is low (1.2–1.5 ×10⁻² pascal-second) due to its liquidity.

Thus the main time-averaged contribution to the work is from Coriolis force, whose size is ${\displaystyle -2\rho \mathbf{\Omega }\times \mathbf{u},}$ though this quantity and ${\displaystyle \mathbf{J}\times \mathbf{B}}$ are related only indirectly and are not in general equal locally (thus they affect each other but not in the same place and time).

The current density J is itself the result of the magnetic field according to Ohm's law. Again, due to matter motion and current flow, this is not necessarily the field at the same place and time. However these relations can still be used to deduce orders of magnitude of the quantities in question.

In terms of order of magnitude, ${\displaystyle JB\sim \rho \mathrm{\Omega }u}$ and ${\displaystyle J\sim \sigma uB}$, giving ${\displaystyle \sigma u{B}^2\sim \rho \mathrm{\Omega }u,}$ or:

$${\displaystyle B\sim \sqrt{\frac{\rho \mathrm{\Omega }}{\sigma }}}$$

The exact ratio between both sides is the square root of Elsasser number.

Note that the magnetic field direction cannot be inferred from this approximation (at least not its sign) as it appears squared, and is, indeed, sometimes reversed, though in general it lies on a similar axis to that of ${\displaystyle \mathbf{\Omega }}$.

For earth outer core, ρ is approximately 10⁴ kg/m³,   Ω = 2π/day = 7.3×10⁻⁵/second   and   σ   is approximately   10⁷Ω⁻¹m⁻¹ . This gives   2.7×10⁻⁴ Tesla.

The magnetic field of a magnetic dipole has an inverse cubic dependence in distance, so its order of magnitude at the earth surface can be approximated by multiplying the above result with (R_{outer core}⁄R_Earth )³ = (2890⁄6370)³ = 0.093 , giving   2.5×10⁻⁵ Tesla, not far from the measured value of 3×10⁻⁵ Tesla at the equator.

Numerical models

A visual representation of the Glatzmaier model before dipole reversal

Broadly, models of the geodynamo attempt to produce magnetic fields consistent with observed data given certain conditions and equations as mentioned in the sections above. Implementing the magnetohydrodynamic equations successfully was of particular significance because they pushed dynamo models to self-consistency. Though geodynamo models are especially prevalent, dynamo models are not necessarily restricted to the geodynamo; solar and general dynamo models are also of interest. Studying dynamo models has utility in the field of geophysics as doing so can identify how various mechanisms form magnetic fields like those produced by astrophysical bodies like Earth and how they cause magnetic fields to exhibit certain features, such as pole reversals.

The equations used in numerical models of dynamo are highly complex. For decades, theorists were confined to two dimensional kinematic dynamo models described above, in which the fluid motion is chosen in advance and the effect on the magnetic field calculated. The progression from linear to nonlinear, three dimensional models of dynamo was largely hindered by the search for solutions to magnetohydrodynamic equations, which eliminate the need for many of the assumptions made in kinematic models and allow self-consistency.

A visual representation of the Glatzmaier model during dipole reversal

The first self-consistent dynamo models, ones that determine both the fluid motions and the magnetic field, were developed by two groups in 1995, one in Japan and one in the United States. The latter was made as a model with regards to the geodynamo and received significant attention because it successfully reproduced some of the characteristics of the Earth's field. Following this breakthrough, there was a large swell in development of reasonable, three dimensional dynamo models.

Though many self-consistent models now exist, there are significant differences among the models, both in the results they produce and the way they were developed. Given the complexity of developing a geodynamo model, there are many places where discrepancies can occur such as when making assumptions involving the mechanisms that provide energy for the dynamo, when choosing values for parameters used in equations, or when normalizing equations. In spite of the many differences that may occur, most models have shared features like clear axial dipoles. In many of these models, phenomena like secular variation and geomagnetic polarity reversals have also been successfully recreated.

Observations

A visual representation of the Glatzmaier model after dipole reversal

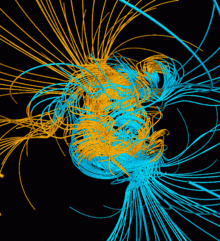
Many observations can be made from dynamo models. Models can be used to estimate how magnetic fields vary with time and can be compared to observed paleomagnetic data to find similarities between the model and the Earth. Due to the uncertainty of paleomagnetic observations, however, comparisons may not be entirely valid or useful. Simplified geodynamo models have shown relationships between the dynamo number (determined by variance in rotational rates in the outer core and mirror-asymmetric convection (e.g. when convection favors one direction in the north and the other in the south)) and magnetic pole reversals as well as found similarities between the geodynamo and the Sun's dynamo. In many models, it appears that magnetic fields have somewhat random magnitudes that follow a normal trend that average to zero. In addition to these observations, general observations about the mechanisms powering the geodynamo can be made based on how accurately the model reflects actual data collected from Earth.

Modern modelling

The complexity of dynamo modelling is so great that models of the geodynamo are limited by the current power of supercomputers, particularly because calculating the Ekman and Rayleigh number of the outer core is extremely difficult and requires a vast number of computations.

Many improvements have been proposed in dynamo modelling since the self-consistent breakthrough in 1995. One suggestion in studying the complex magnetic field changes is applying spectral methods to simplify computations. Ultimately, until considerable improvements in computer power are made, the methods for computing realistic dynamo models will have to be made more efficient, so making improvements in methods for computing the model is of high importance for the advancement of numerical dynamo modelling.

Notable people

• Stanislav I. Braginsky, research geophysicist

Nebular hypothesis

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Nebular_hypothesis

The nebular hypothesis is the most widely accepted model in the field of cosmogony to explain the formation and evolution of the Solar System (as well as other planetary systems). It suggests the Solar System is formed from gas and dust orbiting the Sun which clumped up together to form the planets. The theory was developed by Immanuel Kant and published in his Universal Natural History and Theory of the Heavens (1755) and then modified in 1796 by Pierre Laplace. Originally applied to the Solar System, the process of planetary system formation is now thought to be at work throughout the universe. The widely accepted modern variant of the nebular theory is the solar nebular disk model (SNDM) or solar nebular model. It offered explanations for a variety of properties of the Solar System, including the nearly circular and coplanar orbits of the planets, and their motion in the same direction as the Sun's rotation. Some elements of the original nebular theory are echoed in modern theories of planetary formation, but most elements have been superseded.

According to the nebular theory, stars form in massive and dense clouds of molecular hydrogen—giant molecular clouds (GMC). These clouds are gravitationally unstable, and matter coalesces within them to smaller denser clumps, which then rotate, collapse, and form stars. Star formation is a complex process, which always produces a gaseous protoplanetary disk (proplyd) around the young star. This may give birth to planets in certain circumstances, which are not well known. Thus the formation of planetary systems is thought to be a natural result of star formation. A Sun-like star usually takes approximately 1 million years to form, with the protoplanetary disk evolving into a planetary system over the next 10–100 million years.

The protoplanetary disk is an accretion disk that feeds the central star. Initially very hot, the disk later cools in what is known as the T Tauri star stage; here, formation of small dust grains made of rocks and ice is possible. The grains eventually may coagulate into kilometer-sized planetesimals. If the disk is massive enough, the runaway accretions begin, resulting in the rapid—100,000 to 300,000 years—formation of Moon- to Mars-sized planetary embryos. Near the star, the planetary embryos go through a stage of violent mergers, producing a few terrestrial planets. The last stage takes approximately 100 million to a billion years.

The formation of giant planets is a more complicated process. It is thought to occur beyond the frost line, where planetary embryos mainly are made of various types of ice. As a result, they are several times more massive than in the inner part of the protoplanetary disk. What follows after the embryo formation is not completely clear. Some embryos appear to continue to grow and eventually reach 5–10 Earth masses—the threshold value, which is necessary to begin accretion of the hydrogen–helium gas from the disk. The accumulation of gas by the core is initially a slow process, which continues for several million years, but after the forming protoplanet reaches about 30 Earth masses (M_🜨) it accelerates and proceeds in a runaway manner. Jupiter- and Saturn-like planets are thought to accumulate the bulk of their mass during only 10,000 years. The accretion stops when the gas is exhausted. The formed planets can migrate over long distances during or after their formation. Ice giants such as Uranus and Neptune are thought to be failed cores, which formed too late when the disk had almost disappeared.

History

Main article: History of Solar System formation and evolution hypotheses

There is evidence that Emanuel Swedenborg first proposed parts of the nebular theory in 1734. Immanuel Kant, familiar with Swedenborg's work, developed the theory further in 1755, publishing his own Universal Natural History and Theory of the Heavens, wherein he argued that gaseous clouds (nebulae) slowly rotate, gradually collapse and flatten due to gravity, eventually forming stars and planets.

Pierre-Simon Laplace independently developed and proposed a similar model in 1796 in his Exposition du systeme du monde. He envisioned that the Sun originally had an extended hot atmosphere throughout the volume of the Solar System. His theory featured a contracting and cooling protosolar cloud—the protosolar nebula. As this cooled and contracted, it flattened and spun more rapidly, throwing off (or shedding) a series of gaseous rings of material; and according to him, the planets condensed from this material. His model was similar to Kant's, except more detailed and on a smaller scale. While the Laplacian nebular model dominated in the 19th century, it encountered a number of difficulties. The main problem involved angular momentum distribution between the Sun and planets. The planets have 99% of the angular momentum, and this fact could not be explained by the nebular model. As a result, astronomers largely abandoned this theory of planet formation at the beginning of the 20th century.

A major critique came during the 19th century from James Clerk Maxwell (1831–1879), who maintained that different rotation between the inner and outer parts of a ring could not allow condensation of material. Astronomer Sir David Brewster also rejected Laplace, writing in 1876 that "those who believe in the Nebular Theory consider it as certain that our Earth derived its solid matter and its atmosphere from a ring thrown from the Solar atmosphere, which afterwards contracted into a solid terraqueous sphere, from which the Moon was thrown off by the same process". He argued that under such view, "the Moon must necessarily have carried off water and air from the watery and aerial parts of the Earth and must have an atmosphere". Brewster claimed that Sir Isaac Newton's religious beliefs had previously considered nebular ideas as tending to atheism, and quoted him as saying that "the growth of new systems out of old ones, without the mediation of a Divine power, seemed to him apparently absurd".

The perceived deficiencies of the Laplacian model stimulated scientists to find a replacement for it. During the 20th century many theories addressed the issue, including the planetesimal theory of Thomas Chamberlin and Forest Moulton (1901), the tidal model of James Jeans (1917), the accretion model of Otto Schmidt (1944), the protoplanet theory of William McCrea (1960) and finally the capture theory of Michael Woolfson. In 1978 Andrew Prentice resurrected the initial Laplacian ideas about planet formation and developed the modern Laplacian theory. None of these attempts proved completely successful, and many of the proposed theories were descriptive.

The birth of the modern widely accepted theory of planetary formation—the solar nebular disk model (SNDM)—can be traced to the Soviet astronomer Victor Safronov. His 1969 book Evolution of the protoplanetary cloud and formation of the Earth and the planets, which was translated to English in 1972, had a long-lasting effect on the way scientists think about the formation of the planets. In this book almost all major problems of the planetary formation process were formulated and some of them solved. Safronov's ideas were further developed in the works of George Wetherill, who discovered runaway accretion. While originally applied only to the Solar System, the SNDM was subsequently thought by theorists to be at work throughout the Universe; as of 1 October 2023 astronomers have discovered 5,506 extrasolar planets in our galaxy.

Solar nebular model: achievements and problems

Achievements

Dusty disks surrounding nearby young stars in greater detail.

The star formation process naturally results in the appearance of accretion disks around young stellar objects. At the age of about 1 million years, 100% of stars may have such disks. This conclusion is supported by the discovery of the gaseous and dusty disks around protostars and T Tauri stars as well as by theoretical considerations. Observations of these disks show that the dust grains inside them grow in size on short (thousand-year) time scales, producing 1 centimeter sized particles.

The accretion process, by which 1 km planetesimals grow into 1,000 km sized bodies, is well understood now. This process develops inside any disk where the number density of planetesimals is sufficiently high, and proceeds in a runaway manner. Growth later slows and continues as oligarchic accretion. The end result is formation of planetary embryos of varying sizes, which depend on the distance from the star. Various simulations have demonstrated that the merger of embryos in the inner part of the protoplanetary disk leads to the formation of a few Earth-sized bodies. Thus the origin of terrestrial planets is now considered to be an almost solved problem.

Current issues

The physics of accretion disks encounters some problems. The most important one is how the material, which is accreted by the protostar, loses its angular momentum. One possible explanation suggested by Hannes Alfvén was that angular momentum was shed by the solar wind during its T Tauri star phase. The momentum is transported to the outer parts of the disk by viscous stresses. Viscosity is generated by macroscopic turbulence, but the precise mechanism that produces this turbulence is not well understood. Another possible process for shedding angular momentum is magnetic braking, where the spin of the star is transferred into the surrounding disk via that star's magnetic field. The main processes responsible for the disappearance of the gas in disks are viscous diffusion and photo-evaporation.

Multiple star system AS 205.

The formation of planetesimals is the biggest unsolved problem in the nebular disk model. How 1 cm sized particles coalesce into 1 km planetesimals is a mystery. This mechanism appears to be the key to the question as to why some stars have planets, while others have nothing around them, not even dust belts.

The formation timescale of giant planets is also an important problem. Old theories were unable to explain how their cores could form fast enough to accumulate significant amounts of gas from the quickly disappearing protoplanetary disk. The mean lifetime of the disks, which is less than ten million (10⁷) years, appeared to be shorter than the time necessary for the core formation. Much progress has been done to solve this problem and current models of giant planet formation are now capable of forming Jupiter (or more massive planets) in about 4 million years or less, well within the average lifetime of gaseous disks.

Another potential problem of giant planet formation is their orbital migration. Some calculations show that interaction with the disk can cause rapid inward migration, which, if not stopped, results in the planet reaching the "central regions still as a sub-Jovian object." More recent calculations indicate that disk evolution during migration can mitigate this problem.

Formation of stars and protoplanetary disks

Protostars

Main article: Protostar

The visible-light (left) and infrared (right) views of the Trifid Nebula—a giant star-forming cloud of gas and dust located 5,400 light-years away in the constellation Sagittarius

Stars are thought to form inside giant clouds of cold molecular hydrogen—giant molecular clouds roughly 300,000 times the mass of the Sun (M_☉) and 20 parsecs in diameter. Over millions of years, giant molecular clouds are prone to collapse and fragmentation. These fragments then form small, dense cores, which in turn collapse into stars. The cores range in mass from a fraction to several times that of the Sun and are called protostellar (protosolar) nebulae. They possess diameters of 0.01–0.1 pc (2,000–20,000 AU) and a particle number density of roughly 10,000 to 100,000 cm⁻³.

The initial collapse of a solar-mass protostellar nebula takes around 100,000 years. Every nebula begins with a certain amount of angular momentum. Gas in the central part of the nebula, with relatively low angular momentum, undergoes fast compression and forms a hot hydrostatic (not contracting) core containing a small fraction of the mass of the original nebula. This core forms the seed of what will become a star. As the collapse continues, conservation of angular momentum means that the rotation of the infalling envelope accelerates, which largely prevents the gas from directly accreting onto the central core. The gas is instead forced to spread outwards near its equatorial plane, forming a disk, which in turn accretes onto the core. The core gradually grows in mass until it becomes a young hot protostar. At this stage, the protostar and its disk are heavily obscured by the infalling envelope and are not directly observable. In fact the remaining envelope's opacity is so high that even millimeter-wave radiation has trouble escaping from inside it. Such objects are observed as very bright condensations, which emit mainly millimeter-wave and submillimeter-wave radiation. They are classified as spectral Class 0 protostars. The collapse is often accompanied by bipolar outflows—jets—that emanate along the rotational axis of the inferred disk. The jets are frequently observed in star-forming regions (see Herbig–Haro (HH) objects). The luminosity of the Class 0 protostars is high — a solar-mass protostar may radiate at up to 100 solar luminosities. The source of this energy is gravitational collapse, as their cores are not yet hot enough to begin nuclear fusion.

Infrared image of the molecular outflow from an otherwise hidden newborn star HH 46/47

As the infall of its material onto the disk continues, the envelope eventually becomes thin and transparent and the young stellar object (YSO) becomes observable, initially in far-infrared light and later in the visible. Around this time the protostar begins to fuse deuterium. If the protostar is sufficiently massive (above 80 Jupiter masses (M_J)), hydrogen fusion follows. Otherwise, if its mass is too low, the object becomes a brown dwarf. This birth of a new star occurs approximately 100,000 years after the collapse begins. Objects at this stage are known as Class I protostars, which are also called young T Tauri stars, evolved protostars, or young stellar objects. By this time the forming star has already accreted much of its mass: the total mass of the disk and remaining envelope does not exceed 10–20% of the mass of the central YSO.

At the next stage the envelope completely disappears, having been gathered up by the disk, and the protostar becomes a classical T Tauri star. This happens after about 1 million years. The mass of the disk around a classical T Tauri star is about 1–3% of the stellar mass, and it is accreted at a rate of 10⁻⁷ to 10⁻⁹ M_☉ per year. A pair of bipolar jets is usually present as well. The accretion explains all peculiar properties of classical T Tauri stars: strong flux in the emission lines (up to 100% of the intrinsic luminosity of the star), magnetic activity, photometric variability and jets. The emission lines actually form as the accreted gas hits the "surface" of the star, which happens around its magnetic poles. The jets are byproducts of accretion: they carry away excessive angular momentum. The classical T Tauri stage lasts about 10 million years. The disk eventually disappears due to accretion onto the central star, planet formation, ejection by jets and photoevaporation by UV-radiation from the central star and nearby stars. As a result, the young star becomes a weakly lined T Tauri star, which slowly, over hundreds of millions of years, evolves into an ordinary Sun-like star.

Protoplanetary disks

See also: Protoplanetary disk and planetesimal

Debris disks detected in HST archival images of young stars, HD 141943 and HD 191089, using improved imaging processes (24 April 2014).

Under certain circumstances the disk, which can now be called protoplanetary, may give birth to a planetary system. Protoplanetary disks have been observed around a very high fraction of stars in young star clusters. They exist from the beginning of a star's formation, but at the earliest stages are unobservable due to the opacity of the surrounding envelope. The disk of a Class 0 protostar is thought to be massive and hot. It is an accretion disk, which feeds the central protostar. The temperature can easily exceed 400 K inside 5 AU and 1,000 K inside 1 AU. The heating of the disk is primarily caused by the viscous dissipation of turbulence in it and by the infall of the gas from the nebula. The high temperature in the inner disk causes most of the volatile material—water, organics, and some rocks—to evaporate, leaving only the most refractory elements like iron. The ice can survive only in the outer part of the disk.

A protoplanetary disk forming in the Orion Nebula

The main problem in the physics of accretion disks is the generation of turbulence and the mechanism responsible for the high effective viscosity. The turbulent viscosity is thought to be responsible for the transport of the mass to the central protostar and momentum to the periphery of the disk. This is vital for accretion, because the gas can be accreted by the central protostar only if it loses most of its angular momentum, which must be carried away by the small part of the gas drifting outwards. The result of this process is the growth of both the protostar and of the disk radius, which can reach 1,000 AU if the initial angular momentum of the nebula is large enough. Large disks are routinely observed in many star-forming regions such as the Orion nebula.

The lifespan of the accretion disks is about 10 million years. By the time the star reaches the classical T-Tauri stage, the disk becomes thinner and cools. Less volatile materials start to condense close to its center, forming 0.1–1 μm dust grains that contain crystalline silicates. The transport of the material from the outer disk can mix these newly formed dust grains with primordial ones, which contain organic matter and other volatiles. This mixing can explain some peculiarities in the composition of Solar System bodies such as the presence of interstellar grains in primitive meteorites and refractory inclusions in comets.

Various planet formation processes, including exocomets and other planetesimals, around Beta Pictoris, a very young type A V star (NASA artist's conception).

Dust particles tend to stick to each other in the dense disk environment, leading to the formation of larger particles up to several centimeters in size. The signatures of the dust processing and coagulation are observed in the infrared spectra of the young disks. Further aggregation can lead to the formation of planetesimals measuring 1 km across or larger, which are the building blocks of planets. Planetesimal formation is another unsolved problem of disk physics, as simple sticking becomes ineffective as dust particles grow larger.

One hypothesis is formation by gravitational instability. Particles several centimeters in size or larger slowly settle near the middle plane of the disk, forming a very thin—less than 100 km—and dense layer. This layer is gravitationally unstable and may fragment into numerous clumps, which in turn collapse into planetesimals. However, the differing velocities of the gas disk and the solids near the mid-plane can generate turbulence which prevents the layer from becoming thin enough to fragment due to gravitational instability. This may limit the formation of planetesimals via gravitational instabilities to specific locations in the disk where the concentration of solids is enhanced.

Another possible mechanism for the formation of planetesimals is the streaming instability in which the drag felt by particles orbiting through gas creates a feedback effect causing the growth of local concentrations. These local concentrations push back on the gas creating a region where the headwind felt by the particles is smaller. The concentration is thus able to orbit faster and undergoes less radial drift. Isolated particles join these concentrations as they are overtaken or as they drift inward causing it to grow in mass. Eventually these concentrations form massive filaments which fragment and undergo gravitational collapse forming planetesimals the size of the larger asteroids.

Planetary formation can also be triggered by gravitational instability within the disk itself, which leads to its fragmentation into clumps. Some of them, if they are dense enough, will collapse, which can lead to rapid formation of gas giant planets and even brown dwarfs on the timescale of 1,000 years. If these clumps migrate inward as the collapse proceeds tidal forces from the star can result in a significant mass loss leaving behind a smaller body. However it is only possible in massive disks—more massive than 0.3 M_☉. In comparison, typical disk masses are 0.01–0.03 M_☉. Because the massive disks are rare, this mechanism of planet formation is thought to be infrequent. On the other hand, it may play a major role in the formation of brown dwarfs.

Asteroid collision—building planets (artist concept).

The ultimate dissipation of protoplanetary disks is triggered by a number of different mechanisms. The inner part of the disk is either accreted by the star or ejected by the bipolar jets, whereas the outer part can evaporate under the star's powerful UV radiation during the T Tauri stage or by nearby stars. The gas in the central part can either be accreted or ejected by the growing planets, while the small dust particles are ejected by the radiation pressure of the central star. What is finally left is either a planetary system, a remnant disk of dust without planets, or nothing, if planetesimals failed to form.

Because planetesimals are so numerous, and spread throughout the protoplanetary disk, some survive the formation of a planetary system. Asteroids are understood to be left-over planetesimals, gradually grinding each other down into smaller and smaller bits, while comets are typically planetesimals from the farther reaches of a planetary system. Meteorites are samples of planetesimals that reach a planetary surface, and provide a great deal of information about the formation of the Solar System. Primitive-type meteorites are chunks of shattered low-mass planetesimals, where no thermal differentiation took place, while processed-type meteorites are chunks from shattered massive planetesimals. Interstellar objects could have been captured, and become part of the young Solar system.

Formation of planets

Rocky planets

According to the solar nebular disk model, rocky planets form in the inner part of the protoplanetary disk, within the frost line, where the temperature is high enough to prevent condensation of water ice and other substances into grains. This results in coagulation of purely rocky grains and later in the formation of rocky planetesimals. Such conditions are thought to exist in the inner 3–4 AU part of the disk of a Sun-like star.

After small planetesimals—about 1 km in diameter—have formed by one way or another, runaway accretion begins. It is called runaway because the mass growth rate is proportional to R⁴~M^4/3, where R and M are the radius and mass of the growing body, respectively. The specific (divided by mass) growth accelerates as the mass increases. This leads to the preferential growth of larger bodies at the expense of smaller ones. The runaway accretion lasts between 10,000 and 100,000 years and ends when the largest bodies exceed approximately 1,000 km in diameter. Slowing of the accretion is caused by gravitational perturbations by large bodies on the remaining planetesimals. In addition, the influence of larger bodies stops further growth of smaller bodies.

The next stage is called oligarchic accretion. It is characterized by the dominance of several hundred of the largest bodies—oligarchs, which continue to slowly accrete planetesimals. No body other than the oligarchs can grow. At this stage the rate of accretion is proportional to R², which is derived from the geometrical cross-section of an oligarch. The specific accretion rate is proportional to M^−1/3; and it declines with the mass of the body. This allows smaller oligarchs to catch up to larger ones. The oligarchs are kept at the distance of about 10·H_r (H_r=a(1-e)(M/3M_s)^1/3 is the Hill radius, where a is the semimajor axis, e is the orbital eccentricity, and M_s is the mass of the central star) from each other by the influence of the remaining planetesimals. Their orbital eccentricities and inclinations remain small. The oligarchs continue to accrete until planetesimals are exhausted in the disk around them. Sometimes nearby oligarchs merge. The final mass of an oligarch depends on the distance from the star and surface density of planetesimals and is called the isolation mass. For the rocky planets it is up to 0.1 M_🜨, or one Mars mass. The final result of the oligarchic stage is the formation of about 100 Moon- to Mars-sized planetary embryos uniformly spaced at about 10·H_r. They are thought to reside inside gaps in the disk and to be separated by rings of remaining planetesimals. This stage is thought to last a few hundred thousand years.

The last stage of rocky planet formation is the merger stage. It begins when only a small number of planetesimals remains and embryos become massive enough to perturb each other, which causes their orbits to become chaotic. During this stage embryos expel remaining planetesimals, and collide with each other. The result of this process, which lasts for 10 to 100 million years, is the formation of a limited number of Earth-sized bodies. Simulations show that the number of surviving planets is on average from 2 to 5. In the Solar System they may be represented by Earth and Venus. Formation of both planets required merging of approximately 10–20 embryos, while an equal number of them were thrown out of the Solar System. Some of the embryos, which originated in the asteroid belt, are thought to have brought water to Earth. Mars and Mercury may be regarded as remaining embryos that survived that rivalry. Rocky planets, which have managed to coalesce, settle eventually into more or less stable orbits, explaining why planetary systems are generally packed to the limit; or, in other words, why they always appear to be at the brink of instability.

Giant planets

The dust disk around Fomalhaut—the brightest star in Piscis Austrinus constellation. Asymmetry of the disk may be caused by a giant planet (or planets) orbiting the star.

The formation of giant planets is an outstanding problem in the planetary sciences. In the framework of the solar nebular model two theories for their formation exist. The first one is the disk instability model, where giant planets form in the massive protoplanetary disks as a result of its gravitational fragmentation (see above). The second possibility is the core accretion model, which is also known as the nucleated instability model. The latter scenario is thought to be the most promising one, because it can explain the formation of the giant planets in relatively low-mass disks (less than 0.1 M_☉). In this model giant planet formation is divided into two stages: a) accretion of a core of approximately 10 M_🜨 and b) accretion of gas from the protoplanetary disk. Either method may also lead to the creation of brown dwarfs. Searches as of 2011 have found that core accretion is likely the dominant formation mechanism.

Giant planet core formation is thought to proceed roughly along the lines of the terrestrial planet formation. It starts with planetesimals that undergo runaway growth, followed by the slower oligarchic stage. Hypotheses do not predict a merger stage, due to the low probability of collisions between planetary embryos in the outer part of planetary systems. An additional difference is the composition of the planetesimals, which in the case of giant planets form beyond the so-called frost line and consist mainly of ice—the ice to rock ratio is about 4 to 1. This enhances the mass of planetesimals fourfold. However, the minimum mass nebula capable of terrestrial planet formation can only form 1–2 M_🜨 cores at the distance of Jupiter (5 AU) within 10 million years. The latter number represents the average lifetime of gaseous disks around Sun-like stars. The proposed solutions include enhanced mass of the disk—a tenfold increase would suffice; protoplanet migration, which allows the embryo to accrete more planetesimals; and finally accretion enhancement due to gas drag in the gaseous envelopes of the embryos. Some combination of the above-mentioned ideas may explain the formation of the cores of gas giant planets such as Jupiter and perhaps even Saturn. The formation of planets like Uranus and Neptune is more problematic, since no theory has been capable of providing for the in situ formation of their cores at the distance of 20–30 AU from the central star. One hypothesis is that they initially accreted in the Jupiter-Saturn region, then were scattered and migrated to their present location. Another possible solution is the growth of the cores of the giant planets via pebble accretion. In pebble accretion objects between a cm and a meter in diameter falling toward a massive body are slowed enough by gas drag for them to spiral toward it and be accreted. Growth via pebble accretion may be as much as 1000 times faster than by the accretion of planetesimals.

Once the cores are of sufficient mass (5–10 M_🜨), they begin to gather gas from the surrounding disk. Initially it is a slow process, increasing the core masses up to 30 M_🜨 in a few million years. After that, the accretion rates increase dramatically and the remaining 90% of the mass is accumulated in approximately 10,000 years. The accretion of gas stops when the supply from the disk is exhausted. This happens gradually, due to the formation of a density gap in the protoplanetary disk and to disk dispersal. In this model ice giants—Uranus and Neptune—are failed cores that began gas accretion too late, when almost all gas had already disappeared. The post-runaway-gas-accretion stage is characterized by migration of the newly formed giant planets and continued slow gas accretion. Migration is caused by the interaction of the planet sitting in the gap with the remaining disk. It stops when the protoplanetary disk disappears or when the end of the disk is attained. The latter case corresponds to the so-called hot Jupiters, which are likely to have stopped their migration when they reached the inner hole in the protoplanetary disk.

In this artist's conception, a planet spins through a clearing (gap) in a nearby star's dusty, planet-forming disc.

Giant planets can significantly influence terrestrial planet formation. The presence of giants tends to increase eccentricities and inclinations (see Kozai mechanism) of planetesimals and embryos in the terrestrial planet region (inside 4 AU in the Solar System). If giant planets form too early, they can slow or prevent inner planet accretion. If they form near the end of the oligarchic stage, as is thought to have happened in the Solar System, they will influence the merges of planetary embryos, making them more violent. As a result, the number of terrestrial planets will decrease and they will be more massive. In addition, the size of the system will shrink, because terrestrial planets will form closer to the central star. The influence of giant planets in the Solar System, particularly that of Jupiter, is thought to have been limited because they are relatively remote from the terrestrial planets.

The region of a planetary system adjacent to the giant planets will be influenced in a different way. In such a region, eccentricities of embryos may become so large that the embryos pass close to a giant planet, which may cause them to be ejected from the system. If all embryos are removed, then no planets will form in this region. An additional consequence is that a huge number of small planetesimals will remain, because giant planets are incapable of clearing them all out without the help of embryos. The total mass of remaining planetesimals will be small, because cumulative action of the embryos before their ejection and giant planets is still strong enough to remove 99% of the small bodies. Such a region will eventually evolve into an asteroid belt, which is a full analog of the asteroid belt in the Solar System, located from 2 to 4 AU from the Sun.

Exoplanets

Thousands of exoplanets have been identified in the last twenty years, with, at the very least, billions more, within our observable universe, yet to be discovered. The orbits of many of these planets and systems of planets differ significantly from the planets in the Solar System. The exoplanets discovered include hot-Jupiters, warm-Jupiters, super-Earths, and systems of tightly packed inner planets.

The hot-Jupiters and warm-Jupiters are thought to have migrated to their current orbits during or following their formation. A number of possible mechanisms for this migration have been proposed. Type I or Type II migration could smoothly decrease the semimajor axis of the planet's orbit resulting in a warm- or hot-Jupiter. Gravitational scattering by other planets onto eccentric orbits with a perihelion near the star followed by the circularization of its orbit due to tidal interactions with the star can leave a planet on a close orbit. If a massive companion planet or star on an inclined orbit was present an exchange of inclination for eccentricity via the Kozai mechanism raising eccentricities and lowering perihelion followed by circularization can also result in a close orbit. Many of the Jupiter-sized planets have eccentric orbits which may indicate that gravitational encounters occurred between the planets, although migration while in resonance can also excite eccentricities. The in situ growth of hot Jupiters from closely orbiting super Earths has also been proposed. The cores in this hypothesis could have formed locally or at a greater distance and migrated close to the star.

Super-Earths and other closely orbiting planets are thought to have either formed in situ or ex situ, that is, to have migrated inward from their initial locations. The in situ formation of closely orbiting super-Earths would require a massive disk, the migration of planetary embryos followed by collisions and mergers, or the radial drift of small solids from farther out in the disk. The migration of the super-Earths, or the embryos that collided to form them, is likely to have been Type I due to their smaller mass. The resonant orbits of some of the exoplanet systems indicates that some migration occurred in these systems, while the spacing of the orbits in many of the other systems not in resonance indicates that an instability likely occurred in those systems after the dissipation of the gas disk. The absence of Super-Earths and closely orbiting planets in the Solar System may be due to the previous formation of Jupiter blocking their inward migration.

The amount of gas a super-Earth that formed in situ acquires may depend on when the planetary embryos merged due to giant impacts relative to the dissipation of the gas disk. If the mergers happen after the gas disk dissipates terrestrial planets can form, if in a transition disk a super-Earth with a gas envelope containing a few percent of its mass may form. If the mergers happen too early runaway gas accretion may occur leading to the formation of a gas giant. The mergers begin when the dynamical friction due to the gas disk becomes insufficient to prevent collisions, a process that will begin earlier in a higher metallicity disk. Alternatively gas accretion may be limited due to the envelopes not being in hydrostatic equilibrium, instead gas may flow through the envelope slowing its growth and delaying the onset of runaway gas accretion until the mass of the core reaches 15 Earth masses.

Meaning of accretion

Use of the term "accretion disk" for the protoplanetary disk leads to confusion over the planetary accretion process. The protoplanetary disk is sometimes referred to as an accretion disk, because while the young T Tauri-like protostar is still contracting, gaseous material may still be falling onto it, accreting on its surface from the disk's inner edge. In an accretion disk, there is a net flux of mass from larger radii toward smaller radii.

However, that meaning should not be confused with the process of accretion forming the planets. In this context, accretion refers to the process of cooled, solidified grains of dust and ice orbiting the protostar in the protoplanetary disk, colliding and sticking together and gradually growing, up to and including the high-energy collisions between sizable planetesimals.

In addition, the giant planets probably had accretion disks of their own, in the first meaning of the word. The clouds of captured hydrogen and helium gas contracted, spun up, flattened, and deposited gas onto the surface of each giant protoplanet, while solid bodies within that disk accreted into the giant planet's regular moons.

Atomic and molecular astrophysics

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Atomic_and_molecular_astrophysics

Within a few million years the light from bright stars will have boiled away this molecular cloud of gas and dust. The cloud has broken off from the Carina Nebula. Newly formed stars are visible nearby, their images reddened by blue light being preferentially scattered by the pervasive dust. This image spans about two light years and was taken by the orbiting Hubble Space Telescope in 1999.

Atomic astrophysics is concerned with performing atomic physics calculations that will be useful to astronomers and using atomic data to interpret astronomical observations. Atomic physics plays a key role in astrophysics as astronomers' only information about a particular object comes through the light that it emits, and this light arises through atomic transitions.

Molecular astrophysics, developed into a rigorous field of investigation by theoretical astrochemist Alexander Dalgarno beginning in 1967, concerns the study of emission from molecules in space. There are 110 currently known interstellar molecules. These molecules have large numbers of observable transitions. Lines may also be observed in absorption—for example the highly redshifted lines seen against the gravitationally lensed quasar PKS1830-211. High energy radiation, such as ultraviolet light, can break the molecular bonds which hold atoms in molecules. In general then, molecules are found in cool astrophysical environments. The most massive objects in our galaxy are giant clouds of molecules and dust known as giant molecular clouds. In these clouds, and smaller versions of them, stars and planets are formed. One of the primary fields of study of molecular astrophysics is star and planet formation. Molecules may be found in many environments, however, from stellar atmospheres to those of planetary satellites. Most of these locations are relatively cool, and molecular emission is most easily studied via photons emitted when the molecules make transitions between low rotational energy states. One molecule, composed of the abundant carbon and oxygen atoms, and very stable against dissociation into atoms, is carbon monoxide (CO). The wavelength of the photon emitted when the CO molecule falls from its lowest excited state to its zero energy, or ground, state is 2.6mm, or 115 gigahertz. This frequency is a thousand times higher than typical FM radio frequencies. At these high frequencies, molecules in the Earth's atmosphere can block transmissions from space, and telescopes must be located in dry (water is an important atmospheric blocker), high sites. Radio telescopes must have very accurate surfaces to produce high fidelity images.

On February 21, 2014, NASA announced a greatly upgraded database for tracking polycyclic aromatic hydrocarbons (PAHs) in the universe. According to scientists, more than 20% of the carbon in the universe may be associated with PAHs, possible starting materials for the formation of life. PAHs seem to have been formed shortly after the Big Bang, are widespread throughout the universe, and are associated with new stars and exoplanets.