Black hole information paradox

From Wikipedia, the free encyclopedia

 

Artist's representation of a black hole

The black hole information paradox^[1] is a puzzle resulting from the combination of quantum mechanics and general relativity. Calculations suggest that physical information could permanently disappear in a black hole, allowing many physical states to devolve into the same state. This is controversial because it violates a core precept of modern physics—that in principle the value of a wave function of a physical system at one point in time should determine its value at any other time.^[2][3] A fundamental postulate of the Copenhagen interpretation of quantum mechanics is that complete information about a system is encoded in its wave function up to when the wave function collapses. The evolution of the wave function is determined by a unitary operator, and unitarity implies that information is conserved in the quantum sense.

Relevant principles

There are two main principles in play:^{[citation needed]}

• Quantum determinism means that given a present wave function, its future changes are uniquely determined by the evolution operator.
• Reversibility refers to the fact that the evolution operator has an inverse, meaning that the past wave functions are similarly unique.

The combination of the two means that information must always be preserved.

Starting in the mid-1970s, Stephen Hawking and Jacob Bekenstein put forward theoretical arguments based on general relativity and quantum field theory that not only appeared to be inconsistent with information conservation but were not accounting for the information loss and state no reason for it. Specifically, Hawking's calculations^[4] indicated that black hole evaporation via Hawking radiation does not preserve information. Today, many physicists believe that the holographic principle (specifically the AdS/CFT duality) demonstrates that Hawking's conclusion was incorrect, and that information is in fact preserved.^[5] In 2004 Hawking himself conceded a bet he had made, agreeing that black hole evaporation does in fact preserve information.

Hawking radiation

The Penrose diagram of a black hole which forms, and then completely evaporates away. Information falling into it will hit the singularity.^{[clarification needed]} Time shown on vertical axis from bottom to top; space shown on horizontal axis from left (radius zero) to right (growing radius).

In 1973–75, Stephen Hawking and Jacob Bekenstein showed that black holes should slowly radiate away energy, which poses a problem. From the no-hair theorem, one would expect the Hawking radiation to be completely independent of the material entering the black hole. Nevertheless, if the material entering the black hole were a pure quantum state, the transformation of that state into the mixed state of Hawking radiation would destroy information about the original quantum state. This violates Liouville's theorem and presents a physical paradox.^{[citation needed]}

More precisely, if there is an entangled pure state, and one part of the entangled system is thrown into the black hole while keeping the other part outside, the result is a mixed state after the partial trace is taken into the interior of the black hole. But since everything within the interior of the black hole will hit the singularity within a finite time, the part which is traced over partially might disappear completely from the physical system.^{[citation needed]}

Hawking remained convinced that the equations of black-hole thermodynamics together with the no-hair theorem led to the conclusion that quantum information may be destroyed. This annoyed many physicists, notably John Preskill, who bet Hawking and Kip Thorne in 1997 that information was not lost in black holes. The implications that Hawking had opened led to a "battle" where Leonard Susskind and Gerard 't Hooft publicly 'declared war' on Hawking's solution, with Susskind publishing a popular book, The Black Hole War, about the debate in 2008. (The book carefully notes that the 'war' was purely a scientific one, and that at a personal level, the participants remained friends.^[6]) The solution to the problem that concluded the battle is the holographic principle, which was first proposed by 't Hooft but was given a precise string theory interpretation by Susskind. With this, "Susskind quashes Hawking in quarrel over quantum quandary".^[7]

There are various ideas about how the paradox is solved. Since the 1997 proposal of the AdS/CFT correspondence, the predominant belief among physicists is that information is preserved and that Hawking radiation is not precisely thermal but receives quantum corrections.^{[clarification needed]} Other possibilities include the information being contained in a Planckian remnant left over at the end of Hawking radiation or a modification of the laws of quantum mechanics to allow for non-unitary time evolution.^{[citation needed]}

In July 2004, Stephen Hawking published a paper presenting a theory that quantum perturbations of the event horizon could allow information to escape from a black hole, which would resolve the information paradox.^[8] His argument assumes the unitarity of the AdS/CFT correspondence which implies that an AdS black hole that is dual to a thermal conformal field theory. When announcing his result, Hawking also conceded the 1997 bet, paying Preskill with a baseball encyclopedia "from which information can be retrieved at will."^{[citation needed]}

According to Roger Penrose, loss of unitarity in quantum systems is not a problem: quantum measurements are by themselves already non-unitary. Penrose claims that quantum systems will in fact no longer evolve unitarily as soon as gravitation comes into play, precisely as in black holes. The Conformal Cyclic Cosmology advocated by Penrose critically depends on the condition that information is in fact lost in black holes. This new cosmological model might in future be tested experimentally by detailed analysis of the cosmic microwave background radiation (CMB): if true the CMB should exhibit circular patterns with slightly lower or slightly higher temperatures. In November 2010, Penrose and V. G. Gurzadyan announced they had found evidence of such circular patterns, in data from the Wilkinson Microwave Anisotropy Probe (WMAP) corroborated by data from the BOOMERanG experiment.^[9] The significance of the findings was subsequently debated by others.^{[clarification needed]}

Postulated solutions

• Information is irretrievably lost^[10][11]

  Advantage: Seems to be a direct consequence of relatively non-controversial calculation based on semiclassical gravity.

  Disadvantage: Violates unitarity. (Banks, Susskind and Peskin argued that it also violates energy-momentum conservation or locality, but the argument does not seem to be correct for systems with a large number of degrees of freedom.^[12])

• Information gradually leaks out during the black-hole evaporation^[10][11]

  Advantage: Intuitively appealing because it qualitatively resembles information recovery in a classical process of burning.

  Disadvantage: Requires a large deviation from classical and semiclassical gravity (which do not allow information to leak out from the black hole) even for macroscopic black holes for which classical and semiclassical approximations are expected to be good approximations.

• Information suddenly escapes out during the final stage of black-hole evaporation^[10][11]

  Advantage: A significant deviation from classical and semiclassical gravity is needed only in the regime in which the effects of quantum gravity are expected to dominate.

  Disadvantage: Just before the sudden escape of information, a very small black hole must be able to store an arbitrary amount of information, which violates the Bekenstein bound.

• Information is stored in a Planck-sized remnant^[10][11]

  Advantage: No mechanism for information escape is needed.

  Disadvantage: To contain the information from any evaporated black hole, the remnants would need to have an infinite number of internal states. It has been argued that it would be possible to produce an infinite amount of pairs of these remnants since they are small and indistinguishable from the perspective of the low-energy effective theory.^[13]

• Information is stored in a large remnant^[14][15]

  Advantage: The size of remnant increases with the size of the initial black hole, so there is no need for an infinite number of internal states.

  Disadvantage: Hawking radiation must stop before the black hole reaches the Planck size, which requires a violation of semi-classical gravity at a macroscopic scale.

• Information is stored in a baby universe that separates from our own universe.^[11][16]

  Advantage: This scenario is predicted by the Einstein–Cartan theory of gravity which extends general relativity to matter with intrinsic angular momentum (spin). No violation of known general principles of physics is needed.

  Disadvantage: It is difficult to test the Einstein–Cartan theory because its predictions are significantly different from general-relativistic ones only at extremely high densities.

• Information is encoded in the correlations between future and past^[17][18]

  Advantage: Semiclassical gravity is sufficient, i.e., the solution does not depend on details of (still not well understood) quantum gravity.

  Disadvantage: Contradicts the intuitive view of nature as an entity that evolves with time.

Recent developments

In 2014, Chris Adami argued that analysis using quantum channel theory causes any apparent paradox to disappear; Adami rejects Susskind's analysis of black hole complementarity, arguing instead that no space-like surface contains duplicated quantum information.^[19][20]

In 2015, Modak, Ortíz, Peña and Sudarsky, have argued that the paradox can be dissolved by invoking foundational issues of quantum theory often referred as the measurement problem of quantum mechanics.^[21] This work was built on an earlier proposal by Okon and Sudarsky on the benefits of objective collapse theory in a much broader context.^[22] The original motivation of these studies was the long lasting proposal of Roger Penrose where collapse of the wave-function is said to be inevitable in presence of black holes (and even under the influence of gravitational field).^[23][24] Experimental verification of collapse theories is an ongoing effort.^[25]

In 2016, Hawking et al. proposed new theories of information moving in and out of a black hole.^[26][27] The 2016 work posits that the information is saved in "soft particles", low-energy versions of photons and other particles that exist in zero-energy empty space.^[28]

Quantum tunnelling

From Wikipedia, the free encyclopedia

 

Quantum tunnelling or tunneling (see spelling differences) is the quantum mechanical phenomenon where a particle tunnels through a barrier that it classically cannot surmount. This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the Sun.^[1] It has important applications to modern devices such as the tunnel diode,^[2] quantum computing, and the scanning tunnelling microscope. The effect was predicted in the early 20th century and its acceptance as a general physical phenomenon came mid-century.^[3]

Fundamental quantum mechanical concepts are central to this phenomenon, which makes quantum tunnelling one of the novel implications of quantum mechanics. Quantum tunneling is projected to create physical limits to how small transistors can get, due to electrons being able to tunnel past them if they are too small.^[4]

Tunnelling is often explained in terms of Heisenberg uncertainty principle and the wave–particle duality of matter.

History

Quantum tunnelling was developed from the study of radioactivity,^[3] which was discovered in 1896 by Henri Becquerel.^[5] Radioactivity was examined further by Marie Curie and Pierre Curie, for which they earned the Nobel Prize in Physics in 1903.^[5] Ernest Rutherford and Egon Schweidler studied its nature, which was later verified empirically by Friedrich Kohlrausch. The idea of the half-life and the possibility of predicting decay was created from their work.^[3]

In 1901, Robert Francis Earhart, while investigating the conduction of gases between closely spaced electrodes using the Michelson interferometer to measure the spacing, discovered an unexpected conduction regime. J. J. Thomson commented that the finding warranted further investigation. In 1911 and then 1914, then-graduate student Franz Rother, employing Earhart's method for controlling and measuring the electrode separation but with a sensitive platform galvanometer, directly measured steady field emission currents. In 1926, Rother, using a still newer platform galvanometer of sensitivity 26 pA, measured the field emission currents in a "hard" vacuum between closely spaced electrodes.^[6]

Quantum tunneling was first noticed in 1927 by Friedrich Hund when he was calculating the ground state of the double-well potential^[5] and independently in the same year by Leonid Mandelstam and Mikhail Leontovich in their analysis of the implications of the then new Schrödinger wave equation for the motion of a particle in a confining potential of a limited spatial extent.^[7] Its first application was a mathematical explanation for alpha decay, which was done in 1928 by George Gamow (who was aware of the findings of Mandelstam and Leontovich^[8]) and independently by Ronald Gurney and Edward Condon.^{[9][10][11][12]} The two researchers simultaneously solved the Schrödinger equation for a model nuclear potential and derived a relationship between the half-life of the particle and the energy of emission that depended directly on the mathematical probability of tunnelling.

After attending a seminar by Gamow, Max Born recognised the generality of tunnelling. He realised that it was not restricted to nuclear physics, but was a general result of quantum mechanics that applies to many different systems.^[3] Shortly thereafter, both groups considered the case of particles tunnelling into the nucleus. The study of semiconductors and the development of transistors and diodes led to the acceptance of electron tunnelling in solids by 1957. The work of Leo Esaki, Ivar Giaever and Brian Josephson predicted the tunnelling of superconducting Cooper pairs, for which they received the Nobel Prize in Physics in 1973.^[3] In 2016, the quantum tunneling of water was discovered.^[13]

Introduction to the concept

Play media

Animation showing the tunnel effect and its application to an STM

 

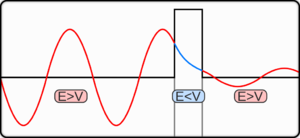
Quantum tunnelling through a barrier. The energy of the tunnelled particle is the same but the probability amplitude is decreased.

 

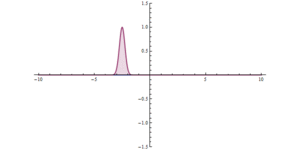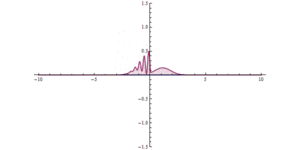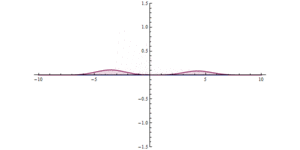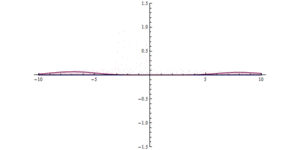
A simulation of a wave packet incident on a potential barrier. In relative units, the barrier energy is 20, greater than the mean wave packet energy of 14. A portion of the wave packet passes through the barrier.

 

Quantum tunnelling through a barrier. At the origin (x=0), there is a very high, but narrow potential barrier. A significant tunnelling effect can be seen.

Quantum tunnelling falls under the domain of quantum mechanics: the study of what happens at the quantum scale. This process cannot be directly perceived, but much of its understanding is shaped by the microscopic world, which classical mechanics cannot adequately explain. To understand the phenomenon, particles attempting to travel between potential barriers can be compared to a ball trying to roll over a hill; quantum mechanics and classical mechanics differ in their treatment of this scenario. Classical mechanics predicts that particles that do not have enough energy to classically surmount a barrier will not be able to reach the other side. Thus, a ball without sufficient energy to surmount the hill would roll back down. Or, lacking the energy to penetrate a wall, it would bounce back (reflection) or in the extreme case, bury itself inside the wall (absorption). In quantum mechanics, these particles can, with a very small probability, tunnel to the other side, thus crossing the barrier. Here, the "ball" could, in a sense, borrow energy from its surroundings to tunnel through the wall or "roll over the hill", paying it back by making the reflected electrons more energetic than they otherwise would have been.^[14]

The reason for this difference comes from the treatment of matter in quantum mechanics as having properties of waves and particles. One interpretation of this duality involves the Heisenberg uncertainty principle, which defines a limit on how precisely the position and the momentum of a particle can be known at the same time.^[5] This implies that there are no solutions with a probability of exactly zero (or one), though a solution may approach infinity if, for example, the calculation for its position was taken as a probability of 1, the other, i.e. its speed, would have to be infinity. Hence, the probability of a given particle's existence on the opposite side of an intervening barrier is non-zero, and such particles will appear on the 'other' (a semantically difficult word in this instance) side with a relative frequency proportional to this probability.

An electron wavepacket directed at a potential barrier. Note the dim spot on the right that represents tunnelling electrons.

 

Play media

Quantum tunnelling in the phase space formulation of quantum mechanics. Wigner function for tunnelling through the potential barrier ${\displaystyle U(x)=8e^{-0.25x^{2}}}$ in atomic units (a.u.). The solid lines represent the level set of the Hamiltonian ${\displaystyle H(x,p)=p^{2}/2+U(x)}$.

The tunnelling problem

The wave function of a particle summarises everything that can be known about a physical system.^[15] Therefore, problems in quantum mechanics center on the analysis of the wave function for a system. Using mathematical formulations of quantum mechanics, such as the Schrödinger equation, the wave function can be solved. This is directly related to the probability density of the particle's position, which describes the probability that the particle is at any given place. In the limit of large barriers, the probability of tunnelling decreases for taller and wider barriers.

For simple tunnelling-barrier models, such as the rectangular barrier, an analytic solution exists. Problems in real life often do not have one, so "semiclassical" or "quasiclassical" methods have been developed to give approximate solutions to these problems, like the WKB approximation. Probabilities may be derived with arbitrary precision, constrained by computational resources, via Feynman's path integral method; such precision is seldom required in engineering practice.^{[citation needed]}

Related phenomena

There are several phenomena that have the same behaviour as quantum tunnelling, and thus can be accurately described by tunnelling. Examples include the tunnelling of a classical wave-particle association,^[16] evanescent wave coupling (the application of Maxwell's wave-equation to light) and the application of the non-dispersive wave-equation from acoustics applied to "waves on strings". Evanescent wave coupling, until recently, was only called "tunnelling" in quantum mechanics; now it is used in other contexts.

These effects are modelled similarly to the rectangular potential barrier. In these cases, there is one transmission medium through which the wave propagates that is the same or nearly the same throughout, and a second medium through which the wave travels differently. This can be described as a thin region of medium B between two regions of medium A. The analysis of a rectangular barrier by means of the Schrödinger equation can be adapted to these other effects provided that the wave equation has travelling wave solutions in medium A but real exponential solutions in medium B.

In optics, medium A is a vacuum while medium B is glass. In acoustics, medium A may be a liquid or gas and medium B a solid. For both cases, medium A is a region of space where the particle's total energy is greater than its potential energy and medium B is the potential barrier. These have an incoming wave and resultant waves in both directions. There can be more mediums and barriers, and the barriers need not be discrete; approximations are useful in this case.

Applications

Tunnelling occurs with barriers of thickness around 1-3 nm and smaller,^[17] but is the cause of some important macroscopic physical phenomena. For instance, tunnelling is a source of current leakage in very-large-scale integration (VLSI) electronics and results in the substantial power drain and heating effects that plague high-speed and mobile technology; it is considered the lower limit on how small computer chips can be made.^[18] Tunnelling is a fundamental technique used to program the floating gates of flash memory, which is one of the most significant inventions that have shaped consumer electronics in the last two decades.

Nuclear fusion in stars

Quantum tunnelling is essential for nuclear fusion in stars. Temperature and pressure in the core of stars are insufficient for nuclei to overcome the Coulomb barrier in order to achieve a thermonuclear fusion. However, there is some probability to penetrate the barrier due to quantum tunnelling. Though the probability is very low, the extreme number of nuclei in a star generates a steady fusion reaction over millions or even billions of years - a precondition for the evolution of life in insolation habitable zones.^[19]

Radioactive decay

Radioactive decay is the process of emission of particles and energy from the unstable nucleus of an atom to form a stable product. This is done via the tunnelling of a particle out of the nucleus (an electron tunnelling into the nucleus is electron capture). This was the first application of quantum tunnelling and led to the first approximations. Radioactive decay is also a relevant issue for astrobiology as this consequence of quantum tunnelling is creating a constant source of energy over a large period of time for environments outside the circumstellar habitable zone where insolation would not be possible (subsurface oceans) or effective.^[19]

Astrochemistry in interstellar clouds

By including quantum tunnelling the astrochemical syntheses of various molecules in interstellar clouds can be explained such as the synthesis of molecular hydrogen, water (ice) and the prebiotic important formaldehyde.^[19]

Quantum biology

Quantum tunnelling is among the central non trivial quantum effects in quantum biology. Here it is important both as electron tunnelling and proton tunnelling. Electron tunnelling is a key factor in many biochemical redox reactions (photosynthesis, cellular respiration) as well as enzymatic catalysis while proton tunnelling is a key factor in spontaneous mutation of DNA.^[19]

Spontaneous mutation of DNA occurs when normal DNA replication takes place after a particularly significant proton has defied the odds in quantum tunnelling in what is called "proton tunnelling"^[20] (quantum biology). A hydrogen bond joins normal base pairs of DNA. There exists a double well potential along a hydrogen bond separated by a potential energy barrier. It is believed that the double well potential is asymmetric with one well deeper than the other so the proton normally rests in the deeper well. For a mutation to occur, the proton must have tunnelled into the shallower of the two potential wells. The movement of the proton from its regular position is called a tautomeric transition. If DNA replication takes place in this state, the base pairing rule for DNA may be jeopardised causing a mutation.^[21] Per-Olov Lowdin was the first to develop this theory of spontaneous mutation within the double helix (quantum bio). Other instances of quantum tunnelling-induced mutations in biology are believed to be a cause of ageing and cancer.^[22]

Cold emission

Cold emission of electrons is relevant to semiconductors and superconductor physics. It is similar to thermionic emission, where electrons randomly jump from the surface of a metal to follow a voltage bias because they statistically end up with more energy than the barrier, through random collisions with other particles. When the electric field is very large, the barrier becomes thin enough for electrons to tunnel out of the atomic state, leading to a current that varies approximately exponentially with the electric field.^[23] These materials are important for flash memory, vacuum tubes, as well as some electron microscopes.

Tunnel junction

A simple barrier can be created by separating two conductors with a very thin insulator. These are tunnel junctions, the study of which requires quantum tunnelling.^[24] Josephson junctions take advantage of quantum tunnelling and the superconductivity of some semiconductors to create the Josephson effect. This has applications in precision measurements of voltages and magnetic fields,^[23] as well as the multijunction solar cell.

Quantum-dot cellular automata

QCA is a molecular binary logic synthesis technology that operates by the inter-island electron tunneling system. This is a very low power and fastest device that can operate at maximum 15 PHz of frequency^[25].

A working mechanism of a resonant tunnelling diode device, based on the phenomenon of quantum tunnelling through the potential barriers.

Tunnel diode

Diodes are electrical semiconductor devices that allow electric current flow in one direction more than the other. The device depends on a depletion layer between N-type and P-type semiconductors to serve its purpose; when these are very heavily doped the depletion layer can be thin enough for tunnelling. Then, when a small forward bias is applied the current due to tunnelling is significant. This has a maximum at the point where the voltage bias is such that the energy level of the p and n conduction bands are the same. As the voltage bias is increased, the two conduction bands no longer line up and the diode acts typically.^[26]

Because the tunnelling current drops off rapidly, tunnel diodes can be created that have a range of voltages for which current decreases as voltage is increased. This peculiar property is used in some applications, like high speed devices where the characteristic tunnelling probability changes as rapidly as the bias voltage.^[26]

The resonant tunnelling diode makes use of quantum tunnelling in a very different manner to achieve a similar result. This diode has a resonant voltage for which there is a lot of current that favors a particular voltage, achieved by placing two very thin layers with a high energy conductance band very near each other. This creates a quantum potential well that has a discrete lowest energy level. When this energy level is higher than that of the electrons, no tunnelling will occur, and the diode is in reverse bias. Once the two voltage energies align, the electrons flow like an open wire. As the voltage is increased further tunnelling becomes improbable and the diode acts like a normal diode again before a second energy level becomes noticeable.^[27]

Tunnel field-effect transistors

A European research project has demonstrated field effect transistors in which the gate (channel) is controlled via quantum tunnelling rather than by thermal injection, reducing gate voltage from ~1 volt to 0.2 volts and reducing power consumption by up to 100×. If these transistors can be scaled up into VLSI chips, they will significantly improve the performance per power of integrated circuits.^[28]

Quantum conductivity

While the Drude model of electrical conductivity makes excellent predictions about the nature of electrons conducting in metals, it can be furthered by using quantum tunnelling to explain the nature of the electron's collisions.^[23] When a free electron wave packet encounters a long array of uniformly spaced barriers the reflected part of the wave packet interferes uniformly with the transmitted one between all barriers so that there are cases of 100% transmission. The theory predicts that if positively charged nuclei form a perfectly rectangular array, electrons will tunnel through the metal as free electrons, leading to an extremely high conductance, and that impurities in the metal will disrupt it significantly.^[23]

Scanning tunnelling microscope

The scanning tunnelling microscope (STM), invented by Gerd Binnig and Heinrich Rohrer, may allow imaging of individual atoms on the surface of a material.^[23] It operates by taking advantage of the relationship between quantum tunnelling with distance. When the tip of the STM's needle is brought very close to a conduction surface that has a voltage bias, by measuring the current of electrons that are tunnelling between the needle and the surface, the distance between the needle and the surface can be measured. By using piezoelectric rods that change in size when voltage is applied over them the height of the tip can be adjusted to keep the tunnelling current constant. The time-varying voltages that are applied to these rods can be recorded and used to image the surface of the conductor.^[23] STMs are accurate to 0.001 nm, or about 1% of atomic diameter.^[27]

Faster than light

Some physicists have claimed that it is possible for spin-zero particles to travel faster than the speed of light when tunnelling.^[3] This apparently violates the principle of causality, since there will be a frame of reference in which it arrives before it has left. In 1998, Francis E. Low reviewed briefly the phenomenon of zero-time tunnelling.^[29] More recently experimental tunnelling time data of phonons, photons, and electrons have been published by Günter Nimtz.^[30]
Other physicists, such as Herbert Winful ^[31], have disputed these claims. Winful argues that the wavepacket of a tunnelling particle propagates locally, so a particle can't tunnel through the barrier non-locally. Winful also argues that the experiments that are purported to show non-local propagation have been misinterpreted. In particular, the group velocity of a wavepacket does not measure its speed, but is related to the amount of time the wavepacket is stored in the barrier.

Mathematical discussions of quantum tunnelling

The following subsections discuss the mathematical formulations of quantum tunnelling.

The Schrödinger equation

The time-independent Schrödinger equation for one particle in one dimension can be written as

${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\Psi (x)+V(x)\Psi (x)=E\Psi (x)}$ or

${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)\Psi (x)\equiv {\frac {2m}{\hbar ^{2}}}M(x)\Psi (x),}$

where ${\displaystyle \hbar }$ is the reduced Planck's constant, m is the particle mass, x represents distance measured in the direction of motion of the particle, Ψ is the Schrödinger wave function, V is the potential energy of the particle (measured relative to any convenient reference level), E is the energy of the particle that is associated with motion in the x-axis (measured relative to V), and M(x) is a quantity defined by V(x) – E which has no accepted name in physics.

The solutions of the Schrödinger equation take different forms for different values of x, depending on whether M(x) is positive or negative. When M(x) is constant and negative, then the Schrödinger equation can be written in the form

${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)=-k^{2}\Psi (x),\;\;\;\;\;\;\mathrm {where} \;\;\;k^{2}=-{\frac {2m}{\hbar ^{2}}}M.}$

The solutions of this equation represent travelling waves, with phase-constant +k or -k. Alternatively, if M(x) is constant and positive, then the Schrödinger equation can be written in the form

${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)={\kappa }^{2}\Psi (x),\;\;\;\;\;\;\mathrm {where} \;\;\;{\kappa }^{2}={\frac {2m}{\hbar ^{2}}}M.}$

The solutions of this equation are rising and falling exponentials in the form of evanescent waves. When M(x) varies with position, the same difference in behaviour occurs, depending on whether M(x) is negative or positive. It follows that the sign of M(x) determines the nature of the medium, with negative M(x) corresponding to medium A as described above and positive M(x) corresponding to medium B. It thus follows that evanescent wave coupling can occur if a region of positive M(x) is sandwiched between two regions of negative M(x), hence creating a potential barrier.

The mathematics of dealing with the situation where M(x) varies with x is difficult, except in special cases that usually do not correspond to physical reality. A discussion of the semi-classical approximate method, as found in physics textbooks, is given in the next section. A full and complicated mathematical treatment appears in the 1965 monograph by Fröman and Fröman noted below. Their ideas have not been incorporated into physics textbooks, but their corrections have little quantitative effect.

The WKB approximation

The wave function is expressed as the exponential of a function:

${\displaystyle \Psi (x)=e^{\Phi (x)}}$, where ${\displaystyle \Phi ''(x)+\Phi '(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right).}$

${\displaystyle \Phi '(x)}$ is then separated into real and imaginary parts:

${\displaystyle \Phi '(x)=A(x)+iB(x)}$, where A(x) and B(x) are real-valued functions.

Substituting the second equation into the first and using the fact that the imaginary part needs to be 0 results in:

${\displaystyle A'(x)+A(x)^{2}-B(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}$.

To solve this equation using the semiclassical approximation, each function must be expanded as a power series in ${\displaystyle \hbar }$. From the equations, the power series must start with at least an order of ${\displaystyle \hbar ^{-1}}$ to satisfy the real part of the equation; for a good classical limit starting with the highest power of Planck's constant possible is preferable, which leads to

${\displaystyle A(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}A_{k}(x)}$

and

${\displaystyle B(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}B_{k}(x)}$,

with the following constraints on the lowest order terms,

${\displaystyle A_{0}(x)^{2}-B_{0}(x)^{2}=2m\left(V(x)-E\right)}$

and

${\displaystyle A_{0}(x)B_{0}(x)=0}$.

At this point two extreme cases can be considered.

Case 1 If the amplitude varies slowly as compared to the phase ${\displaystyle A_{0}(x)=0}$ and

${\displaystyle B_{0}(x)=\pm {\sqrt {2m\left(E-V(x)\right)}}}$

which corresponds to classical motion. Resolving the next order of expansion yields

${\displaystyle \Psi (x)\approx C{\frac {e^{i\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}}+\theta }}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}}}}$

Case 2

If the phase varies slowly as compared to the amplitude, ${\displaystyle B_{0}(x)=0}$ and

${\displaystyle A_{0}(x)=\pm {\sqrt {2m\left(V(x)-E\right)}}}$

which corresponds to tunnelling. Resolving the next order of the expansion yields

${\displaystyle \Psi (x)\approx {\frac {C_{+}e^{+\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}+C_{-}e^{-\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}$

In both cases it is apparent from the denominator that both these approximate solutions are bad near the classical turning points ${\displaystyle E=V(x)}$. Away from the potential hill, the particle acts similar to a free and oscillating wave; beneath the potential hill, the particle undergoes exponential changes in amplitude. By considering the behaviour at these limits and classical turning points a global solution can be made.

To start, choose a classical turning point, ${\displaystyle x_{1}}$ and expand ${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}$ in a power series about ${\displaystyle x_{1}}$:

${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1})+v_{2}(x-x_{1})^{2}+\cdots }$

Keeping only the first order term ensures linearity:

${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1})}$.

Using this approximation, the equation near ${\displaystyle x_{1}}$ becomes a differential equation:

${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)=v_{1}(x-x_{1})\Psi (x)}$.

This can be solved using Airy functions as solutions.

${\displaystyle \Psi (x)=C_{A}Ai\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)+C_{B}Bi\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)}$

Taking these solutions for all classical turning points, a global solution can be formed that links the limiting solutions. Given the two coefficients on one side of a classical turning point, the two coefficients on the other side of a classical turning point can be determined by using this local solution to connect them.

Hence, the Airy function solutions will asymptote into sine, cosine and exponential functions in the proper limits. The relationships between ${\displaystyle C,\theta }$ and ${\displaystyle C_{+},C_{-}}$ are

${\displaystyle C_{+}={\frac {1}{2}}C\cos {\left(\theta -{\frac {\pi }{4}}\right)}}$

and

${\displaystyle C_{-}=-C\sin {\left(\theta -{\frac {\pi }{4}}\right)}}$

With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunnelling through a single potential barrier is

${\displaystyle T(E)=e^{-2\int _{x_{1}}^{x_{2}}\mathrm {d} x{\sqrt {{\frac {2m}{\hbar ^{2}}}\left[V(x)-E\right]}}}}$,

where ${\displaystyle x_{1},x_{2}}$ are the two classical turning points for the potential barrier.

For a rectangular barrier, this expression is simplified to:

${\displaystyle T(E)=e^{-2{\sqrt {{\frac {2m}{\hbar ^{2}}}(V_{0}-E)}}(x_{2}-x_{1})}={\tilde {V}}_{0}^{-(x_{2}-x_{1})}}$.