Higgs boson
Condensed from Wikipedia, the free encyclopedia
| |
| Composition | Elementary particle |
|---|---|
| Statistics | Bosonic |
| Status | A Higgs boson of mass ≈125 GeV has been tentatively confirmed by CERN on 14 March 2013,[1][2][3] although unclear as yet which model the particle best supports or whether multiple Higgs bosons exist.[2] (See: Current status) |
| Symbol | H0 |
| Theorised | R. Brout, F. Englert, P. Higgs, G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble (1964) |
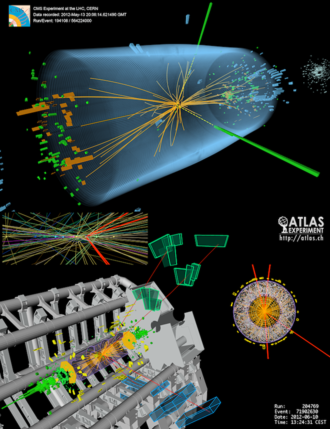
| Discovered | Previously unknown boson confirmed to exist on 4 July 2012, by the ATLAS and CMS teams at the Large Hadron Collider; tentatively confirmed as a Higgs boson of some kind on 14 March 2013 (see above). |
| Mass | 125.03+0.26 −0.27 (stat) +0.13 −0.15 (sys) GeV/c2 ,[4] 125.36 ± 0.37 (stat) ± 0.18 (sys) GeV/c2[5] |
| Mean lifetime | 1.56×10−22 s[Note 2] (predicted in the Standard Model) |
| Decays into | (observed) W and Z bosons, two photons. (Others still being studied) |
| Electric charge | 0 |
| Color charge | 0 |
| Spin | 0 (tentatively confirmed at 125 GeV)[1] |
| Parity | +1 (tentatively confirmed at 125 GeV)[1] |
This unanswered question in fundamental physics is of such importance[10][11] that it led to a search of more than 40 years for the Higgs boson and finally the construction of one of the world's most expensive and complex experimental facilities to date, the Large Hadron Collider,[13] able to create Higgs bosons and other particles for observation and study. On 4 July 2012, it was announced that a previously unknown particle with a mass between 125 and 127 GeV/c2 (134.2 and 136.3 amu) had been detected; physicists suspected at the time that it was the Higgs boson.[14][9][15] By March 2013, the particle had been proven to behave, interact and decay in many of the ways predicted by the Standard Model, and was also tentatively confirmed to have positive parity and zero spin,[1] two fundamental attributes of a Higgs boson. This appears to be the first elementary scalar particle discovered in nature.[16] More data are needed to determine whether the particle discovered exactly matches the predictions of the Standard Model, or whether, as predicted by some theories, multiple Higgs bosons exist.[3]
The Higgs boson is named after Peter Higgs, one of six physicists who, in 1964, proposed the mechanism that suggested the existence of such a particle. Although Higgs's name has come to be associated with this theory, several researchers between about 1960 and 1972 each independently developed different parts of it. In mainstream media the Higgs boson has often been called the "God particle", from a 1993 book on the topic; the nickname is strongly disliked by many physicists, including Higgs, who regard it as inappropriate sensationalism.[17][18] In 2013 two of the original researchers, Peter Higgs and François Englert, were awarded the Nobel Prize in Physics for their work and prediction.[19] Englert's co-researcher Robert Brout had died in 2011 and the Nobel is not given posthumously except in unusual circumstances.
In the Standard Model, the Higgs particle is a boson with no spin, electric charge, or color charge. It is also very unstable, decaying into other particles almost immediately. It is a quantum excitation of one of the four components of the Higgs field. The latter constitutes a scalar field, with two neutral and two electrically charged components, and forms a complex doublet of the weak isospin SU(2) symmetry. The field has a "Mexican hat" shaped potential with nonzero strength everywhere (including otherwise empty space), which in its vacuum state breaks the weak isospin symmetry of the electroweak interaction. When this happens, three components of the Higgs field are "absorbed" by the SU(2) and U(1) gauge bosons (the "Higgs mechanism") to become the longitudinal components of the now-massive W and Z bosons of the weak force. The remaining electrically neutral component separately couples to other particles known as fermions (via Yukawa couplings), causing these to acquire mass as well. Some versions of the theory predict more than one kind of Higgs fields and bosons. Alternative "Higgsless" models would have been considered if the Higgs boson were not discovered.
Overview
In particle physics, elementary particles and forces give rise to the world around us. Nowadays, physicists explain the behaviour of these particles and how they interact using the Standard Model—a widely accepted and "remarkably" accurate[21] framework based on gauge invariance and symmetries, believed to explain almost everything in the world we see, other than gravity.[22]But by around 1960 all attempts to create a gauge invariant theory for two of the four fundamental forces had consistently failed at one crucial point: although gauge invariance seemed extremely important, it seemed to make any theory of electromagnetism and the weak force go haywire, by demanding that either many particles with mass were massless or that non-existent forces and massless particles had to exist. Scientists had no idea how to get past this point.
Work done on superconductivity and "broken" symmetries around 1960 led physicist Philip Anderson to suggest in 1962 a new kind of solution that might hold the key. In 1964 a theory was created by 3 different groups of researchers, that showed the problems could be resolved if an unusual kind of field existed throughout the universe. It would cause existing particles to acquire mass instead of new massless particles being formed. By 1972 it had been developed into a comprehensive theory and proved capable of giving "sensible" results. Although there was not yet any proof of such a field, calculations consistently gave answers and predictions that were confirmed by experiments, including very accurate predictions of several other particles,[Note 7] so scientists began to believe this might be true and to search for proof whether or not a Higgs field exists in nature.
If this field did exist, this would be a monumental discovery for science and human knowledge, and is expected to open doorways to new knowledge in many fields. If not, then other more complicated theories would need to be explored. The easiest proof whether or not the field existed was by searching for a new kind of particle it would have to give off, known as "Higgs bosons" or the "Higgs particle". These would be extremely difficult to find, so it was only many years later that experimental technology became sophisticated enough to answer the question.
While several symmetries in nature are spontaneously broken through a form of the Higgs mechanism, in the context of the Standard Model the term "Higgs mechanism" almost always means symmetry breaking of the electroweak field. It is considered proven, but the exact cause has been exceedingly difficult to prove. After 50 years, the Higgs boson's existence – apparently proven in 2013 – would finally confirm that the Standard Model is essentially correct and allow further development, while its non-existence would mean that other theories are needed instead.
Various analogies have also been invented to describe the Higgs field and boson, including analogies with well-known symmetry breaking effects such as the rainbow and prism, electric fields, ripples, and resistance of macro objects moving through media, like people moving through crowds or some objects moving through syrup or molasses. However, analogies based on simple resistance to motion are inaccurate as the Higgs field does not work by resisting motion.
Significance
Scientific impact
Evidence of the Higgs field and its properties would be extremely significant scientifically, for many reasons. The Higgs boson's importance is largely that it is able to be examined using existing knowledge and experimental technology, as a way to confirm and study the entire Higgs field theory.[10][11] Conversely, proof that the Higgs field and boson do not exist would also be significant. In discussion form, the relevance includes:| Validating the Standard Model, or choosing between extensions and alternatives | Does the Higgs field exist, which fundamentally validates the Standard Model? If it does, then which more advanced extensions are suggested or excluded based upon measurements of its properties? What else can we learn about this fundamental field, now that we have the experimental means to study its behavior and interactions? Alternatively, if the Higgs field doesn't exist, which alternatives and modifications to the Standard Model are likely to be preferred? Will the data suggest an extension, or a completely different approach (such as supersymmetry or string theory)? Related to this, a belief generally exists among physicists that there is likely to be "new" physics beyond the Standard Model—the Standard Model will at some point be extended or superseded. The Higgs field and related issues present a promising "doorway" to understand better the places where the Standard Model might become inadequate or fail, and could provide considerable evidence guiding researchers into future enhancements or successors. | ||
| Finding how symmetry breaking happens within the electroweak interaction | Below an extremely high temperature, electroweak symmetry breaking causes the electroweak interaction to manifest in part as the short-ranged weak force, which is carried by massive gauge bosons. Without this, the universe we see around us could not exist, because atoms and other structures could not form, and reactions in stars such as our Sun would not occur. But it is not clear how this actually happens in nature. Is the Standard Model correct in its approach, and can it be made more exact with actual experimental measurements? If not the Higgs field, then what is breaking symmetry in its place? | ||
| Finding how certain particles acquire mass | Electroweak symmetry breaking (due to a Higgs field or otherwise) is believed proven responsible for the masses of fundamental particles such as elementary fermions (including electrons and quarks) and the massive W and Z gauge bosons. Finding how this happens is pivotal to particle physics. It is worth noting that the Higgs field does not 'create' mass out of nothing (which would violate the law of conservation of energy). Nor is the Higgs field responsible for the mass of all particles. For example, about 99% of the mass of baryons (composite particles such as the proton and neutron) is due instead to the kinetic energy of quarks and to the energies of (massless) gluons of the strong interaction inside the baryons.[23] In Higgs-based theories, the property of 'mass' is a manifestation of potential energy transferred to particles when they interact ("couple") with the Higgs field, which had contained that mass in the form of energy.[24] | ||
| Evidence whether or not scalar fields exist in nature, and "new" physics | Proof of a scalar field such as the Higgs field would be hard to overestimate: "[The] verification of real scalar fields would be nearly as important as its role in generating mass". [9] Rolf-Dieter Heuer, director general of CERN, stated in a 2011 talk on the Higgs field:[25]
| ||
| Insight into cosmic inflation | There has been considerable scientific research on possible links between the Higgs field and the inflaton – a hypothetical field suggested as the explanation for the expansion of space during the first fraction of a second of the universe (known as the "inflationary epoch"). Some theories suggest that a fundamental scalar field might be responsible for this phenomenon; the Higgs field is such a field and therefore has led to papers analysing whether it could also be the inflaton responsible for this exponential expansion of the universe during the Big Bang. Such theories are highly tentative and face significant problems related to unitarity, but may be viable if combined with additional features such as large non-minimal coupling, a Brans–Dicke scalar, or other "new" physics, and have received treatments suggesting that Higgs inflation models are still of interest theoretically. | ||
| Insight into the nature of the universe, and its possible fates |
If measurements of the Higgs boson suggest that our universe lies within a false vacuum of this kind, then it would imply – more than likely in many billions of years[39][Note 8] – that the universe's forces, particles, and structures could cease to exist as we know them (and be replaced by different ones), if a true vacuum happened to nucleate.[39][Note 9] It also suggests that the Higgs self-coupling λ and its βλ function could be very close to zero at the Planck scale, with "intriguing" implications, including theories of gravity and Higgs-based inflation.[26]:218[41][42] A future electron–positron collider would be able to provide the precise measurements of the top quark needed for such calculations.[26] | ||
| Insight into the 'energy of the vacuum' | More speculatively, the Higgs field has also been proposed as the energy of the vacuum, which at the extreme energies of the first moments of the Big Bang caused the universe to be a kind of featureless symmetry of undifferentiated extremely high energy. In this kind of speculation, the single unified field of a Grand Unified Theory is identified as (or modeled upon) the Higgs field, and it is through successive symmetry breakings of the Higgs field or some similar field at phase transitions that the present universe's known forces and fields arise.[43] | ||
| Link to the 'cosmological constant' problem | The relationship (if any) between the Higgs field and the presently observed vacuum energy density of the universe has also come under scientific study. As observed, the present vacuum energy density is extremely close to zero, but the energy density expected from the Higgs field, supersymmetry, and other current theories are typically many orders of magnitude larger. It is unclear how these should be reconciled. This cosmological constant problem remains a further major unanswered problem in physics.
Further information: Zero-point energy and Vacuum state
|
"Real world" impact[edit]
As yet, there are no known immediate technological benefits of finding the Higgs particle. However, observers in both media and science point out that when fundamental discoveries are made about our world, their practical uses can take decades to emerge, but are often world-changing when they do.[44][45][46] A common pattern for fundamental discoveries is for practical applications to follow later, once the discovery has been explored further, at which point they become the basis for social change and new technologies.For example, in the first half of the 20th century it was not expected that quantum mechanics would make possible transistors and microchips, mobile phones and computers, lasers and M.R.I. scanners.[47] Radio waves were described by their co-discoverer in 1888 as "an interesting laboratory experiment" with "no useful purpose" whatsoever,[48] and are now used in innumerable ways (radar, weather prediction, medicine, television, wireless computing and emergency response), positrons are used in hospital tomography scans, and special and general relativity, which explain black holes also enable satellite-based GPS and satellite navigation ("satnav").[47] Electric power generation and transmission, motors, and lighting all stemmed from previous theoretical work on electricity and magnetism; air conditioning and refrigeration resulted from thermodynamics. It is impossible to predict how seemingly esoteric knowledge may affect society in the future.[44][46]
Other observers highlight technological spin-offs from this and related particle physics activities, which have already brought major developments to society. For example, the World Wide Web as used today was created by physicists working in global collaborations on particle experiments at CERN to share their results, and the results of massive amounts of data produced by the Large Hadron Collider have already led to significant advances in distributed and cloud computing, now well established within mainstream services.[45]
Theoretical properties
Theoretical need for the Higgs

"Symmetry breaking illustrated": – At high energy levels (left) the ball settles in the center, and the result is symmetrical. At lower energy levels (right), the overall "rules" remain symmetrical, but the "Mexican hat" potential comes into effect: "local" symmetry inevitably becomes broken since eventually the ball must at random roll one way or another.
Gauge invariance is an important property of modern particle theories such as the Standard Model, partly due to its success in other areas of fundamental physics such as electromagnetism and the strong interaction (quantum chromodynamics). However, there were great difficulties in developing gauge theories for the weak nuclear force or a possible unified electroweak interaction. Fermions with a mass term would violate gauge symmetry and therefore cannot be gauge invariant. (This can be seen by examining the Dirac Lagrangian for a fermion in terms of left and right handed components; we find none of the spin-half particles could ever flip helicity as required for mass, so they must be massless.[Note 12]) W and Z bosons are observed to have mass, but a boson mass term contains terms, which clearly depend on the choice of gauge and therefore these masses too cannot be gauge invariant. Therefore it seems that none of the standard model fermions or bosons could "begin" with mass as an inbuilt property except by abandoning gauge invariance. If gauge invariance were to be retained, then these particles had to be acquiring their mass by some other mechanism or interaction. Additionally, whatever was giving these particles their mass, had to not "break" gauge invariance as the basis for other parts of the theories where it worked well, and had to not require or predict unexpected massless particles and long-range forces (seemingly an inevitable consequence of Goldstone's theorem) which did not actually seem to exist in nature.
A solution to all of these overlapping problems came from the discovery of a previously unnoticed borderline case hidden in the mathematics of Goldstone's theorem,[Note 10] that under certain conditions it might theoretically be possible for a symmetry to be broken without disrupting gauge invariance and without any new massless particles or forces, and having "sensible" (renormalisable) results mathematically: this became known as the Higgs mechanism.
The Standard Model hypothesizes a field which is responsible for this effect, called the Higgs field (symbol:
Properties of the Standard Model Higgs
In the Standard Model, the Higgs field consists of four components, two neutral ones and two charged component fields. Both of the charged components and one of the neutral fields are Goldstone bosons, which act as the longitudinal third-polarization components of the massive W+, W–, and Z bosons. The quantum of the remaining neutral component corresponds to (and is theoretically realised as) the massive Higgs boson.[88] Since the Higgs field is a scalar field (meaning it does not transform under Lorentz transformations), the Higgs boson has no spin. The Higgs boson is also its own antiparticle and is CP-even, and has zero electric and colour charge.[89]The Minimal Standard Model does not predict the mass of the Higgs boson.[90] If that mass is between 115 and 180 GeV/c2, then the Standard Model can be valid at energy scales all the way up to the Planck scale (1019 GeV).[91] Many theorists expect new physics beyond the Standard Model to emerge at the TeV-scale, based on unsatisfactory properties of the Standard Model.[92] The highest possible mass scale allowed for the Higgs boson (or some other electroweak symmetry breaking mechanism) is 1.4 TeV; beyond this point, the Standard Model becomes inconsistent without such a mechanism, because unitarity is violated in certain scattering processes.[93]
It is also possible, although experimentally difficult, to estimate the mass of the Higgs boson indirectly. In the Standard Model, the Higgs boson has a number of indirect effects; most notably, Higgs loops result in tiny corrections to masses of W and Z bosons. Precision measurements of electroweak parameters, such as the Fermi constant and masses of W/Z bosons, can be used to calculate constraints on the mass of the Higgs. As of July 2011, the precision electroweak measurements tell us that the mass of the Higgs boson is likely to be less than about 161 GeV/c2 at 95% confidence level (this upper limit would increase to 185 GeV/c2 if the lower bound of 114.4 GeV/c2 from the LEP-2 direct search is allowed for[85]). These indirect constraints rely on the assumption that the Standard Model is correct. It may still be possible to discover a Higgs boson above these masses if it is accompanied by other particles beyond those predicted by the Standard Model.[94]
Production
 Gluon fusion |  Higgs Strahlung |
 Vector boson fusion |  Top fusion |
The Standard Model predicts that Higgs bosons could be formed in a number of ways,[95][96][97] although the probability of producing a Higgs boson in any collision is always expected to be very small—for example, only 1 Higgs boson per 10 billion collisions in the Large Hadron Collider.[Note 13] The most common expected processes for Higgs boson production are:
- Gluon fusion. If the collided particles are hadrons such as the proton or antiproton—as is the case in the LHC and Tevatron—then it is most likely that two of the gluons binding the hadron together collide. The easiest way to produce a Higgs particle is if the two gluons combine to form a loop of virtual quarks. Since the coupling of particles to the Higgs boson is proportional to their mass, this process is more likely for heavy particles. In practice it is enough to consider the contributions of virtual top and bottom quarks (the heaviest quarks). This process is the dominant contribution at the LHC and Tevatron being about ten times more likely than any of the other processes.[95][96]
- Higgs Strahlung. If an elementary fermion collides with an anti-fermion—e.g., a quark with an anti-quark or an electron with a positron—the two can merge to form a virtual W or Z boson which, if it carries sufficient energy, can then emit a Higgs boson. This process was the dominant production mode at the LEP, where an electron and a positron collided to form a virtual Z boson, and it was the second largest contribution for Higgs production at the Tevatron. At the LHC this process is only the third largest, because the LHC collides protons with protons, making a quark-antiquark collision less likely than at the Tevatron. Higgs Strahlung is also known as associated production.[95][96][97]
- Weak boson fusion. Another possibility when two (anti-)fermions collide is that the two exchange a virtual W or Z boson, which emits a Higgs boson. The colliding fermions do not need to be the same type. So, for example, an up quark may exchange a Z boson with an anti-down quark. This process is the second most important for the production of Higgs particle at the LHC and LEP.[95][97]
- Top fusion. The final process that is commonly considered is by far the least likely (by two orders of magnitude). This process involves two colliding gluons, which each decay into a heavy quark–antiquark pair. A quark and antiquark from each pair can then combine to form a Higgs particle.[95][96]
Decay

The Standard Model prediction for the decay width of the Higgs particle depends on the value of its mass.
Quantum mechanics predicts that if it is possible for a particle to decay into a set of lighter particles, then it will eventually do so.[99] This is also true for the Higgs boson. The likelihood with which this happens depends on a variety of factors including: the difference in mass, the strength of the interactions, etc. Most of these factors are fixed by the Standard Model, except for the mass of the Higgs boson itself. For a Higgs boson with a mass of 126 GeV/c2 the SM predicts a mean life time of about 1.6×10−22 s.[Note 2]

The Standard Model prediction for the branching ratios of the different decay modes of the Higgs particle depends on the value of its mass.
Since it interacts with all the massive elementary particles of the SM, the Higgs boson has many different processes through which it can decay. Each of these possible processes has its own probability, expressed as the branching ratio; the fraction of the total number decays that follows that process. The SM predicts these branching ratios as a function of the Higgs mass (see plot).
One way that the Higgs can decay is by splitting into a fermion–antifermion pair. As general rule, the Higgs is more likely to decay into heavy fermions than light fermions, because the mass of a fermion is proportional to the strength of its interaction with the Higgs.[101] By this logic the most common decay should be into a top–antitop quark pair. However, such a decay is only possible if the Higgs is heavier than ~346 GeV/c2, twice the mass of the top quark. For a Higgs mass of 126 GeV/c2 the SM predicts that the most common decay is into a bottom–antibottom quark pair, which happens 56.1% of the time.[100] The second most common fermion decay at that mass is a tau–antitau pair, which happens only about 6% of the time.[100]
Another possibility is for the Higgs to split into a pair of massive gauge bosons. The most likely possibility is for the Higgs to decay into a pair of W bosons (the light blue line in the plot), which happens about 23.1% of the time for a Higgs boson with a mass of 126 GeV/c2.[100] The W bosons can subsequently decay either into a quark and an antiquark or into a charged lepton and a neutrino. However, the decays of W bosons into quarks are difficult to distinguish from the background, and the decays into leptons cannot be fully reconstructed (because neutrinos are impossible to detect in particle collision experiments). A cleaner signal is given by decay into a pair of Z-bosons (which happens about 2.9% of the time for a Higgs with a mass of 126 GeV/c2),[100] if each of the bosons subsequently decays into a pair of easy-to-detect charged leptons (electrons or muons).
Decay into massless gauge bosons (i.e., gluons or photons) is also possible, but requires intermediate loop of virtual heavy quarks (top or bottom) or massive gauge bosons.[101] The most common such process is the decay into a pair of gluons through a loop of virtual heavy quarks. This process, which is the reverse of the gluon fusion process mentioned above, happens approximately 8.5% of the time for a Higgs boson with a mass of 126 GeV/c2.[100] Much rarer is the decay into a pair of photons mediated by a loop of W bosons or heavy quarks, which happens only twice for every thousand decays.[100] However, this process is very relevant for experimental searches for the Higgs boson, because the energy and momentum of the photons can be measured very precisely, giving an accurate reconstruction of the mass of the decaying particle.[101]


