In theoretical physics, Feynman diagrams are pictorial representations of the mathematical expressions describing the behavior of subatomic particles. The scheme is named after its inventor, American physicist Richard Feynman, and was first introduced in 1948. The interaction of sub-atomic particles can be complex and difficult to understand intuitively. Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. As David Kaiser writes, "since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations", and so "Feynman diagrams have revolutionized nearly every aspect of theoretical physics".[1] While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory.
Feynman used Ernst Stueckelberg's interpretation of the positron as if it were an electron moving backward in time.[2] Thus, antiparticles are represented as moving backward along the time axis in Feynman diagrams.
The calculation of probability amplitudes in theoretical particle physics requires the use of rather large and complicated integrals over a large number of variables. These integrals do, however, have a regular structure, and may be represented graphically as Feynman diagrams.
A Feynman diagram is a contribution of a particular class of particle paths, which join and split as described by the diagram. More precisely, and technically, a Feynman diagram is a graphical representation of a perturbative contribution to the transition amplitude or correlation function of a quantum mechanical or statistical field theory. Within the canonical formulation of quantum field theory, a Feynman diagram represents a term in the Wick's expansion of the perturbative S-matrix. Alternatively, the path integral formulation of quantum field theory represents the transition amplitude as a weighted sum of all possible histories of the system from the initial to the final state, in terms of either particles or fields. The transition amplitude is then given as the matrix element of the S-matrix between the initial and the final states of the quantum system.
Motivation and history
When calculating scattering cross-sections in particle physics, the interaction between particles can be described by starting from a free field that describes the incoming and outgoing particles, and including an interaction Hamiltonian to describe how the particles deflect one another. The amplitude for scattering is the sum of each possible interaction history over all possible intermediate particle states. The number of times the interaction Hamiltonian acts is the order of the perturbation expansion, and the time-dependent perturbation theory for fields is known as the Dyson series. When the intermediate states at intermediate times are energy eigenstates (collections of particles with a definite momentum) the series is called old-fashioned perturbation theory.
The Dyson series can be alternatively rewritten as a sum over Feynman diagrams, where at each vertex both the energy and momentum are conserved, but where the length of the energy-momentum four-vector is not necessarily equal to the mass. The Feynman diagrams are much easier to keep track of than old-fashioned terms, because the old-fashioned way treats the particle and antiparticle contributions as separate. Each Feynman diagram is the sum of exponentially many old-fashioned terms, because each internal line can separately represent either a particle or an antiparticle. In a non-relativistic theory, there are no antiparticles and there is no doubling, so each Feynman diagram includes only one term.
Feynman gave a prescription for calculating the amplitude for any given diagram from a field theory Lagrangian—the Feynman rules. Each internal line corresponds to a factor of the virtual particle's propagator; each vertex where lines meet gives a factor derived from an interaction term in the Lagrangian, and incoming and outgoing lines carry an energy, momentum, and spin.
In addition to their value as a mathematical tool, Feynman diagrams provide deep physical insight into the nature of particle interactions. Particles interact in every way available; in fact, intermediate virtual particles are allowed to propagate faster than light. The probability of each final state is then obtained by summing over all such possibilities. This is closely tied to the functional integral formulation of quantum mechanics, also invented by Feynman—see path integral formulation.
The naïve application of such calculations often produces diagrams whose amplitudes are infinite, because the short-distance particle interactions require a careful limiting procedure, to include particle self-interactions. The technique of renormalization, suggested by Ernst Stueckelberg and Hans Bethe and implemented by Dyson, Feynman, Schwinger, and Tomonaga compensates for this effect and eliminates the troublesome infinities. After renormalization, calculations using Feynman diagrams match experimental results with very high accuracy.
Feynman diagram and path integral methods are also used in statistical mechanics and can even be applied to classical mechanics.[3]
Alternative names
Murray Gell-Mann always referred to Feynman diagrams as Stueckelberg diagrams, after a Swiss physicist, Ernst Stueckelberg, who devised a similar notation many years earlier. Stueckelberg was motivated by the need for a manifestly covariant formalism for quantum field theory, but did not provide as automated a way to handle symmetry factors and loops, although he was first to find the correct physical interpretation in terms of forward and backward in time particle paths, all without the path-integral.[4]Historically, as a book-keeping device of covariant perturbation theory, the graphs were called Feynman–Dyson diagrams or Dyson graphs,[5] because when they were introduced, the path integral was unfamiliar, and Freeman Dyson's derivation from old-fashioned perturbation theory was easier to follow for physicists trained in earlier methods.[6] Feynman had to lobby hard for the diagrams, which confused the establishment physicists trained in equations and graphs.[7]
Representation of physical reality
In their presentations of fundamental interactions,[8][9] written from the particle physics perspective, Gerard 't Hooft and Martinus Veltman gave good arguments for taking the original, non-regularized Feynman diagrams as the most succinct representation of our present knowledge about the physics of quantum scattering of fundamental particles. Their motivations are consistent with the convictions of James Daniel Bjorken and Sidney Drell:[10]The Feynman graphs and rules of calculation summarize quantum field theory in a form in close contact with the experimental numbers one wants to understand. Although the statement of the theory in terms of graphs may imply perturbation theory, use of graphical methods in the many-body problem shows that this formalism is flexible enough to deal with phenomena of nonperturbative characters … Some modification of the Feynman rules of calculation may well outlive the elaborate mathematical structure of local canonical quantum field theory …So far there are no opposing opinions. In quantum field theories the Feynman diagrams are obtained from the Lagrangian by Feynman rules.
Dimensional regularization is a method for regularizing integrals in the evaluation of Feynman diagrams; it assigns values to them that are meromorphic functions of an auxiliary complex parameter d, called the dimension. Dimensional regularization writes a Feynman integral as an integral depending on the spacetime dimension d and spacetime points.
Particle-path interpretation
A Feynman diagram is a representation of quantum field theory processes in terms of particle paths. The particle trajectories are represented by the lines of the diagram, which can be squiggly or straight, with an arrow or without, depending on the type of particle. A point where lines connect to other lines is a vertex, and this is where the particles meet and interact: by emitting or absorbing new particles, deflecting one another, or changing type.There are three different types of lines: internal lines connect two vertices, incoming lines extend from "the past" to a vertex and represent an initial state, and outgoing lines extend from a vertex to "the future" and represent the final state (the latter two are also known as external lines). Sometimes, the bottom of the diagram is the past and the top the future; other times, the past is to the left and the future to the right. When calculating correlation functions instead of scattering amplitudes, there is no past and future and all the lines are internal. The particles then begin and end on little x's, which represent the positions of the operators whose correlation is being calculated.
Feynman diagrams are a pictorial representation of a contribution to the total amplitude for a process that can happen in several different ways. When a group of incoming particles are to scatter off each other, the process can be thought of as one where the particles travel over all possible paths, including paths that go backward in time.
Feynman diagrams are often confused with spacetime diagrams and bubble chamber images because they all describe particle scattering. Feynman diagrams are graphs that represent the trajectories of particles in intermediate stages of a scattering process. Unlike a bubble chamber picture, only the sum of all the Feynman diagrams represent any given particle interaction; particles do not choose a particular diagram each time they interact. The law of summation is in accord with the principle of superposition—every diagram contributes to the total amplitude for the process.
Description
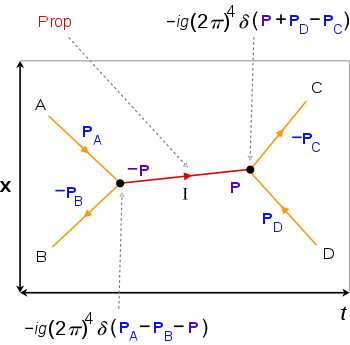
General features of the scattering process A + B → C + D:
• internal lines (red) for intermediate particles and processes, which has a propagator factor ("prop"), external lines (orange) for incoming/outgoing particles to/from vertices (black),
• at each vertex there is 4-momentum conservation using delta functions, 4-momenta entering the vertex are positive while those leaving are negative, the factors at each vertex and internal line are multiplied in the amplitude integral,
• space x and time t axes are not always shown, directions of external lines correspond to passage of time.
• internal lines (red) for intermediate particles and processes, which has a propagator factor ("prop"), external lines (orange) for incoming/outgoing particles to/from vertices (black),
• at each vertex there is 4-momentum conservation using delta functions, 4-momenta entering the vertex are positive while those leaving are negative, the factors at each vertex and internal line are multiplied in the amplitude integral,
• space x and time t axes are not always shown, directions of external lines correspond to passage of time.
A Feynman diagram represents a perturbative contribution to the amplitude of a quantum transition from some initial quantum state to some final quantum state.
For example, in the process of electron-positron annihilation the initial state is one electron and one positron, the final state: two photons.
The initial state is often assumed to be at the left of the diagram and the final state at the right (although other conventions are also used quite often).
A Feynman diagram consists of points, called vertices, and lines attached to the vertices.
The particles in the initial state are depicted by lines sticking out in the direction of the initial state (e.g., to the left), the particles in the final state are represented by lines sticking out in the direction of the final state (e.g., to the right).
In QED there are two types of particles: electrons/positrons (called fermions) and photons (called gauge bosons). They are represented in Feynman diagrams as follows:
- Electron in the initial state is represented by a solid line with an arrow pointing toward the vertex (→•).
- Electron in the final state is represented by a line with an arrow pointing away from the vertex: (•→).
- Positron in the initial state is represented by a solid line with an arrow pointing away from the vertex: (←•).
- Positron in the final state is represented by a line with an arrow pointing toward the vertex: (•←).
- Photon in the initial and the final state is represented by a wavy line (~• and •~).
The vertices might be connected by a bosonic or fermionic propagator. A bosonic propagator is represented by a wavy line connecting two vertices (•~•). A fermionic propagator is represented by a solid line (with an arrow in one or another direction) connecting two vertices, (•←•).
The number of vertices gives the order of the term in the perturbation series expansion of the transition amplitude.
Electron–positron annihilation example
Feynman diagram of electron/positron annihilation
- e+ e− → 2γ
In the initial state (at the bottom; early time) there is one electron (e−) and one positron (e+) and in the final state (at the top; late time) there are two photons (γ).
Canonical quantization formulation
The probability amplitude for a transition of a quantum system from the initial state |i⟩ to the final state | f ⟩ is given by the matrix elementIn the canonical quantum field theory the S-matrix is represented within the interaction picture by the perturbation series in the powers of the interaction Lagrangian,
A Feynman diagram is a graphical representation of a term in the Wick's expansion of the time-ordered product in the nth order term S(n) of the S-matrix,
Feynman rules
The diagrams are drawn according to the Feynman rules, which depend upon the interaction Lagrangian. For the QED interaction Lagrangian- Each integration coordinate xj is represented by a point (sometimes called a vertex);
- A bosonic propagator is represented by a wiggly line connecting two points;
- A fermionic propagator is represented by a solid line connecting two points;
- A bosonic field
is represented by a wiggly line attached to the point xi;
- A fermionic field ψ(xi) is represented by a solid line attached to the point xi with an arrow toward the point;
- An anti-fermionic field ψ(xi) is represented by a solid line attached to the point xi with an arrow away from the point;
Example: second order processes in QED
The second order perturbation term in the S-matrix isScattering of fermions
The Feynman diagram of the term
 |
The Wick's expansion of the integrand gives (among others) the following term
- e− e− scattering (initial state at the right, final state at the left of the diagram);
- e+ e+ scattering (initial state at the left, final state at the right of the diagram);
- e− e+ scattering (initial state at the bottom/top, final state at the top/bottom of the diagram).
Compton scattering and annihilation/generation of e− e+ pairs
Another interesting term in the expansion isPath integral formulation
In a path integral, the field Lagrangian, integrated over all possible field histories, defines the probability amplitude to go from one field configuration to another. In order to make sense, the field theory should have a well-defined ground state, and the integral should be performed a little bit rotated into imaginary time, i.e. a Wick rotation.Scalar field Lagrangian
A simple example is the free relativistic scalar field in d dimensions, whose action integral is:The path integral gives the expectation value of operators between the initial and final state:
The initial-to-final amplitudes are ill-defined if one thinks of the continuum limit right from the beginning, because the fluctuations in the field can become unbounded. So the path-integral can be thought of as on a discrete square lattice, with lattice spacing a and the limit a → 0 should be taken carefully[clarification needed]. If the final results do not depend on the shape of the lattice or the value of a, then the continuum limit exists.
On a lattice
On a lattice, (i), the field can be expanded in Fourier modes:It is also convenient from time to time to consider the space-time volume to be finite, so that the k modes are also a lattice. This is not strictly as necessary as the space-lattice limit, because interactions in k are not localized, but it is convenient for keeping track of the factors in front of the k-integrals and the momentum-conserving delta functions that will arise.
On a lattice, (ii), the action needs to be discretized:
In terms of the lattice Fourier modes, the action can be written:
.
The field φ is real-valued, so the Fourier transform obeys:
For a complex scalar field with action
Integrating over all different values of φ(x) is equivalent to integrating over all Fourier modes, because taking a Fourier transform is a unitary linear transformation of field coordinates. When you change coordinates in a multidimensional integral by a linear transformation, the value of the new integral is given by the determinant of the transformation matrix. If
The matrix that changes coordinates from φ(x) to φ(k) can be read off from the definition of a Fourier transform.
In imaginary time, the Euclidean action becomes positive definite, and can be interpreted as a probability distribution. The probability of a field having values φk is
Monte Carlo
The path integral defines a probabilistic algorithm to generate a Euclidean scalar field configuration. Randomly pick the real and imaginary parts of each Fourier mode at wavenumber k to be a Gaussian random variable with variance 1/k2. This generates a configuration φC(k) at random, and the Fourier transform gives φC(x). For real scalar fields, the algorithm must generate only one of each pair φ(k), φ(−k), and make the second the complex conjugate of the first.To find any correlation function, generate a field again and again by this procedure, and find the statistical average:
For free fields with a quadratic action, the probability distribution is a high-dimensional Gaussian, and the statistical average is given by an explicit formula. But the Monte Carlo method also works well for bosonic interacting field theories where there is no closed form for the correlation functions.
Scalar propagator
Each mode is independently Gaussian distributed. The expectation of field modes is easy to calculate:It is important to emphasize that the delta functions contain factors of 2π, so that they cancel out the 2π factors in the measure for k integrals.
Equation of motion
The form of the propagator can be more easily found by using the equation of motion for the field. From the Lagrangian, the equation of motion is:Wick theorem
Because each field mode is an independent Gaussian, the expectation values for the product of many field modes obeys Wick's theorem:An interpretation of Wick's theorem is that each field insertion can be thought of as a dangling line, and the expectation value is calculated by linking up the lines in pairs, putting a delta function factor that ensures that the momentum of each partner in the pair is equal, and dividing by the propagator.
Higher Gaussian moments — completing Wick's theorem
There is a subtle point left before Wick's theorem is proved—what if more than two of the phis have the same momentum? If it's an odd number, the integral is zero; negative values cancel with the positive values. But if the number is even, the integral is positive. The previous demonstration assumed that the phis would only match up in pairs.But the theorem is correct even when arbitrarily many of the φ are equal, and this is a notable property of Gaussian integration:
Interaction
Interactions are represented by higher order contributions, since quadratic contributions are always Gaussian. The simplest interaction is the quartic self-interaction, with an action:Where SF is the free action, whose correlation functions are given by Wick's theorem. The exponential of S in the path integral can be expanded in powers of λ, giving a series of corrections to the free action.
To compute a correlation function in the interacting theory, there is a contribution from the X terms now. For example, the path-integral for the four-field correlator:
which in the free field was only nonzero when the momenta k were equal in pairs, is now nonzero for all values of k. The momenta of the insertions φ(ki) can now match up with the momenta of the Xs in the expansion. The insertions should also be thought of as half-lines, four in this case, which carry a momentum k, but one that is not integrated.
The lowest-order contribution comes from the first nontrivial term e−SFX in the Taylor expansion of the action. Wick's theorem requires that the momenta in the X half-lines, the φ(k) factors in X, should match up with the momenta of the external half-lines in pairs. The new contribution is equal to:
Feynman diagrams
The expansion of the action in powers of X gives a series of terms with progressively higher number of Xs. The contribution from the term with exactly n Xs is called nth order.The nth order terms has:
- 4n internal half-lines, which are the factors of φ(k) from the Xs. These all end on a vertex, and are integrated over all possible k.
- external half-lines, which are the come from the φ(k) insertions in the integral.
The diagrams that are formed by linking the half-lines in the Xs with the external half-lines, representing insertions, are the Feynman diagrams of this theory. Each line carries a factor of 1/k2, the propagator, and either goes from vertex to vertex, or ends at an insertion. If it is internal, it is integrated over. At each vertex, the total incoming k is equal to the total outgoing k.
The number of ways of making a diagram by joining half-lines into lines almost completely cancels the factorial factors coming from the Taylor series of the exponential and the 4! at each vertex.
Loop order
A forest diagram is one where all the internal lines have momentum that is completely determined by the external lines and the condition that the incoming and outgoing momentum are equal at each vertex. The contribution of these diagrams is a product of propagators, without any integration. A tree diagram is a connected forest diagram.An example of a tree diagram is the one where each of four external lines end on an X. Another is when three external lines end on an X, and the remaining half-line joins up with another X, and the remaining half-lines of this X run off to external lines. These are all also forest diagrams (as every tree is a forest); an example of a forest that is not a tree is when eight external lines end on two Xs.
It is easy to verify that in all these cases, the momenta on all the internal lines is determined by the external momenta and the condition of momentum conservation in each vertex.
A diagram that is not a forest diagram is called a loop diagram, and an example is one where two lines of an X are joined to external lines, while the remaining two lines are joined to each other. The two lines joined to each other can have any momentum at all, since they both enter and leave the same vertex. A more complicated example is one where two Xs are joined to each other by matching the legs one to the other. This diagram has no external lines at all.
The reason loop diagrams are called loop diagrams is because the number of k-integrals that are left undetermined by momentum conservation is equal to the number of independent closed loops in the diagram, where independent loops are counted as in homology theory. The homology is real-valued (actually Rd valued), the value associated with each line is the momentum. The boundary operator takes each line to the sum of the end-vertices with a positive sign at the head and a negative sign at the tail. The condition that the momentum is conserved is exactly the condition that the boundary of the k-valued weighted graph is zero.
A set of valid k-values can be arbitrarily redefined whenever there is a closed loop. A closed loop is a cyclical path of adjacent vertices that never revisits the same vertex. Such a cycle can be thought of as the boundary of a hypothetical 2-cell. The k-labellings of a graph that conserve momentum (i.e. which has zero boundary) up to redefinitions of k (i.e. up to boundaries of 2-cells) define the first homology of a graph. The number of independent momenta that are not determined is then equal to the number of independent homology loops. For many graphs, this is equal to the number of loops as counted in the most intuitive way.
Symmetry factors
The number of ways to form a given Feynman diagram by joining together half-lines is large, and by Wick's theorem, each way of pairing up the half-lines contributes equally. Often, this completely cancels the factorials in the denominator of each term, but the cancellation is sometimes incomplete.The uncancelled denominator is called the symmetry factor of the diagram. The contribution of each diagram to the correlation function must be divided by its symmetry factor.
For example, consider the Feynman diagram formed from two external lines joined to one X, and the remaining two half-lines in the X joined to each other. There are 4 × 3 ways to join the external half-lines to the X, and then there is only one way to join the two remaining lines to each other. The X comes divided by 4! = 4 × 3 × 2, but the number of ways to link up the X half lines to make the diagram is only 4 × 3, so the contribution of this diagram is divided by two.
For another example, consider the diagram formed by joining all the half-lines of one X to all the half-lines of another X. This diagram is called a vacuum bubble, because it does not link up to any external lines. There are 4! ways to form this diagram, but the denominator includes a 2! (from the expansion of the exponential, there are two Xs) and two factors of 4!. The contribution is multiplied by 4!/2 × 4! × 4! = 1/48.
Another example is the Feynman diagram formed from two Xs where each X links up to two external lines, and the remaining two half-lines of each X are joined to each other. The number of ways to link an X to two external lines is 4 × 3, and either X could link up to either pair, giving an additional factor of 2. The remaining two half-lines in the two Xs can be linked to each other in two ways, so that the total number of ways to form the diagram is 4 × 3 × 4 × 3 × 2 × 2, while the denominator is 4! × 4! × 2!. The total symmetry factor is 2, and the contribution of this diagram is divided by 2.
The symmetry factor theorem gives the symmetry factor for a general diagram: the contribution of each Feynman diagram must be divided by the order of its group of automorphisms, the number of symmetries that it has.
An automorphism of a Feynman graph is a permutation M of the lines and a permutation N of the vertices with the following properties:
- If a line l goes from vertex v to vertex v′, then M(l) goes from N(v) to N(v′). If the line is undirected, as it is for a real scalar field, then M(l) can go from N(v′) to N(v) too.
- If a line l ends on an external line, M(l) ends on the same external line.
- If there are different types of lines, M(l) should preserve the type.
Proof: To prove this theorem, label all the internal and external lines of a diagram with a unique name. Then form the diagram by linking a half-line to a name and then to the other half line.
Now count the number of ways to form the named diagram. Each permutation of the Xs gives a different pattern of linking names to half-lines, and this is a factor of n!. Each permutation of the half-lines in a single X gives a factor of 4!. So a named diagram can be formed in exactly as many ways as the denominator of the Feynman expansion.
But the number of unnamed diagrams is smaller than the number of named diagram by the order of the automorphism group of the graph.
Connected diagrams: linked-cluster theorem
Roughly speaking, a Feynman diagram is called connected if all vertices and propagator lines are linked by a sequence of vertices and propagators of the diagram itself. If one views it as an undirected graph it is connected. The remarkable relevance of such diagrams in QFTs is due to the fact that they are sufficient to determine the quantum partition function Z[J]. More precisely, connected Feynman diagrams determineA scheme to successively create such contributions from the Dk to Z[J] is obtained by
Vacuum bubbles
An immediate consequence of the linked-cluster theorem is that all vacuum bubbles, diagrams without external lines, cancel when calculating correlation functions. A correlation function is given by a ratio of path-integrals:The vacuum bubbles then are only useful for determining Z itself, which from the definition of the path integral is equal to:
Sources
Correlation functions are the sum of the connected Feynman diagrams, but the formalism treats the connected and disconnected diagrams differently. Internal lines end on vertices, while external lines go off to insertions. Introducing sources unifies the formalism, by making new vertices where one line can end.Sources are external fields, fields that contribute to the action, but are not dynamical variables. A scalar field source is another scalar field h that contributes a term to the (Lorentz) Lagrangian:
The sum of the connected diagrams in the presence of sources includes a term for each connected diagram in the absence of sources, except now the diagrams can end on the source. Traditionally, a source is represented by a little "×" with one line extending out, exactly as an insertion.
The field h is not dynamical, which means that there is no path integral over h: h is just a parameter in the Lagrangian, which varies from point to point. The path integral for the field is:
The partition function is now a function of the field h, and the physical partition function is the value when h is the zero function:
The correlation functions are derivatives of the path integral with respect to the source:
Spin 1/2; "photons" and "ghosts"
Spin 1/2: Grassmann integrals
The field path integral can be extended to the Fermi case, but only if the notion of integration is expanded. A Grassmann integral of a free Fermi field is a high-dimensional determinant or Pfaffian, which defines the new type of Gaussian integration appropriate for Fermi fields.The two fundamental formulas of Grassmann integration are:
In matrix notation, where ψ and η are Grassmann-valued row vectors, η and ψ are Grassmann-valued column vectors, and M is a real-valued matrix:
where the last equality is a consequence of the translation invariance of the Grassmann integral. The Grassmann variables η are external sources for ψ, and differentiating with respect to η pulls down factors of ψ.
For real Grassmann fields, for Majorana fermions, the path integral a Pfaffian times a source quadratic form, and the formulas give the square root of the determinant, just as they do for real Bosonic fields. The propagator is still the inverse of the quadratic part.
The free Dirac Lagrangian:
where S is the sign of the permutation that reorders the sequence of ψ and ψ to put the ones that are paired up to make the delta-functions next to each other, with the ψ coming right before the ψ. Since a ψ, ψ pair is a commuting element of the Grassmann algebra, it doesn't matter what order the pairs are in. If more than one ψ, ψ pair have the same k, the integral is zero, and it is easy to check that the sum over pairings gives zero in this case (there are always an even number of them). This is the Grassmann analog of the higher Gaussian moments that completed the Bosonic Wick's theorem earlier.
The rules for spin-1/2 Dirac particles are as follows: The propagator is the inverse of the Dirac operator, the lines have arrows just as for a complex scalar field, and the diagram acquires an overall factor of −1 for each closed Fermi loop. If there are an odd number of Fermi loops, the diagram changes sign. Historically, the −1 rule was very difficult for Feynman to discover. He discovered it after a long process of trial and error, since he lacked a proper theory of Grassmann integration.
The rule follows from the observation that the number of Fermi lines at a vertex is always even. Each term in the Lagrangian must always be Bosonic. A Fermi loop is counted by following Fermionic lines until one comes back to the starting point, then removing those lines from the diagram. Repeating this process eventually erases all the Fermionic lines: this is the Euler algorithm to 2-color a graph, which works whenever each vertex has even degree. Note that the number of steps in the Euler algorithm is only equal to the number of independent Fermionic homology cycles in the common special case that all terms in the Lagrangian are exactly quadratic in the Fermi fields, so that each vertex has exactly two Fermionic lines. When there are four-Fermi interactions (like in the Fermi effective theory of the weak nuclear interactions) there are more k-integrals than Fermi loops. In this case, the counting rule should apply the Euler algorithm by pairing up the Fermi lines at each vertex into pairs that together form a bosonic factor of the term in the Lagrangian, and when entering a vertex by one line, the algorithm should always leave with the partner line.
To clarify and prove the rule, consider a Feynman diagram formed from vertices, terms in the Lagrangian, with Fermion fields. The full term is Bosonic, it is a commuting element of the Grassmann algebra, so the order in which the vertices appear is not important. The Fermi lines are linked into loops, and when traversing the loop, one can reorder the vertex terms one after the other as one goes around without any sign cost. The exception is when you return to the starting point, and the final half-line must be joined with the unlinked first half-line. This requires one permutation to move the last ψ to go in front of the first ψ, and this gives the sign.
This rule is the only visible effect of the exclusion principle in internal lines. When there are external lines, the amplitudes are antisymmetric when two Fermi insertions for identical particles are interchanged. This is automatic in the source formalism, because the sources for Fermi fields are themselves Grassmann valued.
Spin 1: photons
The naive propagator for photons is infinite, since the Lagrangian for the A-field is:To fix this problem, one needs to fix a gauge. The most convenient way is to demand that the divergence of A is some function f, whose value is random from point to point. It does no harm to integrate over the values of f, since it only determines the choice of gauge. This procedure inserts the following factor into the path integral for A:
If the averaging over f is done with a coefficient different from 1/2, the two terms don't cancel completely. This gives a covariant Lagrangian with a coefficient
 , which does not affect anything:
, which does not affect anything:Spin 1: non-Abelian ghosts
To find the Feynman rules for non-Abelian gauge fields, the procedure that performs the gauge fixing must be carefully corrected to account for a change of variables in the path-integral.The gauge fixing factor has an extra determinant from popping the delta function:
The factor in front is the volume of the gauge group, and it contributes a constant, which can be discarded. The remaining integral is over the gauge fixed action.
The diagrams are derived from this action. The propagator for the spin-1 fields has the usual Feynman form. There are vertices of degree 3 with momentum factors whose couplings are the structure constants, and vertices of degree 4 whose couplings are products of structure constants. There are additional ghost loops, which cancel out timelike and longitudinal states in A loops.
In the Abelian case, the determinant for covariant gauges does not depend on A, so the ghosts do not contribute to the connected diagrams.
Particle-path representation
Feynman diagrams were originally discovered by Feynman, by trial and error, as a way to represent the contribution to the S-matrix from different classes of particle trajectories.Schwinger representation
The Euclidean scalar propagator has a suggestive representation:The path-integral representation for the propagator is then:
The Schwinger representation is both useful for making manifest the particle aspect of the propagator, and for symmetrizing denominators of loop diagrams.
Combining denominators
The Schwinger representation has an immediate practical application to loop diagrams. For example, for the diagram in the φ4 theory formed by joining two xs together in two half-lines, and making the remaining lines external, the integral over the internal propagators in the loop is:The Jacobian for this transformation of variables is easy to work out from the identities:
.
leaving only the v-integral. This method, invented by Schwinger but usually attributed to Feynman, is called combining denominator. Abstractly, it is the elementary identity:
Once the denominators are combined, a shift in k to k′ = k + vp symmetrizes everything:
This form shows that the moment that p2 is more negative than four times the mass of the particle in the loop, which happens in a physical region of Lorentz space, the integral has a cut. This is exactly when the external momentum can create physical particles.
When the loop has more vertices, there are more denominators to combine:
The Jacobian for the coordinate transformation can be worked out as before:
Since the numerator of the integrand is not involved, the same prescription works for any loop, no matter what the spins are carried by the legs. The interpretation of the parameters vi is that they are the fraction of the total proper time spent on each leg.
Scattering
The correlation functions of a quantum field theory describe the scattering of particles. The definition of "particle" in relativistic field theory is not self-evident, because if you try to determine the position so that the uncertainty is less than the compton wavelength, the uncertainty in energy is large enough to produce more particles and antiparticles of the same type from the vacuum. This means that the notion of a single-particle state is to some extent incompatible with the notion of an object localized in space.In the 1930s, Wigner gave a mathematical definition for single-particle states: they are a collection of states that form an irreducible representation of the Poincaré group. Single particle states describe an object with a finite mass, a well defined momentum, and a spin. This definition is fine for protons and neutrons, electrons and photons, but it excludes quarks, which are permanently confined, so the modern point of view is more accommodating: a particle is anything whose interaction can be described in terms of Feynman diagrams, which have an interpretation as a sum over particle trajectories.
A field operator can act to produce a one-particle state from the vacuum, which means that the field operator φ(x) produces a superposition of Wigner particle states. In the free field theory, the field produces one particle states only. But when there are interactions, the field operator can also produce 3-particle, 5-particle (if there is no +/− symmetry also 2, 4, 6 particle) states too. To compute the scattering amplitude for single particle states only requires a careful limit, sending the fields to infinity and integrating over space to get rid of the higher-order corrections.
The relation between scattering and correlation functions is the LSZ-theorem: The scattering amplitude for n particles to go to m particles in a scattering event is the given by the sum of the Feynman diagrams that go into the correlation function for n + m field insertions, leaving out the propagators for the external legs.
For example, for the λφ4 interaction of the previous section, the order λ contribution to the (Lorentz) correlation function is:
Non-relativistic single particle states are labeled by the momentum k, and they are chosen to have the same norm at every value of k. This is because the nonrelativistic unit operator on single particle states is:
For nonrelativistic values of k, the relativistic normalization is the same as the nonrelativistic normalization (up to a constant factor √m). In this limit, the φ4 invariant scattering amplitude is still constant. The particles created by the field φ scatter in all directions with equal amplitude.
The nonrelativistic potential, which scatters in all directions with an equal amplitude (in the Born approximation), is one whose Fourier transform is constant—a delta-function potential. The lowest order scattering of the theory reveals the non-relativistic interpretation of this theory—it describes a collection of particles with a delta-function repulsion. Two such particles have an aversion to occupying the same point at the same time.
Nonperturbative effects
Thinking of Feynman diagrams as a perturbation series, nonperturbative effects like tunneling do not show up, because any effect that goes to zero faster than any polynomial does not affect the Taylor series. Even bound states are absent, since at any finite order particles are only exchanged a finite number of times, and to make a bound state, the binding force must last forever.But this point of view is misleading, because the diagrams not only describe scattering, but they also are a representation of the short-distance field theory correlations. They encode not only asymptotic processes like particle scattering, they also describe the multiplication rules for fields, the operator product expansion. Nonperturbative tunneling processes involve field configurations that on average get big when the coupling constant gets small, but each configuration is a coherent superposition of particles whose local interactions are described by Feynman diagrams. When the coupling is small, these become collective processes that involve large numbers of particles, but where the interactions between each of the particles is simple.[citation needed]
This means that nonperturbative effects show up asymptotically in resummations of infinite classes of diagrams, and these diagrams can be locally simple. The graphs determine the local equations of motion, while the allowed large-scale configurations describe non-perturbative physics. But because Feynman propagators are nonlocal in time, translating a field process to a coherent particle language is not completely intuitive, and has only been explicitly worked out in certain special cases. In the case of nonrelativistic bound states, the Bethe–Salpeter equation describes the class of diagrams to include to describe a relativistic atom. For quantum chromodynamics, the Shifman Vainshtein Zakharov sum rules describe non-perturbatively excited long-wavelength field modes in particle language, but only in a phenomenological way.
The number of Feynman diagrams at high orders of perturbation theory is very large, because there are as many diagrams as there are graphs with a given number of nodes. Nonperturbative effects leave a signature on the way in which the number of diagrams and resummations diverge at high order. It is only because non-perturbative effects appear in hidden form in diagrams that it was possible to analyze nonperturbative effects in string theory, where in many cases a Feynman description is the only one available.

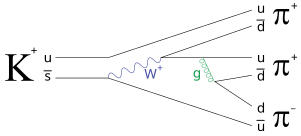























































![iW[J]\equiv \ln Z[J].](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03aef8a72b98aa83afeccb54512c30e74dd0762)
![Z[J]\propto \sum _{k}{D_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c7b6e822c008b3a97c2e25ae9a16d806decc9e7)


![{\displaystyle Z[J]\propto \prod _{i}{\sum _{n_{i}=0}^{\infty }{\frac {C_{i}^{n_{i}}}{n_{i}!}}}=\exp {\sum _{i}{C_{i}}}\propto \exp {W[J]}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50886f901a854ec595c3b9727199e105ad57b73f)




![{\displaystyle \log {\big (}Z[h]{\big )}=\sum _{n,C}h(k_{1})h(k_{2})\cdots h(k_{n})C(k_{1},\cdots ,k_{n})\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bb5547d19ab5fdb64ff700ecc8e3835311e446c)
![{\displaystyle Z[h]=\int e^{iS+i\int h\phi }\,D\phi \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7ea2bd0c5073e68ceff5ddba15e555ce70f92a6)

![{\displaystyle Z[h]=\int e^{iS}e^{i\int _{x}h(x)\phi (x)}\,D\phi =\left\langle e^{ih\phi }\right\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b66d7bcdfcff36ef81756bc3cda53721bd81d685)



![{\displaystyle \left\langle \phi (x)\right\rangle ={\frac {1}{Z}}{\frac {\partial }{\partial h(x)}}Z[h]={\frac {\partial }{\partial h(x)}}\log {\big (}Z[h]{\big )}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/370ee6c83d4c8ed003752105106c84371401dfa1)















































