Quantum mechanics is the science of the very small. It explains the behavior of matter and its interactions with energy on the scale of atoms and subatomic particles. By contrast, classical physics
only explains matter and energy on a scale familiar to human
experience, including the behavior of astronomical bodies such as the
Moon. Classical physics is still used in much of modern science and
technology. However, towards the end of the 19th century, scientists
discovered phenomena in both the large (macro) and the small (micro) worlds that classical physics could not explain.
The desire to resolve inconsistencies between observed phenomena and
classical theory led to two major revolutions in physics that created a
shift in the original scientific paradigm: the theory of relativity and the development of quantum mechanics.
This article describes how physicists discovered the limitations of
classical physics and developed the main concepts of the quantum theory
that replaced it in the early decades of the 20th century. It describes
these concepts in roughly the order in which they were first discovered.
Light behaves in some aspects like particles and in other aspects like waves. Matter—the "stuff" of the universe consisting of particles such as electrons and atoms—exhibits wavelike behavior too. Some light sources, such as neon lights, give off only certain frequencies of light. Quantum mechanics shows that light, along with all other forms of electromagnetic radiation, comes in discrete units, called photons, and predicts its energies, colors, and spectral intensities. A single photon is a quantum, or smallest observable amount, of the electromagnetic field because a partial photon has never been observed. More broadly, quantum mechanics shows that many quantities, such as angular momentum, that appeared continuous in the zoomed-out view of classical mechanics, turn out to be (at the small, zoomed-in scale of quantum mechanics) quantized. Angular momentum is required to take on one of a set of discrete allowable values, and since the gap between these values is so minute, the discontinuity is only apparent at the atomic level.
Many aspects of quantum mechanics are counterintuitive and can seem paradoxical, because they describe behavior quite different from that seen at larger length scales. In the words of quantum physicist Richard Feynman, quantum mechanics deals with "nature as She is – absurd". For example, the uncertainty principle of quantum mechanics means that the more closely one pins down one measurement (such as the position of a particle), the less accurate another measurement pertaining to the same particle (such as its momentum) must become.
Light behaves in some aspects like particles and in other aspects like waves. Matter—the "stuff" of the universe consisting of particles such as electrons and atoms—exhibits wavelike behavior too. Some light sources, such as neon lights, give off only certain frequencies of light. Quantum mechanics shows that light, along with all other forms of electromagnetic radiation, comes in discrete units, called photons, and predicts its energies, colors, and spectral intensities. A single photon is a quantum, or smallest observable amount, of the electromagnetic field because a partial photon has never been observed. More broadly, quantum mechanics shows that many quantities, such as angular momentum, that appeared continuous in the zoomed-out view of classical mechanics, turn out to be (at the small, zoomed-in scale of quantum mechanics) quantized. Angular momentum is required to take on one of a set of discrete allowable values, and since the gap between these values is so minute, the discontinuity is only apparent at the atomic level.
Many aspects of quantum mechanics are counterintuitive and can seem paradoxical, because they describe behavior quite different from that seen at larger length scales. In the words of quantum physicist Richard Feynman, quantum mechanics deals with "nature as She is – absurd". For example, the uncertainty principle of quantum mechanics means that the more closely one pins down one measurement (such as the position of a particle), the less accurate another measurement pertaining to the same particle (such as its momentum) must become.
The first quantum theory: Max Planck and black-body radiation
Hot
metalwork. The yellow-orange glow is the visible part of the thermal
radiation emitted due to the high temperature. Everything else in the
picture is glowing with thermal radiation as well, but less brightly and
at longer wavelengths than the human eye can detect. A far-infrared
camera can observe this radiation.
Thermal radiation
is electromagnetic radiation emitted from the surface of an object due
to the object's internal energy. If an object is heated sufficiently, it
starts to emit light at the red end of the spectrum, as it becomes red hot.
Heating it further causes the color to change from red to
yellow, white, and blue, as it emits light at increasingly shorter
wavelengths (higher frequencies). A perfect emitter is also a perfect
absorber: when it is cold, such an object looks perfectly black,
because it absorbs all the light that falls on it and emits none.
Consequently, an ideal thermal emitter is known as a black body, and the radiation it emits is called black-body radiation.
Predictions
of the amount of thermal radiation of different frequencies emitted by a
body. Correct values predicted by Planck's law (green) contrasted
against the classical values of Rayleigh-Jeans law (red) and Wien approximation (blue).
In the late 19th century, thermal radiation had been fairly well characterized experimentally.
However, classical physics led to the Rayleigh-Jeans law, which, as
shown in the figure, agrees with experimental results well at low
frequencies, but strongly disagrees at high frequencies. Physicists
searched for a single theory that explained all the experimental
results.
The first model that was able to explain the full spectrum of thermal radiation was put forward by Max Planck in 1900. He proposed a mathematical model in which the thermal radiation was in equilibrium with a set of harmonic oscillators.
To reproduce the experimental results, he had to assume that each
oscillator emitted an integer number of units of energy at its single
characteristic frequency, rather than being able to emit any arbitrary
amount of energy. In other words, the energy emitted by an oscillator
was quantized. The quantum
of energy for each oscillator, according to Planck, was proportional to
the frequency of the oscillator; the constant of proportionality is now
known as the Planck constant. The Planck constant, usually written as h, has the value of 6.63×10−34 J s. So, the energy E of an oscillator of frequency f is given by
To change the color of such a radiating body, it is necessary to change its temperature. Planck's law
explains why: increasing the temperature of a body allows it to emit
more energy overall, and means that a larger proportion of the energy is
towards the violet end of the spectrum.
Planck's law
was the first quantum theory in physics, and Planck won the Nobel Prize
in 1918 "in recognition of the services he rendered to the advancement
of Physics by his discovery of energy quanta".
At the time, however, Planck's view was that quantization was purely a
heuristic mathematical construct, rather than (as is now believed) a
fundamental change in our understanding of the world.
Photons: the quantization of light
Albert Einstein c. 1905
In 1905, Albert Einstein
took an extra step. He suggested that quantization was not just a
mathematical construct, but that the energy in a beam of light actually
occurs in individual packets, which are now called photons. The energy of a single photon is given by its frequency multiplied by Planck's constant:
For centuries, scientists had debated between two possible theories of light: was it a wave or did it instead comprise a stream of tiny particles?
By the 19th century, the debate was generally considered to have been
settled in favor of the wave theory, as it was able to explain observed
effects such as refraction, diffraction, interference and polarization. James Clerk Maxwell had shown that electricity, magnetism and light are all manifestations of the same phenomenon: the electromagnetic field. Maxwell's equations, which are the complete set of laws of classical electromagnetism,
describe light as waves: a combination of oscillating electric and
magnetic fields. Because of the preponderance of evidence in favor of
the wave theory, Einstein's ideas were met initially with great
skepticism. Eventually, however, the photon model became favored. One of
the most significant pieces of evidence in its favor was its ability to
explain several puzzling properties of the photoelectric effect,
described in the following section. Nonetheless, the wave analogy
remained indispensable for helping to understand other characteristics
of light: diffraction, refraction and interference.
The photoelectric effect
Light
(red arrows, left) is shone upon a metal. If the light frequency is
high enough (i.e. sufficient energy), electrons are ejected (blue
arrows, right).
In 1887, Heinrich Hertz observed that when light with sufficient frequency hits a metallic surface, it emits electrons. In 1902, Philipp Lenard discovered that the maximum possible energy of an ejected electron is related to the frequency of the light, not to its intensity:
if the frequency is too low, no electrons are ejected regardless of the
intensity. Strong beams of light toward the red end of the spectrum
might produce no electrical potential at all, while weak beams of light
toward the violet end of the spectrum would produce higher and higher
voltages. The lowest frequency of light that can cause electrons to be
emitted, called the threshold frequency, is different for different
metals. This observation is at odds with classical electromagnetism,
which predicts that the electron's energy should be proportional to the
intensity of the radiation.
So when physicists first discovered devices exhibiting the
photoelectric effect, they initially expected that a higher intensity of
light would produce a higher voltage from the photoelectric device.
Einstein explained the effect by postulating that a beam of light is a stream of particles ("photons") and that, if the beam is of frequency f, then each photon has an energy equal to hf. An electron is likely to be struck only by a single photon, which imparts at most an energy hf to the electron. Therefore, the intensity of the beam has no effect and only its frequency determines the maximum energy that can be imparted to the electron.
To explain the threshold effect, Einstein argued that it takes a certain amount of energy, called the work function and denoted by φ, to remove an electron from the metal.
This amount of energy is different for each metal. If the energy of the
photon is less than the work function, then it does not carry
sufficient energy to remove the electron from the metal. The threshold
frequency, f0, is the frequency of a photon whose energy is equal to the work function:
If f is greater than f0, the energy hf is enough to remove an electron. The ejected electron has a kinetic energy, EK, which is, at most, equal to the photon's energy minus the energy needed to dislodge the electron from the metal:
Einstein's description of light as being composed of particles
extended Planck's notion of quantised energy, which is that a single
photon of a given frequency, f, delivers an invariant amount of energy, hf.
In other words, individual photons can deliver more or less energy, but
only depending on their frequencies. In nature, single photons are
rarely encountered. The Sun and emission sources available in the 19th
century emit vast numbers of photons every second, and so the importance
of the energy carried by each individual photon was not obvious.
Einstein's idea that the energy contained in individual units of light
depends on their frequency made it possible to explain experimental
results that had hitherto seemed quite counter intuitive. However,
although the photon is a particle, it was still being described as
having the wave-like property of frequency. Effectively, the account of
light as a particle is insufficient, and its wave-like nature is still
required.
Consequences of light being quantized
The relationship between the frequency of electromagnetic radiation and the energy of each individual photon is why ultraviolet light can cause sunburn, but visible or infrared light cannot. A photon of ultraviolet light delivers a high amount of energy—enough
to contribute to cellular damage such as occurs in a sunburn. A photon
of infrared light delivers less energy—only enough to warm one's skin.
So, an infrared lamp can warm a large surface, perhaps large enough to
keep people comfortable in a cold room, but it cannot give anyone a
sunburn.
All photons of the same frequency have identical energy, and all photons of different frequencies have proportionally (order 1, Ephoton = hf ) different energies.
However, although the energy imparted by photons is invariant at any
given frequency, the initial energy state of the electrons in a
photoelectric device prior to absorption of light is not necessarily
uniform. Anomalous results may occur in the case of individual
electrons. For instance, an electron that was already excited above the
equilibrium level of the photoelectric device might be ejected when it
absorbed uncharacteristically low frequency illumination. Statistically,
however, the characteristic behavior of a photoelectric device reflects
the behavior of the vast majority of its electrons, which are at their
equilibrium level. This point is helpful in comprehending the
distinction between the study of individual particles in quantum
dynamics and the study of massed particles in classical physics.
The quantization of matter: the Bohr model of the atom
By the dawn of the 20th century, evidence required a model of the atom with a diffuse cloud of negatively charged electrons surrounding a small, dense, positively charged nucleus. These properties suggested a model in which electrons circle around the nucleus like planets orbiting a sun.
However, it was also known that the atom in this model would be
unstable: according to classical theory, orbiting electrons are
undergoing centripetal acceleration, and should therefore give off
electromagnetic radiation, the loss of energy also causing them to
spiral toward the nucleus, colliding with it in a fraction of a second.
A second, related, puzzle was the emission spectrum of atoms. When a gas is heated, it gives off light only at discrete frequencies. For example, the visible light given off by hydrogen
consists of four different colors, as shown in the picture below. The
intensity of the light at different frequencies is also different. By
contrast, white light consists of a continuous emission across the whole
range of visible frequencies. By the end of the nineteenth century, a
simple rule known as Balmer's formula showed how the frequencies of the different lines related to each other, though without explaining why
this was, or making any prediction about the intensities. The formula
also predicted some additional spectral lines in ultraviolet and
infrared light that had not been observed at the time. These lines were
later observed experimentally, raising confidence in the value of the
formula.
Emission spectrum of hydrogen.
When excited, hydrogen gas gives off light in four distinct colors
(spectral lines) in the visible spectrum, as well as a number of lines
in the infrared and ultraviolet.
The Bohr model of the atom, showing an electron transitioning from one orbit to another by emitting a photon.
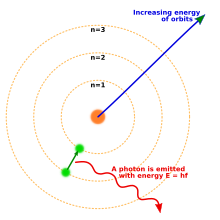
In 1913 Niels Bohr proposed a new model of the atom
that included quantized electron orbits: electrons still orbit the
nucleus much as planets orbit around the sun, but they are only
permitted to inhabit certain orbits, not to orbit at any distance.
When an atom emitted (or absorbed) energy, the electron did not move in
a continuous trajectory from one orbit around the nucleus to another,
as might be expected classically. Instead, the electron would jump
instantaneously from one orbit to another, giving off the emitted light
in the form of a photon.
The possible energies of photons given off by each element were
determined by the differences in energy between the orbits, and so the
emission spectrum for each element would contain a number of lines.
Niels Bohr as a young man
Starting from only one simple assumption about the rule that the
orbits must obey, the Bohr model was able to relate the observed
spectral lines in the emission spectrum of hydrogen to previously known
constants. In Bohr's model the electron simply wasn't allowed to emit
energy continuously and crash into the nucleus: once it was in the
closest permitted orbit, it was stable forever. Bohr's model didn't
explain why the orbits should be quantized in that way, nor was
it able to make accurate predictions for atoms with more than one
electron, or to explain why some spectral lines are brighter than
others.
Some fundamental assumptions of the Bohr model were soon proven
wrong—but the key result that the discrete lines in emission spectra are
due to some property of the electrons in atoms being quantised is
correct. The way that the electrons actually behave is strikingly
different from Bohr's atom, and from what we see in the world of our
everyday experience.
Wave-particle duality
Louis de Broglie in 1929. De Broglie won the Nobel Prize in Physics for his prediction that matter acts as a wave, made in his 1924 PhD thesis.
Just as light has both wave-like and particle-like properties, matter also has wave-like properties.
Matter behaving as a wave was first demonstrated experimentally for electrons: a beam of electrons can exhibit diffraction, just like a beam of light or a water wave. Similar wave-like phenomena were later shown for atoms and even molecules.
The wavelength, λ, associated with any object is related to its momentum, p, through the Planck constant, h:
The relationship, called the de Broglie hypothesis, holds for all
types of matter: all matter exhibits properties of both particles and
waves.
The concept of wave–particle duality says that neither the
classical concept of "particle" nor of "wave" can fully describe the
behavior of quantum-scale objects, either photons or matter.
Wave–particle duality is an example of the principle of complementarity in quantum physics. An elegant example of wave–particle duality, the double slit experiment, is discussed in the section below.
The double-slit experiment
The
diffraction pattern produced when light is shone through one slit (top)
and the interference pattern produced by two slits (bottom). The much
more complex pattern from two slits, with its small-scale interference
fringes, demonstrates the wave-like propagation of light.

The double slit experiment for a classical particle, a wave, and a quantum particle demonstrating wave-particle duality
In the double-slit experiment, as originally performed by Thomas Young and Augustin Fresnel in 1827, a beam of light is directed through two narrow, closely spaced slits, producing an interference pattern
of light and dark bands on a screen. If one of the slits is covered up,
one might naively expect that the intensity of the fringes due to
interference would be halved everywhere. In fact, a much simpler pattern
is seen, a simple diffraction pattern.
Closing one slit results in a much simpler pattern diametrically
opposite the open slit. Exactly the same behavior can be demonstrated in
water waves, and so the double-slit experiment was seen as a
demonstration of the wave nature of light.
Variations of the double-slit experiment have been performed using electrons, atoms, and even large molecules,
and the same type of interference pattern is seen. Thus it has been
demonstrated that all matter possesses both particle and wave
characteristics.
Even if the source intensity is turned down, so that only one
particle (e.g. photon or electron) is passing through the apparatus at a
time, the same interference pattern develops over time. The quantum
particle acts as a wave when passing through the double slits, but as a
particle when it is detected. This is a typical feature of quantum
complementarity: a quantum particle acts as a wave in an experiment to
measure its wave-like properties, and like a particle in an experiment
to measure its particle-like properties. The point on the detector
screen where any individual particle shows up is the result of a random
process. However, the distribution pattern of many individual particles
mimics the diffraction pattern produced by waves.
Application to the Bohr model
De Broglie expanded the Bohr model of the atom by showing that an electron in orbit around a nucleus could be thought of as having wave-like properties. In particular, an electron is observed only in situations that permit a standing wave around a nucleus.
An example of a standing wave is a violin string, which is fixed at
both ends and can be made to vibrate. The waves created by a stringed
instrument appear to oscillate in place, moving from crest to trough in
an up-and-down motion. The wavelength of a standing wave is related to
the length of the vibrating object and the boundary conditions. For
example, because the violin string is fixed at both ends, it can carry
standing waves of wavelengths , where l is the length and n
is a positive integer. De Broglie suggested that the allowed electron
orbits were those for which the circumference of the orbit would be an
integer number of wavelengths. The electron's wavelength therefore
determines that only Bohr orbits of certain distances from the nucleus
are possible. In turn, at any distance from the nucleus smaller than a
certain value it would be impossible to establish an orbit. The minimum
possible distance from the nucleus is called the Bohr radius.
De Broglie's treatment of quantum events served as a starting
point for Schrödinger when he set out to construct a wave equation to
describe quantum theoretical events.
Spin

Quantum spin versus classical magnet in the Stern-Gerlach experiment.
In 1922, Otto Stern and Walther Gerlach
shot silver atoms through an (inhomogeneous) magnetic field. In
classical mechanics, a magnet thrown through a magnetic field may be,
depending on its orientation (if it is pointing with its northern pole
upwards or down, or somewhere in between), deflected a small or large
distance upwards or downwards. The atoms that Stern and Gerlach shot
through the magnetic field acted in a similar way. However, while the
magnets could be deflected variable distances, the atoms would always be
deflected a constant distance either up or down. This implied that the
property of the atom that corresponds to the magnet's orientation must
be quantised, taking one of two values (either up or down), as opposed
to being chosen freely from any angle.
Ralph Kronig
originated the theory that particles such as atoms or electrons behave
as if they rotate, or "spin", about an axis. Spin would account for the
missing magnetic moment, and allow two electrons in the same orbital to occupy distinct quantum states if they "spun" in opposite directions, thus satisfying the exclusion principle. The quantum number represented the sense (positive or negative) of spin.
The choice of orientation of the magnetic field used in the
Stern-Gerlach experiment is arbitrary. In the animation shown here, the
field is vertical and so the atoms are deflected either up or down. If
the magnet is rotated a quarter turn, the atoms are deflected either
left or right. Using a vertical field shows that the spin along the
vertical axis is quantized, and using a horizontal field shows that the
spin along the horizontal axis is quantized.
If, instead of hitting a detector screen, one of the beams of
atoms coming out of the Stern-Gerlach apparatus is passed into another
(inhomogeneous) magnetic field oriented in the same direction, all of
the atoms are deflected the same way in this second field. However, if
the second field is oriented at 90° to the first, then half of the atoms
are deflected one way and half the other, so that the atom's spin about
the horizontal and vertical axes are independent of each other.
However, if one of these beams (e.g. the atoms that were deflected up
then left) is passed into a third magnetic field, oriented the same way
as the first, half of the atoms go one way and half the other, even
though they all went in the same direction originally. The action of
measuring the atoms' spin with respect to a horizontal field has changed
their spin with respect to a vertical field.
The Stern-Gerlach experiment demonstrates a number of important features of quantum mechanics:
- a feature of the natural world has been demonstrated to be quantized, and only able to take certain discrete values
- particles possess an intrinsic angular momentum that is closely analogous to the angular momentum of a classically spinning object
- measurement changes the system being measured in quantum mechanics. Only the spin of an object in one direction can be known, and observing the spin in another direction destroys the original information about the spin.
- quantum mechanics is probabilistic: whether the spin of any individual atom sent into the apparatus is positive or negative is random.
Development of modern quantum mechanics
In 1925, Werner Heisenberg
attempted to solve one of the problems that the Bohr model left
unanswered, explaining the intensities of the different lines in the
hydrogen emission spectrum. Through a series of mathematical analogies,
he wrote out the quantum mechanical analogue for the classical
computation of intensities. Shortly afterwards, Heisenberg's colleague Max Born
realized that Heisenberg's method of calculating the probabilities for
transitions between the different energy levels could best be expressed
by using the mathematical concept of matrices.
In the same year, building on de Broglie's hypothesis, Erwin Schrödinger developed the equation that describes the behavior of a quantum mechanical wave. The mathematical model, called the Schrödinger equation
after its creator, is central to quantum mechanics, defines the
permitted stationary states of a quantum system, and describes how the
quantum state of a physical system changes in time. The wave itself is described by a mathematical function known as a "wave function". Schrödinger said that the wave function provides the "means for predicting probability of measurement results".
Schrödinger was able to calculate the energy levels of hydrogen by treating a hydrogen atom's electron
as a classical wave, moving in a well of electrical potential created
by the proton. This calculation accurately reproduced the energy levels
of the Bohr model.
In May 1926, Schrödinger proved that Heisenberg's matrix mechanics and his own wave mechanics
made the same predictions about the properties and behavior of the
electron; mathematically, the two theories had an underlying common
form. Yet the two men disagreed on the interpretation of their mutual
theory. For instance, Heisenberg accepted the theoretical prediction of
jumps of electrons between orbitals in an atom, but Schrödinger hoped that a theory based on continuous wave-like properties could avoid what he called (as paraphrased by Wilhelm Wien) "this nonsense about quantum jumps."
Copenhagen interpretation
The Niels Bohr Institute
in Copenhagen, which was a focal point for researchers in quantum
mechanics and related subjects in the 1920s and 1930s. Most of the
world's best known theoretical physicists spent time there.
Bohr, Heisenberg and others tried to explain what these experimental
results and mathematical models really mean. Their description, known
as the Copenhagen interpretation of quantum mechanics, aimed to describe
the nature of reality that was being probed by the measurements and
described by the mathematical formulations of quantum mechanics.
The main principles of the Copenhagen interpretation are:
- A system is completely described by a wave function, usually represented by the Greek letter ("psi"). (Heisenberg)
- How changes over time is given by the Schrödinger equation.
- The description of nature is essentially probabilistic. The probability of an event – for example, where on the screen a particle shows up in the double-slit experiment – is related to the square of the absolute value of the amplitude of its wave function. (Born rule, due to Max Born, which gives a physical meaning to the wave function in the Copenhagen interpretation: the probability amplitude)
- It is not possible to know the values of all of the properties of the system at the same time; those properties that are not known with precision must be described by probabilities. (Heisenberg's uncertainty principle)
- Matter, like energy, exhibits a wave–particle duality. An experiment can demonstrate the particle-like properties of matter, or its wave-like properties; but not both at the same time. (Complementarity principle due to Bohr)
- Measuring devices are essentially classical devices, and measure classical properties such as position and momentum.
- The quantum mechanical description of large systems should closely approximate the classical description. (Correspondence principle of Bohr and Heisenberg)
Various consequences of these principles are discussed in more detail in the following subsections.
Uncertainty principle
Werner Heisenberg at the age of 26. Heisenberg won the Nobel Prize in Physics in 1932 for the work that he did at around this time.
Suppose it is desired to measure the position and speed of an
object – for example a car going through a radar speed trap. It can be
assumed that the car has a definite position and speed at a particular
moment in time. How accurately these values can be measured depends on
the quality of the measuring equipment. If the precision of the
measuring equipment is improved, it provides a result closer to the true
value. It might be assumed that the speed of the car and its position
could be operationally defined and measured simultaneously, as precisely
as might be desired.
In 1927, Heisenberg proved that this last assumption is not correct.
Quantum mechanics shows that certain pairs of physical properties, such
as for example position and speed, cannot be simultaneously measured,
nor defined in operational terms, to arbitrary precision: the more
precisely one property is measured, or defined in operational terms, the
less precisely can the other. This statement is known as the uncertainty principle.
The uncertainty principle isn't only a statement about the accuracy of
our measuring equipment, but, more deeply, is about the conceptual
nature of the measured quantities – the assumption that the car had
simultaneously defined position and speed does not work in quantum
mechanics. On a scale of cars and people, these uncertainties are
negligible, but when dealing with atoms and electrons they become
critical.
Heisenberg gave, as an illustration, the measurement of the
position and momentum of an electron using a photon of light. In
measuring the electron's position, the higher the frequency of the
photon, the more accurate is the measurement of the position of the
impact of the photon with the electron, but the greater is the
disturbance of the electron. This is because from the impact with the
photon, the electron absorbs a random amount of energy, rendering the
measurement obtained of its momentum
increasingly uncertain (momentum is velocity multiplied by mass), for
one is necessarily measuring its post-impact disturbed momentum from the
collision products and not its original momentum. With a photon of
lower frequency, the disturbance (and hence uncertainty) in the momentum
is less, but so is the accuracy of the measurement of the position of
the impact.
The uncertainty principle shows mathematically that the product of the uncertainty in the position and momentum
of a particle (momentum is velocity multiplied by mass) could never be
less than a certain value, and that this value is related to Planck's constant.
Wave function collapse
Wave function collapse is a forced expression for whatever just
happened when it becomes appropriate to replace the description of an
uncertain state of a system by a description of the system in a definite
state. Explanations for the nature of the process of becoming certain
are controversial. At any time before a photon "shows up" on a detection
screen it can only be described by a set of probabilities for where it
might show up. When it does show up, for instance in the CCD
of an electronic camera, the time and the space where it interacted
with the device are known within very tight limits. However, the photon
has disappeared, and the wave function has disappeared with it. In its
place some physical change in the detection screen has appeared, e.g.,
an exposed spot in a sheet of photographic film, or a change in electric
potential in some cell of a CCD.
Eigenstates and eigenvalues
Because of the uncertainty principle, statements about both the position and momentum of particles can only assign a probability
that the position or momentum has some numerical value. Therefore, it
is necessary to formulate clearly the difference between the state of
something that is indeterminate, such as an electron in a probability
cloud, and the state of something having a definite value. When an
object can definitely be "pinned-down" in some respect, it is said to
possess an eigenstate.
In the Stern-Gerlach experiment discussed above,
the spin of the atom about the vertical axis has two eigenstates: up
and down. Before measuring it, we can only say that any individual atom
has equal probability of being found to have spin up or spin down. The
measurement process causes the wavefunction to collapse into one of the
two states.
The eigenstates of spin about the vertical axis are not
simultaneously eigenstates of spin about the horizontal axis, so this
atom has equal probability of being found to have either value of spin
about the horizontal axis. As described in the section above,
measuring the spin about the horizontal axis can allow an atom that was
spun up to spin down: measuring its spin about the horizontal axis
collapses its wave function into one of the eigenstates of this
measurement, which means it is no longer in an eigenstate of spin about
the vertical axis, so can take either value.
The Pauli exclusion principle
In 1924, Wolfgang Pauli proposed a new quantum degree of freedom (or quantum number),
with two possible values, to resolve inconsistencies between observed
molecular spectra and the predictions of quantum mechanics. In
particular, the spectrum of atomic hydrogen had a doublet, or pair of lines differing by a small amount, where only one line was expected. Pauli formulated his exclusion principle,
stating that "There cannot exist an atom in such a quantum state that
two electrons within [it] have the same set of quantum numbers."
A year later, Uhlenbeck and Goudsmit identified Pauli's new degree of freedom with the property called spin whose effects were observed in the Stern–Gerlach experiment.
Application to the hydrogen atom
Bohr's model of the atom was essentially a planetary one, with the
electrons orbiting around the nuclear "sun." However, the uncertainty
principle states that an electron cannot simultaneously have an exact
location and velocity in the way that a planet does. Instead of
classical orbits, electrons are said to inhabit atomic orbitals.
An orbital is the "cloud" of possible locations in which an electron
might be found, a distribution of probabilities rather than a precise
location.
Each orbital is three dimensional, rather than the two dimensional
orbit, and is often depicted as a three-dimensional region within which
there is a 95 percent probability of finding the electron.
Schrödinger was able to calculate the energy levels of hydrogen by treating a hydrogen atom's electron as a wave, represented by the "wave function" Ψ, in an electric potential well, V,
created by the proton. The solutions to Schrödinger's equation are
distributions of probabilities for electron positions and locations.
Orbitals have a range of different shapes in three dimensions. The
energies of the different orbitals can be calculated, and they
accurately match the energy levels of the Bohr model.
Within Schrödinger's picture, each electron has four properties:
- An "orbital" designation, indicating whether the particle wave is one that is closer to the nucleus with less energy or one that is farther from the nucleus with more energy;
- The "shape" of the orbital, spherical or otherwise;
- The "inclination" of the orbital, determining the magnetic moment of the orbital around the z-axis.
- The "spin" of the electron.
The collective name for these properties is the quantum state
of the electron. The quantum state can be described by giving a number
to each of these properties; these are known as the electron's quantum numbers.
The quantum state of the electron is described by its wave function.
The Pauli exclusion principle demands that no two electrons within an
atom may have the same values of all four numbers.
The shapes of atomic orbitals. Rows: 1s, 2p, 3d and 4f. From left to right . The colors show the phase of the wave function.
The first property describing the orbital is the principal quantum number, n, which is the same as in Bohr's model. n denotes the energy level of each orbital. The possible values for n are integers:
The next quantum number, the azimuthal quantum number, denoted l, describes the shape of the orbital. The shape is a consequence of the angular momentum
of the orbital. The angular momentum represents the resistance of a
spinning object to speeding up or slowing down under the influence of
external force. The azimuthal quantum number represents the orbital
angular momentum of an electron around its nucleus. The possible values
for l are integers from 0 to n − 1 (where n is the principal quantum number of the electron):
The shape of each orbital is usually referred to by a letter, rather than by its azimuthal quantum number. The first shape (l=0) is denoted by the letter s (a mnemonic being "sphere"). The next shape is denoted by the letter p and has the form of a dumbbell. The other orbitals have more complicated shapes (see atomic orbital), and are denoted by the letters d, f, g, etc.
The third quantum number, the magnetic quantum number, describes the magnetic moment of the electron, and is denoted by ml (or simply m). The possible values for ml are integers from −l to l (where l is the azimuthal quantum number of the electron):
The magnetic quantum number measures the component of the angular
momentum in a particular direction. The choice of direction is
arbitrary, conventionally the z-direction is chosen.
The fourth quantum number, the spin quantum number (pertaining to the "orientation" of the electron's spin) is denoted ms, with values +1⁄2 or −1⁄2.
The chemist Linus Pauling wrote, by way of example:
In the case of a helium atom with two electrons in the 1s orbital, the Pauli Exclusion Principle requires that the two electrons differ in the value of one quantum number. Their values of n, l, and ml are the same. Accordingly they must differ in the value of ms, which can have the value of +1⁄2 for one electron and −1⁄2 for the other.
It is the underlying structure and symmetry of atomic orbitals, and
the way that electrons fill them, that leads to the organization of the periodic table. The way the atomic orbitals on different atoms combine to form molecular orbitals determines the structure and strength of chemical bonds between atoms.
Dirac wave equation
Paul Dirac (1902–1984)
In 1928, Paul Dirac extended the Pauli equation, which described spinning electrons, to account for special relativity.
The result was a theory that dealt properly with events, such as the
speed at which an electron orbits the nucleus, occurring at a
substantial fraction of the speed of light. By using the simplest electromagnetic interaction,
Dirac was able to predict the value of the magnetic moment associated
with the electron's spin, and found the experimentally observed value,
which was too large to be that of a spinning charged sphere governed by classical physics. He was able to solve for the spectral lines of the hydrogen atom, and to reproduce from physical first principles Sommerfeld's successful formula for the fine structure of the hydrogen spectrum.
Dirac's equations sometimes yielded a negative value for energy,
for which he proposed a novel solution: he posited the existence of an antielectron and of a dynamical vacuum. This led to the many-particle quantum field theory.
Quantum entanglement
Superposition of two quantum characteristics, and two resolution possibilities.
The Pauli exclusion principle says that two electrons in one system
cannot be in the same state. Nature leaves open the possibility,
however, that two electrons can have both states "superimposed" over
each of them. Recall that the wave functions that emerge simultaneously
from the double slits arrive at the detection screen in a state of
superposition. Nothing is certain until the superimposed waveforms
"collapse". At that instant an electron shows up somewhere in accordance
with the probability that is the square of the absolute value of the
sum of the complex-valued amplitudes of the two superimposed waveforms.
The situation there is already very abstract. A concrete way of thinking
about entangled photons, photons in which two contrary states are
superimposed on each of them in the same event, is as follows:
Imagine that the superposition of a state labeled blue, and another state labeled red then appear (in imagination) as a purple
state. Two photons are produced as the result of the same atomic event.
Perhaps they are produced by the excitation of a crystal that
characteristically absorbs a photon of a certain frequency and emits two
photons of half the original frequency. So the two photons come out purple. If the experimenter now performs some experiment that determines whether one of the photons is either blue or red, then that experiment changes the photon involved from one having a superposition of blue and red
characteristics to a photon that has only one of those characteristics.
The problem that Einstein had with such an imagined situation was that
if one of these photons had been kept bouncing between mirrors in a
laboratory on earth, and the other one had traveled halfway to the
nearest star, when its twin was made to reveal itself as either blue or
red, that meant that the distant photon now had to lose its purple
status too. So whenever it might be investigated after its twin had
been measured, it would necessarily show up in the opposite state to
whatever its twin had revealed.
In trying to show that quantum mechanics was not a complete
theory, Einstein started with the theory's prediction that two or more
particles that have interacted in the past can appear strongly
correlated when their various properties are later measured. He sought
to explain this seeming interaction in a classical way, through their
common past, and preferably not by some "spooky action at a distance."
The argument is worked out in a famous paper, Einstein, Podolsky, and
Rosen (1935; abbreviated EPR), setting out what is now called the EPR paradox. Assuming what is now usually called local realism,
EPR attempted to show from quantum theory that a particle has both
position and momentum simultaneously, while according to the Copenhagen interpretation,
only one of those two properties actually exists and only at the moment
that it is being measured. EPR concluded that quantum theory is
incomplete in that it refuses to consider physical properties that
objectively exist in nature. (Einstein, Podolsky, & Rosen 1935 is
currently Einstein's most cited publication in physics journals.) In the
same year, Erwin Schrödinger used the word "entanglement" and declared: "I would not call that one but rather the characteristic trait of quantum mechanics." The question of whether entanglement is a real condition is still in dispute. The Bell inequalities are the most powerful challenge to Einstein's claims.
Quantum field theory
The idea of quantum field theory began in the late 1920s with British physicist Paul Dirac, when he attempted to quantise the electromagnetic field – a procedure for constructing a quantum theory starting from a classical theory.
A field in physics is "a region or space in which a given effect (such as magnetism) exists." Other effects that manifest themselves as fields are gravitation and static electricity. In 2008, physicist Richard Hammond wrote that
Sometimes we distinguish between quantum mechanics (QM) and quantum field theory (QFT). QM refers to a system in which the number of particles is fixed, and the fields (such as the electromechanical field) are continuous classical entities. QFT ... goes a step further and allows for the creation and annihilation of particles . . . .
He added, however, that quantum mechanics is often used to refer to "the entire notion of quantum view".
In 1931, Dirac proposed the existence of particles that later became known as antimatter. Dirac shared the Nobel Prize in Physics for 1933 with Schrödinger "for the discovery of new productive forms of atomic theory".
On its face, quantum field theory allows infinite numbers of
particles, and leaves it up to the theory itself to predict how many and
with which probabilities or numbers they should exist. When developed
further, the theory often contradicts observation, so that its creation
and annihilation operators can be empirically tied down.
Furthermore, empirical conservation laws like that of mass-energy
suggest certain constraints on the mathematical form of the theory,
which are mathematically speaking finicky. The latter fact makes quantum
field theories difficult to handle, but has also led to further
restrictions on admissible forms of the theory; the complications are
mentioned below under the rubric of renormalization.
Quantum electrodynamics
Quantum electrodynamics (QED) is the name of the quantum theory of the electromagnetic force. Understanding QED begins with understanding electromagnetism. Electromagnetism can be called "electrodynamics" because it is a dynamic interaction between electrical and magnetic forces. Electromagnetism begins with the electric charge.
Electric charges are the sources of, and create, electric fields.
An electric field is a field that exerts a force on any particles that
carry electric charges, at any point in space. This includes the
electron, proton, and even quarks,
among others. As a force is exerted, electric charges move, a current
flows and a magnetic field is produced. The changing magnetic field, in
turn causes electric current (often moving electrons). The physical description of interacting charged particles, electrical currents, electrical fields, and magnetic fields is called electromagnetism.
In 1928 Paul Dirac
produced a relativistic quantum theory of electromagnetism. This was
the progenitor to modern quantum electrodynamics, in that it had
essential ingredients of the modern theory. However, the problem of
unsolvable infinities developed in this relativistic quantum theory. Years later, renormalization
largely solved this problem. Initially viewed as a suspect, provisional
procedure by some of its originators, renormalization eventually was
embraced as an important and self-consistent tool in QED and other
fields of physics. Also, in the late 1940s Feynman's diagrams
depicted all possible interactions pertaining to a given event. The
diagrams showed in particular that the electromagnetic force is the
exchange of photons between interacting particles.
The Lamb shift
is an example of a quantum electrodynamics prediction that has been
experimentally verified. It is an effect whereby the quantum nature of
the electromagnetic field makes the energy levels in an atom or ion
deviate slightly from what they would otherwise be. As a result,
spectral lines may shift or split.
Similarly, within a freely propagating electromagnetic wave, the current can also be just an abstract displacement current, instead of involving charge carriers. In QED, its full description makes essential use of short lived virtual particles. There, QED again validates an earlier, rather mysterious concept.
Standard Model
In the 1960s physicists realized that QED broke down at extremely high energies. From this inconsistency the Standard Model
of particle physics was discovered, which remedied the higher energy
breakdown in theory. It is another extended quantum field theory that
unifies the electromagnetic and weak interactions into one theory. This is called the electroweak theory.
Additionally the Standard Model contains a high energy unification of the electroweak theory with the strong force, described by quantum chromodynamics. It also postulates a connection with gravity as yet another gauge theory, but the connection is as of 2015 still poorly understood. The theory's successful prediction of the Higgs particle to explain inertial mass was confirmed by the Large Hadron Collider, and thus the Standard model is now considered the basic and more or less complete description of particle physics as we know it.
Interpretations
The physical measurements, equations, and predictions pertinent to
quantum mechanics are all consistent and hold a very high level of
confirmation. However, the question of what these abstract models say
about the underlying nature of the real world has received competing
answers. These interpretations are widely varying and sometimes somewhat
abstract. For instance, the Copenhagen interpretation states that before a measurement, statements about a particles' properties are completely meaningless, while in the Many-worlds interpretation describes the existence of a multiverse made up of every possible universe.
Applications
Applications of quantum mechanics include the laser, the transistor, the electron microscope, and magnetic resonance imaging. A special class of quantum mechanical applications is related to macroscopic quantum phenomena such as superfluid helium and superconductors. The study of semiconductors led to the invention of the diode and the transistor, which are indispensable for modern electronics.
In even the simple light switch, quantum tunneling is absolutely vital, as otherwise the electrons in the electric current could not penetrate the potential barrier made up of a layer of oxide. Flash memory chips found in USB drives also use quantum tunneling, to erase their memory cells.