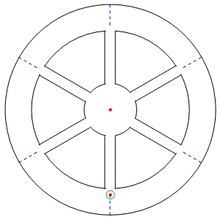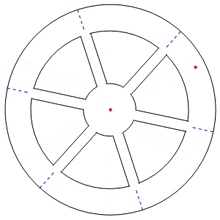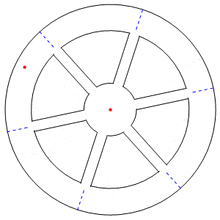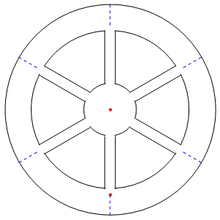
Bouncing ball in a rotating space station: The objective reality of the ball bouncing off the outer hull is confirmed both by a rotating and by a non-rotating observer, hence the rotation of the space station is an "absolute", objective fact regardless of the chosen frame of reference.
In physics, the concept of absolute rotation—rotation independent of any external reference—is a topic of debate about relativity, cosmology, and the nature of physical laws.
For the concept of absolute rotation to be scientifically
meaningful, it must be measurable. In other words, can an observer
distinguish between the rotation of an observed object and their own
rotation? Newton suggested two experiments to resolve this problem. One
is the effects of centrifugal force upon the shape of the surface of water rotating in a bucket, equivalent to the phenomenon of rotational gravity used in proposals for human spaceflight.
The second is the effect of centrifugal force upon the tension in a
string joining two spheres rotating about their center of mass.
Classical mechanics
Newton's bucket argument
Newton suggested the shape of the surface of the water indicates the presence or absence of absolute rotation relative to absolute space:
rotating water has a curved surface, still water has a flat surface.
Because rotating water has a concave surface, if the surface you see is
concave, and the water does not seem to you to be rotating, then you are rotating with the water.
Centrifugal force is needed to explain the concavity of the water
in a co-rotating frame of reference (one that rotates with the water)
because the water appears stationary in this frame, and so should have a
flat surface. Thus, observers looking at the stationary water need the
centrifugal force to explain why the water surface is concave and not
flat. The centrifugal force pushes the water toward the sides of the
bucket, where it piles up deeper and deeper, Pile-up is arrested when
any further climb costs as much work against gravity as is the energy
gained from the centrifugal force, which is greater at larger radius.
If you need a centrifugal force to explain what you see, then you
are rotating. Newton's conclusion was that rotation is absolute.
Other thinkers suggest that pure logic implies only relative rotation makes sense. For example, Bishop Berkeley and Ernst Mach (among others) suggested that it is relative rotation with respect to the fixed stars
that matters, and rotation of the fixed stars relative to an object has
the same effect as rotation of the object with respect to the fixed
stars.
Newton's arguments do not settle this issue; his arguments may be
viewed, however, as establishing centrifugal force as a basis for an operational definition of what we actually mean by absolute rotation.
Rotating spheres
Figure
2: Two spheres tied with a string and rotating at an angular rate ω.
Because of the rotation, the string tying the spheres together is under
tension.
Newton also proposed another experiment to measure one's rate of
rotation: using the tension in a cord joining two spheres rotating about
their center of mass. Non-zero tension in the string indicates rotation
of the spheres, whether or not the observer thinks they are rotating.
This experiment is simpler than the bucket experiment in principle,
because it need not involve gravity.
Beyond a simple "yes or no" answer to rotation, one may actually
calculate one's rotation. To do that, one takes one's measured rate of
rotation of the spheres and computes the tension appropriate to this
observed rate. This calculated tension then is compared to the measured
tension. If the two agree, one is in a stationary (non-rotating) frame.
If the two do not agree, to obtain agreement, one must include a
centrifugal force in the tension calculation; for example, if the
spheres appear to be stationary, but the tension is non-zero, the entire
tension is due to centrifugal force. From the necessary centrifugal
force, one can determine one's speed of rotation; for example, if the
calculated tension is greater than measured, one is rotating in the
sense opposite to the spheres, and the larger the discrepancy the faster
this rotation.
The tension in the wire is the required centripetal force to
sustain the rotation. What is experienced by the physically rotating
observer is the centripetal force and the physical effect arising from
his own inertia. The effect arising from inertia is referred to as reactive centrifugal force.
Whether or not the effects from inertia are attributed to a fictitious centrifugal force is a matter of choice.
Rotating elastic sphere
Figure 3: An ellipsoid
In a similar fashion, if we did not know the Earth rotates about its
axis, we could infer this rotation from the centrifugal force needed to
account for the bulging observed at its equator.
In his Principia, Newton
proposed the shape of the rotating Earth was that of a homogeneous
ellipsoid formed by an equilibrium between the gravitational force
holding it together and the centrifugal force pulling it apart. This
effect is more easily seen with the planet Saturn
which has a radius 8.5 to 9.5 times that of Earth but has a rotational
period of only 10.57 hours. The ratios of Saturn's diameters is
approximately 11 to 10.
Isaac Newton explained this in his Principia Mathematica
(1687) in which he outlined his theory and calculations on the shape of
the Earth. Newton theorized correctly that the Earth was not precisely
a sphere but had an oblate ellipsoidal shape, slightly flattened at the poles due to the centrifugal force
of its rotation. Since the surface of the Earth is closer to its
center at the poles than at the equator, gravity is stronger there.
Using geometric calculations, he gave a concrete argument as to the
hypothetical ellipsoid shape of the Earth.
A modern measurement of the Earth's oblateness leads to an equatorial radius of 6378.14 km and a polar radius of 6356.77 km, about 0.1% less oblate than Newton's estimate.
A theoretical determination of the precise extent of oblateness in
response to a centrifugal force requires an understanding of the
make-up of the planet, not only today but during its formation.
In 1672 Jean Richer found the first evidence that gravity was not constant over the Earth (as it would be if the Earth were a sphere); he took a pendulum clock to Cayenne, French Guiana and found that it lost 2 1⁄2 minutes per day compared to its rate at Paris. This indicated the acceleration of gravity
was less at Cayenne than at Paris. Pendulum gravimeters began to be
taken on voyages to remote parts of the world, and it was slowly
discovered that gravity increases smoothly with increasing latitude,
gravitational acceleration being about 0.5% greater at the poles than at
the equator.
It was only in 1743 that Alexis Clairaut, in Théorie de la figure de la terre, was able to show that Newton's theory that the Earth was ellipsoidal was correct
Clairaut showed how Newton's equations were incorrect, and did not prove an ellipsoid shape to the Earth.
However, he corrected problems with the theory, that in effect would
prove Newton's theory correct. Clairaut believed that Newton had reasons
for choosing the shape that he did, but he did not support it in Principia.
Clairaut's article did not provide a valid equation to back up his
argument as well. This created much controversy in the scientific
community.
Special relativity
French physicist Georges Sagnac in 1913 conducted an experiment that was similar to the Michelson–Morley experiment, but was intended to observe the effects of rotation. Sagnac set up this experiment to prove the existence of the luminiferous aether that Einstein's 1905 theory of special relativity had discarded.
The Sagnac experiment
and later similar experiments showed that a stationary object on the
surface of the Earth will rotate once every rotation of the Earth when
using stars as a stationary reference point. Rotation was thus
concluded to be absolute rather than relative.
General relativity
Mach's principle is the name given by Einstein to a hypothesis often credited to the physicist and philosopher Ernst Mach.
The idea is that the local motion of a rotating reference frame
is determined by the large-scale distribution of matter in the
universe. Mach's principle says that there is a physical law that
relates the motion of the distant stars to the local inertial frame. If
you see all the stars whirling around you, Mach suggests that there is
some physical law which would make it so you would feel a centrifugal force. The principle is often stated in vague ways, like "mass out there influences inertia here".
The example considered by Einstein was the rotating elastic
sphere. Like a rotating planet bulging at the equator, a rotating sphere
deforms into an oblate (squashed) spheroid depending on its rotation.
In classical mechanics, an explanation of this deformation
requires external causes in a frame of reference in the spheroid it is
not rotating, and these external causes may be taken as "absolute
rotation" in classical physics and special relativity.
In general relativity, no external causes are invoked. The rotation is relative to the local geodesics, and since the local geodesics eventually channel information from the distant stars, there appears to be absolute rotation relative to these stars.