Dynamical system

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Dynamical_system

 

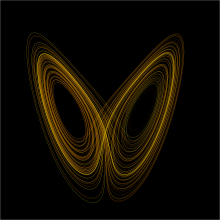
The Lorenz attractor arises in the study of the Lorenz Oscillator, a dynamical system.

 

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a lake.

At any given time, a dynamical system has a state given by a tuple of real numbers (a vector) that can be represented by a point in an appropriate state space (a geometrical manifold). The evolution rule of the dynamical system is a function that describes what future states follow from the current state. Often the function is deterministic, that is, for a given time interval only one future state follows from the current state. However, some systems are stochastic, in that random events also affect the evolution of the state variables. 

In physics, a dynamical system is described as a "particle or ensemble of particles whose state varies over time and thus obeys differential equations involving time derivatives." In order to make a prediction about the system's future behavior, an analytical solution of such equations or their integration over time through computer simulation is realized. 

The study of dynamical systems is the focus of dynamical systems theory, which has applications to a wide variety of fields such as mathematics, physics, biology, chemistry, engineering, economics, history, and medicine. Dynamical systems are a fundamental part of chaos theory, logistic map dynamics, bifurcation theory, the self-assembly and self-organization processes, and the edge of chaos concept. 

Overview

The concept of a dynamical system has its origins in Newtonian mechanics. There, as in other natural sciences and engineering disciplines, the evolution rule of dynamical systems is an implicit relation that gives the state of the system for only a short time into the future. (The relation is either a differential equation, difference equation or other time scale.) To determine the state for all future times requires iterating the relation many times—each advancing time a small step. The iteration procedure is referred to as solving the system or integrating the system. If the system can be solved, given an initial point it is possible to determine all its future positions, a collection of points known as a trajectory or orbit. 

Before the advent of computers, finding an orbit required sophisticated mathematical techniques and could be accomplished only for a small class of dynamical systems. Numerical methods implemented on electronic computing machines have simplified the task of determining the orbits of a dynamical system. 

For simple dynamical systems, knowing the trajectory is often sufficient, but most dynamical systems are too complicated to be understood in terms of individual trajectories. The difficulties arise because:

• The systems studied may only be known approximately—the parameters of the system may not be known precisely or terms may be missing from the equations. The approximations used bring into question the validity or relevance of numerical solutions. To address these questions several notions of stability have been introduced in the study of dynamical systems, such as Lyapunov stability or structural stability. The stability of the dynamical system implies that there is a class of models or initial conditions for which the trajectories would be equivalent. The operation for comparing orbits to establish their equivalence changes with the different notions of stability.
• The type of trajectory may be more important than one particular trajectory. Some trajectories may be periodic, whereas others may wander through many different states of the system. Applications often require enumerating these classes or maintaining the system within one class. Classifying all possible trajectories has led to the qualitative study of dynamical systems, that is, properties that do not change under coordinate changes. Linear dynamical systems and systems that have two numbers describing a state are examples of dynamical systems where the possible classes of orbits are understood.
• The behavior of trajectories as a function of a parameter may be what is needed for an application. As a parameter is varied, the dynamical systems may have bifurcation points where the qualitative behavior of the dynamical system changes. For example, it may go from having only periodic motions to apparently erratic behavior, as in the transition to turbulence of a fluid.
• The trajectories of the system may appear erratic, as if random. In these cases it may be necessary to compute averages using one very long trajectory or many different trajectories. The averages are well defined for ergodic systems and a more detailed understanding has been worked out for hyperbolic systems. Understanding the probabilistic aspects of dynamical systems has helped establish the foundations of statistical mechanics and of chaos.

History

Many people regard French mathematician Henri Poincaré as the founder of dynamical systems. Poincaré published two now classical monographs, "New Methods of Celestial Mechanics" (1892–1899) and "Lectures on Celestial Mechanics" (1905–1910). In them, he successfully applied the results of their research to the problem of the motion of three bodies and studied in detail the behavior of solutions (frequency, stability, asymptotic, and so on). These papers included the Poincaré recurrence theorem, which states that certain systems will, after a sufficiently long but finite time, return to a state very close to the initial state. 

Aleksandr Lyapunov developed many important approximation methods. His methods, which he developed in 1899, make it possible to define the stability of sets of ordinary differential equations. He created the modern theory of the stability of a dynamic system. 

In 1913, George David Birkhoff proved Poincaré's "Last Geometric Theorem", a special case of the three-body problem, a result that made him world-famous. In 1927, he published his Dynamical SystemsBirkhoff's most durable result has been his 1931 discovery of what is now called the ergodic theorem. Combining insights from physics on the ergodic hypothesis with measure theory, this theorem solved, at least in principle, a fundamental problem of statistical mechanics. The ergodic theorem has also had repercussions for dynamics. 

Stephen Smale made significant advances as well. His first contribution is the Smale horseshoe that jumpstarted significant research in dynamical systems. He also outlined a research program carried out by many others. 

Oleksandr Mykolaiovych Sharkovsky developed Sharkovsky's theorem on the periods of discrete dynamical systems in 1964. One of the implications of the theorem is that if a discrete dynamical system on the real line has a periodic point of period 3, then it must have periodic points of every other period. 

In the late 20th century, Palestinian mechanical engineer Ali H. Nayfeh applied nonlinear dynamics in mechanical and engineering systems. His pioneering work in applied nonlinear dynamics has been influential in the construction and maintenance of machines and structures that are common in daily life, such as ships, cranes, bridges, buildings, skyscrapers, jet engines, rocket engines, aircraft and spacecraft.

Basic definitions

A dynamical system is a manifold M called the phase (or state) space endowed with a family of smooth evolution functions Φ^t that for any element of t ∈ T, the time, map a point of the phase space back into the phase space. The notion of smoothness changes with applications and the type of manifold. There are several choices for the set T. When T is taken to be the reals, the dynamical system is called a flow; and if T is restricted to the non-negative reals, then the dynamical system is a semi-flow. When T is taken to be the integers, it is a cascade or a map; and the restriction to the non-negative integers is a semi-cascade. 

Examples

The evolution function Φ ^t is often the solution of a differential equation of motion

${\displaystyle {\dot {x}}=v(x).}$

The equation gives the time derivative, represented by the dot, of a trajectory x(t) on the phase space starting at some point x₀. The vector field v(x) is a smooth function that at every point of the phase space M provides the velocity vector of the dynamical system at that point. (These vectors are not vectors in the phase space M, but in the tangent space T_xM of the point x.) Given a smooth Φ ^t, an autonomous vector field can be derived from it. 

There is no need for higher order derivatives in the equation, nor for time dependence in v(x) because these can be eliminated by considering systems of higher dimensions. Other types of differential equations can be used to define the evolution rule:

${\displaystyle G(x,{\dot {x}})=0}$

is an example of an equation that arises from the modeling of mechanical systems with complicated constraints. 

The differential equations determining the evolution function Φ ^t are often ordinary differential equations; in this case the phase space M is a finite dimensional manifold. Many of the concepts in dynamical systems can be extended to infinite-dimensional manifolds—those that are locally Banach spaces—in which case the differential equations are partial differential equations. In the late 20th century the dynamical system perspective to partial differential equations started gaining popularity. 

Further examples

• Logistic map
• Complex quadratic polynomial
• Dyadic transformation
• Tent map
• Double pendulum
• Arnold's cat map
• Horseshoe map
• Baker's map is an example of a chaotic piecewise linear map
• Billiards and outer billiards
• Hénon map
• Lorenz system
• Circle map
• Rössler map
• Kaplan–Yorke map
• List of chaotic maps
• Swinging Atwood's machine
• Quadratic map simulation system
• Bouncing ball dynamics

Linear dynamical systems

Linear dynamical systems can be solved in terms of simple functions and the behavior of all orbits classified. In a linear system the phase space is the N-dimensional Euclidean space, so any point in phase space can be represented by a vector with N numbers. The analysis of linear systems is possible because they satisfy a superposition principle: if u(t) and w(t) satisfy the differential equation for the vector field (but not necessarily the initial condition), then so will u(t) + w(t). 

Flows

For a flow, the vector field Φ(x) is an affine function of the position in the phase space, that is,

${\displaystyle {\dot {x}}=\phi (x)=Ax+b,}$

with A a matrix, b a vector of numbers and x the position vector. The solution to this system can be found by using the superposition principle (linearity). The case b ≠ 0 with A = 0 is just a straight line in the direction of b:

${\displaystyle \Phi ^{t}(x_{1})=x_{1}+bt.}$

When b is zero and A ≠ 0 the origin is an equilibrium (or singular) point of the flow, that is, if x₀ = 0, then the orbit remains there. For other initial conditions, the equation of motion is given by the exponential of a matrix: for an initial point x₀,

${\displaystyle \Phi ^{t}(x_{0})=e^{tA}x_{0}.}$

When b = 0, the eigenvalues of A determine the structure of the phase space. From the eigenvalues and the eigenvectors of A it is possible to determine if an initial point will converge or diverge to the equilibrium point at the origin.

The distance between two different initial conditions in the case A ≠ 0 will change exponentially in most cases, either converging exponentially fast towards a point, or diverging exponentially fast. Linear systems display sensitive dependence on initial conditions in the case of divergence. For nonlinear systems this is one of the (necessary but not sufficient) conditions for chaotic behavior.

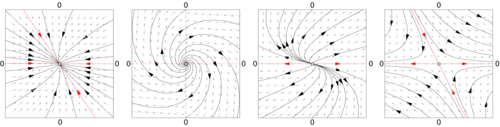
Linear vector fields and a few trajectories.

 

Maps

A discrete-time, affine dynamical system has the form of a matrix difference equation:

${\displaystyle x_{n+1}=Ax_{n}+b,}$

with A a matrix and b a vector. As in the continuous case, the change of coordinates x → x + (1 − A) ^–1b removes the term b from the equation. In the new coordinate system, the origin is a fixed point of the map and the solutions are of the linear system A ⁿx₀. The solutions for the map are no longer curves, but points that hop in the phase space. The orbits are organized in curves, or fibers, which are collections of points that map into themselves under the action of the map.

As in the continuous case, the eigenvalues and eigenvectors of A determine the structure of phase space. For example, if u₁ is an eigenvector of A, with a real eigenvalue smaller than one, then the straight lines given by the points along α u₁, with α ∈ R, is an invariant curve of the map. Points in this straight line run into the fixed point. 

There are also many other discrete dynamical systems. 

Local dynamics

The qualitative properties of dynamical systems do not change under a smooth change of coordinates (this is sometimes taken as a definition of qualitative): a singular point of the vector field (a point where v(x) = 0) will remain a singular point under smooth transformations; a periodic orbit is a loop in phase space and smooth deformations of the phase space cannot alter it being a loop. It is in the neighborhood of singular points and periodic orbits that the structure of a phase space of a dynamical system can be well understood. In the qualitative study of dynamical systems, the approach is to show that there is a change of coordinates (usually unspecified, but computable) that makes the dynamical system as simple as possible. 

Rectification

A flow in most small patches of the phase space can be made very simple. If y is a point where the vector field v(y) ≠ 0, then there is a change of coordinates for a region around y where the vector field becomes a series of parallel vectors of the same magnitude. This is known as the rectification theorem.

The rectification theorem says that away from singular points the dynamics of a point in a small patch is a straight line. The patch can sometimes be enlarged by stitching several patches together, and when this works out in the whole phase space M the dynamical system is integrable. In most cases the patch cannot be extended to the entire phase space. There may be singular points in the vector field (where v(x) = 0); or the patches may become smaller and smaller as some point is approached. The more subtle reason is a global constraint, where the trajectory starts out in a patch, and after visiting a series of other patches comes back to the original one. If the next time the orbit loops around phase space in a different way, then it is impossible to rectify the vector field in the whole series of patches. 

Near periodic orbits

In general, in the neighborhood of a periodic orbit the rectification theorem cannot be used. Poincaré developed an approach that transforms the analysis near a periodic orbit to the analysis of a map. Pick a point x₀ in the orbit γ and consider the points in phase space in that neighborhood that are perpendicular to v(x₀). These points are a Poincaré section S(γ, x₀), of the orbit. The flow now defines a map, the Poincaré map F : S → S, for points starting in S and returning to S. Not all these points will take the same amount of time to come back, but the times will be close to the time it takes x₀.

The intersection of the periodic orbit with the Poincaré section is a fixed point of the Poincaré map F. By a translation, the point can be assumed to be at x = 0. The Taylor series of the map is F(x) = J · x + O(x²), so a change of coordinates h can only be expected to simplify F to its linear part

${\displaystyle h^{-1}\circ F\circ h(x)=J\cdot x.}$

This is known as the conjugation equation. Finding conditions for this equation to hold has been one of the major tasks of research in dynamical systems. Poincaré first approached it assuming all functions to be analytic and in the process discovered the non-resonant condition. If λ₁, ..., λ_ν are the eigenvalues of J they will be resonant if one eigenvalue is an integer linear combination of two or more of the others. As terms of the form λ_i – ∑ (multiples of other eigenvalues) occurs in the denominator of the terms for the function h, the non-resonant condition is also known as the small divisor problem. 

Conjugation results

The results on the existence of a solution to the conjugation equation depend on the eigenvalues of J and the degree of smoothness required from h. As J does not need to have any special symmetries, its eigenvalues will typically be complex numbers. When the eigenvalues of J are not in the unit circle, the dynamics near the fixed point x₀ of F is called hyperbolic and when the eigenvalues are on the unit circle and complex, the dynamics is called elliptic. 

In the hyperbolic case, the Hartman–Grobman theorem gives the conditions for the existence of a continuous function that maps the neighborhood of the fixed point of the map to the linear map J · x. The hyperbolic case is also structurally stable. Small changes in the vector field will only produce small changes in the Poincaré map and these small changes will reflect in small changes in the position of the eigenvalues of J in the complex plane, implying that the map is still hyperbolic. 

The Kolmogorov–Arnold–Moser (KAM) theorem gives the behavior near an elliptic point. 

Bifurcation theory

When the evolution map Φ^t (or the vector field it is derived from) depends on a parameter μ, the structure of the phase space will also depend on this parameter. Small changes may produce no qualitative changes in the phase space until a special value μ₀ is reached. At this point the phase space changes qualitatively and the dynamical system is said to have gone through a bifurcation.

Bifurcation theory considers a structure in phase space (typically a fixed point, a periodic orbit, or an invariant torus) and studies its behavior as a function of the parameter μ. At the bifurcation point the structure may change its stability, split into new structures, or merge with other structures. By using Taylor series approximations of the maps and an understanding of the differences that may be eliminated by a change of coordinates, it is possible to catalog the bifurcations of dynamical systems.

The bifurcations of a hyperbolic fixed point x₀ of a system family F_μ can be characterized by the eigenvalues of the first derivative of the system DF_μ(x₀) computed at the bifurcation point. For a map, the bifurcation will occur when there are eigenvalues of DF_μ on the unit circle. For a flow, it will occur when there are eigenvalues on the imaginary axis. For more information, see the main article on Bifurcation theory.

Some bifurcations can lead to very complicated structures in phase space. For example, the Ruelle–Takens scenario describes how a periodic orbit bifurcates into a torus and the torus into a strange attractor. In another example, Feigenbaum period-doubling describes how a stable periodic orbit goes through a series of period-doubling bifurcations. 

Ergodic systems

In many dynamical systems, it is possible to choose the coordinates of the system so that the volume (really a ν-dimensional volume) in phase space is invariant. This happens for mechanical systems derived from Newton's laws as long as the coordinates are the position and the momentum and the volume is measured in units of (position) × (momentum). The flow takes points of a subset A into the points Φ ^t(A) and invariance of the phase space means that

${\displaystyle \mathrm {vol} (A)=\mathrm {vol} (\Phi ^{t}(A)).}$

In the Hamiltonian formalism, given a coordinate it is possible to derive the appropriate (generalized) momentum such that the associated volume is preserved by the flow. The volume is said to be computed by the Liouville measure.

In a Hamiltonian system, not all possible configurations of position and momentum can be reached from an initial condition. Because of energy conservation, only the states with the same energy as the initial condition are accessible. The states with the same energy form an energy shell Ω, a sub-manifold of the phase space. The volume of the energy shell, computed using the Liouville measure, is preserved under evolution.

For systems where the volume is preserved by the flow, Poincaré discovered the recurrence theorem: Assume the phase space has a finite Liouville volume and let F be a phase space volume-preserving map and A a subset of the phase space. Then almost every point of A returns to A infinitely often. The Poincaré recurrence theorem was used by Zermelo to object to Boltzmann's derivation of the increase in entropy in a dynamical system of colliding atoms.

One of the questions raised by Boltzmann's work was the possible equality between time averages and space averages, what he called the ergodic hypothesis. The hypothesis states that the length of time a typical trajectory spends in a region A is vol(A)/vol(Ω).

The ergodic hypothesis turned out not to be the essential property needed for the development of statistical mechanics and a series of other ergodic-like properties were introduced to capture the relevant aspects of physical systems. Koopman approached the study of ergodic systems by the use of functional analysis. An observable a is a function that to each point of the phase space associates a number (say instantaneous pressure, or average height). The value of an observable can be computed at another time by using the evolution function φ ^t. This introduces an operator U ^t, the transfer operator,

${\displaystyle (U^{t}a)(x)=a(\Phi ^{-t}(x)).}$

By studying the spectral properties of the linear operator U it becomes possible to classify the ergodic properties of Φ ^t. In using the Koopman approach of considering the action of the flow on an observable function, the finite-dimensional nonlinear problem involving Φ ^t gets mapped into an infinite-dimensional linear problem involving U.

The Liouville measure restricted to the energy surface Ω is the basis for the averages computed in equilibrium statistical mechanics. An average in time along a trajectory is equivalent to an average in space computed with the Boltzmann factor exp(−βH). This idea has been generalized by Sinai, Bowen, and Ruelle (SRB) to a larger class of dynamical systems that includes dissipative systems. SRB measures replace the Boltzmann factor and they are defined on attractors of chaotic systems. 

Nonlinear dynamical systems and chaos

Simple nonlinear dynamical systems and even piecewise linear systems can exhibit a completely unpredictable behavior, which might seem to be random, despite the fact that they are fundamentally deterministic. This seemingly unpredictable behavior has been called chaos. Hyperbolic systems are precisely defined dynamical systems that exhibit the properties ascribed to chaotic systems. In hyperbolic systems the tangent space perpendicular to a trajectory can be well separated into two parts: one with the points that converge towards the orbit (the stable manifold) and another of the points that diverge from the orbit (the unstable manifold).

This branch of mathematics deals with the long-term qualitative behavior of dynamical systems. Here, the focus is not on finding precise solutions to the equations defining the dynamical system (which is often hopeless), but rather to answer questions like "Will the system settle down to a steady state in the long term, and if so, what are the possible attractors?" or "Does the long-term behavior of the system depend on its initial condition?"

Note that the chaotic behavior of complex systems is not the issue. Meteorology has been known for years to involve complex—even chaotic—behavior. Chaos theory has been so surprising because chaos can be found within almost trivial systems. The logistic map is only a second-degree polynomial; the horseshoe map is piecewise linear. 

Geometrical definition

A dynamical system is the tuple ${\displaystyle \langle {\mathcal {M}},f,{\mathcal {T}}\rangle }$, with ${\displaystyle {\mathcal {M}}}$ a manifold (locally a Banach space or Euclidean space), ${\displaystyle {\mathcal {T}}}$ the domain for time (non-negative reals, the integers, ...) and f an evolution rule t → f ^t (with ${\displaystyle t\in {\mathcal {T}}}$) such that f ^t is a diffeomorphism of the manifold to itself. So, f is a mapping of the time-domain ${\displaystyle {\mathcal {T}}}$ into the space of diffeomorphisms of the manifold to itself. In other terms, f(t) is a diffeomorphism, for every time t in the domain ${\displaystyle {\mathcal {T}}}$ . 

Measure theoretical definition

A dynamical system may be defined formally, as a measure-preserving transformation of a sigma-algebra, the quadruplet (X, Σ, μ, τ). Here, X is a set, and Σ is a sigma-algebra on X, so that the pair (X, Σ) is a measurable space. μ is a finite measure on the sigma-algebra, so that the triplet (X, Σ, μ) is a probability space. A map τ: X → X is said to be Σ-measurable if and only if, for every σ ∈ Σ, one has ${\displaystyle \tau ^{-1}\sigma \in \Sigma }$. A map τ is said to preserve the measure if and only if, for every σ ∈ Σ, one has ${\displaystyle \mu (\tau ^{-1}\sigma )=\mu (\sigma )}$. Combining the above, a map τ is said to be a measure-preserving transformation of X , if it is a map from X to itself, it is Σ-measurable, and is measure-preserving. The quadruple (X, Σ, μ, τ), for such a τ, is then defined to be a dynamical system.

The map τ embodies the time evolution of the dynamical system. Thus, for discrete dynamical systems the iterates ${\displaystyle \tau ^{n}=\tau \circ \tau \circ \cdots \circ \tau }$ for integer n are studied. For continuous dynamical systems, the map τ is understood to be a finite time evolution map and the construction is more complicated. 

Examples of dynamical systems

• Arnold's cat map
• Baker's map is an example of a chaotic piecewise linear map
• Circle map
• Double pendulum
• Billiards and Outer billiards
• Hénon map
• Horseshoe map
• Irrational rotation
• List of chaotic maps
• Logistic map
• Lorenz system
• Rossler map

Multidimensional generalization

Dynamical systems are defined over a single independent variable, usually thought of as time. A more general class of systems are defined over multiple independent variables and are therefore called multidimensional systems. Such systems are useful for modeling, for example, image processing.

Cultivated plant taxonomy

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Cultivated_plant_taxonomy

 

Some of the traditional tools of cultivated plant taxonomy including: microscope, camera, flowers and book to assist identification.

 

Cultivated plant taxonomy is the study of the theory and practice of the science that identifies, describes, classifies, and names cultigens—those plants whose origin or selection is primarily due to intentional human activity. Cultivated plant taxonomists do, however, work with all kinds of plants in cultivation. 

Cultivated plant taxonomy is one part of the study of horticultural botany which is mostly carried out in botanical gardens, large nurseries, universities, or government departments. Areas of special interest for the cultivated plant taxonomist include: searching for and recording new plants suitable for cultivation (plant hunting); communicating with and advising the general public on matters concerning the classification and nomenclature of cultivated plants and carrying out original research on these topics; describing the cultivated plants of particular regions (horticultural floras); maintaining databases, herbaria and other information about cultivated plants.

Much of the work of the cultivated plant taxonomist is concerned with the naming of plants as prescribed by two plant nomenclatural Codes. The provisions of the International Code of Nomenclature for algae, fungi, and plants (Botanical Code) serve primarily scientific ends and the objectives of the scientific community, while those of the International Code of Nomenclature for Cultivated Plants (Cultivated Plant Code) are designed to serve both scientific and utilitarian ends by making provision for the names of plants used in commerce—the cultigens that have arisen in agriculture, forestry and horticulture. These names, sometimes called variety names, are not in Latin but are added onto the scientific Latin names, and they assist communication among the community of foresters, farmers and horticulturists. 

The history of cultivated plant taxonomy can be traced from the first plant selections that occurred during the agrarian Neolithic Revolution to the first recorded naming of human plant selections by the Romans. The naming and classification of cultigens followed a similar path to that of all plants until the establishment of the first Cultivated Plant Code in 1953 which formally established the cultigen classification category of cultivar. Since that time the classification and naming of cultigens has followed its own path. 

Distinctive characteristics

Cultivated plant taxonomy has been distinguished from the taxonomy of other plants in at least five ways. Firstly, there is a distinction made according to where the plants are growing — that is, whether they are wild or cultivated. This is alluded to by the Cultivated Plant Code which specifies in its title that it is dealing with cultivated plants. Secondly, a distinction is made according to how the plants originated. This is indicated in Principle 2 of the Cultivated Plant Code which defines the scope of the Code as "... plants whose origin or selection is primarily due to the intentional actions of mankind" — plants that have evolved under natural selection with human assistance.Thirdly, cultivated plant taxonomy is concerned with plant variation that requires the use of special classification categories that do not conform with the hierarchy of ranks implicit in the Botanical Code, these categories being the cultivar, Group and grex (which are only loosely equivalent to ranks in the Botanical Code). This feature is also referred to in the Preamble to the Cultivated Plant Code which states that "The purpose of giving a name to a taxon is not to indicate its characters or history, but to supply a means of referring to it and to indicate to which category it is assigned." Fourthly, cultivated plant taxonomy serves a particular community of people: the Botanical Code focuses on the needs of plant taxonomists as they attempt to maintain order and stability for the scientific names of all plants, while the Cultivated Plant Code caters for the needs of people requiring names for plants used in the commercial world of agriculture, forestry and horticulture. Finally, the difference between cultivated plant taxonomy and the taxonomy of other plants has been attributed to the purpose for which the taxonomy has been devised, it being plant-centred in the Botanical Code and human-centred in the Cultivated Plant Code.

Scientific and anthropocentric classification

The key activities of cultivated plant taxonomy relate to classification (taxonomy) and naming (nomenclature). The rules associated with naming plants are separate from the methods, principles or purposes of classification, except that the units of classification, the taxa, are placed in a nested hierarchy of ranks – like species within genera, and genera within families. There are three classification categories used in the Cultivated Plant Code, the cultivar and the Group and the grex, but they are only loosely equivalent to ranks in the Botanical Code.

From the time of the ancient world, at least, plants have been classified in two ways. On the one hand there is the detached academic, philosophical or scientific interest in plants themselves: this groups plants by their relationship to one another according to their similarities and differences in structure and function. Then there is the practical, utilitarian or anthropocentric interest which groups plants according to their human use. Cultivated plant taxonomy is concerned with the special classification categories needed for the plants of agriculture, horticulture and forestry as regulated by the Cultivated Plant Code. This Code serves not only the scientific interests of formal nomenclature, it also caters for the special utilitarian needs of people dealing with the plants of commerce. Those cultigens given names governed by the Cultivated Plant Code fulfill three criteria: they have special features considered of sufficient importance to warrant a name; the special features are the result of deliberate human breeding or selection and are not found in wild populations (except in rare cases where the special features represent desirable part of natural variation found in wild populations that is not covered by a scientific name); it is possible to perpetuate the desirable features by propagation in cultivation.

The terms cultigen and cultivar may be confused with each other. Cultigen is a general-purpose term for plants that have been deliberately altered or specially selected by humans, while cultivar is a formal classification category. Cultigens include not only plants with cultivar names but also those with names in the classification categories of grex and Group. The Cultivated Plant Code points out that cultigens are: deliberately selected plants that may have arisen by intentional or accidental hybridization in cultivation, by selection from existing cultivated stocks, or from variants within wild populations that are maintained as recognizable entities solely by continued propagation. Included within the group of plants known as cultigens are genetically modified plants, plants with binomial Latin names that are the result of ancient human selection, and any plants that have been altered by humans but which have not been given formal names. In practice most cultigens are cultivars.

The following account of the historical development of cultivated plant taxonomy traces the way cultigens have arisen and been incorporated into botanical science; it also demonstrates how two approaches to plant nomenclature and classification have led to the present-day International Code of Nomenclature for algae, fungi, and plants and International Code of Nomenclature for Cultivated Plants. 

Historical development

The history of cultigen nomenclature has been discussed by William T. Stearn and Brandenberg, Hetterscheid and Berg. It has also been examined from a botanical perspective and from the origin of the Cultivated Plant Code in 1953 until 2004.

The early development of cultigen taxonomy follows that of plant taxonomy in general as the early listing and documentation of plants made little distinction between those that were anthropogenic and those that were natural wild kinds. Formal botanical nomenclature and classification evolved from the simple binomial system of folk taxonomy and it was not until the mid-19th century that the nomenclatural path of cultigens began to diverge from mainstream plant taxonomy.

10,000 to 400 BCE – plant domestication

Sumerian harvester's sickle made from baked clay and dated to about 3000 BCE.

 

William T. Stearn (1911–2001), taxonomic botanist, classical scholar and author of the book Botanical Latin has commented that "cultivated plants [cultigens] are mankind's most vital and precious heritage from remote antiquity". Cultigens of our most common economic plants probably date back to the first settled communities of the Neolithic Revolution 10,000 to 12,000 years ago although their exact time and place of true origin will probably remain a mystery. In the Western world among the first cultigens would have been selections of the cereals wheat and barley that arose in the early settlements of the Fertile Crescent (the fertile river valleys of the Nile, Tigris and Euphrates) in the Western Mediterranean. Food plant selections would also have been made in the ten or so other centres of settlement that occurred around the world at this time. Confining crops to local areas gave rise to landraces (selections that are highly adapted to local conditions) although these are now largely replaced by modern cultivars. Cuttings are an extremely effective way of perpetuating desirable characters, especially of woody plants like grapes, figs and olives so it is not surprising that these are among the first known plant selections perpetuated in cultivation in the West. Migrating people would take their plant seeds and cuttings with them; there is evidence of early Fertile Crescent cereal cultigens being transferred from Western Asia to surrounding lands.

400 BCE to 1400 – the ancient world: Greco-Roman influence to the Middle Ages

Aristotle (384–322 BCE)

 

As early as the 5th century BCE the Greek philosopher Hippo expressed the opinion that cultigens (as we call them now) were produced from wild plants as the result of the care bestowed on them by man, a revolutionary view at a time when they were regarded as the special creation and gift of the gods. In devising ways of classifying organisms the philosopher Aristotle (384–322 BCE) established the important idea of a fundamentum divisionis — the principle that groups can be progressively subdivided. This has been assumed in biological classification ever since and is congruent with the relatively recent idea of evolution as descent with modification. All biological classification follows this principle of groups within groups, known as a nested hierarchy, but this form of classification does not necessarily presuppose evolution.

Theophrastus (371–286 BCE)

 

The earliest scientific (rather than utilitarian) approach to plants is attributed to Aristotle's student Theophrastus (371–286 BCE), known as the "father of botany". In his Enquiry into Plants Theophrastus described 480 kinds of plant, dividing the plant kingdom into trees, shrubs, undershrubs and herbs with further subdivision into wild and cultivated, flowering and non-flowering, deciduous or evergreen.

The earliest scientific (rather than utilitarian) approach to plants is attributed to Aristotle's student Theophrastus (371–286 BCE), known as the "father of botany". In his Enquiry into Plants Theophrastus described 480 kinds of plant, dividing the plant kingdom into trees, shrubs, undershrubs and herbs with further subdivision into wild and cultivated, flowering and non-flowering, deciduous or evergreen.

The utilitarian approach, classifying plants according to their medicinal properties, is exemplified by the work of Roman nobleman, scientist and historian, Pliny the Elder (29–79 CE) author of Naturalis historiae. "Cultivars" listed here are named after people, places or special plant characteristics. Most notable is the work of Dioscorides (ca.40–ca.90 CE) a Greek doctor who worked with the Roman army. His five-volume Materia Medica was a forerunner of the herbal which led to the modern pharmacopoeia. This work was endlessly plagiarised by later herbals including those printed between about 1470 and 1670 CE: it listed 600 to 1000 different kinds of plants including the cultigens Gallica, Centifolia, the rose of uncertain origin known as Alba and other rose cultivars grown by the Romans. 

Pliny the Elder (29–79 CE)

 

The first record of a named cultigen occurs in De Agri Cultura. written about 160 BCE by Roman statesman Cato the Elder (234–149 BCE) in a list that includes 120 kinds (cultivars) of figs, grapes, apples and olives. The names are presented in a way that implies that they would have been familiar to fellow Romans. The "cultivar" names were mostly of one word and denoted the provenance of the cultivar (the geographical origin of the place where the plant selections were made). Writers up to the 15th century added little to this early work. In the Middle Ages the book of hours, early herbals, illuminated manuscripts and economic records indicate that plants grown by the Romans found their way into monastery gardens. For example, in 827 CE the following herbs were mentioned in the poem Hortulus by Walafrid Strabo as growing in the monastery garden of St Gallen in Switzerland: sage, rue, southernwood, wormwood, horehound, fennel, German iris, lovage, chervil, Madonna lily, opium poppy, clary, mint, betony, agrimony, catmint, radish, gallica rose, bottle gourd and melon. It seems likely that aromatic and culinary herbs were quite widespread and similar lists of plants occur in records of plants grown in Villa gardens at the time of Charlemagne (742–814 CE).

1400 to 1700 – Renaissance, imperial expansion, herbals

Caspar Bauhin (1550–1624)

 

The revival of learning during the Renaissance reinvigorated the study of plants and their classification. From about 1400 CE European expansion established Latin as the common language of scholars and it was adopted for biological nomenclature. Then, from about 1500 CE, the publication of herbals (books often illustrated with woodcuts describing the appearance, medicinal properties, and other characteristics of plants used in herbal medicine) extended the formal documentation of plants and by the late 16th century the number of different plant kinds described in Europe had risen to about 4,000. In 1623 Gaspard Bauhin published his Pinax theatre botanici an attempt at a comprehensive compilation of all plants known at that time: it included about 6000 kinds. The combined works of a German physician and botanist Valerius Cordus (1515–1544 CE) which were published in 1562 included many named "cultivars" including 30 apples and 49 pears, presumably local German selections. English herbalist John Parkinson's Paradisi in Sole ... (1629) lists 57 apple "cultivars", 62 pears, 61 plums, 35 cherries and 22 peaches.

With increasing trade in economic and medicinal plants the need for a more comprehensive classification system increased. Up to about 1650 CE plants had been grouped either alphabetically or according to utilitarian folk taxonomy – by their medicinal uses or whether they were trees, shrubs or herbs. Between 1650 and 1700 CE there was a move from the utilitarian back to a scientific natural classification based on the characters of the plants themselves.

1700 to 1750 – dawn of scientific classification

In 1700 French botanist J.P. de Tournefort although still using the broad groupings of "trees" and "herbs" for flowering plants, began to use flower characteristics as distinguishing features and, most importantly, provided a clear definition of the genus as a basic unit of classification. In Institutiones Rei Herbariae he listed about 10,000 different plants, which he called species, organised into 698 genera with illustrations. The establishment of this precursor of scientific classification vastly improved the organisation of plant variation into approximately equivalent groups or ranks and many of his genera were later taken up by Carl Linnaeus. There was still at this time no common agreement on the way to present plant names so they ranged in length from one word to lengthy descriptive sentences. As the number of recorded plants increased this naming system became more unwieldy. 

In England the tradition of documenting garden plants was established long before Linnaeus' Species Plantarum starting with the herbals, but the most prominent early chronicler was Philip Miller (1691–1771) who was a master gardener in charge of the Chelsea Physic Garden in London from 1722 to 1770. New plants were coming into Western Europe from southern Europe and the overseas colonies of the Dutch, British and French. These new plants came largely to the botanic gardens of Amsterdam, Leiden, Chelsea and Paris and they needed recording. In 1724 Miller produced a two-volume compendium of garden plants called The Gardeners and Florists Dictionary or a complete System of Horticulture. The first edition was in 1724, subsequently revised and enlarged until the last and 8th edition in 1768 by which time he had adopted Linnaean binomials. For a while this publication was taken as the starting point for "horticultural" nomenclature equivalent to Linnaeus' Species Plantarum which is now taken as the starting point for botanical nomenclature in general. Miller's Dictionary was the first of many English horticultural compendia whose history has been traced by William Stearn.

1750 to 1800 – Linnaeus and binomial nomenclature

Carl Linnaeus (1707–1778) who established the binomial system of plant nomenclature.

 

In the early 18th century colonial expansion and exploration created a demand for the description of thousands of new organisms. This highlighted difficulties in communication about plants, the replication of their descriptions, and the importance of an agreed way of presenting, publishing and applying their names. 

It was the Swedish botanist Carl Linnaeus who finally put order into this situation as he attempted to name all the known organisms of his day. In 1735 his Systema Naturae, which included animals (the tenth edition became the starting point for zoological nomenclature) was followed by Critica Botanica in 1737, and Philosophia Botanica in 1751. But it was his most comprehensive work on plants, the 1753 publication Species Plantarum that formalised the name of a genus with a single epithet to form the name of a species as two words, the binomial thus making secure the biological system of binomial nomenclature. In these works Linnaeus used a third name as a variety within a species. These varieties included both wild and horticultural variants. The horticultural varieties were still written in Latin and some have persisted to this day. 

Linnaeus had very definite and uncomplimentary views about cultigens, regarding them as inferior plants for the amusement of those people he disparagingly called anthophiles (flower-lovers); these were plants not deserving the attention of serious botanists. His views revealed both his prejudice, his stance on special creation, and his recognition of the difficulties entailed in cultivated plant taxonomy: 

“

"anthophiles … practice a floral science all their own, grasped only by their devotees; no botanist in his senses will enlist in their camp." "All the species recognized by Botanists came forth from the Almighty Creator's hand, and the number now and always will be exactly the same, while every day new and different florist's species arise from the true species recognized by botanists, and when they have arisen they eventually revert to their original forms. Accordingly to the former have been assigned by Nature fixed limits, beyond which they cannot go: while the latter display without end the infinite sport of Nature." "... botany has been overborne by the system of varieties for long enough … few, if any, agree as to what constitutes a species, or what a variety; … I wish the system of varieties were entirely excluded from Botany and turned over entirely to the Anthophiles, since it causes nothing but ambiguities, errors, dead weight and vanity …"

”

1800 to 1900 – global plant trade

Linnaeus's Species Plantarum of 1753, his catalogue of all the world's plants known to European science.

 

The natural distribution of plants across the world has determined when and where cultigens have been produced. The botanical and horticultural collection of economically important plants, including ornamentals, was based in Europe. Although economic herbs and spices had a long history in trade, and there are good records of cultivar distribution by the Romans, European botanical and horticultural exploration rapidly increased in the 19th century with the colonial expansion taking place at the time. New plants were brought back to Europe while, at the same time, valuable economic plants, including those from the tropics, were distributed among the colonies. This plant trade has provided the common global heritage of economic and ornamental cultigens that we use today and which formed the stock for modern plant selection, breeding, and genetic engineering. The plant exchange that occurred as a result of European trade can be divided into several phases:

to 1560 mostly within Europe

1560–1620 Near East (esp. bulbous plants from Turkey – "tulipomania")

1620–1686 Canada and Virginia herbaceous plants

1687–1772 Cape of South Africa

1687–1772 North American trees and shrubs

1772–1820 Australia, Tasmania, New Zealand

1820–1900 Tropical glasshouse plants; hardy Japanese plants

1900–1930 West China

1930 Intensive breeding and selection programs

1900 to 1950 – the Botanical Code and cultigen nomenclature

As the community of people dealing with the cultigens of commerce grew so, once again, the divergence between taxonomy serving scientific purposes and utilitarian taxonomy meeting human needs re-emerged. In 1865 German botanist Karl Koch, who became General Secretary of the Berlin Horticultural Society, expressed resentment at the continued use of Latin for cultigen names. Many proposals to deal with this were made, perhaps the most prominent being the Lois de la nomenclature botanique submitted in 1867 to the fourth Horticultural and Botanical Congress by Swiss botanist Alphonse de Candolle who, in Article 40 stated:

"Seedlings, half-breeds (métis) of unknown origin or sports should receive from horticulturists fancy names (noms de fantaisie) in common language, as distinct as possible from the Latin names of species or varieties."

Outstanding American cultivated plant taxonomist Liberty Hyde Bailey (1858–1954).

 

This Article, making provision for the cultigens of horticultural nomenclature was to remain in the Botanical Code (with a minor amendment in 1935 suggesting the use of the letter 'c' before the horticultural name and antedating formal recognition of the cultivar) through 1906, 1912 and 1935 until the separation, in 1953, of the Horticultural Code, precursor to the International Code of Nomenclature for Cultivated Plants (Cultivated Plant Code). In 1900 there was the first International Botanical Congress and in 1905 at the second Congress in Vienna an agreed set of nomenclatural rules was established, the Vienna Rules, which became known from then on as the International Code of Botanical Nomenclature (now the International Code of Nomenclature for algae, fungi, and plants). After World War II the responsibility for the Botanical Code was taken up by the International Association for Plant Taxonomy and meetings to discuss revisions are held at six-yearly intervals, the latest being in 2005.

In horticulture at this time there existed all the problems that had confronted botanists in the 19th century – a plethora of names of various length, written and published in many languages with much duplication. The period between 1867 and 1953 was an uneasy time in which American horticulturists and other groups in Europe, such as the specialist orchid community, made attempts to put order into this chaos within their particular group of interest and devising their own rules for naming the plants of commerce. Friedrich Alefeld (1820–1872), who used Latin variety names, in a monographic study of beans, lentils and other legumes distinguished three infraspecific taxonomic categories: Unterart (subspecies), Varietäten Gruppe and Kultur-Varietät, all with Latin names. In doing this he was probably laying the ground for the later establishment of the cultigen classification categories cultivar and Group. In conjunction with the Brussels International Botanical Congress of 1910 there was an International Horticultural Congress having a horticultural nomenclature component. 

As a result of general dissatisfaction and a submission from the Royal Horticultural Society the Règles de Nomenclature Horticole was established. The use of simple descriptive Latin names (e.g. compactus, nanus, prostratus) for horticultural variants was accepted and so too were names in the local language – which were not to be translated and should preferably consist of one word and a maximum of three. This first Horticultural Code consisted of 16 Articles. With the intercession of a World War I it was not until the 9th Horticultural Congress in London in 1930 that the rules of a Horticulture Nomenclature Committee were agreed and added as an appendix to the 1935 Botanical Code. The rules established in 1935 were accepted but needed to be extended to include the cultigens of agriculture and forestry, but it was only a result of discussions at the 1950 International Botanical Congress in Stockholm and the 18th International Horticultural Congress in London in 1952 the first International Code of Nomenclature for Cultivated Plants was published in 1953. The American horticultural botanist Liberty Hyde Bailey was responsible for coining the word cultigen in 1918 and cultivar in 1923, the word cultivar only coming into general circulation with the new Code of 1953. The use of these two terms belies the multitude of classification terms and categories that had been suggested as designations for cultigens.

1953 – the International Code of Nomenclature for Cultivated Plants

The first Cultivated Plant Code (Wageningen), which was published in 1953, has been followed by eight subsequent editions – in 1958 (Utrecht), 1961 (update of 1958), 1969 (Edinburgh), 1980 (Seattle), 1995 (Edinburgh), 2004 (Toronto) and 2009 (Wageningen).

Following the structure of the Botanical Code the Cultivated Plant Code is set out in the form of an initial set of Principles followed by Rules and Recommendations that are subdivided into Articles. Amendments to the Cultivated Plant Code are prompted by international symposia for cultivated plant taxonomy which allow for rulings made by the International Commission on the Nomenclature of Cultivated Plants. Each new Cultivated Plant Code includes a summary of the changes made to the previous version and these have also been summarised for the period 1953 to 1995.

International Association for Cultivated Plant Taxonomy

Wisley is one of the Royal Horticultural Society's flagship gardens and a focus for cultivated plant taxonomy.

 

Recent concerns have focused on international communication on cultivated plant taxonomy, organisation of international symposia, and general communication on topics of interest. In 1988 a Horticultural Taxonomy Group (Hortax) was formed in the UK and a parallel organisation, the Nomenclature and Registration Working Group of the Vaste Keurings Commissie in the Netherlands. One development promoting discussion was the newsletter Hortax News which was superseded in February 2006 by the first issue of Hanburyana, a journal produced by the Royal Horticultural Society in London and dedicated to horticultural taxonomy. This filled a gap left when the American journal Baileya ceased publication in the early 1990s. Another development was the launch, in 2007, at the Sixth Symposium on the Taxonomy of Cultivated Plants at Wageningen of the International Association for Cultivated Plant Taxonomy. Hortax also publishes Plant Names: A Guide for Horticulturists, Nurserymen, Gardeners and Students.

Presenting cultigen names

Most cultigens have names consisting of a Latin name that is governed by the International Code of Nomenclature for algae, fungi, and plants e.g. Malus domestica, to which is added a cultigen epithet, enclosed in single quotes e.g. Malus domestica 'Granny Smith'. The formation and use of the three classification categories (ranks) used for cultigens, the cultivar, Group and grex, is regulated by the ICNCP. Examples of acceptable ways to present cultigen names are given below:

Prunus serrata Sato-zakura Group 

Prunus serrata (Sato-zakura Group) 'Ojochin'

Prunus 'Ojochin'

Flowering cherry 'Ojochin'

Contemporary issues

Chelsea Physic Garden, summer 2006

 

Current challenges for cultivated plant taxonomists include: the use of large plant name databases; ways of dealing with the use of non-scientific names in commerce (known as trade designations), especially for plant labels in nurseries; intellectual property and plants; adapting modern technology, in particular molecular techniques, to the creation and identification of cultivars; maintaining germplasm collections of cultivars, including herbaria; the recording and registration of cultivars.

The ways in which the plant variation resulting from human activity is named and classified remains contentious. The replacement of the expression "cultivated plant" with the word "cultigen" is not universally accepted. The debate continues concerning the notions of ranks and taxa as applied to cultigens. Is it appropriate to call the highly modified transgenic products of human artificial selection "taxa" in the same way we do for the products of natural selection in the wild? To overcome this difficulty the term culton (pl. culta) has been suggested to replace the word taxon when speaking about cultigens.

Then, most "wild" plants fit neatly into the nested hierarchy of ranks used in Linnaean classification (species into genera, genera into families etc.) which aligns with Darwinian descent with modification. Choosing classification categories for cultigens is not clear-cut. Included among cultigens are: simple selections taken from plants in the wild or in cultivation; artificial hybrids produced both by accident and intention; plants produced by genetic engineering; clonal material reproduced by cuttings, grafting, budding, layering etc.; graft-chimaeras; selections from the wild; ancient selections of crops that date back thousands of years; selections of aberrant growth such as witches brooms; the results of deliberate repeatable single crosses between two pure lines to produce plants of a particular general appearance that is desirable for horticulture, but which are not genetically identical. The question remains as to whether the classification categories of cultivar, Group and grex are the most appropriate and efficient way to deal with this broad range of plant variation.