Spacecraft propulsion (updated)

From Wikipedia, the free encyclopedia

A remote camera captures a close-up view of a Space Shuttle Main Engine during a test firing at the John C. Stennis Space Center in Hancock County, Mississippi.

Spacecraft propulsion is any method used to accelerate spacecraft and artificial satellites. There are many different methods. Each method has drawbacks and advantages, and spacecraft propulsion is an active area of research. However, most spacecraft today are propelled by forcing a gas from the back/rear of the vehicle at very high speed through a supersonic de Laval nozzle. This sort of engine is called a rocket engine.

All current spacecraft use chemical rockets (bipropellant or solid-fuel) for launch, though some (such as the Pegasus rocket and SpaceShipOne) have used air-breathing engines on their first stage. Most satellites have simple reliable chemical thrusters (often monopropellant rockets) or resistojet rockets for orbital station-keeping and some use momentum wheels for attitude control. Soviet bloc satellites have used electric propulsion for decades, and newer Western geo-orbiting spacecraft are starting to use them for north-south stationkeeping and orbit raising. Interplanetary vehicles mostly use chemical rockets as well, although a few have used ion thrusters and Hall effect thrusters (two different types of electric propulsion) to great success.

Requirements

Artificial satellites must be launched into orbit and once there they must be placed in their nominal orbit. Once in the desired orbit, they often need some form of attitude control so that they are correctly pointed with respect to Earth, the Sun, and possibly some astronomical object of interest. They are also subject to drag from the thin atmosphere, so that to stay in orbit for a long period of time some form of propulsion is occasionally necessary to make small corrections (orbital stationkeeping). Many satellites need to be moved from one orbit to another from time to time, and this also requires propulsion. A satellite's useful life is usually over once it has exhausted its ability to adjust its orbit.

Spacecraft designed to travel further also need propulsion methods. They need to be launched out of the Earth's atmosphere just as satellites do. Once there, they need to leave orbit and move around.

For interplanetary travel, a spacecraft must use its engines to leave Earth orbit. Once it has done so, it must somehow make its way to its destination. Current interplanetary spacecraft do this with a series of short-term trajectory adjustments. In between these adjustments, the spacecraft simply falls freely along its trajectory. The most fuel-efficient means to move from one circular orbit to another is with a Hohmann transfer orbit: the spacecraft begins in a roughly circular orbit around the Sun. A short period of thrust in the direction of motion accelerates or decelerates the spacecraft into an elliptical orbit around the Sun which is tangential to its previous orbit and also to the orbit of its destination. The spacecraft falls freely along this elliptical orbit until it reaches its destination, where another short period of thrust accelerates or decelerates it to match the orbit of its destination. Special methods such as aerobraking or aerocapture are sometimes used for this final orbital adjustment.

Artist's concept of a solar sail

Some spacecraft propulsion methods such as solar sails provide very low but inexhaustible thrust; an interplanetary vehicle using one of these methods would follow a rather different trajectory, either constantly thrusting against its direction of motion in order to decrease its distance from the Sun or constantly thrusting along its direction of motion to increase its distance from the Sun. The concept has been successfully tested by the Japanese IKAROS solar sail spacecraft.

Spacecraft for interstellar travel also need propulsion methods. No such spacecraft has yet been built, but many designs have been discussed. Because interstellar distances are very great, a tremendous velocity is needed to get a spacecraft to its destination in a reasonable amount of time. Acquiring such a velocity on launch and getting rid of it on arrival will be a formidable challenge for spacecraft designers.

Effectiveness

When in space, the purpose of a propulsion system is to change the velocity, or v, of a spacecraft. Because this is more difficult for more massive spacecraft, designers generally discuss momentum, mv. The amount of change in momentum is called impulse. So the goal of a propulsion method in space is to create an impulse.

When launching a spacecraft from Earth, a propulsion method must overcome a higher gravitational pull to provide a positive net acceleration. In orbit, any additional impulse, even very tiny, will result in a change in the orbit path.

The rate of change of velocity is called acceleration, and the rate of change of momentum is called force. To reach a given velocity, one can apply a small acceleration over a long period of time, or one can apply a large acceleration over a short time. Similarly, one can achieve a given impulse with a large force over a short time or a small force over a long time. This means that for maneuvering in space, a propulsion method that produces tiny accelerations but runs for a long time can produce the same impulse as a propulsion method that produces large accelerations for a short time. When launching from a planet, tiny accelerations cannot overcome the planet's gravitational pull and so cannot be used.

Earth's surface is situated fairly deep in a gravity well. The escape velocity required to get out of it is 11.2 kilometers/second. As human beings evolved in a gravitational field of 1g (9.8 m/s²), an ideal propulsion system would be one that provides a continuous acceleration of 1g (though human bodies can tolerate much larger accelerations over short periods). The occupants of a rocket or spaceship having such a propulsion system would be free from all the ill effects of free fall, such as nausea, muscular weakness, reduced sense of taste, or leaching of calcium from their bones.

The law of conservation of momentum means that in order for a propulsion method to change the momentum of a space craft it must change the momentum of something else as well. A few designs take advantage of things like magnetic fields or light pressure in order to change the spacecraft's momentum, but in free space the rocket must bring along some mass to accelerate away in order to push itself forward. Such mass is called reaction mass.

In order for a rocket to work, it needs two things: reaction mass and energy. The impulse provided by launching a particle of reaction mass having mass m at velocity v is mv. But this particle has kinetic energy mv²/2, which must come from somewhere. In a conventional solid, liquid, or hybrid rocket, the fuel is burned, providing the energy, and the reaction products are allowed to flow out the back, providing the reaction mass. In an ion thruster, electricity is used to accelerate ions out the back. Here some other source must provide the electrical energy (perhaps a solar panel or a nuclear reactor), whereas the ions provide the reaction mass.

When discussing the efficiency of a propulsion system, designers often focus on effectively using the reaction mass. Reaction mass must be carried along with the rocket and is irretrievably consumed when used. One way of measuring the amount of impulse that can be obtained from a fixed amount of reaction mass is the specific impulse, the impulse per unit weight-on-Earth (typically designated by ${\displaystyle I_{\text{sp}}}$). The unit for this value is seconds. Because the weight on Earth of the reaction mass is often unimportant when discussing vehicles in space, specific impulse can also be discussed in terms of impulse per unit mass. This alternate form of specific impulse uses the same units as velocity (e.g. m/s), and in fact it is equal to the effective exhaust velocity of the engine (typically designated ${\displaystyle v_{e}}$). Confusingly, both values are sometimes called specific impulse. The two values differ by a factor of g_n, the standard acceleration due to gravity 9.80665 m/s² (${\displaystyle I_{\text{sp}}g_{\mathrm {n} }=v_{e}}$).

A rocket with a high exhaust velocity can achieve the same impulse with less reaction mass. However, the energy required for that impulse is proportional to the exhaust velocity, so that more mass-efficient engines require much more energy, and are typically less energy efficient. This is a problem if the engine is to provide a large amount of thrust. To generate a large amount of impulse per second, it must use a large amount of energy per second. So high-mass-efficient engines require enormous amounts of energy per second to produce high thrusts. As a result, most high-mass-efficient engine designs also provide lower thrust due to the unavailability of high amounts of energy.

Methods

Propulsion methods can be classified based on their means of accelerating the reaction mass. There are also some special methods for launches, planetary arrivals, and landings.

Reaction engines

A reaction engine is an engine which provides propulsion by expelling reaction mass, in accordance with Newton's third law of motion. This law of motion is most commonly paraphrased as: "For every action there is an equal, and opposite, reaction".

Examples include both duct engines and rocket engines, and more uncommon variations such as Hall effect thrusters, ion drives and mass drivers. Duct engines are obviously not used for space propulsion due to the lack of air; however some proposed spacecraft have these kinds of engines to assist takeoff and landing.

Delta-v and propellant

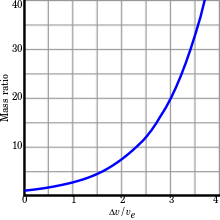
Rocket mass ratios versus final velocity, as calculated from the rocket equation

Exhausting the entire usable propellant of a spacecraft through the engines in a straight line in free space would produce a net velocity change to the vehicle; this number is termed delta-v (${\displaystyle \Delta v}$).

If the exhaust velocity is constant then the total ${\displaystyle \Delta v}$ of a vehicle can be calculated using the rocket equation, where M is the mass of propellant, P is the mass of the payload (including the rocket structure), and ${\displaystyle v_{e}}$ is the velocity of the rocket exhaust. This is known as the Tsiolkovsky rocket equation:

${\displaystyle \Delta v=v_{e}\ln \left({\frac {M+P}{P}}\right).}$

For historical reasons, as discussed above, ${\displaystyle v_{e}}$ is sometimes written as

${\displaystyle v_{e}=I_{\text{sp}}g_{0}}$

where ${\displaystyle I_{\text{sp}}}$ is the specific impulse of the rocket, measured in seconds, and ${\displaystyle g_{0}}$ is the gravitational acceleration at sea level.

For a high delta-v mission, the majority of the spacecraft's mass needs to be reaction mass. Because a rocket must carry all of its reaction mass, most of the initially-expended reaction mass goes towards accelerating reaction mass rather than payload. If the rocket has a payload of mass P, the spacecraft needs to change its velocity by ${\displaystyle \Delta v}$, and the rocket engine has exhaust velocity v_e, then the reaction mass M which is needed can be calculated using the rocket equation and the formula for ${\displaystyle I_{\text{sp}}}$:

${\displaystyle M=P\left(e^{\frac {\Delta v}{v_{e}}}-1\right).}$

For ${\displaystyle \Delta v}$ much smaller than v_e, this equation is roughly linear, and little reaction mass is needed. If ${\displaystyle \Delta v}$ is comparable to v_e, then there needs to be about twice as much fuel as combined payload and structure (which includes engines, fuel tanks, and so on). Beyond this, the growth is exponential; speeds much higher than the exhaust velocity require very high ratios of fuel mass to payload and structural mass.

For a mission, for example, when launching from or landing on a planet, the effects of gravitational attraction and any atmospheric drag must be overcome by using fuel. It is typical to combine the effects of these and other effects into an effective mission delta-v. For example, a launch mission to low Earth orbit requires about 9.3–10 km/s delta-v. These mission delta-vs are typically numerically integrated on a computer.

Some effects such as Oberth effect can only be significantly utilised by high thrust engines such as rockets; i.e., engines that can produce a high g-force (thrust per unit mass, equal to delta-v per unit time).

Power use and propulsive efficiency

For all reaction engines (such as rockets and ion drives) some energy must go into accelerating the reaction mass. Every engine will waste some energy, but even assuming 100% efficiency, to accelerate an exhaust the engine will need energy amounting to

${\displaystyle {\frac {1}{2}}{\dot {m}}v_{e}^{2}}$

This energy is not necessarily lost- some of it usually ends up as kinetic energy of the vehicle, and the rest is wasted in residual motion of the exhaust.

Due to energy carried away in the exhaust, the energy efficiency of a reaction engine varies with the speed of the exhaust relative to the speed of the vehicle, this is called propulsive efficiency

Comparing the rocket equation (which shows how much energy ends up in the final vehicle) and the above equation (which shows the total energy required) shows that even with 100% engine efficiency, certainly not all energy supplied ends up in the vehicle - some of it, indeed usually most of it, ends up as kinetic energy of the exhaust.

The exact amount depends on the design of the vehicle, and the mission. However, there are some useful fixed points:

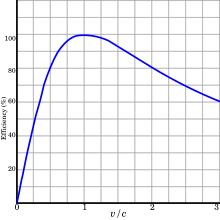
• if the ${\displaystyle I_{\text{sp}}}$ is fixed, for a mission delta-v, there is a particular ${\displaystyle I_{\text{sp}}}$ that minimises the overall energy used by the rocket. This comes to an exhaust velocity of about ⅔ of the mission delta-v (see the energy computed from the rocket equation). Drives with a specific impulse that is both high and fixed such as Ion thrusters have exhaust velocities that can be enormously higher than this ideal for many missions.
• if the exhaust velocity can be made to vary so that at each instant it is equal and opposite to the vehicle velocity then the absolute minimum energy usage is achieved. When this is achieved, the exhaust stops in space and has no kinetic energy; and the propulsive efficiency is 100%- all the energy ends up in the vehicle (in principle such a drive would be 100% efficient, in practice there would be thermal losses from within the drive system and residual heat in the exhaust). However, in most cases this uses an impractical quantity of propellant, but is a useful theoretical consideration. Anyway, the vehicle has to move before the method can be applied.

Some drives (such as VASIMR or electrodeless plasma thruster) actually can significantly vary their exhaust velocity. This can help reduce propellant usage or improve acceleration at different stages of the flight. However the best energetic performance and acceleration is still obtained when the exhaust velocity is close to the vehicle speed. Proposed ion and plasma drives usually have exhaust velocities enormously higher than that ideal (in the case of VASIMR the lowest quoted speed is around 15000 m/s compared to a mission delta-v from high Earth orbit to Mars of about 4000 m/s).

It might be thought that adding power generation capacity is helpful, and although initially this can improve performance, this inevitably increases the weight of the power source, and eventually the mass of the power source and the associated engines and propellant dominates the weight of the vehicle, and then adding more power gives no significant improvement.

For, although solar power and nuclear power are virtually unlimited sources of energy, the maximum power they can supply is substantially proportional to the mass of the powerplant (i.e. specific power takes a largely constant value which is dependent on the particular powerplant technology). For any given specific power, with a large ${\displaystyle v_{e}}$ which is desirable to save propellant mass, it turns out that the maximum acceleration is inversely proportional to ${\displaystyle v_{e}}$. Hence the time to reach a required delta-v is proportional to ${\displaystyle v_{e}}$. Thus the latter should not be too large.

Energy

Plot of instantaneous propulsive efficiency (blue) and overall efficiency for a vehicle accelerating from rest (red) as percentages of the engine efficiency

In the ideal case ${\displaystyle m_{1}}$ is useful payload and ${\displaystyle m_{0}-m_{1}}$ is reaction mass (this corresponds to empty tanks having no mass, etc.). The energy required can simply be computed as

${\displaystyle {\frac {1}{2}}(m_{0}-m_{1})v_{\text{e}}^{2}}$

This corresponds to the kinetic energy the expelled reaction mass would have at a speed equal to the exhaust speed. If the reaction mass had to be accelerated from zero speed to the exhaust speed, all energy produced would go into the reaction mass and nothing would be left for kinetic energy gain by the rocket and payload. However, if the rocket already moves and accelerates (the reaction mass is expelled in the direction opposite to the direction in which the rocket moves) less kinetic energy is added to the reaction mass. To see this, if, for example, ${\displaystyle v_{e}}$=10 km/s and the speed of the rocket is 3 km/s, then the speed of a small amount of expended reaction mass changes from 3 km/s forwards to 7 km/s rearwards. Thus, although the energy required is 50 MJ per kg reaction mass, only 20 MJ is used for the increase in speed of the reaction mass. The remaining 30 MJ is the increase of the kinetic energy of the rocket and payload.

In general:

${\displaystyle d\left({\frac {1}{2}}v^{2}\right)=vdv=vv_{\text{e}}{\frac {dm}{m}}={\frac {1}{2}}\left[v_{\text{e}}^{2}-\left(v-v_{\text{e}}\right)^{2}+v^{2}\right]{\frac {dm}{m}}}$

Thus the specific energy gain of the rocket in any small time interval is the energy gain of the rocket including the remaining fuel, divided by its mass, where the energy gain is equal to the energy produced by the fuel minus the energy gain of the reaction mass. The larger the speed of the rocket, the smaller the energy gain of the reaction mass; if the rocket speed is more than half of the exhaust speed the reaction mass even loses energy on being expelled, to the benefit of the energy gain of the rocket; the larger the speed of the rocket, the larger the energy loss of the reaction mass.

We have

${\displaystyle \Delta \epsilon =\int v\,d(\Delta v)}$

where ${\displaystyle \epsilon }$ is the specific energy of the rocket (potential plus kinetic energy) and ${\displaystyle \Delta v}$ is a separate variable, not just the change in ${\displaystyle v}$. In the case of using the rocket for deceleration; i.e., expelling reaction mass in the direction of the velocity, ${\displaystyle v}$ should be taken negative.

The formula is for the ideal case again, with no energy lost on heat, etc. The latter causes a reduction of thrust, so it is a disadvantage even when the objective is to lose energy (deceleration).

If the energy is produced by the mass itself, as in a chemical rocket, the fuel value has to be ${\displaystyle \scriptstyle {v_{\text{e}}^{2}/2}}$, where for the fuel value also the mass of the oxidizer has to be taken into account. A typical value is ${\displaystyle v_{\text{e}}}$ = 4.5 km/s, corresponding to a fuel value of 10.1 MJ/kg. The actual fuel value is higher, but much of the energy is lost as waste heat in the exhaust that the nozzle was unable to extract.

The required energy ${\displaystyle E}$ is

${\displaystyle E={\frac {1}{2}}m_{1}\left(e^{\frac {\Delta v}{v_{\text{e}}}}-1\right)v_{\text{e}}^{2}}$

Conclusions:

• for ${\displaystyle \Delta v\ll v_{e}}$ we have ${\displaystyle E\approx {\frac {1}{2}}m_{1}v_{\text{e}}\Delta v}$
• for a given ${\displaystyle \Delta v}$, the minimum energy is needed if ${\displaystyle v_{\text{e}}=0.6275\Delta v}$, requiring an energy of

${\displaystyle E=0.772m_{1}(\Delta v)^{2}}$.

In the case of acceleration in a fixed direction, and starting from zero speed, and in the absence of other forces, this is 54.4% more than just the final kinetic energy of the payload. In this optimal case the initial mass is 4.92 times the final mass.

These results apply for a fixed exhaust speed.

Due to the Oberth effect and starting from a nonzero speed, the required potential energy needed from the propellant may be less than the increase in energy in the vehicle and payload. This can be the case when the reaction mass has a lower speed after being expelled than before – rockets are able to liberate some or all of the initial kinetic energy of the propellant.

Also, for a given objective such as moving from one orbit to another, the required ${\displaystyle \Delta v}$ may depend greatly on the rate at which the engine can produce ${\displaystyle \Delta v}$ and maneuvers may even be impossible if that rate is too low. For example, a launch to Low Earth orbit (LEO) normally requires a ${\displaystyle \Delta v}$ of ca. 9.5 km/s (mostly for the speed to be acquired), but if the engine could produce ${\displaystyle \Delta v}$ at a rate of only slightly more than g, it would be a slow launch requiring altogether a very large ${\displaystyle \Delta v}$ (think of hovering without making any progress in speed or altitude, it would cost a ${\displaystyle \Delta v}$ of 9.8 m/s each second). If the possible rate is only ${\displaystyle g}$ or less, the maneuver can not be carried out at all with this engine.

The power is given by

${\displaystyle P={\frac {1}{2}}mav_{\text{e}}={\frac {1}{2}}Fv_{\text{e}}}$

where ${\displaystyle F}$ is the thrust and ${\displaystyle a}$ the acceleration due to it. Thus the theoretically possible thrust per unit power is 2 divided by the specific impulse in m/s. The thrust efficiency is the actual thrust as percentage of this.

If, e.g., solar power is used, this restricts ${\displaystyle a}$; in the case of a large ${\displaystyle v_{\text{e}}}$ the possible acceleration is inversely proportional to it, hence the time to reach a required delta-v is proportional to ${\displaystyle v_{\text{e}}}$; with 100% efficiency:

• for ${\displaystyle \Delta v\ll v_{\text{e}}}$ we have ${\displaystyle t\approx {\frac {mv_{\text{e}}\Delta v}{2P}}}$

Examples:

• power, 1000 W; mass, 100 kg; ${\displaystyle \Delta v}$ = 5 km/s, ${\displaystyle v_{\text{e}}}$ = 16 km/s, takes 1.5 months.
• power, 1000 W; mass, 100 kg; ${\displaystyle \Delta v}$ = 5 km/s, ${\displaystyle v_{\text{e}}}$ = 50 km/s, takes 5 months.

Thus ${\displaystyle v_{\text{e}}}$ should not be too large.

Power to thrust ratio

The power to thrust ratio is simply:

${\displaystyle {\frac {P}{F}}={\frac {{\frac {1}{2}}{{\dot {m}}v^{2}}}{{\dot {m}}v}}={\frac {1}{2}}v}$

Thus for any vehicle power P, the thrust that may be provided is:

${\displaystyle F={\frac {P}{{\frac {1}{2}}v}}={\frac {2P}{v}}}$

Example

Suppose a 10,000 kg space probe will be sent to Mars. The required ${\displaystyle \Delta v}$ from LEO is approximately 3000 m/s, using a Hohmann transfer orbit. For the sake of argument, assume the following thrusters are options to be used:

Engine	Effective exhaust velocity (km/s)	Specific impulse (s)	Mass, propellant (kg)	Energy required (GJ)	Specific energy, propellant (J/kg)	Minimum power/thrust	Power generator mass/thrust
Solid rocket	1	100	190,000	95	500×103	0.5 kW/N	N/A
Bipropellant rocket	5	500	8,200	103	12.6×106	2.5 kW/N	N/A
Ion thruster	50	5,000	620	775	1.25×109	25 kW/N	25 kg/N

1. Assuming 100% energetic efficiency; 50% is more typical in practice.
2. Assumes a specific power of 1 kW/kg

Observe that the more fuel-efficient engines can use far less fuel; their mass is almost negligible (relative to the mass of the payload and the engine itself) for some of the engines. However, note also that these require a large total amount of energy. For Earth launch, engines require a thrust to weight ratio of more than one. To do this with the ion or more theoretical electrical drives, the engine would have to be supplied with one to several gigawatts of power, equivalent to a major metropolitan generating station. From the table it can be seen that this is clearly impractical with current power sources.

Alternative approaches include some forms of laser propulsion, where the reaction mass does not provide the energy required to accelerate it, with the energy instead being provided from an external laser or other beam-powered propulsion system. Small models of some of these concepts have flown, although the engineering problems are complex and the ground-based power systems are not a solved problem.

Instead, a much smaller, less powerful generator may be included which will take much longer to generate the total energy needed. This lower power is only sufficient to accelerate a tiny amount of fuel per second, and would be insufficient for launching from Earth. However, over long periods in orbit where there is no friction, the velocity will be finally achieved. For example, it took the SMART-1 more than a year to reach the Moon, whereas with a chemical rocket it takes a few days. Because the ion drive needs much less fuel, the total launched mass is usually lower, which typically results in a lower overall cost, but the journey takes longer.

Mission planning therefore frequently involves adjusting and choosing the propulsion system so as to minimise the total cost of the project, and can involve trading off launch costs and mission duration against payload fraction.

Rocket engines

SpaceX's Kestrel engine is tested

Most rocket engines are internal combustion heat engines (although non combusting forms exist). Rocket engines generally produce a high temperature reaction mass, as a hot gas. This is achieved by combusting a solid, liquid or gaseous fuel with an oxidiser within a combustion chamber. The extremely hot gas is then allowed to escape through a high-expansion ratio nozzle. This bell-shaped nozzle is what gives a rocket engine its characteristic shape. The effect of the nozzle is to dramatically accelerate the mass, converting most of the thermal energy into kinetic energy. Exhaust speed reaching as high as 10 times the speed of sound at sea level are common.

Rocket engines provide essentially the highest specific powers and high specific thrusts of any engine used for spacecraft propulsion.

Ion propulsion rockets can heat a plasma or charged gas inside a magnetic bottle and release it via a magnetic nozzle, so that no solid matter need come in contact with the plasma. Of course, the machinery to do this is complex, but research into nuclear fusion has developed methods, some of which have been proposed to be used in propulsion systems, and some have been tested in a lab.
See rocket engine for a listing of various kinds of rocket engines using different heating methods, including chemical, electrical, solar, and nuclear.

Electromagnetic propulsion

This test engine accelerates ions using electrostatic forces

Rather than relying on high temperature and fluid dynamics to accelerate the reaction mass to high speeds, there are a variety of methods that use electrostatic or electromagnetic forces to accelerate the reaction mass directly. Usually the reaction mass is a stream of ions. Such an engine typically uses electric power, first to ionize atoms, and then to create a voltage gradient to accelerate the ions to high exhaust velocities.

The idea of electric propulsion dates back to 1906, when Robert Goddard considered the possibility in his personal notebook. Konstantin Tsiolkovsky published the idea in 1911.

For these drives, at the highest exhaust speeds, energetic efficiency and thrust are all inversely proportional to exhaust velocity. Their very high exhaust velocity means they require huge amounts of energy and thus with practical power sources provide low thrust, but use hardly any fuel.

For some missions, particularly reasonably close to the Sun, solar energy may be sufficient, and has very often been used, but for others further out or at higher power, nuclear energy is necessary; engines drawing their power from a nuclear source are called nuclear electric rockets.

With any current source of electrical power, chemical, nuclear or solar, the maximum amount of power that can be generated limits the amount of thrust that can be produced to a small value. Power generation adds significant mass to the spacecraft, and ultimately the weight of the power source limits the performance of the vehicle.

Current nuclear power generators are approximately half the weight of solar panels per watt of energy supplied, at terrestrial distances from the Sun. Chemical power generators are not used due to the far lower total available energy. Beamed power to the spacecraft shows some potential.

6 kW Hall thruster in operation at the NASA Jet Propulsion Laboratory.

Some electromagnetic methods:

• Ion thrusters (accelerate ions first and later neutralize the ion beam with an electron stream emitted from a cathode called a neutralizer)
  • Electrostatic ion thruster
  • Field-emission electric propulsion
  • Hall effect thruster
  • Colloid thruster
• Electrothermal thrusters (electromagnetic fields are used to generate a plasma to increase the heat of the bulk propellant, the thermal energy imparted to the propellant gas is then converted into kinetic energy by a nozzle of either physical material construction or by magnetic means)
  • DC arcjet
  • microwave arcjet
  • Helicon Double Layer Thruster
• Electromagnetic thrusters (ions are accelerated either by the Lorentz Force or by the effect of electromagnetic fields where the electric field is not in the direction of the acceleration)
  • Plasma propulsion engine
  • Magnetoplasmadynamic thruster
  • Electrodeless plasma thruster
  • Pulsed inductive thruster
  • Pulsed plasma thruster
  • Variable specific impulse magnetoplasma rocket (VASIMR)
• Mass drivers (for propulsion)

In electrothermal and electromagnetic thrusters, both ions and electrons are accelerated simultaneously, no neutralizer is required.

Without internal reaction mass

NASA study of a solar sail. The sail would be half a kilometer wide.

The law of conservation of momentum is usually taken to imply that any engine which uses no reaction mass cannot accelerate the center of mass of a spaceship (changing orientation, on the other hand, is possible). But space is not empty, especially space inside the Solar System; there are gravitation fields, magnetic fields, electromagnetic waves, solar wind and solar radiation. Electromagnetic waves in particular are known to contain momentum, despite being massless; specifically the momentum flux density P of an EM wave is quantitatively 1/c^2 times the Poynting vector S, i.e. P = S/c^2, where c is the velocity of light. Field propulsion methods which do not rely on reaction mass thus must try to take advantage of this fact by coupling to a momentum-bearing field such as an EM wave that exists in the vicinity of the craft. However, because many of these phenomena are diffuse in nature, corresponding propulsion structures need to be proportionately large.

There are several different space drives that need little or no reaction mass to function. A tether propulsion system employs a long cable with a high tensile strength to change a spacecraft's orbit, such as by interaction with a planet's magnetic field or through momentum exchange with another object. Solar sails rely on radiation pressure from electromagnetic energy, but they require a large collection surface to function effectively. The magnetic sail deflects charged particles from the solar wind with a magnetic field, thereby imparting momentum to the spacecraft. A variant is the mini-magnetospheric plasma propulsion system, which uses a small cloud of plasma held in a magnetic field to deflect the Sun's charged particles. An E-sail would use very thin and lightweight wires holding an electric charge to deflect these particles, and may have more controllable directionality.
As a proof of concept, NanoSail-D became the first nanosatellite to orbit Earth. There are plans to add them^{[clarification needed]} to future Earth orbit satellites, enabling them to de-orbit and burn up once they are no longer needed. Cubesail will be the first mission to demonstrate solar sailing in low Earth orbit, and the first mission to demonstrate full three-axis attitude control of a solar sail.

Japan also launched its own solar sail powered spacecraft IKAROS in May 2010. IKAROS successfully demonstrated propulsion and guidance and is still flying today.

A satellite or other space vehicle is subject to the law of conservation of angular momentum, which constrains a body from a net change in angular velocity. Thus, for a vehicle to change its relative orientation without expending reaction mass, another part of the vehicle may rotate in the opposite direction. Non-conservative external forces, primarily gravitational and atmospheric, can contribute up to several degrees per day to angular momentum, so secondary systems are designed to "bleed off" undesired rotational energies built up over time. Accordingly, many spacecraft utilize reaction wheels or control moment gyroscopes to control orientation in space.

A gravitational slingshot can carry a space probe onward to other destinations without the expense of reaction mass. By harnessing the gravitational energy of other celestial objects, the spacecraft can pick up kinetic energy. However, even more energy can be obtained from the gravity assist if rockets are used.

Beam-powered propulsion is another method of propulsion without reaction mass. Beamed propulsion includes sails pushed by laser, microwave, or particle beams.

Planetary and atmospheric propulsion

A successful proof of concept Lightcraft test, a subset of beam-powered propulsion.

Launch-assist mechanisms

There have been many ideas proposed for launch-assist mechanisms that have the potential of drastically reducing the cost of getting into orbit. Proposed non-rocket spacelaunch launch-assist mechanisms include:

• Skyhook (requires reusable suborbital launch vehicle, not engineeringly feasible using presently available materials)
• Space elevator (tether from Earth's surface to geostationary orbit, cannot be built with existing materials)
• Launch loop (a very fast enclosed rotating loop about 80 km tall)
• Space fountain (a very tall building held up by a stream of masses fired from its base)
• Orbital ring (a ring around Earth with spokes hanging down off bearings)
• Electromagnetic catapult (railgun, coilgun) (an electric gun)
• Rocket sled launch
• Space gun (Project HARP, ram accelerator) (a chemically powered gun)
• Beam-powered propulsion rockets and jets powered from the ground via a beam
• High-altitude platforms to assist initial stage

Air-breathing engines

Studies generally show that conventional air-breathing engines, such as ramjets or turbojets are basically too heavy (have too low a thrust/weight ratio) to give any significant performance improvement when installed on a launch vehicle itself. However, launch vehicles can be air launched from separate lift vehicles (e.g. B-29, Pegasus Rocket and White Knight) which do use such propulsion systems. Jet engines mounted on a launch rail could also be so used.

On the other hand, very lightweight or very high speed engines have been proposed that take advantage of the air during ascent:

• SABRE - a lightweight hydrogen fueled turbojet with precooler
• ATREX - a lightweight hydrogen fueled turbojet with precooler
• Liquid air cycle engine - a hydrogen fueled jet engine that liquifies the air before burning it in a rocket engine
• Scramjet - jet engines that use supersonic combustion
• Shcramjet - similar to a scramjet engine, however it takes advantage of shockwaves produced from the aircraft in the combustion chamber to assist in increasing overall efficiency.

Normal rocket launch vehicles fly almost vertically before rolling over at an altitude of some tens of kilometers before burning sideways for orbit; this initial vertical climb wastes propellant but is optimal as it greatly reduces airdrag. Airbreathing engines burn propellant much more efficiently and this would permit a far flatter launch trajectory, the vehicles would typically fly approximately tangentially to Earth's surface until leaving the atmosphere then perform a rocket burn to bridge the final delta-v to orbital velocity.

For spacecraft already in very low-orbit, air-breathing electric propulsion would use residual gases in the upper atmosphere as propellant. Air-breathing electric propulsion could make a new class of long-lived, low-orbiting missions feasible on Earth, Mars or Venus.

Planetary arrival and landing

A test version of the MARS Pathfinder airbag system

When a vehicle is to enter orbit around its destination planet, or when it is to land, it must adjust its velocity. This can be done using all the methods listed above (provided they can generate a high enough thrust), but there are a few methods that can take advantage of planetary atmospheres and/or surfaces.

• Aerobraking allows a spacecraft to reduce the high point of an elliptical orbit by repeated brushes with the atmosphere at the low point of the orbit. This can save a considerable amount of fuel because it takes much less delta-V to enter an elliptical orbit compared to a low circular orbit. Because the braking is done over the course of many orbits, heating is comparatively minor, and a heat shield is not required. This has been done on several Mars missions such as Mars Global Surveyor, Mars Odyssey and Mars Reconnaissance Orbiter, and at least one Venus mission, Magellan.
• Aerocapture is a much more aggressive manoeuver, converting an incoming hyperbolic orbit to an elliptical orbit in one pass. This requires a heat shield and much trickier navigation, because it must be completed in one pass through the atmosphere, and unlike aerobraking no preview of the atmosphere is possible. If the intent is to remain in orbit, then at least one more propulsive maneuver is required after aerocapture—otherwise the low point of the resulting orbit will remain in the atmosphere, resulting in eventual re-entry. Aerocapture has not yet been tried on a planetary mission, but the re-entry skip by Zond 6 and Zond 7 upon lunar return were aerocapture maneuvers, because they turned a hyperbolic orbit into an elliptical orbit. On these missions, because there was no attempt to raise the perigee after the aerocapture, the resulting orbit still intersected the atmosphere, and re-entry occurred at the next perigee.
• A ballute is an inflatable drag device.
• Parachutes can land a probe on a planet or moon with an atmosphere, usually after the atmosphere has scrubbed off most of the velocity, using a heat shield.
• Airbags can soften the final landing.
• Lithobraking, or stopping by impacting the surface, is usually done by accident. However, it may be done deliberately with the probe expected to survive (see, for example, Deep Impact (spacecraft)), in which case very sturdy probes are required.

Table of methods

Below is a summary of some of the more popular, proven technologies, followed by increasingly speculative methods.

Four numbers are shown. The first is the effective exhaust velocity: the equivalent speed that the propellant leaves the vehicle. This is not necessarily the most important characteristic of the propulsion method; thrust and power consumption and other factors can be. However:

• if the delta-v is much more than the exhaust velocity, then exorbitant amounts of fuel are necessary (see the section on calculations, above);
• if it is much more than the delta-v, then, proportionally more energy is needed; if the power is limited, as with solar energy, this means that the journey takes a proportionally longer time.

The second and third are the typical amounts of thrust and the typical burn times of the method. Outside a gravitational potential small amounts of thrust applied over a long period will give the same effect as large amounts of thrust over a short period. (This result does not apply when the object is significantly influenced by gravity.)

The fourth is the maximum delta-v this technique can give (without staging). For rocket-like propulsion systems this is a function of mass fraction and exhaust velocity. Mass fraction for rocket-like systems is usually limited by propulsion system weight and tankage weight. For a system to achieve this limit, typically the payload may need to be a negligible percentage of the vehicle, and so the practical limit on some systems can be much lower.

Propulsion methods

Method	Effective exhaust velocity (km/s)	Thrust (N)	Firing duration	Maximum delta-v (km/s)	Technology readiness level
Solid-fuel rocket	<2 .5="" span="">	<10 sup="">7

Minutes 7 9: Flight proven Hybrid rocket

Minutes >3 9: Flight proven Monopropellant rocket 1 – 3 0.1 – 100 Milliseconds – minutes 3 9: Flight proven Liquid-fuel rocket <4 .4="" span=""> <10 sup="">7 Minutes 9 9: Flight proven Electrostatic ion thruster 15 – 210
Months – years >100 9: Flight proven Hall-effect thruster (HET) 8 – 50
Months – years >100 9: Flight proven Resistojet rocket 2 – 6 10⁻² – 10 Minutes ? 8: Flight qualified Arcjet rocket 4 – 16 10⁻² – 10 Minutes ? 8: Flight qualified Field emission
electric propulsion (FEEP) 100 – 130 10⁻⁶ – 10⁻³ Months – years ? 8: Flight qualified Pulsed plasma thruster (PPT) 20 0.1 80 – 400 days ? 7: Prototype demonstrated in space Dual-mode propulsion rocket 1 – 4.7 0.1 – 10⁷ Milliseconds – minutes 3 – 9 7: Prototype demonstrated in space Solar sails 299792, light 9/km² at 1 AU
230/km² at 0.2 AU
10⁻¹⁰/km² at 4 ly Indefinite >40

• 9: Light pressure attitude-control flight proven
• 6: Deploy-only demonstrated in space
• 5: Light-sail validated in medium vacuum

Tripropellant rocket 2.5 – 5.3 0.1 – 10⁷ Minutes 9 6: Prototype demonstrated on ground Magnetoplasmadynamic
thruster (MPD) 20 – 100 100 Weeks ? 6: Model, 1 kW demonstrated in space Nuclear–thermal rocket 9 10⁷ Minutes > 20 6: Prototype demonstrated on ground Propulsive mass drivers 0 – 30 10⁴ – 10⁸ Months ? 6: Model, 32 MJ demonstrated on ground Tether propulsion N/A 1 – 10¹² Minutes 7 6: Model, 31.7 km demonstrated in space Air-augmented rocket 5 – 6 0.1 – 10⁷ Seconds – minutes >7? 6: Prototype demonstrated on ground Liquid-air-cycle engine 4.5 10³ – 10⁷ Seconds – minutes ? 6: Prototype demonstrated on ground Pulsed-inductive thruster (PIT) 10 – 80 20 Months ? 5: Component validated in vacuum Variable-specific-impulse
magnetoplasma rocket
(VASIMR) 10 – 300 40 – 1,200 Days – months >100 5: Component, 200 kW validated in vacuum Magnetic-field oscillating
amplified thruster 10 – 130 0.1 – 1 Days – months >100 5: Component validated in vacuum Solar–thermal rocket 7 – 12 1 – 100 Weeks >20 4: Component validated in lab Radioisotope rocket 7 – 8 1.3 – 1.5 Months ? 4: Component validated in lab Nuclear–electric rocket As electric propulsion method used 4: Component, 400 kW validated in lab Orion Project (near-term
nuclear pulse propulsion) 20 – 100 10⁹ – 10¹² Days 30 – 60 3: Validated, 900 kg proof-of-concept Space elevator N/A N/A Indefinite >12 3: Validated proof-of-concept Reaction Engines SABRE^[19] 30/4.5 0.1 – 10⁷ Minutes 9.4 3: Validated proof-of-concept Electric sails 145 – 750, solar wind ? Indefinite >40 3: Validated proof-of-concept Magnetic sails 145 – 750, solar wind 2/t Indefinite ? 3: Validated proof-of-concept Mini-magnetospheric
plasma propulsion 200 1/kW Months ? 3: Validated proof-of-concept Beam-powered/laser As propulsion method powered by beam 3: Validated, 71 m proof-of-concept Launch loop/orbital ring N/A 10⁴ Minutes 11 – 30 2: Technology concept formulated Nuclear pulse propulsion
(Project Daedalus' drive) 20 – 1,000 10⁹ – 10¹² Years 15,000 2: Technology concept formulated Gas-core reactor rocket 10 – 20 10³ – 10⁶ ? ? 2: Technology concept formulated Nuclear salt-water rocket 100 10³ – 10⁷ Half-hour ? 2: Technology concept formulated Fission sail ? ? ? ? 2: Technology concept formulated Fission-fragment rocket 15,000 ? ? ? 2: Technology concept formulated Nuclear–photonic rocket 299,792 10⁻⁵ – 1 Years – decades ? 2: Technology concept formulated Fusion rocket 100 – 1,000 ? ? ? 2: Technology concept formulated Antimatter-catalyzed
nuclear pulse propulsion 200 – 4,000 ? Days – weeks ? 2: Technology concept formulated Antimatter rocket 10,000 – 100,000 ? ? ? 2: Technology concept formulated Bussard ramjet 2.2 – 20,000 ? Indefinite 30,000 2: Technology concept formulated Method Effective exhaust
velocity (km/s) Thrust (N) Firing
duration Maximum
delta-v (km/s) Technology
readiness level

Testing

Spacecraft propulsion systems are often first statically tested on Earth's surface, within the atmosphere but many systems require a vacuum chamber to test fully. Rockets are usually tested at a rocket engine test facility well away from habitation and other buildings for safety reasons. Ion drives are far less dangerous and require much less stringent safety, usually only a large-ish vacuum chamber is needed.

Famous static test locations can be found at Rocket Ground Test Facilities.

 

Some systems cannot be adequately tested on the ground and test launches may be employed at a Rocket Launch Site.

Speculative methods

Artist's conception of a warp drive design

A variety of hypothetical propulsion techniques have been considered that require a deeper understanding of the properties of space, particularly inertial frames and the vacuum state. To date, such methods are highly speculative and include:

• Black hole starship
• Differential sail
• Faster-than-light
• Field propulsion
  • RF resonant cavity thruster
• Gravitational shielding
  • Diametric drive
  • Disjunction drive
  • Pitch drive
  • Bias drive
• Photon rocket
• Photonic laser thruster
• Quantum vacuum thruster
• Reactionless drive
  • Abraham—Minkowski drive
  • Alcubierre drive
  • Heim drive
  • Dean drive
  • Gyroscopic Inertial Thruster (GIT)
  • Woodward effect

A NASA assessment of its Breakthrough Propulsion Physics Program divides such proposals into those that are non-viable for propulsion purposes, those that are of uncertain potential, and those that are not impossible according to current theories.