Biochemical switches in the cell cycle

From Wikipedia, the free encyclopedia

 

A series of biochemical switches control transitions between and within the various phases of the cell cycle. The cell cycle is a series of complex, ordered, sequential events that control how a single cell divides into two cells, and involves several different phases. The phases include the G1 and G2 phases, DNA replication or S phase, and the actual process of cell division, mitosis or M phase. During the M phase, the chromosomes separate and cytokinesis occurs.

 

The switches maintain the orderly progression of the cell cycle and act as checkpoints to ensure that each phase has been properly completed before progression to the next phase. For example, Cdk, or cyclin dependent kinase, is a major control switch for the cell cycle and it allows the cell to move from G1 to S or G2 to M by adding phosphate to protein substrates. Such multi-component (involving multiple inter-linked proteins) switches have been shown to generate decisive, robust (and potentially irreversible) transitions and trigger stable oscillations. As a result, they are a subject of active research that tries to understand how such complex properties are wired into biological control systems.

Feedback loops

Many biological circuits produce complex outputs by exploiting one or more feedback loops. In a sequence of biochemical events, feedback would refer to a downstream element in the sequence (B in the adjacent image) affecting some upstream component (A in the adjacent image) to affect its own production or activation (output) in the future. If this element acts to enhance its own output, then it engages in positive feedback (blue arrow). A positive feedback loop is also known as a self-reinforcing loop, and it is possible that these loops can be part of a larger loop, as this is characteristic of regulatory circuits.

Conversely, if this element leads to its own inhibition through upstream elements, this is canonically negative feedback (red blunt arrow). A negative feedback loop is also known as a balancing loop, and it may be common to see oscillations in which a delayed negative feedback signal is used to maintain homeostatic balance in the system.

Feedback loops can be used for amplification (positive) or self-correction (negative). The right combination of positive and negative feedback loops can generate ultrasensitivity and bistability, which in turn can generate decisive transitions and oscillations.

Combination of positive and negative feedback loops

Positive and negative feedback loops do not always operate distinctly. In the mechanism of biochemical switches, they work together to create a flexible system. For example, according to Pfeuty & Kaneko (2009), to overcome a drawback in biochemical systems, positive feedback regulation loops may interact with negative regulation loops to facilitate escape from stable states. The coexistence of two stable states is known as bistability, which is often the result of positive feedback regulations. 

An example that reveals the interaction of the multiple negative and positive feedback loops is the activation of cyclin-dependent protein kinases, or Cdks14. Positive feedback loops play a role by switching cells from low to high Cdk-activity. The interaction between the two types of loops is evident in mitosis. While positive feedback initiates mitosis, a negative feedback loop promotes the inactivation of the cyclin-dependent kinases by the anaphase-promoting complex. This example clearly shows the combined effects that positive and negative feedback loops have on cell-cycle regulation.

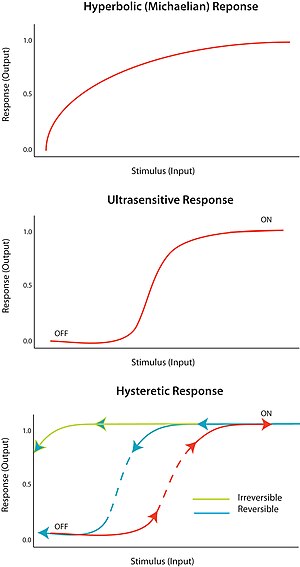
Ultrasensitivity

An "all-or-none" response to a stimulus is termed ultrasensitivity. In other words, a very small change in stimulus causes a very large change in response, producing a sigmoidal dose-response curve. An ultrasensitive response is described by the general equation V = Sⁿ/(Sⁿ + K_m), known as the Hill equation, when n, the Hill coefficient, is more than 1. The steepness of the sigmoidal curve depends on the value of n. A value of n = 1 produces a hyperbolic or Michaelian response. Ultrasensitivity is achieved in a variety of systems; a notable example is the cooperative binding of the enzyme hemoglobin to its substrate. Since an ultrasensitive response is almost ‘digital’, it can be used to amplify a response to a stimulus or cause a decisive sharp transition (between ‘off’ and ‘on’ states).

Ultrasensitivity plays a large role in cell-cycle regulation. For example, Cdk1 and Wee1 are mitotic regulators, and they are able to inactivate each other through inhibitory phosphorylation. This represents a double negative feedback loop in which both regulators inactivate each other. According to Kim et al. (2007), there must be an ultrasensitive element to generate a bistable response. It turns out that Wee1 has an ultrasensitive response to Cdk1, and this likely arises because of substrate competition among the various phosphorylation sites on Wee1.

Bistability

Bistability implies hysteresis, and hysteresis implies multistability. Multistability indicates the presence of two or more stable states for a given input. Therefore, bistability is the ability of a system to exist in two steady states. In other words, there is a range of stimulus values for which the response can have two steady-state values. Bistability is accompanied by hysteresis, which means that the system approaches one of the two steady states preferentially depending on its history. Bistability requires feedback as well as an ultrasensitive circuit element. 

Under the proper circumstances, positive and negative feedback loops can provide the conditions for bistability; for example, by having positive feedback coupled to an ultrasensitive response element with the circuit. A hysteretic bistable system can act as a robust reversible switch because it is harder for the system to transition between ‘on’ and ‘off’ states (compared to the equivalent monostable ultransensitive response). The system could also be poised such that one of the transitions is physically unattainable; for example, no amount of reduction in the stimulus will return the system to the ‘off’-state once it is already in the ‘on’ state. This would form a robust irreversible switch.

There is no one-to-one correspondence between network topology, since many networks have a similar input and output relationship. A network topology does not imply input or output, and similarly input or output does not imply network topology. It is for this reason that parameterization is very important for circuit function. If the dynamics of the input are comparable or faster than the response of the system, the response may appear hysteretic. 

Three cell cycle switches are described below that achieve abrupt and/or irreversible transitions by exploiting some of the mechanisms described above.

The G1/S switch

The G1/S transition, more commonly known as the Start checkpoint in budding yeast (the restriction point in other organisms) regulates cell cycle commitment. At this checkpoint, cells either arrest before DNA replication (due to limiting nutrients or a pheromone signal), prolong G1 (size control), or begin replication and progress through the rest of the cell cycle. The G1/S regulatory network or regulon in budding yeast includes the G1 cyclins Cln1, Cln2 and Cln3, Cdc28 (Cdk1), the transcription factors SBF and MBF, and the transcriptional inhibitor Whi5. Cln3 interacts with Cdk1 to initiate the sequence of events by phosphorylating a large number of targets, including SBF, MBF and Whi5. Phosphorylation of Whi5 causes it to translocate out of the nucleus, preventing it from inhibiting SBF and MBF. Active SBF/MBF drive the G1/S transition by turning on the B-type cyclins and initiating DNA replication, bud formation and spindle body duplication. Moreover, SBF/MBF drives expression of Cln1 and Cln2, which can also interact with Cdk1 to promote phosphorylation of its targets.

This G1/S switch was initially thought to function as a linear sequence of events starting with Cln3 and ending in S phase. However, the observation that any one of the Clns was sufficient to activate the regulon indicated that Cln1 and Cln2 might be able to engage positive feedback to activate their own transcription. This would result in a continuously accelerating cycle that could act as an irreversible bistable trigger. Skotheim et al. used single-cell measurements in budding yeast to show that this positive feedback does indeed occur. A small amount of Cln3 induces Cln1/2 expression and then the feedback loop takes over, leading to rapid and abrupt exit of Whi5 from the nucleus and consequently coherent expression of G1/S regulon genes. In the absence of coherent gene expression, cells take longer to exit G1 and a significant fraction even arrest before S phase, highlighting the importance of positive feedback in sharpening the G1/S switch.

The G1/S cell cycle checkpoint controls the passage of eukaryotic cells from the first gap phase, G1, into the DNA synthesis phase, S. In this switch in mammalian cells, there are two cell cycle kinases that help to control the checkpoint: cell cycle kinases CDK4/6-cyclin D and CDK2-cyclin E. The transcription complex that includes Rb and E2F is important in controlling this checkpoint. In the first gap phase, the Rb-HDAC repressor complex binds to the E2F-DP1 transcription factors, therefore inhibiting the downstream transcription. The phosphorylation of Rb by CDK4/6 and CDK2 dissociates the Rb-repressor complex and serves as an on/off switch for the cell cycle. Once Rb is phosphorylated, the inhibition is released on the E2F transcriptional activity. This allows for the transcription of S phase genes encoding for proteins that amplify the G1 to S phase switch.

Many different stimuli apply checkpoint controls including TGFb, DNA damage, contact inhibition, replicative senescence, and growth factor withdrawal. The first four act by inducing members of the INK4 or Kip/Cip families of cell cycle kinase inhibitors. TGFb inhibits the transcription of Cdc25A, a phosphatase that activates the cell cycle kinases, and growth factor withdrawal activates GSK3b, which phosphorylates cyclin D. This leads to its rapid ubiquitination.

The G2/M switch

G2 is commenced by E2F-mediated transcription of cyclin A, which forms the cyclin A-Cdk2 complex. In order to proceed into mitosis, the cyclin B-Cdk1 complex (first discovered as MPF or M-phase promoting factor; Cdk1 is also known as Cdc2 in fission yeast and Cdc28 in budding yeast) is activated by Cdc25, a protein phosphatase. As mitosis starts, the nuclear envelope disintegrates, chromosomes condense and become visible, and the cell prepares for division. Cyclin B-Cdk1 activation results in nuclear envelope breakdown, which is a characteristic of the initiation of mitosis.

The cyclin B-Cdk1 complex participates in a regulatory circuit in which Cdk1 can phosphorylate and activate its activator, Cdc25 (positive feedback), and phosphorylate and inactivate its inactivator, the kinase Wee1 (double-negative feedback). This circuit could act as a bistable trigger with one stable steady state in G2 (Cdk1 and Cdc25 off, Wee1 on) and a second stable steady state in M phase (Cdk1 and Cdc25 active, Wee1 off). However, Wee1 is itself regulated by other factors, such as Cdr2. 

It was suggested and defended by Jin et al. in their series of experiments with the human HeLa cell line in 1998 that it is the spatial location of cyclin B within the cell that initiates mitosis. Known from previous experiments in both human cells and starfish oocytes, Jin et al. summarize that cyclin B1 is abundant in the cytoplasm during non-dividing phases of mitosis, but is identified in the nucleus, in complex with Cdk1, immediately before the cell enters mitosis. Other experimenters showed that cells would not divide if cyclin B remains in the cytoplasm. In order to further investigate the effect of spatial location of cyclin B on cell division and cycle control, Jin et al. tagged cyclin B with a nuclear localization signal (NLS) that would keep the cyclin within the nucleus. Initially, this NLS cyclin B did not induce the expected effect of accelerated mitotic entry. This result is due to the inhibition detailed in the figure below. Wee1, an inhibitor on the cyclin B-Cdk1 complex, is localized in the nucleus, and likely phosphorylating the NLS cyclin B, rendering it unable to perform as predicted. This postulation was confirmed when Jin et al. employed Cdc2AF, an unphosphorylatable mutant of Cdk1, and saw accelerated entry to cell division due to the nuclear localization of the cyclin B. Therefore, nuclear localization of cyclin B is necessary but not sufficient to trigger cell division.

In investigation of cell cycle regulation, Jin et al. manipulated cells in order to evaluate the localization of cyclin B in cells with DNA damage. Through combination of DNA damage and nuclear localization of exogenous cyclin B, they were able to determine that cells would divide even with DNA damage if the cyclin B were forced to be expressed in the nucleus. This suggests that spatial localization of cyclin B may play a role as a checkpoint of mitosis. If the cells, under normal circumstances, don’t divide when their genetic information is damaged, but will enter mitosis if endogenous cyclin B is expressed in the nucleus, it is likely that the translocation of the cyclin B to the cytoplasm is a mechanism that prevents immature mitotic entry. This hypothesis was further supported by Jin et al.’s analysis of cells arrested in G2 due to DNA damage. In these cells, Jin et al. observed high levels of cyclin B-Cdc2 complex activity in the cytoplasm. This is supporting evidence for the previously mentioned theory because it shows that the Cdc2 can activate the cyclin without immediate translocation to the nucleus. Additionally, the accumulation of cyclin B-Cdk1 complexes in the cytoplasm of cells that are not dividing due to DNA damage supports the theory that it is nuclear localization of cyclin B that initiates mitotic entry.

To conclude, spatial localization of cyclin B plays a role in mitotic entry. Translocation of cyclin B from the cytoplasm to the nucleus is necessary for cell division, but not sufficient, as its inhibitors do not allow the cell to enter mitosis prematurely. In addition to the back up inhibition of the cyclin B-Cdk1 complex, premature cellular division is prevented by the translocation of the cyclin B itself. The cyclin B-Cdk1 complex will remain in the cytoplasm in cells with DNA damage, rather than translocate to the nucleus, keeping the cell inhibiting the cell from entering mitosis. The next question addressed by researchers in this field is by which specific mechanism is this translocation regulated. 

Santos et al. hypothesized that the translocation of cyclin B is regulated by a mechanism of positive feedback, similar to that which regulates the activation of the cyclin B-Cdk1 complex. They believed that the positive feedback loop involves the phosphorylation of the cyclin B and its translocation to the nucleus. To begin to investigate this, they first reconfirmed some of the results of the Jin et al. experiments, utilizing immunofluorescence to show cyclin B in the cytoplasm prior to division, and translocation to the nucleus to initiate mitosis, which they operationalized by comparing relative to nuclear envelope breakdown (NEB). Using nuclear cyclin that cannot be inactivated by Wee1 or Myt1, Santos et al. observed that active nuclear cyclin recruits more cyclin from the cytoplasm to be translocated to the nucleus. They confirmed this observation by employing a rapamycin treatment, iRap. iRap induces translocation of tagged cyclin B from the cytoplasm to the nucleus. Remarkably, Santos et al. saw that untagged cyclin B migrated with the cyclin B influenced by iRap. The untagged cyclin is insentive to the treatment, and moves independently from the treated cyclin. This supports the first part of the positive feedback loop, that nuclear localization of cyclin B, which leads to mitotic entry, promotes increased translocation of cytoplasmic cyclin B to the nucleus, further promoting the remaining cytoplasmic cyclin B to migrate to the nucleus, etc. 

Santos et al. further hypothesize that phosphorylation of the cyclin B is another component of the positive feedback loop. They observed that the cyclin B naturally enters the nucleus before NEB. In contrast, mutated, unphosphorylatable cyclin B enters the nucleus during NEB. This is unexpected because it is characteristic of the cell cycle for the cyclin to translocate to the nucleus prior to NEB in order to induce cell cycle progression into mitotic division. Therefore, Santos et al. conclude that the phosphorylation of the cyclin B promotes the translocation to the nucleus. However, in addition, translocation to the nucleus promotes phosphorylation of the cyclin. It is noted by the authors that phosphorylation of cyclin B is nineteen times more favorable in the nucleus than in the cytoplasm, due to the smaller overall volume of the nucleus, allowing a faster phosphorylation rate. The increased translocation due to phosphorylation and increased phosphorylation due to translocation exemplify the positive feedback loop that resembles that previously discovered, which activates the cyclin B-Cdk1 complex.

In conclusion, nuclear localization of cyclin B is necessary for cellular entry into mitosis. The translocation of the cyclin from the cytoplasm to the nucleus, which allows for cellular division, is regulated by a positive feedback loop. Active cyclin B translocates to the nucleus and promotes activation and translocation of additional units of cyclin residing in the nucleus. This phenomenon is enhanced when considering phosphorylation. Phosphorylation of cyclin B promotes translocation to the nucleus, and cyclin B in the nucleus is much more likely to be phosphorylated, so nuclear localization promotes cyclin B phosphorylation in return. 

Once cells are in mitosis, cyclin B-Cdk1 activates the anaphase-promoting complex (APC), which in turn inactivates cyclin B-Cdk1 by degrading cyclin B, eventually leading to exit from mitosis. Coupling the bistable Cdk1 response function to the negative feedback from the APC could generate what is known as a relaxation oscillator, with sharp spikes of Cdk1 activity triggering robust mitotic cycles. However, in a relaxation oscillator, the control parameter moves slowly relative to the system’s response dynamics which may be an accurate representation of mitotic entry, but not necessarily mitotic exit. 

It is necessary to inactivate the cyclin B-Cdk1 complex in order to exit the mitotic stage of the cell cycle. The cells can then return to the first gap phase G1 and wait until the cycle proceeds yet again.

In 2003 Pomerening et al. provided strong evidence for this hypothesis by demonstrating hysteresis and bistability in the activation of Cdk1 in the cytoplasmic extracts of Xenopus oocytes. They first demonstrated a discontinuous sharp response of Cdk1 to changing concentrations of non-destructible Cyclin B (to decouple the Cdk1 response network from APC-mediated negative feedback). However, such a response would be consistent with both a monostable, ultrasensitive transition and a bistable transition. To distinguish between these two possibilities, they measured the steady-state levels of active Cdk1 in response to changing cyclin levels, but in two separate experiments, one starting with an interphase extract and one starting with an extract already in mitosis. At intermediate concentrations of cyclin they found two steady-state concentrations of active Cdk1. Which of the two steady states was occupied depended on the history of the system, i.e.whether they started with interphase or mitotic extract, effectively demonstrating hysteresis and bistability.

In the same year, Sha et al. independently reached the same conclusion revealing the hysteretic loop also using Xenopus laevis egg extracts. In this article, three predictions of the Novak-Tyson model were tested in an effort to conclude that hysteresis is the driving force for "cell-cycle transitions into and out of mitosis". The predictions of the Novak-Tyson model are generic to all saddle-node bifurcations. Saddle-node bifurcations are extremely useful bifurcations in an imperfect world because they help describe biological systems which are not perfect. The first prediction was that the threshold concentration of cyclin to enter mitosis is higher than the threshold concentration of cyclin to exit mitosis, and this was confirmed by supplementing cycling egg extracts with non-degradable cyclin B and measuring the activation and inactivation threshold after the addition of cycloheximide (CHX), which is a protein synthesis inhibitor. Furthermore, the second prediction of the Novak-Tyson model was also validated: unreplicated deoxyribonucleic acid, or DNA, increases the threshold concentration of cyclin that is required to enter mitosis. In order to arrive at this conclusion, cytostatic factor released extracts were supplemented with CHX, APH (a DNA polymerase inhibitor), or both, and non-degradable cyclin B was added. The third and last prediction that was tested and proven true in this article was that the rate of Cdc2 activation slows down near the activation threshold concentration of cyclin. These predictions and experiments demonstrate the toggle-like switching behavior that can be described by hysteresis in a dynamical system.

Metaphase-anaphase switch

In the transition from metaphase to anaphase, it is crucial that sister chromatids are properly and simultaneously separated to opposite ends of the cell. Separation of sister-chromatids is initially strongly inhibited to prevent premature separation in late mitosis, but this inhibition is relieved through destruction of the inhibitory elements by the anaphase-promoting complex (APC) once sister-chromatid bi-orientation is achieved. One of these inhibitory elements is securin, which prevents the destruction of cohesin, the complex that holds the sister-chromatids together, by binding the protease separase which targets Scc1, a subunit of the cohesin complex, for destruction. In this system, the phosphatase Cdc14 can remove an inhibitory phosphate from securin, thereby facilitating the destruction of securin by the APC, releasing separase. As shown by Uhlmann et al., during the attachment of chromosomes to the mitotic spindle the chromatids remain paired because cohesion between the sisters prevents separation. Cohesion is established during DNA replication and depends on cohesin, which is a multisubunit complex composed of Scc1, Scc3, Smc2, and Smc3. In yeast at the metaphase-to-anaphase transition, Scc1 dissociates from the chromosomes and the sister chromatids separate. This action is controlled by the Esp1 protein, which is tightly bound by the anaphase inhibitor Pds1 that is destroyed by the anaphase-promoting complex. In order to verify that Esp1 does play a role in regulating Scc1 chromosome association, cell strains were arrested in G1 with an alpha factor. These cells stayed in arrest during the development. Esp1-1 mutant cells were used and the experiment was repeated, and Scc1 successfully bound to the chromosomes and remained associated even after the synthesis was terminated. This was crucial in showing that with Esp1, Scc1 is hindered in its ability to become stably associated with chromosomes during G1, and Esp1 can in fact directly remove Scc1 from chromosomes. 

It has been shown by Holt et al. that separase activates Cdc14, which in turn acts on securin, thus creating a positive feedback loop that increases the sharpness of the metaphase to anaphase transition and coordination of sister-chromatid separation. Holt et al. probed the basis for the effect of positive feedback in securin phosphorylation by using mutant 'securin' strains of yeast, and testing how changes in the phosphoregulation of securin affects the synchrony of sister chromatid separation. Their results indicate that interfering with this positive securin-separase-cdc14 loop decreases sister chromatid separation synchrony. This positive feedback can hypothetically generate bistability in the transition to anaphase, causing the cell to make the irreversible decision to separate sister-chromatids.

Mitotic exit

Mitotic exit is an important transition point that signifies the end of mitosis and the onset of new G1 phase for a cell, and the cell needs to rely on specific control mechanisms to ensure that once it exits mitosis, it never returns to mitosis until it has gone through G1, S, and G2 phases and passed all the necessary checkpoints. Many factors including cyclins, cyclin-dependent kinases (CDKs), ubiquitin ligases, inhibitors of cyclin-dependent kinases, and reversible phosphorylations regulate mitotic exit to ensure that cell cycle events occur in correct order with the fewest errors. The end of mitosis is characterized by spindle breakdown, shortened kinetochore microtubules, and pronounced outgrowth of astral (non-kinetochore) microtubules. For a normal eukaryotic cell, mitotic exit is irreversible.

Proteolytic degradation

Fig. 1 Immunofluorescence patterns of cyclin B and phosphorylated cyclin-dependent kinase1 (Cdk1) in HeLa cells change as they go from G2 to anaphase.

 

Many speculations were made with regard to the control mechanisms employed by a cell to promote the irreversibility of mitotic exit in a eukaryotic model organism, the budding yeast Saccharomyces cerevisiae. Proteolytic degradation of cell cycle regulators and corresponding effects on the levels of cyclin-dependent kinases were proposed as a mechanism that promotes eukaryotic cell cycle and metaphase-to-anaphase transition in particular. In this theory, anaphase promoting complex (APC), a class of ubiquitin ligase, facilitates degradation of mitotic cyclins (Clb2) and anaphase-inhibiting factors (PDS1, CUT2) to promote mitotic exit. APC ubiquitinates nine-amino acid motif known as the destruction box (D box) in the NH2-terminal domain of mitotic cyclins for degradation by proteasome. APC in association with Cdc20 (APC-Cdc20) ubiquitinates and targets mitotic cyclins (Clb2) for degradation at initial phase. Simultaneously, APC-Cdc20 mediates degradation of securins, which inhibit separases through binding, at anaphase onset. Released and active separase cleaves cohesin that held sister chromatids together, facilitating separation of sister chromatids and initiates mitotic exit by promoting release of Cdc14 from nucleolus. At later phase, downregulation of Cdk1 and activation of Cdc14, a Cdh1-activating phosphatase, promotes formation of APC in association with Cdh1 (APC-Cdh1) to degrade Clb2s. Cdc20 and Cdh1, which are the activators of APC, recruit substrates such as securin and B-type cyclins(Clb) for ubiquitination. Without Cdk1-Clb2 complexes to phosphorylate proteins that are involved in spindle dynamics such as Sli15, Ase1, and Ask1, spindle elongation and chromosomal segregation are promoted, facilitating mitotic exit. The importance of proteolytic degradation in eukaryotic cell cycle changed the view of cell division as a simple kinase cascade to a more complex process in which interactions among phosphorylation, ubiquitination, and proteolysis are necessary. However, experiments using budding yeast cells with cdc28-as1, a INM-PP1 (ATP analog)-sensitive Cdk allele, proved that destruction of B-type cyclins (Clb) is not necessary for triggering irreversible mitotic exit. Clb2 degradation did shorten the Cdk1-inhibition period required for triggering irreversible mitotic exit indicating that cyclin proteolysis contributes to the dynamic nature of the eukaryotic cell cycle due to slower timescale of its action but is unlikely to be the major determining factor in triggering irreversible cell cycle transitions.

Sic1 levels

Discoveries were made which indicated the importance of the level of the inhibitors of cyclin-dependent kinases in regulating eukaryotic cell cycle. In particular, the level of Sic1, a stoichiometric inhibitor of Clb-CDK complexes in budding yeast, was shown to be particularly important in irreversible G1-S transition by irreversibly activating S phase kinases. Sic1 level was shown to play a major role in triggering irreversible mitotic exit (M-G1 transition) as well as in G1-S transition. During mitosis, decreasing levels of Cdk1 leads to the activation of Cdc14, a phosphatase that counteracts Cdk1 via activation of Cdh1 and Swi5, a transcriptional activator of Sic1 proteins. While degradation of Sic1 to a certain low level triggered the onset of S phase, accumulation of Sic1 to a certain high level was required to trigger irreversible mitotic exit. Cdk1-inhibitors could induce mitotic exit even when degradation of B-type cyclins was blocked by expression of non-degradable Clbs or proteasome inhibitors. However, sister chromatids failed to segregate, and cells reverted to mitosis once the inhibitors were washed away, indicating that a threshold level of the inhibitors needs to be achieved to trigger irreversible mitotic exit independently of cyclin degradations. Despite different thresholds of Sic1 level that are required to trigger mitotic exit compared to G1-S transition, the level of Sic1 was shown to play a key role in regulating eukaryotic cell cycle by inhibiting the activity of CDKs.

Dynamical systems approach

Fig. 2 Irreversible and bistable switch in mitotic exit with control parameter being Sic1 level and order parameter being cell cycle phases.

Because eukaryotic cell cycle involves a variety of proteins and regulatory interactions, dynamical systems approach can be taken to simplify a complex biological circuit into a general framework for better analysis. Among the four possible input/output relationships, the relationship between Sic1 level and mitotic exit seems to show the characteristics of an irreversible bistable switch, driven by feedback between APC-Cdh1, Sic1, and Clb2-Cdk1. Bistability is known to control biological functions such as cell cycle control and cellular differentiation and play a key role in many cellular regulatory networks. Bistable input/output relationship is characterized by two stable states with two bifurcation points. Multiple outputs are possible for one specific input in the region of bistability, marked by two bifurcation points. In addition, the bistable relationship displays hysteresis: the final state/output depends on the history of the input as well as the current value of input because the system has a memory. One bifurcation point has a negative control parameter value (the bifurcation point is on the other side of the axis), resulting in disconnection between the two stable states and irreversibility of the transition from one state to the other. With regard to mitotic exit, the two stable states are defined by mitosis and G1 phase. Once Sic1 level (input) accumulates beyond the threshold, irreversible transition occurs from mitosis (stable state I) to G1 phase (stable state II). In the imperfect environment, the only bifurcation that remains intact is saddle-node bifurcation. Saddle-node bifurcation does not break down (saddle-node is the expected generic behavior), while transcritical and pitchfork bifurcations break down in the presence of imperfections. Thus, the only one-dimensional bifurcation that can exist in imperfect biological world is the saddle-node bifurcation. The bistable relation between M-G1 transition and Sic1 level can be represented as a diagram of two saddle-node bifurcations in which the system’s behavior changes qualitatively with a small change in control parameter, the amount of Sic1.

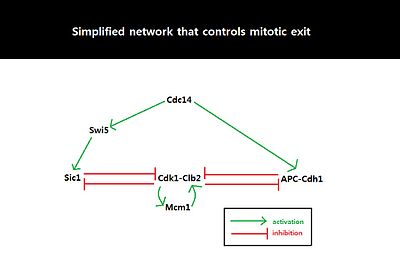
Systems-level feedback

Fig. 3 Simplified network involving Cdk1-Clb2, APC-Cdh1, Sic1, and Cdc14. Double negative feedback loop, mediated by APC-Cdh1 and Sic1, is required to suppress Cdk1-Clb2 and trigger mitotic exit.

 

Because the behavior of cell cycle critically depends on the amount of Sic1 at the M-G1 transition state, the amount of Sic1 is tightly regulated by systems-level feedbacks. Because Cdk1-Clb2 inhibits Sic1 by phosphorylating Sic1 and making Sic1 available for degradation via ubiquitylation, APC-Cdh1-dependent degradation of Cdk1-Clb2 not only decreases the level of available Cdk1-Clb2 complexes but also increases the level of Sic1 which in turn further inhibits the function of Cdk1-Clb2. This activation of the double negative feedback loop is initiated from APC-Cdc20-dependent degradation of Cdk1-Clb2 and release of Cdc14 from nucleolar protein Net1/Cfi1. FEAR (Cdc14 early anaphase release) pathway facilitates Clb2-Cdk1-dependent phosphorylation of Net1 which transiently releases Cdc14 from Net1. The released Cdc14 and Clb2-Cdk1 complexes go onto form spindles that activates mitotic exit network (MEN). MEN allows sustained release of Cdc14 from the nucleolus, and Cdc14 counters the activity of Clb2-Cdk1 by activating Cdh1 and stabilizing Sic1 through activation of Sic1-transcriptional activator Swi5. Sic1 positively regulates itself by inhibiting Cdk1-Clb2 to release inhibition of Swi5, and Cdh1 also positively regulates itself by inhibiting Clb2-Cdk1 to release inhibition of MEN which can activate Cdc14 and subsequently Cdh1 itself. The double-negative feedback loop, formed by APC-Cdh1 and Sic1, is required to maintain low Clb2-Cdk1 activity because Clb2 auto-activates its synthesis by activating transcriptional factors, Fkh2–Mcm1 Ndd1 complex.

Implications

Eukaryotic cell cycle consists of various checkpoints and feedback loops to ensure faithful and successful cell division. During mitosis for example, when duplicated chromosomes are improperly attached to mitotic spindle, spindle assembly checkpoint (SAC) proteins including Mad and Bub inhibit APC-Cdc20 to delay entry into anaphase and B-type cyclin degradations. In addition, when mitotic spindles are misaligned, MEN and subsequently Cdc14 are inhibited in a Bub2 and Bfa1-dependent manner to prevent degradation of mitotic cyclins and anaphase entry. Sic1 is a nice example demonstrating how systems-level feedbacks interact to sense the environmental conditions and trigger cell cycle transitions. Even though actual M-G1 transition is vastly complex with numerous proteins and regulations involved, dynamical systems approach allows simplification of this complex system into bistable input/output relation with two saddle-node bifurcations in which the output (mitotic exit) depends on critical concentration of Sic1. Using one-dimensional analysis, it might be possible to explain many of the irreversible transition points in the eukaryotic cell cycle that are governed by systems-level control and feedback. Other examples of irreversible transition points include Start (irreversible commitment to a new cell division cycle) that can be explained by irreversible bistable switch whose control parameter is tightly regulated by the systemic feedbacks involving Cln2, Whi5, and SBF.