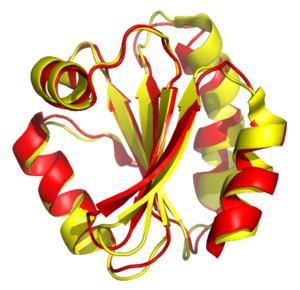
Structural alignment of thioredoxins from humans and the fly Drosophila melanogaster. The proteins are shown as ribbons, with the human protein in red, and the fly protein in yellow. Generated from PDB 3TRX and 1XWC.
Structural alignment attempts to establish homology between two or more polymer structures based on their shape and three-dimensional conformation. This process is usually applied to protein tertiary structures but can also be used for large RNA
molecules. In contrast to simple structural superposition, where at
least some equivalent residues of the two structures are known,
structural alignment requires no a priori knowledge of equivalent
positions. Structural alignment is a valuable tool for the comparison
of proteins with low sequence similarity, where evolutionary
relationships between proteins cannot be easily detected by standard sequence alignment techniques. Structural alignment can therefore be used to imply evolutionary
relationships between proteins that share very little common sequence.
However, caution should be used in using the results as evidence for
shared evolutionary ancestry because of the possible confounding effects
of convergent evolution by which multiple unrelated amino acid sequences converge on a common tertiary structure.
Structural alignments can compare two sequences or multiple sequences.
Because these alignments rely on information about all the query
sequences' three-dimensional conformations, the method can only be used
on sequences where these structures are known. These are usually found
by X-ray crystallography or NMR spectroscopy. It is possible to perform a structural alignment on structures produced by structure prediction
methods. Indeed, evaluating such predictions often requires a
structural alignment between the model and the true known structure to
assess the model's quality. Structural alignments are especially useful
in analyzing data from structural genomics and proteomics efforts, and they can be used as comparison points to evaluate alignments produced by purely sequence-based bioinformatics methods.
The outputs of a structural alignment are a superposition of the atomic coordinate sets and a minimal root mean square deviation (RMSD)
between the structures. The RMSD of two aligned structures indicates
their divergence from one another. Structural alignment can be
complicated by the existence of multiple protein domains
within one or more of the input structures, because changes in relative
orientation of the domains between two structures to be aligned can
artificially inflate the RMSD.
Data produced by structural alignment
The
minimum information produced from a successful structural alignment is a
set of residues that are considered equivalent between the structures.
This set of equivalences is then typically used to superpose the
three-dimensional coordinates for each input structure. (Note that one
input element may be fixed as a reference and therefore its superposed
coordinates do not change.) The fitted structures can be used to
calculate mutual RMSD values, as well as other more sophisticated
measures of structural similarity such as the global distance test (GDT, the metric used in CASP). The structural alignment also implies a corresponding one-dimensional sequence alignment
from which a sequence identity, or the percentage of residues that are
identical between the input structures, can be calculated as a measure
of how closely the two sequences are related.
Types of comparisons
Because protein structures are composed of amino acids whose side chains
are linked by a common protein backbone, a number of different possible
subsets of the atoms that make up a protein macromolecule can be used
in producing a structural alignment and calculating the corresponding
RMSD values. When aligning structures with very different sequences, the
side chain atoms generally are not taken into account because their
identities differ between many aligned residues. For this reason it is
common for structural alignment methods to use by default only the
backbone atoms included in the peptide bond. For simplicity and efficiency, often only the alpha carbon positions are considered, since the peptide bond has a minimally variant planar
conformation. Only when the structures to be aligned are highly similar
or even identical is it meaningful to align side-chain atom positions,
in which case the RMSD reflects not only the conformation of the protein
backbone but also the rotameric states of the side chains. Other comparison criteria that reduce noise and bolster positive matches include secondary structure assignment, native contact maps or residue interaction patterns, measures of side chain packing, and measures of hydrogen bond retention.
Structural superposition
The
most basic possible comparison between protein structures makes no
attempt to align the input structures and requires a precalculated
alignment as input to determine which of the residues in the sequence
are intended to be considered in the RMSD calculation. Structural
superposition is commonly used to compare multiple conformations of the
same protein (in which case no alignment is necessary, since the
sequences are the same) and to evaluate the quality of alignments
produced using only sequence information between two or more sequences
whose structures are known. This method traditionally uses a simple
least-squares fitting algorithm, in which the optimal rotations and
translations are found by minimizing the sum of the squared distances
among all structures in the superposition.
More recently, maximum likelihood and Bayesian methods have greatly
increased the accuracy of the estimated rotations, translations, and
covariance matrices for the superposition.
Algorithms based on multidimensional rotations and modified quaternions
have been developed to identify topological relationships between
protein structures without the need for a predetermined alignment. Such
algorithms have successfully identified canonical folds such as the four-helix bundle. The SuperPose method is sufficiently extensible to correct for relative domain rotations and other structural pitfalls.
Algorithmic complexity
Optimal solution
The optimal "threading"
of a protein sequence onto a known structure and the production of an
optimal multiple sequence alignment have been shown to be NP-complete.
However, this does not imply that the structural alignment problem is
NP-complete. Strictly speaking, an optimal solution to the protein
structure alignment problem is only known for certain protein structure
similarity measures, such as the measures used in protein structure
prediction experiments, GDT_TS and MaxSub.
These measures can be rigorously optimized using an algorithm capable
of maximizing the number of atoms in two proteins that can be
superimposed under a predefined distance cutoff.
Unfortunately, the algorithm for optimal solution is not practical,
since its running time depends not only on the lengths but also on the
intrinsic geometry of input proteins.
Approximate solution
Approximate polynomial-time
algorithms for structural alignment that produce a family of "optimal"
solutions within an approximation parameter for a given scoring function
have been developed.
Although these algorithms theoretically classify the approximate
protein structure alignment problem as "tractable", they are still
computationally too expensive for large-scale protein structure
analysis. As a consequence, practical algorithms that converge to the
global solutions of the alignment, given a scoring function, do not
exist. Most algorithms are, therefore, heuristic, but algorithms that
guarantee the convergence to at least local maximizers of the scoring
functions, and are practical, have been developed.
Representation of structures
Protein
structures have to be represented in some coordinate-independent space
to make them comparable. This is typically achieved by constructing a
sequence-to-sequence matrix or series of matrices that encompass
comparative metrics: rather than absolute distances relative to a fixed
coordinate space. An intuitive representation is the distance matrix, which is a two-dimensional matrix containing all pairwise distances between some subset of the atoms in each structure (such as the alpha carbons).
The matrix increases in dimensionality as the number of structures to
be simultaneously aligned increases. Reducing the protein to a coarse
metric such as secondary structure
elements (SSEs) or structural fragments can also produce sensible
alignments, despite the loss of information from discarding distances,
as noise is also discarded. Choosing a representation to facilitate computation is critical to developing an efficient alignment mechanism.
Methods
Structural
alignment techniques have been used in comparing individual structures
or sets of structures as well as in the production of "all-to-all"
comparison databases that measure the divergence between every pair of
structures present in the Protein Data Bank (PDB). Such databases are used to classify proteins by their fold.
DALI

Illustration
of the atom-to-atom vectors calculated in SSAP. From these vectors a
series of vector differences, e.g., between (FA) in Protein 1 and (SI)
in Protein 2 would be constructed. The two sequences are plotted on the
two dimensions of a matrix to form a difference matrix between the two
proteins. Dynamic programming is applied to all possible difference
matrices to construct a series of optimal local alignment paths that are
then summed to form the summary matrix, on which a second round of
dynamic programming is performed.
A common and
popular structural alignment method is the DALI, or Distance-matrix
ALIgnment method, which breaks the input structures into hexapeptide
fragments and calculates a distance matrix by evaluating the contact
patterns between successive fragments. Secondary structure features that involve residues that are contiguous in sequence appear on the matrix's main diagonal;
other diagonals in the matrix reflect spatial contacts between residues
that are not near each other in the sequence. When these diagonals are
parallel to the main diagonal, the features they represent are parallel;
when they are perpendicular, their features are anti-parallel. This
representation is memory-intensive because the features in the square
matrix are symmetrical (and thus redundant) about the main diagonal.
When two proteins' distance matrices share the same or similar
features in approximately the same positions, they can be said to have
similar folds with similar-length loops connecting their secondary
structure elements. DALI's actual alignment process requires a
similarity search after the two proteins' distance matrices are built;
this is normally conducted via a series of overlapping submatrices of
size 6x6. Submatrix matches are then reassembled into a final alignment
via a standard score-maximization algorithm — the original version of
DALI used a Monte Carlo
simulation to maximize a structural similarity score that is a function
of the distances between putative corresponding atoms. In particular,
more distant atoms within corresponding features are exponentially
downweighted to reduce the effects of noise introduced by loop mobility,
helix torsions, and other minor structural variations.
Because DALI relies on an all-to-all distance matrix, it can account
for the possibility that structurally aligned features might appear in
different orders within the two sequences being compared.
The DALI method has also been used to construct a database known as FSSP
(Fold classification based on Structure-Structure alignment of
Proteins, or Families of Structurally Similar Proteins) in which all
known protein structures are aligned with each other to determine their
structural neighbors and fold classification. There is an searchable database based on DALI as well as a downloadable program and web search based on a standalone version known as DaliLite.
Combinatorial extension
The
combinatorial extension (CE) method is similar to DALI in that it too
breaks each structure in the query set into a series of fragments that
it then attempts to reassemble into a complete alignment. A series of
pairwise combinations of fragments called aligned fragment pairs, or
AFPs, are used to define a similarity matrix through which an optimal
path is generated to identify the final alignment. Only AFPs that meet
given criteria for local similarity are included in the matrix as a
means of reducing the necessary search space and thereby increasing
efficiency.
A number of similarity metrics are possible; the original definition of
the CE method included only structural superpositions and inter-residue
distances but has since been expanded to include local environmental
properties such as secondary structure, solvent exposure,
hydrogen-bonding patterns, and dihedral angles.
An alignment path is calculated as the optimal path through the
similarity matrix by linearly progressing through the sequences and
extending the alignment with the next possible high-scoring AFP pair.
The initial AFP pair that nucleates the alignment can occur at any point
in the sequence matrix. Extensions then proceed with the next AFP that
meets given distance criteria restricting the alignment to low gap
sizes. The size of each AFP and the maximum gap size are required input
parameters but are usually set to empirically determined values of 8 and
30 respectively. Like DALI and SSAP, CE has been used to construct an all-to-all fold classification database from the known protein structures in the PDB.
The RCSB PDB has recently released an updated version of CE and FATCAT as part of the RCSB PDB Protein Comparison Tool. It provides a new variation of CE that can detect circular permutations in protein structures.
SSAP
The SSAP (Sequential Structure Alignment Program) method uses double dynamic programming to produce a structural alignment based on atom-to-atom vectors in structure space. Instead of the alpha carbons typically used in structural alignment, SSAP constructs its vectors from the beta carbons
for all residues except glycine, a method which thus takes into
account the rotameric state of each residue as well as its location
along the backbone. SSAP works by first constructing a series of
inter-residue distance vectors between each residue and its nearest
non-contiguous neighbors on each protein. A series of matrices are then
constructed containing the vector differences between neighbors for each
pair of residues for which vectors were constructed. Dynamic
programming applied to each resulting matrix determines a series of
optimal local alignments which are then summed into a "summary" matrix
to which dynamic programming is applied again to determine the overall
structural alignment.
SSAP originally produced only pairwise alignments but has since been extended to multiple alignments as well. It has been applied in an all-to-all fashion to produce a hierarchical fold classification scheme known as CATH (Class, Architecture, Topology, Homology), which has been used to construct the CATH Protein Structure Classification database.
Recent developments
Improvements
in structural alignment methods constitute an active area of research,
and new or modified methods are often proposed that are claimed to offer
advantages over the older and more widely distributed techniques. A
recent example, TM-align, uses a novel method for weighting its distance
matrix, to which standard dynamic programming is then applied.
The weighting is proposed to accelerate the convergence of dynamic
programming and correct for effects arising from alignment lengths. In a
benchmarking study, TM-align has been reported to improve in both speed
and accuracy over DALI and CE.
Other promising methods of structural alignment are local
structural alignment methods. These provide comparison of pre-selected
parts of proteins (e.g. binding sites, user-defined structural motifs) against binding sites or whole-protein structural databases. The MultiBind and MAPPIS servers allow the identification of common spatial arrangements of
physicochemical properties such as H-bond donor, acceptor, aliphatic,
aromatic or hydrophobic in a set of user provided protein binding sites
defined by interactions with small molecules (MultiBind) or in a set of
user-provided protein–protein interfaces (MAPPIS). Others provide
comparison of entire protein structures against a number of user submitted structures or against a large database of protein structures in reasonable time (ProBiS).
Unlike global alignment approaches, local structural alignment
approaches are suited to detection of locally conserved patterns of
functional groups, which often appear in binding sites and have
significant involvement in ligand binding. As an example, comparing G-Losa,
a local structure alignment tool, with TM-align, a global structure
alignment based method. While G-Losa predicts drug-like ligands’
positions in single-chain protein targets more precisely than TM-align,
the overall success rate of TM-align is better.
However, as algorithmic improvements and computer performance
have erased purely technical deficiencies in older approaches, it has
become clear that there is no one universal criterion for the 'optimal'
structural alignment. TM-align, for instance, is particularly robust in
quantifying comparisons between sets of proteins with great disparities
in sequence lengths, but it only indirectly captures hydrogen bonding or
secondary structure order conservation which might be better metrics
for alignment of evolutionarily related proteins. Thus recent
developments have focused on optimizing particular attributes such as
speed, quantification of scores, correlation to alternative gold
standards, or tolerance of imperfection in structural data or ab initio
structural models. An alternative methodology that is gaining popularity
is to use the consensus of various methods to ascertain proteins structural similarities.
RNA structural alignment
Structural alignment techniques have traditionally been applied exclusively to proteins, as the primary biological macromolecules that assume characteristic three-dimensional structures. However, large RNA molecules also form characteristic tertiary structures, which are mediated primarily by hydrogen bonds formed between base pairs as well as base stacking. Functionally similar noncoding RNA molecules can be especially difficult to extract from genomics data because structure is more strongly conserved than sequence in RNA as well as in proteins, and the more limited alphabet of RNA decreases the information content of any given nucleotide at any given position.
However, because of the increasing interest in RNA structures and
because of the growth of the number of experimentally determined 3D RNA
structures, few RNA structure similarity methods have been developed
recently. One of those methods is, e.g., SETTER
which decomposes each RNA structure into smaller parts called general
secondary structure units (GSSUs). GSSUs are subsequently aligned and
these partial alignments are merged into the final RNA structure
alignment and scored. The method has been implemented into the SETTER web server.
A recent method for pairwise structural alignment of RNA
sequences with low sequence identity has been published and implemented
in the program FOLDALIGN.
However, this method is not truly analogous to protein structural
alignment techniques because it computationally predicts the structures
of the RNA input sequences rather than requiring experimentally
determined structures as input. Although computational prediction of the
protein folding process has not been particularly successful to date, RNA structures without pseudoknots can often be sensibly predicted using free energy-based scoring methods that account for base pairing and stacking.
Software
Choosing a software tool for structural alignment can be a challenge
due to the large variety of available packages that differ significantly
in methodology and reliability. A partial solution to this problem was
presented in
and made publicly accessible through the ProCKSI webserver. A more
complete list of currently available and freely distributed structural
alignment software can be found in structural alignment software.
Properties of some structural alignment servers and software packages are summarized and tested with examples at Structural Alignment Tools in Proteopedia.Org.