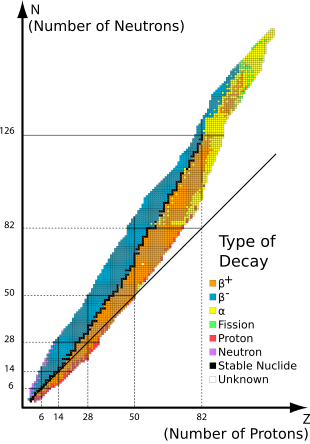Environmental isotopes

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Environmental_isotopes 

The environmental isotopes are a subset of the isotopes, both stable and radioactive, which are the object of isotope geochemistry. They are primarily used as tracers to see how things move around within the ocean-atmosphere system, within terrestrial biomes, within the Earth's surface, and between these broad domains.

Isotope Geochemistry

Chemical elements are defined by their number of protons, but the mass of the atom is determined by the number of protons and neutrons in the nucleus. Isotopes are atoms that are of a specific element, but have different numbers of neutrons and thus different masses. In a specific object, you can have a ratio between two isotopes of an element. This ratio varies slightly in the world, so in order to study isotopic ratio changes across the world, changes in isotope ratios are defined as deviations from a standard, multiplied by 1000. This unit is a "per mil". As a convention, the ratio is of the heavier isotope to the lower isotope.

${\displaystyle \delta {\ce {^{13}C}}=\left({\frac {\left({\frac {{\ce {^{13}C}}}{{\ce {^{12}C}}}}\right)_{sample}}{\left({\frac {{\ce {^{13}C}}}{{\ce {^{12}C}}}}\right)_{standard}}}-1\right)\times 1000}$ ‰

These variations in isotopes can occur through many types of fractionation. They are generally classified as mass independent fractionation and mass dependent fractionation. An example of a mass independent process is the fractionation of oxygen atoms in ozone. This is due to the kinetic isotope effect (KIE) and is caused by different isotope molecules reacting at different speeds. An example of a mass dependent process is the fractionation of water as it transitions from the liquid to gas phase. Water molecules with heavier isotopes (¹⁸O and ²H) tend to stay in the liquid phase as water molecules with lighter isotopes (¹⁶O and ¹H) preferentially move to the gas phase.

Of the different isotopes that exist, one common classification is distinguishing radioactive isotopes from stable isotopes. Radioactive isotopes are isotopes that will decay into a different isotope. For example, ³H (tritium) is a radioactive isotope of hydrogen. It decays into ³He with a half-life of ~12.3 years. By comparison, stable isotopes are more stable, decaying much more slowly and having much longer half-lives. Examples of stable isotopes are ⁸⁶Sr and ⁸⁷Sr. These isotopes of strontium have half-lives on the order of billions of years or are unmeasured because of how stable they are. On timescales that geologists and environmental scientists investigate, these isotopes are stable. Both of these types of isotopes are useful to scientists. Radioactive isotopes are generally more useful on shorter timescales, such as investigating modern circulation of the ocean using ¹⁴C, while stable isotopes are generally more useful on longer timescales, such as investigating differences in river flow with strontium stable isotopes.

These isotopes are used as tracers to study various phenomena of interest. These tracers have a certain distribution spatially, and so scientists need to deconvolve the different processes that affect these tracer distributions. One way tracer distributions are set is by conservative mixing. In conservative mixing, the amount of the tracer is conserved. An example of this is mixing two water masses with different salinities. The salt from the saltier water mass moves to the less salty water mass, keeping the total amount of salinity constant. This way of mixing tracers is very important, giving a baseline of what value of a tracer one should expect. The value of a tracer as a point is expected to be an average value of the sources that flow into that region. Deviations from this are indicative of other processes. These can be called nonconservative mixing, where there are other processes that do not conserve the amount of tracer. An example of this is 𝛿¹⁴C. This mixes between water masses, but it also decays over time, reducing the amount of ¹⁴C in the region.

Useful Elements

The most used environmental isotopes are:

• deuterium
• tritium
• carbon-13
• carbon-14
• nitrogen-15
• oxygen-18
• silicon-29
• chlorine-36
• isotopes of uranium
• isotopes of strontium

Ocean Circulation

One topic that environmental isotopes are used to study is the circulation of the ocean. Treating the ocean as a box is only useful in some studies; in depth consideration of the oceans in general circulation models (GCM's) requires knowing how the ocean circulates. This leads to an understanding of how the oceans (along with the atmosphere) transfer heat from the tropics to the poles. This also helps deconvolve circulation effects from other phenomena that affect certain tracers such as radioactive and biological processes.

A summary of the path of the thermohaline circulation. Blue paths represent deep-water currents, while red paths represent surface currents.

Using rudimentary observation techniques, the circulation of the surface ocean can be determined. In the Atlantic basin, surface waters flow from the south towards the north in general, while also creating gyres in the northern and southern Atlantic. In the Pacific Ocean, the gyres still form, but there is comparatively very little large scale meridional (North-South) movement. For deep waters, there are two areas where density causes waters to sink into the deep ocean. These are in the North Atlantic and the Antarctic. The deep water masses formed are North Atlantic Deep Water (NADW) and Antarctic Bottom Water (AABW). Deep waters are mixtures of these two waters, and understanding how waters are composed of these two water masses can tell us about how water masses move around in the deep ocean.

This can be investigated with environmental isotopes, including ¹⁴C. ¹⁴C is predominantly produced in the upper atmosphere and from nuclear testing, with no major sources or sinks in the ocean. This ¹⁴C from the atmosphere becomes oxidized into ¹⁴CO₂, allowing it to enter the surface ocean through gas transfer. This is transferred into the deep ocean through NADW and AABW. In NADW, the 𝛿¹⁴C is approximately -60‰, and in AABW, the 𝛿¹⁴C is approximately -160‰. Thus, using conservative mixing of radiocarbon, the expected amount of radiocarbon in various locations can be determined using the percent compositions of NADW and AABW at that location. This can be determined using other tracers, such as phosphate star or salinity. Deviations from this expected value are indicative of other processes that affect the delta ratio of radiocarbon, namely radioactive decay. This deviation can be converted to a time, giving the age of the water at that location. Doing this over the world's ocean can yield a circulation pattern of the ocean and the rate at which water flow through the deep ocean. Using this circulation in conjunction with the surface circulation allows scientists to understand the energy balance of the world. Warmer surface waters flow northward while colder deep waters flow southward, leading to net heat transfer towards the pole.

Paleoclimate

Isotopes are also used to study paleoclimate. This is the study of how climate was in the past, from hundreds of years ago to hundreds of thousands of years ago. The only records of these times that we have are buried in rocks, sediments, biological shells, stalagmites and stalactites, etc. The isotope ratios in these samples were affected by the temperature, salinity, circulation of the ocean, precipitation, etc. of the climate at the time, causing a measurable change from the standards for isotope measurements. This is how climate information is encoded in these geological formations. Some of the many isotopes useful for environmental science are discussed below.

Delta O18

One useful isotope for reconstructing past climates is oxygen-18. It is another stable isotope of oxygen along with oxygen-16, and its incorporation into water and carbon dioxide/carbonate molecules is strongly temperature dependent. Higher temperature implies more incorporation of oxygen-18, and vice versa. Thus, the ratio of ¹⁸O/¹⁶O can tell something about temperature. For water, the isotope ratio standard is Vienna Standard Mean Ocean Water, and for carbonates, the standard is Pee Dee Belemnite. Using ice cores and sediment cores that record information about the water and shells from past times, this ratio can tell scientists about the temperature of those times.

 

Climate record as reconstructed by Lisiecki and Raymo (2005) showing oscillations in the Earth's temperature over time. These oscillations have a 41 kyr cycle until about 1.2 million years ago, switching to a 100 kyr cycle that we see now.

This ratio is used with ice cores to determine the temperature at the spot in the ice core. Depth in an ice core is proportional to time, and it is "wiggle-matched" with other records to determine the true time of the ice at that depth. This can be done by comparing δ¹⁸O in calcium carbonate shells in sediment cores to these records to match large scale changes in the temperature of the Earth. Once the ice cores are matched to sediment cores, highly accurate dating methods such as U-series dating can be used to accurately determine the time of these events. There are some processes that mix water from different times into the same depth in the ice core, such as firn production and sloped landscape floes.

Lisiecki and Raymo (2005) used measurements of δ¹⁸O in benthic foraminifera from 57 globally distributed deep sea sediment cores, taken as a proxy for the total global mass of glacial ice sheets, to reconstruct the climate for the past five million years. This record shows oscillations of 2-10 degrees Celsius over this time. Between 5 million and 1.2 million years ago, these oscillations had a period of 41,000 years (41 kyr), but about 1.2 million years ago the period switch to 100 kyr. These changes in global temperature match with changes in orbital parameters of the Earth's orbit around the Sun. These are called Milankovitch cycles, and these are related to eccentricity, obliquity (axial tilt), and precession of Earth around its axis. These correspond to cycles with periods of 100 kyr, 40 kyr, and 20 kyr.

δ¹⁸O can also be used to investigate smaller scale climate phenomena. Koutavas et al. (2006) used δ¹⁸O of G. ruber foraminifera to study the El Niño–Southern Oscillation (ENSO) and it's variability through the mid-Holocene.^[6] By isolating individual foram shells, Koutavas et al. were able to obtain a spread of δ¹⁸O values at a specific depth. Because these forams live for approximately a month and that the individual forams were from many different months, clumped together in a small depth range in the coral, the variability of δ¹⁸O was able to be determined. In the eastern Pacific, where these cores were taken, the primary driver of this variability is ENSO, making this a record of ENSO variability over the core's time span. Koutavas et al. found that ENSO was much less variable in the mid Holocene (~6,000 years ago) than it is currently.

Strontium isotopes

Another set of environmental isotopes used in paleoclimate is strontium isotopes. Strontium-86 and strontium-87 are both stable isotopes of strontium, but strontium-87 is radiogenic, coming from the decay of rubidium-87. The ratio of these two isotopes depends on the concentration of rubidium-87 initially and the age of the sample, assuming that the background concentration of strontium-87 is known. This is useful because ⁸⁷Rb is predominantly found in continental rocks. Particles from these rocks come into the ocean through weathering by rivers, meaning that this strontium isotope ratio is related to the weathering ion flux coming from rivers into the ocean. The background concentration in the ocean for ⁸⁷Sr/⁸⁶Sr is 0.709 ± 0.0012. Because the strontium ratio is recorded in sedimentary records, the oscillations of this ratio over time can be studied. These oscillations are related to the riverine input into the oceans or into the local basin. Richter and Turekian have done work on this, finding that over glacial-interglacial timescales (10⁵ years), the ⁸⁷Sr/⁸⁶Sr ratio varies by 3*10⁻⁵.

Decay series of Actinides, including Uranium, Protactinium, Thorium, and Lead

Uranium and related isotopes

Uranium has many radioactive isotopes that continue emitting particles down a decay chain.

Uranium-235 is in one such chain, and decays into protactinium-231 and then into other products. Uranium-238 is in a separate chain, decaying into a series of elements, including thorium-230. Both of these series end up forming lead, either lead-207 from uranium-235 or lead-206 from uranium-238. All of these decays are alpha or beta decays, meaning that they all follow first order rate equations of the form ${\displaystyle dN/dt=\lambda N}$, where λ is the half-life of the isotope in question. This makes it simple to determine the age of a sample based on the various ratios of radioactive isotopes that exist.

One way uranium isotopes are used is to date rocks from millions to billions of years ago. This is through uranium-lead dating. This technique uses zircon samples and measures the lead content in them. Zircon incorporates uranium and thorium atoms into its crystal structure, but strongly rejects lead. Thus, the only sources of lead in a zircon crystal are through decay of uranium and thorium. Both the uranium-235 and uranium-238 series decay into an isotope of lead. The "half-life" of converting ²³⁵U to ²⁰⁷Pb is 710 million years, and the "half-life" of converting ²³⁸U to ²⁰⁶Pb is 4.47 billion years. Because of high resolution mass-spectroscopy, both chains can be used to date rocks, giving complementary information about the rocks. The large difference in half-lives makes the technique robust over long time scales, from on the order of millions of years to on the order of billions of years.

Another way uranium isotopes are used in environmental science is the ratio of ²³¹Pa/²³⁰Th. These radiogenic isotopes have different uranium parents, but have very different reactivities in the ocean. The uranium profile in the ocean is constant because uranium has a very large residence time compared to the residence time of the ocean. The decay of uranium is thus also isotropic, but the daughter isotopes react differently. Thorium is readily scavenged by particles, leading to rapid removal from the ocean into sediments. By contrast, ²³¹Pa is not as particle-reactive, feeling the circulation of the ocean in small amounts before settling into the sediment. Thus, knowing the decay rates of both isotopes and the fractions of each uranium isotopes, the expected ratio of ²³¹Pa/²³⁰Th can be determined, with any deviation from this value being due to circulation. Circulation leads to a higher ²³¹Pa/²³⁰Th ratio downstream and a lower ratio upstream, with the magnitude of the deviation being related to flow rate. This technique has been used to quantify the Atlantic Meridional Overturning Circulation (AMOC) during the Last Glacial Maximum (LGM) and during abrupt climate change events in Earth's past, such as Heinrich events and Dansgaard-Oeschger events.

Neodymium

Neodymium isotopes are also used to determine circulation in the ocean. All of the isotopes of neodymium are stable on the timescales of glacial-interglacial cycles, but ¹⁴³Nd is a daughter of ¹⁴⁷Sm, a radioactive isotope in the ocean. Samarium-147 has higher concentrations in mantle rocks vs crust rocks, so areas that receive river inputs from mantle-derived rocks have higher concentrations of ¹⁴⁷Sm and ¹⁴³Nd. However, these differences are so small, the standard notation of a delta value are no blunt for it; a more precise epsilon value is used to describe variations in this ratio of neodymium isotopes. It 

is defined as ${\displaystyle \epsilon {\ce {_{Nd}}}=\left({\frac {\left({\frac {{\ce {^{143}Nd}}}{{\ce {^{144}Nd}}}}\right)_{sample}}{\left({\frac {{\ce {^{143}Nd}}}{{\ce {^{144}Nd}}}}\right)_{standard}}}-1\right)\times 10000}$

The only major sources of this in the ocean are in the North Atlantic and in the deep Pacific Ocean. Because one of the end-members is set in the interior of the ocean, this technique has the potential to tell us complementary information about paleoclimate compared to all other ocean tracers that are only set in the surface ocean.

Isotope geochemistry

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Isotope_geochemistry 

Isotope geochemistry is an aspect of geology based upon the study of natural variations in the relative abundances of isotopes of various elements. Variations in isotopic abundance are measured by isotope ratio mass spectrometry, and can reveal information about the ages and origins of rock, air or water bodies, or processes of mixing between them.

Stable isotope geochemistry is largely concerned with isotopic variations arising from mass-dependent isotope fractionation, whereas radiogenic isotope geochemistry is concerned with the products of natural radioactivity.

Stable isotope geochemistry

For most stable isotopes, the magnitude of fractionation from kinetic and equilibrium fractionation is very small; for this reason, enrichments are typically reported in "per mil" (‰, parts per thousand).

 These enrichments (δ) represent the ratio of heavy isotope to light isotope in the sample over the ratio of a standard. That is,

${\displaystyle \delta {\ce {^{13}C}}=\left({\frac {\left({\frac {{\ce {^{13}C}}}{{\ce {^{12}C}}}}\right)_{sample}}{\left({\frac {{\ce {^{13}C}}}{{\ce {^{12}C}}}}\right)_{standard}}}-1\right)\times 1000}$ ‰

Carbon

Carbon has two stable isotopes, ¹²C and ¹³C, and one radioactive isotope, ¹⁴C.

The stable carbon isotope ratio, δ¹³C, is measured against Vienna Pee Dee Belemnite (VPDB). The stable carbon isotopes are fractionated primarily by photosynthesis (Faure, 2004). The ¹³C/¹²C ratio is also an indicator of paleoclimate: a change in the ratio in the remains of plants indicates a change in the amount of photosynthetic activity, and thus in how favorable the environment was for the plants. During photosynthesis, organisms using the C₃ pathway show different enrichments compared to those using the C₄ pathway, allowing scientists not only to distinguish organic matter from abiotic carbon, but also what type of photosynthetic pathway the organic matter was using. Occasional spikes in the global ¹³C/¹²C ratio have also been useful as stratigraphic markers for chemostratigraphy, especially during the Paleozoic.

The ¹⁴C ratio has been used to track ocean circulation, among other things.

Nitrogen

Nitrogen has two stable isotopes, ¹⁴N and ¹⁵N. The ratio between these is measured relative to nitrogen in ambient air. Nitrogen ratios are frequently linked to agricultural activities. Nitrogen isotope data has also been used to measure the amount of exchange of air between the stratosphere and troposphere using data from the greenhouse gas N₂O.

Oxygen

Oxygen has three stable isotopes, ¹⁶O, ¹⁷O, and ¹⁸O. Oxygen ratios are measured relative to Vienna Standard Mean Ocean Water (VSMOW) or Vienna Pee Dee Belemnite (VPDB). Variations in oxygen isotope ratios are used to track both water movement, paleoclimate, and atmospheric gases such as ozone and carbon dioxide. Typically, the VPDB oxygen reference is used for paleoclimate, while VSMOW is used for most other applications. Oxygen isotopes appear in anomalous ratios in atmospheric ozone, resulting from mass-independent fractionation. Isotope ratios in fossilized foraminifera have been used to deduce the temperature of ancient seas.

Sulfur

Sulfur has four stable isotopes, with the following abundances: ³²S (0.9502), ³³S (0.0075), ³⁴S (0.0421) and ³⁶S (0.0002). These abundances are compared to those found in Cañon Diablo troilite. Variations in sulfur isotope ratios are used to study the origin of sulfur in an orebody and the temperature of formation of sulfur–bearing minerals.

Radiogenic isotope geochemistry

Radiogenic isotopes provide powerful tracers for studying the ages and origins of Earth systems. They are particularly useful to understand mixing processes between different components, because (heavy) radiogenic isotope ratios are not usually fractionated by chemical processes.

Radiogenic isotope tracers are most powerful when used together with other tracers: The more tracers used, the more control on mixing processes. An example of this application is to the evolution of the Earth's crust and Earth's mantle through geological time.

Lead–lead isotope geochemistry

Lead has four stable isotopes: ²⁰⁴Pb, ²⁰⁶Pb, ²⁰⁷Pb, and ²⁰⁸Pb.

Lead is created in the Earth via decay of actinide elements, primarily uranium and thorium.

Lead isotope geochemistry is useful for providing isotopic dates on a variety of materials. Because the lead isotopes are created by decay of different transuranic elements, the ratios of the four lead isotopes to one another can be very useful in tracking the source of melts in igneous rocks, the source of sediments and even the origin of people via isotopic fingerprinting of their teeth, skin and bones.

It has been used to date ice cores from the Arctic shelf, and provides information on the source of atmospheric lead pollution.

Lead–lead isotopes has been successfully used in forensic science to fingerprint bullets, because each batch of ammunition has its own peculiar ²⁰⁴Pb/²⁰⁶Pb vs ²⁰⁷Pb/²⁰⁸Pb ratio.

Samarium–neodymium

Samarium–neodymium is an isotope system which can be utilised to provide a date as well as isotopic fingerprints of geological materials, and various other materials including archaeological finds (pots, ceramics).

¹⁴⁷Sm decays to produce ¹⁴³Nd with a half life of 1.06x10¹¹ years.

Dating is achieved usually by trying to produce an isochron of several minerals within a rock specimen. The initial ¹⁴³Nd/¹⁴⁴Nd ratio is determined.

This initial ratio is modelled relative to CHUR - the Chondritic Uniform Reservoir - which is an approximation of the chondritic material which formed the solar system. CHUR was determined by analysing chondrite and achondrite meteorites.

The difference in the ratio of the sample relative to CHUR can give information on a model age of extraction from the mantle (for which an assumed evolution has been calculated relative to CHUR) and to whether this was extracted from a granitic source (depleted in radiogenic Nd), the mantle, or an enriched source.

Rhenium–osmium

Rhenium and osmium are siderophile elements which are present at very low abundances in the crust. Rhenium undergoes radioactive decay to produce osmium. The ratio of non-radiogenic osmium to radiogenic osmium throughout time varies.

Rhenium prefers to enter sulfides more readily than osmium. Hence, during melting of the mantle, rhenium is stripped out, and prevents the osmium–osmium ratio from changing appreciably. This locks in an initial osmium ratio of the sample at the time of the melting event. Osmium–osmium initial ratios are used to determine the source characteristic and age of mantle melting events.

Noble gas isotopes

Natural isotopic variations amongst the noble gases result from both radiogenic and nucleogenic production processes. Because of their unique properties, it is useful to distinguish them from the conventional radiogenic isotope systems described above.

Helium-3

Helium-3 was trapped in the planet when it formed. Some ³He is being added by meteoric dust, primarily collecting on the bottom of oceans (although due to subduction, all oceanic tectonic plates are younger than continental plates). However, ³He will be degassed from oceanic sediment during subduction, so cosmogenic ³He is not affecting the concentration or noble gas ratios of the mantle.

Helium-3 is created by cosmic ray bombardment, and by lithium spallation reactions which generally occur in the crust. Lithium spallation is the process by which a high-energy neutron bombards a lithium atom, creating a ³He and a ⁴He ion. This requires significant lithium to adversely affect the ³He/⁴He ratio.

All degassed helium is lost to space eventually, due to the average speed of helium exceeding the escape velocity for the Earth. Thus, it is assumed the helium content and ratios of Earth's atmosphere have remained essentially stable.

It has been observed that ³He is present in volcano emissions and oceanic ridge samples. How ³He is stored in the planet is under investigation, but it is associated with the mantle and is used as a marker of material of deep origin.

Due to similarities in helium and carbon in magma chemistry, outgassing of helium requires the loss of volatile components (water, carbon dioxide) from the mantle, which happens at depths of less than 60 km. However, ³He is transported to the surface primarily trapped in the crystal lattice of minerals within fluid inclusions.

Helium-4 is created by radiogenic production (by decay of uranium/thorium-series elements). The continental crust has become enriched with those elements relative to the mantle and thus more He⁴ is produced in the crust than in the mantle.

The ratio (R) of ³He to ⁴He is often used to represent ³He content. R usually is given as a multiple of the present atmospheric ratio (Ra).

Common values for R/Ra:

• Old continental crust: less than 1
• mid-ocean ridge basalt (MORB): 7 to 9
• Spreading ridge rocks: 9.1 plus or minus 3.6
• Hotspot rocks: 5 to 42
• Ocean and terrestrial water: 1
• Sedimentary formation water: less than 1
• Thermal spring water: 3 to 11

³He/⁴He isotope chemistry is being used to date groundwaters, estimate groundwater flow rates, track water pollution, and provide insights into hydrothermal processes, igneous geology and ore genesis.

• (U-Th)/He dating of apatite as a thermal history tool
• USGS: Helium Discharge at Mammoth Mountain Fumarole (MMF)

Isotopes in actinide decay chains

Isotopes in the decay chains of actinides are unique amongst radiogenic isotopes because they are both radiogenic and radioactive. Because their abundances are normally quoted as activity ratios rather than atomic ratios, they are best considered separately from the other radiogenic isotope systems.

Protactinium/Thorium – ²³¹Pa / ²³⁰Th

Uranium is well mixed in the ocean, and its decay produces ²³¹Pa and ²³⁰Th at a constant activity ratio (0.093). The decay products are rapidly removed by adsorption on settling particles, but not at equal rates. ²³¹Pa has a residence equivalent to the residence time of deep water in the Atlantic basin (around 1000 yrs) but ²³⁰Th is removed more rapidly (centuries). Thermohaline circulation effectively exports ²³¹Pa from the Atlantic into the Southern Ocean, while most of the ²³⁰Th remains in Atlantic sediments. As a result, there is a relationship between ²³¹Pa/²³⁰Th in Atlantic sediments and the rate of overturning: faster overturning produces lower sediment ²³¹Pa/²³⁰Th ratio, while slower overturning increases this ratio. The combination of δ¹³C and ²³¹Pa/²³⁰Th can therefore provide a more complete insight into past circulation changes.

Anthropogenic isotopes

Tritium/helium-3

Tritium was released to the atmosphere during atmospheric testing of nuclear bombs. Radioactive decay of tritium produces the noble gas helium-3. Comparing the ratio of tritium to helium-3 (³H/³He) allows estimation of the age of recent ground waters.

• USGS Tritium/Helium-3 Dating
• Hydrologic Isotope Tracers - Helium

Stable nuclide

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Stable_nuclide 

 

Graph of nuclides (isotopes) by type of decay. Orange and blue nuclides are unstable, with the black squares between these regions representing stable nuclides. The continuous line passing below most of the nuclides comprises the positions on the graph of the (mostly hypothetical) nuclides for which proton number would the same as neutron number. The graph reflects the fact that elements with more than 20 protons either have more neutrons than protons or are unstable.

Stable nuclides are nuclides that are not radioactive and so (unlike radionuclides) do not spontaneously undergo radioactive decay. When such nuclides are referred to in relation to specific elements, they are usually termed stable isotopes.

The 80 elements with one or more stable isotopes comprise a total of 252 nuclides that have not been known to decay using current equipment (see list at the end of this article). Of these elements, 26 have only one stable isotope; they are thus termed monoisotopic. The rest have more than one stable isotope. Tin has ten stable isotopes, the largest number of stable isotopes known for an element.

Definition of stability, and naturally occurring nuclides

Most naturally occurring nuclides are stable (about 252; see list at the end of this article), and about 34 more (total of 286) are known to be radioactive with sufficiently long half-lives (also known) to occur primordially. If the half-life of a nuclide is comparable to, or greater than, the Earth's age (4.5 billion years), a significant amount will have survived since the formation of the Solar System, and then is said to be primordial. It will then contribute in that way to the natural isotopic composition of a chemical element. Primordially present radioisotopes are easily detected with half-lives as short as 700 million years (e.g., ²³⁵U). This is the present limit of detection, as shorter-lived nuclides have not yet been detected undisputedly in nature.

Many naturally occurring radioisotopes (another 53 or so, for a total of about 339) exhibit still shorter half-lives than 700 million years, but they are made freshly, as daughter products of decay processes of primordial nuclides (for example, radium from uranium) or from ongoing energetic reactions, such as cosmogenic nuclides produced by present bombardment of Earth by cosmic rays (for example, ¹⁴C made from nitrogen).

Some isotopes that are classed as stable (i.e. no radioactivity has been observed for them) are predicted to have extremely long half-lives (sometimes as high as 10¹⁸ years or more). If the predicted half-life falls into an experimentally accessible range, such isotopes have a chance to move from the list of stable nuclides to the radioactive category, once their activity is observed. For example, ²⁰⁹Bi and ¹⁸⁰W were formerly classed as stable, but were found to be alpha-active in 2003. However, such nuclides do not change their status as primordial when they are found to be radioactive.

Most stable isotopes on Earth are believed to have been formed in processes of nucleosynthesis, either in the Big Bang, or in generations of stars that preceded the formation of the solar system. However, some stable isotopes also show abundance variations in the earth as a result of decay from long-lived radioactive nuclides. These decay-products are termed radiogenic isotopes, in order to distinguish them from the much larger group of 'non-radiogenic' isotopes.

Isotopes per element

Of the known chemical elements, 80 elements have at least one stable nuclide. These comprise the first 82 elements from hydrogen to lead, with the two exceptions, technetium (element 43) and promethium (element 61), that do not have any stable nuclides. As of December 2016, there were a total of 252 known "stable" nuclides. In this definition, "stable" means a nuclide that has never been observed to decay against the natural background. Thus, these elements have half lives too long to be measured by any means, direct or indirect.

Stable isotopes:

• 1 element (tin) has 10 stable isotopes
• 5 elements have 7 stable isotopes apiece
• 7 elements have 6 stable isotopes apiece
• 11 elements have 5 stable isotopes apiece
• 9 elements have 4 stable isotopes apiece
• 5 elements have 3 stable isotopes apiece
• 16 elements have 2 stable isotopes apiece
• 26 elements have 1 single stable isotope.

These last 26 are thus called monoisotopic elements. The mean number of stable isotopes for elements which have at least one stable isotope is 252/80 = 3.15.

Physical magic numbers and odd and even proton and neutron count

Stability of isotopes is affected by the ratio of protons to neutrons, and also by presence of certain magic numbers of neutrons or protons which represent closed and filled quantum shells. These quantum shells correspond to a set of energy levels within the shell model of the nucleus; filled shells, such as the filled shell of 50 protons for tin, confers unusual stability on the nuclide. As in the case of tin, a magic number for Z, the atomic number, tends to increase the number of stable isotopes for the element.

Just as in the case of electrons, which have the lowest energy state when they occur in pairs in a given orbital, nucleons (both protons and neutrons) exhibit a lower energy state when their number is even, rather than odd. This stability tends to prevent beta decay (in two steps) of many even–even nuclides into another even–even nuclide of the same mass number but lower energy (and of course with two more protons and two fewer neutrons), because decay proceeding one step at a time would have to pass through an odd–odd nuclide of higher energy. Such nuclei thus instead undergo double beta decay (or are theorized to do so) with half-lives several orders of magnitude larger than the age of the universe. This makes for a larger number of stable even-even nuclides, which account for 151 of the 252 total. Stable even–even nuclides number as many as three isobars for some mass numbers, and up to seven isotopes for some atomic numbers.

Conversely, of the 252 known stable nuclides, only five have both an odd number of protons and odd number of neutrons: hydrogen-2 (deuterium), lithium-6, boron-10, nitrogen-14, and tantalum-180m. Also, only four naturally occurring, radioactive odd–odd nuclides have a half-life over a billion years: potassium-40, vanadium-50, lanthanum-138, and lutetium-176. Odd–odd primordial nuclides are rare because most odd–odd nuclei are unstable with respect to beta decay, because the decay products are even–even, and are therefore more strongly bound, due to nuclear pairing effects.

Yet another effect of the instability of an odd number of either type of nucleons is that odd-numbered elements tend to have fewer stable isotopes. Of the 26 monoisotopic elements (those with only a single stable isotope), all but one have an odd atomic number, and all but one has an even number of neutrons—the single exception to both rules being beryllium.

The end of the stable elements in the periodic table occurs after lead, largely due to the fact that nuclei with 128 neutrons are extraordinarily unstable and almost immediately shed alpha particles. This also contributes to the very short half-lives of astatine, radon, and francium relative to heavier elements. This may also be seen to a much lesser extent with 84 neutrons, which exhibits as a certain number of isotopes in the lanthanide series which exhibit alpha decay.

Nuclear isomers, including a "stable" one

The count of 252 known stable nuclides includes tantalum-180m, since even though its decay and instability is automatically implied by its notation of "metastable", this has still not yet been observed. All "stable" isotopes (stable by observation, not theory) are the ground states of nuclei, with the exception of tantalum-180m, which is a nuclear isomer or excited state. The ground state of this particular nucleus, tantalum-180, is radioactive with a comparatively short half-life of 8 hours; in contrast, the decay of the excited nuclear isomer is extremely strongly forbidden by spin-parity selection rules. It has been reported experimentally by direct observation that the half-life of ^180mTa to gamma decay must be more than 10¹⁵ years. Other possible modes of ^180mTa decay (beta decay, electron capture and alpha decay) have also never been observed.

Binding energy per nucleon of common isotopes.

Still-unobserved decay

It is expected that some continual improvement of experimental sensitivity will allow discovery of very mild radioactivity (instability) of some isotopes that are considered to be stable today. For an example of a recent discovery, it was not until 2003 that bismuth-209 (the only primordial isotope of bismuth) was shown to be very mildly radioactive, confirming theoretical predictions from nuclear physics that bismuth-209 would decay very slowly by alpha emission.

Isotopes that are theoretically believed to be unstable but have not been observed to decay are termed as observationally stable.

Summary table for numbers of each class of nuclides

This is a summary table from List of nuclides. Note that numbers are not exact and may change slightly in the future, as nuclides are observed to be radioactive, or new half-lives are determined to some precision.

Type of nuclide by stability class	Number of nuclides in class	Running total of nuclides in all classes to this point	Notes
Theoretically stable to all but proton decay	90	90	Includes first 40 elements. If protons decay, then there are no stable nuclides.
Theoretically stable to alpha decay, beta decay, isomeric transition, and double beta decay but not spontaneous fission, which is possible for "stable" nuclides ≥ niobium-93	56	146	(Note that spontaneous fission has never been observed for nuclides with mass number < 230).
Energetically unstable to one or more known decay modes, but no decay yet seen. Considered stable until radioactivity confirmed.	106	252	Total is the observationally stable nuclides.
Radioactive primordial nuclides.	34	286	Includes Bi, Th, U.
Radioactive nonprimordial, but naturally occurring on Earth.	~61 significant	~347 significant	Cosmogenic nuclides from cosmic rays; daughters of radioactive primordials such as francium, etc.

List of stable nuclides

1. Hydrogen-1
2. Hydrogen-2
3. Helium-3
4. Helium-4

   no mass number 5

5. Lithium-6
6. Lithium-7
   no mass number 8
7. Beryllium-9
8. Boron-10
9. Boron-11
10. Carbon-12
11. Carbon-13
12. Nitrogen-14
13. Nitrogen-15
14. Oxygen-16
15. Oxygen-17
16. Oxygen-18
17. Fluorine-19
18. Neon-20
19. Neon-21
20. Neon-22
21. Sodium-23
22. Magnesium-24
23. Magnesium-25
24. Magnesium-26
25. Aluminium-27
26. Silicon-28
27. Silicon-29
28. Silicon-30
29. Phosphorus-31
30. Sulfur-32
31. Sulfur-33
32. Sulfur-34
33. Sulfur-36
34. Chlorine-35
35. Chlorine-37
36. Argon-36 (2E)
37. Argon-38
38. Argon-40
39. Potassium-39
40. Potassium-41
41. Calcium-40 (2E)*
42. Calcium-42
43. Calcium-43
44. Calcium-44
45. Calcium-46 (2B)*
46. Scandium-45
47. Titanium-46
48. Titanium-47
49. Titanium-48
50. Titanium-49
51. Titanium-50
52. Vanadium-51
53. Chromium-50 (2E)*
54. Chromium-52
55. Chromium-53
56. Chromium-54
57. Manganese-55
58. Iron-54 (2E)*
59. Iron-56
60. Iron-57
61. Iron-58
62. Cobalt-59
63. Nickel-58 (2E)*
64. Nickel-60
65. Nickel-61
66. Nickel-62
67. Nickel-64
68. Copper-63
69. Copper-65
70. Zinc-64 (2E)*
71. Zinc-66
72. Zinc-67
73. Zinc-68
74. Zinc-70 (2B)*
75. Gallium-69
76. Gallium-71
77. Germanium-70
78. Germanium-72
79. Germanium-73
80. Germanium-74
81. Arsenic-75
82. Selenium-74 (2E)
83. Selenium-76
84. Selenium-77
85. Selenium-78
86. Selenium-80 (2B)
87. Bromine-79
88. Bromine-81
89. Krypton-80
90. Krypton-82
91. Krypton-83
92. Krypton-84
93. Krypton-86 (2B)
94. Rubidium-85
95. Strontium-84 (2E)
96. Strontium-86
97. Strontium-87
98. Strontium-88
99. Yttrium-89
100. Zirconium-90
101. Zirconium-91
102. Zirconium-92
103. Zirconium-94 (2B)*
104. Niobium-93
105. Molybdenum-92 (2E)*
106. Molybdenum-94
107. Molybdenum-95
108. Molybdenum-96
109. Molybdenum-97
110. Molybdenum-98 (2B)*
     Technetium - No stable isotopes
111. Ruthenium-96 (2E)*
112. Ruthenium-98
113. Ruthenium-99
114. Ruthenium-100
115. Ruthenium-101
116. Ruthenium-102
117. Ruthenium-104 (2B)
118. Rhodium-103
119. Palladium-102 (2E)
120. Palladium-104
121. Palladium-105
122. Palladium-106
123. Palladium-108
124. Palladium-110 (2B)*
125. Silver-107
126. Silver-109
127. Cadmium-106 (2E)*
128. Cadmium-108 (2E)*
129. Cadmium-110
130. Cadmium-111
131. Cadmium-112
132. Cadmium-114 (2B)*
133. Indium-113
134. Tin-112 (2E)
135. Tin-114
136. Tin-115
137. Tin-116
138. Tin-117
139. Tin-118
140. Tin-119
141. Tin-120
142. Tin-122 (2B)
143. Tin-124 (2B)*
144. Antimony-121
145. Antimony-123
146. Tellurium-120 (2E)*
147. Tellurium-122
148. Tellurium-123 (E)*
149. Tellurium-124
150. Tellurium-125
151. Tellurium-126
152. Iodine-127
153. Xenon-126 (2E)
154. Xenon-128
155. Xenon-129
156. Xenon-130
157. Xenon-131
158. Xenon-132
159. Xenon-134 (2B)*
160. Caesium-133
161. Barium-132 (2E)*
162. Barium-134
163. Barium-135
164. Barium-136
165. Barium-137
166. Barium-138
167. Lanthanum-139
168. Cerium-136 (2E)*
169. Cerium-138 (2E)*
170. Cerium-140
171. Cerium-142 (A, 2B)*
172. Praseodymium-141
173. Neodymium-142
174. Neodymium-143
175. Neodymium-145 (A)*
176. Neodymium-146 (2B)
     no mass number 147
177. Neodymium-148 (A, 2B)*
     Promethium - No stable isotopes
178. Samarium-144 (2E)
179. Samarium-149 (A)*
180. Samarium-150
     no mass number 151
181. Samarium-152
182. Samarium-154 (2B)*
183. Europium-153
184. Gadolinium-154
185. Gadolinium-155
186. Gadolinium-156
187. Gadolinium-157
188. Gadolinium-158
189. Gadolinium-160 (2B)*
190. Terbium-159
191. Dysprosium-156 (A, 2E)*
192. Dysprosium-158
193. Dysprosium-160
194. Dysprosium-161
195. Dysprosium-162
196. Dysprosium-163
197. Dysprosium-164
198. Holmium-165
199. Erbium-162 (A, 2E)*
200. Erbium-164
201. Erbium-166
202. Erbium-167
203. Erbium-168
204. Erbium-170 (A, 2B)*
205. Thulium-169
206. Ytterbium-168 (A, 2E)*
207. Ytterbium-170
208. Ytterbium-171
209. Ytterbium-172
210. Ytterbium-173
211. Ytterbium-174
212. Ytterbium-176 (A, 2B)*
213. Lutetium-175
214. Hafnium-176
215. Hafnium-177
216. Hafnium-178
217. Hafnium-179
218. Hafnium-180
219. Tantalum-180m (A, B, E, IT)* ^
220. Tantalum-181
221. Tungsten-182 (A)*
222. Tungsten-183 (A)*
223. Tungsten-184 (A)*
224. Tungsten-186 (A, 2B)*
225. Rhenium-185
226. Osmium-184 (A, 2E)*
227. Osmium-187
228. Osmium-188
229. Osmium-189
230. Osmium-190
231. Osmium-192 (A, 2B)*
232. Iridium-191
233. Iridium-193
234. Platinum-192 (A)*
235. Platinum-194
236. Platinum-195
237. Platinum-196
238. Platinum-198 (A, 2B)*
239. Gold-197
240. Mercury-196 (A, 2E)*
241. Mercury-198
242. Mercury-199
243. Mercury-200
244. Mercury-201
245. Mercury-202
246. Mercury-204 (2B)
247. Thallium-203
248. Thallium-205
249. Lead-204 (A)*
250. Lead-206 (A)
251. Lead-207 (A)
252. Lead-208 (A)*
     Bismuth ^^ and above – No stable isotopes
     no mass number 209 and above

Abbreviations for predicted unobserved decay:

A for alpha decay, B for beta decay, 2B for double beta decay, E for electron capture, 2E for double electron capture, IT for isomeric transition, SF for spontaneous fission, * for the nuclides whose half-lives have lower bound.

^ Tantalum-180m is a "metastable isotope" meaning that it is an excited nuclear isomer of tantalum-180. See isotopes of tantalum. However, the half-life of this nuclear isomer is so long that it has never been observed to decay, and it thus occurs as an "observationally nonradioactive" primordial nuclide, as a minor isotope of tantalum. This is the only case of a nuclear isomer which has a half-life so long that it has never been observed to decay. It is thus included in this list.

^^ Bismuth-209 had long been believed to be stable, due to its unusually long half-life of 2.01×10¹⁹ years, which is more than a billion (1000 million) times the age of the universe.