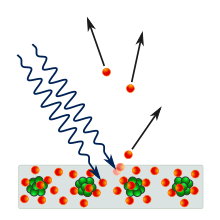
The Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in a state of equilibrium, devised by Ludwig Boltzmann in 1872. The classic example of such a system is a fluid with temperature gradients in space causing heat to flow from hotter regions to colder ones, by the random but biased transport of the particles making up that fluid. In the modern literature the term Boltzmann equation is often used in a more general sense, referring to any kinetic equation that describes the change of a macroscopic quantity in a thermodynamic system, such as energy, charge or particle number.
The equation arises not by analyzing the individual positions and momenta of each particle in the fluid but rather by considering a probability distribution for the position and momentum of a typical particle—that is, the probability that the particle occupies a given very small region of space (mathematically the volume element ) centered at the position , and has momentum nearly equal to a given momentum vector (thus occupying a very small region of momentum space ), at an instant of time.
The Boltzmann equation can be used to determine how physical quantities change, such as heat energy and momentum, when a fluid is in transport. One may also derive other properties characteristic to fluids such as viscosity, thermal conductivity, and electrical conductivity (by treating the charge carriers in a material as a gas).
The equation is a nonlinear integro-differential equation, and the unknown function in the equation is a probability density function in six-dimensional space of a particle position and momentum. The problem of existence and uniqueness of solutions is still not fully resolved, but some recent results are quite promising.
Overview
The phase space and density function
The set of all possible positions r and momenta p is called the phase space of the system; in other words a set of three coordinates for each position coordinate x, y, z, and three more for each momentum component px, py, pz. The entire space is 6-dimensional: a point in this space is (r, p) = (x, y, z, px, py, pz), and each coordinate is parameterized by time t. The small volume ("differential volume element") is written
Since the probability of N molecules which all have r and p within is in question, at the heart of the equation is a quantity f which gives this probability per unit phase-space volume, or probability per unit length cubed per unit momentum cubed, at an instant of time t. This is a probability density function: f(r, p, t), defined so that,
is the number of molecules which all have positions lying within a volume element about r and momenta lying within a momentum space element about p, at time t. Integrating over a region of position space and momentum space gives the total number of particles which have positions and momenta in that region:
which is a 6-fold integral. While f is associated with a number of particles, the phase space is for one-particle (not all of them, which is usually the case with deterministic many-body systems), since only one r and p is in question. It is not part of the analysis to use r1, p1 for particle 1, r2, p2 for particle 2, etc. up to rN, pN for particle N.
It is assumed the particles in the system are identical (so each has an identical mass m). For a mixture of more than one chemical species, one distribution is needed for each, see below.
Principal statement
The general equation can then be written as
where the "force" term corresponds to the forces exerted on the particles by an external influence (not by the particles themselves), the "diff" term represents the diffusion of particles, and "coll" is the collision term – accounting for the forces acting between particles in collisions. Expressions for each term on the right side are provided below.
Note that some authors use the particle velocity v instead of momentum p; they are related in the definition of momentum by p = mv.
The force and diffusion terms
Consider particles described by f, each experiencing an external force F not due to other particles (see the collision term for the latter treatment).
Suppose at time t some number of particles all have position r within element and momentum p within . If a force F instantly acts on each particle, then at time t + Δt their position will be r + Δr = r + pΔt/m and momentum p + Δp = p + FΔt. Then, in the absence of collisions, f must satisfy
Note that we have used the fact that the phase space volume element is constant, which can be shown using Hamilton's equations (see the discussion under Liouville's theorem). However, since collisions do occur, the particle density in the phase-space volume ' changes, so
-
(1)
where Δf is the total change in f. Dividing (1) by Δt and taking the limits Δt → 0 and Δf → 0, we have
-
(2)
The total differential of f is:
-
(3)
where ∇ is the gradient operator, · is the dot product,
is a shorthand for the momentum analogue of ∇, and êx, êy, êz are Cartesian unit vectors.
Final statement
Dividing (3) by dt and substituting into (2) gives:
In this context, F(r, t) is the force field acting on the particles in the fluid, and m is the mass of the particles. The term on the right hand side is added to describe the effect of collisions between particles; if it is zero then the particles do not collide. The collisionless Boltzmann equation, where individual collisions are replaced with long-range aggregated interactions, e.g. Coulomb interactions, is often called the Vlasov equation.
This equation is more useful than the principal one above, yet still incomplete, since f cannot be solved unless the collision term in f is known. This term cannot be found as easily or generally as the others – it is a statistical term representing the particle collisions, and requires knowledge of the statistics the particles obey, like the Maxwell–Boltzmann, Fermi–Dirac or Bose–Einstein distributions.
The collision term (Stosszahlansatz) and molecular chaos
Two-body collision term
A key insight applied by Boltzmann was to determine the collision term resulting solely from two-body collisions between particles that are assumed to be uncorrelated prior to the collision. This assumption was referred to by Boltzmann as the "Stosszahlansatz" and is also known as the "molecular chaos assumption". Under this assumption the collision term can be written as a momentum-space integral over the product of one-particle distribution functions:
where pA and pB are the momenta of any two particles (labeled as A and B for convenience) before a collision, p′A and p′B are the momenta after the collision,
is the magnitude of the relative momenta (see relative velocity for more on this concept), and I(g, Ω) is the differential cross section of the collision, in which the relative momenta of the colliding particles turns through an angle θ into the element of the solid angle dΩ, due to the collision.
Simplifications to the collision term
Since much of the challenge in solving the Boltzmann equation originates with the complex collision term, attempts have been made to "model" and simplify the collision term. The best known model equation is due to Bhatnagar, Gross and Krook. The assumption in the BGK approximation is that the effect of molecular collisions is to force a non-equilibrium distribution function at a point in physical space back to a Maxwellian equilibrium distribution function and that the rate at which this occurs is proportional to the molecular collision frequency. The Boltzmann equation is therefore modified to the BGK form:
where is the molecular collision frequency, and is the local Maxwellian distribution function given the gas temperature at this point in space.
General equation (for a mixture)
For a mixture of chemical species labelled by indices i = 1, 2, 3, ..., n the equation for species i is
where fi = fi(r, pi, t), and the collision term is
where f′ = f′(p′i, t), the magnitude of the relative momenta is
and Iij is the differential cross-section, as before, between particles i and j. The integration is over the momentum components in the integrand (which are labelled i and j). The sum of integrals describes the entry and exit of particles of species i in or out of the phase-space element.
Applications and extensions
Conservation equations
The Boltzmann equation can be used to derive the fluid dynamic conservation laws for mass, charge, momentum, and energy. For a fluid consisting of only one kind of particle, the number density n is given by
The average value of any function A is
Since the conservation equations involve tensors, the Einstein summation convention will be used where repeated indices in a product indicate summation over those indices. Thus and , where is the particle velocity vector. Define as some function of momentum only, which is conserved in a collision. Assume also that the force is a function of position only, and that f is zero for . Multiplying the Boltzmann equation by A and integrating over momentum yields four terms, which, using integration by parts, can be expressed as
where the last term is zero, since A is conserved in a collision. Letting , the mass of the particle, the integrated Boltzmann equation becomes the conservation of mass equation:
where is the mass density, and is the average fluid velocity.
Letting , the momentum of the particle, the integrated Boltzmann equation becomes the conservation of momentum equation:
where is the pressure tensor (the viscous stress tensor plus the hydrostatic pressure).
Letting , the kinetic energy of the particle, the integrated Boltzmann equation becomes the conservation of energy equation:
where is the kinetic thermal energy density, and is the heat flux vector.
Hamiltonian mechanics
In Hamiltonian mechanics, the Boltzmann equation is often written more generally as
where L is the Liouville operator (there is an inconsistent definition between the Liouville operator as defined here and the one in the article linked) describing the evolution of a phase space volume and C is the collision operator. The non-relativistic form of L is
Quantum theory and violation of particle number conservation
It is possible to write down relativistic quantum Boltzmann equations for relativistic quantum systems in which the number of particles is not conserved in collisions. This has several applications in physical cosmology, including the formation of the light elements in Big Bang nucleosynthesis, the production of dark matter and baryogenesis. It is not a priori clear that the state of a quantum system can be characterized by a classical phase space density f. However, for a wide class of applications a well-defined generalization of f exists which is the solution of an effective Boltzmann equation that can be derived from first principles of quantum field theory.
General relativity and astronomy
The Boltzmann equation is of use in galactic dynamics. A galaxy, under certain assumptions, may be approximated as a continuous fluid; its mass distribution is then represented by f; in galaxies, physical collisions between the stars are very rare, and the effect of gravitational collisions can be neglected for times far longer than the age of the universe.
Its generalization in general relativity is
where Γαβγ is the Christoffel symbol of the second kind (this assumes there are no external forces, so that particles move along geodesics in the absence of collisions), with the important subtlety that the density is a function in mixed contravariant-covariant (xi, pi) phase space as opposed to fully contravariant (xi, pi) phase space.
In physical cosmology the fully covariant approach has been used to study the cosmic microwave background radiation. More generically the study of processes in the early universe often attempt to take into account the effects of quantum mechanics and general relativity. In the very dense medium formed by the primordial plasma after the Big Bang, particles are continuously created and annihilated. In such an environment quantum coherence and the spatial extension of the wavefunction can affect the dynamics, making it questionable whether the classical phase space distribution f that appears in the Boltzmann equation is suitable to describe the system. In many cases it is, however, possible to derive an effective Boltzmann equation for a generalized distribution function from first principles of quantum field theory. This includes the formation of the light elements in Big Bang nucleosynthesis, the production of dark matter and baryogenesis.
Solving the equation
Exact solutions to the Boltzmann equations have been proven to exist in some cases; this analytical approach provides insight, but is not generally usable in practical problems.
Instead, numerical methods (including finite elements) are generally used to find approximate solutions to the various forms of the Boltzmann equation. Example applications range from hypersonic aerodynamics in rarefied gas flows to plasma flows.
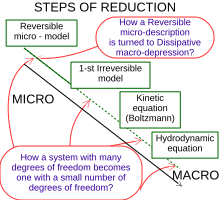
Close to local equilibrium, solution of the Boltzmann equation can be represented by an asymptotic expansion in powers of Knudsen number (the Chapman-Enskog expansion). The first two terms of this expansion give the Euler equations and the Navier-Stokes equations. The higher terms have singularities. The problem of developing mathematically the limiting processes, which lead from the atomistic view (represented by Boltzmann's equation) to the laws of motion of continua, is an important part of Hilbert's sixth problem.







![{\displaystyle {\begin{aligned}N&=\int \limits _{\mathrm {momenta} }{\text{d}}^{3}\mathbf {p} \int \limits _{\mathrm {positions} }{\text{d}}^{3}\mathbf {r} \,f(\mathbf {r} ,\mathbf {p} ,t)\\[5pt]&=\iiint \limits _{\mathrm {momenta} }\quad \iiint \limits _{\mathrm {positions} }f(x,y,z,p_{x},p_{y},p_{z},t)\,{\text{d}}x\,{\text{d}}y\,{\text{d}}z\,{\text{d}}p_{x}\,{\text{d}}p_{y}\,{\text{d}}p_{z}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6a934912a1eafc8d0599defe591b5d69bed1eab)



![{\displaystyle {\begin{aligned}dN_{\mathrm {coll} }&=\left({\frac {\partial f}{\partial t}}\right)_{\mathrm {coll} }\Delta td^{3}\mathbf {r} d^{3}\mathbf {p} \\[5pt]&=f\left(\mathbf {r} +{\frac {\mathbf {p} }{m}}\Delta t,\mathbf {p} +\mathbf {F} \Delta t,t+\Delta t\right)d^{3}\mathbf {r} d^{3}\mathbf {p} -f(\mathbf {r} ,\mathbf {p} ,t)\,d^{3}\mathbf {r} \,d^{3}\mathbf {p} \\[5pt]&=\Delta f\,d^{3}\mathbf {r} \,d^{3}\mathbf {p} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9960aaf286aba914dcba4b7f12302770507e8971)

![{\displaystyle {\begin{aligned}df&={\frac {\partial f}{\partial t}}\,dt+\left({\frac {\partial f}{\partial x}}\,dx+{\frac {\partial f}{\partial y}}\,dy+{\frac {\partial f}{\partial z}}\,dz\right)+\left({\frac {\partial f}{\partial p_{x}}}\,dp_{x}+{\frac {\partial f}{\partial p_{y}}}\,dp_{y}+{\frac {\partial f}{\partial p_{z}}}\,dp_{z}\right)\\[5pt]&={\frac {\partial f}{\partial t}}dt+\nabla f\cdot d\mathbf {r} +{\frac {\partial f}{\partial \mathbf {p} }}\cdot d\mathbf {p} \\[5pt]&={\frac {\partial f}{\partial t}}dt+\nabla f\cdot {\frac {\mathbf {p} }{m}}dt+{\frac {\partial f}{\partial \mathbf {p} }}\cdot \mathbf {F} \,dt\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67b56caf51cf42cf7be79adca5e50c89f25d72e8)


![{\displaystyle \left({\frac {\partial f}{\partial t}}\right)_{\text{coll}}=\iint gI(g,\Omega )[f(\mathbf {r} ,\mathbf {p'} _{A},t)f(\mathbf {r} ,\mathbf {p'} _{B},t)-f(\mathbf {r} ,\mathbf {p} _{A},t)f(\mathbf {r} ,\mathbf {p} _{B},t)]\,d\Omega \,d^{3}\mathbf {p} _{A}\,d^{3}\mathbf {p} _{B},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03cce4b7cc659415722008bf9a14459fb719613)





![{\displaystyle \left({\frac {\partial f_{i}}{\partial t}}\right)_{\mathrm {coll} }=\sum _{j=1}^{n}\iint g_{ij}I_{ij}(g_{ij},\Omega )[f'_{i}f'_{j}-f_{i}f_{j}]\,d\Omega \,d^{3}\mathbf {p'} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69babd72938f7fdae1b4f65310c002d4fa752b2b)

























![\hat{\mathbf{L}}[f]=\mathbf{C}[f], \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/43189f13a6621f7dfff96d4735117f11065461f5)