Speed of sound

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Speed_of_sound

Sound measurements
Characteristic	Symbols
Sound pressure	p, SPL,LPA
Particle velocity	v, SVL
Particle displacement	δ
Sound intensity	I, SIL
Sound power	P, SWL, LWA
Sound energy	W
Sound energy density	w
Sound exposure	E, SEL
Acoustic impedance	Z
Audio frequency	AF
Transmission loss	TL

The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. At 20 °C (68 °F), the speed of sound in air is about 343 metres per second (1,235 km/h; 1,125 ft/s; 767 mph; 667 kn), or a kilometre in 2.9 s or a mile in 4.7 s. It depends strongly on temperature as well as the medium through which a sound wave is propagating. At 0 °C (32 °F), the speed-of-sound is 1,192 km/h, 741 mph.

The speed of sound in an ideal gas depends only on its temperature and composition. The speed has a weak dependence on frequency and pressure in ordinary air, deviating slightly from ideal behavior.

In colloquial speech, speed of sound refers to the speed of sound waves in air. However, the speed of sound varies from substance to substance: typically, sound travels most slowly in gases, faster in liquids, and fastest in solids. For example, while sound travels at 343 m/s in air, it travels at 1,481 m/s in water (almost 4.3 times as fast) and at 5,120 m/s in iron (almost 15 times as fast). In an exceptionally stiff material such as diamond, sound travels at 12,000 metres per second (39,000 ft/s),— about 35 times its speed in air and about the fastest it can travel under normal conditions.

Sound waves in solids are composed of compression waves (just as in gases and liquids), and a different type of sound wave called a shear wave, which occurs only in solids. Shear waves in solids usually travel at different speeds than compression waves, as exhibited in seismology. The speed of compression waves in solids is determined by the medium's compressibility, shear modulus and density. The speed of shear waves is determined only by the solid material's shear modulus and density.

In fluid dynamics, the speed of sound in a fluid medium (gas or liquid) is used as a relative measure for the speed of an object moving through the medium. The ratio of the speed of an object to the speed of sound (in the same medium) is called the object's Mach number. Objects moving at speeds greater than the speed of sound (Mach1) are said to be traveling at supersonic speeds.

History

Sir Isaac Newton's 1687 Principia includes a computation of the speed of sound in air as 979 feet per second (298 m/s). This is too low by about 15%. The discrepancy is due primarily to neglecting the (then unknown) effect of rapidly-fluctuating temperature in a sound wave (in modern terms, sound wave compression and expansion of air is an adiabatic process, not an isothermal process). This error was later rectified by Laplace.

During the 17th century there were several attempts to measure the speed of sound accurately, including attempts by Marin Mersenne in 1630 (1,380 Parisian feet per second), Pierre Gassendi in 1635 (1,473 Parisian feet per second) and Robert Boyle (1,125 Parisian feet per second). In 1709, the Reverend William Derham, Rector of Upminster, published a more accurate measure of the speed of sound, at 1,072 Parisian feet per second. (The Parisian foot was 325 mm. This is longer than the standard "international foot" in common use today, which was officially defined in 1959 as 304.8 mm, making the speed of sound at 20 °C (68 °F) 1,055 Parisian feet per second).

Derham used a telescope from the tower of the church of St. Laurence, Upminster to observe the flash of a distant shotgun being fired, and then measured the time until he heard the gunshot with a half-second pendulum. Measurements were made of gunshots from a number of local landmarks, including North Ockendon church. The distance was known by triangulation, and thus the speed that the sound had travelled was calculated.

Basic concepts

The transmission of sound can be illustrated by using a model consisting of an array of spherical objects interconnected by springs.

In real material terms, the spheres represent the material's molecules and the springs represent the bonds between them. Sound passes through the system by compressing and expanding the springs, transmitting the acoustic energy to neighboring spheres. This helps transmit the energy in-turn to the neighboring sphere's springs (bonds), and so on.

The speed of sound through the model depends on the stiffness/rigidity of the springs, and the mass of the spheres. As long as the spacing of the spheres remains constant, stiffer springs/bonds transmit energy quicker, while larger spheres transmit the energy slower.

In a real material, the stiffness of the springs is known as the "elastic modulus", and the mass corresponds to the material density. Given that all other things being equal (ceteris paribus), sound will travel slower in spongy materials, and faster in stiffer ones. Effects like dispersion and reflection can also be understood using this model.

For instance, sound will travel 1.59 times faster in nickel than in bronze, due to the greater stiffness of nickel at about the same density. Similarly, sound travels about 1.41 times faster in light hydrogen (protium) gas than in heavy hydrogen (deuterium) gas, since deuterium has similar properties but twice the density. At the same time, "compression-type" sound will travel faster in solids than in liquids, and faster in liquids than in gases, because the solids are more difficult to compress than liquids, while liquids, in turn, are more difficult to compress than gases.

Some textbooks mistakenly state that the speed of sound increases with density. This notion is illustrated by presenting data for three materials, such as air, water, and steel, they each have vastly different compressibility, which more than makes up for the density differences. An illustrative example of the two effects is that sound travels only 4.3 times faster in water than air, despite enormous differences in compressibility of the two media. The reason is that the larger density of water, which works to slow sound in water relative to air, nearly makes up for the compressibility differences in the two media.

A practical example can be observed in Edinburgh when the "One o'Clock Gun" is fired at the eastern end of Edinburgh Castle. Standing at the base of the western end of the Castle Rock, the sound of the Gun can be heard through the rock, slightly before it arrives by the air route, partly delayed by the slightly longer route. It is particularly effective if a multi-gun salute such as for "The Queen's Birthday" is being fired.

Compression and shear waves

Pressure-pulse or compression-type wave (longitudinal wave) confined to a plane. This is the only type of sound wave that travels in fluids (gases and liquids). A pressure-type wave may also travel in solids, along with other types of waves (transverse waves, see below)

Transverse wave affecting atoms initially confined to a plane. This additional type of sound wave (additional type of elastic wave) travels only in solids, for it requires a sideways shearing motion which is supported by the presence of elasticity in the solid. The sideways shearing motion may take place in any direction which is at right-angle to the direction of wave-travel (only one shear direction is shown here, at right angles to the plane). Furthermore, the right-angle shear direction may change over time and distance, resulting in different types of polarization of shear-waves

In a gas or liquid, sound consists of compression waves. In solids, waves propagate as two different types. A longitudinal wave is associated with compression and decompression in the direction of travel, and is the same process in gases and liquids, with an analogous compression-type wave in solids. Only compression waves are supported in gases and liquids. An additional type of wave, the transverse wave, also called a shear wave, occurs only in solids because only solids support elastic deformations. It is due to elastic deformation of the medium perpendicular to the direction of wave travel; the direction of shear-deformation is called the "polarization" of this type of wave. In general, transverse waves occur as a pair of orthogonal polarizations.

These different waves (compression waves and the different polarizations of shear waves) may have different speeds at the same frequency. Therefore, they arrive at an observer at different times, an extreme example being an earthquake, where sharp compression waves arrive first and rocking transverse waves seconds later.

The speed of a compression wave in a fluid is determined by the medium's compressibility and density. In solids, the compression waves are analogous to those in fluids, depending on compressibility and density, but with the additional factor of shear modulus which affects compression waves due to off-axis elastic energies which are able to influence effective tension and relaxation in a compression. The speed of shear waves, which can occur only in solids, is determined simply by the solid material's shear modulus and density.

Equations

The speed of sound in mathematical notation is conventionally represented by c, from the Latin celeritas meaning "velocity".

For fluids in general, the speed of sound c is given by the Newton–Laplace equation:

${\displaystyle c={\sqrt {\frac {K_{s}}{\rho }}},}$

where

• K_s is a coefficient of stiffness, the isentropic bulk modulus (or the modulus of bulk elasticity for gases);
• ${\displaystyle \rho }$ is the density.

Thus, the speed of sound increases with the stiffness (the resistance of an elastic body to deformation by an applied force) of the material and decreases with an increase in density. For ideal gases, the bulk modulus K is simply the gas pressure multiplied by the dimensionless adiabatic index, which is about 1.4 for air under normal conditions of pressure and temperature.

For general equations of state, if classical mechanics is used, the speed of sound c can be derived as follows:

Consider the sound wave propagating at speed ${\displaystyle v}$ through a pipe aligned with the ${\displaystyle x}$ axis and with a cross-sectional area of ${\displaystyle A}$. In time interval ${\displaystyle dt}$ it moves length ${\displaystyle dx=vdt}$. In steady state, the mass flow rate ${\displaystyle {\dot {m}}=\rho vA}$ must be the same at the two ends of the tube, therefore the mass flux ${\displaystyle j=\rho v=const.\,\rightarrow vd\rho =-\rho dv}$. Per Newton's second law, the pressure-gradient force provides the acceleration:

${\displaystyle {\begin{aligned}{\frac {dv}{dt}}&=-{\frac {1}{\rho }}{\frac {dP}{dx}}\\\rightarrow dP&=(-\rho dv){\frac {dx}{dt}}=(vd\rho )v\\\rightarrow v^{2}&\equiv c^{2}={\frac {dP}{d\rho }}\end{aligned}}}$

And therefore:

${\displaystyle c={\sqrt {\left({\frac {\partial P}{\partial \rho }}\right)_{s}}},}$

where

• P is the pressure;
• ${\displaystyle \rho }$ is the density and the derivative is taken isentropically, that is, at constant entropy s. This is because a sound wave travels so fast that its propagation can be approximated as an adiabatic process.

If relativistic effects are important, the speed of sound is calculated from the relativistic Euler equations.

In a non-dispersive medium, the speed of sound is independent of sound frequency, so the speeds of energy transport and sound propagation are the same for all frequencies. Air, a mixture of oxygen and nitrogen, constitutes a non-dispersive medium. However, air does contain a small amount of CO₂ which is a dispersive medium, and causes dispersion to air at ultrasonic frequencies (> 28 kHz).

In a dispersive medium, the speed of sound is a function of sound frequency, through the dispersion relation. Each frequency component propagates at its own speed, called the phase velocity, while the energy of the disturbance propagates at the group velocity. The same phenomenon occurs with light waves; see optical dispersion for a description.

Dependence on the properties of the medium

The speed of sound is variable and depends on the properties of the substance through which the wave is travelling. In solids, the speed of transverse (or shear) waves depends on the shear deformation under shear stress (called the shear modulus), and the density of the medium. Longitudinal (or compression) waves in solids depend on the same two factors with the addition of a dependence on compressibility.

In fluids, only the medium's compressibility and density are the important factors, since fluids do not transmit shear stresses. In heterogeneous fluids, such as a liquid filled with gas bubbles, the density of the liquid and the compressibility of the gas affect the speed of sound in an additive manner, as demonstrated in the hot chocolate effect.

In gases, adiabatic compressibility is directly related to pressure through the heat capacity ratio (adiabatic index), while pressure and density are inversely related to the temperature and molecular weight, thus making only the completely independent properties of temperature and molecular structure important (heat capacity ratio may be determined by temperature and molecular structure, but simple molecular weight is not sufficient to determine it).

Sound propagates faster in low molecular weight gases such as helium than it does in heavier gases such as xenon. For monatomic gases, the speed of sound is about 75% of the mean speed that the atoms move in that gas.

For a given ideal gas the molecular composition is fixed, and thus the speed of sound depends only on its temperature. At a constant temperature, the gas pressure has no effect on the speed of sound, since the density will increase, and since pressure and density (also proportional to pressure) have equal but opposite effects on the speed of sound, and the two contributions cancel out exactly. In a similar way, compression waves in solids depend both on compressibility and density—just as in liquids—but in gases the density contributes to the compressibility in such a way that some part of each attribute factors out, leaving only a dependence on temperature, molecular weight, and heat capacity ratio which can be independently derived from temperature and molecular composition (see derivations below). Thus, for a single given gas (assuming the molecular weight does not change) and over a small temperature range (for which the heat capacity is relatively constant), the speed of sound becomes dependent on only the temperature of the gas.

In non-ideal gas behavior regimen, for which the Van der Waals gas equation would be used, the proportionality is not exact, and there is a slight dependence of sound velocity on the gas pressure.

Humidity has a small but measurable effect on the speed of sound (causing it to increase by about 0.1%–0.6%), because oxygen and nitrogen molecules of the air are replaced by lighter molecules of water. This is a simple mixing effect.

Altitude variation and implications for atmospheric acoustics

Density and pressure decrease smoothly with altitude, but temperature (red) does not. The speed of sound (blue) depends only on the complicated temperature variation at altitude and can be calculated from it since isolated density and pressure effects on the speed of sound cancel each other. The speed of sound increases with height in two regions of the stratosphere and thermosphere, due to heating effects in these regions.

In the Earth's atmosphere, the chief factor affecting the speed of sound is the temperature. For a given ideal gas with constant heat capacity and composition, the speed of sound is dependent solely upon temperature; see Details below. In such an ideal case, the effects of decreased density and decreased pressure of altitude cancel each other out, save for the residual effect of temperature.

Since temperature (and thus the speed of sound) decreases with increasing altitude up to 11 km, sound is refracted upward, away from listeners on the ground, creating an acoustic shadow at some distance from the source. The decrease of the speed of sound with height is referred to as a negative sound speed gradient.

However, there are variations in this trend above 11 km. In particular, in the stratosphere above about 20 km, the speed of sound increases with height, due to an increase in temperature from heating within the ozone layer. This produces a positive speed of sound gradient in this region. Still another region of positive gradient occurs at very high altitudes, in the aptly-named thermosphere above 90 km.

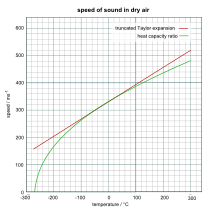
Practical formula for dry air

Approximation of the speed of sound in dry air based on the heat capacity ratio (in green) against the truncated Taylor expansion (in red).

The approximate speed of sound in dry (0% humidity) air, in metres per second, at temperatures near 0 °C, can be calculated from

${\displaystyle c_{\mathrm {air} }=(331.3+0.606\cdot \vartheta )~~~\mathrm {m/s} ,}$

where ${\displaystyle \vartheta }$ is the temperature in degrees Celsius (°C).

This equation is derived from the first two terms of the Taylor expansion of the following more accurate equation:

${\displaystyle c_{\mathrm {air} }=331.3~{\sqrt {1+{\frac {\vartheta }{273.15}}}}~~~~\mathrm {m/s} .}$

Dividing the first part, and multiplying the second part, on the right hand side, by √273.15 gives the exactly equivalent form

${\displaystyle c_{\mathrm {air} }=20.05~{\sqrt {\vartheta +273.15}}~~~~\mathrm {m/s} .}$

which can also be written as

${\displaystyle c_{\mathrm {air} }=20.05~{\sqrt {T}}~~~~\mathrm {m/s} }$

where T denotes the thermodynamic temperature.

The value of 331.3 m/s, which represents the speed at 0 °C (or 273.15 K), is based on theoretical (and some measured) values of the heat capacity ratio, γ, as well as on the fact that at 1 atm real air is very well described by the ideal gas approximation. Commonly found values for the speed of sound at 0 °C may vary from 331.2 to 331.6 due to the assumptions made when it is calculated. If ideal gas γ is assumed to be 7/5 = 1.4 exactly, the 0 °C speed is calculated (see section below) to be 331.3 m/s, the coefficient used above.

This equation is correct to a much wider temperature range, but still depends on the approximation of heat capacity ratio being independent of temperature, and for this reason will fail, particularly at higher temperatures. It gives good predictions in relatively dry, cold, low-pressure conditions, such as the Earth's stratosphere. The equation fails at extremely low pressures and short wavelengths, due to dependence on the assumption that the wavelength of the sound in the gas is much longer than the average mean free path between gas molecule collisions. A derivation of these equations will be given in the following section.

A graph comparing results of the two equations is at right, using the slightly different value of 331.5 m/s for the speed of sound at 0 °C.

Details

Speed of sound in ideal gases and air

For an ideal gas, K (the bulk modulus in equations above, equivalent to C, the coefficient of stiffness in solids) is given by

${\displaystyle K=\gamma \cdot p,}$

thus, from the Newton–Laplace equation above, the speed of sound in an ideal gas is given by

${\displaystyle c={\sqrt {\gamma \cdot {p \over \rho }}},}$

where

• γ is the adiabatic index also known as the isentropic expansion factor. It is the ratio of the specific heat of a gas at constant pressure to that of a gas at constant volume (${\displaystyle C_{p}/C_{v}}$) and arises because a classical sound wave induces an adiabatic compression, in which the heat of the compression does not have enough time to escape the pressure pulse, and thus contributes to the pressure induced by the compression;
• p is the pressure;
• ρ is the density.

Using the ideal gas law to replace p with nRT/V, and replacing ρ with nM/V, the equation for an ideal gas becomes

${\displaystyle c_{\mathrm {ideal} }={\sqrt {\gamma \cdot {p \over \rho }}}={\sqrt {\gamma \cdot R\cdot T \over M}}={\sqrt {\gamma \cdot k\cdot T \over m}},}$

where

• c_ideal is the speed of sound in an ideal gas;
• R (approximately 8.314463 J·K⁻¹·mol⁻¹) is the molar gas constant (universal gas constant);
• k is the Boltzmann constant;
• γ (gamma) is the adiabatic index. At room temperature, where thermal energy is fully partitioned into rotation (rotations are fully excited) but quantum effects prevent excitation of vibrational modes, the value is 7/5 = 1.400 for diatomic molecules, according to kinetic theory. Gamma is actually experimentally measured over a range from 1.3991 to 1.403 at 0 °C, for air. Gamma is exactly 5/3 = 1.6667 for monatomic gases such as noble gases and it is 8/6 = 1.3333 for triatomic molecule gases that, like H2O, are not co-linear (a co-linear triatomic gas such as CO2 is equivalent to a diatomic gas for our purposes here);
• T is the absolute temperature;
• M is the molar mass of the gas. The mean molar mass for dry air is about 0.028,964,5 kg/mol;
• n is the number of moles;
• m is the mass of a single molecule.

This equation applies only when the sound wave is a small perturbation on the ambient condition, and the certain other noted conditions are fulfilled, as noted below. Calculated values for c_air have been found to vary slightly from experimentally determined values.

Newton famously considered the speed of sound before most of the development of thermodynamics and so incorrectly used isothermal calculations instead of adiabatic. His result was missing the factor of γ but was otherwise correct.

Numerical substitution of the above values gives the ideal gas approximation of sound velocity for gases, which is accurate at relatively low gas pressures and densities (for air, this includes standard Earth sea-level conditions). Also, for diatomic gases the use of γ = 1.4000 requires that the gas exists in a temperature range high enough that rotational heat capacity is fully excited (i.e., molecular rotation is fully used as a heat energy "partition" or reservoir); but at the same time the temperature must be low enough that molecular vibrational modes contribute no heat capacity (i.e., insignificant heat goes into vibration, as all vibrational quantum modes above the minimum-energy-mode, have energies too high to be populated by a significant number of molecules at this temperature). For air, these conditions are fulfilled at room temperature, and also temperatures considerably below room temperature (see tables below). See the section on gases in specific heat capacity for a more complete discussion of this phenomenon.

For air, we introduce the shorthand

${\displaystyle R_{*}=R/M_{\mathrm {air} }.}$

In addition, we switch to the Celsius temperature ${\displaystyle \vartheta }$ = T − 273.15, which is useful to calculate air speed in the region near 0 °C (about 273 kelvin). Then, for dry air,

${\displaystyle c_{\mathrm {air} }={\sqrt {\gamma \cdot R_{*}\cdot T}}={\sqrt {\gamma \cdot R_{*}\cdot (\vartheta +273.15)}},}$

${\displaystyle c_{\mathrm {air} }={\sqrt {\gamma \cdot R_{*}\cdot 273.15}}\cdot {\sqrt {1+{\frac {\vartheta }{273.15}}}},}$

where ${\displaystyle \vartheta }$ (theta) is the temperature in degrees Celsius(°C).

Substituting numerical values

${\displaystyle R=8.314\,463~\mathrm {J/(mol\cdot K)} }$

for the molar gas constant in J/mole/Kelvin, and

${\displaystyle M_{\mathrm {air} }=0.028\,964\,5~\mathrm {kg/mol} }$

for the mean molar mass of air, in kg; and using the ideal diatomic gas value of γ = 1.4000, we have

${\displaystyle c_{\mathrm {air} }=331.3~~{\sqrt {1+{\frac {\vartheta }{273.15}}}}~~~\mathrm {m/s} .}$

Finally, Taylor expansion of the remaining square root in ${\displaystyle \vartheta }$ yields

${\displaystyle c_{\mathrm {air} }=331.3~(1+{\frac {\vartheta }{2\cdot 273.15}})~~~\mathrm {m/s} ,}$

${\displaystyle c_{\mathrm {air} }=(331.3+0.606\cdot \vartheta )~~~\mathrm {m/s} .}$

The above derivation includes the first two equations given in the "Practical formula for dry air" section above.

Effects due to wind shear

The speed of sound varies with temperature. Since temperature and sound velocity normally decrease with increasing altitude, sound is refracted upward, away from listeners on the ground, creating an acoustic shadow at some distance from the source. Wind shear of 4 m/(s · km) can produce refraction equal to a typical temperature lapse rate of 7.5 °C/km. Higher values of wind gradient will refract sound downward toward the surface in the downwind direction, eliminating the acoustic shadow on the downwind side. This will increase the audibility of sounds downwind. This downwind refraction effect occurs because there is a wind gradient; the sound is not being carried along by the wind.

For sound propagation, the exponential variation of wind speed with height can be defined as follows:

${\displaystyle U(h)=U(0)h^{\zeta },}$

${\displaystyle {\frac {\mathrm {d} U}{\mathrm {d} H}}(h)=\zeta {\frac {U(h)}{h}},}$

where

• U(h) is the speed of the wind at height h;
• ζ is the exponential coefficient based on ground surface roughness, typically between 0.08 and 0.52;
• dU/dH(h) is the expected wind gradient at height h.

In the 1862 American Civil War Battle of Iuka, an acoustic shadow, believed to have been enhanced by a northeast wind, kept two divisions of Union soldiers out of the battle, because they could not hear the sounds of battle only 10 km (six miles) downwind.

Tables

In the standard atmosphere:

• T₀ is 273.15 K (= 0 °C = 32 °F), giving a theoretical value of 331.3 m/s (= 1086.9 ft/s = 1193 km/h = 741.1 mph = 644.0 kn). Values ranging from 331.3 to 331.6 m/s may be found in reference literature, however;
• T₂₀ is 293.15 K (= 20 °C = 68 °F), giving a value of 343.2 m/s (= 1126.0 ft/s = 1236 km/h = 767.8 mph = 667.2 kn);
• T₂₅ is 298.15 K (= 25 °C = 77 °F), giving a value of 346.1 m/s (= 1135.6 ft/s = 1246 km/h = 774.3 mph = 672.8 kn).

In fact, assuming an ideal gas, the speed of sound c depends on temperature only, not on the pressure or density (since these change in lockstep for a given temperature and cancel out). Air is almost an ideal gas. The temperature of the air varies with altitude, giving the following variations in the speed of sound using the standard atmosphere—actual conditions may vary.

Effect of temperature on properties of air

Tempe­rature, T (°C)	Speed of sound, c (m/s)	Density of air, ρ (kg/m3)	Characteristic specific acoustic impedance, z0 (Pa·s/m)
35	351.88	1.1455	403.2
30	349.02	1.1644	406.5
25	346.13	1.1839	409.4
20	343.21	1.2041	413.3
15	340.27	1.2250	416.9
10	337.31	1.2466	420.5
5	334.32	1.2690	424.3
0	331.30	1.2922	428.0
−5	328.25	1.3163	432.1
−10	325.18	1.3413	436.1
−15	322.07	1.3673	440.3
−20	318.94	1.3943	444.6
−25	315.77	1.4224	449.1

Given normal atmospheric conditions, the temperature, and thus speed of sound, varies with altitude:

Altitude	Temperature	m/s	km/h	mph	kn
Sea level	15 °C (59 °F)	340	1,225	761	661
11,000 m−20,000 m (Cruising altitude of commercial jets, and first supersonic flight)	−57 °C (−70 °F)	295	1,062	660	573
29,000 m (Flight of X-43A)	−48 °C (−53 °F)	301	1,083	673	585

Effect of frequency and gas composition

General physical considerations

The medium in which a sound wave is travelling does not always respond adiabatically, and as a result, the speed of sound can vary with frequency.

The limitations of the concept of speed of sound due to extreme attenuation are also of concern. The attenuation which exists at sea level for high frequencies applies to successively lower frequencies as atmospheric pressure decreases, or as the mean free path increases. For this reason, the concept of speed of sound (except for frequencies approaching zero) progressively loses its range of applicability at high altitudes. The standard equations for the speed of sound apply with reasonable accuracy only to situations in which the wavelength of the sound wave is considerably longer than the mean free path of molecules in a gas.

The molecular composition of the gas contributes both as the mass (M) of the molecules, and their heat capacities, and so both have an influence on speed of sound. In general, at the same molecular mass, monatomic gases have slightly higher speed of sound (over 9% higher) because they have a higher γ (5/3 = 1.66...) than diatomics do (7/5 = 1.4). Thus, at the same molecular mass, the speed of sound of a monatomic gas goes up by a factor of

${\displaystyle {c_{\mathrm {gas,monatomic} } \over c_{\mathrm {gas,diatomic} }}={\sqrt {{5/3} \over {7/5}}}={\sqrt {25 \over 21}}=1.091\ldots }$

This gives the 9% difference, and would be a typical ratio for speeds of sound at room temperature in helium vs. deuterium, each with a molecular weight of 4. Sound travels faster in helium than deuterium because adiabatic compression heats helium more since the helium molecules can store heat energy from compression only in translation, but not rotation. Thus helium molecules (monatomic molecules) travel faster in a sound wave and transmit sound faster. (Sound travels at about 70% of the mean molecular speed in gases; the figure is 75% in monatomic gases and 68% in diatomic gases).

Note that in this example we have assumed that temperature is low enough that heat capacities are not influenced by molecular vibration. However, vibrational modes simply cause gammas which decrease toward 1, since vibration modes in a polyatomic gas give the gas additional ways to store heat which do not affect temperature, and thus do not affect molecular velocity and sound velocity. Thus, the effect of higher temperatures and vibrational heat capacity acts to increase the difference between the speed of sound in monatomic vs. polyatomic molecules, with the speed remaining greater in monatomics.

Practical application to air

By far, the most important factor influencing the speed of sound in air is temperature. The speed is proportional to the square root of the absolute temperature, giving an increase of about 0.6 m/s per degree Celsius. For this reason, the pitch of a musical wind instrument increases as its temperature increases.

The speed of sound is raised by humidity. The difference between 0% and 100% humidity is about 1.5 m/s at standard pressure and temperature, but the size of the humidity effect increases dramatically with temperature.

The dependence on frequency and pressure are normally insignificant in practical applications. In dry air, the speed of sound increases by about 0.1 m/s as the frequency rises from 10 Hz to 100 Hz. For audible frequencies above 100 Hz it is relatively constant. Standard values of the speed of sound are quoted in the limit of low frequencies, where the wavelength is large compared to the mean free path.

As shown above, the approximate value 1000/3 = 333.33... m/s is exact a little below 5 °C and is a good approximation for all "usual" outside temperatures (in temperate climates, at least), hence the usual rule of thumb to determine how far lightning has struck: count the seconds from the start of the lightning flash to the start of the corresponding roll of thunder and divide by 3: the result is the distance in kilometers to the nearest point of the lightning bolt.

Mach number

Main article: Mach number

Mach number, a useful quantity in aerodynamics, is the ratio of air speed to the local speed of sound. At altitude, for reasons explained, Mach number is a function of temperature.

Aircraft flight instruments, however, operate using pressure differential to compute Mach number, not temperature. The assumption is that a particular pressure represents a particular altitude and, therefore, a standard temperature. Aircraft flight instruments need to operate this way because the stagnation pressure sensed by a Pitot tube is dependent on altitude as well as speed.

Experimental methods

A range of different methods exist for the measurement of sound in air.

The earliest reasonably accurate estimate of the speed of sound in air was made by William Derham and acknowledged by Isaac Newton. Derham had a telescope at the top of the tower of the Church of St Laurence in Upminster, England. On a calm day, a synchronized pocket watch would be given to an assistant who would fire a shotgun at a pre-determined time from a conspicuous point some miles away, across the countryside. This could be confirmed by telescope. He then measured the interval between seeing gunsmoke and arrival of the sound using a half-second pendulum. The distance from where the gun was fired was found by triangulation, and simple division (distance/time) provided velocity. Lastly, by making many observations, using a range of different distances, the inaccuracy of the half-second pendulum could be averaged out, giving his final estimate of the speed of sound. Modern stopwatches enable this method to be used today over distances as short as 200–400 metres, and not needing something as loud as a shotgun.

Single-shot timing methods

The simplest concept is the measurement made using two microphones and a fast recording device such as a digital storage scope. This method uses the following idea.

If a sound source and two microphones are arranged in a straight line, with the sound source at one end, then the following can be measured:

1. The distance between the microphones (x), called microphone basis.
2. The time of arrival between the signals (delay) reaching the different microphones (t).

Then v = x/t.

Other methods

In these methods, the time measurement has been replaced by a measurement of the inverse of time (frequency).

Kundt's tube is an example of an experiment which can be used to measure the speed of sound in a small volume. It has the advantage of being able to measure the speed of sound in any gas. This method uses a powder to make the nodes and antinodes visible to the human eye. This is an example of a compact experimental setup.

A tuning fork can be held near the mouth of a long pipe which is dipping into a barrel of water. In this system it is the case that the pipe can be brought to resonance if the length of the air column in the pipe is equal to (1 + 2n)λ/4 where n is an integer. As the antinodal point for the pipe at the open end is slightly outside the mouth of the pipe it is best to find two or more points of resonance and then measure half a wavelength between these.

Here it is the case that v = fλ.

High-precision measurements in air

The effect of impurities can be significant when making high-precision measurements. Chemical desiccants can be used to dry the air, but will, in turn, contaminate the sample. The air can be dried cryogenically, but this has the effect of removing the carbon dioxide as well; therefore many high-precision measurements are performed with air free of carbon dioxide rather than with natural air. A 2002 review found that a 1963 measurement by Smith and Harlow using a cylindrical resonator gave "the most probable value of the standard speed of sound to date." The experiment was done with air from which the carbon dioxide had been removed, but the result was then corrected for this effect so as to be applicable to real air. The experiments were done at 30 °C but corrected for temperature in order to report them at 0 °C. The result was 331.45 ± 0.01 m/s for dry air at STP, for frequencies from 93 Hz to 1,500 Hz.

Non-gaseous media

Speed of sound in solids

Three-dimensional solids

In a solid, there is a non-zero stiffness both for volumetric deformations and shear deformations. Hence, it is possible to generate sound waves with different velocities dependent on the deformation mode. Sound waves generating volumetric deformations (compression) and shear deformations (shearing) are called pressure waves (longitudinal waves) and shear waves (transverse waves), respectively. In earthquakes, the corresponding seismic waves are called P-waves (primary waves) and S-waves (secondary waves), respectively. The sound velocities of these two types of waves propagating in a homogeneous 3-dimensional solid are respectively given by

${\displaystyle c_{\mathrm {solid,p} }={\sqrt {\frac {K+{\frac {4}{3}}G}{\rho }}}={\sqrt {\frac {E(1-\nu )}{\rho (1+\nu )(1-2\nu )}}},}$

${\displaystyle c_{\mathrm {solid,s} }={\sqrt {\frac {G}{\rho }}},}$

where

• K is the bulk modulus of the elastic materials;
• G is the shear modulus of the elastic materials;
• E is the Young's modulus;
• ρ is the density;
• ν is Poisson's ratio.

The last quantity is not an independent one, as E = 3K(1 − 2ν). Note that the speed of pressure waves depends both on the pressure and shear resistance properties of the material, while the speed of shear waves depends on the shear properties only.

Typically, pressure waves travel faster in materials than do shear waves, and in earthquakes this is the reason that the onset of an earthquake is often preceded by a quick upward-downward shock, before arrival of waves that produce a side-to-side motion. For example, for a typical steel alloy, K = 170 GPa, G = 80 GPa and ρ = 7,700 kg/m³, yielding a compressional speed c_solid,p of 6,000 m/s. This is in reasonable agreement with c_solid,p measured experimentally at 5,930 m/s for a (possibly different) type of steel. The shear speed c_solid,s is estimated at 3,200 m/s using the same numbers.

One-dimensional solids

The speed of sound for pressure waves in stiff materials such as metals is sometimes given for "long rods" of the material in question, in which the speed is easier to measure. In rods where their diameter is shorter than a wavelength, the speed of pure pressure waves may be simplified and is given by:

${\displaystyle c_{\mathrm {solid} }={\sqrt {\frac {E}{\rho }}},}$

where E is Young's modulus. This is similar to the expression for shear waves, save that Young's modulus replaces the shear modulus. This speed of sound for pressure waves in long rods will always be slightly less than the same speed in homogeneous 3-dimensional solids, and the ratio of the speeds in the two different types of objects depends on Poisson's ratio for the material.

Speed of sound in liquids

Speed of sound in water vs temperature.

In a fluid, the only non-zero stiffness is to volumetric deformation (a fluid does not sustain shear forces).

Hence the speed of sound in a fluid is given by

${\displaystyle c_{\mathrm {fluid} }={\sqrt {\frac {K}{\rho }}},}$

where K is the bulk modulus of the fluid.

Water

In fresh water, sound travels at about 1481 m/s at 20 °C (see the External Links section below for online calculators). Applications of underwater sound can be found in sonar, acoustic communication and acoustical oceanography.

Seawater

See also: Sound speed profile

Speed of sound as a function of depth at a position north of Hawaii in the Pacific Ocean derived from the 2005 World Ocean Atlas. The SOFAR channel spans the minimum in the speed of sound at about 750-m depth.

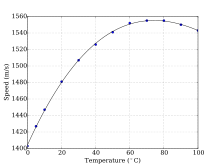
In salt water that is free of air bubbles or suspended sediment, sound travels at about 1500 m/s (1500.235 m/s at 1000 kilopascals, 10 °C and 3% salinity by one method). The speed of sound in seawater depends on pressure (hence depth), temperature (a change of 1 °C ~ 4 m/s), and salinity (a change of 1‰ ~ 1 m/s), and empirical equations have been derived to accurately calculate the speed of sound from these variables. Other factors affecting the speed of sound are minor. Since in most ocean regions temperature decreases with depth, the profile of the speed of sound with depth decreases to a minimum at a depth of several hundred metres. Below the minimum, sound speed increases again, as the effect of increasing pressure overcomes the effect of decreasing temperature (right). For more information see Dushaw et al.

An empirical equation for the speed of sound in sea water is provided by Mackenzie:

${\displaystyle c(T,S,z)=a_{1}+a_{2}T+a_{3}T^{2}+a_{4}T^{3}+a_{5}(S-35)+a_{6}z+a_{7}z^{2}+a_{8}T(S-35)+a_{9}Tz^{3},}$

where

• T is the temperature in degrees Celsius;
• S is the salinity in parts per thousand;
• z is the depth in metres.

The constants a₁, a₂, ..., a₉ are

${\displaystyle {\begin{aligned}a_{1}&=1,448.96,&a_{2}&=4.591,&a_{3}&=-5.304\times 10^{-2},\\a_{4}&=2.374\times 10^{-4},&a_{5}&=1.340,&a_{6}&=1.630\times 10^{-2},\\a_{7}&=1.675\times 10^{-7},&a_{8}&=-1.025\times 10^{-2},&a_{9}&=-7.139\times 10^{-13},\end{aligned}}}$

with check value 1550.744 m/s for T = 25 °C, S = 35 parts per thousand, z = 1,000 m. This equation has a standard error of 0.070 m/s for salinity between 25 and 40 ppt.

(Note: The Sound Speed vs. Depth graph does not correlate directly to the MacKenzie formula. This is due to the fact that the temperature and salinity varies at different depths. When T and S are held constant, the formula itself is always increasing with depth.)

Other equations for the speed of sound in sea water are accurate over a wide range of conditions, but are far more complicated, e.g., that by V. A. Del Grosso and the Chen-Millero-Li Equation.

Speed of sound in plasma

The speed of sound in a plasma for the common case that the electrons are hotter than the ions (but not too much hotter) is given by the formula

${\displaystyle c_{s}=(\gamma ZkT_{\mathrm {e} }/m_{\mathrm {i} })^{1/2}=90.85(\gamma ZT_{e}/\mu )^{1/2}~\mathrm {m/s} ,}$

where

• m_i is the ion mass;
• μ is the ratio of ion mass to proton mass μ = m_i/m_p;
• T_e is the electron temperature;
• Z is the charge state;
• k is Boltzmann constant;
• γ is the adiabatic index.

In contrast to a gas, the pressure and the density are provided by separate species: the pressure by the electrons and the density by the ions. The two are coupled through a fluctuating electric field.

Gradients

Main article: Sound speed gradient

When sound spreads out evenly in all directions in three dimensions, the intensity drops in proportion to the inverse square of the distance. However, in the ocean, there is a layer called the 'deep sound channel' or SOFAR channel which can confine sound waves at a particular depth.

In the SOFAR channel, the speed of sound is lower than that in the layers above and below. Just as light waves will refract towards a region of higher index, sound waves will refract towards a region where their speed is reduced. The result is that sound gets confined in the layer, much the way light can be confined to a sheet of glass or optical fiber. Thus, the sound is confined in essentially two dimensions. In two dimensions the intensity drops in proportion to only the inverse of the distance. This allows waves to travel much further before being undetectably faint.

A similar effect occurs in the atmosphere. Project Mogul successfully used this effect to detect a nuclear explosion at a considerable distance.

Speed of electricity

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Speed_of_electricity 

The word electricity refers generally to the movement of electrons (or other charge carriers) through a conductor in the presence of a potential difference or an electric field. The speed of this flow has multiple meanings. In everyday electrical and electronic devices, the signals travel as electromagnetic waves typically at 50%–99% of the speed of light, while the electrons themselves move much more slowly, see Drift velocity and Electron mobility.

Electromagnetic waves

Main article: Wave propagation speed

The speed at which energy or signals travel down a cable is actually the speed of the electromagnetic wave traveling along (guided by) the cable. I.e., a cable is a form of a waveguide. The propagation of the wave is affected by the interaction with the material(s) in and surrounding the cable, caused by the presence of electric charge carriers (interacting with the electric field component) and magnetic dipoles (interacting with the magnetic field component). These interactions are typically described using mean field theory by the permeability and the permittivity of the materials involved. The energy/signal usually flows overwhelmingly outside the electric conductor of a cable; the purpose of the conductor is thus not to conduct energy, but to guide the energy-carrying wave.

Speed of electromagnetic waves in good dielectrics

The speed of electromagnetic waves in a low-loss dielectric is given by

${\displaystyle \quad v={\frac {1}{\sqrt {\epsilon \mu }}}={\frac {c}{\sqrt {\epsilon _{r}\mu _{r}}}}}$ .

where

${\displaystyle \quad c}$ = speed of light in vacuum.

${\displaystyle \quad \mu _{0}}$ = the permeability of free space = 4π x 10⁻⁷ H/m.

${\displaystyle \quad \mu _{r}}$ = relative magnetic permeability of the material. Usually in good dielectrics, eg. vacuum, air, Teflon, ${\displaystyle \mu _{r}=1}$.

${\displaystyle \quad \mu }$ = ${\displaystyle \mu _{r}}$ ${\displaystyle \mu _{0}}$.

${\displaystyle \quad \epsilon _{0}}$ = the permitivity of free space = 8.854 x 10⁻¹² F/m.

${\displaystyle \quad \epsilon _{r}}$ = relative permitivity of the material. Usually in good conductors eg. copper, silver, gold, ${\displaystyle \epsilon _{r}=1}$.

${\displaystyle \quad \epsilon }$ = ${\displaystyle \epsilon _{r}}$ ${\displaystyle \epsilon _{0}}$.

Speed of electromagnetic waves in good conductors

The speed of electromagnetic waves in a good conductor is given by

${\displaystyle \quad v={\sqrt {\frac {2\omega }{\sigma \mu }}}={\sqrt {\frac {4\pi }{\sigma _{c}\mu _{0}}}}{\sqrt {\frac {f}{\sigma _{r}\mu _{r}}}}\approx \left(0.41~\mathrm {m/s} \right){\sqrt {\frac {f/(1~\mathrm {Hz} )}{\sigma _{r}\mu _{r}}}}}$.

where

${\displaystyle \quad f}$ = frequency.

${\displaystyle \quad \omega }$ = angular frequency = 2πf.

${\displaystyle \quad \sigma _{c}}$ = conductivity of annealed copper = 5.96×10⁷ S/m.

${\displaystyle \quad \sigma _{r}}$ = conductivity of the material relative to the conductivity of copper. For hard drawn copper ${\displaystyle \sigma _{r}}$ may be as low as 0.97.

${\displaystyle \quad \sigma }$ = ${\displaystyle \sigma _{r}\sigma _{c}}$.

and permeability is defined as above in § Speed of electromagnetic waves in good dielectrics

${\displaystyle \quad \mu _{0}}$ = the permeability of free space = 4π x 10⁻⁷ H/m.

${\displaystyle \quad \mu _{r}}$ = relative magnetic permeability of the material. Magnetically conductive materials such as copper typically have a ${\displaystyle \mu _{r}}$ near 1.

${\displaystyle \quad \mu }$ = ${\displaystyle \mu _{r}}$ ${\displaystyle \mu _{0}}$.

In copper at 60 Hz, ${\displaystyle v\approx }$ 3.2 m/s. As a consequence of Snell's Law and the extremely low speed, electromagnetic waves always enter good conductors in a direction that is within a milliradian of normal to the surface, regardless of the angle of incidence. This velocity is the speed with which electromagnetic waves penetrate into the conductor and is not the drift velocity of the conduction electrons.

Electromagnetic waves in circuits

In the theoretical investigation of electric circuits, the velocity of propagation of the electromagnetic field through space is usually not considered; the field is assumed, as a precondition, to be present throughout space. The magnetic component of the field is considered to be in phase with the current, and the electric component is considered to be in phase with the voltage. The electric field starts at the conductor, and propagates through space at the velocity of light (which depends on the material it is traveling through). Note that the electromagnetic fields do not move through space. It is the electromagnetic energy that moves; the corresponding fields simply grow and decline in a region of space in response to the flow of energy. At any point in space, the electric field corresponds not to the condition of the electric energy flow at that moment, but to that of the flow at a moment earlier. The latency is determined by the time required for the field to propagate from the conductor to the point under consideration. In other words, the greater the distance from the conductor, the more the electric field lags.

Since the velocity of propagation is very high – about 300,000 kilometers per second – the wave of an alternating or oscillating current, even of high frequency, is of considerable length. At 60 cycles per second, the wavelength is 5,000 kilometers, and even at 100,000 hertz, the wavelength is 3 kilometers. This is a very large distance compared to those typically used in field measurement and application.

The important part of the electric field of a conductor extends to the return conductor, which usually is only a few feet distant. At greater distance, the aggregate field can be approximated by the differential field between conductor and return conductor, which tend to cancel. Hence, the intensity of the electric field is usually inappreciable at a distance which is still small compared to the wavelength. Within the range in which an appreciable field exists, this field is practically in phase with the flow of energy in the conductor. That is, the velocity of propagation has no appreciable effect unless the return conductor is very distant, or entirely absent, or the frequency is so high that the distance to the return conductor is an appreciable portion of the wavelength.

Electric drift

Main article: Drift velocity

The drift velocity deals with the average velocity of a particle, such as an electron, due to an electric field. In general, an electron will propagate randomly in a conductor at the Fermi velocity. Free electrons in a conductor follow a random path. Without the presence of an electric field, the electrons have no net velocity. When a DC voltage is applied, the electron drift velocity will increase in speed proportionally to the strength of the electric field. The drift velocity in a 2 mm diameter copper wire in 1 ampere current is approximately 8 cm per hour. AC voltages cause no net movement; the electrons oscillate back and forth in response to the alternating electric field.

Speed of gravity

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Speed_of_gravity 

 

Speed of gravity

Exact values
metres per second	299792458
Approximate values (to three significant digits)
kilometres per hour	1080000000
miles per second	186000
miles per hour	671000000
astronomical units per day	173
parsecs per year	0.307
Approximate light signal travel times
Distance	Time
one foot	1.0 ns
one metre	3.3 ns
from geostationary orbit to Earth	119 ms
the length of Earth's equator	134 ms
from Moon to Earth	1.3 s
from Sun to Earth (1 AU)	8.3 min
one light year	1.0 year
one parsec	3.26 years
from nearest star to Sun (1.3 pc)	4.2 years
from the nearest galaxy (the Canis Major Dwarf Galaxy) to Earth	25000 years
across the Milky Way	100000 years
from the Andromeda Galaxy to Earth	2.5 million years

In classical theories of gravitation, the changes in a gravitational field propagate. A change in the distribution of energy and momentum of matter results in subsequent alteration, at a distance, of the gravitational field which it produces. In the relativistic sense, the "speed of gravity" refers to the speed of a gravitational wave, which, as predicted by general relativity and confirmed by observation of the GW170817 neutron star merger, is the same speed as the speed of light (c).

Introduction

The speed of gravitational waves in the general theory of relativity is equal to the speed of light in a vacuum, c. Within the theory of special relativity, the constant c is not only about light; instead it is the highest possible speed for any interaction in nature. Formally, c is a conversion factor for changing the unit of time to the unit of space. This makes it the only speed which does not depend either on the motion of an observer or a source of light and / or gravity. Thus, the speed of "light" is also the speed of gravitational waves, and further the speed of any massless particle. Such particles include the gluon (carrier of the strong force), the photons that make up light (hence carrier of electromagnetic force), and the hypothetical gravitons (which are the presumptive field particles associated with gravity; however, an understanding of the graviton, if any exist, requires an as-yet unavailable theory of quantum gravity).

Static fields

The speed of physical changes in a gravitational or electromagnetic field should not be confused with "changes" in the behavior of static fields that are due to pure observer-effects. These changes in direction of a static field are, because of relativistic considerations, the same for an observer when a distant charge is moving, as when an observer (instead) decides to move with respect to a distant charge. Thus, constant motion of an observer with regard to a static charge and its extended static field (either a gravitational or electric field) does not change the field. For static fields, such as the electrostatic field connected with electric charge, or the gravitational field connected to a massive object, the field extends to infinity, and does not propagate. Motion of an observer does not cause the direction of such a field to change, and by symmetrical considerations, changing the observer frame so that the charge appears to be moving at a constant rate, also does not cause the direction of its field to change, but requires that it continue to "point" in the direction of the charge, at all distances from the charge.

The consequence of this is that static fields (either electric or gravitational) always point directly to the actual position of the bodies that they are connected to, without any delay that is due to any "signal" traveling (or propagating) from the charge, over a distance to an observer. This remains true if the charged bodies and their observers are made to "move" (or not), by simply changing reference frames. This fact sometimes causes confusion about the "speed" of such static fields, which sometimes appear to change infinitely quickly when the changes in the field are mere artifacts of the motion of the observer, or of observation.

In such cases, nothing actually changes infinitely quickly, save the point of view of an observer of the field. For example, when an observer begins to move with respect to a static field that already extends over light years, it appears as though "immediately" the entire field, along with its source, has begun moving at the speed of the observer. This, of course, includes the extended parts of the field. However, this "change" in the apparent behavior of the field source, along with its distant field, does not represent any sort of propagation that is faster than light.

Newtonian gravitation

Isaac Newton's formulation of a gravitational force law requires that each particle with mass respond instantaneously to every other particle with mass irrespective of the distance between them. In modern terms, Newtonian gravitation is described by the Poisson equation, according to which, when the mass distribution of a system changes, its gravitational field instantaneously adjusts. Therefore, the theory assumes the speed of gravity to be infinite. This assumption was adequate to account for all phenomena with the observational accuracy of that time. It was not until the 19th century that an anomaly in astronomical observations which could not be reconciled with the Newtonian gravitational model of instantaneous action was noted: the French astronomer Urbain Le Verrier determined in 1859 that the elliptical orbit of Mercury precesses at a significantly different rate from that predicted by Newtonian theory.

Laplace

The first attempt to combine a finite gravitational speed with Newton's theory was made by Laplace in 1805. Based on Newton's force law he considered a model in which the gravitational field is defined as a radiation field or fluid. Changes in the motion of the attracting body are transmitted by some sort of waves. Therefore, the movements of the celestial bodies should be modified in the order v/c, where v is the relative speed between the bodies and c is the speed of gravity. The effect of a finite speed of gravity goes to zero as c goes to infinity, but not as 1/c² as it does in modern theories. This led Laplace to conclude that the speed of gravitational interactions is at least 7×10⁶ times the speed of light. This velocity was used by many in the 19th century to criticize any model based on a finite speed of gravity, like electrical or mechanical explanations of gravitation.

Figure 1. One possible consequence of combining Newtonian Mechanics with a finite speed of gravity. If we assume a Fatio/La Sage mechanism for the origin of gravity, the Earth spirals outwards with violation of conservation of energy and of angular momentum. In 1776, Laplace considered a different mechanism whereby gravity is caused by "the impulse of a fluid directed towards the centre of the attracting body". In such a theory, a finite speed of gravity results in the Earth spiraling inwards towards the Sun.

From a modern point of view, Laplace's analysis is incorrect. Not knowing about Lorentz invariance of static fields, Laplace assumed that when an object like the Earth is moving around the Sun, the attraction of the Earth would not be toward the instantaneous position of the Sun, but toward where the Sun had been if its position was retarded using the relative velocity (this retardation actually does happen with the optical position of the Sun, and is called annual solar aberration). Putting the Sun immobile at the origin, when the Earth is moving in an orbit of radius R with velocity v presuming that the gravitational influence moves with velocity c, moves the Sun's true position ahead of its optical position, by an amount equal to vR/c, which is the travel time of gravity from the sun to the Earth times the relative velocity of the sun and the Earth. As seem in Fig. 1, the pull of gravity (if it behaved like a wave, such as light) would then always be displaced in the direction of the Earth's velocity, so that the Earth would always be pulled toward the optical position of the Sun, rather than its actual position. This would cause a pull ahead of the Earth, which would cause the orbit of the Earth to spiral outward. Such an outspiral would be suppressed by an amount v/c compared to the force which keeps the Earth in orbit; and since the Earth's orbit is observed to be stable, Laplace's c must be very large. As is now known, it may be considered to be infinite in the limit of straight-line motion, since as a static influence it is instantaneous at distance when seen by observers at constant transverse velocity. For orbits in which velocity (direction of speed) changes slowly, it is almost infinite.

The attraction toward an object moving with a steady velocity is towards its instantaneous position with no delay, for both gravity and electric charge. In a field equation consistent with special relativity (i.e., a Lorentz invariant equation), the attraction between static charges moving with constant relative velocity is always toward the instantaneous position of the charge (in this case, the "gravitational charge" of the Sun), not the time-retarded position of the Sun. When an object is moving in orbit at a steady speed but changing velocity v, the effect on the orbit is order v²/c², and the effect preserves energy and angular momentum, so that orbits do not decay.

Electrodynamical analogies

Early theories

At the end of the 19th century, many tried to combine Newton's force law with the established laws of electrodynamics, like those of Wilhelm Eduard Weber, Carl Friedrich Gauss, Bernhard Riemann and James Clerk Maxwell. Those theories are not invalidated by Laplace's critique, because although they are based on finite propagation speeds, they contain additional terms which maintain the stability of the planetary system. Those models were used to explain the perihelion advance of Mercury, but they could not provide exact values. One exception was Maurice Lévy in 1890, who succeeded in doing so by combining the laws of Weber and Riemann, whereby the speed of gravity is equal to the speed of light. However, those hypotheses were rejected.

However, a more important variation of those attempts was the theory of Paul Gerber, who derived in 1898 the identical formula, which was also derived later by Einstein for the perihelion advance. Based on that formula, Gerber calculated a propagation speed for gravity of 305000 km/s, i.e. practically the speed of light. But Gerber's derivation of the formula was faulty, i.e., his conclusions did not follow from his premises, and therefore many (including Einstein) did not consider it to be a meaningful theoretical effort. Additionally, the value it predicted for the deflection of light in the gravitational field of the sun was too high by the factor 3/2.

Lorentz

In 1900, Hendrik Lorentz tried to explain gravity on the basis of his ether theory and the Maxwell equations. After proposing (and rejecting) a Le Sage type model, he assumed like Ottaviano-Fabrizio Mossotti and Johann Karl Friedrich Zöllner that the attraction of opposite charged particles is stronger than the repulsion of equal charged particles. The resulting net force is exactly what is known as universal gravitation, in which the speed of gravity is that of light. This leads to a conflict with the law of gravitation by Isaac Newton, in which it was shown by Pierre-Simon Laplace that a finite speed of gravity leads to some sort of aberration and therefore makes the orbits unstable. However, Lorentz showed that the theory is not concerned by Laplace's critique, because due to the structure of the Maxwell equations only effects in the order v²/c² arise. But Lorentz calculated that the value for the perihelion advance of Mercury was much too low. He wrote:

The special form of these terms may perhaps be modified. Yet, what has been said is sufficient to show that gravitation may be attributed to actions which are propagated with no greater velocity than that of light.

In 1908, Henri Poincaré examined the gravitational theory of Lorentz and classified it as compatible with the relativity principle, but (like Lorentz) he criticized the inaccurate indication of the perihelion advance of Mercury.

Lorentz covariant models

Henri Poincaré argued in 1904 that a propagation speed of gravity which is greater than c would contradict the concept of local time (based on synchronization by light signals) and the principle of relativity. He wrote:

What would happen if we could communicate by signals other than those of light, the velocity of propagation of which differed from that of light? If, after having regulated our watches by the optimal method, we wished to verify the result by means of these new signals, we should observe discrepancies due to the common translatory motion of the two stations. And are such signals inconceivable, if we take the view of Laplace, that universal gravitation is transmitted with a velocity a million times as great as that of light?

However, in 1905 Poincaré calculated that changes in the gravitational field can propagate with the speed of light if it is presupposed that such a theory is based on the Lorentz transformation. He wrote:

Laplace showed in effect that the propagation is either instantaneous or much faster than that of light. However, Laplace examined the hypothesis of finite propagation velocity ceteris non mutatis [all other things being unchanged]; here, on the contrary, this hypothesis is conjoined with many others, and it may be that between them a more or less perfect compensation takes place. The application of the Lorentz transformation has already provided us with numerous examples of this.

Similar models were also proposed by Hermann Minkowski (1907) and Arnold Sommerfeld (1910). However, those attempts were quickly superseded by Einstein's theory of general relativity. Whitehead's theory of gravitation (1922) explains gravitational red shift, light bending, perihelion shift and Shapiro delay.

General relativity

Background

General relativity predicts that gravitational radiation should exist and propagate as a wave at lightspeed: A slowly evolving and weak gravitational field will produce, according to general relativity, effects like those of Newtonian gravitation (it does not depend on the existence of gravitons, mentioned above, or any similar force-carrying particles).

Suddenly displacing one of two gravitoelectrically interacting particles would, after a delay corresponding to lightspeed, cause the other to feel the displaced particle's absence: accelerations due to the change in quadrupole moment of star systems, like the Hulse–Taylor binary, have removed much energy (almost 2% of the energy of our own Sun's output) as gravitational waves, which would theoretically travel at the speed of light.

Two gravitoelectrically interacting particle ensembles, e.g., two planets or stars moving at constant velocity with respect to each other, each feel a force toward the instantaneous position of the other body without a speed-of-light delay because Lorentz invariance demands that what a moving body in a static field sees and what a moving body that emits that field sees be symmetrical.

A moving body's seeing no aberration in a static field emanating from a "motionless body" therefore causes Lorentz invariance to require that in the previously moving body's reference frame the (now moving) emitting body's field lines must not at a distance be retarded or aberred. Moving charged bodies (including bodies that emit static gravitational fields) exhibit static field lines that bend not with distance and show no speed of light delay effects, as seen from bodies moving with regard to them.

In other words, since the gravitoelectric field is, by definition, static and continuous, it does not propagate. If such a source of a static field is accelerated (for example stopped) with regard to its formerly constant velocity frame, its distant field continues to be updated as though the charged body continued with constant velocity. This effect causes the distant fields of unaccelerated moving charges to appear to be "updated" instantly for their constant velocity motion, as seen from distant positions, in the frame where the source-object is moving at constant velocity. However, as discussed, this is an effect which can be removed at any time, by transitioning to a new reference frame in which the distant charged body is now at rest.

The static and continuous gravitoelectric component of a gravitational field is not a gravitomagnetic component (gravitational radiation); see Petrov classification. The gravitoelectric field is a static field and therefore cannot superluminally transmit quantized (discrete) information, i.e., it could not constitute a well-ordered series of impulses carrying a well-defined meaning (this is the same for gravity and electromagnetism).

Aberration of field direction in general relativity, for a weakly accelerated observer

Main article: Liénard–Wiechert potential

The finite speed of gravitational interaction in general relativity does not lead to the sorts of problems with the aberration of gravity that Newton was originally concerned with, because there is no such aberration in static field effects. Because the acceleration of the Earth with regard to the Sun is small (meaning, to a good approximation, the two bodies can be regarded as traveling in straight lines past each other with unchanging velocity), the orbital results calculated by general relativity are the same as those of Newtonian gravity with instantaneous action at a distance, because they are modelled by the behavior of a static field with constant-velocity relative motion, and no aberration for the forces involved. Although the calculations are considerably more complicated, one can show that a static field in general relativity does not suffer from aberration problems as seen by an unaccelerated observer (or a weakly accelerated observer, such as the Earth). Analogously, the "static term" in the electromagnetic Liénard–Wiechert potential theory of the fields from a moving charge does not suffer from either aberration or positional-retardation. Only the term corresponding to acceleration and electromagnetic emission in the Liénard–Wiechert potential shows a direction toward the time-retarded position of the emitter.

It is in fact not very easy to construct a self-consistent gravity theory in which gravitational interaction propagates at a speed other than the speed of light, which complicates discussion of this possibility.

Formulaic conventions

In general relativity the metric tensor symbolizes the gravitational potential, and Christoffel symbols of the spacetime manifold symbolize the gravitational force field. The tidal gravitational field is associated with the curvature of spacetime.

Measurements

For the reader who desires a deeper background, a comprehensive review of the definition of the speed of gravity and its measurement with high-precision astrometric and other techniques appears in the textbook Relativistic Celestial Mechanics in the Solar System.

PSR 1913+16 orbital decay

The speed of gravity (more correctly, the speed of gravitational waves) can be calculated from observations of the orbital decay rate of binary pulsars PSR 1913+16 (the Hulse–Taylor binary system noted above) and PSR B1534+12. The orbits of these binary pulsars are decaying due to loss of energy in the form of gravitational radiation. The rate of this energy loss ("gravitational damping") can be measured, and since it depends on the speed of gravity, comparing the measured values to theory shows that the speed of gravity is equal to the speed of light to within 1%. However, according to PPN formalism setting, measuring the speed of gravity by comparing theoretical results with experimental results will depend on the theory; use of a theory other than that of general relativity could in principle show a different speed, although the existence of gravitational damping at all implies that the speed cannot be infinite.

Jovian occultation of QSO J0842+1835 (contested)

In September 2002, Sergei Kopeikin and Edward Fomalont announced that they had measured the speed of gravity indirectly, using their data from VLBI measurement of the retarded position of Jupiter on its orbit during Jupiter's transit across the line-of-sight of the bright radio source quasar QSO J0842+1835. Kopeikin and Fomalont concluded that the speed of gravity is between 0.8 and 1.2 times the speed of light, which would be fully consistent with the theoretical prediction of general relativity that the speed of gravity is exactly the same as the speed of light.

Several physicists, including Clifford M. Will and Steve Carlip, have criticized these claims on the grounds that they have allegedly misinterpreted the results of their measurements. Notably, prior to the actual transit, Hideki Asada in a paper to the Astrophysical Journal Letters theorized that the proposed experiment was essentially a roundabout confirmation of the speed of light instead of the speed of gravity.

It is important to keep in mind that none of the debaters in this controversy are claiming that general relativity is "wrong". Rather, the debated issue is whether or not Kopeikin and Fomalont have really provided yet another verification of one of its fundamental predictions.

Kopeikin and Fomalont, however, continue to vigorously argue their case and the means of presenting their result at the press conference of the American Astronomical Society (AAS) that was offered after the results of the Jovian experiment had been peer-reviewed by the experts of the AAS scientific organizing committee. In a later publication by Kopeikin and Fomalont, which uses a bi-metric formalism that splits the space-time null cone in two — one for gravity and another one for light — the authors claimed that Asada's claim was theoretically unsound. The two null cones overlap in general relativity, which makes tracking the speed-of-gravity effects difficult and requires a special mathematical technique of gravitational retarded potentials, which was worked out by Kopeikin and co-authors but was never properly employed by Asada and/or the other critics.

Stuart Samuel also showed that the experiment did not actually measure the speed of gravity because the effects were too small to have been measured. A response by Kopeikin and Fomalont challenges this opinion.

GW170817 and the demise of two neutron stars

The detection of GW170817 in 2017, the finalé of a neutron star inspiral observed through both gravitational waves and gamma rays, currently provides by far the best limit on the difference between the speed of light and that of gravity. Photons were detected 1.7 seconds after peak gravitational wave emission; assuming a delay of zero to 10 seconds, the difference between the speeds of gravitational and electromagnetic waves, v_GW − v_EM, is constrained to between −3×10⁻¹⁵ and +7×10⁻¹⁶ times the speed of light.

This also excluded some alternatives to general relativity, including variants of scalar–tensor theory, instances of Horndeski's theory, and Hořava–Lifshitz gravity.