Differential of a function

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Differential_of_a_function

In calculus, the differential represents the principal part of the change in a function ${\displaystyle y=f(x)}$ with respect to changes in the independent variable. The differential ${\displaystyle dy}$ is defined by

$${\displaystyle dy=f^{\prime }(x)dx,}$$

where ${\displaystyle f^{\prime }(x)}$ is the derivative of f with respect to ${\displaystyle x}$, and ${\displaystyle dx}$ is an additional real variable (so that ${\displaystyle dy}$ is a function of ${\displaystyle x}$ and ${\displaystyle dx}$). The notation is such that the equation

$${\displaystyle dy=\frac{dy}{dx}dx}$$

holds, where the derivative is represented in the Leibniz notation ${\displaystyle dy/dx}$, and this is consistent with regarding the derivative as the quotient of the differentials. One also writes

$${\displaystyle df(x)=f^{\prime }(x)dx.}$$

The precise meaning of the variables ${\displaystyle dy}$ and ${\displaystyle dx}$ depends on the context of the application and the required level of mathematical rigor. The domain of these variables may take on a particular geometrical significance if the differential is regarded as a particular differential form, or analytical significance if the differential is regarded as a linear approximation to the increment of a function. Traditionally, the variables ${\displaystyle dx}$ and ${\displaystyle dy}$ are considered to be very small (infinitesimal), and this interpretation is made rigorous in non-standard analysis.

History and usage

The differential was first introduced via an intuitive or heuristic definition by Isaac Newton and furthered by Gottfried Leibniz, who thought of the differential dy as an infinitely small (or infinitesimal) change in the value y of the function, corresponding to an infinitely small change dx in the function's argument x. For that reason, the instantaneous rate of change of y with respect to x, which is the value of the derivative of the function, is denoted by the fraction

$${\displaystyle \frac{dy}{dx}}$$

in what is called the Leibniz notation for derivatives. The quotient ${\displaystyle dy/dx}$ is not infinitely small; rather it is a real number.

The use of infinitesimals in this form was widely criticized, for instance by the famous pamphlet The Analyst by Bishop Berkeley. Augustin-Louis Cauchy (1823) defined the differential without appeal to the atomism of Leibniz's infinitesimals. Instead, Cauchy, following d'Alembert, inverted the logical order of Leibniz and his successors: the derivative itself became the fundamental object, defined as a limit of difference quotients, and the differentials were then defined in terms of it. That is, one was free to define the differential ${\displaystyle dy}$ by an expression

$${\displaystyle dy=f^{\prime }(x)dx}$$

in which ${\displaystyle dy}$ and ${\displaystyle dx}$ are simply new variables taking finite real values, not fixed infinitesimals as they had been for Leibniz.

According to Boyer (1959, p. 12), Cauchy's approach was a significant logical improvement over the infinitesimal approach of Leibniz because, instead of invoking the metaphysical notion of infinitesimals, the quantities ${\displaystyle dy}$ and ${\displaystyle dx}$ could now be manipulated in exactly the same manner as any other real quantities in a meaningful way. Cauchy's overall conceptual approach to differentials remains the standard one in modern analytical treatments, although the final word on rigor, a fully modern notion of the limit, was ultimately due to Karl Weierstrass.

In physical treatments, such as those applied to the theory of thermodynamics, the infinitesimal view still prevails. Courant & John (1999, p. 184) reconcile the physical use of infinitesimal differentials with the mathematical impossibility of them as follows. The differentials represent finite non-zero values that are smaller than the degree of accuracy required for the particular purpose for which they are intended. Thus "physical infinitesimals" need not appeal to a corresponding mathematical infinitesimal in order to have a precise sense.

Following twentieth-century developments in mathematical analysis and differential geometry, it became clear that the notion of the differential of a function could be extended in a variety of ways. In real analysis, it is more desirable to deal directly with the differential as the principal part of the increment of a function. This leads directly to the notion that the differential of a function at a point is a linear functional of an increment ${\displaystyle \mathrm{\Delta }x}$. This approach allows the differential (as a linear map) to be developed for a variety of more sophisticated spaces, ultimately giving rise to such notions as the Fréchet or Gateaux derivative. Likewise, in differential geometry, the differential of a function at a point is a linear function of a tangent vector (an "infinitely small displacement"), which exhibits it as a kind of one-form: the exterior derivative of the function. In non-standard calculus, differentials are regarded as infinitesimals, which can themselves be put on a rigorous footing (see differential (infinitesimal)).

Definition

The differential of a function ${\displaystyle f(x)}$ at a point ${\displaystyle x_0}$.

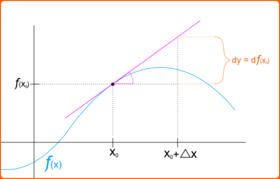
The differential is defined in modern treatments of differential calculus as follows. The differential of a function ${\displaystyle f(x)}$ of a single real variable ${\displaystyle x}$ is the function ${\displaystyle df}$ of two independent real variables ${\displaystyle x}$ and ${\displaystyle \mathrm{\Delta }x}$ given by

$${\displaystyle df(x,\mathrm{\Delta }x)\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}{f}^{\prime }(x)\mathrm{\Delta }x.}$$

One or both of the arguments may be suppressed, i.e., one may see ${\displaystyle df(x)}$ or simply ${\displaystyle df}$. If ${\displaystyle y=f(x)}$, the differential may also be written as ${\displaystyle dy}$. Since ${\displaystyle dx(x,\mathrm{\Delta }x)=\mathrm{\Delta }x}$, it is conventional to write ${\displaystyle dx=\mathrm{\Delta }x}$ so that the following equality holds:

$${\displaystyle df(x)=f^{\prime }(x)dx}$$

This notion of differential is broadly applicable when a linear approximation to a function is sought, in which the value of the increment ${\displaystyle \mathrm{\Delta }x}$ is small enough. More precisely, if ${\displaystyle f}$ is a differentiable function at ${\displaystyle x}$, then the difference in ${\displaystyle y}$-values

$${\displaystyle \mathrm{\Delta }y\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}f(x+\mathrm{\Delta }x)-f(x)}$$

satisfies

$${\displaystyle \mathrm{\Delta }y=f^{\prime }(x)\mathrm{\Delta }x+\epsilon =df(x)+\epsilon }$$

where the error ${\displaystyle \epsilon }$ in the approximation satisfies ${\displaystyle \epsilon /\mathrm{\Delta }x\to 0}$ as ${\displaystyle \mathrm{\Delta }x\to 0}$. In other words, one has the approximate identity

$${\displaystyle \mathrm{\Delta }y\approx dy}$$

in which the error can be made as small as desired relative to ${\displaystyle \mathrm{\Delta }x}$ by constraining ${\displaystyle \mathrm{\Delta }x}$ to be sufficiently small; that is to say,

$${\displaystyle \frac{\mathrm{\Delta }y-dy}{\mathrm{\Delta }x}\to 0}$$

as ${\displaystyle \mathrm{\Delta }x\to 0}$. For this reason, the differential of a function is known as the principal (linear) part in the increment of a function: the differential is a linear function of the increment ${\displaystyle \mathrm{\Delta }x}$, and although the error ${\displaystyle \epsilon }$ may be nonlinear, it tends to zero rapidly as ${\displaystyle \mathrm{\Delta }x}$ tends to zero.

Differentials in several variables

Operator / Function	${\displaystyle f(x)}$	${\displaystyle f(x,y,u(x,y),v(x,y))}$
Differential	1: ${\displaystyle df\stackrel{\underset{\mathrm{d}\mathrm{e}\mathrm{f}}{}}{=}{f}_x^{\prime }dx}$	2: ${\displaystyle d_{x}f\stackrel{\underset{\mathrm{d}\mathrm{e}\mathrm{f}}{}}{=}{f}_x^{\prime }dx}$ 3: ${\displaystyle df\stackrel{\underset{\mathrm{d}\mathrm{e}\mathrm{f}}{}}{=}{f}_x^{\prime }dx+f_y^{\prime }dy+f_u^{\prime }du+f_v^{\prime }dv}$
Partial derivative	${\displaystyle f_x^{\prime }\stackrel{\underset{(1)}{}}{=}\frac{df}{dx}}$	${\displaystyle f_x^{\prime }\stackrel{\underset{(2)}{}}{=}\frac{d_{x}f}{dx}=\frac{\mathrm{\partial }f}{\mathrm{\partial }x}}$
Total derivative	${\displaystyle \frac{df}{dx}\stackrel{\underset{(1)}{}}{=}{f}_x^{\prime }}$	${\displaystyle \frac{df}{dx}\stackrel{\underset{(3)}{}}{=}{f}_x^{\prime }+f_u^{\prime }\frac{du}{dx}+f_v^{\prime }\frac{dv}{dx};(f_y^{\prime }\frac{dy}{dx}=0)}$

Following Goursat (1904, I, §15), for functions of more than one independent variable,

$${\displaystyle y=f(x_1,\dots ,x_n),}$$

the partial differential of y with respect to any one of the variables x₁ is the principal part of the change in y resulting from a change dx₁ in that one variable. The partial differential is therefore

$${\displaystyle \frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_1}d{x}_1}$$

involving the partial derivative of y with respect to x₁. The sum of the partial differentials with respect to all of the independent variables is the total differential

$${\displaystyle dy=\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_1}d{x}_1+\cdots +\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_n}d{x}_n,}$$

which is the principal part of the change in y resulting from changes in the independent variables x_i.

More precisely, in the context of multivariable calculus, following Courant (1937b), if f is a differentiable function, then by the definition of differentiability, the increment

$${\displaystyle \begin{array}{rl}\mathrm{\Delta }y& \stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}f(x_1+\mathrm{\Delta }{x}_1,\dots ,x_n+\mathrm{\Delta }{x}_n)-f(x_1,\dots ,x_n)\\ & =\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_1}\mathrm{\Delta }{x}_1+\cdots +\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_n}\mathrm{\Delta }{x}_n+{\epsilon }_1\mathrm{\Delta }{x}_1+\cdots +{\epsilon }_n\mathrm{\Delta }{x}_n\end{array}}$$

where the error terms ε _i tend to zero as the increments Δx_i jointly tend to zero. The total differential is then rigorously defined as

$${\displaystyle dy=\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_1}\mathrm{\Delta }{x}_1+\cdots +\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_n}\mathrm{\Delta }{x}_n.}$$

Since, with this definition,

$${\displaystyle d{x}_i(\mathrm{\Delta }{x}_1,\dots ,\mathrm{\Delta }{x}_n)=\mathrm{\Delta }{x}_i,}$$

one has

$${\displaystyle dy=\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_1}d{x}_1+\cdots +\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_n}d{x}_n.}$$

As in the case of one variable, the approximate identity holds

$${\displaystyle dy\approx \mathrm{\Delta }y}$$

in which the total error can be made as small as desired relative to $\sqrt{\mathrm{\Delta }{x}_1^2+\cdots +\mathrm{\Delta }{x}_n^2}$ by confining attention to sufficiently small increments.

Application of the total differential to error estimation

In measurement, the total differential is used in estimating the error ${\displaystyle \mathrm{\Delta }f}$ of a function ${\displaystyle f}$ based on the errors ${\displaystyle \mathrm{\Delta }x,\mathrm{\Delta }y,\dots }$ of the parameters ${\displaystyle x,y,\dots }$. Assuming that the interval is short enough for the change to be approximately linear:

$${\displaystyle \mathrm{\Delta }f(x)=f^{\prime }(x)\mathrm{\Delta }x}$$

and that all variables are independent, then for all variables,

$${\displaystyle \mathrm{\Delta }f=f_x\mathrm{\Delta }x+f_y\mathrm{\Delta }y+\cdots }$$

This is because the derivative ${\displaystyle f_x}$ with respect to the particular parameter ${\displaystyle x}$ gives the sensitivity of the function ${\displaystyle f}$ to a change in ${\displaystyle x}$, in particular the error ${\displaystyle \mathrm{\Delta }x}$. As they are assumed to be independent, the analysis describes the worst-case scenario. The absolute values of the component errors are used, because after simple computation, the derivative may have a negative sign. From this principle the error rules of summation, multiplication etc. are derived, e.g.:

Let ${\displaystyle f(a,b)=ab}$. Then, the finite error can be approximated as

$${\displaystyle \mathrm{\Delta }f=f_a\mathrm{\Delta }a+f_b\mathrm{\Delta }b.}$$

Evaluating the derivatives:

$${\displaystyle \mathrm{\Delta }f=b\mathrm{\Delta }a+a\mathrm{\Delta }b.}$$

Dividing by f, which is a × b

$${\displaystyle \frac{\mathrm{\Delta }f}{f}=\frac{\mathrm{\Delta }a}{a}+\frac{\mathrm{\Delta }b}{b}}$$

That is to say, in multiplication, the total relative error is the sum of the relative errors of the parameters.

To illustrate how this depends on the function considered, consider the case where the function is ${\displaystyle f(a,b)=a\ln b}$ instead. Then, it can be computed that the error estimate is

$${\displaystyle \frac{\mathrm{\Delta }f}{f}=\frac{\mathrm{\Delta }a}{a}+\frac{\mathrm{\Delta }b}{b\ln b}}$$

with an extra 'ln b' factor not found in the case of a simple product. This additional factor tends to make the error smaller, as ln b is not as large as a bare b.

Higher-order differentials

Higher-order differentials of a function y = f(x) of a single variable x can be defined via:

$${\displaystyle d^{2}y=d(dy)=d(f^{\prime }(x)dx)=(d{f}^{\prime }(x))dx=f^{″}(x)(dx{)}^2,}$$

and, in general,

$${\displaystyle d^{n}y=f^{(n)}(x)(dx{)}^n.}$$

Informally, this motivates Leibniz's notation for higher-order derivatives

$${\displaystyle f^{(n)}(x)=\frac{d^{n}f}{d{x}^n}.}$$

When the independent variable x itself is permitted to depend on other variables, then the expression becomes more complicated, as it must include also higher order differentials in x itself. Thus, for instance,

$${\displaystyle \begin{array}{rl}{d}^{2}y& =f^{″}(x)(dx{)}^2+f^{\prime }(x)d^{2}x\\ d^{3}y& =f^{‴}(x)(dx{)}^3+3f^{″}(x)dx{d}^{2}x+f^{\prime }(x)d^{3}x\end{array}}$$

and so forth.

Similar considerations apply to defining higher order differentials of functions of several variables. For example, if f is a function of two variables x and y, then

$${\displaystyle d^{n}f=\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})\frac{{\mathrm{\partial }}^{n}f}{\mathrm{\partial }{x}^k\mathrm{\partial }{y}^{n-k}}(dx{)}^k(dy{)}^{n-k},}$$

where $(\genfrac{}{}{0ex}{}{n}{k})$ is a binomial coefficient. In more variables, an analogous expression holds, but with an appropriate multinomial expansion rather than binomial expansion.

Higher order differentials in several variables also become more complicated when the independent variables are themselves allowed to depend on other variables. For instance, for a function f of x and y which are allowed to depend on auxiliary variables, one has

$${\displaystyle d^{2}f=\left(\frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}^2}(dx{)}^2+2\frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }x\mathrm{\partial }y}dxdy+\frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{y}^2}(dy{)}^2\right)+\frac{\mathrm{\partial }f}{\mathrm{\partial }x}{d}^{2}x+\frac{\mathrm{\partial }f}{\mathrm{\partial }y}{d}^{2}y.}$$

Because of this notational awkwardness, the use of higher order differentials was roundly criticized by Hadamard (1935), who concluded:

Enfin, que signifie ou que représente l'égalité

$${\displaystyle d^{2}z=rd{x}^2+2sdxdy+td{y}^2?}$$

A mon avis, rien du tout.

That is: Finally, what is meant, or represented, by the equality [...]? In my opinion, nothing at all. In spite of this skepticism, higher order differentials did emerge as an important tool in analysis.

In these contexts, the n-th order differential of the function f applied to an increment Δx is defined by

$${\displaystyle d^{n}f(x,\mathrm{\Delta }x)={\frac{d^n}{d{t}^n}f(x+t\mathrm{\Delta }x)|}_{t=0}}$$

or an equivalent expression, such as

$${\displaystyle \underset{t\to 0}{lim}\frac{{\mathrm{\Delta }}_{t\mathrm{\Delta }x}^{n}f}{t^n}}$$

where ${\displaystyle {\mathrm{\Delta }}_{t\mathrm{\Delta }x}^{n}f}$ is an nth forward difference with increment tΔx.

This definition makes sense as well if f is a function of several variables (for simplicity taken here as a vector argument). Then the n-th differential defined in this way is a homogeneous function of degree n in the vector increment Δx. Furthermore, the Taylor series of f at the point x is given by

$${\displaystyle f(x+\mathrm{\Delta }x)\sim f(x)+df(x,\mathrm{\Delta }x)+\frac{1}{2}{d}^{2}f(x,\mathrm{\Delta }x)+\cdots +\frac{1}{n!}{d}^{n}f(x,\mathrm{\Delta }x)+\cdots }$$

The higher order Gateaux derivative generalizes these considerations to infinite dimensional spaces.

Properties

A number of properties of the differential follow in a straightforward manner from the corresponding properties of the derivative, partial derivative, and total derivative. These include:

• Linearity: For constants a and b and differentiable functions f and g,
  $${\displaystyle d(af+bg)=adf+bdg.}$$

  
• Product rule: For two differentiable functions f and g,
  $${\displaystyle d(fg)=fdg+gdf.}$$

  

An operation d with these two properties is known in abstract algebra as a derivation. They imply the power rule

$${\displaystyle d(f^n)=n{f}^{n-1}df}$$

In addition, various forms of the chain rule hold, in increasing level of generality:

• If y = f(u) is a differentiable function of the variable u and u = g(x) is a differentiable function of x, then
  $${\displaystyle dy=f^{\prime }(u)du=f^{\prime }(g(x))g^{\prime }(x)dx.}$$

  
• If y = f(x₁, ..., x_n) and all of the variables x₁, ..., x_n depend on another variable t, then by the chain rule for partial derivatives, one has
  $${\displaystyle \begin{array}{rl}dy=\frac{dy}{dt}dt& =\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_1}d{x}_1+\cdots +\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_n}d{x}_n\\ & =\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_1}\frac{d{x}_1}{dt}dt+\cdots +\frac{\mathrm{\partial }y}{\mathrm{\partial }{x}_n}\frac{d{x}_n}{dt}dt.\end{array}}$$

  
  Heuristically, the chain rule for several variables can itself be understood by dividing through both sides of this equation by the infinitely small quantity dt.
• More general analogous expressions hold, in which the intermediate variables x_i depend on more than one variable.

General formulation

See also: Fréchet derivative and Gateaux derivative

A consistent notion of differential can be developed for a function f : Rⁿ → R^m between two Euclidean spaces. Let x,Δx ∈ Rⁿ be a pair of Euclidean vectors. The increment in the function f is

$${\displaystyle \mathrm{\Delta }f=f(\mathbf{x}+\mathrm{\Delta }\mathbf{x})-f(\mathbf{x}).}$$

If there exists an m × n matrix A such that

$${\displaystyle \mathrm{\Delta }f=A\mathrm{\Delta }\mathbf{x}+\Vert \mathrm{\Delta }\mathbf{x}\Vert \mathit{\epsilon }}$$

in which the vector ε → 0 as Δx → 0, then f is by definition differentiable at the point x. The matrix A is sometimes known as the Jacobian matrix, and the linear transformation that associates to the increment Δx ∈ Rⁿ the vector AΔx ∈ R^m is, in this general setting, known as the differential df(x) of f at the point x. This is precisely the Fréchet derivative, and the same construction can be made to work for a function between any Banach spaces.

Another fruitful point of view is to define the differential directly as a kind of directional derivative:

$${\displaystyle df(\mathbf{x},\mathbf{h})=\underset{t\to 0}{lim}\frac{f(\mathbf{x}+t\mathbf{h})-f(\mathbf{x})}{t}={\frac{d}{dt}f(\mathbf{x}+t\mathbf{h})|}_{t=0},}$$

which is the approach already taken for defining higher order differentials (and is most nearly the definition set forth by Cauchy). If t represents time and x position, then h represents a velocity instead of a displacement as we have heretofore regarded it. This yields yet another refinement of the notion of differential: that it should be a linear function of a kinematic velocity. The set of all velocities through a given point of space is known as the tangent space, and so df gives a linear function on the tangent space: a differential form. With this interpretation, the differential of f is known as the exterior derivative, and has broad application in differential geometry because the notion of velocities and the tangent space makes sense on any differentiable manifold. If, in addition, the output value of f also represents a position (in a Euclidean space), then a dimensional analysis confirms that the output value of df must be a velocity. If one treats the differential in this manner, then it is known as the pushforward since it "pushes" velocities from a source space into velocities in a target space.

Other approaches

Main article: Differential (infinitesimal)

Although the notion of having an infinitesimal increment dx is not well-defined in modern mathematical analysis, a variety of techniques exist for defining the infinitesimal differential so that the differential of a function can be handled in a manner that does not clash with the Leibniz notation. These include:

• Defining the differential as a kind of differential form, specifically the exterior derivative of a function. The infinitesimal increments are then identified with vectors in the tangent space at a point. This approach is popular in differential geometry and related fields, because it readily generalizes to mappings between differentiable manifolds.
• Differentials as nilpotent elements of commutative rings. This approach is popular in algebraic geometry.
• Differentials in smooth models of set theory. This approach is known as synthetic differential geometry or smooth infinitesimal analysis and is closely related to the algebraic geometric approach, except that ideas from topos theory are used to hide the mechanisms by which nilpotent infinitesimals are introduced.
• Differentials as infinitesimals in hyperreal number systems, which are extensions of the real numbers which contain invertible infinitesimals and infinitely large numbers. This is the approach of nonstandard analysis pioneered by Abraham Robinson.

Examples and applications

Differentials may be effectively used in numerical analysis to study the propagation of experimental errors in a calculation, and thus the overall numerical stability of a problem (Courant 1937a). Suppose that the variable x represents the outcome of an experiment and y is the result of a numerical computation applied to x. The question is to what extent errors in the measurement of x influence the outcome of the computation of y. If the x is known to within Δx of its true value, then Taylor's theorem gives the following estimate on the error Δy in the computation of y:

$${\displaystyle \mathrm{\Delta }y=f^{\prime }(x)\mathrm{\Delta }x+\frac{(\mathrm{\Delta }x{)}^2}{2}{f}^{″}(\xi )}$$

where ξ = x + θΔx for some 0 < θ < 1. If Δx is small, then the second order term is negligible, so that Δy is, for practical purposes, well-approximated by dy = f'(x) Δx.

The differential is often useful to rewrite a differential equation

$${\displaystyle \frac{dy}{dx}=g(x)}$$

in the form

$${\displaystyle dy=g(x)dx,}$$

in particular when one wants to separate the variables.

Lithium–sulfur battery

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Lithium%E2%80%93sulfur_battery 

 

Lithium–sulfur battery

Working principle of lithium-sulfur battery and "shuttle" effect
Specific energy	450 [Wh/kg]
Energy density	550 [Wh/L]
Charge/discharge efficiency	C/5 nominal
Cycle durability	disputed
Nominal cell voltage	cell voltage varies nonlinearly in the range 2.5–1.7 V during discharge; batteries often packaged for 3 V

The lithium–sulfur battery (Li–S battery) is a type of rechargeable battery. It is notable for its high specific energy. The low atomic weight of lithium and moderate atomic weight of sulfur means that Li–S batteries are relatively light (about the density of water). They were used on the longest and highest-altitude unmanned solar-powered aeroplane flight (at the time) by Zephyr 6 in August 2008.

Lithium–sulfur batteries may displace lithium-ion cells because of their higher energy density and reduced cost. This is due to the use of sulfur instead of cobalt, a common element in lithium-ion batteries. Li–S batteries offer specific energies on the order of 550 Wh/kg, while lithium-ion batteries are in the range of 150–260 Wh/kg.

Li–S batteries with up to 1,500 charge and discharge cycles were demonstrated in 2017, but cycle life tests at commercial scale and with lean electrolyte have not been completed. As of early 2021, none were commercially available.

Issues that have slowed acceptance include the polysulfide "shuttle" effect that is responsible for the progressive leakage of active material from the cathode, resulting in too-few recharge cycles. Also, sulfur cathodes have low conductivity, requiring extra mass for a conducting agent in order to exploit the contribution of active mass to the capacity. Volume expansion of the sulfur cathode during S to Li₂S conversion and the large amount of electrolyte needed are also issues.

History

Li–S batteries were invented in the 1960s, when Herbert and Ulam patented a primary battery employing lithium or lithium alloys as anodic material, sulfur as cathodic material and an electrolyte composed of aliphatic saturated amines. A few years later the technology was improved by the introduction of organic solvents as PC, DMSO and DMF yielding a 2.35-2.5 V battery. By the end of the 1980s a rechargeable Li–S battery was demonstrated employing ethers, in particular DOL, as the electrolyte solvent.

In 2020 Manthiram identified the critical parameters needed for achieving commercial acceptance. Specifically, Li-S batteries need to achieve a sulfur loading of >5 mg cm⁻², a carbon content of <5%, electrolyte-to-sulfur ratio of <5 μL mg⁻¹, electrolyte-to-capacity ratio of <5 μL (mA h)⁻¹, and negative-to-positive capacity ratio of <5 in pouch-type cells.

In 2021, researchers announced the use of a sugar-based anode additive that prevented the release of polysulfide chains from the cathodes that pollute the anode. A prototype cell demonstrated 1,000 charge cycles with a capacity of 700 mAh/g.

In 2022, an interlayer was introduced that claimed to reduce polysulfide movement (protecting the anode) and facilitate lithium ion transfer to reduce charge/discharge times. Also that year, researchers employed aramid nanofibers (nanoscale Kevlar fibers), fashioned into cell membrane-like networks. This prevented dendrite formation. It addressed polysulfide shuttle by using ion selectivity, by integrating tiny channels into the network and adding an electrical charge.

Also in 2022, Researchers at Drexel University produced a prototype lithium-sulfur battery that did not degrade over 4000 charge cycles. Analysis has shown that the battery contained monoclinic gamma-phase sulfur, which has been thought to be unstable below 95 degrees Celsius, and only a few studies have shown this type of sulfur to be stable longer than 20 to 30 minutes.

Chemistry

Chemical processes in the Li–S cell include lithium dissolution from the anode surface (and incorporation into alkali metal polysulfide salts) during discharge, and reverse lithium plating to the anode while charging.

Anode

At the anodic surface, dissolution of the metallic lithium occurs, with the production of electrons and lithium ions during the discharge and electrodeposition during the charge. The half-reaction is expressed as:

${\displaystyle \text{Li}\stackrel{-\rightharpoonup }{\leftharpoondown -}{\text{Li}}^{+}+{\text{e}}^{-}}$

In analogy with lithium batteries, the dissolution / electrodeposition reaction causes over time problems of unstable growth of the solid-electrolyte interface (SEI), generating active sites for the nucleation and dendritic growth of lithium. Dendritic growth is responsible for the internal short circuit in lithium batteries and leads to the death of the battery itself.

Cathode

In Li-S batteries, energy is stored in the sulfur cathode (S₈). During discharge, the lithium ions in the electrolyte migrate to the cathode where the sulfur is reduced to lithium sulphide (Li₂S). The sulfur is reoxidized to S₈ during the recharge phase. The semi-reaction is therefore expressed as:

${\displaystyle \text{S}+2{\text{Li}}^{+}+2{\text{e}}^{-}\stackrel{-\rightharpoonup }{\leftharpoondown -}{\text{Li}}_2^{}\text{S}}$ (E ° ≈ 2.15 V vs Li / Li⁺ )

Actually the sulfur reduction reaction to lithium sulphide is much more complex and involves the formation of lithium polysulphides (Li₂S_x, 2 ≤ x ≤ 8) at decreasing chain length according to the order:

${\displaystyle {\text{Li}}_2^{}{\text{S}}_8^{}⟶{\text{Li}}_2^{}{\text{S}}_6^{}⟶{\text{Li}}_2^{}{\text{S}}_4^{}⟶{\text{Li}}_2^{}{\text{S}}_2^{}⟶{\text{Li}}_2^{}\text{S}}$

The final product is actually a mixture of Li₂S₂ and Li₂S rather than pure Li₂S, due to the slow reduction kinetics at Li₂S. This contrasts with conventional lithium-ion cells, where the lithium ions are intercalated in the anode and cathodes. Each sulfur atom can host two lithium ions. Typically, lithium-ion batteries accommodate only 0.5–0.7 lithium ions per host atom. Consequently, Li–S allows for a much higher lithium storage density. Polysulfides are reduced on the cathode surface in sequence while the cell is discharging:

S
₈ → Li
₂S
₈ → Li
₂S
₆ → Li
₂S
₄ → Li
₂S
₃

Across a porous diffusion separator, sulfur polymers form at the cathode as the cell charges:

Li
₂S → Li
₂S
₂ → Li
₂S
₃ → Li
₂S
₄ → Li
₂S
₆ → Li
₂S
₈ → S
₈

These reactions are analogous to those in the sodium–sulfur battery.

The main challenges of Li–S batteries is the low conductivity of sulfur and its considerable volume change upon discharging and finding a suitable cathode is the first step for commercialization of Li–S batteries. Therefore, most researchers use a carbon/sulfur cathode and a lithium anode. Sulfur is very cheap, but has practically no electroconductivity, 5×10⁻³⁰ S⋅cm⁻¹ at 25 °C. A carbon coating provides the missing electroconductivity. Carbon nanofibers provide an effective electron conduction path and structural integrity, at the disadvantage of higher cost.

One problem with the lithium–sulfur design is that when the sulfur in the cathode absorbs lithium, volume expansion of the Li_xS compositions occurs, and predicted volume expansion of Li₂S is nearly 80% of the volume of the original sulfur. This causes large mechanical stresses on the cathode, which is a major cause of rapid degradation. This process reduces the contact between the carbon and the sulfur, and prevents the flow of lithium ions to the carbon surface.

Mechanical properties of the lithiated sulfur compounds are strongly contingent on the lithium content, and with increasing lithium content, the strength of lithiated sulfur compounds improves, although this increment is not linear with lithiation.

One of the primary shortfalls of most Li–S cells is unwanted reactions with the electrolytes. While S and Li
₂S are relatively insoluble in most electrolytes, many intermediate polysulfides are not. Dissolving Li
₂S
_n into electrolytes causes irreversible loss of active sulfur. Use of highly reactive lithium as a negative electrode causes dissociation of most of the commonly used other type electrolytes. Use of a protective layer in the anode surface has been studied to improve cell safety, i.e., using Teflon coating showed improvement in the electrolyte stability, LIPON, Li₃N also exhibited promising performance.

Polysulfide "shuttle"

Historically, the "shuttle" effect is the main cause of degradation in a Li–S battery. The lithium polysulfide Li₂S_x (6≤x≤8) is highly soluble in the common electrolytes used for Li–S batteries. They are formed and leaked from the cathode and they diffuse to the anode, where they are reduced to short-chain polysulfides and diffuse back to the cathode where long-chain polysulfides are formed again. This process results in the continuous leakage of active material from the cathode, lithium corrosion, low coulombic efficiency and low battery life. Moreover, the "shuttle" effect is responsible for the characteristic self-discharge of Li–S batteries, because of slow dissolution of polysulfide, which occurs also in rest state. The "shuttle" effect in a Li–S battery can be quantified by a factor f_c (0<f_c<1), evaluated by the extension of the charge voltage plateau. The factor f_c is given by the expression:

${\displaystyle fc=\frac{k_{\text{s}}{q}_{\text{up}}[S_{\text{tot}}]}{I_c}}$

where k_s, q_up, [S_tot] and I_c are respectively the kinetic constant, specific capacity contributing to the anodic plateau, the total sulfur concentration and charge current.

In 2022, researchers reported the use of a cathode made from carbon nanofibers. Elemental sulfur was deposited onto the carbon substrate (cf. physical vapor deposition), which formed the rare and usually metastable monoclinic γ-Sulfur allotrope. This allotrope reversibly reacts to Li
₂S without the formation of intermediate polysulfides Li
₂S
_x. Therefore, carbonate electrolytes, which commonly react with those polysulfides, can be used instead of the rather dangerous ether based electrolytes (low flash and boiling points).

Its initial capacity was 800 Ah/kg (classical LiCoO2/graphite batteries have a cell capacity of 100 Ah/kg). It decayed only very slowly, on average 0.04% each cycle, and retained 658 Ah/kg after 4000 cycles (82%).

Electrolyte

Conventionally, Li–S batteries employ a liquid organic electrolyte, contained in the pores of PP separator. The electrolyte plays a key role in Li–S batteries, acting both on "shuttle" effect by the polysulfide dissolution and the SEI stabilization at anode surface. It has been demonstrated that the electrolytes based on organic carbonates commonly employed in Li-ion batteries (i.e. PC, EC, DEC and mixtures of them) are not compatible with the chemistry of Li–S batteries. Long-chain polysulfides undergo nucleophilic attack on electrophilic sites of carbonates, resulting in the irreversible formation of by-products as ethanol, methanol, ethylene glycol and thiocarbonates. In Li–S batteries are conventionally employed cyclic ethers (as DOL) or short-chain ethers (as DME) as well as the family of glycol ethers, including DEGDME and TEGDME. One common electrolyte is 1M LiTFSI in DOL:DME 1:1 vol. with1%w/w di LiNO₃ as additive for lithium surface passivation.

Safety

Because of the high potential energy density and the nonlinear discharge and charging response of the cell, a microcontroller and other safety circuitry is sometimes used along with voltage regulators to manage cell operation and prevent rapid discharge.