Superconductivity

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Superconductivity

A high-temperature superconductor levitating above a magnet. Persistent electric current flows on the surface of the superconductor, acting to exclude the magnetic field of the magnet (Meissner effect). This current effectively forms an electromagnet that repels the magnet.

Superconductivity is a set of physical properties observed in superconductors: materials where electrical resistance vanishes and magnetic fields are expelled from the material. Unlike an ordinary metallic conductor, whose resistance decreases gradually as its temperature is lowered, even down to near absolute zero, a superconductor has a characteristic critical temperature below which the resistance drops abruptly to zero. An electric current through a loop of superconducting wire can persist indefinitely with no power source.

The superconductivity phenomenon was discovered in 1911 by Dutch physicist Heike Kamerlingh Onnes. Like ferromagnetism and atomic spectral lines, superconductivity is a phenomenon which can only be explained by quantum mechanics. It is characterized by the Meissner effect, the complete cancellation of the magnetic field in the interior of the superconductor during its transitions into the superconducting state. The occurrence of the Meissner effect indicates that superconductivity cannot be understood simply as the idealization of perfect conductivity in classical physics.

In 1986, it was discovered that some cuprate-perovskite ceramic materials have a critical temperature above 35 K (−238 °C). It was shortly found (by Ching-Wu Chu) that replacing the lanthanum with yttrium, i.e. making YBCO, raised the critical temperature to 92 K (−181 °C), which was important because liquid nitrogen could then be used as a refrigerant. Such a high transition temperature is theoretically impossible for a conventional superconductor, leading the materials to be termed high-temperature superconductors. The cheaply available coolant liquid nitrogen boils at 77 K (−196 °C) and thus the existence of superconductivity at higher temperatures than this facilitates many experiments and applications that are less practical at lower temperatures.

History

Main article: History of superconductivity

Timeline of superconducting materials. Colors represent different classes of materials:

•   BCS (dark green circle)
•   Heavy fermion-based (light green star)
•   Cuprate (blue diamond)
•   Buckminsterfullerene-based (purple inverted triangle)
•   Carbon-allotrope (red triangle)
•   Iron-pnictogen-based (orange square)
•   Strontium ruthenate (grey pentagon)
•   Nickel-based (pink six-point star)

Heike Kamerlingh Onnes (right), the discoverer of superconductivity. Paul Ehrenfest, Hendrik Lorentz, Niels Bohr stand to his left.

Superconductivity was discovered on April 8, 1911, by Heike Kamerlingh Onnes, who was studying the resistance of solid mercury at cryogenic temperatures using the recently produced liquid helium as a refrigerant. At the temperature of 4.2 K, he observed that the resistance abruptly disappeared. In the same experiment, he also observed the superfluid transition of helium at 2.2 K, without recognizing its significance. The precise date and circumstances of the discovery were only reconstructed a century later, when Onnes's notebook was found. In subsequent decades, superconductivity was observed in several other materials. In 1913, lead was found to superconduct at 7 K, and in 1941 niobium nitride was found to superconduct at 16 K.

Great efforts have been devoted to finding out how and why superconductivity works; the important step occurred in 1933, when Meissner and Ochsenfeld discovered that superconductors expelled applied magnetic fields, a phenomenon which has come to be known as the Meissner effect. In 1935, Fritz and Heinz London showed that the Meissner effect was a consequence of the minimization of the electromagnetic free energy carried by superconducting current.

London constitutive equations

The theoretical model that was first conceived for superconductivity was completely classical: it is summarized by London constitutive equations. It was put forward by the brothers Fritz and Heinz London in 1935, shortly after the discovery that magnetic fields are expelled from superconductors. A major triumph of the equations of this theory is their ability to explain the Meissner effect, wherein a material exponentially expels all internal magnetic fields as it crosses the superconducting threshold. By using the London equation, one can obtain the dependence of the magnetic field inside the superconductor on the distance to the surface.

The two constitutive equations for a superconductor by London are:

$${\displaystyle \frac{\mathrm{\partial }\mathbf{j}}{\mathrm{\partial }t}=\frac{n{e}^2}{m}\mathbf{E},\mathrm{\nabla }\times \mathbf{j}=-\frac{n{e}^2}{m}\mathbf{B}.}$$

The first equation follows from Newton's second law for superconducting electrons.

Conventional theories (1950s)

During the 1950s, theoretical condensed matter physicists arrived at an understanding of "conventional" superconductivity, through a pair of remarkable and important theories: the phenomenological Ginzburg–Landau theory (1950) and the microscopic BCS theory (1957).

In 1950, the phenomenological Ginzburg–Landau theory of superconductivity was devised by Landau and Ginzburg. This theory, which combined Landau's theory of second-order phase transitions with a Schrödinger-like wave equation, had great success in explaining the macroscopic properties of superconductors. In particular, Abrikosov showed that Ginzburg–Landau theory predicts the division of superconductors into the two categories now referred to as Type I and Type II. Abrikosov and Ginzburg were awarded the 2003 Nobel Prize for their work (Landau had received the 1962 Nobel Prize for other work, and died in 1968). The four-dimensional extension of the Ginzburg–Landau theory, the Coleman-Weinberg model, is important in quantum field theory and cosmology.

Also in 1950, Maxwell and Reynolds et al. found that the critical temperature of a superconductor depends on the isotopic mass of the constituent element. This important discovery pointed to the electron–phonon interaction as the microscopic mechanism responsible for superconductivity.

The complete microscopic theory of superconductivity was finally proposed in 1957 by Bardeen, Cooper and Schrieffer. This BCS theory explained the superconducting current as a superfluid of Cooper pairs, pairs of electrons interacting through the exchange of phonons. For this work, the authors were awarded the Nobel Prize in 1972.

The BCS theory was set on a firmer footing in 1958, when N. N. Bogolyubov showed that the BCS wavefunction, which had originally been derived from a variational argument, could be obtained using a canonical transformation of the electronic Hamiltonian. In 1959, Lev Gor'kov showed that the BCS theory reduced to the Ginzburg–Landau theory close to the critical temperature.

Generalizations of BCS theory for conventional superconductors form the basis for the understanding of the phenomenon of superfluidity, because they fall into the lambda transition universality class. The extent to which such generalizations can be applied to unconventional superconductors is still controversial.

Niobium

The first practical application of superconductivity was developed in 1954 with Dudley Allen Buck's invention of the cryotron. Two superconductors with greatly different values of the critical magnetic field are combined to produce a fast, simple switch for computer elements.

Soon after discovering superconductivity in 1911, Kamerlingh Onnes attempted to make an electromagnet with superconducting windings but found that relatively low magnetic fields destroyed superconductivity in the materials he investigated. Much later, in 1955, G. B. Yntema succeeded in constructing a small 0.7-tesla iron-core electromagnet with superconducting niobium wire windings. Then, in 1961, J. E. Kunzler, E. Buehler, F. S. L. Hsu, and J. H. Wernick made the startling discovery that, at 4.2 kelvin, niobium–tin, a compound consisting of three parts niobium and one part tin, was capable of supporting a current density of more than 100,000 amperes per square centimeter in a magnetic field of 8.8 tesla. The alloy was brittle and difficult to fabricate, but niobium–tin proved useful for generating magnetic fields as high as 20 tesla.

In 1962, T. G. Berlincourt and R. R. Hake discovered that more ductile alloys of niobium and titanium are suitable for applications up to 10 tesla. Commercial production of niobium–titanium supermagnet wire immediately commenced at Westinghouse Electric Corporation and at Wah Chang Corporation. Although niobium–titanium boasts less-impressive superconducting properties than those of niobium–tin, niobium–titanium became the most widely used "workhorse" supermagnet material, in large measure a consequence of its very high ductility and ease of fabrication. However, both niobium–tin and niobium–titanium found wide application in MRI medical imagers, bending and focusing magnets for enormous high-energy-particle accelerators, and other applications. Conectus, a European superconductivity consortium, estimated that in 2014, global economic activity for which superconductivity was indispensable amounted to about five billion euros, with MRI systems accounting for about 80% of that total.

Josephson effect

In 1962, Josephson made the important theoretical prediction that a supercurrent can flow between two pieces of superconductor separated by a thin layer of insulator. This phenomenon, now called the Josephson effect, is exploited by superconducting devices such as SQUIDs. It is used in the most accurate available measurements of the magnetic flux quantum Φ₀ = h/(2e), where h is the Planck constant. Coupled with the quantum Hall resistivity, this leads to a precise measurement of the Planck constant. Josephson was awarded the Nobel Prize for this work in 1973.

In 2008, it was proposed that the same mechanism that produces superconductivity could produce a superinsulator state in some materials, with almost infinite electrical resistance. The first development and study of superconducting Bose–Einstein condensate (BEC) in 2020 suggested a "smooth transition between" BEC and Bardeen-Cooper-Shrieffer regimes.

2D materials

Multiple types of superconductivity are reported in devices made of single-layer materials. Some of these materials can switch between conducting, insulating, and other behaviors.

Twisting materials imbues them with a “moiré” pattern involving tiled hexagonal cells that act like atoms and host electrons. In this environment, the electrons move slowly enough for their collective interactions to guide their behavior. When each cell has a single electron, the electrons take on an antiferromagnetic arrangement; each electron can have a preferred location and magnetic orientation. Their intrinsic magnetic fields tend to alternate between pointing up and down. Adding electrons allows superconductivity by causing Cooper pairs to form. Fu and Schrade argued that electron-on-electron action was allowing both antiferromagnetic and superconducting states.

The first success with 2D materials involved a twisted bilayer graphene sheet (2018, Tc ~1.7 K, 1.1° twist). A twisted three-layer graphene device was later shown to superconduct (2021, Tc ~2.8 K). Then an untwisted trilayer graphene device was reported to superconduct (2022, Tc 1-2 K). The latter was later shown to be tunable, easily reproducing behavior found in millions of other configurations. Directly observing what happens when electrons are added to a material or slightly weakening its electric field enables quick testing of an unprecedented number of recipes to see which lead to superconductivity.

In four and five layer rhombohedral graphene, a form of superconductivity with spontaneously broken time reversal symmetry known as "chiral superconductivity" was recently observed. These systems were not observed to have any superlattice effects, and they can flip between two possible magnetic states without exiting the superconducting phase. This is in strong contrast to other observations of superconductivity and magnetic fields.

These devices have applications in quantum computing.

2D materials other than graphene have also been made to superconduct. Transition metal dichalcogenide (TMD) sheets twisted at 5 degrees intermittently achieved superconduction by creating a Josephson junction. The device used used thin layers of palladium to connect to the sides of a tungsten telluride layer surrounded and protected by boron nitride. Another group demonstrated superconduction in molybdenum telluride (MoTe₂) in 2D van der Waals materials using ferroelectric domain walls. The Tc was implied to be higher than typical TMDs (~5–10 K).

A Cornell group added a 3.5-degree twist to an insulator that allowed electrons to slow down and interact strongly, leaving one electron per cell, exhibiting superconduction. Existing theories do not explain this behavior.

Fu and collaborators proposed that electrons arrange to form a repeating crystal that allows the electron grid to float independently of the background atomic nuclei and the electron grid to relax. Its ripples pair electrons the way phonons do, although this is unconfirmed.

Classification

Main article: Superconductor classification

Superconductors are classified according to many criteria. The most common are:

Response to a magnetic field

A superconductor can be Type I, meaning it has a single critical field, above which superconductivity is lost and below which the magnetic field is completely expelled from the superconductor; or Type II, meaning it has two critical fields, between which it allows partial penetration of the magnetic field through isolated points called vortices. Furthermore, in multicomponent superconductors it is possible to combine the two behaviours. In that case the superconductor is of Type-1.5.

Theory of operation

A superconductor is conventional if it is driven by electron–phonon interaction and explained by the BCS theory or its extension, the Eliashberg theory. Otherwise, it is unconventional. Alternatively, a superconductor is called unconventional if the superconducting order parameter transforms according to a non-trivial irreducible representation of the system's point group or space group.

Critical temperature

A superconductor is generally considered high-temperature if it reaches a superconducting state above a temperature of 30 K (−243.15 °C); as in the initial discovery by Georg Bednorz and K. Alex Müller. It may also reference materials that transition to superconductivity when cooled using liquid nitrogen – that is, at only T_c > 77 K, although this is generally used only to emphasize that liquid nitrogen coolant is sufficient. Low temperature superconductors refer to materials with a critical temperature below 30 K, and are cooled mainly by liquid helium (T_c > 4.2 K). One exception to this rule is the iron pnictide group of superconductors that display behaviour and properties typical of high-temperature superconductors, yet some of the group have critical temperatures below 30 K.

Material

Top: Periodic table of superconducting elemental solids and their experimental critical temperature (T)
Bottom: Periodic table of superconducting binary hydrides (0–300 GPa). Theoretical predictions indicated in blue and experimental results in red

Superconductor material classes include chemical elements (e.g. mercury or lead), alloys (such as niobium–titanium, germanium–niobium, and niobium nitride), ceramics (YBCO and magnesium diboride), superconducting pnictides (like fluorine-doped LaOFeAs), single-layer materials such as graphene and transition metal dichalcogenides, or organic superconductors (fullerenes and carbon nanotubes; though perhaps these examples should be included among the chemical elements, as they are composed entirely of carbon).

Elementary properties

Several physical properties of superconductors vary from material to material, such as the critical temperature, the value of the superconducting gap, the critical magnetic field, and the critical current density at which superconductivity is destroyed. On the other hand, there is a class of properties that are independent of the underlying material. The Meissner effect, the quantization of the magnetic flux or permanent currents, i.e. the state of zero resistance are the most important examples. The existence of these "universal" properties is rooted in the nature of the broken symmetry of the superconductor and the emergence of off-diagonal long range order. Superconductivity is a thermodynamic phase, and thus possesses certain distinguishing properties which are largely independent of microscopic details. Off diagonal long range order is closely connected to the formation of Cooper pairs.

Zero electrical DC resistance

Electric cables for accelerators at CERN. Both the massive and slim cables are rated for 12,500 A. Top: regular cables for LEP; bottom: superconductor-based cables for the LHC

Cross section of a preformed superconductor rod from the abandoned Texas Superconducting Super Collider (SSC)

The simplest method to measure the electrical resistance of a sample of some material is to place it in an electrical circuit in series with a current source I and measure the resulting voltage V across the sample. The resistance of the sample is given by Ohm's law as R = V / I. If the voltage is zero, this means that the resistance is zero.

Superconductors are also able to maintain a current with no applied voltage whatsoever, a property exploited in superconducting electromagnets such as those found in MRI machines. Experiments have demonstrated that currents in superconducting coils can persist for years without any measurable degradation. Experimental evidence points to a lifetime of at least 100,000 years. Theoretical estimates for the lifetime of a persistent current can exceed the estimated lifetime of the universe, depending on the wire geometry and the temperature. In practice, currents injected in superconducting coils persisted for 28 years, 7 months, 27 days in a superconducting gravimeter in Belgium, from August 4, 1995 until March 31, 2024. In such instruments, the measurement is based on the monitoring of the levitation of a superconducting niobium sphere with a mass of four grams.

In a normal conductor, an electric current may be visualized as a fluid of electrons moving across a heavy ionic lattice. The electrons are constantly colliding with the ions in the lattice, and during each collision some of the energy carried by the current is absorbed by the lattice and converted into heat, which is essentially the vibrational kinetic energy of the lattice ions. As a result, the energy carried by the current is constantly being dissipated. This is the phenomenon of electrical resistance and Joule heating.

The situation is different in a superconductor. In a conventional superconductor, the electronic fluid cannot be resolved into individual electrons. Instead, it consists of bound pairs of electrons known as Cooper pairs. This pairing is caused by an attractive force between electrons from the exchange of phonons. This pairing is very weak, and small thermal vibrations can fracture the bond. Due to quantum mechanics, the energy spectrum of this Cooper pair fluid possesses an energy gap, meaning there is a minimum amount of energy ΔE that must be supplied in order to excite the fluid. Therefore, if ΔE is larger than the thermal energy of the lattice, given by kT, where k is the Boltzmann constant and T is the temperature, the fluid will not be scattered by the lattice. The Cooper pair fluid is thus a superfluid, meaning it can flow without energy dissipation.

In the class of superconductors known as type II superconductors, including all known high-temperature superconductors, an extremely low but non-zero resistivity appears at temperatures not too far below the nominal superconducting transition when an electric current is applied in conjunction with a strong magnetic field, which may be caused by the electric current. This is due to the motion of magnetic vortices in the electronic superfluid, which dissipates some of the energy carried by the current. If the current is sufficiently small, the vortices are stationary, and the resistivity vanishes. The resistance due to this effect is minuscule compared with that of non-superconducting materials, but must be taken into account in sensitive experiments. However, as the temperature decreases far enough below the nominal superconducting transition, these vortices can become frozen into a disordered but stationary phase known as a "vortex glass". Below this vortex glass transition temperature, the resistance of the material becomes truly zero.

Phase transition

Behavior of heat capacity (c_v, blue) and resistivity (ρ, green) at the superconducting phase transition

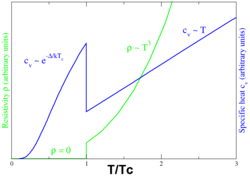
In superconducting materials, the characteristics of superconductivity appear when the temperature T is lowered below a critical temperature T_c. The value of this critical temperature varies from material to material. Conventional superconductors usually have critical temperatures ranging from around 20 K to less than 1 K. Solid mercury, for example, has a critical temperature of 4.2 K. As of 2015, the highest critical temperature found for a conventional superconductor is 203 K for H₂S, although high pressures of approximately 90 gigapascals were required. Cuprate superconductors can have much higher critical temperatures: YBa₂Cu₃O₇, one of the first cuprate superconductors to be discovered, has a critical temperature above 90 K, and mercury-based cuprates have been found with critical temperatures in excess of 130 K. The basic physical mechanism responsible for the high critical temperature is not yet clear. However, it is clear that a two-electron pairing is involved, although the nature of the pairing (${\displaystyle s}$ wave vs. ${\displaystyle d}$ wave) remains controversial.

Similarly, at a fixed temperature below the critical temperature, superconducting materials cease to superconduct when an external magnetic field is applied which is greater than the critical magnetic field. This is because the Gibbs free energy of the superconducting phase increases quadratically with the magnetic field while the free energy of the normal phase is roughly independent of the magnetic field. If the material superconducts in the absence of a field, then the superconducting phase free energy is lower than that of the normal phase and so for some finite value of the magnetic field (proportional to the square root of the difference of the free energies at zero magnetic field) the two free energies will be equal and a phase transition to the normal phase will occur. More generally, a higher temperature and a stronger magnetic field lead to a smaller fraction of electrons that are superconducting and consequently to a longer London penetration depth of external magnetic fields and currents. The penetration depth becomes infinite at the phase transition.

The onset of superconductivity is accompanied by abrupt changes in various physical properties, which is the hallmark of a phase transition. For example, the electronic heat capacity is proportional to the temperature in the normal (non-superconducting) regime. At the superconducting transition, it suffers a discontinuous jump and thereafter ceases to be linear. At low temperatures, it varies instead as e^−α/T for some constant, α. This exponential behavior is one of the pieces of evidence for the existence of the energy gap.

The order of the superconducting phase transition was long a matter of debate. Experiments indicate that the transition is second-order, meaning there is no latent heat. However, in the presence of an external magnetic field there is latent heat, because the superconducting phase has a lower entropy below the critical temperature than the normal phase. It has been experimentally demonstrated that, as a consequence, when the magnetic field is increased beyond the critical field, the resulting phase transition leads to a decrease in the temperature of the superconducting material.

Calculations in the 1970s suggested that it may actually be weakly first-order due to the effect of long-range fluctuations in the electromagnetic field. In the 1980s it was shown theoretically with the help of a disorder field theory, in which the vortex lines of the superconductor play a major role, that the transition is of second order within the type II regime and of first order (i.e., latent heat) within the type I regime, and that the two regions are separated by a tricritical point. The results were strongly supported by Monte Carlo computer simulations.

Meissner effect

Main article: Meissner effect

When a superconductor is placed in a weak external magnetic field H, and cooled below its transition temperature, the magnetic field is ejected. The Meissner effect does not cause the field to be completely ejected but instead, the field penetrates the superconductor but only to a very small distance, characterized by a parameter λ, called the London penetration depth, decaying exponentially to zero within the bulk of the material. The Meissner effect is a defining characteristic of superconductivity. For most superconductors, the London penetration depth is on the order of 100 nm.

The Meissner effect is sometimes confused with the kind of diamagnetism one would expect in a perfect electrical conductor: according to Lenz's law, when a changing magnetic field is applied to a conductor, it will induce an electric current in the conductor that creates an opposing magnetic field. In a perfect conductor, an arbitrarily large current can be induced, and the resulting magnetic field exactly cancels the applied field.

The Meissner effect is distinct from this – it is the spontaneous expulsion that occurs during transition to superconductivity. Suppose we have a material in its normal state, containing a constant internal magnetic field. When the material is cooled below the critical temperature, we would observe the abrupt expulsion of the internal magnetic field, which we would not expect based on Lenz's law.

The Meissner effect was given a phenomenological explanation by the brothers Fritz and Heinz London, who showed that the electromagnetic free energy in a superconductor is minimized provided $${\displaystyle {\mathrm{\nabla }}^2\mathbf{H}={\lambda }^{-2}\mathbf{H}}$$ where H is the magnetic field and λ is the London penetration depth.

This equation, which is known as the London equation, predicts that the magnetic field in a superconductor decays exponentially from whatever value it possesses at the surface.

A superconductor with little or no magnetic field within it is said to be in the Meissner state. The Meissner state breaks down when the applied magnetic field is too large. Superconductors can be divided into two classes according to how this breakdown occurs. In Type I superconductors, superconductivity is abruptly destroyed when the strength of the applied field rises above a critical value H_c. Depending on the geometry of the sample, one may obtain an intermediate state consisting of a baroque pattern of regions of normal material carrying a magnetic field mixed with regions of superconducting material containing no field. In Type II superconductors, raising the applied field past a critical value H_c1 leads to a mixed state (also known as the vortex state) in which an increasing amount of magnetic flux penetrates the material, but there remains no resistance to the flow of electric current as long as the current is not too large. At a second critical field strength H_c2, superconductivity is destroyed. The mixed state is actually caused by vortices in the electronic superfluid, sometimes called fluxons because the flux carried by these vortices is quantized. Most pure elemental superconductors, except niobium and carbon nanotubes, are Type I, while almost all impure and compound superconductors are Type II.

London moment

Main article: London moment

Conversely, a spinning superconductor generates a magnetic field, precisely aligned with the spin axis. The effect, the London moment, was put to good use in Gravity Probe B. This experiment measured the magnetic fields of four superconducting gyroscopes to determine their spin axes. This was critical to the experiment since it is one of the few ways to accurately determine the spin axis of an otherwise featureless sphere.

High-temperature superconductivity

A sample of bismuth strontium calcium copper oxide (BSCCO), which is currently one of the most practical high-temperature superconductors. Notably, it does not contain rare-earths. BSCCO is a cuprate superconductor based on bismuth and strontium. Thanks to its higher operating temperature, cuprates are now becoming competitors for more ordinary niobium-based superconductors, as well as magnesium diboride superconductors.

High-temperature superconductivity (high-T_c or HTS) is superconductivity in materials with a critical temperature (the temperature below which the material behaves as a superconductor) above 77 K (−196.2 °C; −321.1 °F), the boiling point of liquid nitrogen. They are "high-temperature" only relative to previously known superconductors, which function only closer to absolute zero. The first high-temperature superconductor was discovered in 1986 by IBM researchers Georg Bednorz and K. Alex Müller. Although the critical temperature is around 35.1 K (−238.1 °C; −396.5 °F), this material was modified by Ching-Wu Chu to make the first high-temperature superconductor with critical temperature 93 K (−180.2 °C; −292.3 °F). Bednorz and Müller were awarded the Nobel Prize in Physics in 1987 "for their important break-through in the discovery of superconductivity in ceramic materials". Most high-T_c materials are type-II superconductors.

The major advantage of high-temperature superconductors is that they can be cooled using liquid nitrogen, in contrast to previously known superconductors, which require expensive and hard-to-handle coolants, primarily liquid helium. A second advantage of high-T_c materials is they retain their superconductivity in higher magnetic fields than previous materials. This is important when constructing superconducting magnets, a primary application of high-T_c materials.

The majority of high-temperature superconductors are ceramics, rather than the previously known metallic materials. Ceramic superconductors are suitable for some practical uses but encounter manufacturing issues. For example, most ceramics are brittle, which complicates wire fabrication.

The main class of high-temperature superconductors is copper oxides combined with other metals, especially the rare-earth barium copper oxides (REBCOs) such as yttrium barium copper oxide (YBCO). The second class of high-temperature superconductors in the practical classification is the iron-based compounds. Magnesium diboride is sometimes included in high-temperature superconductors: It is relatively simple to manufacture, but it superconducts only below 39 K (−234.2 °C), which makes it unsuitable for liquid nitrogen cooling.

Applications

Main article: Technological applications of superconductivity

Superconductors are promising candidate materials for devising fundamental circuit elements of electronic, spintronic, and quantum technologies. One such example is a superconducting diode, in which supercurrent flows along one direction only, that promise dissipationless superconducting and semiconducting-superconducting hybrid technologies.

Superconducting magnets are some of the most powerful electromagnets known. They are used in MRI/NMR machines, mass spectrometers, the beam-steering magnets used in particle accelerators and plasma confining magnets in some tokamaks. They can also be used for magnetic separation, where weakly magnetic particles are extracted from a background of less or non-magnetic particles, as in the pigment industries. They can also be used in large wind turbines to overcome the restrictions imposed by high electrical currents, with an industrial grade 3.6 megawatt superconducting windmill generator having been tested successfully in Denmark.

In the 1950s and 1960s, superconductors were used to build experimental digital computers using cryotron switches. More recently, superconductors have been used to make digital circuits based on rapid single flux quantum technology and RF and microwave filters for mobile phone base stations.

Superconductors are used to build Josephson junctions which are the building blocks of SQUIDs (superconducting quantum interference devices), the most sensitive magnetometers known. SQUIDs are used in scanning SQUID microscopes and magnetoencephalography. Series of Josephson devices are used to realize the SI volt. Superconducting photon detectors can be realised in a variety of device configurations. Depending on the particular mode of operation, a superconductor–insulator–superconductor Josephson junction can be used as a photon detector or as a mixer. The large resistance change at the transition from the normal to the superconducting state is used to build thermometers in cryogenic micro-calorimeter photon detectors. The same effect is used in ultrasensitive bolometers made from superconducting materials. Superconducting nanowire single-photon detectors offer high speed, low noise single-photon detection and have been employed widely in advanced photon-counting applications.

Other early markets are arising where the relative efficiency, size and weight advantages of devices based on high-temperature superconductivity outweigh the additional costs involved. For example, in wind turbines the lower weight and volume of superconducting generators could lead to savings in construction and tower costs, offsetting the higher costs for the generator and lowering the total levelized cost of electricity (LCOE).

Promising future applications include high-performance smart grid, electric power transmission, transformers, power storage devices, compact fusion power devices, electric motors (e.g. for vehicle propulsion, as in vactrains or maglev trains), magnetic levitation devices, fault current limiters, enhancing spintronic devices with superconducting materials, and superconducting magnetic refrigeration. However, superconductivity is sensitive to moving magnetic fields, so applications that use alternating current (e.g. transformers) will be more difficult to develop than those that rely upon direct current. Compared to traditional power lines, superconducting transmission lines are more efficient and require only a fraction of the space, which would not only lead to a better environmental performance but could also improve public acceptance for expansion of the electric grid. Another attractive industrial aspect is the ability for high power transmission at lower voltages. Advancements in the efficiency of cooling systems and use of cheap coolants such as liquid nitrogen have also significantly decreased cooling costs needed for superconductivity.

Nobel Prizes

As of 2022, there have been five Nobel Prizes in Physics for superconductivity related subjects:

• Heike Kamerlingh Onnes (1913), "for his investigations on the properties of matter at low temperatures which led, inter alia, to the production of liquid helium".
• John Bardeen, Leon N. Cooper, and J. Robert Schrieffer (1972), "for their jointly developed theory of superconductivity, usually called the BCS-theory".
• Leo Esaki, Ivar Giaever, and Brian D. Josephson (1973), "for their experimental discoveries regarding tunneling phenomena in semiconductors and superconductors, respectively" and "for his theoretical predictions of the properties of a supercurrent through a tunnel barrier, in particular those phenomena which are generally known as the Josephson effects".
• Georg Bednorz and K. Alex Müller (1987), "for their important break-through in the discovery of superconductivity in ceramic materials".
• Alexei A. Abrikosov, Vitaly L. Ginzburg, and Anthony J. Leggett (2003), "for pioneering contributions to the theory of superconductors and superfluids".

Superconducting computing

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Superconducting_computing 

Superconducting logic refers to a class of logic circuits or logic gates that use the unique properties of superconductors, including zero-resistance wires, ultrafast Josephson junction switches, and quantization of magnetic flux (fluxoid). As of 2023, superconducting computing is a form of cryogenic computing, as superconductive electronic circuits require cooling to cryogenic temperatures for operation, typically below 10 kelvin. Often superconducting computing is applied to quantum computing, with an important application known as superconducting quantum computing.

Superconducting digital logic circuits use single flux quanta (SFQ), also known as magnetic flux quanta, to encode, process, and transport data. SFQ circuits are made up of active Josephson junctions and passive elements such as inductors, resistors, transformers, and transmission lines. Whereas voltages and capacitors are important in semiconductor logic circuits such as CMOS, currents and inductors are most important in SFQ logic circuits. Power can be supplied by either direct current or alternating current, depending on the SFQ logic family.

Fundamental concepts

The primary advantage of superconducting computing is improved power efficiency over conventional CMOS technology. Much of the power consumed, and heat dissipated, by conventional processors comes from moving information between logic elements rather than the actual logic operations. Because superconductors have zero electrical resistance, little energy is required to move bits within the processor. This is expected to result in power consumption savings of a factor of 500 for an exascale computer. For comparison, in 2014 it was estimated that a 1 exaFLOPS computer built in CMOS logic is estimated to consume some 500 megawatts of electrical power. Superconducting logic can be an attractive option for ultrafast CPUs, where switching times are measured in picoseconds and operating frequencies approach 770 GHz. However, since transferring information between the processor and the outside world does still dissipate energy, superconducting computing was seen as well-suited for computations-intensive tasks where the data largely stays in the cryogenic environment, rather than big data applications where large amounts of information are streamed from outside the processor.

As superconducting logic supports standard digital machine architectures and algorithms, the existing knowledge base for CMOS computing will still be useful in constructing superconducting computers. However, given the reduced heat dissipation, it may enable innovations such as three-dimensional stacking of components. However, as they require inductors, it is harder to reduce their size. As of 2014, devices using niobium as the superconducting material operating at 4 K were considered state-of-the-art. Important challenges for the field were reliable cryogenic memory, as well as moving from research on individual components to large-scale integration.

Josephson junction count is a measure of superconducting circuit or device complexity, similar to the transistor count used for semiconductor integrated circuits.

History

Superconducting computing research has been pursued by the U. S. National Security Agency since the mid-1950s. However, progress could not keep up with the increasing performance of standard CMOS technology. As of 2016 there are no commercial superconducting computers, although research and development continues.

Research in the mid-1950s to early 1960s focused on the cryotron invented by Dudley Allen Buck, but the liquid-helium temperatures and the slow switching time between superconducting and resistive states caused this research to be abandoned. In 1962 Brian Josephson established the theory behind the Josephson effect, and within a few years IBM had fabricated the first Josephson junction. IBM invested heavily in this technology from the mid-1960s to 1983. By the mid-1970s IBM had constructed a superconducting quantum interference device using these junctions, mainly working with lead-based junctions and later switching to lead/niobium junctions. In 1980 the Josephson computer revolution was announced by IBM through the cover page of the May issue of Scientific American. One of the reasons which justified such a large-scale investment lies in that Moore's law - enunciated in 1965 - was expected to slow down and reach a plateau 'soon'. However, on the one hand Moore's law kept its validity, while the costs of improving superconducting devices were basically borne entirely by IBM alone and the latter, however big, could not compete with the whole world of semiconductors which provided nearly limitless resources. Thus, the program was shut down in 1983 because the technology was not considered competitive with standard semiconductor technology. Founded by researchers with this IBM program, HYPRES developed and commercialized superconductor integrated circuits from its commercial superconductor foundry in Elmsford, New York. The Japanese Ministry of International Trade and Industry funded a superconducting research effort from 1981 to 1989 that produced the ETL-JC1, which was a 4-bit machine with 1,000 bits of RAM.

In 1983, Bell Labs created niobium/aluminum oxide Josephson junctions that were more reliable and easier to fabricate. In 1985, the Rapid single flux quantum logic scheme, which had improved speed and energy efficiency, was developed by researchers at Moscow State University. These advances led to the United States' Hybrid Technology Multi-Threaded project, started in 1997, which sought to beat conventional semiconductors to the petaflop computing scale. The project was abandoned in 2000, however, and the first conventional petaflop computer was constructed in 2008. After 2000, attention turned to superconducting quantum computing. The 2011 introduction of reciprocal quantum logic by Quentin Herr of Northrop Grumman, as well as energy-efficient rapid single flux quantum by Hypres, were seen as major advances.

The push for exascale computing beginning in the mid-2010s, as codified in the National Strategic Computing Initiative, was seen as an opening for superconducting computing research as exascale computers based on CMOS technology would be expected to require impractical amounts of electrical power. The Intelligence Advanced Research Projects Activity, formed in 2006, currently coordinates the U. S. Intelligence Community's research and development efforts in superconducting computing.

Conventional computing techniques

Despite the names of many of these techniques containing the word "quantum", they are not necessarily platforms for quantum computing.

Rapid single flux quantum (RSFQ)

Main article: Rapid single flux quantum

Rapid single flux quantum (RSFQ) superconducting logic was developed in the Soviet Union in the 1980s. Information is carried by the presence or absence of a single flux quantum (SFQ). The Josephson junctions are critically damped, typically by addition of an appropriately sized shunt resistor, to make them switch without a hysteresis. Clocking signals are provided to logic gates by separately distributed SFQ voltage pulses.

Power is provided by bias currents distributed using resistors that can consume more than 10 times as much static power than the dynamic power used for computation. The simplicity of using resistors to distribute currents can be an advantage in small circuits and RSFQ continues to be used for many applications where energy efficiency is not of critical importance.

RSFQ has been used to build specialized circuits for high-throughput and numerically intensive applications, such as communications receivers and digital signal processing.

Josephson junctions in RSFQ circuits are biased in parallel. Therefore, the total bias current grows linearly with the Josephson junction count. This currently presents the major limitation on the integration scale of RSFQ circuits, which does not exceed a few tens of thousands of Josephson junctions per circuit.

LR-RSFQ

Reducing the resistor (R) used to distribute currents in traditional RSFQ circuits and adding an inductor (L) in series can reduce the static power dissipation and improve energy efficiency.

Low Voltage RSFQ (LV-RSFQ)

Reducing the bias voltage in traditional RSFQ circuits can reduce the static power dissipation and improve energy efficiency.

Energy-Efficient Single Flux Quantum Technology (ERSFQ/eSFQ)

Efficient rapid single flux quantum (ERSFQ) logic was developed to eliminate the static power losses of RSFQ by replacing bias resistors with sets of inductors and current-limiting Josephson junctions.

Efficient single flux quantum (eSFQ) logic is also powered by direct current, but differs from ERSFQ in the size of the bias current limiting inductor and how the limiting Josephson junctions are regulated.

Reciprocal Quantum Logic (RQL)

Reciprocal Quantum Logic (RQL) was developed to fix some of the problems of RSFQ logic. RQL uses reciprocal pairs of SFQ pulses to encode a logical '1'. Both power and clock are provided by multi-phase alternating current signals. RQL gates do not use resistors to distribute power and thus dissipate negligible static power.

Major RQL gates include: AndOr, AnotB, Set/Reset (with nondestructive readout), which together form a universal logic set and provide memory capabilities.

Adiabatic Quantum Flux Parametron (AQFP)

Main article: Quantum flux parametron

Adiabatic Quantum flux parametron (AQFP) logic was developed for energy-efficient operation and is powered by alternating current.

On January 13, 2021, it was announced that a 2.5 GHz prototype AQFP-based processor called MANA (Monolithic Adiabatic iNtegration Architecture) had achieved an energy efficiency that was 80 times that of traditional semiconductor processors, even accounting for the cooling.

Quantum computing techniques

Main article: Superconducting quantum computing

Superconducting quantum computing is a promising implementation of quantum information technology that involves nanofabricated superconducting electrodes coupled through Josephson junctions. As in a superconducting electrode, the phase and the charge are conjugate variables. There exist three families of superconducting qubits, depending on whether the charge, the phase, or neither of the two are good quantum numbers. These are respectively termed charge qubits, flux qubits, and hybrid qubits.

Connection Machine

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Connection_Machine 

Connection Machine
A Connection Machine CM-2 (1987) and accompanying DataVault on display at the Mimms Museum of Technology and Art in Roswell, Georgia. The CM-2 used the same casing as the CM-1.

The Connection Machine (CM) is a member of a series of massively parallel supercomputers sold by Thinking Machines Corporation. The idea for the Connection Machine grew out of doctoral research on alternatives to the traditional von Neumann architecture of computers by Danny Hillis at Massachusetts Institute of Technology (MIT) in the early 1980s. Starting with CM-1, the machines were intended originally for applications in artificial intelligence (AI) and symbolic processing, but later versions found greater success in the field of computational science.

Origin of idea

Danny Hillis and Sheryl Handler founded Thinking Machines Corporation (TMC) in Waltham, Massachusetts, in 1983, moving in 1984 to Cambridge, MA. At TMC, Hillis assembled a team to develop what would become the CM-1 Connection Machine, a design for a massively parallel hypercube-based arrangement of thousands of microprocessors, springing from his PhD thesis work at MIT in Electrical Engineering and Computer Science (1985). The dissertation won the ACM Distinguished Dissertation prize in 1985, and was presented as a monograph that overviewed the philosophy, architecture, and software for the first Connection Machine, including information on its data routing between central processing unit (CPU) nodes, its memory handling, and the programming language Lisp applied in the parallel machine. Very early concepts contemplated just over a million processors, each connected in a 20-dimensional hypercube, which was later scaled down.

Designs

Thinking Machines Connection Machine models
		1984	1985	1986	1987	1988	1989	1990	1991			1992	1993	1994
		Custom architecture									RISC-based (SPARC)
Entry		—				CM-2a					—
Mainstream		—	CM-1		CM-2			—			CM-5		CM-5E
Hi-end		—				CM-200
expansions
Storage		—			DataVault							—

Thinking Machines CM-2 at the Computer History Museum in Mountain View, California. One of the face plates has been partly removed to show the circuit boards inside.

Each CM-1 microprocessor has its own 4 kilobits of random-access memory (RAM), and the hypercube-based array of them was designed to perform the same operation on multiple data points simultaneously, i.e., to execute tasks in single instruction, multiple data (SIMD) fashion. The CM-1, depending on the configuration, has as many as 65,536 individual processors, each extremely simple, processing one bit at a time. CM-1 and its successor CM-2 take the form of a cube 1.5 meters on a side, divided equally into eight smaller cubes. Each subcube contains 16 printed circuit boards and a main processor called a sequencer. Each circuit board contains 32 chips. Each chip contains a router, 16 processors, and 16 RAMs. The CM-1 as a whole has a 12-dimensional hypercube-based routing network (connecting the 2¹² chips), a main RAM, and an input-output processor (a channel controller). Each router contains five buffers to store the data being transmitted when a clear channel is not available. The engineers had originally calculated that seven buffers per chip would be needed, but this made the chip slightly too large to build. Nobel Prize-winning physicist Richard Feynman had previously calculated that five buffers would be enough, using a differential equation involving the average number of 1 bits in an address. They resubmitted the design of the chip with only five buffers, and when they put the machine together, it worked fine. Each chip is connected to a switching device called a nexus. The CM-1 uses Feynman's algorithm for computing logarithms that he had developed at Los Alamos National Laboratory for the Manhattan Project. It is well suited to the CM-1, using as it did, only shifting and adding, with a small table shared by all the processors. Feynman also discovered that the CM-1 would compute the Feynman diagrams for quantum chromodynamics (QCD) calculations faster than an expensive special-purpose machine developed at Caltech.

To improve its commercial viability, TMC launched the CM-2 in 1987, adding Weitek 3132 floating-point numeric coprocessors and more RAM to the system. Thirty-two of the original one-bit processors shared each numeric processor. The CM-2 can be configured with up to 512 MB of RAM, and a redundant array of independent disks (RAID) hard disk system, called a DataVault, of up to 25 GB. Two later variants of the CM-2 were also produced, the smaller CM-2a with either 4096 or 8192 single-bit processors, and the faster CM-200.

The light panels of FROSTBURG, a CM-5, on display at the National Cryptologic Museum. The panels were used to check the usage of the processing nodes, and to run diagnostics.

Due to its origins in AI research, the software for the CM-1/2/200 single-bit processor was influenced by the Lisp programming language and a version of Common Lisp, *Lisp (spoken: Star-Lisp), was implemented on the CM-1. Other early languages included Karl Sims' IK and Cliff Lasser's URDU. Much system utility software for the CM-1/2 was written in *Lisp. Many applications for the CM-2, however, were written in C*, a data-parallel superset of ANSI C.

With the CM-5, announced in 1991, TMC switched from the CM-2's hypercubic architecture of simple processors to a new and different multiple instruction, multiple data (MIMD) architecture based on a fat tree network of reduced instruction set computing (RISC) SPARC processors. To make programming easier, it was made to simulate a SIMD design. The later CM-5E replaces the SPARC processors with faster SuperSPARCs. A CM-5 was the fastest computer in the world in 1993 according to the TOP500 list, running 1024 cores with Rpeak of 131.0 GFLOPS, and for several years many of the top 10 fastest computers were CM-5s.

Visual design

The CM-5 LED panels could show randomly generated moving patterns that served purely as eye candy, as seen in Jurassic Park.

Connection Machines were noted for their striking visual design. The CM-1 and CM-2 design teams were led by Tamiko Thiel. The physical form of the CM-1, CM-2, and CM-200 chassis was a cube-of-cubes, referencing the machine's internal 12-dimensional hypercube network, with the red light-emitting diodes (LEDs), by default indicating the processor status, visible through the doors of each cube.

By default, when a processor is executing an instruction, its LED is on. In a SIMD program, the goal is to have as many processors as possible working the program at the same time – indicated by having all LEDs being steady on. Those unfamiliar with the use of the LEDs wanted to see the LEDs blink – or even spell out messages to visitors. The result is that finished programs often have superfluous operations to blink the LEDs.

The CM-5, in plan view, had a staircase-like shape, and also had large panels of red blinking LEDs. Prominent sculptor-architect Maya Lin contributed to the CM-5 design.

Surviving examples

Permanent exhibits

• The very first CM-1 is on permanent display in the Computer History Museum, Mountain View, California, which also has two other CM-1s and CM-5.
• There is a decommissioned CM-1 or CM-2 on display in the main building of the Karlsruhe Institute of Technology computer science department. Students have converted it into a Bluetooth-controlled LED matrix display which can be used to play games or display art.
• A CM-2 with flashing red LED arrays and its accompanying DataVault storage unit are on permanent display at the Mimms Museum of Technology and Art in Roswell, Georgia.
• There is a CM-200 on permanent display at École Polytechnique Fédérale de Lausanne in Switzerland, part of the exhibition space of Musée Bolo.

Past exhibits, Museum collections

• The Museum of Modern Art in New York City displayed a CM-2 in 2018. They continue to house the machine in their collection.
• A CM-2 is in the collection of the Swedish National Museum of Science and Technology (Tekniska Museet) in Stockholm, Sweden.
• Several parts of a CM-1 are in the collection of the Smithsonian Institution National Museum of American History, though it may not be a complete example.
• The Living Computers: Museum + Labs in Seattle displayed a CM-2 with flashing LEDs prior to its closing in 2020.^{[19][better source needed]} It is possible this machine is now in private hands, though it is not listed among the objects auctioned by Christie's.

Private collections

• As of 2007, a preserved CM-2a was owned by the Corestore, a type of online-only museum.

References in popular culture

A CM-5 was featured in the film Jurassic Park in the control room for the island (instead of a Cray X-MP supercomputer as in the novel). Two banks, one bank of 4 Units and a single off to the right of the set could be seen in the control room.

The computer mainframes in Fallout 3 were inspired heavily by the CM-5.

Cyberpunk 2077 features numerous CM-1/CM-2 style units in various portions of the game.

The b-side to Clock DVA's 1989 single "The Hacker" is titled "The Connection Machine" in reference to the CM-1.

Nitric oxide

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Nitric_oxide

 

Nitric oxide

Nitric oxide (nitrogen oxide, nitrogen monooxide, or nitrogen monoxide) is a colorless gas with the formula NO. It is one of the principal oxides of nitrogen. Nitric oxide is a free radical: it has an unpaired electron, which is sometimes denoted by a dot in its chemical formula (^•N=O or ^•NO). Nitric oxide is also a heteronuclear diatomic molecule, a class of molecules whose study spawned early modern theories of chemical bonding.

An important intermediate in industrial chemistry, nitric oxide forms in combustion systems and can be generated by lightning in thunderstorms. In mammals, including humans, nitric oxide is a signaling molecule in many physiological and pathological processes. It was proclaimed the "Molecule of the Year" in 1992. The 1998 Nobel Prize in Physiology or Medicine was awarded for discovering nitric oxide's role as a cardiovascular signalling molecule. Its impact extends beyond biology, with applications in medicine, such as the development of sildenafil (Viagra), and in industry, including semiconductor manufacturing.

Nitric oxide should not be confused with nitrogen dioxide (NO₂), a brown gas and major air pollutant, or with nitrous oxide (N₂O), an anesthetic gas.

History

Nitric oxide (NO) was first identified by Joseph Priestley in the late 18th century, originally seen as merely a toxic byproduct of combustion and an environmental pollutant. Its biological significance was later uncovered in the 1980s when researchers Robert F. Furchgott, Louis J. Ignarro, and Ferid Murad discovered its critical role as a vasodilator in the cardiovascular system, a breakthrough that earned them the 1998 Nobel Prize in Physiology or Medicine.

Physical properties

Electronic configuration

The ground-state electronic configuration of NO in united-atom notation is $${\displaystyle (1\sigma {)}^2(2\sigma {)}^2(3\sigma {)}^2(4{\sigma }^{\ast }{)}^2(5\sigma {)}^2(1\pi {)}^4(2{\pi }^{\ast }{)}^1.}$$ The first two orbitals are actually pure atomic 1s_O and 1s_N from oxygen and nitrogen respectively and therefore are usually not noted in the united-atom notation. Orbitals noted with an asterisk are antibonding. The ordering of 5σ and 1π according to their binding energies is subject to discussion. Removal of a 1π electron leads to 6 states whose energies span over a range starting at a lower level than a 5σ electron an extending to a higher level. This is due to the different orbital momentum couplings between a 1π and a 2π electron.

The lone electron in the 2π orbital makes NO a doublet (X ²Π) in its ground state, whose degeneracy is split in the fine structure from spin–orbit coupling with a total momentum J = 3/2 or J = 1/2.

Dipole

The dipole of NO has been measured experimentally to 0.15740 D and is oriented from O to N (⁻NO⁺) due to the transfer of negative electronic charge from oxygen to nitrogen.

Reactions

With di- and triatomic molecules

Upon condensing to a neat liquid, nitric oxide dimerizes to colorless dinitrogen dioxide (O=N–N=O), but the association is weak and reversible. The N–N distance in crystalline NO is 218 pm, nearly twice the N–O distance. Condensation in a highly polar environment instead gives the red alternant isomer O=N–O⁺=N⁻.

Since the heat of formation of ^•NO is endothermic, NO can be decomposed to the elements. Catalytic converters in cars exploit this reaction:

2 ^•NO → O₂ + N₂

When exposed to oxygen, nitric oxide converts into nitrogen dioxide:

2 ^•NO + O₂ → 2 ^•NO₂

This reaction is thought to occur via the intermediates ONOO^• and the red compound ONOONO.

In water, nitric oxide reacts with oxygen to form nitrous acid (HNO₂). The reaction is thought to proceed via the following stoichiometry:

4 ^•NO + O₂ + 2 H₂O → 4 HNO₂

Nitric oxide reacts with fluorine, chlorine, and bromine to form the nitrosyl halides, such as nitrosyl chloride:

2 ^•NO + Cl₂ → 2 NOCl

With NO₂, also a radical, NO combines to form the intensely blue dinitrogen trioxide:

^•NO + ^•NO₂ ⇌ ON−NO₂

Organic chemistry

"Traube reaction" redirects here; not to be confused with Traube purine synthesis.

Nitric oxide rarely sees organic chemistry use. Most reactions with it produce complex mixtures of salts, separable only through careful recrystallization.

The addition of a nitric oxide moiety to another molecule is often referred to as nitrosylation. The Traube reaction is the addition of a two equivalents of nitric oxide onto an enolate, giving a diazeniumdiolate (also called a nitrosohydroxylamine). The product can undergo a subsequent retro-aldol reaction, giving an overall process similar to the haloform reaction. For example, nitric oxide reacts with acetone and an alkoxide to form a diazeniumdiolate on each α position, with subsequent loss of methyl acetate as a by-product:

This reaction, which was discovered around 1898, remains of interest in nitric oxide prodrug research. Nitric oxide can also react directly with sodium methoxide, ultimately forming sodium formate and nitrous oxide by way of an N-methoxydiazeniumdiolate.

Sufficiently basic secondary amines undergo a Traube-like reaction to give NONOates. However, very few nucleophiles undergo the Traube reaction, either failing to adduce NO or immediately decomposing with nitrous oxide release.

Coordination complexes

Main article: Metal nitrosyl

Nitric oxide reacts with transition metals to give complexes called metal nitrosyls. The most common bonding mode of nitric oxide is the terminal linear type (M−NO). Alternatively, nitric oxide can serve as a one-electron pseudohalide. In such complexes, the M−N−O group is characterized by an angle between 120° and 140°. The NO group can also bridge between metal centers through the nitrogen atom in a variety of geometries.

Production and preparation

In commercial settings, nitric oxide is produced by the oxidation of ammonia at 750–900 °C (normally at 850 °C) with platinum as catalyst in the Ostwald process:

4 NH₃ + 5 O₂ → 4 ^•NO + 6 H₂O

The uncatalyzed endothermic reaction of oxygen (O₂) and nitrogen (N₂), which is effected at high temperature (>2000 °C) by lightning has not been developed into a practical commercial synthesis (see Birkeland–Eyde process):

N₂ + O₂ → 2 ^•NO

Laboratory methods

In the laboratory, nitric oxide is conveniently generated by reduction of dilute nitric acid with copper:

8 HNO₃ + 3 Cu → 3 Cu(NO₃)₂ + 4 H₂O + 2 ^•NO

An alternative route involves the reduction of nitrous acid in the form of sodium nitrite or potassium nitrite:

2 NaNO₂ + 2 NaI + 2 H₂SO₄ → I₂ + 2 Na₂SO₄ + 2 H₂O + 2 ^•NO

2 NaNO₂ + 2 FeSO₄ + 3 H₂SO₄ → Fe₂(SO₄)₃ + 2 NaHSO₄ + 2 H₂O + 2 ^•NO

3 KNO₂ + KNO₃ + Cr₂O₃ → 2 K₂CrO₄ + 4 ^•NO

The iron(II) sulfate route is simple and has been used in undergraduate laboratory experiments.

So-called NONOate compounds are also used for nitric oxide generation, especially in biological laboratories. However, other Traube adducts may decompose to instead give nitrous oxide.^[22]

Detection and assay

Nitric oxide (white) in conifer cells, visualized using DAF-2 DA (diaminofluorescein diacetate)

Nitric oxide concentration can be determined using a chemiluminescent reaction involving ozone. A sample containing nitric oxide is mixed with a large quantity of ozone. The nitric oxide reacts with the ozone to produce oxygen and nitrogen dioxide, accompanied with emission of light (chemiluminescence):

^•NO + O₃ → ^•NO₂ + O₂ + hν

which can be measured with a photodetector. The amount of light produced is proportional to the amount of nitric oxide in the sample.

Other methods of testing include electroanalysis (amperometric approach), where ·NO reacts with an electrode to induce a current or voltage change. The detection of NO radicals in biological tissues is particularly difficult due to the short lifetime and concentration of these radicals in tissues. One of the few practical methods is spin trapping of nitric oxide with iron-dithiocarbamate complexes and subsequent detection of the mono-nitrosyl-iron complex with electron paramagnetic resonance (EPR).

A group of fluorescent dye indicators that are also available in acetylated form for intracellular measurements exist. The most common compound is 4,5-diaminofluorescein (DAF-2).

Environmental effects

Main article: NOx

Acid rain deposition

Nitric oxide reacts with the hydroperoxyl radical (HO^•
₂) to form nitrogen dioxide (NO₂), which then can react with a hydroxyl radical (HO^•) to produce nitric acid (HNO₃):

^•NO + HO^•
₂ → ^•NO₂ + HO^•

^•NO₂ + HO^• → HNO₃

Nitric acid, along with sulfuric acid, contributes to acid rain deposition.

Ozone depletion

^•NO participates in ozone layer depletion. Nitric oxide reacts with stratospheric ozone to form O₂ and nitrogen dioxide:

^•NO + O₃ → ^•NO₂ + O₂

This reaction is also utilized to measure concentrations of ^•NO in control volumes.

Precursor to NO₂

As seen in the acid deposition section, nitric oxide can transform into nitrogen dioxide (this can happen with the hydroperoxy radical, HO^•
₂, or diatomic oxygen, O₂). Symptoms of short-term nitrogen dioxide exposure include nausea, dyspnea and headache. Long-term effects could include impaired immune and respiratory function.

Biological functions

Main article: Biological functions of nitric oxide

NO is a gaseous signaling molecule. It is a key vertebrate biological messenger, playing a role in a variety of biological processes. It is a bioproduct in almost all types of organisms, including bacteria, plants, fungi, and animal cells.

Nitric oxide, an endothelium-derived relaxing factor (EDRF), is biosynthesized endogenously from L-arginine, oxygen, and NADPH by various nitric oxide synthase (NOS) enzymes. Reduction of inorganic nitrate may also make nitric oxide. One of the main enzymatic targets of nitric oxide is guanylyl cyclase. The binding of nitric oxide to the heme region of the enzyme leads to activation, in the presence of iron. Nitric oxide is highly reactive (having a lifetime of a few seconds), yet diffuses freely across membranes. These attributes make nitric oxide ideal for a transient paracrine (between adjacent cells) and autocrine (within a single cell) signaling molecule. Once nitric oxide is converted to nitrates and nitrites by oxygen and water, cell signaling is deactivated.

The endothelium (inner lining) of blood vessels uses nitric oxide to signal the surrounding smooth muscle to relax, resulting in vasodilation and increasing blood flow. Sildenafil (Viagra) is a drug that uses the nitric oxide pathway. Sildenafil does not produce nitric oxide, but enhances the signals that are downstream of the nitric oxide pathway by protecting cyclic guanosine monophosphate (cGMP) from degradation by cGMP-specific phosphodiesterase type 5 (PDE5) in the corpus cavernosum, allowing for the signal to be enhanced, and thus vasodilation. Another endogenous gaseous transmitter, hydrogen sulfide (H₂S) works with NO to induce vasodilation and angiogenesis in a cooperative manner.

Nasal breathing produces higher levels of exhaled nitric oxide compared to oral breathing.

Occupational safety and health

In the U.S., the Occupational Safety and Health Administration (OSHA) has set the legal limit (permissible exposure limit) for nitric oxide exposure in the workplace as 25 ppm (30 mg/m³) over an 8-hour workday. The National Institute for Occupational Safety and Health (NIOSH) has set a recommended exposure limit (REL) of 25 ppm (30 mg/m³) over an 8-hour workday. At levels of 100 ppm, nitric oxide is immediately dangerous to life and health.

Explosion hazard

Liquid nitrogen oxide is very sensitive to detonation even in the absence of fuel, and can be initiated as readily as nitroglycerin. Detonation of the endothermic liquid oxide close to its boiling point (−152 °C or −241.6 °F or 121.1 K) generated a 100 kbar pulse and fragmented the test equipment. It is the simplest molecule that is capable of detonation in all three phases. The liquid oxide is sensitive and may explode during distillation, and this has been the cause of industrial accidents. Gaseous nitric oxide detonates at about 2,300 metres per second (8,300 km/h; 5,100 mph), but as a solid it can reach a detonation velocity of 6,100 metres per second (22,000 km/h; 13,600 mph).