Automata-based programming is a programming paradigm in which the program or part of it is thought of as a model of a finite state machine (FSM) or any other (often more complicated) formal automaton.
Sometimes a potentially infinite set of possible states is introduced,
and such a set can have a complicated structure, not just an
enumeration.
FSM-based programming is generally the same, but, formally speaking, doesn't cover all possible variants, as FSM stands for finite state machine, and automata-based programming doesn't necessarily employ FSMs in the strict sense.
The following properties are key indicators for automata-based programming:
Another reason for using the notion of automata-based programming is that the programmer's style of thinking about the program in this technique is very similar to the style of thinking used to solve mathematical tasks using Turing machines, Markov algorithms, etc.
FSM-based programming is generally the same, but, formally speaking, doesn't cover all possible variants, as FSM stands for finite state machine, and automata-based programming doesn't necessarily employ FSMs in the strict sense.
The following properties are key indicators for automata-based programming:
- The time period of the program's execution is clearly separated down to the steps of the automaton. Each of the steps is effectively an execution of a code section (same for all the steps), which has a single entry point. Such a section can be a function or other routine, or just a cycle body. The step section might be divided down to subsections to be executed depending on different states, although this is not necessary.
- Any communication between the steps is only possible via the explicitly noted set of variables named the state. Between any two steps, the program (or its part created using the automata-based technique) can not have implicit components of its state, such as local (stack) variables' values, return addresses, the current instruction pointer, etc. That is, the state of the whole program, taken at any two moments of entering the step of the automaton, can only differ in the values of the variables being considered as the state of the automaton.
Another reason for using the notion of automata-based programming is that the programmer's style of thinking about the program in this technique is very similar to the style of thinking used to solve mathematical tasks using Turing machines, Markov algorithms, etc.
Example
Traditional (imperative) program in C
The program which solves the example task in traditional (imperative) style can look something like this:#include
Automata-based style program
The same task can be solved by thinking in terms of finite state machines. Note that line parsing has three stages: skipping the leading spaces, printing the word and skipping the trailing characters. Let's call them statesbefore, inside and after. The program may now look like this:#include
Although the code now looks longer, it has at least one significant advantage: there's only one reading (that is, call to the
getchar() function) instruction in the program. Besides that, there's only one loop instead of the four the previous versions had.In this program, the body of the
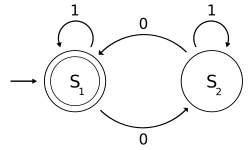
while loop is the automaton step, and the loop itself is the cycle of the automaton's work. The program implements (models) the work of a finite state machine shown on the picture. The N denotes the end of line character, the S denotes spaces, and the A stands for all the other characters. The automaton follows exactly one arrow on each step depending on the current state and the encountered character. Some state switches are accompanied with printing the character; such arrows are marked with asterisks.
It is not absolutely necessary to divide the code down to separate handlers for each unique state. Furthermore, in some cases the very notion of the state can be composed of several variables' values, so that it could be impossible to handle each possible state explicitly. In the discussed program it is possible to reduce the code length by noticing that the actions taken in response to the end of line character are the same for all the possible states. The following program is equal to the previous one but is a bit shorter:
#include
A separate function for the automation step
The most important property of the previous program is that the automaton step code section is clearly localized. With a separate function for it, we can better demonstrate this property:#include
This example clearly demonstrates the basic properties of automata-based code:
- time periods of automaton step executions may not overlap
- the only information passed from the previous step to the next is the explicitly specified automaton state
Explicit state transition table
A finite automaton can be defined by an explicit state transition table. Generally speaking, an automata-based program code can naturally reflect this approach. In the program below there's an array namedthe_table, which defines the table. The rows of the table stand for three states,
while columns reflect the input characters (first for spaces, second
for the end of line character, and the last is for all the other
characters).For every possible combination, the table contains the new state number and the flag, which determines whether the automaton must print the symbol. In a real life task, this could be more complicated; e.g., the table could contain pointers to functions to be called on every possible combination of conditions.
#include
Automation and Automata
Automata-based programming indeed closely matches the programming needs found in the field of automation.A production cycle is commonly modeled as:
- A sequence of stages stepping according to input data (from captors).
- A set of actions performed depending on the current stage.
Example Program
The example presented above could be expressed according to this view like in the following program. Here pseudo-code uses such conventions:- 'set' and 'reset' respectively activate & inactivate a logic variable (here a stage)
- ':' is assignment, '=' is equality test
SPC : ' '
EOL : '\n'
states : (before, inside, after, end, endplusnl)
setState(c) {
if c=EOF then if inside or after then set endplusnl else set end
if before and (c!=SPC and c!=EOL) then set inside
if inside and (c=SPC or c=EOL) then set after
if after and c=EOL then set before
}
doAction(c) {
if inside then write(c)
else if c=EOL or endplusnl then write(EOL)
}
cycle {
set before
loop {
c : readCharacter
setState(c)
doAction(c)
}
until end or endplusnl
}
The separation of routines expressing cycle progression on one side, and actual action on the other (matching input & output) allows clearer and simpler code.
Automation & Events
In the field of automation, stepping from step to step depends on input data coming from the machine itself. This is represented in the program by reading characters from a text. In reality, those data inform about position, speed, temperature, etc. of critical elements of a machine.Like in GUI programming, changes in the machine state can thus be considered as events causing the passage from a state to another, until the final one is reached. The combination of possible states can generate a wide variety of events, thus defining a more complex production cycle. As a consequence, cycles are usually far to be simple linear sequences. There are commonly parallel branches running together and alternatives selected according to different events, schematically represented below:
s:stage c:condition
s1
|
|-c2
|
s2
|
----------
| |
|-c31 |-c32
| |
s31 s32
| |
|-c41 |-c42
| |
----------
|
s4
Using object-oriented capabilities
If the implementation language supports object-oriented programming, a simple refactoring is to encapsulate the automaton into an object, thus hiding its implementation details. For example, an object-oriented version in C++ of the same program is below. A more sophisticated refactoring could employ the State pattern.#include
Note: To minimize changes not directly related to the subject of the article, the input/output functions from the standard library of C are being used. Note the use of the ternary operator, which could also be implemented as if-else.
Applications
Automata-based programming is widely used in lexical and syntactic analyses.Besides that, thinking in terms of automata (that is, breaking the execution process down to automaton steps and passing information from step to step through the explicit state) is necessary for event-driven programming as the only alternative to using parallel processes or threads.
The notions of states and state machines are often used in the field of formal specification. For instance, UML-based software architecture development uses state diagrams to specify the behaviour of the program. Also various communication protocols are often specified using the explicit notion of state.
Thinking in terms of automata (steps and states) can also be used to describe semantics of some programming languages. For example, the execution of a program written in the Refal language is described as a sequence of steps of a so-called abstract Refal machine; the state of the machine is a view (an arbitrary Refal expression without variables).
Continuations in the Scheme language require thinking in terms of steps and states, although Scheme itself is in no way automata-related (it is recursive). To make it possible the call/cc feature to work, implementation needs to be able to catch a whole state of the executing program, which is only possible when there's no implicit part in the state. Such a caught state is the very thing called continuation, and it can be considered as the state of a (relatively complicated) automaton. The step of the automaton is deducing the next continuation from the previous one, and the execution process is the cycle of such steps.
Alexander Ollongren in his book explains the so-called Vienna method of programming languages semantics description which is fully based on formal automata.
The STAT system is a good example of using the automata-based approach; this system, besides other features, includes an embedded language called STATL which is purely automata-oriented.
History
Automata-based techniques were used widely in the domains where there are algorithms based on automata theory, such as formal language analyses.One of the early papers on this is by Johnson et al., 1968.
One of the earliest mentions of automata-based programming as a general technique is found in the paper by Peter Naur, 1963. The author calls the technique Turing machine approach, however no real Turing machine is given in the paper; instead, the technique based on states and steps is described.
Compared against imperative and procedural programming
The notion of state is not exclusive property of automata-based programming. Generally speaking, state (or program state) appears during execution of any computer program, as a combination of all information that can change during the execution. For instance, a state of a traditional imperative program consists of- values of all variables and the information stored within dynamic memory
- values stored in registers
- stack contents (including local variables' values and return addresses)
- current value of the instruction pointer
Having said this, an automata-based program can be considered as a special case of an imperative program, in which implicit part of the state is minimized. The state of the whole program taken at the two distinct moments of entering the step code section can differ in the automaton state only. This simplifies the analysis of the program.
Object-oriented programming relationship
In the theory of object-oriented programming an object is said to have an internal state and is capable of receiving messages, responding to them, sending messages to other objects and changing the internal state during message handling. In more practical terminology, to call an object's method is considered the same as to send a message to the object.Thus, on the one hand, objects from object-oriented programming can be considered as automata (or models of automata) whose state is the combination of internal fields, and one or more methods are considered to be the step. Such methods must not call each other nor themselves, neither directly nor indirectly, otherwise the object can not be considered to be implemented in an automata-based manner.
On the other hand, object is good for implementing a model of an automaton. When the automata-based approach is used within an object-oriented language, an automaton model is usually implemented by a class, the state is represented with internal (private) fields of the class, and the step is implemented as a method; such a method is usually the only non-constant public method of the class (besides constructors and destructors). Other public methods could query the state but don't change it. All the secondary methods (such as particular state handlers) are usually hidden within the private part of the class.






























![{\begin{aligned}&P\left({\text{Searched}}\mid {\text{Known}}\wedge \delta \wedge \pi \right)\\={}&\sum _{\text{Free}}\left[P\left({\text{Searched}}\wedge {\text{Free}}\mid {\text{Known}}\wedge \delta \wedge \pi \right)\right]\\={}&{\frac {\displaystyle \sum _{\text{Free}}\left[P\left({\text{Searched}}\wedge {\text{Free}}\wedge {\text{Known}}\mid \delta \wedge \pi \right)\right]}{\displaystyle P\left({\text{Known}}\mid \delta \wedge \pi \right)}}\\={}&{\frac {\displaystyle \sum _{\text{Free}}\left[P\left({\text{Searched}}\wedge {\text{Free}}\wedge {\text{Known}}\mid \delta \wedge \pi \right)\right]}{\displaystyle \sum _{{\text{Free}}\wedge {\text{Searched}}}\left[P\left({\text{Searched}}\wedge {\text{Free}}\wedge {\text{Known}}\mid \delta \wedge \pi \right)\right]}}\\={}&{\frac {1}{Z}}\times \sum _{\text{Free}}\left[P\left({\text{Searched}}\wedge {\text{Free}}\wedge {\text{Known}}\mid \delta \wedge \pi \right)\right]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8e89d4673f42532ccdc53d02fb71a3435bba866)

![{\begin{aligned}&P\left({\text{Searched}}\mid {\text{Known}}\wedge \delta \wedge \pi \right)\\={}&{\frac {1}{Z}}\sum _{\text{Free}}\left[\prod _{k=1}^{K}\left[P\left(L_{i}\mid K_{i}\wedge \pi \right)\right]\right]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9949ce61882e0abfcd9ddd5e3c24bac2d42f22ae)









![P([{\text{Spam}}=1])=0.75](https://wikimedia.org/api/rest_v1/media/math/render/svg/28323086cc18aa32cd855cad0c2a6895ff317214)

![P(W_{n}\mid [{\text{Spam}}={\text{false}}])={\frac {1+a_{f}^{n}}{2+a_{f}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/993948361ac4f01d716daee166ac993e88dc4fa4)
![P(W_{n}\mid [{\text{Spam}}={\text{true}}])={\frac {1+a_{t}^{n}}{2+a_{t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60b5a547cf7753bb7bc52f2a3b6d6dc841cb87eb)








![{\begin{aligned}&P({\text{Spam}}\mid w_{0}\wedge \cdots \wedge w_{N-1})\\={}&{\frac {\displaystyle P({\text{Spam}})\prod _{n=0}^{N-1}[P(w_{n}\mid {\text{Spam}})]}{\displaystyle \sum _{\text{Spam}}[P({\text{Spam}})\prod _{n=0}^{N-1}[P(w_{n}\mid {\text{Spam}})]]}}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f2f48d2a47db007ecbfd26c3ab235518d3bad7e)
![{\begin{aligned}&{\frac {P([{\text{Spam}}={\text{true}}]\mid w_{0}\wedge \cdots \wedge w_{N-1})}{P([{\text{Spam}}={\text{false}}]\mid w_{0}\wedge \cdots \wedge w_{N-1})}}\\={}&{\frac {P([{\text{Spam}}={\text{true}}])}{P([{\text{Spam}}={\text{false}}])}}\times \prod _{n=0}^{N-1}\left[{\frac {P(w_{n}\mid [{\text{Spam}}={\text{true}}])}{P(w_{n}\mid [{\text{Spam}}={\text{false}}])}}\right]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97e9cfd466e7d8bd8cdb01c3da2e12e2adec4a78)

![\Pr {\begin{cases}Ds{\begin{cases}Sp(\pi ){\begin{cases}Va:{\text{Spam}},W_{0},W_{1}\ldots W_{N-1}\\Dc:{\begin{cases}P({\text{Spam}}\land W_{0}\land \ldots \land W_{n}\land \ldots \land W_{N-1})\\=P({\text{Spam}})\prod _{n=0}^{N-1}P(W_{n}\mid {\text{Spam}})\end{cases}}\\Fo:{\begin{cases}P({\text{Spam}}):{\begin{cases}P([{\text{Spam}}={\text{false}}])=0.25\\P([{\text{Spam}}={\text{true}}])=0.75\end{cases}}\\P(W_{n}\mid {\text{Spam}}):{\begin{cases}P(W_{n}\mid [{\text{Spam}}={\text{false}}])\\={\frac {1+a_{f}^{n}}{2+a_{f}}}\\P(W_{n}\mid [{\text{Spam}}={\text{true}}])\\={\frac {1+a_{t}^{n}}{2+a_{t}}}\end{cases}}\\\end{cases}}\\\end{cases}}\\{\text{Identification (based on }}\delta )\end{cases}}\\Qu:P({\text{Spam}}\mid w_{0}\land \ldots \land w_{n}\land \ldots \land w_{N-1})\end{cases}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/298794c932a3de3a1ecf61aca016e058488bd396)



















![Pr{\begin{cases}Ds{\begin{cases}Sp(\pi ){\begin{cases}Va:\\S^{0},\cdots ,S^{T},O^{0},\cdots ,O^{T}\\Dc:\\{\begin{cases}&P\left(S^{0}\wedge \cdots \wedge S^{T}\wedge O^{0}\wedge \cdots \wedge O^{T}|\pi \right)\\=&P\left(S^{0}\wedge O^{0}\right)\times \prod _{t=1}^{T}\left[P\left(S^{t}|S^{t-1}\right)\times P\left(O^{t}|S^{t}\right)\right]\end{cases}}\\Fo:\\{\begin{cases}P\left(S^{0}\wedge O^{0}\right)\\P\left(S^{t}|S^{t-1}\right)\\P\left(O^{t}|S^{t}\right)\end{cases}}\end{cases}}\\Id\end{cases}}\\Qu:\\{\begin{cases}{\begin{array}{l}P\left(S^{t+k}|O^{0}\wedge \cdots \wedge O^{t}\right)\\\left(k=0\right)\equiv {\text{Filtering}}\\\left(k>0\right)\equiv {\text{Prediction}}\\\left(k<0\right)\equiv {\text{Smoothing}}\end{array}}\end{cases}}\end{cases}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0afa2e8c338bbd3139f5bda7b207e7a4c982e260)
![Pr{\begin{cases}Ds{\begin{cases}Sp(\pi ){\begin{cases}Va:\\S^{0},\cdots ,S^{T},O^{0},\cdots ,O^{T}\\Dc:\\{\begin{cases}&P\left(S^{0}\wedge \cdots \wedge O^{T}|\pi \right)\\=&\left[{\begin{array}{c}P\left(S^{0}\wedge O^{0}|\pi \right)\\\prod _{t=1}^{T}\left[P\left(S^{t}|S^{t-1}\wedge \pi \right)\times P\left(O^{t}|S^{t}\wedge \pi \right)\right]\end{array}}\right]\end{cases}}\\Fo:\\{\begin{cases}P\left(S^{t}\mid S^{t-1}\wedge \pi \right)\equiv G\left(S^{t},A\bullet S^{t-1},Q\right)\\P\left(O^{t}\mid S^{t}\wedge \pi \right)\equiv G\left(O^{t},H\bullet S^{t},R\right)\end{cases}}\end{cases}}\\Id\end{cases}}\\Qu:\\P\left(S^{T}\mid O^{0}\wedge \cdots \wedge O^{T}\wedge \pi \right)\end{cases}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84763c1c72220bff2b98a20efd9aeee8910ac015)



![\Pr {\begin{cases}Ds{\begin{cases}Sp(\pi ){\begin{cases}Va:\\S^{0},\ldots ,S^{T},O^{0},\ldots ,O^{T}\\Dc:\\{\begin{cases}&P\left(S^{0}\wedge \cdots \wedge O^{T}\mid \pi \right)\\=&\left[{\begin{array}{c}P\left(S^{0}\wedge O^{0}\mid \pi \right)\\\prod _{t=1}^{T}\left[P\left(S^{t}\mid S^{t-1}\wedge \pi \right)\times P\left(O^{t}\mid S^{t}\wedge \pi \right)\right]\end{array}}\right]\end{cases}}\\Fo:\\{\begin{cases}P\left(S^{0}\wedge O^{0}\mid \pi \right)\equiv {\text{Matrix}}\\P\left(S^{t}\mid S^{t-1}\wedge \pi \right)\equiv {\text{Matrix}}\\P\left(O^{t}\mid S^{t}\wedge \pi \right)\equiv {\text{Matrix}}\end{cases}}\end{cases}}\\Id\end{cases}}\\Qu:\\\max _{S^{1}\wedge \cdots \wedge S^{T-1}}\left[P\left(S^{1}\wedge \cdots \wedge S^{T-1}\mid S^{T}\wedge O^{0}\wedge \cdots \wedge O^{T}\wedge \pi \right)\right]\end{cases}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fdb4b04f2fcf2e32cd28a2505e30d2b6b534351)


