According to the Big Bang model, the
universe expanded from an extremely dense and hot state and continues to expand.
The
Big Bang theory is the prevailing
cosmological model for the
universe from the
earliest known periods through its subsequent large-scale evolution.
[1][2][3] The model accounts for the fact that the universe
expanded from a very high density and high temperature state,
[4][5] and offers a comprehensive explanation for a broad range of phenomena, including the abundance of light elements, the
cosmic microwave background,
large scale structure and
Hubble's Law.
[6] If the known laws of physics are extrapolated beyond where they are valid, there is a
singularity. Modern measurements place this moment at approximately 13.8
billion years ago, which is thus considered the
age of the universe.
[7] After the initial expansion, the universe cooled sufficiently to allow the formation of
subatomic particles, and later simple
atoms. Giant clouds of these primordial elements later coalesced through
gravity to form
stars and
galaxies.
Since
Georges Lemaître first noted, in 1927, that an expanding universe might be traced back in time to an originating single point, scientists have built on his idea of cosmic expansion. While the scientific community was once divided between supporters of two different expanding universe theories, the Big Bang and the
Steady State theory, accumulated
empirical evidence provides strong support for the former.
[8] In 1929, from analysis of galactic
redshifts,
Edwin Hubble concluded that galaxies are drifting apart, important observational evidence consistent with the hypothesis of an expanding universe. In 1965, the
cosmic microwave background radiation was discovered, which was crucial evidence in favor of the Big Bang model, since that theory predicted the existence of background radiation throughout the universe before it was discovered. More recently, measurements of the redshifts of supernovae indicate that the
expansion of the universe is accelerating, an observation attributed to
dark energy's existence.
[9] The known
physical laws of nature can be used to calculate the characteristics of the universe in detail back in time to an initial state of extreme
density and
temperature.
[10][11][12]
Overview
Hubble observed that the distances to faraway galaxies were strongly correlated with their
redshifts. This was interpreted to mean that all distant galaxies and clusters are receding away from our vantage point with an apparent velocity proportional to their distance: that is, the farther they are, the faster they move away from us, regardless of direction.
[17] Assuming the
Copernican principle (that the Earth is not the center of the universe), the only remaining interpretation is that all observable regions of the universe are receding from all others. Since we know that the distance between galaxies increases today, it must mean that in the past galaxies were closer together. The continuous expansion of the universe implies that the universe was denser and hotter in the past.
Large
particle accelerators can replicate the conditions that prevailed after the early moments of the universe, resulting in confirmation and refinement of the details of the Big Bang model. However, these accelerators can only probe so far into
high energy regimes. Consequently, the state of the universe in the earliest instants of the Big Bang expansion is still poorly understood and an area of open investigation and indeed, speculation.
The first
subatomic particles included
protons,
neutrons, and
electrons. Though simple
atomic nuclei formed within the first three minutes after the Big Bang, thousands of years passed before the first
electrically neutral atoms formed. The majority of atoms produced by the Big Bang were
hydrogen, along with
helium and traces of
lithium. Giant clouds of these primordial elements later coalesced through
gravity to form
stars and galaxies, and the heavier elements were synthesized either
within stars or
during supernovae.
The Big Bang theory offers a comprehensive explanation for a broad range of observed phenomena, including the abundance of light elements, the
cosmic microwave background,
large scale structure, and
Hubble's Law.
[6] The framework for the Big Bang model relies on
Albert Einstein's theory of
general relativity and on simplifying assumptions such as
homogeneity and
isotropy of space. The governing equations were formulated by
Alexander Friedmann, and similar solutions were worked on by
Willem de Sitter. Since then, astrophysicists have incorporated observational and theoretical additions into the Big Bang model, and its
parametrization as the
Lambda-CDM model serves as the framework for current investigations of theoretical cosmology. The
Lambda-CDM model is the standard model of Big Bang cosmology, the simplest model that provides a reasonably good account of various observations about the universe.
Timeline
Singularity
Extrapolation of the expansion of the universe backwards in time using general relativity yields an
infinite density and temperature at a finite time in the past.
[18] This
singularity signals the breakdown of
general relativity and thus, all the
laws of physics. How closely this can be extrapolated toward the singularity is debated—certainly no closer than the end of the
Planck epoch. This singularity is sometimes called "the Big Bang",
[19] but the term can also refer to the early hot, dense phase itself,
[20][notes 1] which can be considered the "birth" of our universe. Based on measurements of the expansion using
Type Ia supernovae and measurements of temperature fluctuations in the
cosmic microwave background, the universe has an estimated
age of 13.799 ± 0.021 billion years.
[21] The agreement of these three independent measurements strongly supports the
ΛCDM model that describes in detail the contents of the universe.
Inflation and baryogenesis
The earliest phases of the Big Bang are subject to much speculation. In the most common models the universe was filled
homogeneously and
isotropically with a very high
energy density and huge temperatures and
pressures and was very rapidly expanding and cooling. Approximately 10
−37 seconds into the expansion, a
phase transition caused a
cosmic inflation, during which the universe grew
exponentially.
[22] After inflation stopped, the universe consisted of a
quark–gluon plasma, as well as all other
elementary particles.
[23] Temperatures were so high that the random motions of particles were at
relativistic speeds, and
particle–antiparticle pairs of all kinds were being continuously created and destroyed in collisions.
[4] At some point an unknown reaction called
baryogenesis violated the conservation of
baryon number, leading to a very small excess of
quarks and
leptons over antiquarks and antileptons—of the order of one part in 30 million. This resulted in the predominance of
matter over
antimatter in the present universe.
[24]
Cooling
Panoramic view of the entire
near-infrared sky reveals the distribution of galaxies beyond the Milky Way. Galaxies are color-coded by
redshift.
The universe continued to decrease in density and fall in temperature, hence the typical energy of each particle was decreasing.
Symmetry breaking phase transitions put the
fundamental forces of physics and the parameters of
elementary particles into their present form.
[25] After about 10
−11 seconds, the picture becomes less speculative, since particle energies drop to values that can be attained in
particle physics experiments. At about 10
−6 seconds, quarks and gluons combined to form
baryons such as protons and neutrons. The small excess of quarks over antiquarks led to a small excess of baryons over antibaryons. The temperature was now no longer high enough to create new proton–antiproton pairs (similarly for neutrons–antineutrons), so a mass annihilation immediately followed, leaving just one in 10
10 of the original protons and neutrons, and none of their antiparticles. A similar process happened at about 1 second for electrons and positrons. After these annihilations, the remaining protons, neutrons and electrons were no longer moving relativistically and the energy density of the universe was dominated by
photons (with a minor contribution from
neutrinos).
A few minutes into the expansion, when the temperature was about a billion (one thousand million; 10
9; SI prefix
giga-)
kelvin and the density was about that of air, neutrons combined with protons to form the universe's
deuterium and helium
nuclei in a process called
Big Bang nucleosynthesis.
[26] Most protons remained uncombined as hydrogen nuclei. As the universe cooled, the
rest mass energy density of matter came to gravitationally dominate that of the photon
radiation. After about 379,000 years the electrons and nuclei combined into atoms (mostly hydrogen); hence the radiation decoupled from matter and continued through space largely unimpeded. This relic radiation is known as the
cosmic microwave background radiation.
[27] The
chemistry of life may have begun shortly after the Big Bang,
13.8 billion years ago, during a habitable epoch when the
universe was only 10–17 million years old.
[28][29][30]
Structure formation

Over a long period of time, the slightly denser regions of the nearly uniformly distributed matter gravitationally attracted nearby matter and thus grew even denser, forming gas clouds, stars, galaxies, and the other astronomical structures observable today.
[4] The details of this process depend on the amount and type of matter in the universe. The four possible types of matter are known as
cold dark matter,
warm dark matter,
hot dark matter, and
baryonic matter. The best measurements available (from
WMAP) show that the data is well-fit by a Lambda-CDM model in which dark matter is assumed to be cold (warm dark matter is ruled out by early
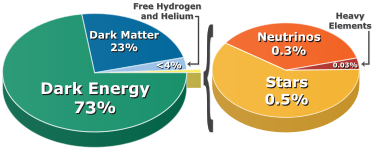
reionization[32]), and is estimated to make up about 23% of the matter/energy of the universe, while baryonic matter makes up about 4.6%.
[33] In an "extended model" which includes hot dark matter in the form of
neutrinos, then if the "physical baryon density" Ω
bh
2 is estimated at about 0.023 (this is different from the 'baryon density' Ω
b expressed as a fraction of the total matter/energy density, which as noted above is about 0.046), and the corresponding cold dark matter density Ω
ch
2 is about 0.11, the corresponding neutrino density Ω
vh
2 is estimated to be less than 0.0062.
[33]
Cosmic acceleration

Lambda-CDM, accelerated expansion of the universe. The time-line in this schematic diagram extends from the big bang/inflation era 13.7 Gyr ago to the present cosmological time.
Independent lines of evidence from Type Ia supernovae and the
CMB imply that the universe today is dominated by a mysterious form of energy known as
dark energy, which apparently permeates all of space. The observations suggest 73% of the total energy density of today's universe is in this form. When the universe was very young, it was likely infused with dark energy, but with less space and everything closer together, gravity predominated, and it was slowly braking the expansion. But eventually, after numerous billion years of expansion, the growing abundance of dark energy caused the
expansion of the universe to slowly begin to accelerate. Dark energy in its simplest formulation takes the form of the
cosmological constant term in
Einstein's field equations of general relativity, but its composition and mechanism are unknown and, more generally, the details of its
equation of state and relationship with the
Standard Model of particle physics continue to be investigated both observationally and theoretically.
[9]
All of this cosmic evolution after the
inflationary epoch can be rigorously described and modelled by the ΛCDM model of cosmology, which uses the independent frameworks of quantum mechanics and Einstein's General Relativity. There is no well-supported model describing the action prior to 10
−15 seconds or so. Apparently a new unified theory of
quantum gravitation is needed to break this barrier. Understanding this earliest of eras in the history of the universe is currently one of the greatest
unsolved problems in physics.
Underlying assumptions
The Big Bang theory depends on two major assumptions: the universality of
physical laws and the
cosmological principle. The cosmological principle states that on large scales the universe is
homogeneous and
isotropic.
These ideas were initially taken as postulates, but today there are efforts to test each of them. For example, the first assumption has been tested by observations showing that largest possible deviation of the
fine structure constant over much of the
age of the universe is of order 10
−5.
[34] Also, general relativity has passed stringent
tests on the scale of the Solar System and binary stars.
[notes 2]
If the large-scale universe appears isotropic as viewed from Earth, the cosmological principle can be derived from the simpler
Copernican principle, which states that there is no preferred (or special) observer or vantage point. To this end, the cosmological principle has been confirmed to a level of 10
−5 via observations of the CMB. The universe has been measured to be homogeneous on the largest scales at the 10% level.
[35]
Expansion of space
General relativity describes spacetime by a
metric, which determines the distances that separate nearby points. The points, which can be galaxies, stars, or other objects, themselves are specified using a
coordinate chart or "grid" that is laid down over all
spacetime. The cosmological principle implies that the metric should be
homogeneous and
isotropic on large scales, which uniquely singles out the
Friedmann–Lemaître–Robertson–Walker metric (FLRW metric). This metric contains a
scale factor, which describes how the size of the universe changes with time. This enables a convenient choice of a
coordinate system to be made, called
comoving coordinates. In this coordinate system the grid expands along with the universe, and objects that are moving only due to the expansion of the universe remain at fixed points on the grid. While their
coordinate distance (
comoving distance) remains constant, the
physical distance between two such comoving points expands proportionally with the
scale factor of the universe.
[36]
The Big Bang is not an explosion of matter moving outward to fill an empty universe. Instead,
space itself expands with time everywhere and increases the physical distance between two comoving points. In other words, the Big Bang is not an explosion
in space, but rather an expansion
of space.
[4] Because the FLRW metric assumes a uniform distribution of mass and energy, it applies to our universe only on large scales—local concentrations of matter such as our galaxy are gravitationally bound and as such do not experience the large-scale expansion of space.
[37]
Horizons
An important feature of the Big Bang spacetime is the presence of
horizons. Since the universe has a finite age, and light travels at a finite speed, there may be events in the past whose light has not had time to reach us. This places a limit or a
past horizon on the most distant objects that can be observed. Conversely, because space is expanding, and more distant objects are receding ever more quickly, light emitted by us today may never "catch up" to very distant objects. This defines a
future horizon, which limits the events in the future that we will be able to influence. The presence of either type of horizon depends on the details of the FLRW model that describes our universe. Our understanding of the universe back to very early times
suggests that there is a past horizon, though in practice our view is also limited by the opacity of the universe at early times. So our view cannot extend further backward in time, though the horizon recedes in space. If the expansion of the universe continues to
accelerate, there is a future horizon as well.
[38]
History
Etymology
English astronomer
Fred Hoyle is credited with coining the term "Big Bang" during a 1949 BBC radio broadcast. It is popularly reported that Hoyle, who favored an alternative "
steady state" cosmological model, intended this to be pejorative, but Hoyle explicitly denied this and said it was just a striking image meant to highlight the difference between the two models.
[39][40][41]:129
Development
XDF size compared to the size of the
moon - several thousand
galaxies, each consisting of billions of
stars, are in this small view.
XDF (2012) view - each light speck is a galaxy - some of these are as old as 13.2 billion years
[42] - the universe is estimated to contain 200 billion galaxies.
XDF image shows fully mature galaxies in the foreground plane - nearly mature galaxies from 5 to 9 billion years ago -
protogalaxies, blazing with
young stars, beyond 9 billion years.
The Big Bang theory developed from observations of the structure of the universe and from theoretical considerations. In 1912
Vesto Slipher measured the first
Doppler shift of a "
spiral nebula" (spiral nebula is the obsolete term for spiral galaxies), and soon discovered that almost all such nebulae were receding from Earth. He did not grasp the cosmological implications of this fact, and indeed at the time it was
highly controversial whether or not these nebulae were "island universes" outside our
Milky Way.
[43][44] Ten years later, Alexander Friedmann, a
Russian cosmologist and
mathematician, derived the
Friedmann equations from
Albert Einstein's equations of general relativity, showing that the universe might be expanding in contrast to the
static universe model advocated by Einstein at that time.
[45] In 1924 Edwin Hubble's measurement of the great distance to the nearest spiral nebulae showed that these systems were indeed other galaxies. Independently deriving Friedmann's equations in 1927,
Georges Lemaître, a Belgian physicist and
Roman Catholic priest, proposed that the inferred recession of the nebulae was due to the expansion of the universe.
[46]
In 1931 Lemaître went further and suggested that the evident expansion of the universe, if projected back in time, meant that the further in the past the smaller the universe was, until at some finite time in the past all the mass of the universe was concentrated into a single point, a "primeval atom" where and when the fabric of time and space came into existence.
[47]
Starting in 1924, Hubble painstakingly developed a series of distance indicators, the forerunner of the
cosmic distance ladder, using the 100-inch (2.5 m)
Hooker telescope at
Mount Wilson Observatory. This allowed him to estimate distances to galaxies whose redshifts had already been measured, mostly by Slipher. In 1929 Hubble discovered a correlation between distance and recession velocity—now known as
Hubble's law.
[17][48] Lemaître had already shown that this was expected, given the
cosmological principle.
[9]
In the 1920s and 1930s almost every major cosmologist preferred an eternal
steady state universe, and several complained that the beginning of time implied by the Big Bang imported religious concepts into physics; this objection was later repeated by supporters of the steady state theory.
[49] This perception was enhanced by the fact that the originator of the Big Bang theory, Monsignor
Georges Lemaître, was a Roman Catholic priest.
[50] Arthur Eddington agreed with
Aristotle that the universe did not have a beginning in time, viz., that
matter is eternal. A beginning in time was "repugnant" to him.
[51][52] Lemaître, however, thought that
If the world has begun with a single quantum, the notions of space and time would altogether fail to have any meaning at the beginning; they would only begin to have a sensible meaning when the original quantum had been divided into a sufficient number of quanta. If this suggestion is correct, the beginning of the world happened a little before the beginning of space and time.[53]
During the 1930s other ideas were proposed as
non-standard cosmologies to explain Hubble's observations, including the
Milne model,
[54] the
oscillatory universe (originally suggested by Friedmann, but advocated by Albert Einstein and
Richard Tolman)
[55] and
Fritz Zwicky's
tired light hypothesis.
[56]
After
World War II, two distinct possibilities emerged. One was Fred Hoyle's
steady state model, whereby new matter would be created as the universe seemed to expand. In this model the universe is roughly the same at any point in time.
[57] The other was Lemaître's Big Bang theory, advocated and developed by
George Gamow, who introduced
big bang nucleosynthesis (BBN)
[58] and whose associates,
Ralph Alpher and
Robert Herman, predicted the
cosmic microwave background radiation (CMB).
[59] Ironically, it was Hoyle who coined the phrase that came to be applied to Lemaître's theory, referring to it as "this
big bang idea" during a
BBC Radio broadcast in March 1949.
[41]:129[notes 3] For a while, support was split between these two theories. Eventually, the observational evidence, most notably from radio
source counts, began to favor Big Bang over Steady State. The discovery and confirmation of the cosmic microwave background radiation in 1965
[61] secured the Big Bang as the best theory of the origin and evolution of the universe. Much of the current work in cosmology includes understanding how galaxies form in the context of the Big Bang, understanding the physics of the universe at earlier and earlier times, and reconciling observations with the basic theory.
In 1968 and 1970,
Roger Penrose,
Stephen Hawking, and
George F. R. Ellis published papers where they showed that
mathematical singularities were an inevitable initial condition of
general relativistic models of the Big Bang.
[62][63] Then, from the 1970s to the 1990s, cosmologists worked on characterizing the features of the Big Bang universe and resolving outstanding problems. In 1981,
Alan Guth made a breakthrough in theoretical work on resolving certain outstanding theoretical
problems in the Big Bang theory with the introduction of an epoch of rapid expansion in the early universe he called "
inflation".
[64] Meanwhile, during these decades, two questions in
observational cosmology that generated much discussion and disagreement were over the precise values of the
Hubble Constant[65] and the matter-density of the universe (before the discovery of
dark energy, thought to be the key predictor for the eventual
fate of the universe).
[66] In the mid-1990s observations of certain
globular clusters appeared to indicate that they were about 15 billion years old, which
conflicted with most then-current estimates of the age of the universe (and indeed with the age measured today). This issue was later resolved when new computer simulations, which included the effects of mass loss due to
stellar winds, indicated a much younger age for globular clusters.
[67] While there still remain some questions as to how accurately the ages of the clusters are measured, globular clusters are of interest to cosmology as some of the oldest objects in the universe.
Significant progress in Big Bang cosmology have been made since the late 1990s as a result of advances in
telescope technology as well as the analysis of data from satellites such as
COBE,
[68] the
Hubble Space Telescope and
WMAP.
[69] Cosmologists now have fairly precise and accurate measurements of many of the parameters of the Big Bang model, and have made the unexpected discovery that the expansion of the universe appears to be accelerating.
Observational evidence

Artist's depiction of the
WMAP satellite gathering data to help scientists understand the Big Bang
The earliest and most direct observational evidence of the validity of the theory are the expansion of the universe according to
Hubble's law (as indicated by the redshifts of galaxies), discovery and measurement of the
cosmic microwave background and the relative abundances of light elements produced by
Big Bang nucleosynthesis. More recent evidence includes observations of
galaxy formation and evolution, and the distribution of
large-scale cosmic structures,
[71] These are sometimes called the "four pillars" of the Big Bang theory.
[72]
Precise modern models of the Big Bang appeal to various exotic physical phenomena that have not been observed in terrestrial laboratory experiments or incorporated into the
Standard Model of
particle physics. Of these features,
dark matter is currently subjected to the most active laboratory investigations.
[73] Remaining issues include the
cuspy halo problem and the
dwarf galaxy problem of cold dark matter. Dark energy is also an area of intense interest for scientists, but it is not clear whether direct detection of dark energy will be possible.
[74] Inflation and baryogenesis remain more speculative features of current Big Bang models. Viable, quantitative explanations for such phenomena are still being sought. These are currently unsolved problems in physics.
Hubble's law and the expansion of space
Observations of distant galaxies and
quasars show that these objects are redshifted—the
light emitted from them has been shifted to longer wavelengths. This can be seen by taking a
frequency spectrum of an object and matching the
spectroscopic pattern of
emission lines or
absorption lines corresponding to
atoms of the
chemical elements interacting with the light. These redshifts are
uniformly isotropic, distributed evenly among the observed objects in all directions. If the redshift is interpreted as a Doppler shift, the recessional
velocity of the object can be calculated. For some galaxies, it is possible to estimate distances via the
cosmic distance ladder. When the recessional velocities are plotted against these distances, a linear relationship known as Hubble's law is observed:
[17]
- v = H0D,
where
Hubble's law has two possible explanations. Either we are at the center of an explosion of galaxies—which is untenable given the
Copernican principle—or the universe is
uniformly expanding everywhere. This universal expansion was predicted from general relativity by Alexander Friedmann in 1922
[45] and Georges Lemaître in 1927,
[46] well before Hubble made his 1929 analysis and observations, and it remains the cornerstone of the Big Bang theory as developed by
Friedmann, Lemaître, Robertson, and Walker.
The theory requires the relation
v =
HD to hold at all times, where
D is the
comoving distance,
v is the
recessional velocity, and
v,
H, and
D vary as the universe expands (hence we write
H0 to denote the present-day Hubble "constant"). For distances much smaller than the size of the
observable universe, the Hubble redshift can be thought of as the Doppler shift corresponding to the recession velocity
v. However, the redshift is not a true Doppler shift, but rather the result of the expansion of the universe between the time the light was emitted and the time that it was detected.
[75]
That
space is undergoing metric expansion is shown by direct observational evidence of the
Cosmological principle and the Copernican principle, which together with Hubble's law have no other explanation. Astronomical redshifts are extremely
isotropic and
homogeneous,
[17] supporting the Cosmological principle that the universe looks the same in all directions, along with much other evidence. If the redshifts were the result of an explosion from a center distant from us, they would not be so similar in different directions.
Measurements of the effects of the
cosmic microwave background radiation on the dynamics of distant astrophysical systems in 2000 proved the Copernican principle, that, on a cosmological scale, the Earth is not in a central position.
[76] Radiation from the Big Bang was demonstrably warmer at earlier times throughout the universe. Uniform cooling of the cosmic microwave background over billions of years is explainable only if the universe is experiencing a metric expansion, and excludes the possibility that we are near the unique center of an explosion.
Cosmic microwave background radiation

9 year
WMAP image of the cosmic microwave background radiation (2012).
[77][78] The radiation is
isotropic to roughly one part in 100,000.
[79]
In 1965,
Arno Penzias and
Robert Wilson serendipitously discovered the cosmic background radiation, an omnidirectional signal in the
microwave band.
[61] Their discovery provided substantial confirmation of the big-bang predictions by Alpher, Herman and Gamow around 1950. Through the 1970s the radiation was found to be approximately consistent with a black body spectrum in all directions; this spectrum has been redshifted by the expansion of the universe, and today corresponds to approximately 2.725 K. This tipped the balance of evidence in favor of the Big Bang model, and Penzias and Wilson were awarded a
Nobel Prize in 1978.

The cosmic microwave background spectrum measured by the FIRAS instrument on the COBE satellite is the most-precisely measured black body spectrum in nature.
[80] The
data points and
error bars on this graph are obscured by the theoretical curve.
The
surface of last scattering corresponding to emission of the CMB occurs shortly after
recombination, the epoch when neutral hydrogen becomes stable. Prior to this, the universe comprised a hot dense photon-baryon plasma sea where photons were quickly
scattered from free charged particles. Peaking at around
7013117394272000000♠372±14 kyr,
[32] the mean free path for a photon becomes long enough to reach the present day and the universe becomes transparent.
In 1989
NASA launched the
Cosmic Background Explorer satellite (COBE) which made two major advances: in 1990, high-precision spectrum measurements showed the CMB frequency spectrum is an almost perfect
blackbody with no deviations at a level of 1 part in 10
4, and measured a residual temperature of 2.726 K (more recent measurements have revised this figure down slightly to 2.7255 K); then in 1992 further COBE measurements discovered tiny fluctuations (anisotropies) in the CMB temperature across the sky, at a level of about one part in 10
5.
[68] John C. Mather and
George Smoot were awarded the 2006 Nobel Prize in Physics for their leadership in these results. During the following decade, CMB anisotropies were further investigated by a large number of ground-based and balloon experiments. In 2000–2001 several experiments, most notably
BOOMERanG, found the
shape of the universe to be spatially almost flat by measuring the typical angular size (the size on the sky) of the anisotropies.
[81][82][83]
In early 2003 the first results of the
Wilkinson Microwave Anisotropy Probe (WMAP) were released, yielding what were at the time the most accurate values for some of the cosmological parameters. The results disproved several specific
cosmic inflation models, but are consistent with the
inflation theory in general.
[69] The
Planck space probe was launched in May 2009. Other ground and balloon based
cosmic microwave background experiments are ongoing.
Abundance of primordial elements
Using the Big Bang model it is possible to calculate the concentration of
helium-4,
helium-3, deuterium, and
lithium-7 in the universe as ratios to the amount of ordinary hydrogen.
[26] The relative abundances depend on a single parameter, the ratio of
photons to baryons. This value can be calculated independently from the detailed structure of
CMB fluctuations. The ratios predicted (by mass, not by number) are about 0.25 for
4He/
H, about 10
−3 for
2H/
H, about 10
−4 for
3He/
H and about 10
−9 for
7Li/
H.
[26]
The measured abundances all agree at least roughly with those predicted from a single value of the baryon-to-photon ratio. The agreement is excellent for deuterium, close but formally discrepant for
4He, and off by a factor of two for
7Li; in the latter two cases there are substantial
systematic uncertainties. Nonetheless, the general consistency with abundances predicted by Big Bang nucleosynthesis is strong evidence for the Big Bang, as the theory is the only known explanation for the relative abundances of light elements, and it is virtually impossible to "tune" the Big Bang to produce much more or less than 20–30% helium.
[84] Indeed, there is no obvious reason outside of the Big Bang that, for example, the young universe (i.e., before star formation, as determined by studying matter supposedly free of
stellar nucleosynthesis products) should have more helium than deuterium or more deuterium than
3He, and in constant ratios, too.
[85]:182–185
Galactic evolution and distribution
Detailed observations of the
morphology and
distribution of galaxies and
quasars are in agreement with the current state of the Big Bang theory. A combination of observations and theory suggest that the first quasars and galaxies formed about a billion years after the Big Bang, and since then larger structures have been forming, such as
galaxy clusters and
superclusters. Populations of stars have been aging and evolving, so that distant galaxies (which are observed as they were in the early universe) appear very different from nearby galaxies (observed in a more recent state). Moreover, galaxies that formed relatively recently appear markedly different from galaxies formed at similar distances but shortly after the Big Bang. These observations are strong arguments against the steady-state model. Observations of
star formation, galaxy and quasar distributions and larger structures agree well with Big Bang simulations of the formation of structure in the universe and are helping to complete details of the theory.
[86][87]
Primordial gas clouds
In 2011 astronomers found what they believe to be pristine clouds of primordial gas, by analyzing absorption lines in the spectra of distant quasars. Before this discovery, all other astronomical objects have been observed to contain heavy elements that are formed in stars. These two clouds of gas contain no elements heavier than hydrogen and deuterium.
[88][89] Since the clouds of gas have no heavy elements, they likely formed in the first few minutes after the Big Bang, during
Big Bang nucleosynthesis.
Other lines of evidence
The age of the universe as estimated from the Hubble expansion and the
CMB is now in good agreement with other estimates using the ages of the oldest stars, both as measured by applying the theory of
stellar evolution to
globular clusters and through
radiometric dating of individual
Population II stars.
[90]
The prediction that the CMB temperature was higher in the past has been experimentally supported by observations of very low temperature absorption lines in gas clouds at high redshift.
[91] This prediction also implies that the amplitude of the
Sunyaev–Zel'dovich effect in
clusters of galaxies does not depend directly on redshift. Observations have found this to be roughly true, but this effect depends on cluster properties that do change with cosmic time, making precise measurements difficult.
[92][93]
On 17 March 2014, astronomers at the
Harvard-Smithsonian Center for Astrophysics announced the apparent detection of primordial
gravitational waves, which, if confirmed, may provide strong evidence for
inflation and the Big Bang.
[13][14][15][16] However, on 19 June 2014, lowered confidence in confirming the findings was reported;
[94][95][96] and on 19 September 2014, even more lowered confidence.
[97][98]
Problems and related issues in physics
As with any theory, a number of mysteries and problems have arisen as a result of the development of the Big Bang theory. Some of these mysteries and problems have been resolved while others are still outstanding. Proposed solutions to some of the problems in the Big Bang model have revealed new mysteries of their own. For example, the
horizon problem, the
magnetic monopole problem, and the
flatness problem are most commonly resolved with
inflationary theory, but the details of the inflationary universe are still left unresolved and alternatives to inflation are even still entertained in the literature.
[99][100] What follows are a list of the mysterious aspects of the Big Bang theory still under intense investigation by cosmologists and astrophysicists.
Baryon asymmetry
It is not yet understood why the universe has more matter than antimatter.
[101] It is generally assumed that when the universe was young and very hot, it was in statistical equilibrium and contained equal numbers of baryons and antibaryons. However, observations suggest that the universe, including its most distant parts, is made almost entirely of matter. A process called baryogenesis was hypothesized to account for the asymmetry. For baryogenesis to occur, the
Sakharov conditions must be satisfied. These require that baryon number is not conserved, that
C-symmetry and
CP-symmetry are violated and that the universe depart from
thermodynamic equilibrium.
[102] All these conditions occur in the
Standard Model, but the effect is not strong enough to explain the present baryon asymmetry.
Dark energy
Measurements of the
redshift–
magnitude relation for
type Ia supernovae indicate that the expansion of the universe has been
accelerating since the universe was about half its present age. To explain this acceleration, general relativity requires that much of the energy in the universe consists of a component with large
negative pressure, dubbed "dark energy".
[9] Dark energy, though speculative, solves numerous problems. Measurements of the
cosmic microwave background indicate that the universe is very nearly spatially flat, and therefore according to general relativity the universe must have almost exactly the
critical density of mass/energy. But the mass density of the universe can be measured from its gravitational clustering, and is found to have only about 30% of the critical density.
[9] Since theory suggests that dark energy does not cluster in the usual way it is the best explanation for the "missing" energy density. Dark energy also helps to explain two geometrical measures of the overall curvature of the universe, one using the frequency of
gravitational lenses, and the other using the characteristic pattern of the
large-scale structure as a cosmic ruler.
Negative pressure is believed to be a property of
vacuum energy, but the exact nature and existence of dark energy remains one of the great mysteries of the Big Bang. Results from the WMAP team in 2008 are in accordance with a universe that consists of 73% dark energy, 23% dark matter, 4.6% regular matter and less than 1% neutrinos.
[33] According to theory, the energy density in matter decreases with the expansion of the universe, but the dark energy density remains constant (or nearly so) as the universe expands. Therefore, matter made up a larger fraction of the total energy of the universe in the past than it does today, but its fractional contribution will fall in the
far future as dark energy becomes even more dominant.
The dark energy component of the universe has been explained by theorists using a variety of competing theories including Einstein's
cosmological constant but also extending to more exotic forms of
quintessence or other modified gravity schemes.
[103] A
cosmological constant problem sometimes called the "most embarrassing problem in physics" results from the apparent discrepancy between the measured energy density of dark energy and the one naively predicted from
Planck units.
[104]
Dark matter
During the 1970s and 80s, various observations showed that there is not sufficient visible matter in the universe to account for the apparent strength of gravitational forces within and between galaxies. This led to the idea that up to 90% of the matter in the universe is dark matter that does not emit light or interact with normal
baryonic matter. In addition, the assumption that the universe is mostly normal matter led to predictions that were strongly inconsistent with observations. In particular, the universe today is far more lumpy and contains far less deuterium than can be accounted for without dark matter. While dark matter has always been controversial, it is inferred by various observations: the anisotropies in the CMB,
galaxy cluster velocity dispersions, large-scale structure distributions,
gravitational lensing studies, and
X-ray measurements of galaxy clusters.
[105]
Indirect evidence for dark matter comes from its gravitational influence on other matter, as no dark matter particles have been observed in laboratories. Many
particle physics candidates for dark matter have been proposed, and several projects to detect them directly are underway.
[106]
Additionally, there are outstanding problems associated with the currently favored
cold dark matter model which include the
dwarf galaxy problem[107] and the
cuspy halo problem.
[108] Alternative theories have been proposed that do not require a large amount of undetected matter but instead modify the laws of gravity established by Newton and Einstein, but no alternative theory as been as successful as the cold dark matter proposal in explaining all extant observations.
[109]
Horizon problem
The
horizon problem results from the premise that information cannot travel
faster than light. In a universe of finite age this sets a limit—the
particle horizon—on the separation of any two regions of space that are in
causal contact.
[110] The observed isotropy of the
CMB is problematic in this regard: if the universe had been dominated by radiation or matter at all times up to the epoch of last scattering, the particle horizon at that time would correspond to about 2 degrees on the sky. There would then be no mechanism to cause wider regions to have the same temperature.
[85]:191–202
A resolution to this apparent inconsistency is offered by
inflationary theory in which a homogeneous and isotropic scalar energy field dominates the universe at some very early period (before baryogenesis). During inflation, the universe undergoes exponential expansion, and the particle horizon expands much more rapidly than previously assumed, so that regions presently on opposite sides of the observable universe are well inside each other's particle horizon. The observed isotropy of the CMB then follows from the fact that this larger region was in causal contact before the beginning of inflation.
[22]:180–186
Heisenberg's uncertainty principle predicts that during the inflationary phase there would be
quantum thermal fluctuations, which would be magnified to cosmic scale. These fluctuations serve as the seeds of all current structure in the universe.
[85]:207 Inflation predicts that the
primordial fluctuations are nearly
scale invariant and
Gaussian, which has been accurately confirmed by measurements of the CMB.
[111]:sec 6
If inflation occurred, exponential expansion would push large regions of space well beyond our observable horizon.
[22]:180–186
A related issue to the classic horizon problem arises due to the fact that in most standard cosmological inflation models, inflation ceases well before
electroweak symmetry breaking occurs, so inflation should not be able to prevent large-scale discontinuities in the
electroweak vacuum since distant parts of the observable universe were causally separate when the
electroweak epoch ended.
[112]
Magnetic monopoles
The
magnetic monopole objection was raised in the late 1970s.
Grand unification theories predicted
topological defects in space that would manifest as
magnetic monopoles. These objects would be produced efficiently in the hot early universe, resulting in a density much higher than is consistent with observations, given that no monopoles have been found. This problem is also resolved by
cosmic inflation, which removes all point defects from the observable universe, in the same way that it drives the geometry to flatness.
[110]
Flatness problem
The
flatness problem (also known as the oldness problem) is an observational problem associated with a
Friedmann–Lemaître–Robertson–Walker metric.
[110] The universe may have positive, negative, or zero spatial
curvature depending on its total energy density. Curvature is negative if its density is less than the
critical density, positive if greater, and zero at the critical density, in which case space is said to be
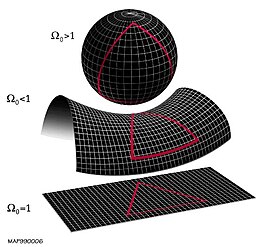
flat. The problem is that any small departure from the critical density grows with time, and yet the universe today remains very close to flat.
[notes 4] Given that a natural timescale for departure from flatness might be the
Planck time, 10
−43 seconds,
[4] the fact that the universe has reached neither a
heat death nor a
Big Crunch after billions of years requires an explanation. For instance, even at the relatively late age of a few minutes (the time of nucleosynthesis), the universe density must have been within one part in 10
14 of its critical value, or it would not exist as it does today.
[113]
Ultimate fate of the Universe
Before observations of dark energy, cosmologists considered two scenarios for the future of the universe. If the mass
density of the universe were greater than the
critical density, then the universe would reach a maximum size and then begin to collapse. It would become denser and hotter again, ending with a state similar to that in which it started—a Big Crunch.
[38] Alternatively, if the density in the universe were equal to or below the critical density, the expansion would slow down but never stop. Star formation would cease with the consumption of interstellar gas in each galaxy; stars would burn out leaving
white dwarfs,
neutron stars, and
black holes. Very gradually, collisions between these would result in mass accumulating into larger and larger black holes. The average temperature of the universe would asymptotically approach
absolute zero—a
Big Freeze.
[114] Moreover, if the proton were
unstable, then baryonic matter would disappear, leaving only radiation and black holes.