Nebular hypothesis

From Wikipedia, the free encyclopedia

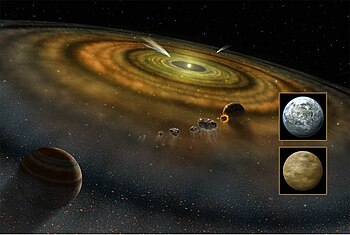
The nebular hypothesis is the most widely accepted model in the field of cosmogony to explain the formation and evolution of the Solar System (as well as other planetary systems). It suggests that the Solar System formed from nebulous material. The theory was developed by Immanuel Kant and published in his Allgemeine Naturgeschichte und Theorie des Himmels ("Universal Natural History and Theory of the Heavens"), published in 1755. Originally applied to the Solar System, the process of planetary system formation is now thought to be at work throughout the Universe. The widely accepted modern variant of the nebular hypothesis is the solar nebular disk model (SNDM) or solar nebular model. It offered explanations for a variety of properties of the Solar System, including the nearly circular and coplanar orbits of the planets, and their motion in the same direction as the Sun's rotation. Some elements of the original nebular hypothesis are echoed in modern theories of planetary formation, but most elements have been superseded.

According to the nebular hypothesis, stars form in massive and dense clouds of molecular hydrogen—giant molecular clouds (GMC). These clouds are gravitationally unstable, and matter coalesces within them to smaller denser clumps, which then rotate, collapse, and form stars. Star formation is a complex process, which always produces a gaseous protoplanetary disk, proplyd, around the young star. This may give birth to planets in certain circumstances, which are not well known. Thus the formation of planetary systems is thought to be a natural result of star formation. A Sun-like star usually takes approximately 1 million years to form, with the protoplanetary disk evolving into a planetary system over the next 10–100 million years.

The protoplanetary disk is an accretion disk that feeds the central star. Initially very hot, the disk later cools in what is known as the T Tauri star stage; here, formation of small dust grains made of rocks and ice is possible. The grains eventually may coagulate into kilometer-sized planetesimals. If the disk is massive enough, the runaway accretions begin, resulting in the rapid—100,000 to 300,000 years—formation of Moon- to Mars-sized planetary embryos. Near the star, the planetary embryos go through a stage of violent mergers, producing a few terrestrial planets. The last stage takes approximately 100 million to a billion years.

The formation of giant planets is a more complicated process. It is thought to occur beyond the frost line, where planetary embryos mainly are made of various types of ice. As a result, they are several times more massive than in the inner part of the protoplanetary disk. What follows after the embryo formation is not completely clear. Some embryos appear to continue to grow and eventually reach 5–10 Earth masses—the threshold value, which is necessary to begin accretion of the hydrogen–helium gas from the disk. The accumulation of gas by the core is initially a slow process, which continues for several million years, but after the forming protoplanet reaches about 30 Earth masses (M_⊕) it accelerates and proceeds in a runaway manner. Jupiter- and Saturn-like planets are thought to accumulate the bulk of their mass during only 10,000 years. The accretion stops when the gas is exhausted. The formed planets can migrate over long distances during or after their formation. Ice giants such as Uranus and Neptune are thought to be failed cores, which formed too late when the disk had almost disappeared.

History

There is evidence that Emanuel Swedenborg first proposed parts of the nebular hypothesis in 1734. Immanuel Kant, familiar with Swedenborg's work, developed the theory further in 1755, publishing his own Universal Natural History and Theory of the Heavens, wherein he argued that gaseous clouds (nebulae) slowly rotate, gradually collapse and flatten due to gravity, eventually forming stars and planets.

Pierre-Simon Laplace independently developed and proposed a similar model in 1796 in his Exposition du systeme du monde. He envisioned that the Sun originally had an extended hot atmosphere throughout the volume of the Solar System. His theory featured a contracting and cooling protosolar cloud—the protosolar nebula. As this cooled and contracted, it flattened and spun more rapidly, throwing off (or shedding) a series of gaseous rings of material; and according to him, the planets condensed from this material. His model was similar to Kant's, except more detailed and on a smaller scale. While the Laplacian nebular model dominated in the 19th century, it encountered a number of difficulties. The main problem involved angular momentum distribution between the Sun and planets. The planets have 99% of the angular momentum, and this fact could not be explained by the nebular model. As a result, astronomers largely abandoned this theory of planet formation at the beginning of the 20th century.

A major critique came during the 19th century from James Clerk Maxwell (1831-1879), who maintained that different rotation between the inner and outer parts of a ring could not allow condensation of material. Astronomer Sir David Brewster also rejected Laplace, writing in 1876 that "those who believe in the Nebular Theory consider it as certain that our Earth derived its solid matter and its atmosphere from a ring thrown from the Solar atmosphere, which afterwards contracted into a solid terraqueous sphere, from which the Moon was thrown off by the same process". He argued that under such view, "the Moon must necessarily have carried off water and air from the watery and aerial parts of the Earth and must have an atmosphere". Brewster claimed that Sir Isaac Newton's religious beliefs had previously considered nebular ideas as tending to atheism, and quoted him as saying that "the growth of new systems out of old ones, without the mediation of a Divine power, seemed to him apparently absurd".

The perceived deficiencies of the Laplacian model stimulated scientists to find a replacement for it. During the 20th century many theories addressed the issue, including the planetesimal theory of Thomas Chamberlin and Forest Moulton (1901), the tidal model of Jeans (1917), the accretion model of Otto Schmidt (1944), the protoplanet theory of William McCrea (1960) and finally the capture theory of Michael Woolfson. In 1978 Andrew Prentice resurrected the initial Laplacian ideas about planet formation and developed the modern Laplacian theory. None of these attempts proved completely successful, and many of the proposed theories were descriptive.

The birth of the modern widely accepted theory of planetary formation—the solar nebular disk model (SNDM)—can be traced to the Soviet astronomer Victor Safronov. His 1969 book Evolution of the protoplanetary cloud and formation of the Earth and the planets, which was translated to English in 1972, had a long-lasting effect on the way scientists think about the formation of the planets. In this book almost all major problems of the planetary formation process were formulated and some of them solved. Safronov's ideas were further developed in the works of George Wetherill, who discovered runaway accretion. While originally applied only to the Solar System, the SNDM was subsequently thought by theorists to be at work throughout the Universe; as of 1 September 2018 astronomers have discovered 3,823 extrasolar planets in our galaxy.

Solar nebular model: achievements and problems

Achievements

Dusty discs surrounding nearby young stars in greater detail.

 

The star formation process naturally results in the appearance of accretion disks around young stellar objects. At the age of about 1 million years, 100% of stars may have such disks. This conclusion is supported by the discovery of the gaseous and dusty disks around protostars and T Tauri stars as well as by theoretical considerations. Observations of these disks show that the dust grains inside them grow in size on short (thousand-year) time scales, producing 1 centimeter sized particles.

The accretion process, by which 1 km planetesimals grow into 1,000 km sized bodies, is well understood now. This process develops inside any disk where the number density of planetesimals is sufficiently high, and proceeds in a runaway manner. Growth later slows and continues as oligarchic accretion. The end result is formation of planetary embryos of varying sizes, which depend on the distance from the star. Various simulations have demonstrated that the merger of embryos in the inner part of the protoplanetary disk leads to the formation of a few Earth-sized bodies. Thus the origin of terrestrial planets is now considered to be an almost solved problem.

Current issues

The physics of accretion disks encounters some problems. The most important one is how the material, which is accreted by the protostar, loses its angular momentum. One possible explanation suggested by Hannes Alfvén was that angular momentum was shed by the solar wind during its T Tauri star phase. The momentum is transported to the outer parts of the disk by viscous stresses. Viscosity is generated by macroscopic turbulence, but the precise mechanism that produces this turbulence is not well understood. Another possible process for shedding angular momentum is magnetic braking, where the spin of the star is transferred into the surrounding disk via that star's magnetic field. The main processes responsible for the disappearance of the gas in disks are viscous diffusion and photo-evaporation.

The formation of planetesimals is the biggest unsolved problem in the nebular disk model. How 1 cm sized particles coalesce into 1 km planetesimals is a mystery. This mechanism appears to be the key to the question as to why some stars have planets, while others have nothing around them, not even dust belts.

The formation timescale of giant planets is also an important problem. Old theories were unable to explain how their cores could form fast enough to accumulate significant amounts of gas from the quickly disappearing protoplanetary disk. The mean lifetime of the disks, which is less than ten million (10⁷) years, appeared to be shorter than the time necessary for the core formation. Much progress has been done to solve this problem and current models of giant planet formation are now capable of forming Jupiter (or more massive planets) in about 4 million years or less, well within the average lifetime of gaseous disks.

Another potential problem of giant planet formation is their orbital migration. Some calculations show that interaction with the disk can cause rapid inward migration, which, if not stopped, results in the planet reaching the "central regions still as a sub-Jovian object." More recent calculations indicate that disk evolution during migration can mitigate this problem.

Formation of stars and protoplanetary disks

Protostars

The visible-light (left) and infrared (right) views of the Trifid Nebula—a giant star-forming cloud of gas and dust located 5,400 light-years away in the constellation Sagittarius

Stars are thought to form inside giant clouds of cold molecular hydrogen—giant molecular clouds roughly 300,000 times the mass of the Sun (M_☉) and 20 parsecs in diameter. Over millions of years, giant molecular clouds are prone to collapse and fragmentation. These fragments then form small, dense cores, which in turn collapse into stars. The cores range in mass from a fraction to several times that of the Sun and are called protostellar (protosolar) nebulae. They possess diameters of 0.01–0.1 pc (2,000–20,000 AU) and a particle number density of roughly 10,000 to 100,000 cm⁻³.

The initial collapse of a solar-mass protostellar nebula takes around 100,000 years. Every nebula begins with a certain amount of angular momentum. Gas in the central part of the nebula, with relatively low angular momentum, undergoes fast compression and forms a hot hydrostatic (not contracting) core containing a small fraction of the mass of the original nebula. This core forms the seed of what will become a star. As the collapse continues, conservation of angular momentum means that the rotation of the infalling envelop accelerates, which largely prevents the gas from directly accreting onto the central core. The gas is instead forced to spread outwards near its equatorial plane, forming a disk, which in turn accretes onto the core. The core gradually grows in mass until it becomes a young hot protostar. At this stage, the protostar and its disk are heavily obscured by the infalling envelope and are not directly observable. In fact the remaining envelope's opacity is so high that even millimeter-wave radiation has trouble escaping from inside it. Such objects are observed as very bright condensations, which emit mainly millimeter-wave and submillimeter-wave radiation.They are classified as spectral Class 0  protostars. The collapse is often accompanied by bipolar outflows—jets—that emanate along the rotational axis of the inferred disk. The jets are frequently observed in star-forming regions (see Herbig–Haro (HH) objects). The luminosity of the Class 0 protostars is high — a solar-mass protostar may radiate at up to 100 solar luminosities. The source of this energy is gravitational collapse, as their cores are not yet hot enough to begin nuclear fusion.

Infrared image of the molecular outflow from an otherwise hidden newborn star HH 46/47

As the infall of its material onto the disk continues, the envelope eventually becomes thin and transparent and the young stellar object (YSO) becomes observable, initially in far-infrared light and later in the visible. Around this time the protostar begins to fuse deuterium. If the protostar is sufficiently massive (above 80 Jupiter masses (M_J)), hydrogen fusion follows. Otherwise, if its mass is too low, the object becomes a brown dwarf. This birth of a new star occurs approximately 100,000 years after the collapse begins. Objects at this stage are known as Class I protostars, which are also called young T Tauri stars, evolved protostars, or young stellar objects. By this time the forming star has already accreted much of its mass: the total mass of the disk and remaining envelope does not exceed 10–20% of the mass of the central YSO.

At the next stage the envelope completely disappears, having been gathered up by the disk, and the protostar becomes a classical T Tauri star. This happens after about 1 million years. The mass of the disk around a classical T Tauri star is about 1–3% of the stellar mass, and it is accreted at a rate of 10⁻⁷ to 10⁻⁹ M_☉ per year. A pair of bipolar jets is usually present as well. The accretion explains all peculiar properties of classical T Tauri stars: strong flux in the emission lines (up to 100% of the intrinsic luminosity of the star), magnetic activity, photometric variability and jets. The emission lines actually form as the accreted gas hits the "surface" of the star, which happens around its magnetic poles. The jets are byproducts of accretion: they carry away excessive angular momentum. The classical T Tauri stage lasts about 10 million years. The disk eventually disappears due to accretion onto the central star, planet formation, ejection by jets and photoevaporation by UV-radiation from the central star and nearby stars. As a result, the young star becomes a weakly lined T Tauri star, which slowly, over hundreds of millions of years, evolves into an ordinary Sun-like star.

Protoplanetary disks

Debris disks detected in HST archival images of young stars, HD 141943 and HD 191089, using improved imaging processes (24 April 2014).

 

Under certain circumstances the disk, which can now be called protoplanetary, may give birth to a planetary system. Protoplanetary disks have been observed around a very high fraction of stars in young star clusters. They exist from the beginning of a star's formation, but at the earliest stages are unobservable due to the opacity of the surrounding envelope. The disk of a Class 0 protostar is thought to be massive and hot. It is an accretion disk, which feeds the central protostar. The temperature can easily exceed 400 K inside 5 AU and 1,000 K inside 1 AU. The heating of the disk is primarily caused by the viscous dissipation of turbulence in it and by the infall of the gas from the nebula. The high temperature in the inner disk causes most of the volatile material—water, organics, and some rocks to evaporate, leaving only the most refractory elements like iron. The ice can survive only in the outer part of the disk.

A protoplanetary disk forming in the Orion Nebula

The main problem in the physics of accretion disks is the generation of turbulence and the mechanism responsible for the high effective viscosity. The turbulent viscosity is thought to be responsible for the transport of the mass to the central protostar and momentum to the periphery of the disk. This is vital for accretion, because the gas can be accreted by the central protostar only if it loses most of its angular momentum, which must be carried away by the small part of the gas drifting outwards. The result of this process is the growth of both the protostar and of the disk radius, which can reach 1,000 AU if the initial angular momentum of the nebula is large enough. Large disks are routinely observed in many star-forming regions such as the Orion nebula.

Play media

Artist's impression of the disc and gas streams around young star HD 142527.

 

The lifespan of the accretion disks is about 10 million years. By the time the star reaches the classical T-Tauri stage, the disk becomes thinner and cools. Less volatile materials start to condense close to its center, forming 0.1–1 μm dust grains that contain crystalline silicates. The transport of the material from the outer disk can mix these newly formed dust grains with primordial ones, which contain organic matter and other volatiles. This mixing can explain some peculiarities in the composition of Solar System bodies such as the presence of interstellar grains in the primitive meteorites and refractory inclusions in comets.

Various planet formation processes, including exocomets and other planetesimals, around Beta Pictoris, a very young type A V star (NASA artist's conception).

Dust particles tend to stick to each other in the dense disk environment, leading to the formation of larger particles up to several centimeters in size. The signatures of the dust processing and coagulation are observed in the infrared spectra of the young disks. Further aggregation can lead to the formation of planetesimals measuring 1 km across or larger, which are the building blocks of planets. Planetesimal formation is another unsolved problem of disk physics, as simple sticking becomes ineffective as dust particles grow larger.

One hypothesis is formation by the gravitational instability. Particles several centimeters in size or larger slowly settle near the middle plane of the disk, forming a very thin—less than 100 km—and dense layer. This layer is gravitationally unstable and may fragment into numerous clumps, which in turn collapse into planetesimals. However, the differing velocities of the gas disk and the solids near the mid-plane can generate turbulence which prevents the layer from becoming thin enough to fragment due to gravitational instability. This may limit the formation of planetesimals via gravitational instabilities to specific locations in the disk where the concentration of solids is enhanced.

Another possible mechanism for the formation of planetesimals is the streaming instability in which the drag felt by particles orbiting through gas creates a feedback effect causing the growth of local concentrations. These local concentration push back on the gas creating a region where the headwind felt by the particles is smaller. The concentration is thus able to orbit faster and undergoes less radial drift. Isolated particles join these concentrations as they are overtaken or as they drift inward causing it to grow in mass. Eventually these concentrations form massive filaments which fragment and undergo gravitational collapse forming planetesimals the size of the larger asteroids.

Planetary formation can also be triggered by gravitational instability within the disk itself, which leads to its fragmentation into clumps. Some of them, if they are dense enough, will collapse, which can lead to rapid formation of gas giant planets and even brown dwarfs on the timescale of 1,000 years. If these clumps migrate inward as the collapse proceeds tidal forces from the star can result in a significant mass loss leaving behind a smaller body. However it is only possible in massive disks—more massive than 0.3 M_☉. In comparison, typical disk masses are 0.01–0.03 M_☉. Because the massive disks are rare, this mechanism of the planet formation is thought to be infrequent. On the other hand, this mechanism may play a major role in the formation of brown dwarfs.

Asteroid collision—building planets (artist concept).

The ultimate dissipation of protoplanetary disks is triggered by a number of different mechanisms. The inner part of the disk is either accreted by the star or ejected by the bipolar jets, whereas the outer part can evaporate under the star's powerful UV radiation during the T Tauri stage or by nearby stars. The gas in the central part can either be accreted or ejected by the growing planets, while the small dust particles are ejected by the radiation pressure of the central star. What is finally left is either a planetary system, a remnant disk of dust without planets, or nothing, if planetesimals failed to form.

Because planetesimals are so numerous, and spread throughout the protoplanetary disk, some survive the formation of a planetary system. Asteroids are understood to be left-over planetesimals, gradually grinding each other down into smaller and smaller bits, while comets are typically planetesimals from the farther reaches of a planetary system. Meteorites are samples of planetesimals that reach a planetary surface, and provide a great deal of information about the formation of the Solar System. Primitive-type meteorites are chunks of shattered low-mass planetesimals, where no thermal differentiation took place, while processed-type meteorites are chunks from shattered massive planetesimals.

Formation of planets

Rocky planets

According to the solar nebular disk model, rocky planets form in the inner part of the protoplanetary disk, within the frost line, where the temperature is high enough to prevent condensation of water ice and other substances into grains. This results in coagulation of purely rocky grains and later in the formation of rocky planetesimals. Such conditions are thought to exist in the inner 3–4 AU part of the disk of a Sun-like star.

After small planetesimals—about 1 km in diameter—have formed by one way or another, runaway accretion begins. It is called runaway because the mass growth rate is proportional to R⁴~M^4/3, where R and M are the radius and mass of the growing body, respectively. The specific (divided by mass) growth accelerates as the mass increases. This leads to the preferential growth of larger bodies at the expense of smaller ones. The runaway accretion lasts between 10,000 and 100,000 years and ends when the largest bodies exceed approximately 1,000 km in diameter. Slowing of the accretion is caused by gravitational perturbations by large bodies on the remaining planetesimals. In addition, the influence of larger bodies stops further growth of smaller bodies.

The next stage is called oligarchic accretion. It is characterized by the dominance of several hundred of the largest bodies—oligarchs, which continue to slowly accrete planetesimals. No body other than the oligarchs can grow. At this stage the rate of accretion is proportional to R², which is derived from the geometrical cross-section of an oligarch. The specific accretion rate is proportional to M^−1/3; and it declines with the mass of the body. This allows smaller oligarchs to catch up to larger ones. The oligarchs are kept at the distance of about 10·H_r (H_r=a(1-e)(M/3M_s)^1/3 is the Hill radius, where a is the semimajor axis, e is the orbital eccentricity, and M_s is the mass of the central star) from each other by the influence of the remaining planetesimals. Their orbital eccentricities and inclinations remain small. The oligarchs continue to accrete until planetesimals are exhausted in the disk around them. Sometimes nearby oligarchs merge. The final mass of an oligarch depends on the distance from the star and surface density of planetesimals and is called the isolation mass. For the rocky planets it is up to 0.1 M_⊕, or one Mars mass. The final result of the oligarchic stage is the formation of about 100 Moon- to Mars-sized planetary embryos uniformly spaced at about 10·H_r. They are thought to reside inside gaps in the disk and to be separated by rings of remaining planetesimals. This stage is thought to last a few hundred thousand years.

The last stage of rocky planet formation is the merger stage. It begins when only a small number of planetesimals remains and embryos become massive enough to perturb each other, which causes their orbits to become chaotic. During this stage embryos expel remaining planetesimals, and collide with each other. The result of this process, which lasts for 10 to 100 million years, is the formation of a limited number of Earth sized bodies. Simulations show that the number of surviving planets is on average from 2 to 5. In the Solar System they may be represented by Earth and Venus. Formation of both planets required merging of approximately 10–20 embryos, while an equal number of them were thrown out of the Solar System. Some of the embryos, which originated in the asteroid belt, are thought to have brought water to Earth. Mars and Mercury may be regarded as remaining embryos that survived that rivalry. Rocky planets, which have managed to coalesce, settle eventually into more or less stable orbits, explaining why planetary systems are generally packed to the limit; or, in other words, why they always appear to be at the brink of instability.

Giant planets

The dust disk around Fomalhaut—the brightest star in Piscis Austrinus constellation. Asymmetry of the disk may be caused by a giant planet (or planets) orbiting the star.

The formation of giant planets is an outstanding problem in the planetary sciences. In the framework of the solar nebular model two theories for their formation exist. The first one is the disk instability model, where giant planets form in the massive protoplanetary disks as a result of its gravitational fragmentation (see above). The second possibility is the core accretion model, which is also known as the nucleated instability model. The latter scenario is thought to be the most promising one, because it can explain the formation of the giant planets in relatively low-mass disks (less than 0.1 M_☉). In this model giant planet formation is divided into two stages: a) accretion of a core of approximately 10 M_⊕ and b) accretion of gas from the protoplanetary disk. Either method may also lead to the creation of brown dwarfs. Searches as of 2011 have found that core accretion is likely the dominant formation mechanism.

Giant planet core formation is thought to proceed roughly along the lines of the terrestrial planet formation. It starts with planetesimals that undergo runaway growth, followed by the slower oligarchic stage. Hypotheses do not predict a merger stage, due to the low probability of collisions between planetary embryos in the outer part of planetary systems. An additional difference is the composition of the planetesimals, which in the case of giant planets form beyond the so-called snow line and consist mainly of ice—the ice to rock ratio is about 4 to 1. This enhances the mass of planetesimals fourfold. However, the minimum mass nebula capable of terrestrial planet formation can only form 1–2 M_⊕ cores at the distance of Jupiter (5 AU) within 10 million years. The latter number represents the average lifetime of gaseous disks around Sun-like stars. The proposed solutions include enhanced mass of the disk—a tenfold increase would suffice; protoplanet migration, which allows the embryo to accrete more planetesimals; and finally accretion enhancement due to gas drag in the gaseous envelopes of the embryos. Some combination of the above-mentioned ideas may explain the formation of the cores of gas giant planets such as Jupiter and perhaps even Saturn. The formation of planets like Uranus and Neptune is more problematic, since no theory has been capable of providing for the in situ formation of their cores at the distance of 20–30 AU from the central star. One hypothesis is that they initially accreted in the Jupiter-Saturn region, then were scattered and migrated to their present location. Another possible solution is the growth of the cores of the giant planets via pebble accretion. In pebble accretion objects between a cm and a meter in diameter falling toward a massive body are slowed enough by gas drag for them to spiral toward it and be accreted. Growth via pebble accretion may be as much as 1000 times faster than by the accretion of planetesimals.

Once the cores are of sufficient mass (5–10 M_⊕), they begin to gather gas from the surrounding disk. Initially it is a slow process, increasing the core masses up to 30 M_⊕ in a few million years. After that, the accretion rates increase dramatically and the remaining 90% of the mass is accumulated in approximately 10,000 years. The accretion of gas stops when the supply from the disk is exhausted. This happens gradually, due to the formation of a density gap in the protoplanetary disk and to disk dispersal. In this model ice giants—Uranus and Neptune—are failed cores that began gas accretion too late, when almost all gas had already disappeared. The post-runaway-gas-accretion stage is characterized by migration of the newly formed giant planets and continued slow gas accretion. Migration is caused by the interaction of the planet sitting in the gap with the remaining disk. It stops when the protoplanetary disk disappears or when the end of the disk is attained. The latter case corresponds to the so-called hot Jupiters, which are likely to have stopped their migration when they reached the inner hole in the protoplanetary disk.

In this artist's conception, a planet spins through a clearing (gap) in a nearby star's dusty, planet-forming disc.

Giant planets can significantly influence terrestrial planet formation. The presence of giants tends to increase eccentricities and inclinations of planetesimals and embryos in the terrestrial planet region (inside 4 AU in the Solar System). If giant planets form too early, they can slow or prevent inner planet accretion. If they form near the end of the oligarchic stage, as is thought to have happened in the Solar System, they will influence the merges of planetary embryos, making them more violent. As a result, the number of terrestrial planets will decrease and they will be more massive. In addition, the size of the system will shrink, because terrestrial planets will form closer to the central star. The influence of giant planets in the Solar System, particularly that of Jupiter, is thought to have been limited because they are relatively remote from the terrestrial planets.

The region of a planetary system adjacent to the giant planets will be influenced in a different way. In such a region, eccentricities of embryos may become so large that the embryos pass close to a giant planet, which may cause them to be ejected from the system. If all embryos are removed, then no planets will form in this region. An additional consequence is that a huge number of small planetesimals will remain, because giant planets are incapable of clearing them all out without the help of embryos. The total mass of remaining planetesimals will be small, because cumulative action of the embryos before their ejection and giant planets is still strong enough to remove 99% of the small bodies. Such a region will eventually evolve into an asteroid belt, which is a full analog of the asteroid belt in the Solar System, located from 2 to 4 AU from the Sun.

Exoplanets

Thousands of exoplanets have been identified in the last twenty years. The orbits of many of these planets and systems of planets differ significantly from the planets in the Solar System. The exoplanets discovered include hot-Jupiters, warm-Jupiters, super-Earths, and systems of tightly packed inner planets.

The hot-Jupiters and warm-Jupiters are thought to have migrated to their current orbits during or following their formation. A number of possible mechanisms for this migration have been proposed. Type I or Type II migration could smoothly decrease the semimajor axis of the planet's orbit resulting in a warm- or hot-Jupiter. Gravitational scattering by other planets onto eccentric orbits with a perihelion near the star followed by the circularization of its orbit due to tidal interactions with the star can leave a planet on a close orbit. If a massive companion planet or star on an inclined orbit was present an exchange of inclination for eccentricity via the Kozai mechanism raising eccentricities and lowering perihelion followed by circularization can also result in a close orbit. Many of the Jupiter sized planets have eccentric orbits which may indicate that gravitational encounters occurred between the planets, although migration while in resonance can also excite eccentricities. The in situ growth of hot Jupiters from closely orbiting super Earths has also been proposed. The cores in this hypothesis could have formed locally or at a greater distance and migrated close to the star.

Super-Earths and other closely orbiting planets are thought to have either formed in situ or to have migrated inward from their initial locations. The in situ formation of closely orbiting super-Earths would require a massive disk, the migration of planetary embryos followed by collisions and mergers, or the radial drift of small solids from farther out in the disk. The migration of the super-Earths, or the embryos that collided to form them, is likely to have been Type I due to their smaller mass. The resonant orbits of some of the exoplanet systems indicates that some migration occurred in these systems, while the spacing of the orbits in many of the other systems not in resonance indicates that an instability likely occurred in those systems after the dissipation of the gas disk. The absence of Super-Earths and closely orbiting planets in the Solar System may be due to the previous formation of Jupiter blocking their inward migration.

The amount of gas a super-Earth that formed in situ acquires may depend on when the planetary embryos merged due to giant impacts relative to the dissipation of the gas disk. If the mergers happen after the gas disk dissipates terrestrial planets can form, if in a transition disk a super-Earth with a gas envelope containing a few percent of its mass may form. If the mergers happen too early runaway gas accretion may occur leading to the formation of a gas giant. The mergers begin when the dynamical friction due to the gas disk becomes insufficient to prevent collisions, a process that will begin earlier in a higher metallicity disk. Alternatively gas accretion may be limited due to the envelopes not being in hydrostatic equilibrium, instead gas may flow through the envelope slowing its growth and delaying the onset of runaway gas accretion until the mass of the core reaches 15 Earth masses.

Meaning of accretion

Use of the term "accretion disk" for the protoplanetary disk leads to confusion over the planetary accretion process. The protoplanetary disk is sometimes referred to as an accretion disk, because while the young T Tauri-like protostar is still contracting, gaseous material may still be falling onto it, accreting on its surface from the disk's inner edge. In an accretion disk, there is a net flux of mass from larger radii toward smaller radii.

However, that meaning should not be confused with the process of accretion forming the planets. In this context, accretion refers to the process of cooled, solidified grains of dust and ice orbiting the protostar in the protoplanetary disk, colliding and sticking together and gradually growing, up to and including the high-energy collisions between sizable planetesimals.
In addition, the giant planets probably had accretion disks of their own, in the first meaning of the word. The clouds of captured hydrogen and helium gas contracted, spun up, flattened, and deposited gas onto the surface of each giant protoplanet, while solid bodies within that disk accreted into the giant planet's regular moons.

Molecular cloud

From Wikipedia, the free encyclopedia

 

Within a few million years the light from bright stars will have boiled away this molecular cloud of gas and dust. The cloud has broken off from the Carina Nebula. Newly formed stars are visible nearby, their images reddened by blue light being preferentially scattered by the pervasive dust. This image spans about two light-years and was taken by the Hubble Space Telescope in 1999.

A molecular cloud, sometimes called a stellar nursery (if star formation is occurring within), is a type of interstellar cloud, the density and size of which permit the formation of molecules, most commonly molecular hydrogen (H₂). This is in contrast to other areas of the interstellar medium that contain predominantly ionized gas.

Molecular hydrogen is difficult to detect by infrared and radio observations, so the molecule most often used to determine the presence of H₂ is carbon monoxide (CO). The ratio between CO luminosity and H₂ mass is thought to be constant, although there are reasons to doubt this assumption in observations of some other galaxies.

Within molecular clouds are regions with higher density, where lots of dust and gas cores reside, called clumps. These clumps are the beginning of star formation, if gravity can overcome the high density and force the dust and gas to collapse.

Occurrence

Molecular cloud Barnard 68, about 500 ly distant and 0.5 ly in diameter.

Within the Milky Way, molecular gas clouds account for less than one percent of the volume of the interstellar medium (ISM), yet it is also the densest part of the medium, comprising roughly half of the total gas mass interior to the Sun's galactic orbit. The bulk of the molecular gas is contained in a ring between 3.5 and 7.5 kiloparsecs (11,000 and 24,000 light-years) from the center of the Milky Way (the Sun is about 8.5 kiloparsecs from the center). Large scale CO maps of the galaxy show that the position of this gas correlates with the spiral arms of the galaxy. That molecular gas occurs predominantly in the spiral arms suggests that molecular clouds must form and dissociate on a timescale shorter than 10 million years—the time it takes for material to pass through the arm region.

Circinus molecular cloud has a mass around 250,000 times that of the Sun.

 

Vertically to the plane of the galaxy, the molecular gas inhabits the narrow midplane of the galactic disc with a characteristic scale height, Z, of approximately 50 to 75 parsecs, much thinner than the warm atomic (Z from 130 to 400 parsecs) and warm ionized (Z around 1000 parsecs) gaseous components of the ISM. The exception to the ionized-gas distribution are H II regions, which are bubbles of hot ionized gas created in molecular clouds by the intense radiation given off by young massive stars and as such they have approximately the same vertical distribution as the molecular gas.

This distribution of molecular gas is averaged out over large distances; however, the small scale distribution of the gas is highly irregular with most of it concentrated in discrete clouds and cloud complexes.

Types of molecular cloud

Giant molecular clouds

Part of the Taurus Molecular Cloud.

 

A vast assemblage of molecular gas with a mass of approximately 10³ to 10⁷ times the mass of the Sun is called a giant molecular cloud (GMC). GMCs are around 15 to 600 light-years in diameter (5 to 200 parsecs). Whereas the average density in the solar vicinity is one particle per cubic centimetre, the average density of a GMC is a hundred to a thousand times as great. Although the Sun is much more dense than a GMC, the volume of a GMC is so great that it contains much more mass than the Sun. The substructure of a GMC is a complex pattern of filaments, sheets, bubbles, and irregular clumps.

The densest parts of the filaments and clumps are called "molecular cores", while the densest molecular cores are called "dense molecular cores" and have densities in excess of 10⁴ to 10⁶ particles per cubic centimeter. Observationally, typical molecular cores are traced with CO and dense molecular cores are traced with ammonia. The concentration of dust within molecular cores is normally sufficient to block light from background stars so that they appear in silhouette as dark nebulae.

GMCs are so large that "local" ones can cover a significant fraction of a constellation; thus they are often referred to by the name of that constellation, e.g. the Orion Molecular Cloud (OMC) or the Taurus Molecular Cloud (TMC). These local GMCs are arrayed in a ring in the neighborhood of the Sun coinciding with the Gould Belt. The most massive collection of molecular clouds in the galaxy forms an asymmetrical ring about the galactic center at a radius of 120 parsecs; the largest component of this ring is the Sagittarius B2 complex. The Sagittarius region is chemically rich and is often used as an exemplar by astronomers searching for new molecules in interstellar space.

Distribution of molecular gas in 30 merging galaxies.

Small molecular clouds

Isolated gravitationally-bound small molecular clouds with masses less than a few hundred times that of the Sun are called Bok globules. The densest parts of small molecular clouds are equivalent to the molecular cores found in GMCs and are often included in the same studies.

High-latitude diffuse molecular clouds

In 1984 IRAS identified a new type of diffuse molecular cloud. These were diffuse filamentary clouds that are visible at high galactic latitudes. These clouds have a typical density of 30 particles per cubic centimeter.

Processes

Young stars in and around molecular cloud Cepheus B. Radiation from one bright, massive star is destroying the cloud (from top to bottom in this image) while simultaneously triggering the formation of new stars.

Star formation

The formation of stars occurs exclusively within molecular clouds. This is a natural consequence of their low temperatures and high densities, because the gravitational force acting to collapse the cloud must exceed the internal pressures that are acting "outward" to prevent a collapse. There is observed evidence that the large, star-forming clouds are confined to a large degree by their own gravity (like stars, planets, and galaxies) rather than by external pressure. The evidence comes from the fact that the "turbulent" velocities inferred from CO linewidth scale in the same manner as the orbital velocity (a virial relation).

Physics

The Serpens South star cluster is embedded in a filamentary molecular cloud, seen as a dark ribbon passing vertically through the cluster. This cloud has served as a testbed for studies of molecular cloud stability.

 

The physics of molecular clouds is poorly understood and much debated. Their internal motions are governed by turbulence in a cold, magnetized gas, for which the turbulent motions are highly supersonic but comparable to the speeds of magnetic disturbances. This state is thought to lose energy rapidly, requiring either an overall collapse or a steady reinjection of energy. At the same time, the clouds are known to be disrupted by some process—most likely the effects of massive stars—before a significant fraction of their mass has become stars.

Molecular clouds, and especially GMCs, are often the home of astronomical masers.

Structure formation

From Wikipedia, the free encyclopedia

 

In physical cosmology, structure formation is the formation of galaxies, galaxy clusters and larger structures from small early density fluctuations. The universe, as is now known from observations of the cosmic microwave background radiation, began in a hot, dense, nearly uniform state approximately 13.8 billion years ago. However, looking in the sky today, we see structures on all scales, from stars and planets to galaxies and, on still larger scales, galaxy clusters and sheet-like structures of galaxies separated by enormous voids containing few galaxies. Structure formation attempts to model how these structures formed by gravitational instability of small early density ripples.

 

The modern Lambda-CDM model is successful at predicting the observed large-scale distribution of galaxies, clusters and voids; but on the scale of individual galaxies there are many complications due to highly nonlinear processes involving baryonic physics, gas heating and cooling, star formation and feedback. Understanding the processes of galaxy formation is a major topic of modern cosmology research, both via observations such as the Hubble Ultra-Deep Field and via large computer simulations.

Overview

Under present models, the structure of the visible universe was formed in the following stages:

Very early universe

In this stage, some mechanism, such as cosmic inflation, was responsible for establishing the initial conditions of the universe: homogeneity, isotropy, and flatness. Cosmic inflation also would have amplified minute quantum fluctuations (pre-inflation) into slight density ripples of overdensity and underdensity (post-inflation).

Growth of structure

The early universe was dominated by radiation; in this case density fluctuations larger than the cosmic horizon grow proportional to the scale factor, as the gravitational potential fluctuations remain constant. Structures smaller than the horizon remained essentially frozen due to radiation domination impeding growth. As the universe expanded, the density of radiation drops faster than matter (due to redshifting of photon energy); this led to a crossover called matter-radiation equality at ~ 50,000 years after the Big Bang. After this all dark matter ripples could grow freely, forming seeds into which the baryons could later fall. The size of the universe at this epoch forms a turnover in the matter power spectrum which can be measured in large redshift surveys.

Recombination

The universe was dominated by radiation for most of this stage, and due to the intense heat and radiation, the primordial hydrogen and helium were fully ionized into nuclei and free electrons. In this hot and dense situation, the radiation (photons) could not travel far before Thomson scattering off an electron. The universe was very hot and dense, but expanding rapidly and therefore cooling. Finally, at a little less than 400,000 years after the 'bang', it become cool enough (around 3000 K) for the protons to capture negatively charged electrons, forming neutral hydrogen atoms. (Helium atoms formed somewhat earlier due to their larger binding energy). Once nearly all the charged particles were bound in neutral atoms, the photons no longer interacted with them and were free to propagate for the next 13.8 billion years; we currently detect those photons redshifted by a factor 1090 down to 2.725 K as the Cosmic Microwave Background Radiation (CMB) filling today's universe. Several remarkable space-based missions (COBE, WMAP, Planck), have detected very slight variations in the density and temperature of the CMB. These variations were subtle, and the CMB appears very nearly uniformly the same in every direction. However, the slight temperature variations of order a few parts in 100,000 are of enormous importance, for they essentially were early "seeds" from which all subsequent complex structures in the universe ultimately developed.

The theory of what happened after the universe's first 400,000 years is one of hierarchical structure formation: the smaller gravitationally bound structures such as matter peaks containing the first stars and stellar clusters formed first, and these subsequently merged with gas and dark matter to form galaxies, followed by groups, clusters and superclusters of galaxies.

Very early universe

The very early universe is still a poorly understood epoch, from the viewpoint of fundamental physics. The prevailing theory, cosmic inflation, does a good job explaining the observed flatness, homogeneity and isotropy of the universe, as well as the absence of exotic relic particles (such as magnetic monopoles). Another prediction borne out by observation is that tiny perturbations in the primordial universe seed the later formation of structure. These fluctuations, while they form the foundation for all structure, appear most clearly as tiny temperature fluctuations at one part in 100,000. (To put this in perspective, the same level of fluctuations on a topographic map of the United States would show no feature taller than a few centimeters.) These fluctuations are critical, because they provide the seeds from which the largest structures can grow and eventually collapse to form galaxies and stars. COBE (Cosmic Background Explorer) provided the first detection of the intrinsic fluctuations in the cosmic microwave background radiation in the 1990s.

These perturbations are thought to have a very specific character: they form a Gaussian random field whose covariance function is diagonal and nearly scale-invariant. Observed fluctuations appear to have exactly this form, and in addition the spectral index measured by WMAP—the spectral index measures the deviation from a scale-invariant (or Harrison-Zel'dovich) spectrum—is very nearly the value predicted by the simplest and most robust models of inflation. Another important property of the primordial perturbations, that they are adiabatic (or isentropic between the various kinds of matter that compose the universe), is predicted by cosmic inflation and has been confirmed by observations.
Other theories of the very early universe have been proposed that are claimed to make similar predictions, such as the brane gas cosmology, cyclic model, pre-big bang model and holographic universe, but they remain nascent and are not widely accepted. Some theories, such as cosmic strings, have largely been refuted by increasingly precise data.

The horizon problem

The physical size of the Hubble radius (solid line) as a function of the scale factor of the universe. The physical wavelength of a perturbation mode (dashed line) is shown as well. The plot illustrates how the perturbation mode exits the horizon during cosmic inflation in order to reenter during radiation domination. If cosmic inflation never happened, and radiation domination continued back until a gravitational singularity, then the mode would never have exited the horizon in the very early universe.

An important concept in structure formation is the notion of the Hubble radius, often called simply the horizon, as it is closely related to the particle horizon. The Hubble radius, which is related to the Hubble parameter ${\displaystyle H}$ as ${\displaystyle R=c/H}$, where ${\displaystyle c}$ is the speed of light, defines, roughly speaking, the volume of the nearby universe that has recently (in the last expansion time) been in causal contact with an observer. Since the universe is continually expanding, its energy density is continually decreasing (in the absence of truly exotic matter such as phantom energy). The Friedmann equation relates the energy density of the universe to the Hubble parameter and shows that the Hubble radius is continually increasing.

The horizon problem of big bang cosmology says that, without inflation, perturbations were never in causal contact before they entered the horizon and thus the homogeneity and isotropy of, for example, the large scale galaxy distributions cannot be explained. This is because, in an ordinary Friedmann–Lemaître–Robertson–Walker cosmology, the Hubble radius increases more rapidly than space expands, so perturbations only enter the Hubble radius, and are not pushed out by the expansion. This paradox is resolved by cosmic inflation, which suggests that during a phase of rapid expansion in the early universe the Hubble radius was nearly constant. Thus, large scale isotropy is due to quantum fluctuations produced during cosmic inflation that are pushed outside the horizon.

Primordial plasma

The end of inflation is called reheating, when the inflation particles decay into a hot, thermal plasma of other particles. In this epoch, the energy content of the universe is entirely radiation, with standard model particles having relativistic velocities. As the plasma cools, baryogenesis and leptogenesis are thought to occur, as the quark–gluon plasma cools, electroweak symmetry breaking occurs and the universe becomes principally composed of ordinary protons, neutrons and electrons. As the universe cools further, big bang nucleosynthesis occurs and small quantities of deuterium, helium and lithium nuclei are created. As the universe cools and expands, the energy in photons begins to redshift away, particles become non-relativistic and ordinary matter begins to dominate the universe. Eventually, atoms begin to form as free electrons bind to nuclei. This suppresses Thomson scattering of photons. Combined with the rarefaction of the universe (and consequent increase in the mean free path of photons), this makes the universe transparent and the cosmic microwave background is emitted at recombination (the surface of last scattering).

Acoustic oscillations

The primordial plasma would have had very slight overdensities of matter, thought to have derived from the enlargement of quantum fluctuations during inflation. Whatever the source, these overdensities gravitationally attract matter. But the intense heat of the near constant photon-matter interactions of this epoch rather forcefully seeks thermal equilibrium, which creates a large amount of outward pressure. These counteracting forces of gravity and pressure create oscillations, analogous to sound waves created in air by pressure differences.

These perturbations are important, as they are responsible for the subtle physics that result in the cosmic microwave background anisotropy. In this epoch, the amplitude of perturbations that enter the horizon oscillate sinusoidally, with dense regions becoming more rarefied and then becoming dense again, with a frequency which is related to the size of the perturbation. If the perturbation oscillates an integral or half-integral number of times between coming into the horizon and recombination, it appears as an acoustic peak of the cosmic microwave background anisotropy. (A half-oscillation, in which a dense region becomes a rarefied region or vice versa, appears as a peak because the anisotropy is displayed as a power spectrum, so underdensities contribute to the power just as much as overdensities.) The physics that determines the detailed peak structure of the microwave background is complicated, but these oscillations provide the essence.

Linear structure

Evolution of two perturbations to the ΛCDM homogeneous big bang model. Between entering the horizon and decoupling, the dark matter perturbation (dashed line) grows logarithmically, before the growth accelerates in matter domination. On the other hand, between entering the horizon and decoupling, the perturbation in the baryon-photon fluid (solid line) oscillates rapidly. After decoupling, it grows rapidly to match the dominant matter perturbation, the dark matter mode.

One of the key realizations made by cosmologists in the 1970s and 1980s was that the majority of the matter content of the universe was composed not of atoms, but rather a mysterious form of matter known as dark matter. Dark matter interacts through the force of gravity, but it is not composed of baryons, and it is known with very high accuracy that it does not emit or absorb radiation. It may be composed of particles that interact through the weak interaction, such as neutrinos, but it cannot be composed entirely of the three known kinds of neutrinos (although some have suggested it is a sterile neutrino). Recent evidence indicates that there are about five times as much dark matter as baryonic matter, and thus the dynamics of the universe in this epoch are dominated by dark matter.

Dark matter plays a crucial role in structure formation because it feels only the force of gravity: the gravitational Jeans instability which allows compact structures to form is not opposed by any force, such as radiation pressure. As a result, dark matter begins to collapse into a complex network of dark matter halos well before ordinary matter, which is impeded by pressure forces. Without dark matter, the epoch of galaxy formation would occur substantially later in the universe than is observed.

The physics of structure formation in this epoch is particularly simple, as dark matter perturbations with different wavelengths evolve independently. As the Hubble radius grows in the expanding universe, it encompasses larger and larger disturbances. During matter domination, all causal dark matter perturbations grow through gravitational clustering. However, the shorter-wavelength perturbations that are included during radiation domination have their growth retarded until matter domination. At this stage, luminous, baryonic matter is expected to mirror the evolution of the dark matter simply, and their distributions should closely trace one another.

It is a simple matter to calculate this "linear power spectrum" and, as a tool for cosmology, it is of comparable importance to the cosmic microwave background. Galaxy surveys have measured the power spectrum, such as the Sloan Digital Sky Survey, and by surveys of the Lyman-α forest. Since these studies observe radiation emitted from galaxies and quasars, they do not directly measure the dark matter, but the large-scale distribution of galaxies (and of absorption lines in the Lyman-α forest) is expected to mirror the distribution of dark matter closely. This depends on the fact that galaxies will be larger and more numerous in denser parts of the universe, whereas they will be comparatively scarce in rarefied regions.

Nonlinear structure

When the perturbations have grown sufficiently, a small region might become substantially denser than the mean density of the universe. At this point, the physics involved becomes substantially more complicated. When the deviations from homogeneity are small, the dark matter may be treated as a pressureless fluid and evolves by very simple equations. In regions which are significantly denser than the background, the full Newtonian theory of gravity must be included. (The Newtonian theory is appropriate because the masses involved are much less than those required to form a black hole, and the speed of gravity may be ignored as the light-crossing time for the structure is still smaller than the characteristic dynamical time.) One sign that the linear and fluid approximations become invalid is that dark matter starts to form caustics in which the trajectories of adjacent particles cross, or particles start to form orbits. These dynamics are best understood using N-body simulations (although a variety of semi-analytic schemes, such as the Press–Schechter formalism, can be used in some cases). While in principle these simulations are quite simple, in practice they are tough to implement, as they require simulating millions or even billions of particles. Moreover, despite the large number of particles, each particle typically weighs 10⁹ solar masses and discretization effects may become significant. The largest such simulation as of 2005 is the Millennium simulation.

The result of N-body simulations suggests that the universe is composed largely of voids, whose densities might be as low as one-tenth the cosmological mean. The matter condenses in large filaments and haloes which have an intricate web-like structure. These form galaxy groups, clusters and superclusters. While the simulations appear to agree broadly with observations, their interpretation is complicated by the understanding of how dense accumulations of dark matter spur galaxy formation. In particular, many more small haloes form than we see in astronomical observations as dwarf galaxies and globular clusters. This is known as the galaxy bias problem, and a variety of explanations have been proposed. Most account for it as an effect in the complicated physics of galaxy formation, but some have suggested that it is a problem with our model of dark matter and that some effect, such as warm dark matter, prevents the formation of the smallest haloes.

Gas evolution

The final stage in evolution comes when baryons condense in the centres of galaxy haloes to form galaxies, stars and quasars. Dark matter greatly accelerates the formation of dense haloes. As dark matter does not have radiation pressure, the formation of smaller structures from dark matter is impossible. This is because dark matter cannot dissipate angular momentum, whereas ordinary baryonic matter can collapse to form dense objects by dissipating angular momentum through radiative cooling. Understanding these processes is an enormously difficult computational problem, because they can involve the physics of gravity, magnetohydrodynamics, atomic physics, nuclear reactions, turbulence and even general relativity. In most cases, it is not yet possible to perform simulations that can be compared quantitatively with observations, and the best that can be achieved are approximate simulations that illustrate the main qualitative features of a process such as a star formation.

Modelling structure formation

Snapshot from a computer simulation of large scale structure formation in a Lambda-CDM universe.

Cosmological perturbations

Much of the difficulty, and many of the disputes, in understanding the large-scale structure of the universe can be resolved by better understanding the choice of gauge in general relativity. By the scalar-vector-tensor decomposition, the metric includes four scalar perturbations, two vector perturbations, and one tensor perturbation. Only the scalar perturbations are significant: the vectors are exponentially suppressed in the early universe, and the tensor mode makes only a small (but important) contribution in the form of primordial gravitational radiation and the B-modes of the cosmic microwave background polarization. Two of the four scalar modes may be removed by a physically meaningless coordinate transformation. Which modes are eliminated determine the infinite number of possible gauge fixings. The most popular gauge is Newtonian gauge (and the closely related conformal Newtonian gauge), in which the retained scalars are the Newtonian potentials Φ and Ψ, which correspond exactly to the Newtonian potential energy from Newtonian gravity. Many other gauges are used, including synchronous gauge, which can be an efficient gauge for numerical computation (it is used by CMBFAST). Each gauge still includes some unphysical degrees of freedom. There is a so-called gauge-invariant formalism, in which only gauge invariant combinations of variables are considered.

Inflation and initial conditions

The initial conditions for the universe are thought to arise from the scale invariant quantum mechanical fluctuations of cosmic inflation. The perturbation of the background energy density at a given point ${\displaystyle \rho (\mathbf {x} ,t)}$ in space is then given by an isotropic, homogeneous Gaussian random field of mean zero. This means that the spatial Fourier transform of ${\displaystyle \rho }$ – ${\displaystyle {\hat {\rho }}(\mathbf {k} ,t)}$ has the following correlation functions

${\displaystyle \langle {\hat {\rho }}(\mathbf {k} ,t){\hat {\rho }}(\mathbf {k} ',t)\rangle =f(k)\delta ^{(3)}(\mathbf {k} -\mathbf {k'} )}$,

where ${\displaystyle \delta ^{(3)}}$ is the three-dimensional Dirac delta function and ${\displaystyle k=|\mathbf {k} |}$ is the length of ${\displaystyle \mathbf {k} }$. Moreover, the spectrum predicted by inflation is nearly scale invariant, which means

${\displaystyle \langle {\hat {\rho }}(\mathbf {k} ,t){\hat {\rho }}(\mathbf {k} ',t)\rangle =k^{n_{s}-1}\delta ^{(3)}(\mathbf {k} -\mathbf {k'} )}$,

where ${\displaystyle n_{s}-1}$ is a small number. Finally, the initial conditions are adiabatic or isentropic, which means that the fractional perturbation in the entropy of each species of particle is equal. The resulting predictions fit very well with observations, however there is a conceptual problem with the physical picture presented above. The quantum state from which the quantum fluctuations are extracted, is in fact completely homogeneous and isotropic, and thus it can not be argued that the quantum fluctuations represent the primordial inhomogeneities and anisotropies. The interpretation of quantum uncertainties in the value of the inflation field (which is what the so-called quantum fluctuations really are) as if they were statistical fluctuations in a Gaussian random field does not follow from the application of standard rules of quantum theory. The issue is sometimes presented in terms of the "quantum to classical transition", which is a confusing manner to refer to the problem at hand, as there are very few physicists, if any, that would argue that there is any entity that is truly classical at the fundamental level. In fact, the consideration of these issues brings us face to face with the so called measurement problem in quantum theory. If anything, the problem becomes exacerbated in the cosmological context, as the early universe contains no entities that might be taken as playing the role of "observers" or of "measuring devices", both of which are essential for the standard usage of quantum mechanics. The most popular posture among cosmologists, in this regard, is to rely on arguments based on decoherence and some form of "Many Worlds Interpretation" of quantum theory. There is an intense ongoing debate about the reasonableness of that posture.