Biological applications of bifurcation theory

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Biological_applications_of_bifurcation_theory

Biological applications of bifurcation theory provide a framework for understanding the behavior of biological networks modeled as dynamical systems. In the context of a biological system, bifurcation theory describes how small changes in an input parameter can cause a bifurcation or qualitative change in the behavior of the system. The ability to make dramatic change in system output is often essential to organism function, and bifurcations are therefore ubiquitous in biological networks such as the switches of the cell cycle.

Biological networks and dynamical systems

Biological networks originate from evolution and therefore have less standardized components and potentially more complex interactions than networks designed by humans, such as electrical networks. At the cellular level, components of a network can include a large variety of proteins, many of which differ between organisms. Network interactions occur when one or more proteins affect the function of another through transcription, translation, translocation, phosphorylation, or other mechanisms. These interactions either activate or inhibit the action of the target protein in some way. While humans build networks with a concern for simplicity and order, biological networks acquire redundancy and complexity over the course of evolution. Therefore, it can be impossible to predict the quantitative behavior of a biological network from knowledge of its organization. Similarly, it is impossible to describe its organization purely from its behavior, though behavior can indicate the presence of certain network motifs.

Figure 1. Example of a biological network between genes and proteins that controls entry into S phase.

However, with knowledge of network interactions and a set of parameters for the proteins and protein interactions (usually obtained through empirical research), it is often possible to construct a model of the network as a dynamical system. In general, for n proteins, the dynamical system takes the following form where x is typically protein concentration:

${\displaystyle {\dot{x}}_1=\frac{d{x}_1}{dt}=f_1(x_1,\dots ,x_n)}$

${\displaystyle ⋮}$

${\displaystyle {\dot{x}}_i=\frac{d{x}_i}{dt}=f_i(x_1,\dots ,x_n)}$

${\displaystyle ⋮}$

${\displaystyle {\dot{x}}_n=\frac{d{x}_n}{dt}=f_n(x_1,\dots ,x_n)}$

These systems are often very difficult to solve, so modeling of networks as a linear dynamical systems is easier. Linear systems contain no products between xs and are always solvable. They have the following form for all i:

${\displaystyle f_i=a_{i1}{x}_1+a_{i2}{x}_2+\cdots +a_{in}{x}_n}$

Unfortunately, biological systems are often nonlinear and therefore need nonlinear models.

Input/output motifs

Despite the great potential complexity and diversity of biological networks, all first-order network behavior generalizes to one of four possible input-output motifs: hyperbolic or Michaelis–Menten, ultra-sensitive, bistable, and bistable irreversible (a bistability where negative and therefore biologically impossible input is needed to return from a state of high output). Examples of each in biological contexts can be found on their respective pages.

Ultrasensitive, bistable, and irreversibly bistable networks all show qualitative change in network behavior around certain parameter values – these are their bifurcation points.

Basic bifurcations in the presence of error

Figure 2. Saddle-node bifurcation phase portrait, where the control parameter is varied (labelled ε instead of r, but functionally equivalent). As ε decreases, the fixed points come together and annihilate one another; As ε increases, the fixed points appear. dx/dt is denoted as v.

Nonlinear dynamical systems can be most easily understood with a one-dimensional example system where the change in some quantity x (e.g. protein concentration) abundance depends only on itself:

${\displaystyle \dot{x}=\frac{dx}{dt}=f(x)}$

Instead of solving the system analytically, which can be difficult or impossible for many functions, it is often quickest and most informative to take a geometric approach and draw a phase portrait. A phase portrait is a qualitative sketch of the differential equation's behavior that shows equilibrium solutions or fixed points and the vector field on the real line.

Bifurcations describe changes in the stability or existence of fixed points as a control parameter in the system changes. As a very simple explanation of a bifurcation in a dynamical system, consider an object balanced on top of a vertical beam. The mass of the object can be thought of as the control parameter, r, and the beam's deflection from the vertical axis is the dynamic variable, x. As r increases, x remains relatively stable. But when the mass reaches a certain point – the bifurcation point – the beam will suddenly buckle, in a direction dependent on minor imperfections in the setup. This is an example of a pitchfork bifurcation. Changes in the control parameter eventually changed the qualitative behavior of the system.

Saddle-node bifurcation

For a more rigorous example, consider the dynamical system shown in Figure 2, described by the following equation:

${\displaystyle \dot{x}=-x^2+r}$

where r is once again the control parameter (labeled ε in Figure 2). The system's fixed points are represented by where the phase portrait curve crosses the x-axis. The stability of a given fixed point can be determined by the direction of flow on the x-axis; for instance, in Figure 2, the green point is unstable (divergent flow), and the red one is stable (convergent flow). At first, when r is greater than 0, the system has one stable fixed point and one unstable fixed point. As r decreases the fixed points move together, briefly collide into a semi-stable fixed point at r = 0, and then cease to exist when r < 0.

In this case, because the behavior of the system changes significantly when the control parameter r is 0, 0 is a bifurcation point. By tracing the position of the fixed points in Figure 2 as r varies, one is able to generate the bifurcation diagram shown in Figure 3.

Other types of bifurcations are also important in dynamical systems, but the saddle-node bifurcation tends to be most important in biology. Real biological systems are subject to small stochastic variations that introduce error terms into the dynamical equations, and this usually leads to more complex bifurcations simplifying into separate saddle nodes and fixed points. Two such examples of "imperfect" bifurcations that can appear in biology are discussed below. Note that the saddle node itself in the presence of error simply translates in the x-r plane, with no change in qualitative behavior; this can be proven using the same analysis as presented below.

Figure 4. Unperturbed (black) and imperfect (red) transcritical bifurcations, overlaid. u and p are referred to as x and r, respectively, in the rest of the article. As before, solid lines are stable, and dotted unstable.

Imperfect transcritical bifurcation

A common simple bifurcation is the transcritical bifurcation, given by

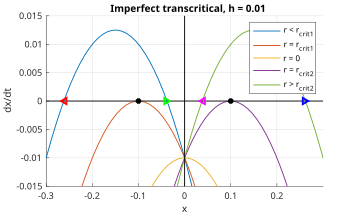
${\displaystyle \frac{dx}{dt}=rx-x^2}$ and the bifurcation diagram in Figure 4 (black curves). The phase diagrams are shown in Figure 5. Tracking the x-intercepts in the phase diagram as r changes, there are two fixed point trajectories which intersect at the origin; this is the bifurcation point (intuitively, when the number of x-intercepts in the phase portrait changes). The left fixed point is always unstable, and the right one stable.

Figure 5. Ideal transcritical bifurcation phase portraits. Fixed points are marked on the x-axis, each trajectory in a different color. The direction of the arrows indicates which direction they move as r increases. The red point is unstable, and the blue point is unstable. The black dot at the origin is stable for r < 0, and unstable for r > 0.

Now consider the addition of an error term h, where 0 < h << 1. That is,

${\displaystyle \frac{dx}{dt}=rx-x^2-h}$

The error term translates all the phase portraits vertically, downward if h is positive. In the left half of Figure 6 (x < 0), the black, red, and green fixed points are semistable, unstable, and stable, respectively. This is mirrored by the magenta, black, and blue points on the right half (x > 0). Each of these halves thus behaves like a saddle-node bifurcation; in other words, the imperfect transcritical bifurcation can be approximated by two saddle-node bifurcations when close to the critical points, as evident in the red curves of Figure 4.

Linear stability analysis

Figure 6. Imperfect transcritical bifurcation phase portraits. Five values of r are shown, given relative to the two critical points. Note that the y-intercept value is the same as h, or the magnitude of the imperfection. The green and blue points are stable, while the green red and magenta are unstable. The black dots indicate semistable fixed points.

Besides observing the flow in the phase diagrams, it is also possible to demonstrate the stability of various fixed points using linear stability analysis. First, find the fixed points in the phase portrait by setting the bifurcation equation to 0:

${\displaystyle \begin{array}{rl}\frac{dx}{dt}=f(x)& =rx-(x{)}^2-h\\ 0& =r{x}^{\ast }-(x^{\ast }{)}^2-h\end{array}}$

Using the quadratic formula to find the fixed points x*:

${\displaystyle \begin{array}{rl}{x}^{\ast }& =\frac{-r\pm \sqrt{r^2-4(-1)h}}{2(-1)}\\ & =\frac{r\pm \sqrt{r^2+4h}}{2}\\ & \approx \frac{r\pm \sqrt{r^2}}{2}\end{array}}$

where in the last step the approximation 4h << r ² has been used, which is reasonable for studying fixed points well past the bifurcation point, such as the light blue and green curves in Figure 6. Simplifying further,

${\displaystyle \begin{array}{rl}{x}^{\ast }& \approx \frac{r\pm r}{2}\\ & =\{\begin{array}{ll}0,& \text{fixed point closer to origin}\\ r,& \text{fixed point further from origin}\end{array}\end{array}}$

Next, determine whether the phase portrait curve is increasing or decreasing at the fixed points, which can be assessed by plugging x* into the first derivative of the bifurcation equation.

${\displaystyle \begin{array}{rl}{f}^{\prime }(x)& =r-2x\\ f^{\prime }(0)& =r=\{\begin{array}{ll}>0,& \text{if }r>0\to \text{unstable (magenta)}\\ <0,& \text{if }r<0\to \text{stable (green)}\end{array}\\ f^{\prime }(r)& =-r=\{\begin{array}{ll}<0,& \text{if }r>0\to \text{stable (blue)}\\ >0,& \text{if }r<0\to \text{unstable (red)}\end{array}\end{array}}$

The results are complicated by the fact that r can be both positive and negative; nonetheless, the conclusions are the same as before regarding the stability of each fixed point. This comes as no surprise, since the first derivative contains the same information as the phase diagram flow analysis. The colors in the above solution correspond to the arrows in Figure 6.

Imperfect pitchfork bifurcation

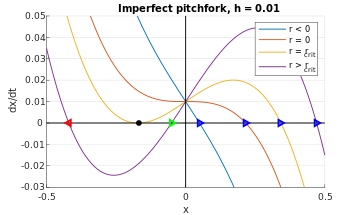
The buckling beam example from earlier is an example of a pitchfork bifurcation (perhaps more appropriately dubbed a "trifurcation"). The "ideal" pitchfork is shown on the left of Figure 7, given by

${\displaystyle \frac{dx}{dt}=rx-x^3}$

and r = 0 is where the bifurcation occurs, represented by the black dot at the origin of Figure 8. As r increases past 0, the black dot splits into three trajectories: the blue stable fixed point that moves right, the red stable point that moves left, and a third unstable point that stays at the origin. The blue and red are solid lines in Figure 7 (left), while the black unstable trajectory is the dotted portion along the positive x-axis.

As before, consider an error term h, where 0 < h << 1, i.e.

Figure 8. Ideal pitchfork bifurcation phase portraits. Fixed points are marked on the x-axis, each trajectory in a different color. The direction of the arrows indicates which direction they move as r increases. The red and blue points are stable, and there is a third unstable fixed point at the origin, indicated by the black dot. For r = r_crit = 0, the black dot also indicates a semi-stable point that appears and splits into the other three trajectories as r increases.

${\displaystyle \frac{dx}{dt}=rx-x^3+h}$

Once again, the phase portraits are translated upward an infinitesimal amount, as shown in Figure 9.Tracking the x-intercepts in the phase diagram as r changes yields the fixed points, which recapitulate the qualitative result from Figure 7 (right). More specifically, the blue fixed point from Figure 9 corresponds to the upper trajectory in Figure 7 (right); the green fixed point is the dotted trajectory; and the red fixed point is the bottommost trajectory. Thus, in the imperfect case (h ≠ 0), the pitchfork bifurcation simplifies into a single stable fixed point coupled with a saddle-node bifurcation.

A linear stability analysis can also be performed here, except using the generalized solution for a cubic equation instead of quadratic. The process is the same: 1) set the differential equation to zero and find the analytical form of the fixed points x*, 2) plug each x* into the first derivative ${\displaystyle f^{\prime }(x)=\frac{d}{dx}\frac{dx}{dt}}$, then 3) evaluate stability based on whether ${\displaystyle f^{\prime }(x^{\ast })}$ is positive or negative.

Figure 9. Imperfect pitchfork bifurcation phase portraits. Four different values of r relative to r_crit are shown. Note that the y-intercept value is the same as h, or the magnitude of the imperfection. The red and blue points are stable, while the green one (previously hidden at the origin) is unstable. As in Figure 5, the black dot indicates a semi-stable point that appears and splits into the red and green ones as r increases.

Multistability

Combined saddle-node bifurcations in a system can generate multistability. Bistability (a special case of multistability) is an important property in many biological systems, often the result of network architecture containing a mix of positive feedback interactions and ultra-sensitive elements. Bistable systems are hysteretic, i.e. the state of the system depends on the history of inputs, which can be crucial for switch-like control of cellular processes. For instance, this is important in contexts where a cell decides whether to commit to a particular pathway; a non-hysteretic response might switch the system on-and-off rapidly when subject to random thermal fluctuations close to the activation threshold, which can be resource-inefficient.

Specific examples in biology

Networks with bifurcation in their dynamics control many important transitions in the cell cycle. The G1/S, G2/M, and Metaphase–Anaphase transitions all act as biochemical switches in the cell cycle. For instance, egg extracts of Xenopus laevis are driven in and out of mitosis irreversibly by positive feedback in the phosphorylation of Cdc2, a cyclin-dependent kinase.

In population ecology, the dynamics of food web interactions networks can exhibit Hopf bifurcations. For instance, in an aquatic system consisting of a primary producer, a mineral resource, and an herbivore, researchers found that patterns of equilibrium, cycling, and extinction of populations could be qualitatively described with a simple nonlinear model with a Hopf Bifurcation.

Galactose utilization in budding yeast (S. cerevisiae) is measurable through GFP expression induced by the GAL promoter as a function of changing galactose concentrations. The system exhibits bistable switching between induced and non-induced states.

Similarly, lactose utilization in E. coli as a function of thio-methylgalactoside (a lactose analogue) concentration measured by a GFP-expressing lac promoter exhibits bistability and hysteresis (Figure 10, left and right respectively).

Mathematical and theoretical biology

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Mathematical_and_theoretical_biology

Yellow chamomile head showing the Fibonacci numbers in spirals consisting of 21 (blue) and 13 (aqua). Such arrangements have been noticed since the Middle Ages and can be used to make mathematical models of a wide variety of plants.

Mathematical and theoretical biology, or biomathematics, is a branch of biology which employs theoretical analysis, mathematical models and abstractions of living organisms to investigate the principles that govern the structure, development and behavior of the systems, as opposed to experimental biology which deals with the conduction of experiments to test scientific theories. The field is sometimes called mathematical biology or biomathematics to stress the mathematical side, or theoretical biology to stress the biological side. Theoretical biology focuses more on the development of theoretical principles for biology while mathematical biology focuses on the use of mathematical tools to study biological systems, even though the two terms are sometimes interchanged.

Mathematical biology aims at the mathematical representation and modeling of biological processes, using techniques and tools of applied mathematics. It can be useful in both theoretical and practical research. Describing systems in a quantitative manner means their behavior can be better simulated, and hence properties can be predicted that might not be evident to the experimenter. This requires precise mathematical models.

Because of the complexity of the living systems, theoretical biology employs several fields of mathematics, and has contributed to the development of new techniques.

History

Early history

Mathematics has been used in biology as early as the 13th century, when Fibonacci used the famous Fibonacci series to describe a growing population of rabbits. In the 18th century, Daniel Bernoulli applied mathematics to describe the effect of smallpox on the human population. Thomas Malthus' 1789 essay on the growth of the human population was based on the concept of exponential growth. Pierre François Verhulst formulated the logistic growth model in 1836.

Fritz Müller described the evolutionary benefits of what is now called Müllerian mimicry in 1879, in an account notable for being the first use of a mathematical argument in evolutionary ecology to show how powerful the effect of natural selection would be, unless one includes Malthus's discussion of the effects of population growth that influenced Charles Darwin: Malthus argued that growth would be exponential (he uses the word "geometric") while resources (the environment's carrying capacity) could only grow arithmetically.

The term "theoretical biology" was first used as a monograph title by Johannes Reinke in 1901, and soon after by Jakob von Uexküll in 1920. One founding text is considered to be On Growth and Form (1917) by D'Arcy Thompson, and other early pioneers include Ronald Fisher, Hans Leo Przibram, Vito Volterra, Nicolas Rashevsky and Conrad Hal Waddington.

Recent growth

Interest in the field has grown rapidly from the 1960s onwards. Some reasons for this include:

• The rapid growth of data-rich information sets, due to the genomics revolution, which are difficult to understand without the use of analytical tools
• Recent development of mathematical tools such as chaos theory to help understand complex, non-linear mechanisms in biology
• An increase in computing power, which facilitates calculations and simulations not previously possible
• An increasing interest in in silico experimentation due to ethical considerations, risk, unreliability and other complications involved in human and non-human animal research

Areas of research

Several areas of specialized research in mathematical and theoretical biology as well as external links to related projects in various universities are concisely presented in the following subsections, including also a large number of appropriate validating references from a list of several thousands of published authors contributing to this field. Many of the included examples are characterised by highly complex, nonlinear, and supercomplex mechanisms, as it is being increasingly recognised that the result of such interactions may only be understood through a combination of mathematical, logical, physical/chemical, molecular and computational models.

Abstract relational biology

Abstract relational biology (ARB) is concerned with the study of general, relational models of complex biological systems, usually abstracting out specific morphological, or anatomical, structures. Some of the simplest models in ARB are the Metabolic-Replication, or (M,R)--systems introduced by Robert Rosen in 1957–1958 as abstract, relational models of cellular and organismal organization.

Other approaches include the notion of autopoiesis developed by Maturana and Varela, Kauffman's Work-Constraints cycles, and more recently the notion of closure of constraints.

Algebraic biology

Algebraic biology (also known as symbolic systems biology) applies the algebraic methods of symbolic computation to the study of biological problems, especially in genomics, proteomics, analysis of molecular structures and study of genes.

Complex systems biology

An elaboration of systems biology to understand the more complex life processes was developed since 1970 in connection with molecular set theory, relational biology and algebraic biology.

Computer models and automata theory

A monograph on this topic summarizes an extensive amount of published research in this area up to 1986, including subsections in the following areas: computer modeling in biology and medicine, arterial system models, neuron models, biochemical and oscillation networks, quantum automata, quantum computers in molecular biology and genetics, cancer modelling, neural nets, genetic networks, abstract categories in relational biology, metabolic-replication systems, category theory applications in biology and medicine, automata theory, cellular automata, tessellation models and complete self-reproduction, chaotic systems in organisms, relational biology and organismic theories.

Modeling cell and molecular biology

This area has received a boost due to the growing importance of molecular biology.

• Mechanics of biological tissues
• Theoretical enzymology and enzyme kinetics
• Cancer modelling and simulation
• Modelling the movement of interacting cell populations
• Mathematical modelling of scar tissue formation
• Mathematical modelling of intracellular dynamics
• Mathematical modelling of the cell cycle
• Mathematical modelling of apoptosis

Modelling physiological systems

• Modelling of arterial disease
• Multi-scale modelling of the heart
• Modelling electrical properties of muscle interactions, as in bidomain and monodomain models

Computational neuroscience

Computational neuroscience (also known as theoretical neuroscience or mathematical neuroscience) is the theoretical study of the nervous system.

Evolutionary biology

Ecology and evolutionary biology have traditionally been the dominant fields of mathematical biology.

Evolutionary biology has been the subject of extensive mathematical theorizing. The traditional approach in this area, which includes complications from genetics, is population genetics. Most population geneticists consider the appearance of new alleles by mutation, the appearance of new genotypes by recombination, and changes in the frequencies of existing alleles and genotypes at a small number of gene loci. When infinitesimal effects at a large number of gene loci are considered, together with the assumption of linkage equilibrium or quasi-linkage equilibrium, one derives quantitative genetics. Ronald Fisher made fundamental advances in statistics, such as analysis of variance, via his work on quantitative genetics. Another important branch of population genetics that led to the extensive development of coalescent theory is phylogenetics. Phylogenetics is an area that deals with the reconstruction and analysis of phylogenetic (evolutionary) trees and networks based on inherited characteristics Traditional population genetic models deal with alleles and genotypes, and are frequently stochastic.

Many population genetics models assume that population sizes are constant. Variable population sizes, often in the absence of genetic variation, are treated by the field of population dynamics. Work in this area dates back to the 19th century, and even as far as 1798 when Thomas Malthus formulated the first principle of population dynamics, which later became known as the Malthusian growth model. The Lotka–Volterra predator-prey equations are another famous example. Population dynamics overlap with another active area of research in mathematical biology: mathematical epidemiology, the study of infectious disease affecting populations. Various models of the spread of infections have been proposed and analyzed, and provide important results that may be applied to health policy decisions.

In evolutionary game theory, developed first by John Maynard Smith and George R. Price, selection acts directly on inherited phenotypes, without genetic complications. This approach has been mathematically refined to produce the field of adaptive dynamics.

Mathematical biophysics

The earlier stages of mathematical biology were dominated by mathematical biophysics, described as the application of mathematics in biophysics, often involving specific physical/mathematical models of biosystems and their components or compartments.

The following is a list of mathematical descriptions and their assumptions.

Deterministic processes (dynamical systems)

A fixed mapping between an initial state and a final state. Starting from an initial condition and moving forward in time, a deterministic process always generates the same trajectory, and no two trajectories cross in state space.

• Difference equations/Maps – discrete time, continuous state space.
• Ordinary differential equations – continuous time, continuous state space, no spatial derivatives. See also: Numerical ordinary differential equations.
• Partial differential equations – continuous time, continuous state space, spatial derivatives. See also: Numerical partial differential equations.
• Logical deterministic cellular automata – discrete time, discrete state space. See also: Cellular automaton.

Stochastic processes (random dynamical systems)

A random mapping between an initial state and a final state, making the state of the system a random variable with a corresponding probability distribution.

• Non-Markovian processes – generalized master equation – continuous time with memory of past events, discrete state space, waiting times of events (or transitions between states) discretely occur.
• Jump Markov process – master equation – continuous time with no memory of past events, discrete state space, waiting times between events discretely occur and are exponentially distributed. See also: Monte Carlo method for numerical simulation methods, specifically dynamic Monte Carlo method and Gillespie algorithm.
• Continuous Markov process – stochastic differential equations or a Fokker–Planck equation – continuous time, continuous state space, events occur continuously according to a random Wiener process.

Spatial modelling

One classic work in this area is Alan Turing's paper on morphogenesis entitled The Chemical Basis of Morphogenesis, published in 1952 in the Philosophical Transactions of the Royal Society.

• Travelling waves in a wound-healing assay
• Swarming behaviour
• A mechanochemical theory of morphogenesis
• Biological pattern formation
• Spatial distribution modeling using plot samples
• Turing patterns

Mathematical methods

A model of a biological system is converted into a system of equations, although the word 'model' is often used synonymously with the system of corresponding equations. The solution of the equations, by either analytical or numerical means, describes how the biological system behaves either over time or at equilibrium. There are many different types of equations and the type of behavior that can occur is dependent on both the model and the equations used. The model often makes assumptions about the system. The equations may also make assumptions about the nature of what may occur.

Molecular set theory

Molecular set theory is a mathematical formulation of the wide-sense chemical kinetics of biomolecular reactions in terms of sets of molecules and their chemical transformations represented by set-theoretical mappings between molecular sets. It was introduced by Anthony Bartholomay, and its applications were developed in mathematical biology and especially in mathematical medicine. In a more general sense, Molecular set theory is the theory of molecular categories defined as categories of molecular sets and their chemical transformations represented as set-theoretical mappings of molecular sets. The theory has also contributed to biostatistics and the formulation of clinical biochemistry problems in mathematical formulations of pathological, biochemical changes of interest to Physiology, Clinical Biochemistry and Medicine.

Organizational biology

Theoretical approaches to biological organization aim to understand the interdependence between the parts of organisms. They emphasize the circularities that these interdependences lead to. Theoretical biologists developed several concepts to formalize this idea.

For example, abstract relational biology (ARB) is concerned with the study of general, relational models of complex biological systems, usually abstracting out specific morphological, or anatomical, structures. Some of the simplest models in ARB are the Metabolic-Replication, or (M,R)--systems introduced by Robert Rosen in 1957–1958 as abstract, relational models of cellular and organismal organization.

Model example: the cell cycle

Main article: Cellular model

The eukaryotic cell cycle is very complex and has been the subject of intense study, since its misregulation leads to cancers. It is possibly a good example of a mathematical model as it deals with simple calculus but gives valid results. Two research groups have produced several models of the cell cycle simulating several organisms. They have recently produced a generic eukaryotic cell cycle model that can represent a particular eukaryote depending on the values of the parameters, demonstrating that the idiosyncrasies of the individual cell cycles are due to different protein concentrations and affinities, while the underlying mechanisms are conserved (Csikasz-Nagy et al., 2006).

By means of a system of ordinary differential equations these models show the change in time (dynamical system) of the protein inside a single typical cell; this type of model is called a deterministic process (whereas a model describing a statistical distribution of protein concentrations in a population of cells is called a stochastic process).

To obtain these equations an iterative series of steps must be done: first the several models and observations are combined to form a consensus diagram and the appropriate kinetic laws are chosen to write the differential equations, such as rate kinetics for stoichiometric reactions, Michaelis-Menten kinetics for enzyme substrate reactions and Goldbeter–Koshland kinetics for ultrasensitive transcription factors, afterwards the parameters of the equations (rate constants, enzyme efficiency coefficients and Michaelis constants) must be fitted to match observations; when they cannot be fitted the kinetic equation is revised and when that is not possible the wiring diagram is modified. The parameters are fitted and validated using observations of both wild type and mutants, such as protein half-life and cell size.

To fit the parameters, the differential equations must be studied. This can be done either by simulation or by analysis. In a simulation, given a starting vector (list of the values of the variables), the progression of the system is calculated by solving the equations at each time-frame in small increments.

In analysis, the properties of the equations are used to investigate the behavior of the system depending on the values of the parameters and variables. A system of differential equations can be represented as a vector field, where each vector described the change (in concentration of two or more protein) determining where and how fast the trajectory (simulation) is heading. Vector fields can have several special points: a stable point, called a sink, that attracts in all directions (forcing the concentrations to be at a certain value), an unstable point, either a source or a saddle point, which repels (forcing the concentrations to change away from a certain value), and a limit cycle, a closed trajectory towards which several trajectories spiral towards (making the concentrations oscillate).

A better representation, which handles the large number of variables and parameters, is a bifurcation diagram using bifurcation theory. The presence of these special steady-state points at certain values of a parameter (e.g. mass) is represented by a point and once the parameter passes a certain value, a qualitative change occurs, called a bifurcation, in which the nature of the space changes, with profound consequences for the protein concentrations: the cell cycle has phases (partially corresponding to G1 and G2) in which mass, via a stable point, controls cyclin levels, and phases (S and M phases) in which the concentrations change independently, but once the phase has changed at a bifurcation event (Cell cycle checkpoint), the system cannot go back to the previous levels since at the current mass the vector field is profoundly different and the mass cannot be reversed back through the bifurcation event, making a checkpoint irreversible. In particular the S and M checkpoints are regulated by means of special bifurcations called a Hopf bifurcation and an infinite period bifurcation.

Doublespeak

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Doublespeak

Doublespeak is language that deliberately obscures, disguises, distorts, or reverses the meaning of words. Doublespeak may take the form of euphemisms (e.g., "downsizing" for layoffs and "servicing the target" for bombing), in which case it is primarily meant to make the truth sound more palatable. It may also refer to intentional ambiguity in language or to actual inversions of meaning. In such cases, doublespeak disguises the nature of the truth.

Doublespeak is most closely associated with political language used by large entities such as corporations and governments.

Origins and concepts

The term doublespeak derives from two concepts in George Orwell's novel, Nineteen Eighty-Four, "doublethink" and "Newspeak", despite the term itself not being used in the novel. Another version of the term, doubletalk, also referring to intentionally ambiguous speech, did exist at the time Orwell wrote his book, but the usage of doublespeak, as well as of "doubletalk", in the sense of emphasizing ambiguity, clearly predates the publication of the novel. Parallels have also been drawn between doublespeak and Orwell's classic essay, Politics and the English Language, which discusses linguistic distortion for purposes related to politics. In the essay, he observes that political language often serves to distort and obscure reality. Orwell's description of political speech is extremely similar to the popular definition of the term, doublespeak:

In our time, political speech and writing are largely the defence of the indefensible… Thus political language has to consist largely of euphemism, question-begging and sheer cloudy vagueness… the great enemy of clear language is insincerity. Where there is a gap between one's real and one's declared aims, one turns as it were instinctively to long words and exhausted idioms…

The writer Edward S. Herman cited what he saw as examples of doublespeak and doublethink in modern society. Herman describes in his book, Beyond Hypocrisy, the principal characteristics of doublespeak:

What is really important in the world of doublespeak is the ability to lie, whether knowingly or unconsciously, and to get away with it; and the ability to use lies and choose and shape facts selectively, blocking out those that don’t fit an agenda or program.

Examples

In politics

Edward S. Herman and Noam Chomsky comment in their book Manufacturing Consent: the Political Economy of the Mass Media that Orwellian doublespeak is an important component of the manipulation of the English language in American media, through a process called dichotomization, a component of media propaganda involving "deeply embedded double standards in the reporting of news." For example, the use of state funds by the poor and financially needy is commonly referred to as "social welfare" or "handouts," which the "coddled" poor "take advantage of". These terms, however, are not as often applied to other beneficiaries of government spending such as military spending. The bellicose language used interchangeably with calls for peace towards Armenia by Azerbaijani president Aliyev after the Second Nagorno-Karabakh War were described as doublespeak in media.

In advertising

Advertisers can use doublespeak to mask their commercial intent from users, as users' defenses against advertising become more entrenched. Some are attempting to counter this technique with a number of systems offering diverse views and information to highlight the manipulative and dishonest methods that advertisers employ.

According to Jacques Ellul, "the aim is not to even modify people’s ideas on a given subject, rather, it is to achieve conformity in the way that people act." He demonstrates this view by offering an example from drug advertising. Use of doublespeak in advertisements resulted in aspirin production rates rising by almost 50 percent from over 23 million pounds in 1960 to over 35 million pounds in 1970.

In comedy

Doublespeak, particularly when exaggerated, can be used as a device in satirical comedy and social commentary to ironically parody political or bureaucratic establishments' intent on obfuscation or prevarication. The television series Yes Minister is notable for its use of this device. Oscar Wilde was an early proponent of this device and a significant influence on Orwell.

Intensify/downplay pattern

This pattern was formulated by Hugh Rank and is a simple tool designed to teach some basic patterns of persuasion used in political propaganda and commercial advertising. The function of the intensify/downplay pattern is not to dictate what should be discussed but to encourage coherent thought and systematic organization. The pattern works in two ways: intensifying and downplaying. All people intensify, and this is done via repetition, association and composition. Downplaying is commonly done via omission, diversion and confusion as they communicate in words, gestures, numbers, et cetera. Individuals can better cope with organized persuasion by recognizing the common ways whereby communication is intensified or downplayed, so as to counter doublespeak.

In social media

In 2022 and 2023, it was widely reported that social media users were using a form of doublespeak – sometimes called "algospeak" – to subvert content moderation on platforms such as TikTok. Examples include using the word "unalive" instead of "dead" or "kill", or using "leg booty" instead of LGBT, which users believed would prevent moderation algorithms from banning or shadow banning their accounts.

Doublespeak Award

Main article: Doublespeak Award

Doublespeak is often used by politicians to advance their agenda. The Doublespeak Award is an "ironic tribute to public speakers who have perpetuated language that is grossly deceptive, evasive, euphemistic, confusing, or self-centered." It has been issued by the US National Council of Teachers of English (NCTE) since 1974. The recipients of the Doublespeak Award are usually politicians, national administration or departments. An example of this is the United States Department of Defense, which won the award three times, in 1991, 1993, and 2001. For the 1991 award, the United States Department of Defense "swept the first six places in the Doublespeak top ten" for using euphemisms like "servicing the target" (bombing) and "force packages" (warplanes). Among the other phrases in contention were "difficult exercise in labor relations", meaning a strike, and "meaningful downturn in aggregate output", an attempt to avoid saying the word "recession".

NCTE Committee on Public Doublespeak

Main article: National Council of Teachers of English

The US National Council of Teachers of English (NCTE) Committee on Public Doublespeak was formed in 1971, in the midst of the Watergate scandal. It was at a point when there was widespread skepticism about the degree of truth which characterized relationships between the public and the worlds of politics, the military, and business.

NCTE passed two resolutions. One called for the council to find means to study dishonest and inhumane uses of language and literature by advertisers, to bring offenses to public attention, and to propose classroom techniques for preparing children to cope with commercial propaganda. The other called for the council to find means to study the relationships between language and public policy and to track, publicize, and combat semantic distortion by public officials, candidates for office, political commentators, and all others whose language is transmitted through the mass media.

The two resolutions were accomplished by forming NCTE's Committee on Public Doublespeak, a body which has made significant contributions in describing the need for reform where clarity in communication has been deliberately distorted.

Hugh Rank

Hugh Rank helped form the Doublespeak committee in 1971 and was its first chairman. Under his editorship, the committee produced a book called Language and Public Policy (1974), with the aim of informing readers of the extensive scope of doublespeak being used to deliberately mislead and deceive the audience. He highlighted the deliberate public misuses of language and provided strategies for countering doublespeak by focusing on educating people in the English language so as to help them identify when doublespeak is being put into play. He was also the founder of the Intensify/Downplay pattern that has been widely used to identify instances of doublespeak being used.

Daniel Dieterich

Daniel Dieterich, former chair of the National Council of Teachers of English, served as the second chairman of the Doublespeak committee after Hugh Rank in 1975. He served as editor of its second publication, Teaching about Doublespeak (1976), which carried forward the committee's charge to inform teachers of ways of teaching students how to recognize and combat language designed to mislead and misinform.

William D. Lutz

William D. Lutz, professor emeritus at Rutgers University-Camden has served as the third chairman of the Doublespeak Committee since 1975. In 1989, both his own book Doublespeak and, under his editorship, the committee's third book, Beyond Nineteen Eighty-Four, were published. Beyond Nineteen Eighty-Four consists of 220 pages and eighteen articles contributed by long-time Committee members and others whose bodies of work have contributed to public understanding about language, as well as a bibliography of 103 sources on doublespeak. Lutz was also the former editor of the now defunct Quarterly Review of Doublespeak, which examined the use of vocabulary by public officials to obscure the underlying meaning of what they tell the public. Lutz is one of the main contributors to the committee as well as promoting the term "doublespeak" to a mass audience to inform them of its deceptive qualities. He mentions:

There is more to being an effective consumer of language than just expressing dismay at dangling modifiers, faulty subject and verb agreement, or questionable usage. All who use language should be concerned whether statements and facts agree, whether language is, in Orwell's words, "largely the defense of the indefensible" and whether language "is designed to make lies sound truthful and murder respectable, and to give an appearance of solidity to pure wind".

Education against doublespeak

Charles Weingartner, one of the founding members of the NCTE committee on Public Doublespeak mentioned: "people do not know enough about the subject (the reality) to recognize that the language being used conceals, distorts, misleads. Teachers of English should teach our students that words are not things, but verbal tokens or signs of things that should finally be carried back to the things that they stand for to be verified."