Many-worlds interpretation (of Quantum mechanics)

From Wikipedia, the free encyclopedia

The quantum-mechanical "Schrödinger's cat" theorem according to the many-worlds interpretation. In this interpretation, every event is a branch point; the cat is both alive and dead, even before the box is opened, but the "alive" and "dead" cats are in different branches of the universe, both of which are equally real, but which do not interact with each other.^[1]

The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction and denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternate histories and futures are real, each representing an actual "world" (or "universe"). In layman's terms, the hypothesis states there is a very large—perhaps infinite^[2]—number of universes, and everything that could possibly have happened in our past, but did not, has occurred in the past of some other universe or universes. The theory is also referred to as MWI, the relative state formulation, the Everett interpretation, the theory of the universal wavefunction, many-universes interpretation, multiverse theory or just many-worlds.

The original relative state formulation is due to Hugh Everett in 1957.^[3][4] Later, this formulation was popularized and renamed many-worlds by Bryce Seligman DeWitt in the 1960s and 1970s.^[1][5][6][7] The decoherence approaches to interpreting quantum theory have been further explored and developed,^[8][9][10] becoming quite popular. MWI is one of many multiverse hypotheses in physics and philosophy. It is currently considered a mainstream interpretation along with the other decoherence interpretations, collapse theories (including the historical Copenhagen interpretation),^[11] and hidden variable theories such as the Bohmian mechanics.

Before many-worlds, reality had always been viewed as a single unfolding history. Many-worlds, however, views historical reality as a many-branched tree, wherein every possible quantum outcome is realised.^[12] Many-worlds reconciles the observation of non-deterministic events, such as random radioactive decay, with the fully deterministic equations of quantum physics.

In many-worlds, the subjective appearance of wavefunction collapse is explained by the mechanism of quantum decoherence, and this is supposed to resolve all of the correlation paradoxes of quantum theory, such as the EPR paradox^[13][14] and Schrödinger's cat,^[1] since every possible outcome of every event defines or exists in its own "history" or "world".

Origin

In Dublin in 1952 Erwin Schrödinger gave a lecture in which at one point he jocularly warned his audience that what he was about to say might "seem lunatic". He went on to assert that when the equation that won him a Nobel prize seems to be describing several different histories, they are "not alternatives but all really happen simultaneously". This is the earliest known reference to the many-worlds.^[15][16]

Outline

Although several versions of many-worlds have been proposed since Hugh Everett's original work,^[4] they all contain one key idea: the equations of physics that model the time evolution of systems without embedded observers are sufficient for modelling systems which do contain observers; in particular there is no observation-triggered wave function collapse which the Copenhagen interpretation proposes. Provided the theory is linear with respect to the wavefunction, the exact form of the quantum dynamics modelled, be it the non-relativistic Schrödinger equation, relativistic quantum field theory or some form of quantum gravity or string theory, does not alter the validity of MWI since MWI is a metatheory applicable to all linear quantum theories, and there is no experimental evidence for any non-linearity of the wavefunction in physics.^[17][18] MWI's main conclusion is that the universe (or multiverse in this context) is composed of a quantum superposition of very many, possibly even non-denumerably infinitely^[2] many, increasingly divergent, non-communicating parallel universes or quantum worlds.^[7]

The idea of MWI originated in Everett's Princeton Ph.D. thesis "The Theory of the Universal Wavefunction",^[7] developed under his thesis advisor John Archibald Wheeler, a shorter summary of which was published in 1957 entitled "Relative State Formulation of Quantum Mechanics" (Wheeler contributed the title "relative state";^[19] Everett originally called his approach the "Correlation Interpretation", where "correlation" refers to quantum entanglement). The phrase "many-worlds" is due to Bryce DeWitt,^[7] who was responsible for the wider popularisation of Everett's theory, which had been largely ignored for the first decade after publication. DeWitt's phrase "many-worlds" has become so much more popular than Everett's "Universal Wavefunction" or Everett–Wheeler's "Relative State Formulation" that many forget that this is only a difference of terminology; the content of both of Everett's papers and DeWitt's popular article is the same.

The many-worlds interpretation shares many similarities with later, other "post-Everett" interpretations of quantum mechanics which also use decoherence to explain the process of measurement or wavefunction collapse. MWI treats the other histories or worlds as real since it regards the universal wavefunction as the "basic physical entity"^[20] or "the fundamental entity, obeying at all times a deterministic wave equation".^[21] The other decoherent interpretations, such as consistent histories, the Existential Interpretation etc., either regard the extra quantum worlds as metaphorical in some sense, or are agnostic about their reality; it is sometimes hard to distinguish between the different varieties. MWI is distinguished by two qualities: it assumes realism,^[20][21] which it assigns to the wavefunction, and it has the minimal formal structure possible, rejecting any hidden variables, quantum potential, any form of a collapse postulate (i.e., Copenhagenism) or mental postulates (such as the many-minds interpretation makes).

Decoherent interpretations of many-worlds using einselection to explain how a small number of classical pointer states can emerge from the enormous Hilbert space of superpositions have been proposed by Wojciech H. Zurek. "Under scrutiny of the environment, only pointer states remain unchanged. Other states decohere into mixtures of stable pointer states that can persist, and, in this sense, exist: They are einselected."^[22] These ideas complement MWI and bring the interpretation in line with our perception of reality.

Many-worlds is often referred to as a theory, rather than just an interpretation, by those who propose that many-worlds can make testable predictions (such as David Deutsch) or is falsifiable (such as Everett) or by those who propose that all the other, non-MW interpretations, are inconsistent, illogical or unscientific in their handling of measurements; Hugh Everett argued that his formulation was a metatheory, since it made statements about other interpretations of quantum theory; that it was the "only completely coherent approach to explaining both the contents of quantum mechanics and the appearance of the world."^[23] Deutsch is dismissive that many-worlds is an "interpretation", saying that calling it an interpretation "is like talking about dinosaurs as an 'interpretation' of fossil records."^[24]

Interpreting wavefunction collapse

As with the other interpretations of quantum mechanics, the many-worlds interpretation is motivated by behavior that can be illustrated by the double-slit experiment. When particles of light (or anything else) are passed through the double slit, a calculation assuming wave-like behavior of light can be used to identify where the particles are likely to be observed. Yet when the particles are observed in this experiment, they appear as particles (i.e., at definite places) and not as non-localized waves.

Some versions of the Copenhagen interpretation of quantum mechanics proposed a process of "collapse" in which an indeterminate quantum system would probabilistically collapse down onto, or select, just one determinate outcome to "explain" this phenomenon of observation. Wavefunction collapse was widely regarded as artificial and ad hoc^{[citation needed]}, so an alternative interpretation in which the behavior of measurement could be understood from more fundamental physical principles was considered desirable.

Everett's Ph.D. work provided such an alternative interpretation. Everett stated that for a composite system – for example a subject (the "observer" or measuring apparatus) observing an object (the "observed" system, such as a particle) – the statement that either the observer or the observed has a well-defined state is meaningless; in modern parlance, the observer and the observed have become entangled; we can only specify the state of one relative to the other, i.e., the state of the observer and the observed are correlated after the observation is made. This led Everett to derive from the unitary, deterministic dynamics alone (i.e., without assuming wavefunction collapse) the notion of a relativity of states.

Everett noticed that the unitary, deterministic dynamics alone decreed that after an observation is made each element of the quantum superposition of the combined subject–object wavefunction contains two "relative states": a "collapsed" object state and an associated observer who has observed the same collapsed outcome; what the observer sees and the state of the object have become correlated by the act of measurement or observation. The subsequent evolution of each pair of relative subject–object states proceeds with complete indifference as to the presence or absence of the other elements, as if wavefunction collapse has occurred, which has the consequence that later observations are always consistent with the earlier observations. Thus the appearance of the object's wavefunction's collapse has emerged from the unitary, deterministic theory itself. (This answered Einstein's early criticism of quantum theory, that the theory should define what is observed, not for the observables to define the theory).^[25] Since the wavefunction merely appears to have collapsed then, Everett reasoned, there was no need to actually assume that it had collapsed. And so, invoking Occam's razor, he removed the postulate of wavefunction collapse from the theory.

The unreal/real interpretation

According to Martin Gardner, the "other" worlds of MWI have two different interpretations: real or unreal; he claims that Stephen Hawking and Steven Weinberg both favour the unreal interpretation.^[26] Gardner also claims that the nonreal interpretation is favoured by the majority of physicists, whereas the "realist" view is only supported by MWI experts such as Deutsch and Bryce DeWitt. Hawking has said that "according to Feynman's idea", all the other histories are as "equally real" as our own,^[27] and Martin Gardner reports Hawking saying that MWI is "trivially true".^[28] In a 1983 interview, Hawking also said he regarded the MWI as "self-evidently correct" but was dismissive towards questions about the interpretation of quantum mechanics, saying, "When I hear of Schrödinger's cat, I reach for my gun." In the same interview, he also said, "But, look: All that one does, really, is to calculate conditional probabilities—in other words, the probability of A happening, given B. I think that that's all the many worlds interpretation is. Some people overlay it with a lot of mysticism about the wave function splitting into different parts. But all that you're calculating is conditional probabilities."^[29] Elsewhere Hawking contrasted his attitude towards the "reality" of physical theories with that of his colleague Roger Penrose, saying, "He's a Platonist and I'm a positivist. He's worried that Schrödinger's cat is in a quantum state, where it is half alive and half dead. He feels that can't correspond to reality. But that doesn't bother me. I don't demand that a theory correspond to reality because I don't know what it is. Reality is not a quality you can test with litmus paper. All I'm concerned with is that the theory should predict the results of measurements. Quantum theory does this very successfully."^[30] For his own part, Penrose agrees with Hawking that QM applied to the universe implies MW, although he considers the current lack of a successful theory of quantum gravity negates the claimed universality of conventional QM.^[31]

Similarities with the de Broglie–Bohm interpretation

Kim Joris Boström has proposed a non-relativistic quantum mechanical theory that combines elements of the de Broglie–Bohm mechanics and that of Everett’s many-‘worlds’. In particular, the unreal MW interpretation of Hawking and Weinberg is similar to the Bohmian concept of unreal empty branch ‘worlds’:

The second issue with Bohmian mechanics may at first sight appear rather harmless, but which on a closer look develops considerable destructive power: the issue of empty branches. These are the components of the post-measurement state that do not guide any particles because they do not have the actual configuration q in their support. At first sight, the empty branches do not appear problematic but on the contrary very helpful as they enable the theory to explain unique outcomes of measurements. Also, they seem to explain why there is an effective “collapse of the wavefunction”, as in ordinary quantum mechanics. On a closer view, though, one must admit that these empty branches do not actually disappear. As the wavefunction is taken to describe a really existing field, all their branches really exist and will evolve forever by the Schrödinger dynamics, no matter how many of them will become empty in the course of the evolution. Every branch of the global wavefunction potentially describes a complete world which is, according to Bohm’s ontology, only a possible world that would be the actual world if only it were filled with particles, and which is in every respect identical to a corresponding world in Everett’s theory. Only one branch at a time is occupied by particles, thereby representing the actual world, while all other branches, though really existing as part of a really existing wavefunction, are empty and thus contain some sort of “zombie worlds” with planets, oceans, trees, cities, cars and people who talk like us and behave like us, but who do not actually exist. Now, if the Everettian theory may be accused of ontological extravagance, then Bohmian mechanics could be accused of ontological wastefulness. On top of the ontology of empty branches comes the additional ontology of particle positions that are, on account of the quantum equilibrium hypothesis, forever unknown to the observer. Yet, the actual configuration is never needed for the calculation of the statistical predictions in experimental reality, for these can be obtained by mere wavefunction algebra. From this perspective, Bohmian mechanics may appear as a wasteful and redundant theory. I think it is considerations like these that are the biggest obstacle in the way of a general acceptance of Bohmian mechanics.^[32]

Probability

Attempts have been made, by many-world advocates and others, over the years to derive the Born rule, rather than just conventionally assume it, so as to reproduce all the required statistical behaviour associated with quantum mechanics. There is no consensus on whether this has been successful.^[33][34][35]

Frequency-based approaches

Everett (1957) briefly derived the Born rule by showing that the Born rule was the only possible rule, and that its derivation was as justified as the procedure for defining probability in classical mechanics. Everett stopped doing research in theoretical physics shortly after obtaining his Ph.D., but his work on probability has been extended by a number of people. Andrew Gleason (1957) and James Hartle (1965) independently reproduced Everett's work^[36] which was later extended.^[37][38] These results are closely related to Gleason's theorem, a mathematical result according to which the Born probability measure is the only one on Hilbert space that can be constructed purely from the quantum state vector.^[39]

Bryce DeWitt and his doctoral student R. Neill Graham later provided alternative (and longer) derivations to Everett's derivation of the Born rule.^[7] They demonstrated that the norm of the worlds where the usual statistical rules of quantum theory broke down vanished, in the limit where the number of measurements went to infinity.

Decision theory

A decision-theoretic derivation of the Born rule from Everettarian assumptions, was produced by David Deutsch (1999)^[40] and refined by Wallace (2002–2009)^{[41][42][43][44]} and Saunders (2004).^[45][46] Some reviews have been positive, although the status of these arguments remains highly controversial; some theoretical physicists have taken them as supporting the case for parallel universes.^[47] In the New Scientist article, reviewing their presentation at a September 2007 conference,^[48][49] Andy Albrecht, a physicist at the University of California at Davis, is quoted as saying "This work will go down as one of the most important developments in the history of science."^[47]

The Born rule and the collapse of the wave function have been obtained in the framework of the relative-state formulation of quantum mechanics by Armando V. D. B. Assis. He has proved that the Born rule and the collapse of the wave function follow from a game-theoretical strategy, namely the Nash equilibrium within a von Neumann zero-sum game between nature and observer.^[50]

Symmetries and invariance

Wojciech H. Zurek (2005)^[51] has produced a derivation of the Born rule, where decoherence has replaced Deutsch's informatic assumptions.^[52] Lutz Polley (2000) has produced Born rule derivations where the informatic assumptions are replaced by symmetry arguments.^[53][54]

Charles Sebens and Sean M. Carroll, building on work by Lev Vaidman,^[55] proposed a similar approach based on self-locating uncertainty.^[56] In this approach, decoherence creates multiple identical copies of observers, who can assign credences to being on different branches using the Born rule.

MWI overview

In Everett's formulation, a measuring apparatus M and an object system S form a composite system, each of which prior to measurement exists in well-defined (but time-dependent) states. Measurement is regarded as causing M and S to interact. After S interacts with M, it is no longer possible to describe either system by an independent state. According to Everett, the only meaningful descriptions of each system are relative states: for example the relative state of S given the state of M or the relative state of M given the state of S. In DeWitt's formulation, the state of S after a sequence of measurements is given by a quantum superposition of states, each one corresponding to an alternative measurement history of S.

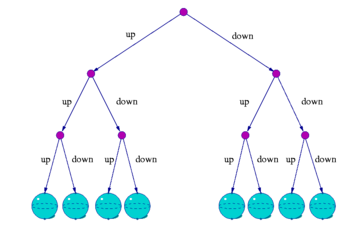
Schematic illustration of splitting as a result of a repeated measurement.

For example, consider the smallest possible truly quantum system S, as shown in the illustration. This describes for instance, the spin-state of an electron. Considering a specific axis (say the z-axis) the north pole represents spin "up" and the south pole, spin "down". The superposition states of the system are described by (the surface of) a sphere called the Bloch sphere. To perform a measurement on S, it is made to interact with another similar system M. After the interaction, the combined system is described by a state that ranges over a six-dimensional space (the reason for the number six is explained in the article on the Bloch sphere). This six-dimensional object can also be regarded as a quantum superposition of two "alternative histories" of the original system S, one in which "up" was observed and the other in which "down" was observed. Each subsequent binary measurement (that is interaction with a system M) causes a similar split in the history tree. Thus after three measurements, the system can be regarded as a quantum superposition of 8 = 2 × 2 × 2 copies of the original system S.

The accepted terminology is somewhat misleading because it is incorrect to regard the universe as splitting at certain times; at any given instant there is one state in one universe.

Relative state

In his 1957 doctoral dissertation, Everett proposed that rather than modeling an isolated quantum system subject to external observation, one could mathematically model an object as well as its observers as purely physical systems within the mathematical framework developed by Paul Dirac, von Neumann and others, discarding altogether the ad hoc mechanism of wave function collapse.

Since Everett's original work, there have appeared a number of similar formalisms in the literature. One such is the relative state formulation. It makes two assumptions: first, the wavefunction is not simply a description of the object's state, but that it actually is entirely equivalent to the object, a claim it has in common with some other interpretations. Secondly, observation or measurement has no special laws or mechanics, unlike in the Copenhagen interpretation which considers the wavefunction collapse as a special kind of event which occurs as a result of observation. Instead, measurement in the relative state formulation is the consequence of a configuration change in the memory of an observer described by the same basic wave physics as the object being modeled.

The many-worlds interpretation is DeWitt's popularisation of Everett's work, who had referred to the combined observer–object system as being split by an observation, each split corresponding to the different or multiple possible outcomes of an observation. These splits generate a possible tree as shown in the graphic below. Subsequently, DeWitt introduced the term "world" to describe a complete measurement history of an observer, which corresponds roughly to a single branch of that tree. Note that "splitting" in this sense is hardly new or even quantum mechanical. The idea of a space of complete alternative histories had already been used in the theory of probability since the mid-1930s for instance to model Brownian motion.

Partial trace as relative state. Light blue rectangle on upper left denotes system in pure state. Trellis shaded rectangle in upper right denotes a (possibly) mixed state. Mixed state from observation is partial trace of a linear superposition of states as shown in lower right-hand corner.

Successive measurements with successive splittings

Under the many-worlds interpretation, the Schrödinger equation, or relativistic analog, holds all the time everywhere. An observation or measurement is modeled by applying the wave equation to the entire system comprising the observer and the object. One consequence is that every observation can be thought of as causing the combined observer–object's wavefunction to change into a quantum superposition of two or more non-interacting branches, or split into many "worlds". Since many observation-like events have happened and are constantly happening, there are an enormous and growing number of simultaneously existing states.

If a system is composed of two or more subsystems, the system's state will be a superposition of products of the subsystems' states. Each product of subsystem states in the overall superposition evolves over time independently of other products. Once the subsystems interact, their states have become correlated or entangled and it is no longer possible to consider them independent of one another. In Everett's terminology each subsystem state was now correlated with its relative state, since each subsystem must now be considered relative to the other subsystems with which it has interacted.

Properties of the theory

MWI removes the observer-dependent role in the quantum measurement process by replacing wavefunction collapse with quantum decoherence. Since the role of the observer lies at the heart of most if not all "quantum paradoxes," this automatically resolves a number of problems; see for example Schrödinger's cat thought experiment, the EPR paradox, von Neumann's "boundary problem" and even wave-particle duality. Quantum cosmology also becomes intelligible, since there is no need anymore for an observer outside of the universe.^{[citation needed]}

MWI is a realist, deterministic, arguably local theory, akin to classical physics (including the theory of relativity), at the expense of losing counterfactual definiteness. MWI achieves this by removing wavefunction collapse, which is indeterministic and non-local, from the deterministic and local equations of quantum theory.^[57]

MWI (or other, broader multiverse considerations) provides a context for the anthropic principle which may provide an explanation for the fine-tuned universe.^[58][59]

MWI, being a decoherent formulation, is axiomatically more streamlined than the Copenhagen and other collapse interpretations; and thus favoured under certain interpretations of Occam's razor.^{[60][unreliable source?]} Of course there are other decoherent interpretations that also possess this advantage with respect to the collapse interpretations.

Comparative properties and possible experimental tests

One of the salient properties of the many-worlds interpretation is that it does not require an exceptional method of wave function collapse to explain it. "It seems that there is no experiment distinguishing the MWI from other no-collapse theories such as Bohmian mechanics or other variants of MWI... In most no-collapse interpretations, the evolution of the quantum state of the Universe is the same. Still, one might imagine that there is an experiment distinguishing the MWI from another no-collapse interpretation based on the difference in the correspondence between the formalism and the experience (the results of experiments)."^[61]

However, in 1985, David Deutsch published three related thought experiments which could test the theory vs the Copenhagen interpretation.^[62] The experiments require macroscopic quantum state preparation and quantum erasure by a hypothetical quantum computer which is currently outside experimental possibility. Since then Lockwood (1989), Vaidman and others have made similar proposals.^[61] These proposals also require an advanced technology which is able to place a macroscopic object in a coherent superposition, another task which it is uncertain will ever be possible to perform. Many other controversial ideas have been put forward though, such as a recent claim that cosmological observations could test the theory,^[63] and another claim by Rainer Plaga (1997), published in Foundations of Physics, that communication might be possible between worlds.^[64]

Copenhagen interpretation

In the Copenhagen interpretation, the mathematics of quantum mechanics allows one to predict probabilities for the occurrence of various events. When an event occurs, it becomes part of the definite reality, and alternative possibilities do not. There is no necessity to say anything definite about what is not observed.

The universe decaying to a new vacuum state

Any event that changes the number of observers in the universe may have experimental consequences.^[65] Quantum tunnelling to a new vacuum state would reduce the number of observers to zero (i.e., kill all life).^{[citation needed]} Some cosmologists^{[citation needed]} argue that the universe is in a false vacuum state and that consequently the universe should have already experienced quantum tunnelling to a true vacuum state. This has not happened and is cited as evidence in favor of many-worlds. In some worlds, quantum tunnelling to a true vacuum state has happened but most other worlds escape this tunneling and remain viable. This can be thought of as a variation on quantum suicide.

Many-minds

The many-minds interpretation is a multi-world interpretation that defines the splitting of reality on the level of the observers' minds. In this, it differs from Everett's many-worlds interpretation, in which there is no special role for the observer's mind.^[64]

Dual manifolds

Our world ${\displaystyle W}$ always manifests a mirrored pair in the imaginary part or a conjugate pair of the complex manifolds, such that the physical nature of ${\displaystyle P}$ functions is associated with its virtual or dark nature of ${\displaystyle V}$ functions to constitute a duality of the real world functions. Today, the most popular topology, for example, is a duality of the virtual and physical manifolds of Entanglement Topology^[66], which represents the foundation of Quantum entanglement^[67] as well as microcosmic ontology^[68].

Among the real world functions, the most fundamental dynamics are our dark resources of the universal energies, known as physical Yin “−” and/or dark Yang “+” objects, with neutral balance “0” that appears as if there were nothing. Each type of the physical of virtual dark objects (−,0,+) appearing as energy fields has their own domain of the relational manifolds such that one defines a ${\displaystyle Y^{-}}$ (Yin) manifold while the other the ${\displaystyle Y^{+}}$ (Yang) manifold, respectively. They jointly present the two-sidedness of any events, operations, transportations, and entanglements, each dissolving into the other in the alternating streams that generates the life of entanglements, conceals the inanimacy of resources, and operates the event actions. As a two-dimensional plane, the physical position of ${\displaystyle {\bf {r}}}$ and virtual positions of ${\displaystyle \pm i{\bf {k}}}$ naturally form a duality of the conjugate manifolds: ${\displaystyle Y^{-}\{{\bf {r}}+i{\bf {k}}\}}$ and ${\displaystyle Y^{+}\{{\bf {r}}-i{\bf {k}}\}}$. Each of the system constitutes its world plane ${\displaystyle W^{\pm }}$ distinctively, forms a duality of the universal topology ${\displaystyle W=P\pm iV}$ cohesively, and maintains its own sub-coordinate system {${\displaystyle {\bf {r}}}$} or {${\displaystyle {\bf {k}}}$} respectively. Because of the two dimensions of the world planes {${\displaystyle {\bf {r}}\pm i{\bf {k}}}$}, each transcends its event operations further down to its sub-coordinate system with extra degrees of freedoms for either physical dimensions ${\displaystyle {\bf {r}}=\{x_{1},x_{2},x_{3}\}}$ or virtual dimensions ${\displaystyle {i{\bf {k}}}=\{x^{0},x^{-1},x^{-2},\cdots \}}$. For example, in the scope of space and time duality, the compound dimensions become the tetrad coordinates, known as the following:

${\displaystyle \qquad x_{m}\in {\check {x}}\{x_{0},x_{1},x_{2},x_{3}\}\subset Y^{-}\{{\bf {r}}+i{\bf {k}}\}\qquad :x_{0}=ict}$

${\displaystyle \qquad x^{\mu }\in {\hat {x}}\{x^{0},x^{1},x^{2},\cdots \}\subset Y^{+}\{{\bf {r}}-i{\bf {k}}\}\qquad :x^{0}=-ict}$

where ${\displaystyle \pm i{\bf {k}}=x_{0}=-x^{0}}$. As a consequence, a manifold appears as or is combined into the higher dimensional coordinates, which results in the spacetime manifolds in the four-dimensional spaces. Together, the two world planes ${\displaystyle Y^{\mp }\{{\bf {r}}\pm i{\bf {k}}\}}$ compose the two dimensional dynamics of Boost, an inertial for generators, and Spiral, a rotational contortions for stresses, which function as a reciprocal or conjugate duality transporting and transforming global events among sub-coordinates. Consequently, for any type of the events, the ${\displaystyle Y^{-}Y^{+}}$ manifolds are always connected, coupled, and conjugated between each other, a duality of which defines entanglements as the virtually inseparable and physically reciprocal pairs of all natural functions.

Popular Comments

The many-worlds interpretation is very vague about the ways to determine when splitting happens, and nowadays usually the criterion is that the two branches have decohered.

Objections

However, present day understanding of decoherence does not allow a completely precise, self-contained way to say when the two branches have decohered/"do not interact", and hence many-worlds interpretation remains arbitrary. This objection is saying that it is not clear what is precisely meant by branching, and point to the lack of self-contained criteria specifying branching.

MWI response: the decoherence or "splitting" or "branching" is complete when the measurement is complete. In Dirac notation a measurement is complete when:

${\displaystyle \langle O_{i}|O_{j}\rangle =\delta _{ij}}$^[69]

where ${\displaystyle O_{i}}$ represents the observer having detected the object system in the ith state. Before the measurement has started the observer states are identical; after the measurement is complete the observer states are orthonormal.^[4][7] Thus a measurement defines the branching process: the branching is as well- or ill-defined as the measurement is; the branching is as complete as the measurement is complete – which is to say that the delta function above represents an idealised measurement. Although true "for all practical purposes" in reality the measurement, and hence the branching, is never fully complete, since delta functions are unphysical,^[70]

Since the role of the observer and measurement per se plays no special role in MWI (measurements are handled as all other interactions are) there is no need for a precise definition of what an observer or a measurement is — just as in Newtonian physics no precise definition of either an observer or a measurement was required or expected. In all circumstances the universal wavefunction is still available to give a complete description of reality.

Also, it is a common misconception to think that branches are completely separate. In Everett's formulation, they may in principle quantum interfere (i.e., "merge" instead of "splitting") with each other in the future,^[71] although this requires all "memory" of the earlier branching event to be lost, so no observer ever sees two branches of reality.^[72][73]

MWI states that there is no special role, or need for precise definition of measurement in MWI, yet Everett uses the word "measurement" repeatedly throughout its exposition.

MWI response: "measurements" are treated as a subclass of interactions, which induce subject–object correlations in the combined wavefunction. There is nothing special about measurements (such as the ability to trigger a wave function collapse), that cannot be dealt with by the usual unitary time development process.^[3] This is why there is no precise definition of measurement in Everett's formulation, although some other formulations emphasize that measurements must be effectively irreversible or create classical information.

The splitting of worlds forward in time, but not backwards in time (i.e., merging worlds), is time asymmetric and incompatible with the time symmetric nature of Schrödinger's equation, or CPT invariance in general.^[74]

MWI response: The splitting is time asymmetric; this observed temporal asymmetry is due to the boundary conditions imposed by the Big Bang^[75]

There is circularity in Everett's measurement theory. Under the assumptions made by Everett, there are no 'good observations' as defined by him, and since his analysis of the observational process depends on the latter, it is void of any meaning. The concept of a 'good observation' is the projection postulate in disguise and Everett's analysis simply derives this postulate by having assumed it, without any discussion.^{[76][unreliable source?]}

MWI response: Everett's treatment of observations / measurements covers both idealised good measurements and the more general bad or approximate cases.^[77] Thus it is legitimate to analyse probability in terms of measurement; no circularity is present.

Talk of probability in Everett presumes the existence of a preferred basis to identify measurement outcomes for the probabilities to range over. But the existence of a preferred basis can only be established by the process of decoherence, which is itself probabilistic^[78] or arbitrary.^[79]

MWI response: Everett analysed branching using what we now call the "measurement basis". It is fundamental theorem of quantum theory that nothing measurable or empirical is changed by adopting a different basis. Everett was therefore free to choose whatever basis he liked. The measurement basis was simply the simplest basis in which to analyse the measurement process.^[80][81]

We cannot be sure that the universe is a quantum multiverse until we have a theory of everything and, in particular, a successful theory of quantum gravity.^[31] If the final theory of everything is non-linear with respect to wavefunctions then many-worlds would be invalid.^{[1][4][5][6][7]}

MWI response: All accepted quantum theories of fundamental physics are linear with respect to the wavefunction. While quantum gravity or string theory may be non-linear in this respect there is no evidence to indicate this at the moment.^[17][18]

Conservation of energy is grossly violated if at every instant near-infinite amounts of new matter are generated to create the new universes.

MWI response: There are two responses to this objection. First, the law of conservation of energy says that energy is conserved within each universe. Hence, even if "new matter" were being generated to create new universes, this would not violate conservation of energy. Second, conservation of energy is not violated since the energy of each branch has to be weighted by its probability, according to the standard formula for the conservation of energy in quantum theory. This results in the total energy of the multiverse being conserved.^{[82][unreliable source?]}

Occam's razor rules against a plethora of unobservable universes – Occam would prefer just one universe; i.e., any non-MWI.

MWI response: Occam's razor actually is a constraint on the complexity of physical theory, not on the number of universes. MWI is a simpler theory since it has fewer postulates.^{[60][unreliable source?]} Occams's razor is often cited by MWI adherents as an advantage of MWI.

Unphysical universes: If a state is a superposition of two states ${\displaystyle \Psi _{A}}$ and ${\displaystyle \Psi _{B}}$, i.e., ${\displaystyle \Psi =(a\Psi _{A}+b\Psi _{B})}$, i.e., weighted by coefficients a and b, then if ${\displaystyle b\ll a}$, what principle allows a universe with vanishingly small probability b to be instantiated on an equal footing with the much more probable one with probability a? This seems to throw away the information in the probability amplitudes.

MWI response: The magnitude of the coefficients provides the weighting that makes the branches or universes "unequal", as Everett and others have shown, leading the emergence of the conventional probabilistic rules.^{[1][4][5][6][7][83][unreliable source?]}

Violation of the principle of locality, which contradicts special relativity: MWI splitting is instant and total: this may conflict with relativity, since an alien in the Andromeda galaxy can't know I collapse an electron over here before she collapses hers there: the relativity of simultaneity says we can't say which electron collapsed first – so which one splits off another universe first? This leads to a hopeless muddle with everyone splitting differently. Note: EPR is not a get-out here, as the alien's and my electrons need never have been part of the same quantum, i.e., entangled.

MWI response: the splitting can be regarded as causal, local and relativistic, spreading at, or below, the speed of light (e.g., we are not split by Schrödinger's cat until we look in the box).^{[84][unreliable source?]} For spacelike separated splitting you can't say which occurred first — but this is true of all spacelike separated events, simultaneity is not defined for them. Splitting is no exception; many-worlds is a local theory.^[57]

Reception

There is a wide range of claims that are considered "many-worlds" interpretations. It was often claimed by those who do not believe in MWI^[85] that Everett himself was not entirely clear^[86] as to what he believed; however, MWI adherents (such as DeWitt, Tegmark, Deutsch and others) believe they fully understand Everett's meaning as implying the literal existence of the other worlds. Additionally, recent biographical sources make it clear that Everett believed in the literal reality of the other quantum worlds.^[24] Everett's son reported that Hugh Everett "never wavered in his belief over his many-worlds theory".^[87] Also Everett was reported to believe "his many-worlds theory guaranteed him immortality".^[88]

One of MWI's strongest advocates is David Deutsch.^[89] According to Deutsch, the single photon interference pattern observed in the double slit experiment can be explained by interference of photons in multiple universes. Viewed in this way, the single photon interference experiment is indistinguishable from the multiple photon interference experiment. In a more practical vein, in one of the earliest papers on quantum computing,^[90] he suggested that parallelism that results from the validity of MWI could lead to "a method by which certain probabilistic tasks can be performed faster by a universal quantum computer than by any classical restriction of it". Deutsch has also proposed that when reversible computers become conscious that MWI will be testable (at least against "naive" Copenhagenism) via the reversible observation of spin.^[72]

Asher Peres was an outspoken critic of MWI. For example, a section in his 1993 textbook had the title Everett's interpretation and other bizarre theories. Peres not only questioned whether MWI is really an "interpretation", but rather, if any interpretations of quantum mechanics are needed at all. An interpretation can be regarded as a purely formal transformation, which adds nothing to the rules of the quantum mechanics.^{[citation needed]} Peres seems to suggest^{[according to whom?]} that positing the existence of an infinite number of non-communicating parallel universes is highly suspect per those^[who?] who interpret it as a violation of Occam's razor, i.e., that it does not minimize the number of hypothesized entities. However, it is understood^{[by whom?]} that the number of elementary particles are not a gross violation of Occam's razor, one counts the types, not the tokens. Max Tegmark remarks^[where?] that the alternative to many-worlds is "many words", an allusion to the complexity of von Neumann's collapse postulate. On the other hand, the same derogatory qualification "many words" is often applied to MWI by its critics^[who?] who see it as a word game which obfuscates rather than clarifies by confounding the von Neumann branching of possible worlds with the Schrödinger parallelism of many worlds in superposition.^{[citation needed]}

MWI is considered by some^[who?] to be unfalsifiable and hence unscientific because the multiple parallel universes are non-communicating, in the sense that no information can be passed between them. Others^[72] claim MWI is directly testable. Everett regarded MWI as falsifiable since any test that falsifies conventional quantum theory would also falsify MWI.^[23]

Polls

Advocates of MWI often cite a poll of 72 "leading cosmologists and other quantum field theorists" ^[91] conducted by the American political scientist David Raub in 1995 showing 58% agreement with "Yes, I think MWI is true".^[92]

However, the poll is controversial. For example, Victor J. Stenger remarks that Murray Gell-Mann's published work explicitly rejects the existence of simultaneous parallel universes. Collaborating with James Hartle, Gell-Mann is working toward the development a more "palatable" post-Everett quantum mechanics. Stenger thinks it's fair to say that most physicists dismiss the many-world interpretation as too extreme, while noting it "has merit in finding a place for the observer inside the system being analyzed and doing away with the troublesome notion of wave function collapse".^[93]

Max Tegmark also reports the result of a "highly unscientific" poll taken at a 1997 quantum mechanics workshop.^[94] According to Tegmark, "The many worlds interpretation (MWI) scored second, comfortably ahead of the consistent histories and Bohm interpretations." Such polls have been taken at other conferences, for example, in response to Sean Carroll's observation, "As crazy as it sounds, most working physicists buy into the many-worlds theory" ^[95] Michael Nielsen counters: "at a quantum computing conference at Cambridge in 1998, a many-worlder surveyed the audience of approximately 200 people... Many-worlds did just fine, garnering support on a level comparable to, but somewhat below, Copenhagen and decoherence." However, Nielsen notes that it seemed most attendees found it to be a waste of time: Asher Peres "got a huge and sustained round of applause… when he got up at the end of the polling and asked 'And who here believes the laws of physics are decided by a democratic vote?'" ^[96]

A 2005 poll of fewer than 40 students and researchers taken after a course on the Interpretation of Quantum Mechanics at the Institute for Quantum Computing University of Waterloo found "Many Worlds (and decoherence)" to be the least favored.^[97]

A 2011 poll of 33 participants at an Austrian conference found 6 endorsed MWI, 8 "Information-based/information-theoretical", and 14 Copenhagen;^[98] the authors remark that the results are similar to the previous Tegmark's 1998 poll.

Speculative implications

Speculative physics deals with questions which are also discussed in science fiction.

Quantum suicide thought experiment

Quantum suicide, as a thought experiment, was published independently by Hans Moravec in 1987^[99][100] and Bruno Marchal in 1988^[101][102] and was independently developed further by Max Tegmark in 1998.^[103] It attempts to distinguish between the Copenhagen interpretation of quantum mechanics and the Everett many-worlds interpretation by means of a variation of the Schrödinger's cat thought experiment, from the cat's point of view. Quantum immortality refers to the subjective experience of surviving quantum suicide regardless of the odds.^[104]

Weak coupling

Another speculation is that the separate worlds remain weakly coupled (e.g., by gravity) permitting "communication between parallel universes". A possible test of this using quantum-optical equipment is described in a 1997 Foundations of Physics article by Rainer Plaga.^[64] It involves an isolated ion in an ion trap, a quantum measurement that would yield two parallel worlds (their difference just being in the detection of a single photon), and the excitation of the ion from only one of these worlds. If the excited ion can be detected from the other parallel universe, then this would constitute direct evidence in support of the many-worlds interpretation and would automatically exclude the orthodox, "logical", and "many-histories" interpretations. The reason the ion is isolated is to make it not participate immediately in the decoherence which insulates the parallel world branches, therefore allowing it to act as a gateway between the two worlds, and if the measure apparatus could perform the measurements quickly enough before the gateway ion is decoupled then the test would succeed (with electronic computers the necessary time window between the two worlds would be in a time scale of milliseconds or nanoseconds, and if the measurements are taken by humans then a few seconds would still be enough). R. Plaga shows that macroscopic decoherence timescales are a possibility. The proposed test is based on technical equipment described in a 1993 Physical Review article by Itano et al.^[105] and R. Plaga says that this level of technology is enough to realize the proposed inter-world communication experiment. The necessary technology for precision measurements of single ions already exists since the 1970s, and the ion recommended for excitation is ¹⁹⁹Hg⁺. The excitation methodology is described by Itano et al. and the time needed for it is given by the Rabi flopping formula.^[106]

Such a test as described by R. Plaga would mean that energy transfer is possible between parallel worlds. This does not violate the fundamental principles of physics because these require energy conservation only for the whole universe and not for the single parallel branches.^[64] Neither the excitation of the single ion (which is a degree of freedom of the proposed system) leads to decoherence, something which is proven by Welcher Weg detectors which can excite atoms without momentum transfer (which causes the loss of coherence).^[107]

The proposed test would allow for low-bandwidth inter-world communication, the limiting factors of bandwidth and time being dependent on the technology of the equipment. Because of the time needed to determine the state of the partially decohered isolated excited ion based on Itano et al.'s methodology, the ion would decohere by the time its state is determined during the experiment, so Plaga's proposal would pass just enough information between the two worlds to confirm their parallel existence and nothing more. The author contemplates that with increased bandwidth, one could even transfer television imagery across the parallel worlds.^[64] For example, Itano et al.'s methodology could be improved (by lowering the time needed for state determination of the excited ion) if a more efficient process were found for the detection of fluorescence radiation using 194 nm photons.^[64]

A 1991 article by J. Polchinski also supports the view that inter-world communication is a theoretical possibility.^[108] Other authors in a 1994 preprint article also contemplated similar ideas.^[109]

The reason inter-world communication seems like a possibility is because decoherence which separates the parallel worlds is never fully complete,^[110][111] therefore weak influences from one parallel world to another can still pass between them,^[110][112] and these should be measurable with advanced technology. Deutsch proposed such an experiment in a 1985 International Journal of Theoretical Physics article,^[113] but the technology it requires involves human-level artificial intelligence.^[64]

Absurd/ highly improbable timelines

Many MWI proponents assert that every physically possible event has to be represented in the multiversal stack, and by definition this would include highly unlikely scenarios and timelines. Bryce Seligman DeWitt has stated that "Everett/ Wheeler/ Graham do not in the end exclude any element of the superposition. All the worlds are there, even those in which everything goes wrong and all the statistical laws break down." ^[114] Murray Gell-Man has stated that "Everything not forbidden is compulsory." (a quote reappropriated from T.H. White to describe the implications of the Totalitarian principle) ^[115] Max Tegmark has affirmed in numerous statements that absurd/ highly unlikely events are inevitable under the MWI interpretation. To quote Tegmark, "Things inconsistent with the laws of physics will never happen - everything else will... it's important to keep track of the statistics, since even if everything conceivable happens somewhere, really freak events happen only exponentially rarely".^[116] Frank J. Tipler, although a strong advocate for the many-worlds interpretation, has expressed some skepticism regarding this aspect of the theory. In a 2015 interview he stated "We simply don't know...it might be that the modulus over the wavefunction of that possibility [i.e. an extremely absurd yet physically possible event] is zero in which case there is no such world...There are universes out there, which you could imagine which...would not be actualized." ^[117]

Similarity to modal realism

The many-worlds interpretation has some similarity to modal realism in philosophy, which is the view that the possible worlds used to interpret modal claims exist and are of a kind with the actual world. Unlike the possible worlds of philosophy, however, in quantum mechanics counterfactual alternatives can influence the results of experiments, as in the Elitzur–Vaidman bomb-testing problem or the Quantum Zeno effect. Also, while the worlds of the many-worlds interpretation all share the same physical laws, modal realism postulates a world for every way things could conceivably have been.

Time travel

The many-worlds interpretation could be one possible way to resolve the paradoxes^[89] that one would expect to arise if time travel turns out to be permitted by physics (permitting closed timelike curves and thus violating causality). Entering the past would itself be a quantum event causing branching, and therefore the timeline accessed by the time traveller simply would be another timeline of many. In that sense, it would make the Novikov self-consistency principle unnecessary.

Many-worlds in literature and science fiction

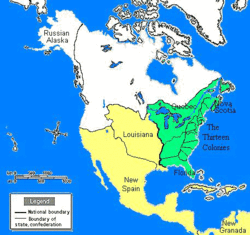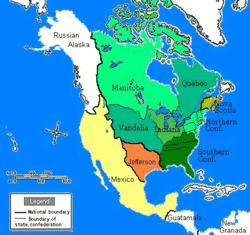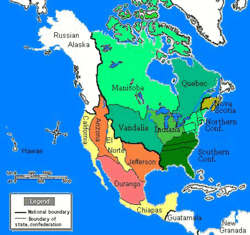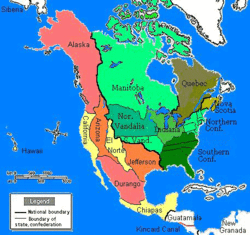
A map from Robert Sobel's novel For Want of a Nail, an artistic illustration of how small events – in this example the branching or point of divergence from our timeline's history is in October 1777 – can profoundly alter the course of history. According to the many-worlds interpretation every event, even microscopic, is a branch point; all possible alternative histories actually exist.^[1]

The many-worlds interpretation (and the somewhat related concept of possible worlds) has been associated to numerous themes in literature, art and science fiction.

Some of these stories or films violate fundamental principles of causality and relativity, since the information-theoretic structure of the path space of multiple universes (that is, information flow between different paths) is very likely complex.

Another kind of popular illustration of many-worlds splittings, which does not involve information flow between paths, or information flow backwards in time considers alternate outcomes of historical events. According to the many-worlds interpretation, all of the historical speculations entertained within the alternate history genre are realized in parallel universes.^[1]

The many-worlds interpretation of reality was anticipated with remarkable fidelity in Olaf Stapledon's 1937 science fiction novel Star Maker, in a paragraph describing one of the many universes created by the Star Maker god of the title. "In one inconceivably complex cosmos, whenever a creature was faced with several possible courses of action, it took them all, thereby creating many distinct temporal dimensions and distinct histories of the cosmos. Since in every evolutionary sequence of the cosmos there were very many creatures, and each was constantly faced with many possible courses, and the combinations of all their courses were innumerable, an infinity of distinct universes exfoliated from every moment of every temporal sequence in this cosmos."

Star Trek uses many-worlds in many stories. In the Original Series, Spock and Kirk make a crossover into a mirror universe and encounter versions of themselves from the other universe. In an episode of Star Trek: The Next Generation, Worf crosses over into a parallel universe while piloting a shuttlecraft and manages to encounter several other universes. The TNG finale "All Good Things" uses the concept heavily as Picard jumps between times. This is continued in Star Trek: Deep Space 9 with the episodes arching between the Terran empire and the Alliance, where Sisko and Kira also find mirror versions of themselves and other characters who are currently dead in the central universe, or dead in the parallel universe.

The author Neal Stephenson drew on the many-worlds theory for some aspects of his 2008 novel Anathem.

A more recent iteration, Rick and Morty on the channel Adult Swim, uses the many-worlds interpretation as a basis for the occurrences in the show. The cartoon also makes an allusion to Schrödinger's Cat in an episode in which they split their existence into two hypothetical, equally possible existences.

In episode 5 of the Netflix series, Stranger Things, the protagonists' middle school teacher Scott Clarke specifically mentions the many-worlds theory when asked about the possibility of "theoretical" alternate dimensions.

Many worlds interpretation was also used in The time Ships by Stephen Baxter.^{[citation needed]}

Many-minds interpretation (of Quantum Mechanics)

From Wikipedia, the free encyclopedia

The many-minds interpretation of quantum mechanics extends the many-worlds interpretation by proposing that the distinction between worlds should be made at the level of the mind of an individual observer. The concept was first introduced in 1970 by H. Dieter Zeh as a variant of the Hugh Everett interpretation in connection with quantum decoherence,^[1] and later (in 1981) explicitly called a many or multi-consciousness interpretation. The name many-minds interpretation was first used by David Albert and Barry Loewer in 1988.^[2]

History

Interpretations of quantum mechanics

The various interpretations of quantum mechanics typically involve explaining the mathematical formalism of quantum mechanics, or to create a physical picture of the theory. While the mathematical structure has a strong foundation, there is still much debate about the physical and philosophical interpretation of the theory. These interpretations aim to tackle various concepts such as:

1. Evolution of the state of a quantum system (given by the wavefunction), typically through the use of the Schrödinger equation. This concept is almost universally accepted, and is rarely put up to debate.
2. The measurement problem, which relates to what we call wavefunction collapse – the collapse of a quantum state into a definite measurement (i.e. a specific eigenstate of the wavefunction). The debate on whether this collapse actually occurs is a central problem in interpreting quantum mechanics.

The standard solution to the measurement problem is the "Orthodox" or "Cophenhagen" interpretation, which claims that the wave function collapses as the result of a measurement by an observer or apparatus external to the quantum system. An alternative interpretation, the Many-worlds Interpretation, was first described by Hugh Everett in 1957^[3][4] (where it was called the relative state interpretation, the name Many-worlds was coined by Bryce Seligman DeWitt starting in the 1960s and finalized in the 70s^[5]). His formalism of quantum mechanics denied that a measurement requires a wave collapse, instead suggesting that all that is truly necessary of a measurement is that a quantum connection is formed between the particle, the measuring device, and the observer.^[4]

The many-worlds interpretation

In the original relative state formulation, Everett proposed that there is one universal wavefunction that describes the objective reality of the whole universe. He stated that when subsystems interact, the total system becomes a superposition of these subsystems. This includes observers and measurement systems, which become part of one universal state (the wavefunction) that is always described via the Schrödinger Equation (or its relativistic alternative). That is, the states of the subsystems that interacted become "entangled" in such a way that any definition of one must necessarily involve the other. Thus, each subsystem's state can only be described relative to each subsystem with which it interacts (hence the name relative state).
This has some interesting implications. For starters, Everett suggested that the universe is actually indeterminate as a whole. To see this, consider an observer measuring some particle that starts in an undetermined state, as both spin-up and spin-down, for example - a superposition of both possibilites. When an observer measures that particle's spin, however, it always registers as either up or down. The problem of how to understand this sudden shift from "both up and down" to "either up or down" is called the Measurement problem. According to the many-worlds interpretation, the act of measurement forced a “splitting” of the universe into two states, one spin-up and the other spin-down, and the two branches that extend from those two subsequently independent states. One branch measures up. The other measures down. Looking at the instrument informs the observer which branch she's on, but the system itself is indeterminate at this and, by logical extension, presumably any higher level.

The “worlds” in the many worlds theory is then just the complete measurement history up until and during the measurement in question, where splitting happens. These “worlds” each describe a different state of the universal wave function and cannot communicate. There is no collapse of the wavefunction into one state or another, but rather you just find yourself in the world leading up to what measurement you have made and are unaware of the other possibilities that are equally real.

The many-minds interpretation

The many-minds interpretation of quantum theory is many-worlds with the distinction between worlds constructed at the level of the individual observer. Rather than the worlds that branch, it is the observer’s mind.^[6]

The purpose of this interpretation is to overcome the fundamentally strange concept of observers being in a superposition with themselves. In their 1988 paper, Albert and Loewer argue that it simply makes no sense for one to think of the mind of an observer to be in an indefinite state. Rather, when someone answers the question about which state of a system they have observed, they must answer with complete certainty. If they are in a superposition of states, then this certainty is not possible and we arrive at a contradiction.^[2] To overcome this, they then suggest that it is merely the “bodies” of the minds that are in a superposition, and that the minds must have definite states that are never in superposition^[2]

When an observer measures a quantum system and becomes entangled with it, it now constitutes a larger quantum system. In regards to each possibility within the wave function, a mental state of the brain corresponds. And ultimately, only one mind is experienced, leading the others to branch off and become inaccessible, albeit real.^[7] In this way, every sentient being is attributed with an infinity of minds, whose prevalence correspond to the amplitude of the wavefunction. As an observer checks a measurement, the probability of realizing a specific measurement directly correlates to the number of minds they have where they see that measurement. It is in this way that the probabilistic nature of quantum measurements are obtained by the Many-minds Interpretation.

Quantum non-locality in the many-minds interpretation

The body remains in an indeterminate state while the minds picks a stochastic result.

Now, consider an experiment where we are measuring the polarization of two photons. When the photon is created it has an indeterminate polarization. If a stream of these photons is passed through a polarization filter, 50% of the light is passed through. This corresponds to each photon having a 50% chance of aligning perfectly with the filter and thus passing, or being misaligned (by 90 degrees relative to the polarization filter) and being absorbed. Quantum mechanically, this means the photon is in a superposition of states where it is either passed or observed. Now, consider the inclusion of another photon and polarization detector. Now, the photons are created in such a way that they are entangled. That is, when one photon takes on a polarization state, the other photon will always behave if it has the same polarization. For simplicity, take the second filter to either be perfectly aligned with the first, or to be perfectly misaligned ( 90 degree difference in angle, such that it is absorbed). If the detectors are aligned, both photons are passed (i.e. we say they agree). If they are misaligned, only the first passes and the second is absorbed (now they disagree). Thus, the entanglement causes perfect correlations between the two measurements - regardless of separation distance, making the interaction non-local. This sort of experiment is further explained in Tim Maudlin's Quantum Non-Locality and Relativity,^[8] and can be related to Bell test experiments. Now, consider the analysis of this experiment from the many minds point of view:

No sentient observer

Consider the case where there is no sentient observer, i.e. no mind around to observe the experiment. In this case, the detector will be in an indefinite state. The photon is both passed and absorbed, and will remain in this state. The correlations are withheld in that none of the possible "minds", or wave function states, correspond to non correlated results.^[8]

One sentient observer

Now expand the situation to have one sentient being observing the device. Now, he too enters the indefinite state. His eyes, body, and brain are seeing both spins at the same time. The mind however, stochastically chooses one of the directions, and that is what the mind sees. When this observer goes over to the second detector, his body will see both results. His mind will choose the result that agrees with the first detector, and the observer will see the expected results. However, the observer's mind seeing one result does not directly affect the distant state - there is just no wave function in which the expected correlations do not exist. The true correlation only happens when he actually goes over to the second detector.^[8]

Two sentient observers

When two people look at two different detectors that scan entangled particles, both observers will enter an indefinite state, as with one observer. These results need not agree – the second observer's mind does not have to have results that correlate with the first's. When one observer tells the results to the second observer, their two minds cannot communicate and thus will only interact with the other's body, which is still indefinite. When the second observer responds, his body will respond with whatever result agrees with the first observer's mind. This means that both observer's minds will be in a state of the wavefunction that always get the expected results, but individually their results could be different.^[8]

Locality of the many-minds interpretation

As we have thus seen, any correlations seen in the wavefunction of each observer's minds are only concrete after interaction between the different polarizers. Even though the correlations on the level of individual minds correspond to the appearance of non-locality (or equivalently, violation of Bell's inequality). However, since the interactions only take place in individual minds they are local, since there is no real interaction between space-like separated events that could influence the minds of observers at two distant points. This, like the many worlds theory, makes the many-minds theory completely local.^[8]

Support

There is currently no empirical evidence for the many-minds interpretation. However, there are theories that do not discredit the many-minds interpretation. In light of Bell’s analysis of the consequences of quantum non-locality, empirical evidence is needed to avoid inventing novel fundamental concepts (hidden variables).^[9] Two different solutions of the measurement problem then appear conceivable: von Neumann’s collapse or Everett’s relative state interpretation.^[10] In both cases a (suitably modified) psycho-physical parallelism can be re-established.

Since conscious awareness has to be coupled with local physical systems, the observer’s physical environment has to interact and can influence the brain. The brain itself must have some physico-chemical processes that affect the states of awareness. If these neural processes can be described and analyzed then some experiments could potentially be created to test whether affecting neural processes can have an effect on a quantum system. Speculation about the details of this awareness-local physical system coupling on a purely theoretical basis could occur, however experimentally searching for them through neurological and psychological studies would be ideal.^[11]

When considering psycho-physical parallelism, superpositions appear rich enough to represent primitive conscious awareness. It seems that quantum superpositions have never been considered, for example, in neuronal models, since only classical states of definite neuronal excitation are usually taken into account. These quasi-classical states are also measured by external neurobiologists. Quantum theory would admit their superpositions, too, thus giving rise to a far greater variety of physical states which may be experienced by the subjective observer. When used for information processing, such superpositions would now be called “quantumbits” or qubits. As demonstrated by M. Tegmark, they can not be relevant for neuronal and similar processes in the brain.^[12]

Objections

Objections that apply to the Many-worlds Interpretation also apply to the Many-minds Interpretation. On the surface both of these theories arguably violate Occam's Razor; proponents counter that in fact these solutions minimize entities by simplifying the rules that would be required to describe the universe.

Nothing within quantum theory itself requires each possibility within a wave function to complement a mental state. As all physical states (i.e. brain states) are quantum states, their associated mental states should be also. Nonetheless, it is not what we experience within physical reality. Albert and Loewer argue that the mind must be intrinsically different than the physical reality as described by quantum theory.^[6] Thereby, they reject type-identity physicalism in favour of a non-reductive stance. However, Lockwood saves materialism through the notion of supervenience of the mental on the physical.^[7]

Nonetheless, the Many-minds Interpretation does not solve the mindless hulks problem as a problem of supervenience. Mental states do not supervene on brain states as a given brain state is compatible with different configurations of mental states.^[13]

Another serious objection is that workers in No Collapse interpretations have produced no more than elementary models based on the definite existence of specific measuring devices. They have assumed, for example, that the Hilbert space of the universe splits naturally into a tensor product structure compatible with the measurement under consideration. They have also assumed, even when describing the behaviour of macroscopic objects, that it is appropriate to employ models in which only a few dimensions of Hilbert space are used to describe all the relevant behaviour.

Furthermore, as the Many-minds Interpretation is corroborated by our experience of physical reality, a notion of many unseen worlds and its compatibility with other physical theories (i.e. the principle of the conservation of mass) is difficult to reconcile.^[6] According to Schrödinger's equation, the mass-energy of the combined observed system and measurement apparatus is the same before and after. However, with every measurement process (i.e. splitting), the total mass-energy would seemingly increase^[14]

Peter J. Lewis argues that the Many-minds Interpretation of quantum mechanics has absurd implications for agents facing life-or-death decisions.^[15]

In general, the Many-minds theory holds that a conscious being who observes the outcome of a random zero-sum experiment will evolve into two successors in different observer states, each of whom observes one of the possible outcomes. Moreover, the theory advises you to favour choices in such situations in proportion to the probability that they will bring good results to your various successors. But in a life-or-death case like getting into the box with Schrödinger's cat, you will only have one successor, since one of the outcomes will ensure your death. So it seems that the Many-minds Interpretation advises you to get in the box with the cat, since it is certain that your only successor will emerge unharmed. See also quantum suicide and immortality.

Finally, it supposes that there is some physical distinction between a conscious observer and a non-conscious measuring device, so it seems to require eliminating the strong Church–Turing hypothesis or postulating a physical model for consciousness.