Mercury in enhanced color, imaged by MESSENGER (2008)
|
|||||||||||||
| Designations | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pronunciation | /ˈmɜːrkjəri/ ( |
||||||||||||
| Adjectives | Mercurian,[1] mercurial[2] | ||||||||||||
| Orbital characteristics[5] | |||||||||||||
| Epoch J2000 | |||||||||||||
| Aphelion |
|
||||||||||||
| Perihelion |
|
||||||||||||
|
|||||||||||||
| Eccentricity | 0.205 630[3] | ||||||||||||
| 115.88 d[3] | |||||||||||||
|
Average orbital speed
|
47.362 km/s[3] | ||||||||||||
| 174.796° | |||||||||||||
| Inclination |
|
||||||||||||
| 48.331° | |||||||||||||
| 29.124° | |||||||||||||
| Satellites | None | ||||||||||||
| Physical characteristics | |||||||||||||
|
Mean radius
|
|||||||||||||
| Flattening | 0[7] | ||||||||||||
|
|||||||||||||
| Volume |
|
||||||||||||
| Mass |
|
||||||||||||
|
Mean density
|
5.427 g/cm3[6] | ||||||||||||
| 0.346±0.014[9] | |||||||||||||
| 4.25 km/s[6] | |||||||||||||
|
Sidereal rotation period
|
|
||||||||||||
|
Equatorial rotation velocity
|
10.892 km/h (3.026 m/s) | ||||||||||||
| 2.04′ ± 0.08′ (to orbit)[9] (0.034°)[3] |
|||||||||||||
|
North pole right ascension
|
|
||||||||||||
|
North pole declination
|
61.45°[3] | ||||||||||||
| Albedo | |||||||||||||
|
|||||||||||||
| −2.6[12] to 5.7[3][13] | |||||||||||||
| 4.5–13″[3] | |||||||||||||
| Atmosphere[14] | |||||||||||||
|
Surface pressure
|
trace (≲ 0.5 nPa) | ||||||||||||
| Composition by volume | |||||||||||||
Like Venus, Mercury orbits the Sun within Earth's orbit as an inferior planet, and never exceeds 28° away from the Sun. When viewed from Earth, this proximity to the Sun means the planet can only be seen near the western or eastern horizon during the early evening or early morning. At this time it may appear as a bright star-like object, but is often far more difficult to observe than Venus. The planet telescopically displays the complete range of phases, similar to Venus and the Moon, as it moves in its inner orbit relative to Earth, which reoccurs over the so-called synodic period approximately every 116 days.
Mercury is gravitationally locked with the Sun in a 3:2 spin-orbit resonance,[15] and rotates in a way that is unique in the Solar System. As seen relative to the fixed stars, it rotates on its axis exactly three times for every two revolutions it makes around the Sun.[a][16] As seen from the Sun, in a frame of reference that rotates with the orbital motion, it appears to rotate only once every two Mercurian years. An observer on Mercury would therefore see only one day every two years.
Mercury's axis has the smallest tilt of any of the Solar System's planets (about 1⁄30 degree). Its orbital eccentricity is the largest of all known planets in the Solar System;[b] at perihelion, Mercury's distance from the Sun is only about two-thirds (or 66%) of its distance at aphelion. Mercury's surface appears heavily cratered and is similar in appearance to the Moon's, indicating that it has been geologically inactive for billions of years. Having almost no atmosphere to retain heat, it has surface temperatures that vary diurnally more than on any other planet in the Solar System, ranging from 100 K (−173 °C; −280 °F) at night to 700 K (427 °C; 800 °F) during the day across the equatorial regions. The polar regions are constantly below 180 K (−93 °C; −136 °F). The planet has no known natural satellites.
Two spacecraft have visited Mercury: Mariner 10 flew by in 1974 and 1975; and MESSENGER, launched in 2004, orbited Mercury over 4,000 times in four years before exhausting its fuel and crashing into the planet's surface on April 30, 2015.[17][18][19]
Physical characteristics
Internal structure
Internal structure of Mercury:
- Crust: 100–300 km thick
- Mantle: 600 km thick
- Core: 1,800 km radius
Gravity anomalies on Mercury—mass concentrations (red) suggest subsurface structure and evolution
Mercury appears to have a solid silicate crust and mantle overlying a solid, iron sulfide outer core layer, a deeper liquid core layer, and possibly a solid inner core.[20]
Mercury is one of four terrestrial planets in the Solar System, and is a rocky body like Earth. It is the smallest planet in the Solar System, with an equatorial radius of 2,439.7 kilometres (1,516.0 mi).[3] Mercury is also smaller—albeit more massive—than the largest natural satellites in the Solar System, Ganymede and Titan. Mercury consists of approximately 70% metallic and 30% silicate material.[21] Mercury's density is the second highest in the Solar System at 5.427 g/cm3, only slightly less than Earth's density of 5.515 g/cm3.[3] If the effect of gravitational compression were to be factored out from both planets, the materials of which Mercury is made would be denser than those of Earth, with an uncompressed density of 5.3 g/cm3 versus Earth's 4.4 g/cm3.[22]
Mercury's density can be used to infer details of its inner structure. Although Earth's high density results appreciably from gravitational compression, particularly at the core, Mercury is much smaller and its inner regions are not as compressed. Therefore, for it to have such a high density, its core must be large and rich in iron.[23]
Geologists estimate that Mercury's core occupies about 55% of its volume; for Earth this proportion is 17%. Research published in 2007 suggests that Mercury has a molten core.[24][25] Surrounding the core is a 500–700 km mantle consisting of silicates.[26][27] Based on data from the Mariner 10 mission and Earth-based observation, Mercury's crust is estimated to be 35 km thick.[28] One distinctive feature of Mercury's surface is the presence of numerous narrow ridges, extending up to several hundred kilometers in length. It is thought that these were formed as Mercury's core and mantle cooled and contracted at a time when the crust had already solidified.[29]
Mercury's core has a higher iron content than that of any other major planet in the Solar System, and several theories have been proposed to explain this. The most widely accepted theory is that Mercury originally had a metal–silicate ratio similar to common chondrite meteorites, thought to be typical of the Solar System's rocky matter, and a mass approximately 2.25 times its current mass.[30] Early in the Solar System's history, Mercury may have been struck by a planetesimal of approximately 1/6 that mass and several thousand kilometers across.[30] The impact would have stripped away much of the original crust and mantle, leaving the core behind as a relatively major component.[30] A similar process, known as the giant impact hypothesis, has been proposed to explain the formation of the Moon.[30]
Alternatively, Mercury may have formed from the solar nebula before the Sun's energy output had stabilized. It would initially have had twice its present mass, but as the protosun contracted, temperatures near Mercury could have been between 2,500 and 3,500 K and possibly even as high as 10,000 K.[31] Much of Mercury's surface rock could have been vaporized at such temperatures, forming an atmosphere of "rock vapor" that could have been carried away by the solar wind.[31]
A third hypothesis proposes that the solar nebula caused drag on the particles from which Mercury was accreting, which meant that lighter particles were lost from the accreting material and not gathered by Mercury.[32] Each hypothesis predicts a different surface composition, and there are two space missions set to make observations. MESSENGER, which ended in 2015, found higher-than-expected potassium and sulfur levels on the surface, suggesting that the giant impact hypothesis and vaporization of the crust and mantle did not occur because potassium and sulfur would have been driven off by the extreme heat of these events.[33] BepiColombo, which will arrive at Mercury in 2025, will make observations to test these hypotheses.[34] The findings so far would seem to favor the third hypothesis; however, further analysis of the data is needed.[35]
Surface geology

|
Mercury's surface
Albedo features are areas of markedly different reflectivity, as seen by telescopic observation. Mercury has dorsa (also called "wrinkle-ridges"), Moon-like highlands, montes (mountains), planitiae (plains), rupes (escarpments), and valles (valleys).[38][39]
Names for features on Mercury come from a variety of sources. Names coming from people are limited to the deceased. Craters are named for artists, musicians, painters, and authors who have made outstanding or fundamental contributions to their field. Ridges, or dorsa, are named for scientists who have contributed to the study of Mercury. Depressions or fossae are named for works of architecture. Montes are named for the word "hot" in a variety of languages. Plains or planitiae are named for Mercury in various languages. Escarpments or rupēs are named for ships of scientific expeditions. Valleys or valles are named for radio telescope facilities.[40]
Mercury was heavily bombarded by comets and asteroids during and shortly following its formation 4.6 billion years ago, as well as during a possibly separate subsequent episode called the Late Heavy Bombardment that ended 3.8 billion years ago.[41] During this period of intense crater formation, Mercury received impacts over its entire surface,[39] facilitated by the lack of any atmosphere to slow impactors down.[42] During this time Mercury was volcanically active; basins such as the Caloris Basin were filled by magma, producing smooth plains similar to the maria found on the Moon.[43][44]
Data from the October 2008 flyby of MESSENGER gave researchers a greater appreciation for the jumbled nature of Mercury's surface. Mercury's surface is more heterogeneous than either Mars's or the Moon's, both of which contain significant stretches of similar geology, such as maria and plateaus.[45]
Impact basins and craters
Perspective view of Caloris Basin – high (red); low (blue).
Craters on Mercury range in diameter from small bowl-shaped cavities to multi-ringed impact basins hundreds of kilometers across. They appear in all states of degradation, from relatively fresh rayed craters to highly degraded crater remnants. Mercurian craters differ subtly from lunar craters in that the area blanketed by their ejecta is much smaller, a consequence of Mercury's stronger surface gravity.[46] According to IAU rules, each new crater must be named after an artist that was famous for more than fifty years, and dead for more than three years, before the date the crater is named.[47]
Enhanced-color image of Munch, Sander and Poe craters amid volcanic plains (orange) near Caloris Basin
The largest known crater is Caloris Basin, with a diameter of 1,550 km.[48] The impact that created the Caloris Basin was so powerful that it caused lava eruptions and left a concentric ring over 2 km tall surrounding the impact crater. At the antipode of the Caloris Basin is a large region of unusual, hilly terrain known as the "Weird Terrain". One hypothesis for its origin is that shock waves generated during the Caloris impact traveled around Mercury, converging at the basin's antipode (180 degrees away). The resulting high stresses fractured the surface.[49] Alternatively, it has been suggested that this terrain formed as a result of the convergence of ejecta at this basin's antipode.[50]
Overall, about 15 impact basins have been identified on the imaged part of Mercury. A notable basin is the 400 km wide, multi-ring Tolstoj Basin that has an ejecta blanket extending up to 500 km from its rim and a floor that has been filled by smooth plains materials. Beethoven Basin has a similar-sized ejecta blanket and a 625 km diameter rim.[46] Like the Moon, the surface of Mercury has likely incurred the effects of space weathering processes, including Solar wind and micrometeorite impacts.[51]
Interior of Abedin crater
Plains
Degas crater
There are two geologically distinct plains regions on Mercury.[46][52] Gently rolling, hilly plains in the regions between craters are Mercury's oldest visible surfaces,[46] predating the heavily cratered terrain. These inter-crater plains appear to have obliterated many earlier craters, and show a general paucity of smaller craters below about 30 km in diameter.[52]
The so-called "Weird Terrain" formed at the point antipodal to the Caloris Basin impact
Smooth plains are widespread flat areas that fill depressions of various sizes and bear a strong resemblance to the lunar maria. Notably, they fill a wide ring surrounding the Caloris Basin. Unlike lunar maria, the smooth plains of Mercury have the same albedo as the older inter-crater plains. Despite a lack of unequivocally volcanic characteristics, the localisation and rounded, lobate shape of these plains strongly support volcanic origins.[46] All the smooth plains of Mercury formed significantly later than the Caloris basin, as evidenced by appreciably smaller crater densities than on the Caloris ejecta blanket.[46] The floor of the Caloris Basin is filled by a geologically distinct flat plain, broken up by ridges and fractures in a roughly polygonal pattern. It is not clear whether they are volcanic lavas induced by the impact, or a large sheet of impact melt.[46]
Compressional features
One unusual feature of Mercury's surface is the numerous compression folds, or rupes, that crisscross the plains. As Mercury's interior cooled, it contracted and its surface began to deform, creating wrinkle ridges and lobate scarps associated with thrust faults. The scarps can reach lengths of 1000 km and heights of 3 km.[53] These compressional features can be seen on top of other features, such as craters and smooth plains, indicating they are more recent.[54] Mapping of the features has suggested a total shrinkage of Mercury's radius in the range of ~1 to 7 km.[55] Small-scale thrust fault scarps have been found, tens of meters in height and with lengths in the range of a few km, that appear to be less than 50 million years old, indicating that compression of the interior and consequent surface geological activity continue to the present.[53][55]The Lunar Reconnaissance Orbiter discovered that similar small thrust faults exist on the Moon.
Volcanology
Picasso crater
— the large arc-shaped pit located on the eastern side of its floor are
postulated to have formed when subsurface magma subsided or drained,
causing the surface to collapse into the resulting void.
Images obtained by MESSENGER have revealed evidence for pyroclastic flows on Mercury from low-profile shield volcanoes.[56][57][58] MESSENGER data has helped identify 51 pyroclastic deposits on the surface,[59] where 90% of them are found within impact craters.[59] A study of the degradation state of the impact craters that host pyroclastic deposits suggests that pyroclastic activity occurred on Mercury over a prolonged interval.[59]
A "rimless depression" inside the southwest rim of the Caloris Basin consists of at least nine overlapping volcanic vents, each individually up to 8 km in diameter. It is thus a "compound volcano".[60] The vent floors are at a least 1 km below their brinks and they bear a closer resemblance to volcanic craters sculpted by explosive eruptions or modified by collapse into void spaces created by magma withdrawal back down into a conduit.[60] The scientists could not quantify the age of the volcanic complex system, but reported that it could be of the order of a billion years.[60]
Surface conditions and exosphere

Composite image of Mercury taken by MESSENGER
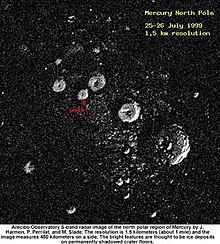
Radar image of Mercury's north pole
Composite of the north pole of Mercury, where NASA confirmed the
discovery of a large volume of water ice, in permanently dark craters
that exist there.[61]
The surface temperature of Mercury ranges from 100 K to 700 K[62] at the most extreme places: 0°N, 0°W, or 180°W. It never rises above 180 K at the poles,[11] due to the absence of an atmosphere and a steep temperature gradient between the equator and the poles. The subsolar point reaches about 700 K during perihelion (0°W or 180°W), but only 550 K at aphelion (90° or 270°W).[63] On the dark side of the planet, temperatures average 110 K.[11][64] The intensity of sunlight on Mercury's surface ranges between 4.59 and 10.61 times the solar constant (1,370 W·m−2).[65]
Although the daylight temperature at the surface of Mercury is generally extremely high, observations strongly suggest that ice (frozen water) exists on Mercury. The floors of deep craters at the poles are never exposed to direct sunlight, and temperatures there remain below 102 K; far lower than the global average.[66] Water ice strongly reflects radar, and observations by the 70-meter Goldstone Solar System Radar and the VLA in the early 1990s revealed that there are patches of high radar reflection near the poles.[67] Although ice was not the only possible cause of these reflective regions, astronomers think it was the most likely.[68]
The icy regions are estimated to contain about 1014–1015 kg of ice,[69] and may be covered by a layer of regolith that inhibits sublimation.[70] By comparison, the Antarctic ice sheet on Earth has a mass of about 4×1018 kg, and Mars's south polar cap contains about 1016 kg of water.[69] The origin of the ice on Mercury is not yet known, but the two most likely sources are from outgassing of water from the planet's interior or deposition by impacts of comets.[69]
Mercury is too small and hot for its gravity to retain any significant atmosphere over long periods of time; it does have a tenuous surface-bounded exosphere[71] containing hydrogen, helium, oxygen, sodium, calcium, potassium and others at a surface pressure of less than approximately 0.5 nPa (0.005 picobars).[14] This exosphere is not stable—atoms are continuously lost and replenished from a variety of sources. Hydrogen atoms and helium atoms probably come from the solar wind, diffusing into Mercury's magnetosphere before later escaping back into space. Radioactive decay of elements within Mercury's crust is another source of helium, as well as sodium and potassium. MESSENGER found high proportions of calcium, helium, hydroxide, magnesium, oxygen, potassium, silicon and sodium. Water vapor is present, released by a combination of processes such as: comets striking its surface, sputtering creating water out of hydrogen from the solar wind and oxygen from rock, and sublimation from reservoirs of water ice in the permanently shadowed polar craters. The detection of high amounts of water-related ions like O+, OH−, and H2O+ was a surprise.[72][73] Because of the quantities of these ions that were detected in Mercury's space environment, scientists surmise that these molecules were blasted from the surface or exosphere by the solar wind.[74][75]
Sodium, potassium and calcium were discovered in the atmosphere during the 1980–1990s, and are thought to result primarily from the vaporization of surface rock struck by micrometeorite impacts[76] including presently from Comet Encke.[77] In 2008, magnesium was discovered by MESSENGER.[78] Studies indicate that, at times, sodium emissions are localized at points that correspond to the planet's magnetic poles. This would indicate an interaction between the magnetosphere and the planet's surface.[79]
On November 29, 2012, NASA confirmed that images from MESSENGER had detected that craters at the north pole contained water ice. MESSENGER's principal investigator Sean Solomon is quoted in The New York Times estimating the volume of the ice to be large enough to "encase Washington, D.C., in a frozen block two and a half miles deep".[61][c]
Magnetic field and magnetosphere

Graph showing relative strength of Mercury's magnetic field
Despite its small size and slow 59-day-long rotation, Mercury has a significant, and apparently global, magnetic field. According to measurements taken by Mariner 10, it is about 1.1% the strength of Earth's. The magnetic-field strength at Mercury's equator is about 300 nT.[80][81] Like that of Earth, Mercury's magnetic field is dipolar.[79] Unlike Earth's, Mercury's poles are nearly aligned with the planet's spin axis.[82] Measurements from both the Mariner 10 and MESSENGER space probes have indicated that the strength and shape of the magnetic field are stable.[82]
It is likely that this magnetic field is generated by a dynamo effect, in a manner similar to the magnetic field of Earth.[83][84] This dynamo effect would result from the circulation of the planet's iron-rich liquid core. Particularly strong tidal effects caused by the planet's high orbital eccentricity would serve to keep the core in the liquid state necessary for this dynamo effect.[85]
Mercury's magnetic field is strong enough to deflect the solar wind around the planet, creating a magnetosphere. The planet's magnetosphere, though small enough to fit within Earth,[79] is strong enough to trap solar wind plasma. This contributes to the space weathering of the planet's surface.[82] Observations taken by the Mariner 10 spacecraft detected this low energy plasma in the magnetosphere of the planet's nightside. Bursts of energetic particles in the planet's magnetotail indicate a dynamic quality to the planet's magnetosphere.[79]
During its second flyby of the planet on October 6, 2008, MESSENGER discovered that Mercury's magnetic field can be extremely "leaky". The spacecraft encountered magnetic "tornadoes" – twisted bundles of magnetic fields connecting the planetary magnetic field to interplanetary space – that were up to 800 km wide or a third of the radius of the planet. These twisted magnetic flux tubes, technically known as flux transfer events, form open windows in the planet's magnetic shield through which the solar wind may enter and directly impact Mercury's surface via magnetic reconnection[86] This also occurs in Earth's magnetic field. The MESSENGER observations showed the reconnection rate is ten times higher at Mercury, but its proximity to the Sun only accounts for about a third of the reconnection rate observed by MESSENGER.[86]
Orbit, rotation, and longitude
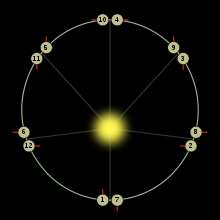
Mercury has the most eccentric orbit of all the planets; its eccentricity is 0.21 with its distance from the Sun ranging from 46,000,000 to 70,000,000 km (29,000,000 to 43,000,000 mi). It takes 87.969 Earth days to complete an orbit. The diagram on the right illustrates the effects of the eccentricity, showing Mercury's orbit overlaid with a circular orbit having the same semi-major axis. Mercury's higher velocity when it is near perihelion is clear from the greater distance it covers in each 5-day interval. In the diagram the varying distance of Mercury to the Sun is represented by the size of the planet, which is inversely proportional to Mercury's distance from the Sun. This varying distance to the Sun leads to Mercury's surface being flexed by tidal bulges raised by the Sun that are about 17 times stronger than the Moon's on Earth.[87] Combined with a 3:2 spin–orbit resonance of the planet's rotation around its axis, it also results in complex variations of the surface temperature.[21] The resonance makes a single solar day on Mercury last exactly two Mercury years, or about 176 Earth days.[88]
Mercury's orbit is inclined by 7 degrees to the plane of Earth's orbit (the ecliptic), as shown in the diagram on the right. As a result, transits of Mercury across the face of the Sun can only occur when the planet is crossing the plane of the ecliptic at the time it lies between Earth and the Sun. This occurs about every seven years on average.[89]
Mercury's axial tilt is almost zero,[90] with the best measured value as low as 0.027 degrees.[91] This is significantly smaller than that of Jupiter, which has the second smallest axial tilt of all planets at 3.1 degrees. This means that to an observer at Mercury's poles, the center of the Sun never rises more than 2.1 arcminutes above the horizon.[91]
At certain points on Mercury's surface, an observer would be able to see the Sun peek up about halfway over the horizon, then reverse and set before rising again, all within the same Mercurian day. This is because approximately four Earth days before perihelion, Mercury's angular orbital velocity equals its angular rotational velocity so that the Sun's apparent motion ceases; closer to perihelion, Mercury's angular orbital velocity then exceeds the angular rotational velocity. Thus, to a hypothetical observer on Mercury, the Sun appears to move in a retrograde direction. Four Earth days after perihelion, the Sun's normal apparent motion resumes.[21] A similar effect would have occurred if Mercury had been in synchronous rotation: the alternating gain and loss of rotation over revolution would have caused a libration of 23.65° in longitude.[92]
For the same reason, there are two points on Mercury's equator, 180 degrees apart in longitude, at either of which, around perihelion in alternate Mercurian years (once a Mercurian day), the Sun passes overhead, then reverses its apparent motion and passes overhead again, then reverses a second time and passes overhead a third time, taking a total of about 16 Earth-days for this entire process. In the other alternate Mercurian years, the same thing happens at the other of these two points. The amplitude of the retrograde motion is small, so the overall effect is that, for two or three weeks, the Sun is almost stationary overhead, and is at its most brilliant because Mercury is at perihelion, its closest to the Sun. This prolonged exposure to the Sun at its brightest makes these two points the hottest places on Mercury. Conversely, there are two other points on the equator, 90 degrees of longitude apart from the first ones, where the Sun passes overhead only when the planet is at aphelion in alternate years, when the apparent motion of the Sun in Mercury's sky is relatively rapid. These points, which are the ones on the equator where the apparent retrograde motion of the Sun happens when it is crossing the horizon as described in the preceding paragraph, receive much less solar heat than the first ones described above.
Mercury attains inferior conjunction (nearest approach to Earth) every 116 Earth days on average,[3] but this interval can range from 105 days to 129 days due to the planet's eccentric orbit. Mercury can come as near as 82.2 gigametres (0.549 astronomical units; 51.1 million miles) to Earth, and that is slowly declining: The next approach to within 82.1 Gm (51.0 million miles) is in 2679, and to within 82.0 Gm (51.0 million miles) in 4487, but it will not be closer to Earth than 80 Gm (50 million miles) until 28,622.[93] Its period of retrograde motion as seen from Earth can vary from 8 to 15 days on either side of inferior conjunction. This large range arises from the planet's high orbital eccentricity.[21]
Longitude convention
The longitude convention for Mercury puts the zero of longitude at one of the two hottest points on the surface, as described above. However, when this area was first visited, by Mariner 10, this zero meridian was in darkness, so it was impossible to select a feature on the surface to define the exact position of the meridian. Therefore, a small crater further west was chosen, called Hun Kal, which provides the exact reference point for measuring longitude. The center of Hun Kal defines the 20° West meridian. A 1970 International Astronomical Union resolution suggests that longitudes be measured positively in the westerly direction on Mercury.[94] The two hottest places on the equator are therefore at longitudes 0°W and 180°W, and the coolest points on the equator are at longitudes 90°W and 270°W. However, the MESSENGER project uses an east-positive convention.[95]Spin–orbit resonance
After one orbit, Mercury has rotated 1.5 times, so after two complete orbits the same hemisphere is again illuminated.
For many years it was thought that Mercury was synchronously tidally locked with the Sun, rotating once for each orbit and always keeping the same face directed towards the Sun, in the same way that the same side of the Moon always faces Earth. Radar observations in 1965 proved that the planet has a 3:2 spin–orbit resonance, rotating three times for every two revolutions around the Sun. The eccentricity of Mercury's orbit makes this resonance stable—at perihelion, when the solar tide is strongest, the Sun is nearly still in Mercury's sky.[96]
The rare 3:2 resonant tidal locking is stabilized by the variance of the tidal force along Mercury's eccentric orbit, acting on a permanent dipole component of Mercury's mass distribution.[97] In a circular orbit there is no such variance, so the only resonance stabilized in such an orbit is at 1:1 (e.g., Earth–Moon), when the tidal force, stretching a body along the "center-body" line, exerts a torque that aligns the body's axis of least inertia (the "longest" axis, and the axis of the aforementioned dipole) to always point at the center. However, with noticeable eccentricity, like that of Mercury's orbit, the tidal force has a maximum at perihelion and thus stabilizes resonances, like 3:2, enforcing that the planet points its axis of least inertia roughly at the Sun when passing through perihelion.[97]
The original reason astronomers thought it was synchronously locked was that, whenever Mercury was best placed for observation, it was always nearly at the same point in its 3:2 resonance, hence showing the same face. This is because, coincidentally, Mercury's rotation period is almost exactly half of its synodic period with respect to Earth. Due to Mercury's 3:2 spin–orbit resonance, a solar day (the length between two meridian transits of the Sun) lasts about 176 Earth days.[21] A sidereal day (the period of rotation) lasts about 58.7 Earth days.[21]
Simulations indicate that the orbital eccentricity of Mercury varies chaotically from nearly zero (circular) to more than 0.45 over millions of years due to perturbations from the other planets.[21][98] This was thought to explain Mercury's 3:2 spin–orbit resonance (rather than the more usual 1:1), because this state is more likely to arise during a period of high eccentricity.[99] However, accurate modeling based on a realistic model of tidal response has demonstrated that Mercury was captured into the 3:2 spin–orbit state at a very early stage of its history, within 20 (more likely, 10) million years after its formation.[100]
Numerical simulations show that a future secular orbital resonant perihelion interaction with Jupiter may cause the eccentricity of Mercury's orbit to increase to the point where there is a 1% chance that the planet may collide with Venus within the next five billion years.[101][102]
Advance of perihelion
In 1859, the French mathematician and astronomer Urbain Le Verrier reported that the slow precession of Mercury's orbit around the Sun could not be completely explained by Newtonian mechanics and perturbations by the known planets. He suggested, among possible explanations, that another planet (or perhaps instead a series of smaller 'corpuscules') might exist in an orbit even closer to the Sun than that of Mercury, to account for this perturbation.[103] (Other explanations considered included a slight oblateness of the Sun.) The success of the search for Neptune based on its perturbations of the orbit of Uranus led astronomers to place faith in this possible explanation, and the hypothetical planet was named Vulcan, but no such planet was ever found.[104]The perihelion precession of Mercury is 5,600 arcseconds (1.5556°) per century relative to Earth, or 574.10±0.65 arcseconds per century[105] relative to the inertial ICRF. Newtonian mechanics, taking into account all the effects from the other planets, predicts a precession of 5,557 arcseconds (1.5436°) per century.[105] In the early 20th century, Albert Einstein's general theory of relativity provided the explanation for the observed precession, by formalizing gravitation as being mediated by the curvature of spacetime. The effect is small: just 42.98 arcseconds per century for Mercury; it therefore requires a little over twelve million orbits for a full excess turn. Similar, but much smaller, effects exist for other Solar System bodies: 8.62 arcseconds per century for Venus, 3.84 for Earth, 1.35 for Mars, and 10.05 for 1566 Icarus.[106][107]
Albert Einstein's formula for the perihelion shift per revolution is
 , where
, where  is the orbital eccentricity,
is the orbital eccentricity,  the semi-major axis, and
the semi-major axis, and  the orbital period. Filling in the values gives a result of 0.1035
arcseconds per revolution or 0.4297 arcseconds per Earth year, i.e.,
42.97 arcseconds per century.
the orbital period. Filling in the values gives a result of 0.1035
arcseconds per revolution or 0.4297 arcseconds per Earth year, i.e.,
42.97 arcseconds per century.Observation
Image mosaic by Mariner 10, 1974
Mercury's apparent magnitude varies between −2.6[12] (brighter than the brightest star Sirius) and about +5.7 (approximating the theoretical limit of naked-eye visibility). The extremes occur when Mercury is close to the Sun in the sky.[12][13] Observation of Mercury is complicated by its proximity to the Sun, as it is lost in the Sun's glare for much of the time. Mercury can be observed for only a brief period during either morning or evening twilight.[108]
Mercury can, like several other planets and the brightest stars, be seen during a total solar eclipse.[109]
Like the Moon and Venus, Mercury exhibits phases as seen from Earth. It is "new" at inferior conjunction and "full" at superior conjunction. The planet is rendered invisible from Earth on both of these occasions because of its being obscured by the Sun,[108] except its new phase during a transit.
Mercury is technically brightest as seen from Earth when it is at a full phase. Although Mercury is farthest from Earth when it is full, the greater illuminated area that is visible and the opposition brightness surge more than compensates for the distance.[12] The opposite is true for Venus, which appears brightest when it is a crescent, because it is much closer to Earth than when gibbous.[12][110]
False-color map showing the maximum temperatures of the north polar region
Nonetheless, the brightest (full phase) appearance of Mercury is an essentially impossible time for practical observation, because of the extreme proximity of the Sun. Mercury is best observed at the first and last quarter, although they are phases of lesser brightness. The first and last quarter phases occur at greatest elongation east and west of the Sun, respectively. At both of these times Mercury's separation from the Sun ranges anywhere from 17.9° at perihelion to 27.8° at aphelion.[111][112] At greatest western elongation, Mercury rises at its earliest before sunrise, and at greatest eastern elongation, it sets at its latest after sunset.[113]
Mercury can be easily seen from the tropics and subtropics more than from higher latitudes. Viewed from low latitudes and at the right times of year, the ecliptic intersects the horizon at a steep angle. Mercury is 10° above the horizon when the planet appears directly above the Sun (i.e. its orbit appears vertical) and is at maximum elongation from the Sun (28°) and also when the Sun is 18° below the horizon, so the sky is just completely dark.[d] This angle is the maximum altitude at which Mercury is visible in a completely dark sky.
False-color image of Carnegie Rupes, a tectonic landform—high terrain (red); low (blue).
At middle latitudes, Mercury is more often and easily visible from the Southern Hemisphere than from the Northern. This is because Mercury's maximum western elongation occurs only during early autumn in the Southern Hemisphere, whereas its greatest eastern elongation happens only during late winter in the Southern Hemisphere.[113] In both of these cases, the angle at which the planet's orbit intersects the horizon is maximized, allowing it to rise several hours before sunrise in the former instance and not set until several hours after sundown in the latter from southern mid-latitudes, such as Argentina and South Africa.[113]
An alternate method for viewing Mercury involves observing the planet during daylight hours when conditions are clear, ideally when it is at its greatest elongation. This allows the planet to be found easily, even when using telescopes with 8 cm (3.1 in) apertures. Care must be taken to ensure the instrument isn't pointed directly towards the Sun because of the risk for eye damage. This method bypasses the limitation of twilight observing when the ecliptic is located at a low elevation (e.g. on autumn evenings).
Ground-based telescope observations of Mercury reveal only an illuminated partial disk with limited detail. The first of two spacecraft to visit the planet was Mariner 10, which mapped about 45% of its surface from 1974 to 1975. The second is the MESSENGER spacecraft, which after three Mercury flybys between 2008 and 2009, attained orbit around Mercury on March 17, 2011,[114] to study and map the rest of the planet.[115]
The Hubble Space Telescope cannot observe Mercury at all, due to safety procedures that prevent its pointing too close to the Sun.[116]
Because the shift of 0.15 revolutions in a year makes up a seven-year cycle (0.15 × 7 ≈ 1.0), in the seventh year Mercury follows almost exactly (earlier by 7 days) the sequence of phenomena it showed seven years before.[111]
Observation history
Ancient astronomers
Mercury, from Liber astronomiae, 1550
The earliest known recorded observations of Mercury are from the Mul.Apin tablets. These observations were most likely made by an Assyrian astronomer around the 14th century BC.[117] The cuneiform name used to designate Mercury on the Mul.Apin tablets is transcribed as Udu.Idim.Gu\u4.Ud ("the jumping planet").[e][118] Babylonian records of Mercury date back to the 1st millennium BC. The Babylonians called the planet Nabu after the messenger to the gods in their mythology.[119]
The ancient Greeks knew the planet as Στίλβων (Stilbon), meaning "the gleaming", Ἑρμάων (Hermaon) and Ἑρμής (Hermes),[120] a planetary name that is retained in modern Greek (Ερμής: Ermis).[121] The Romans named the planet after the swift-footed Roman messenger god, Mercury (Latin Mercurius), which they equated with the Greek Hermes, because it moves across the sky faster than any other planet.[122][123] The astronomical symbol for Mercury is a stylized version of Hermes' caduceus.[124]
The Roman-Egyptian astronomer Ptolemy wrote about the possibility of planetary transits across the face of the Sun in his work Planetary Hypotheses. He suggested that no transits had been observed either because planets such as Mercury were too small to see, or because the transits were too infrequent.[125]
Ibn al-Shatir's model for the appearances of Mercury, showing the multiplication of epicycles using the Tusi couple, thus eliminating the Ptolemaic eccentrics and equant.
In ancient China, Mercury was known as "the Hour Star" (Chen-xing 辰星). It was associated with the direction north and the phase of water in the Five Phases system of metaphysics.[126] Modern Chinese, Korean, Japanese and Vietnamese cultures refer to the planet literally as the "water star" (水星), based on the Five elements.[127][128][129] Hindu mythology used the name Budha for Mercury, and this god was thought to preside over Wednesday.[130] The god Odin (or Woden) of Germanic paganism was associated with the planet Mercury and Wednesday.[131] The Maya may have represented Mercury as an owl (or possibly four owls; two for the morning aspect and two for the evening) that served as a messenger to the underworld.[132]
In medieval Islamic astronomy, the Andalusian astronomer Abū Ishāq Ibrāhīm al-Zarqālī in the 11th century described the deferent of Mercury's geocentric orbit as being oval, like an egg or a pignon, although this insight did not influence his astronomical theory or his astronomical calculations.[133][134] In the 12th century, Ibn Bajjah observed "two planets as black spots on the face of the Sun", which was later suggested as the transit of Mercury and/or Venus by the Maragha astronomer Qotb al-Din Shirazi in the 13th century.[135] (Note that most such medieval reports of transits were later taken as observations of sunspots.[136])
In India, the Kerala school astronomer Nilakantha Somayaji in the 15th century developed a partially heliocentric planetary model in which Mercury orbits the Sun, which in turn orbits Earth, similar to the Tychonic system later proposed by Tycho Brahe in the late 16th century.[137]
Ground-based telescopic research
Transit of Mercury. Mercury is visible as a black dot below and to the left of center. The dark area above the center of the solar disk is a sunspot.
Elongation is the angle between the Sun and the planet, with Earth as the reference point. Mercury appears close to the Sun.
The first telescopic observations of Mercury were made by Galileo in the early 17th century. Although he observed phases when he looked at Venus, his telescope was not powerful enough to see the phases of Mercury. In 1631, Pierre Gassendi made the first telescopic observations of the transit of a planet across the Sun when he saw a transit of Mercury predicted by Johannes Kepler. In 1639, Giovanni Zupi used a telescope to discover that the planet had orbital phases similar to Venus and the Moon. The observation demonstrated conclusively that Mercury orbited around the Sun.[21]
A rare event in astronomy is the passage of one planet in front of another (occultation), as seen from Earth. Mercury and Venus occult each other every few centuries, and the event of May 28, 1737 is the only one historically observed, having been seen by John Bevis at the Royal Greenwich Observatory.[138] The next occultation of Mercury by Venus will be on December 3, 2133.[139]
The difficulties inherent in observing Mercury mean that it has been far less studied than the other planets. In 1800, Johann Schröter made observations of surface features, claiming to have observed 20-kilometre-high (12 mi) mountains. Friedrich Bessel used Schröter's drawings to erroneously estimate the rotation period as 24 hours and an axial tilt of 70°.[140] In the 1880s, Giovanni Schiaparelli mapped the planet more accurately, and suggested that Mercury's rotational period was 88 days, the same as its orbital period due to tidal locking.[141] This phenomenon is known as synchronous rotation. The effort to map the surface of Mercury was continued by Eugenios Antoniadi, who published a book in 1934 that included both maps and his own observations.[79] Many of the planet's surface features, particularly the albedo features, take their names from Antoniadi's map.[142]
In June 1962, Soviet scientists at the Institute of Radio-engineering and Electronics of the USSR Academy of Sciences, led by Vladimir Kotelnikov, became the first to bounce a radar signal off Mercury and receive it, starting radar observations of the planet.[143][144][145] Three years later, radar observations by Americans Gordon Pettengill and R. Dyce, using the 300-meter Arecibo Observatory radio telescope in Puerto Rico, showed conclusively that the planet's rotational period was about 59 days.[146][147] The theory that Mercury's rotation was synchronous had become widely held, and it was a surprise to astronomers when these radio observations were announced. If Mercury were tidally locked, its dark face would be extremely cold, but measurements of radio emission revealed that it was much hotter than expected. Astronomers were reluctant to drop the synchronous rotation theory and proposed alternative mechanisms such as powerful heat-distributing winds to explain the observations.[148]
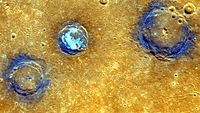
Water ice (yellow) at Mercury's north polar region
Italian astronomer Giuseppe Colombo noted that the rotation value was about two-thirds of Mercury's orbital period, and proposed that the planet's orbital and rotational periods were locked into a 3:2 rather than a 1:1 resonance.[149] Data from Mariner 10 subsequently confirmed this view.[150] This means that Schiaparelli's and Antoniadi's maps were not "wrong". Instead, the astronomers saw the same features during every second orbit and recorded them, but disregarded those seen in the meantime, when Mercury's other face was toward the Sun, because the orbital geometry meant that these observations were made under poor viewing conditions.[140]
Ground-based optical observations did not shed much further light on Mercury, but radio astronomers using interferometry at microwave wavelengths, a technique that enables removal of the solar radiation, were able to discern physical and chemical characteristics of the subsurface layers to a depth of several meters.[151][152] Not until the first space probe flew past Mercury did many of its most fundamental morphological properties become known. Moreover, recent technological advances have led to improved ground-based observations. In 2000, high-resolution lucky imaging observations were conducted by the Mount Wilson Observatory 1.5 meter Hale telescope. They provided the first views that resolved surface features on the parts of Mercury that were not imaged in the Mariner 10 mission.[153] Most of the planet has been mapped by the Arecibo radar telescope, with 5 km (3.1 mi) resolution, including polar deposits in shadowed craters of what may be water ice.[154]
Research with space probes

MESSENGER being prepared for launch
Reaching Mercury from Earth poses significant technical challenges, because it orbits so much closer to the Sun than Earth. A Mercury-bound spacecraft launched from Earth must travel over 91 million kilometres (57 million miles) into the Sun's gravitational potential well. Mercury has an orbital speed of 48 km/s (30 mi/s), whereas Earth's orbital speed is 30 km/s (19 mi/s). Therefore, the spacecraft must make a large change in velocity (delta-v) to enter a Hohmann transfer orbit that passes near Mercury, as compared to the delta-v required for other planetary missions.[156]
The potential energy liberated by moving down the Sun's potential well becomes kinetic energy; requiring another large delta-v change to do anything other than rapidly pass by Mercury. To land safely or enter a stable orbit the spacecraft would rely entirely on rocket motors. Aerobraking is ruled out because Mercury has a negligible atmosphere. A trip to Mercury requires more rocket fuel than that required to escape the Solar System completely. As a result, only two space probes have visited it so far.[157] A proposed alternative approach would use a solar sail to attain a Mercury-synchronous orbit around the Sun.[158]
Mariner 10

Mariner 10, the first probe to visit Mercury
The first spacecraft to visit Mercury was NASA's Mariner 10 (1974–1975).[122] The spacecraft used the gravity of Venus to adjust its orbital velocity so that it could approach Mercury, making it both the first spacecraft to use this gravitational "slingshot" effect and the first NASA mission to visit multiple planets.[156] Mariner 10 provided the first close-up images of Mercury's surface, which immediately showed its heavily cratered nature, and revealed many other types of geological features, such as the giant scarps that were later ascribed to the effect of the planet shrinking slightly as its iron core cools.[159] Unfortunately, the same face of the planet was lit at each of Mariner 10's close approaches. This made close observation of both sides of the planet impossible,[160] and resulted in the mapping of less than 45% of the planet's surface.[161]
The spacecraft made three close approaches to Mercury, the closest of which took it to within 327 km (203 mi) of the surface.[162] At the first close approach, instruments detected a magnetic field, to the great surprise of planetary geologists—Mercury's rotation was expected to be much too slow to generate a significant dynamo effect. The second close approach was primarily used for imaging, but at the third approach, extensive magnetic data were obtained. The data revealed that the planet's magnetic field is much like Earth's, which deflects the solar wind around the planet. For many years after the Mariner 10 encounters, the origin of Mercury's magnetic field remained the subject of several competing theories.[163][164]
On March 24, 1975, just eight days after its final close approach, Mariner 10 ran out of fuel. Because its orbit could no longer be accurately controlled, mission controllers instructed the probe to shut down.[165] Mariner 10 is thought to be still orbiting the Sun, passing close to Mercury every few months.[166]
MESSENGER

Estimated details of the impact of MESSENGER on 30 April 2015
A second NASA mission to Mercury, named MESSENGER (MErcury Surface, Space ENvironment, GEochemistry, and Ranging), was launched on 3 August 2004. It made a fly-by of Earth in August 2005, and of Venus in October 2006 and June 2007 to place it onto the correct trajectory to reach an orbit around Mercury.[167] A first fly-by of Mercury occurred on January 14, 2008, a second on October 6, 2008,[168] and a third on September 29, 2009.[169] Most of the hemisphere not imaged by Mariner 10 was mapped during these fly-bys. The probe successfully entered an elliptical orbit around the planet on March 18, 2011. The first orbital image of Mercury was obtained on March 29, 2011. The probe finished a one-year mapping mission,[168] and then entered a one-year extended mission into 2013. In addition to continued observations and mapping of Mercury, MESSENGER observed the 2012 solar maximum.[170]
The mission was designed to clear up six key issues: Mercury's high density, its geological history, the nature of its magnetic field, the structure of its core, whether it has ice at its poles, and where its tenuous atmosphere comes from. To this end, the probe carried imaging devices that gathered much-higher-resolution images of much more of Mercury than Mariner 10, assorted spectrometers to determine abundances of elements in the crust, and magnetometers and devices to measure velocities of charged particles. Measurements of changes in the probe's orbital velocity were expected to be used to infer details of the planet's interior structure.[171] MESSENGER's final maneuver was on April 24, 2015, and it crashed into Mercury's surface on April 30, 2015.[172][173][174] The spacecraft's impact with Mercury occurred near 3:26 PM EDT on April 30, 2015, leaving a crater estimated to be 16 m (52 ft) in diameter.[175]
First (29 March 2011) and last (30 April 2015) images of
Mercury by MESSENGER