Age of the universe

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Age_of_the_universe

In physical cosmology, the age of the universe is the time elapsed since the Big Bang. Today, astronomers have derived two different measurements of the age of the universe: a measurement based on direct observations of an early state of the universe, which indicate an age of 13.772±0.040 billion years within the Lambda-CDM concordance model as of 2018; and a measurement based on the observations of the local, modern universe which suggest a younger age. The uncertainty of the first kind of measurement has been narrowed down to 20 million years, based on a number of studies which all gave extremely similar figures for the age. These include studies of the microwave background radiation by the Planck spacecraft, the Wilkinson Microwave Anisotropy Probe and other space probes. Measurements of the cosmic background radiation give the cooling time of the universe since the Big Bang, and measurements of the expansion rate of the universe can be used to calculate its approximate age by extrapolating backwards in time. The range of the estimate is also within the range of the estimate for the oldest observed star in the universe.

Explanation

The Lambda-CDM concordance model describes the evolution of the universe from a very uniform, hot, dense primordial state to its present state over a span of about 13.77 billion years of cosmological time. This model is well understood theoretically and strongly supported by recent high-precision astronomical observations such as WMAP. In contrast, theories of the origin of the primordial state remain very speculative. If one extrapolates the Lambda-CDM model backward from the earliest well-understood state, it quickly (within a small fraction of a second) reaches a singularity. This is known as the "initial singularity" or the "Big Bang singularity". This singularity is not understood as having a physical significance in the usual sense, but it is convenient to quote times measured "since the Big Bang" even though they do not correspond to a physically measurable time. For example, "10⁻⁶ seconds after the Big Bang" is a well-defined era in the universe's evolution. If one referred to the same era as "13.77 billion years minus 10⁻⁶ seconds ago", the precision of the meaning would be lost because the minuscule latter time interval is eclipsed by uncertainty in the former.

Though the universe might in theory have a longer history, the International Astronomical Union presently uses the term "age of the universe" to mean the duration of the Lambda-CDM expansion, or equivalently the elapsed time since the Big Bang in the current observable universe.

Observational limits

Since the universe must be at least as old as the oldest things in it, there are a number of observations which put a lower limit on the age of the universe; these include the temperature of the coolest white dwarfs, which gradually cool as they age, and the dimmest turnoff point of main sequence stars in clusters (lower-mass stars spend a greater amount of time on the main sequence, so the lowest-mass stars that have evolved away from the main sequence set a minimum age).

Cosmological parameters

The age of the universe can be determined by measuring the Hubble constant today and extrapolating back in time with the observed value of density parameters (Ω). Before the discovery of dark energy, it was believed that the universe was matter-dominated (Einstein–de Sitter universe, green curve). Note that the de Sitter universe has infinite age, while the closed universe has the least age.

 

The value of the age correction factor, F, is shown as a function of two cosmological parameters: the current fractional matter density Ω_m and cosmological constant density Ω_Λ. The best-fit values of these parameters are shown by the box in the upper left; the matter-dominated universe is shown by the star in the lower right.

The problem of determining the age of the universe is closely tied to the problem of determining the values of the cosmological parameters. Today this is largely carried out in the context of the ΛCDM model, where the universe is assumed to contain normal (baryonic) matter, cold dark matter, radiation (including both photons and neutrinos), and a cosmological constant. The fractional contribution of each to the current energy density of the universe is given by the density parameters Ω_m, Ω_r, and Ω_Λ. The full ΛCDM model is described by a number of other parameters, but for the purpose of computing its age these three, along with the Hubble parameter ${\displaystyle H_{0}}$, are the most important.

If one has accurate measurements of these parameters, then the age of the universe can be determined by using the Friedmann equation. This equation relates the rate of change in the scale factor a(t) to the matter content of the universe. Turning this relation around, we can calculate the change in time per change in scale factor and thus calculate the total age of the universe by integrating this formula. The age t₀ is then given by an expression of the form

${\displaystyle t_{0}={\frac {1}{H_{0}}}F(\Omega _{r},\Omega _{m},\Omega _{\Lambda },\dots )}$

where ${\displaystyle H_{0}}$ is the Hubble parameter and the function F depends only on the fractional contribution to the universe's energy content that comes from various components. The first observation that one can make from this formula is that it is the Hubble parameter that controls that age of the universe, with a correction arising from the matter and energy content. So a rough estimate of the age of the universe comes from the Hubble time, the inverse of the Hubble parameter. With a value for ${\displaystyle H_{0}}$ around 69 km/s/Mpc, the Hubble time evaluates to ${\displaystyle 1/H_{0}}$ = 14.5 billion years.

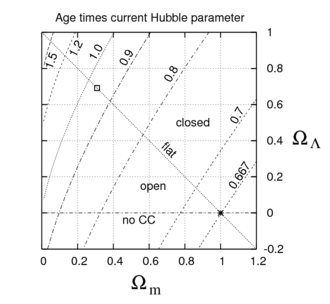
To get a more accurate number, the correction factor F must be computed. In general this must be done numerically, and the results for a range of cosmological parameter values are shown in the figure. For the Planck values (Ω_m, Ω_Λ) = (0.3086, 0.6914), shown by the box in the upper left corner of the figure, this correction factor is about F = 0.956. For a flat universe without any cosmological constant, shown by the star in the lower right corner, F = 2⁄3 is much smaller and thus the universe is younger for a fixed value of the Hubble parameter. To make this figure, Ω_r is held constant (roughly equivalent to holding the CMB temperature constant) and the curvature density parameter is fixed by the value of the other three.

Apart from the Planck satellite, the Wilkinson Microwave Anisotropy Probe (WMAP) was instrumental in establishing an accurate age of the universe, though other measurements must be folded in to gain an accurate number. CMB measurements are very good at constraining the matter content Ω_m and curvature parameter Ω_k. It is not as sensitive to Ω_Λ directly, partly because the cosmological constant becomes important only at low redshift. The most accurate determinations of the Hubble parameter H₀ come from Type Ia supernovae. Combining these measurements leads to the generally accepted value for the age of the universe quoted above.

The cosmological constant makes the universe "older" for fixed values of the other parameters. This is significant, since before the cosmological constant became generally accepted, the Big Bang model had difficulty explaining why globular clusters in the Milky Way appeared to be far older than the age of the universe as calculated from the Hubble parameter and a matter-only universe. Introducing the cosmological constant allows the universe to be older than these clusters, as well as explaining other features that the matter-only cosmological model could not.

WMAP

NASA's Wilkinson Microwave Anisotropy Probe (WMAP) project's nine-year data release in 2012 estimated the age of the universe to be (13.772±0.059)×10⁹ years (13.772 billion years, with an uncertainty of plus or minus 59 million years).

However, this age is based on the assumption that the project's underlying model is correct; other methods of estimating the age of the universe could give different ages. Assuming an extra background of relativistic particles, for example, can enlarge the error bars of the WMAP constraint by one order of magnitude.

This measurement is made by using the location of the first acoustic peak in the microwave background power spectrum to determine the size of the decoupling surface (size of the universe at the time of recombination). The light travel time to this surface (depending on the geometry used) yields a reliable age for the universe. Assuming the validity of the models used to determine this age, the residual accuracy yields a margin of error near one percent.

Planck

In 2015, the Planck Collaboration estimated the age of the universe to be 13.813±0.038 billion years, slightly higher but within the uncertainties of the earlier number derived from the WMAP data.

In the table below, figures are within 68% confidence limits for the base ΛCDM model.

Legend:

• TT, TE, EE: Planck Cosmic microwave background (CMB) power spectra
• lowP: Planck polarization data in the low-ℓ likelihood
• lensing: CMB lensing reconstruction
• ext: External data (BAO+JLA+H0). BAO: Baryon acoustic oscillations, JLA: Joint Light-curve Analysis, H0: Hubble constant

Cosmological parameters from 2015 Planck results

Parameter	Symbol	TT+lowP	TT+lowP +lensing	TT+lowP +lensing+ext	TT,TE,EE+lowP	TT,TE,EE+lowP +lensing	TT,TE,EE+lowP +lensing+ext
Age of the universe (Ga)	${\displaystyle t_{0}}$	13.813±0.038	13.799±0.038	13.796±0.029	13.813±0.026	13.807±0.026	13.799±0.021
Hubble constant (km⁄Mpc⋅s)	${\displaystyle H_{0}}$	67.31±0.96	67.81±0.92	67.90±0.55	67.27±0.66	67.51±0.64	67.74±0.46

In 2018, the Planck Collaboration updated its estimate for the age of the universe to 13.772±0.040 billion years.

Assumption of strong priors

Calculating the age of the universe is accurate only if the assumptions built into the models being used to estimate it are also accurate. This is referred to as strong priors and essentially involves stripping the potential errors in other parts of the model to render the accuracy of actual observational data directly into the concluded result. Although this is not a valid procedure in all contexts (as noted in the accompanying caveat: "based on the fact we have assumed the underlying model we used is correct"), the age given is thus accurate to the specified error (since this error represents the error in the instrument used to gather the raw data input into the model).

The age of the universe based on the best fit to Planck 2018 data alone is 13.772±0.040 billion years. This number represents an accurate "direct" measurement of the age of the universe (other methods typically involve Hubble's law and the age of the oldest stars in globular clusters, etc.). It is possible to use different methods for determining the same parameter (in this case – the age of the universe) and arrive at different answers with no overlap in the "errors". To best avoid the problem, it is common to show two sets of uncertainties; one related to the actual measurement and the other related to the systematic errors of the model being used.

An important component to the analysis of data used to determine the age of the universe (e.g. from Planck) therefore is to use a Bayesian statistical analysis, which normalizes the results based upon the priors (i.e. the model). This quantifies any uncertainty in the accuracy of a measurement due to a particular model used.

History

Main articles: Cosmic age problem and Cosmic microwave background

Nature timeline
−13 — – −12 — – −11 — – −10 — – −9 — – −8 — – −7 — – −6 — – −5 — – −4 — – −3 — – −2 — – −1 — – 0 —	Dark Ages Reionization Matter-dominated era Accelerated expansion Water Single-celled life Photosynthesis Multicellular life Vertebrates	← Earliest Universe ← Earliest stars ← Earliest galaxy ← Quasar / black hole ← Omega Centauri ← Andromeda Galaxy ← Milky Way spirals ← NGC 188 star cluster ← Alpha Centauri ← Earth / Solar System ← Earliest life ← Earliest oxygen ← Atmospheric oxygen ← Sexual reproduction ← Earliest fungi ← Earliest animals / plants ← Cambrian explosion ← Earliest mammals ← Earliest apes / humans L i f e
(billion years ago)

In the 18th century, the concept that the age of the Earth was millions, if not billions, of years began to appear. However, most scientists throughout the 19th century and into the first decades of the 20th century presumed that the universe itself was Steady State and eternal, possibly with stars coming and going but no changes occurring at the largest scale known at the time.

The first scientific theories indicating that the age of the universe might be finite were the studies of thermodynamics, formalized in the mid-19th century. The concept of entropy dictates that if the universe (or any other closed system) were infinitely old, then everything inside would be at the same temperature, and thus there would be no stars and no life. No scientific explanation for this contradiction was put forth at the time.

In 1915 Albert Einstein published the theory of general relativity and in 1917 constructed the first cosmological model based on his theory. In order to remain consistent with a steady state universe, Einstein added what was later called a cosmological constant to his equations. Einstein's model of a static universe was proved unstable by Arthur Eddington.

The first direct observational hint that the universe was not static but expanding came from the observations of 'recession velocities', mostly by Vesto Slipher, combined with distances to the 'nebulae' (galaxies) by Edwin Hubble in a work published in 1929. Earlier in the 20th century, Hubble and others resolved individual stars within certain nebulae, thus determining that they were galaxies, similar to, but external to, our Milky Way Galaxy. In addition, these galaxies were very large and very far away. Spectra taken of these distant galaxies showed a red shift in their spectral lines presumably caused by the Doppler effect, thus indicating that these galaxies were moving away from the Earth. In addition, the farther away these galaxies seemed to be (the dimmer they appeared to us) the greater was their redshift, and thus the faster they seemed to be moving away. This was the first direct evidence that the universe is not static but expanding. The first estimate of the age of the universe came from the calculation of when all of the objects must have started speeding out from the same point. Hubble's initial value for the universe's age was very low, as the galaxies were assumed to be much closer than later observations found them to be.

The first reasonably accurate measurement of the rate of expansion of the universe, a numerical value now known as the Hubble constant, was made in 1958 by astronomer Allan Sandage. His measured value for the Hubble constant came very close to the value range generally accepted today.

However Sandage, like Einstein, did not believe his own results at the time of discovery. Sandage proposed new theories of cosmogony to explain this discrepancy. This issue was more or less resolved by improvements in the theoretical models used for estimating the ages of stars. As of 2013, using the latest models for stellar evolution, the estimated age of the oldest known star is 14.46±0.8 billion years.

The discovery of microwave cosmic background radiation announced in 1965 finally brought an effective end to the remaining scientific uncertainty over the expanding universe. It was a chance result from work by two teams less than 60 miles apart. In 1964, Arno Penzias and Robert Wilson were trying to detect radio wave echoes with a supersensitive antenna. The antenna persistently detected a low, steady, mysterious noise in the microwave region that was evenly spread over the sky, and was present day and night. After testing, they became certain that the signal did not come from the Earth, the Sun, or our galaxy, but from outside our own galaxy, but could not explain it. At the same time another team, Robert H. Dicke, Jim Peebles, and David Wilkinson, were attempting to detect low level noise which might be left over from the Big Bang and could prove whether the Big Bang theory was correct. The two teams realized that the detected noise was in fact radiation left over from the Big Bang, and that this was strong evidence that the theory was correct. Since then, a great deal of other evidence has strengthened and confirmed this conclusion, and refined the estimated age of the universe to its current figure.

The space probes WMAP, launched in 2001, and Planck, launched in 2009, produced data that determines the Hubble constant and the age of the universe independent of galaxy distances, removing the largest source of error.

Eternity of the world

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Eternity_of_the_world 

The eternity of the world is the question of whether the world has a beginning in time or has existed from eternity. It was a concern for both ancient philosophers and the medieval theologians and medieval philosophers of the 13th century. The problem became a focus of a dispute in the 13th century, when some of the works of Aristotle, who believed in the eternity of the world, were rediscovered in the Latin West. This view conflicted with the view of the Catholic Church that the world had a beginning in time. The Aristotelian view was prohibited in the Condemnations of 1210–1277.

Aristotle

The ancient Greek philosopher Aristotle argued that the world must have existed from eternity in his Physics as follows. In Book I, he argues that everything that comes into existence does so from a substratum. Therefore, if the underlying matter of the universe came into existence, it would come into existence from a substratum. But the nature of matter is precisely to be the substratum from which other things arise. Consequently, the underlying matter of the universe could have come into existence only from an already existing matter exactly like itself; to assume that the underlying matter of the universe came into existence would require assuming that an underlying matter already existed. As this assumption is self-contradictory, Aristotle argued, matter must be eternal.

In Book VIII, his argument from motion is that if an absolute beginning of motion should be assumed, the object to undergo the first motion must either

(A) have come into existence and begun to move, or

(B) have existed in an eternal state of rest before beginning to move.

Option A is self-contradictory because an object cannot move before it comes into existence, and the act of coming into existence is itself a "movement," so that the first movement requires a movement before it, that is, the act of coming into existence. Option B is also unsatisfactory for two reasons.

• First, if the world began at a state of rest, the coming into existence of that state of rest would itself have been motion.
• Second, if the world changed from a state of rest to a state of motion, the cause of that change to motion would itself have been a motion.

He concludes that motion is necessarily eternal.

Aristotle argued that a "vacuum" (that is, a place where there is no matter) is impossible. Material objects can come into existence only in place, that is, occupy space. Were something to come from nothing, "the place to be occupied by what comes into existence would previously have been occupied by a vacuum, inasmuch as no body existed." But a vacuum is impossible, and matter must be eternal.

The Greek philosopher Critolaus (c. 200-c. 118 BC) of Phaselis defended Aristotle's doctrine of the eternity of the world, and of the human race in general, against the Stoics. There is no observed change in the natural order of things; humankind recreates itself in the same manner according to the capacity given by Nature, and the various ills to which it is heir, though fatal to individuals, do not avail to modify the whole. Just as it is absurd to suppose that humans are merely earth-born, so the possibility of their ultimate destruction is inconceivable. The world, as the manifestation of eternal order, must itself be eternal.

The Neo-Platonists

The Neoplatonist philosopher Proclus (412 – 485 AD) advanced in his De Aeternitate Mundi (On the Eternity of the World) eighteen proofs for the eternity of the world, resting on the divinity of its creator.

John Philoponus in 529 wrote his critique Against Proclus On the Eternity of the World in which he systematically argued against every proposition put forward for the eternity of the world. The intellectual battle against eternalism became one of Philoponus’ major preoccupations and dominated several of his publications (some now lost) over the following decade.

Philoponus originated the argument now known as the Traversal of the infinite. If the existence of something requires that something else exist before it, then the first thing cannot come into existence without the thing before it existing. An infinite number cannot actually exist, nor be counted through or 'traversed', or be increased. Something cannot come into existence if this requires an infinite number of other things existing before it. Therefore, the world cannot be infinite.

The Aristotelian commentator Simplicius of Cilicia and contemporary of Philoponus argued against the Aristotelian view. Simplicius adhered to the Aristotelian doctrine of the eternity of the world and strongly opposed Philoponus, who asserted the beginning of the world through divine creation.

Philoponus' arguments

Philoponus' arguments for temporal finitism were severalfold. Contra Aristotlem has been lost, and is chiefly known through the citations used by Simplicius of Cilicia in his commentaries on Aristotle's Physics and De Caelo. Philoponus' refutation of Aristotle extended to six books, the first five addressing De Caelo and the sixth addressing Physics, and from comments on Philoponus made by Simplicius can be deduced to have been quite lengthy.

A full exposition of Philoponus' several arguments, as reported by Simplicius, can be found in Sorabji. One such argument was based upon Aristotle's own theorem that there were not multiple infinities, and ran as follows: If time were infinite, then as the universe continued in existence for another hour, the infinity of its age since creation at the end of that hour must be one hour greater than the infinity of its age since creation at the start of that hour. But since Aristotle holds that such treatments of infinity are impossible and ridiculous, the world cannot have existed for infinite time.

Philoponus's works were adopted by many; his first argument against an infinite past being the "argument from the impossibility of the existence of an actual infinite", which states:

"An actual infinite cannot exist."

"An infinite temporal regress of events is an actual infinite."

"Thus an infinite temporal regress of events cannot exist."

This argument defines event as equal increments of time. Philoponus argues that the second premise is not controversial since the number of events prior to today would be an actual infinite without beginning if the universe is eternal. The first premise is defended by a reductio ad absurdum where Philoponus shows that actual infinites can not exist in the actual world because they would lead to contradictions albeit being a possible mathematical enterprise. Since an actual infinite in reality would create logical contradictions, it can not exist including the actual infinite set of past events. The second argument, the "argument from the impossibility of completing an actual infinite by successive addition", states:

"An actual infinite cannot be completed by successive addition."

"The temporal series of past events has been completed by successive addition."

"Thus the temporal series of past events cannot be an actual infinite."

The first statement states, correctly, that a finite (number) cannot be made into an infinite one by the finite addition of more finite numbers. The second skirts around this; the analogous idea in mathematics, that the (infinite) sequence of negative integers "..-3, -2, -1" may be extended by appending zero, then one, and so forth; is perfectly valid.

Medieval period

Avicenna argued that prior to a thing's coming into actual existence, its existence must have been 'possible.' Were its existence necessary, the thing would already have existed, and were its existence impossible, the thing would never exist. The possibility of the thing must therefore in some sense have its own existence. Possibility cannot exist in itself, but must reside within a subject. If an already existent matter must precede everything coming into existence, clearly nothing, including matter, can come into existence ex nihilo, that is, from absolute nothingness. An absolute beginning of the existence of matter is therefore impossible.

The Aristotelian commentator Averroes supported Aristotle's view, particularly in his work The Incoherence of the Incoherence (Tahafut al-tahafut), in which he defended Aristotelian philosophy against al-Ghazali's claims in The Incoherence of the Philosophers (Tahafut al-falasifa).

Averroes' contemporary Maimonides challenged Aristotle's assertion that "everything in existence comes from a substratum," on that basis that his reliance on induction and analogy is a fundamentally flawed means of explaining unobserved phenomenon. According to Maimonides, to argue that "because I have never observed something coming into existence without coming from a substratum it cannot occur" is equivalent to arguing that "because I cannot empirically observe eternity it does not exist."

Maimonides himself held that neither creation nor Aristotle's infinite time were provable, or at least that no proof was available. (According to scholars of his work, he didn't make a formal distinction between unprovability and the simple absence of proof.) However, some of Maimonides' Jewish successors, including Gersonides and Crescas, conversely held that the question was decidable, philosophically.

In the West, the 'Latin Averroists' were a group of philosophers writing in Paris in the middle of the thirteenth century, who included Siger of Brabant, Boethius of Dacia. They supported Aristotle's doctrine of the eternity of the world against conservative theologians such as John Pecham and Bonaventure. The conservative position is that the world can be logically proved to have begun in time, of which the classic exposition is Bonaventure's argument in the second book of his commentary on Peter Lombard's sentences, where he repeats Philoponus' case against a traversal of the infinite.

Thomas Aquinas, like Maimonides, argued against both the conservative theologians and the Averroists, claiming that neither the eternity nor the finite nature of the world could be proved by logical argument alone. According to Aquinas the possible eternity of the world and its creation would be contradictory if an efficient cause were precede its effect in duration or if non-existence precedes existence in duration. But an efficient cause, such as God, which instantaneously produces its effect would not necessarily precede its effect in duration. God can also be distinguished from a natural cause which produces its effect by motion, for a cause that produces motion must precede its effect. God could be an instantaneous and motionless creator, and could have created the world without preceding it in time. To Aquinas, that the world began was an article of faith.

The position of the Averroists was condemned by Stephen Tempier in 1277.

Conservation of energy

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Conservation_of_energy

In physics and chemistry, the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be conserved over time. This law, first proposed and tested by Émilie du Châtelet, means that energy can neither be created nor destroyed; rather, it can only be transformed or transferred from one form to another. For instance, chemical energy is converted to kinetic energy when a stick of dynamite explodes. If one adds up all forms of energy that were released in the explosion, such as the kinetic energy and potential energy of the pieces, as well as heat and sound, one will get the exact decrease of chemical energy in the combustion of the dynamite.

Classically, conservation of energy was distinct from conservation of mass; however, special relativity showed that mass is related to energy and vice versa by E = mc², and science now takes the view that mass-energy as a whole is conserved. Theoretically, this implies that any object with mass can itself be converted to pure energy, and vice versa, though this is believed to be possible only under the most extreme of physical conditions, such as likely existed in the universe very shortly after the Big Bang or when black holes emit Hawking radiation.

Conservation of energy can be rigorously proven by Noether's theorem as a consequence of continuous time translation symmetry; that is, from the fact that the laws of physics do not change over time.

A consequence of the law of conservation of energy is that a perpetual motion machine of the first kind cannot exist, that is to say, no system without an external energy supply can deliver an unlimited amount of energy to its surroundings. For systems which do not have time translation symmetry, it may not be possible to define conservation of energy. Examples include curved spacetimes in general relativity or time crystals in condensed matter physics.

History

Ancient philosophers as far back as Thales of Miletus c. 550 BCE had inklings of the conservation of some underlying substance of which everything is made. However, there is no particular reason to identify their theories with what we know today as "mass-energy" (for example, Thales thought it was water). Empedocles (490–430 BCE) wrote that in his universal system, composed of four roots (earth, air, water, fire), "nothing comes to be or perishes"; instead, these elements suffer continual rearrangement. Epicurus (c. 350 BCE) on the other hand believed everything in the universe to be composed of indivisible units of matter—the ancient precursor to 'atoms'—and he too had some idea of the necessity of conservation, stating that "the sum total of things was always such as it is now, and such it will ever remain."

In 1605, Simon Stevinus was able to solve a number of problems in statics based on the principle that perpetual motion was impossible.

In 1639, Galileo published his analysis of several situations—including the celebrated "interrupted pendulum"—which can be described (in modern language) as conservatively converting potential energy to kinetic energy and back again. Essentially, he pointed out that the height a moving body rises is equal to the height from which it falls, and used this observation to infer the idea of inertia. The remarkable aspect of this observation is that the height to which a moving body ascends on a frictionless surface does not depend on the shape of the surface.

In 1669, Christiaan Huygens published his laws of collision. Among the quantities he listed as being invariant before and after the collision of bodies were both the sum of their linear momenta as well as the sum of their kinetic energies. However, the difference between elastic and inelastic collision was not understood at the time. This led to the dispute among later researchers as to which of these conserved quantities was the more fundamental. In his Horologium Oscillatorium, he gave a much clearer statement regarding the height of ascent of a moving body, and connected this idea with the impossibility of a perpetual motion. Huygens' study of the dynamics of pendulum motion was based on a single principle: that the center of gravity of a heavy object cannot lift itself.

Gottfried Leibniz

It was Leibniz during 1676–1689 who first attempted a mathematical formulation of the kind of energy which is connected with motion (kinetic energy). Using Huygens' work on collision, Leibniz noticed that in many mechanical systems (of several masses, m_i each with velocity v_i),

${\displaystyle \sum _{i}m_{i}v_{i}^{2}}$

was conserved so long as the masses did not interact. He called this quantity the vis viva or living force of the system. The principle represents an accurate statement of the approximate conservation of kinetic energy in situations where there is no friction. Many physicists at that time, such as Newton, held that the conservation of momentum, which holds even in systems with friction, as defined by the momentum:

${\displaystyle \sum _{i}m_{i}v_{i}}$

was the conserved vis viva. It was later shown that both quantities are conserved simultaneously, given the proper conditions such as an elastic collision.

In 1687, Isaac Newton published his Principia, which was organized around the concept of force and momentum. However, the researchers were quick to recognize that the principles set out in the book, while fine for point masses, were not sufficient to tackle the motions of rigid and fluid bodies. Some other principles were also required.

Daniel Bernoulli

The law of conservation of vis viva was championed by the father and son duo, Johann and Daniel Bernoulli. The former enunciated the principle of virtual work as used in statics in its full generality in 1715, while the latter based his Hydrodynamica, published in 1738, on this single conservation principle. Daniel's study of loss of vis viva of flowing water led him to formulate the Bernoulli's principle, which relates the loss to be proportional to the change in hydrodynamic pressure. Daniel also formulated the notion of work and efficiency for hydraulic machines; and he gave a kinetic theory of gases, and linked the kinetic energy of gas molecules with the temperature of the gas.

This focus on the vis viva by the continental physicists eventually led to the discovery of stationarity principles governing mechanics, such as the D'Alembert's principle, Lagrangian, and Hamiltonian formulations of mechanics.

Emilie du Chatelet

Émilie du Châtelet (1706–1749) proposed and tested the hypothesis of the conservation of total energy, as distinct from momentum. Inspired by the theories of Gottfried Leibniz, she repeated and publicized an experiment originally devised by Willem 's Gravesande in 1722 in which balls were dropped from different heights into a sheet of soft clay. Each ball's kinetic energy—as indicated by the quantity of material displaced—was shown to be proportional to the square of the velocity. The deformation of the clay was found to be directly proportional to the height from which the balls were dropped, equal to the initial potential energy. Earlier workers, including Newton and Voltaire, had all believed that "energy" (so far as they understood the concept at all) was not distinct from momentum and therefore proportional to velocity. According to this understanding, the deformation of the clay should have been proportional to the square root of the height from which the balls were dropped. In classical physics the correct formula is ${\displaystyle E_{k}={\frac {1}{2}}mv^{2}}$, where ${\displaystyle E_{k}}$ is the kinetic energy of an object, ${\displaystyle m}$ its mass and ${\displaystyle v}$ its speed. On this basis, du Châtelet proposed that energy must always have the same dimensions in any form, which is necessary to be able to relate it in different forms (kinetic, potential, heat, ...).

Engineers such as John Smeaton, Peter Ewart, Carl Holtzmann, Gustave-Adolphe Hirn and Marc Seguin recognized that conservation of momentum alone was not adequate for practical calculation and made use of Leibniz's principle. The principle was also championed by some chemists such as William Hyde Wollaston. Academics such as John Playfair were quick to point out that kinetic energy is clearly not conserved. This is obvious to a modern analysis based on the second law of thermodynamics, but in the 18th and 19th centuries, the fate of the lost energy was still unknown.

Gradually it came to be suspected that the heat inevitably generated by motion under friction was another form of vis viva. In 1783, Antoine Lavoisier and Pierre-Simon Laplace reviewed the two competing theories of vis viva and caloric theory. Count Rumford's 1798 observations of heat generation during the boring of cannons added more weight to the view that mechanical motion could be converted into heat and (as important) that the conversion was quantitative and could be predicted (allowing for a universal conversion constant between kinetic energy and heat). Vis viva then started to be known as energy, after the term was first used in that sense by Thomas Young in 1807.

Gaspard-Gustave Coriolis

The recalibration of vis viva to

${\displaystyle {\frac {1}{2}}\sum _{i}m_{i}v_{i}^{2}}$

which can be understood as converting kinetic energy to work, was largely the result of Gaspard-Gustave Coriolis and Jean-Victor Poncelet over the period 1819–1839. The former called the quantity quantité de travail (quantity of work) and the latter, travail mécanique (mechanical work), and both championed its use in engineering calculation.

In a paper Über die Natur der Wärme(German "On the Nature of Heat/Warmth"), published in the Zeitschrift für Physik in 1837, Karl Friedrich Mohr gave one of the earliest general statements of the doctrine of the conservation of energy: "besides the 54 known chemical elements there is in the physical world one agent only, and this is called Kraft [energy or work]. It may appear, according to circumstances, as motion, chemical affinity, cohesion, electricity, light and magnetism; and from any one of these forms it can be transformed into any of the others."

Mechanical equivalent of heat

A key stage in the development of the modern conservation principle was the demonstration of the mechanical equivalent of heat. The caloric theory maintained that heat could neither be created nor destroyed, whereas conservation of energy entails the contrary principle that heat and mechanical work are interchangeable.

In the middle of the eighteenth century, Mikhail Lomonosov, a Russian scientist, postulated his corpusculo-kinetic theory of heat, which rejected the idea of a caloric. Through the results of empirical studies, Lomonosov came to the conclusion that heat was not transferred through the particles of the caloric fluid.

In 1798, Count Rumford (Benjamin Thompson) performed measurements of the frictional heat generated in boring cannons, and developed the idea that heat is a form of kinetic energy; his measurements refuted caloric theory, but were imprecise enough to leave room for doubt.

James Prescott Joule

The mechanical equivalence principle was first stated in its modern form by the German surgeon Julius Robert von Mayer in 1842. Mayer reached his conclusion on a voyage to the Dutch East Indies, where he found that his patients' blood was a deeper red because they were consuming less oxygen, and therefore less energy, to maintain their body temperature in the hotter climate. He discovered that heat and mechanical work were both forms of energy and in 1845, after improving his knowledge of physics, he published a monograph that stated a quantitative relationship between them.

Joule's apparatus for measuring the mechanical equivalent of heat. A descending weight attached to a string causes a paddle immersed in water to rotate.

Meanwhile, in 1843, James Prescott Joule independently discovered the mechanical equivalent in a series of experiments. In the most famous, now called the "Joule apparatus", a descending weight attached to a string caused a paddle immersed in water to rotate. He showed that the gravitational potential energy lost by the weight in descending was equal to the internal energy gained by the water through friction with the paddle.

Over the period 1840–1843, similar work was carried out by engineer Ludwig A. Colding, although it was little known outside his native Denmark.

Both Joule's and Mayer's work suffered from resistance and neglect but it was Joule's that eventually drew the wider recognition.

For the dispute between Joule and Mayer over priority, see Mechanical equivalent of heat: Priority.

In 1844, William Robert Grove postulated a relationship between mechanics, heat, light, electricity and magnetism by treating them all as manifestations of a single "force" (energy in modern terms). In 1846, Grove published his theories in his book The Correlation of Physical Forces. In 1847, drawing on the earlier work of Joule, Sadi Carnot and Émile Clapeyron, Hermann von Helmholtz arrived at conclusions similar to Grove's and published his theories in his book Über die Erhaltung der Kraft (On the Conservation of Force, 1847). The general modern acceptance of the principle stems from this publication.

In 1850, William Rankine first used the phrase the law of the conservation of energy for the principle.

In 1877, Peter Guthrie Tait claimed that the principle originated with Sir Isaac Newton, based on a creative reading of propositions 40 and 41 of the Philosophiae Naturalis Principia Mathematica. This is now regarded as an example of Whig history.

Mass–energy equivalence

Main article: Mass–energy equivalence

Matter is composed of atoms and what makes up atoms. Matter has intrinsic or rest mass. In the limited range of recognized experience of the nineteenth century it was found that such rest mass is conserved. Einstein's 1905 theory of special relativity showed that rest mass corresponds to an equivalent amount of rest energy. This means that rest mass can be converted to or from equivalent amounts of (non-material) forms of energy, for example kinetic energy, potential energy, and electromagnetic radiant energy. When this happens, as recognized in twentieth century experience, rest mass is not conserved, unlike the total mass or total energy. All forms of energy contribute to the total mass and total energy.

For example, an electron and a positron each have rest mass. They can perish together, converting their combined rest energy into photons having electromagnetic radiant energy, but no rest mass. If this occurs within an isolated system that does not release the photons or their energy into the external surroundings, then neither the total mass nor the total energy of the system will change. The produced electromagnetic radiant energy contributes just as much to the inertia (and to any weight) of the system as did the rest mass of the electron and positron before their demise. Likewise, non-material forms of energy can perish into matter, which has rest mass.

Thus, conservation of energy (total, including material or rest energy), and conservation of mass (total, not just rest), each still holds as an (equivalent) law. In the 18th century these had appeared as two seemingly-distinct laws.

Conservation of energy in beta decay

Main article: Beta decay § Neutrinos in beta decay

The discovery in 1911 that electrons emitted in beta decay have a continuous rather than a discrete spectrum appeared to contradict conservation of energy, under the then-current assumption that beta decay is the simple emission of an electron from a nucleus. This problem was eventually resolved in 1933 by Enrico Fermi who proposed the correct description of beta-decay as the emission of both an electron and an antineutrino, which carries away the apparently missing energy.

First law of thermodynamics

Main article: First law of thermodynamics

For a closed thermodynamic system, the first law of thermodynamics may be stated as:

${\displaystyle \delta Q=\mathrm {d} U+\delta W}$, or equivalently, ${\displaystyle \mathrm {d} U=\delta Q-\delta W,}$

where ${\displaystyle \delta Q}$ is the quantity of energy added to the system by a heating process, ${\displaystyle \delta W}$ is the quantity of energy lost by the system due to work done by the system on its surroundings and ${\displaystyle \mathrm {d} U}$ is the change in the internal energy of the system.

The δ's before the heat and work terms are used to indicate that they describe an increment of energy which is to be interpreted somewhat differently than the ${\displaystyle \mathrm {d} U}$ increment of internal energy. Work and heat refer to kinds of process which add or subtract energy to or from a system, while the internal energy ${\displaystyle U}$ is a property of a particular state of the system when it is in unchanging thermodynamic equilibrium. Thus the term "heat energy" for ${\displaystyle \delta Q}$ means "that amount of energy added as the result of heating" rather than referring to a particular form of energy. Likewise, the term "work energy" for ${\displaystyle \delta W}$ means "that amount of energy lost as the result of work". Thus one can state the amount of internal energy possessed by a thermodynamic system that one knows is presently in a given state, but one cannot tell, just from knowledge of the given present state, how much energy has in the past flowed into or out of the system as a result of its being heated or cooled, nor as the result of work being performed on or by the system.

Entropy is a function of the state of a system which tells of limitations of the possibility of conversion of heat into work.

For a simple compressible system, the work performed by the system may be written:

${\displaystyle \delta W=P\,\mathrm {d} V,}$

where ${\displaystyle P}$ is the pressure and ${\displaystyle dV}$ is a small change in the volume of the system, each of which are system variables. In the fictive case in which the process is idealized and infinitely slow, so as to be called quasi-static, and regarded as reversible, the heat being transferred from a source with temperature infinitesimally above the system temperature, then the heat energy may be written

${\displaystyle \delta Q=T\,\mathrm {d} S,}$

where ${\displaystyle T}$ is the temperature and ${\displaystyle \mathrm {d} S}$ is a small change in the entropy of the system. Temperature and entropy are variables of state of a system.

If an open system (in which mass may be exchanged with the environment) has several walls such that the mass transfer is through rigid walls separate from the heat and work transfers, then the first law may be written:

${\displaystyle \mathrm {d} U=\delta Q-\delta W+u'\,dM,}$

where ${\displaystyle dM}$ is the added mass and ${\displaystyle u'}$ is the internal energy per unit mass of the added mass, measured in the surroundings before the process.

Noether's theorem

Main article: Noether's theorem

 

Emmy Noether (1882-1935) was an influential mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics.

The conservation of energy is a common feature in many physical theories. From a mathematical point of view it is understood as a consequence of Noether's theorem, developed by Emmy Noether in 1915 and first published in 1918. The theorem states every continuous symmetry of a physical theory has an associated conserved quantity; if the theory's symmetry is time invariance then the conserved quantity is called "energy". The energy conservation law is a consequence of the shift symmetry of time; energy conservation is implied by the empirical fact that the laws of physics do not change with time itself. Philosophically this can be stated as "nothing depends on time per se". In other words, if the physical system is invariant under the continuous symmetry of time translation then its energy (which is canonical conjugate the quantity to time) is conserved. Conversely, systems that are not invariant under shifts in time (an example, systems with time-dependent potential energy) do not exhibit conservation of energy – unless we consider them to exchange energy with another, an external system so that the theory of the enlarged system becomes time-invariant again. Conservation of energy for finite systems is valid in such physical theories as special relativity and quantum theory (including QED) in the flat space-time.

Relativity

With the discovery of special relativity by Henri Poincaré and Albert Einstein, the energy was proposed to be one component of an energy-momentum 4-vector. Each of the four components (one of energy and three of momentum) of this vector is separately conserved across time, in any closed system, as seen from any given inertial reference frame. Also conserved is the vector length (Minkowski norm), which is the rest mass for single particles, and the invariant mass for systems of particles (where momenta and energy are separately summed before the length is calculated).

The relativistic energy of a single massive particle contains a term related to its rest mass in addition to its kinetic energy of motion. In the limit of zero kinetic energy (or equivalently in the rest frame) of a massive particle, or else in the center of momentum frame for objects or systems which retain kinetic energy, the total energy of particle or object (including internal kinetic energy in systems) is related to its rest mass or its invariant mass via the famous equation ${\displaystyle E=mc^{2}}$.

Thus, the rule of conservation of energy over time in special relativity continues to hold, so long as the reference frame of the observer is unchanged. This applies to the total energy of systems, although different observers disagree as to the energy value. Also conserved, and invariant to all observers, is the invariant mass, which is the minimal system mass and energy that can be seen by any observer, and which is defined by the energy–momentum relation.

In general relativity, energy–momentum conservation is not well-defined except in certain special cases. Energy-momentum is typically expressed with the aid of a stress–energy–momentum pseudotensor. However, since pseudotensors are not tensors, they do not transform cleanly between reference frames. If the metric under consideration is static (that is, does not change with time) or asymptotically flat (that is, at an infinite distance away spacetime looks empty), then energy conservation holds without major pitfalls. In practice, some metrics such as the Friedmann–Lemaître–Robertson–Walker metric do not satisfy these constraints and energy conservation is not well defined. The theory of general relativity leaves open the question of whether there is a conservation of energy for the entire universe.

Quantum theory

In quantum mechanics, energy of a quantum system is described by a self-adjoint (or Hermitian) operator called the Hamiltonian, which acts on the Hilbert space (or a space of wave functions) of the system. If the Hamiltonian is a time-independent operator, emergence probability of the measurement result does not change in time over the evolution of the system. Thus the expectation value of energy is also time independent. The local energy conservation in quantum field theory is ensured by the quantum Noether's theorem for energy-momentum tensor operator. Due to the lack of the (universal) time operator in quantum theory, the uncertainty relations for time and energy are not fundamental in contrast to the position-momentum uncertainty principle, and merely holds in specific cases (see Uncertainty principle). Energy at each fixed time can in principle be exactly measured without any trade-off in precision forced by the time-energy uncertainty relations. Thus the conservation of energy in time is a well defined concept even in quantum mechanics.