Tensor

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Tensor 

The second-order Cauchy stress tensor (${\displaystyle \mathbf {T} }$) describes the stress forces experienced by a material at a given point. The product ${\displaystyle \mathbf {T} \cdot \mathbf {v} }$ of the stress tensor and a unit vector ${\displaystyle \mathbf {v} }$, pointing in a given direction, is a vector describing the stress forces experienced by a material at the point described by the stress tensor, along a plane perpendicular to ${\displaystyle \mathbf {v} }$. This image shows the stress vectors along three perpendicular directions, each represented by a face of the cube. Since the stress tensor describes a mapping that takes one vector as input, and gives one vector as output, it is a second-order tensor.

In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Objects that tensors may map between include vectors and scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system.

Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics (stress, elasticity, fluid mechanics, moment of inertia, ...), electrodynamics (electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), or general relativity (stress–energy tensor, curvature tensor, ...) and others. In applications, it is common to study situations in which a different tensor can occur at each point of an object; for example the stress within an object may vary from one location to another. This leads to the concept of a tensor field. In some areas, tensor fields are so ubiquitous that they are often simply called "tensors".

Tullio Levi-Civita and Gregorio Ricci-Curbastro popularised tensors in 1900 – continuing the earlier work of Bernhard Riemann and Elwin Bruno Christoffel and others – as part of the absolute differential calculus. The concept enabled an alternative formulation of the intrinsic differential geometry of a manifold in the form of the Riemann curvature tensor.

Definition

Although seemingly different, the various approaches to defining tensors describe the same geometric concept using different language and at different levels of abstraction.

As multidimensional arrays

A tensor may be represented as an array (potentially multidimensional). Just as a vector in an n-dimensional space is represented by a one-dimensional array with n components with respect to a given basis, any tensor with respect to a basis is represented by a multidimensional array. For example, a linear operator is represented in a basis as a two-dimensional square n × n array. The numbers in the multidimensional array are known as the scalar components of the tensor or simply its components. They are denoted by indices giving their position in the array, as subscripts and superscripts, following the symbolic name of the tensor. For example, the components of an order 2 tensor T could be denoted T_ij , where i and j are indices running from 1 to n, or also by T ⁱ
_j. Whether an index is displayed as a superscript or subscript depends on the transformation properties of the tensor, described below. Thus while T_ij and T ⁱ
_j can both be expressed as n by n matrices, and are numerically related via index juggling, the difference in their transformation laws indicates it would be improper to add them together. The total number of indices required to identify each component uniquely is equal to the dimension of the array, and is called the order, degree or rank of the tensor. However, the term "rank" generally has another meaning in the context of matrices and tensors.

Just as the components of a vector change when we change the basis of the vector space, the components of a tensor also change under such a transformation. Each type of tensor comes equipped with a transformation law that details how the components of the tensor respond to a change of basis. The components of a vector can respond in two distinct ways to a change of basis (see covariance and contravariance of vectors), where the new basis vectors ${\displaystyle \mathbf {\hat {e}} _{i}}$ are expressed in terms of the old basis vectors ${\displaystyle \mathbf {e} _{j}}$ as,

${\displaystyle \mathbf {\hat {e}} _{i}=\sum _{j=1}^{n}\mathbf {e} _{j}R_{i}^{j}=\mathbf {e} _{j}R_{i}^{j}.}$

Here R ^j_i are the entries of the change of basis matrix, and in the rightmost expression the summation sign was suppressed: this is the Einstein summation convention, which will be used throughout this article. The components vⁱ of a column vector v transform with the inverse of the matrix R,

${\displaystyle {\hat {v}}^{i}=\left(R^{-1}\right)_{j}^{i}v^{j},}$

where the hat denotes the components in the new basis. This is called a contravariant transformation law, because the vector components transform by the inverse of the change of basis. In contrast, the components, w_i, of a covector (or row vector), w transform with the matrix R itself,

${\displaystyle {\hat {w}}_{i}=w_{j}R_{i}^{j}.}$

This is called a covariant transformation law, because the covector components transforms by the same matrix as the change of basis matrix. The components of a more general tensor transform by some combination of covariant and contravariant transformations, with one transformation law for each index. If the transformation matrix of an index is the inverse matrix of the basis transformation, then the index is called contravariant and is conventionally denoted with an upper index (superscript). If the transformation matrix of an index is the basis transformation itself, then the index is called covariant and is denoted with a lower index (subscript).

As a simple example, the matrix of a linear operator with respect to a basis is a rectangular array ${\displaystyle T}$ that transforms under a change of basis matrix ${\displaystyle R=\left(R_{i}^{j}\right)}$ by ${\displaystyle {\hat {T}}=R^{-1}TR}$. For the individual matrix entries, this transformation law has the form ${\displaystyle {\hat {T}}_{j'}^{i'}=\left(R^{-1}\right)_{i}^{i'}T_{j}^{i}R_{j'}^{j}}$ so the tensor corresponding to the matrix of a linear operator has one covariant and one contravariant index: it is of type (1,1).

Combinations of covariant and contravariant components with the same index allow us to express geometric invariants. For example, the fact that a vector is the same object in different coordinate systems can be captured by the following equations, using the formulas defined above:

${\displaystyle \mathbf {v} ={\hat {v}}^{i}\,\mathbf {\hat {e}} _{i}=\left(\left(R^{-1}\right)_{j}^{i}{v}^{j}\right)\left(\mathbf {e} _{k}R_{i}^{k}\right)=\left(\left(R^{-1}\right)_{j}^{i}R_{i}^{k}\right){v}^{j}\mathbf {e} _{k}=\delta _{j}^{k}{v}^{j}\mathbf {e} _{k}={v}^{k}\,\mathbf {e} _{k}={v}^{i}\,\mathbf {e} _{i}}$,

where ${\displaystyle \delta _{j}^{k}}$ is the Kronecker delta, which functions similarly to the identity matrix, and has the effect of renaming indices (j into k in this example). This shows several features of the component notation: the ability to re-arrange terms at will (commutativity), the need to use different indices when working with multiple objects in the same expression, the ability to rename indices, and the manner in which contravariant and covariant tensors combine so that all instances of the transformation matrix and its inverse cancel, so that expressions like ${\displaystyle {v}^{i}\,\mathbf {e} _{i}}$ can immediately be seen to be geometrically identical in all coordinate systems.

Similarly, a linear operator, viewed as a geometric object, does not actually depend on a basis: it is just a linear map that accepts a vector as an argument and produces another vector. The transformation law for how the matrix of components of a linear operator changes with the basis is consistent with the transformation law for a contravariant vector, so that the action of a linear operator on a contravariant vector is represented in coordinates as the matrix product of their respective coordinate representations. That is, the components ${\displaystyle (Tv)^{i}}$ are given by ${\displaystyle (Tv)^{i}=T_{j}^{i}v^{j}}$. These components transform contravariantly, since

${\displaystyle \left({\widehat {Tv}}\right)^{i'}={\hat {T}}_{j'}^{i'}{\hat {v}}^{j'}=\left[\left(R^{-1}\right)_{i}^{i'}T_{j}^{i}R_{j'}^{j}\right]\left[\left(R^{-1}\right)_{j}^{j'}v^{j}\right]=\left(R^{-1}\right)_{i}^{i'}(Tv)^{i}.}$

The transformation law for an order p + q tensor with p contravariant indices and q covariant indices is thus given as,

${\displaystyle {\hat {T}}_{j'_{1},\ldots ,j'_{q}}^{i'_{1},\ldots ,i'_{p}}=\left(R^{-1}\right)_{i_{1}}^{i'_{1}}\cdots \left(R^{-1}\right)_{i_{p}}^{i'_{p}}}$ ${\displaystyle T_{j_{1},\ldots ,j_{q}}^{i_{1},\ldots ,i_{p}}}$ ${\displaystyle R_{j'_{1}}^{j_{1}}\cdots R_{j'_{q}}^{j_{q}}.}$

Here the primed indices denote components in the new coordinates, and the unprimed indices denote the components in the old coordinates. Such a tensor is said to be of order or type (p, q). The terms "order", "type", "rank", "valence", and "degree" are all sometimes used for the same concept. Here, the term "order" or "total order" will be used for the total dimension of the array (or its generalization in other definitions), p + q in the preceding example, and the term "type" for the pair giving the number of contravariant and covariant indices. A tensor of type (p, q) is also called a (p, q)-tensor for short.

This discussion motivates the following formal definition:

Definition. A tensor of type (p, q) is an assignment of a multidimensional array

${\displaystyle T_{j_{1}\dots j_{q}}^{i_{1}\dots i_{p}}[\mathbf {f} ]}$

to each basis f = (e₁, ..., e_n) of an n-dimensional vector space such that, if we apply the change of basis

${\displaystyle \mathbf {f} \mapsto \mathbf {f} \cdot R=\left(\mathbf {e} _{i}R_{1}^{i},\dots ,\mathbf {e} _{i}R_{n}^{i}\right)}$

then the multidimensional array obeys the transformation law

${\displaystyle T_{j'_{1}\dots j'_{q}}^{i'_{1}\dots i'_{p}}[\mathbf {f} \cdot R]=\left(R^{-1}\right)_{i_{1}}^{i'_{1}}\cdots \left(R^{-1}\right)_{i_{p}}^{i'_{p}}}$ ${\displaystyle T_{j_{1},\ldots ,j_{q}}^{i_{1},\ldots ,i_{p}}[\mathbf {f} ]}$ ${\displaystyle R_{j'_{1}}^{j_{1}}\cdots R_{j'_{q}}^{j_{q}}.}$

The definition of a tensor as a multidimensional array satisfying a transformation law traces back to the work of Ricci.

An equivalent definition of a tensor uses the representations of the general linear group. There is an action of the general linear group on the set of all ordered bases of an n-dimensional vector space. If ${\displaystyle \mathbf {f} =(\mathbf {f} _{1},\dots ,\mathbf {f} _{n})}$ is an ordered basis, and ${\displaystyle R=\left(R_{j}^{i}\right)}$ is an invertible ${\displaystyle n\times n}$ matrix, then the action is given by

${\displaystyle \mathbf {f} R=\left(\mathbf {f} _{i}R_{1}^{i},\dots ,\mathbf {f} _{i}R_{n}^{i}\right).}$

Let F be the set of all ordered bases. Then F is a principal homogeneous space for GL(n). Let W be a vector space and let ${\displaystyle \rho }$ be a representation of GL(n) on W (that is, a group homomorphism ${\displaystyle \rho :{\text{GL}}(n)\to {\text{GL}}(W)}$). Then a tensor of type ${\displaystyle \rho }$ is an equivariant map ${\displaystyle T:F\to W}$. Equivariance here means that

${\displaystyle T(FR)=\rho \left(R^{-1}\right)T(F).}$

When ${\displaystyle \rho }$ is a tensor representation of the general linear group, this gives the usual definition of tensors as multidimensional arrays. This definition is often used to describe tensors on manifolds, and readily generalizes to other groups.

As multilinear maps

Main article: Multilinear map

A downside to the definition of a tensor using the multidimensional array approach is that it is not apparent from the definition that the defined object is indeed basis independent, as is expected from an intrinsically geometric object. Although it is possible to show that transformation laws indeed ensure independence from the basis, sometimes a more intrinsic definition is preferred. One approach that is common in differential geometry is to define tensors relative to a fixed (finite-dimensional) vector space V, which is usually taken to be a particular vector space of some geometrical significance like the tangent space to a manifold. In this approach, a type (p, q) tensor T is defined as a multilinear map,

${\displaystyle T:\underbrace {V^{*}\times \dots \times V^{*}} _{p{\text{ copies}}}\times \underbrace {V\times \dots \times V} _{q{\text{ copies}}}\rightarrow \mathbf {R} ,}$

where V^∗ is the corresponding dual space of covectors, which is linear in each of its arguments. The above assumes V is a vector space over the real numbers, ℝ. More generally, V can be taken over any field F (e.g. the complex numbers), with F replacing ℝ as the codomain of the multilinear maps.

By applying a multilinear map T of type (p, q) to a basis {e_j} for V and a canonical cobasis {εⁱ} for V^∗,

${\displaystyle T_{j_{1}\dots j_{q}}^{i_{1}\dots i_{p}}\equiv T\left({\boldsymbol {\varepsilon }}^{i_{1}},\ldots ,{\boldsymbol {\varepsilon }}^{i_{p}},\mathbf {e} _{j_{1}},\ldots ,\mathbf {e} _{j_{q}}\right),}$

a (p + q)-dimensional array of components can be obtained. A different choice of basis will yield different components. But, because T is linear in all of its arguments, the components satisfy the tensor transformation law used in the multilinear array definition. The multidimensional array of components of T thus form a tensor according to that definition. Moreover, such an array can be realized as the components of some multilinear map T. This motivates viewing multilinear maps as the intrinsic objects underlying tensors.

In viewing a tensor as a multilinear map, it is conventional to identify the double dual V^∗∗ of the vector space V, i.e., the space of linear functionals on the dual vector space V^∗, with the vector space V. There is always a natural linear map from V to its double dual, given by evaluating a linear form in V^∗ against a vector in V. This linear mapping is an isomorphism in finite dimensions, and it is often then expedient to identify V with its double dual.

Using tensor products

Main article: Tensor (intrinsic definition)

For some mathematical applications, a more abstract approach is sometimes useful. This can be achieved by defining tensors in terms of elements of tensor products of vector spaces, which in turn are defined through a universal property. A type (p, q) tensor is defined in this context as an element of the tensor product of vector spaces,

${\displaystyle T\in \underbrace {V\otimes \dots \otimes V} _{p{\text{ copies}}}\otimes \underbrace {V^{*}\otimes \dots \otimes V^{*}} _{q{\text{ copies}}}.}$

A basis v_i of V and basis w_j of W naturally induce a basis v_i ⊗ w_j of the tensor product V ⊗ W. The components of a tensor T are the coefficients of the tensor with respect to the basis obtained from a basis {e_i} for V and its dual basis {ε^j}, i.e.

${\displaystyle T=T_{j_{1}\dots j_{q}}^{i_{1}\dots i_{p}}\;\mathbf {e} _{i_{1}}\otimes \cdots \otimes \mathbf {e} _{i_{p}}\otimes {\boldsymbol {\varepsilon }}^{j_{1}}\otimes \cdots \otimes {\boldsymbol {\varepsilon }}^{j_{q}}.}$

Using the properties of the tensor product, it can be shown that these components satisfy the transformation law for a type (p, q) tensor. Moreover, the universal property of the tensor product gives a 1-to-1 correspondence between tensors defined in this way and tensors defined as multilinear maps.

This 1 to 1 correspondence can be archived the following way, because in the finite dimensional case there exists a canonical isomorphism between a vectorspace and its double dual:

${\displaystyle U\otimes V\cong \left(U^{**}\right)\otimes \left(V^{**}\right)\cong \left(U^{*}\otimes V^{*}\right)^{*}\cong \operatorname {Hom} ^{2}\left(U^{*}\times V^{*};\mathbb {F} \right)}$

The last line is using the universal property of the tensor product, that there is a 1 to 1 correspondence between maps from ${\displaystyle \operatorname {Hom} ^{2}\left(U^{*}\times V^{*};\mathbb {F} \right)}$ and ${\displaystyle \operatorname {Hom} \left(U^{*}\otimes V^{*};\mathbb {F} \right)}$.

Tensor products can be defined in great generality – for example, involving arbitrary modules over a ring. In principle, one could define a "tensor" simply to be an element of any tensor product. However, the mathematics literature usually reserves the term tensor for an element of a tensor product of any number of copies of a single vector space V and its dual, as above.

Tensors in infinite dimensions

This discussion of tensors so far assumes finite dimensionality of the spaces involved, where the spaces of tensors obtained by each of these constructions are naturally isomorphic. Constructions of spaces of tensors based on the tensor product and multilinear mappings can be generalized, essentially without modification, to vector bundles or coherent sheaves. For infinite-dimensional vector spaces, inequivalent topologies lead to inequivalent notions of tensor, and these various isomorphisms may or may not hold depending on what exactly is meant by a tensor (see topological tensor product). In some applications, it is the tensor product of Hilbert spaces that is intended, whose properties are the most similar to the finite-dimensional case. A more modern view is that it is the tensors' structure as a symmetric monoidal category that encodes their most important properties, rather than the specific models of those categories.

Tensor fields

Main article: Tensor field

In many applications, especially in differential geometry and physics, it is natural to consider a tensor with components that are functions of the point in a space. This was the setting of Ricci's original work. In modern mathematical terminology such an object is called a tensor field, often referred to simply as a tensor.

In this context, a coordinate basis is often chosen for the tangent vector space. The transformation law may then be expressed in terms of partial derivatives of the coordinate functions,

${\displaystyle {\bar {x}}^{i}\left(x^{1},\ldots ,x^{n}\right),}$

defining a coordinate transformation,

${\displaystyle {\hat {T}}_{j'_{1}\dots j'_{q}}^{i'_{1}\dots i'_{p}}\left({\bar {x}}^{1},\ldots ,{\bar {x}}^{n}\right)={\frac {\partial {\bar {x}}^{i'_{1}}}{\partial x^{i_{1}}}}\cdots {\frac {\partial {\bar {x}}^{i'_{p}}}{\partial x^{i_{p}}}}{\frac {\partial x^{j_{1}}}{\partial {\bar {x}}^{j'_{1}}}}\cdots {\frac {\partial x^{j_{q}}}{\partial {\bar {x}}^{j'_{q}}}}T_{j_{1}\dots j_{q}}^{i_{1}\dots i_{p}}\left(x^{1},\ldots ,x^{n}\right).}$

Examples

See also: Dyadic tensor

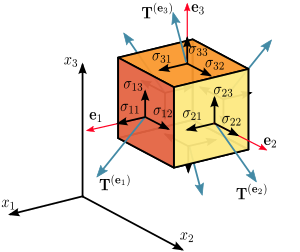
An elementary example of a mapping describable as a tensor is the dot product, which maps two vectors to a scalar. A more complex example is the Cauchy stress tensor T, which takes a directional unit vector v as input and maps it to the stress vector T^(v), which is the force (per unit area) exerted by material on the negative side of the plane orthogonal to v against the material on the positive side of the plane, thus expressing a relationship between these two vectors, shown in the figure (right). The cross product, where two vectors are mapped to a third one, is strictly speaking not a tensor because it changes its sign under those transformations that change the orientation of the coordinate system. The totally anti-symmetric symbol ${\displaystyle \varepsilon _{ijk}}$ nevertheless allows a convenient handling of the cross product in equally oriented three dimensional coordinate systems.

This table shows important examples of tensors on vector spaces and tensor fields on manifolds. The tensors are classified according to their type (n, m), where n is the number of contravariant indices, m is the number of covariant indices, and n + m gives the total order of the tensor. For example, a bilinear form is the same thing as a (0, 2)-tensor; an inner product is an example of a (0, 2)-tensor, but not all (0, 2)-tensors are inner products. In the (0, M)-entry of the table, M denotes the dimensionality of the underlying vector space or manifold because for each dimension of the space, a separate index is needed to select that dimension to get a maximally covariant antisymmetric tensor.

Example tensors on vector spaces and tensor fields on manifolds

		m
		0	1	2	3	⋯	M	⋯
n	0	Scalar, e.g. scalar curvature	Covector, linear functional, 1-form, e.g. dipole moment, gradient of a scalar field	Bilinear form, e.g. inner product, quadrupole moment, metric tensor, Ricci curvature, 2-form, symplectic form	3-form E.g. octupole moment		E.g. M-form i.e. volume form
	1	Euclidean vector	Linear transformation, Kronecker delta	E.g. cross product in three dimensions	E.g. Riemann curvature tensor
	2	Inverse metric tensor, bivector, e.g., Poisson structure		E.g. elasticity tensor
	⋮
	N	Multivector
	⋮

Raising an index on an (n, m)-tensor produces an (n + 1, m − 1)-tensor; this corresponds to moving diagonally down and to the left on the table. Symmetrically, lowering an index corresponds to moving diagonally up and to the right on the table. Contraction of an upper with a lower index of an (n, m)-tensor produces an (n − 1, m − 1)-tensor; this corresponds to moving diagonally up and to the left on the table.

Orientation defined by an ordered set of vectors.

Reversed orientation corresponds to negating the exterior product.

Geometric interpretation of grade n elements in a real exterior algebra for n = 0 (signed point), 1 (directed line segment, or vector), 2 (oriented plane element), 3 (oriented volume). The exterior product of n vectors can be visualized as any n-dimensional shape (e.g. n-parallelotope, n-ellipsoid); with magnitude (hypervolume), and orientation defined by that on its n − 1-dimensional boundary and on which side the interior is.

Properties

Assuming a basis of a real vector space, e.g., a coordinate frame in the ambient space, a tensor can be represented as an organized multidimensional array of numerical values with respect to this specific basis. Changing the basis transforms the values in the array in a characteristic way that allows to define tensors as objects adhering to this transformational behavior. For example, there are invariants of tensors that must be preserved under any change of the basis, thereby making only certain multidimensional arrays of numbers a tensor. Compare this to the array representing ${\displaystyle \varepsilon _{ijk}}$ not being a tensor, for the sign change under transformations changing the orientation.

Because the components of vectors and their duals transform differently under the change of their dual bases, there is a covariant and/or contravariant transformation law that relates the arrays, which represent the tensor with respect to one basis and that with respect to the other one. The numbers of, respectively, vectors: n (contravariant indices) and dual vectors: m (covariant indices) in the input and output of a tensor determine the type (or valence) of the tensor, a pair of natural numbers (n, m), which determine the precise form of the transformation law. The order of a tensor is the sum of these two numbers.

The order (also degree or rank) of a tensor is thus the sum of the orders of its arguments plus the order of the resulting tensor. This is also the dimensionality of the array of numbers needed to represent the tensor with respect to a specific basis, or equivalently, the number of indices needed to label each component in that array. For example, in a fixed basis, a standard linear map that maps a vector to a vector, is represented by a matrix (a 2-dimensional array), and therefore is a 2nd-order tensor. A simple vector can be represented as a 1-dimensional array, and is therefore a 1st-order tensor. Scalars are simple numbers and are thus 0th-order tensors. This way the tensor representing the scalar product, taking two vectors and resulting in a scalar has order 2 + 0 = 2, the same as the stress tensor, taking one vector and returning another 1 + 1 = 2. The ${\displaystyle \varepsilon _{ijk}}$-symbol, mapping two vectors to one vector, would have order 2 + 1 = 3.

The collection of tensors on a vector space and its dual forms a tensor algebra, which allows products of arbitrary tensors. Simple applications of tensors of order 2, which can be represented as a square matrix, can be solved by clever arrangement of transposed vectors and by applying the rules of matrix multiplication, but the tensor product should not be confused with this.

Notation

There are several notational systems that are used to describe tensors and perform calculations involving them.

Ricci calculus

Ricci calculus is the modern formalism and notation for tensor indices: indicating inner and outer products, covariance and contravariance, summations of tensor components, symmetry and antisymmetry, and partial and covariant derivatives.

Einstein summation convention

The Einstein summation convention dispenses with writing summation signs, leaving the summation implicit. Any repeated index symbol is summed over: if the index i is used twice in a given term of a tensor expression, it means that the term is to be summed for all i. Several distinct pairs of indices may be summed this way.

Penrose graphical notation

Penrose graphical notation is a diagrammatic notation which replaces the symbols for tensors with shapes, and their indices by lines and curves. It is independent of basis elements, and requires no symbols for the indices.

Abstract index notation

The abstract index notation is a way to write tensors such that the indices are no longer thought of as numerical, but rather are indeterminates. This notation captures the expressiveness of indices and the basis-independence of index-free notation.

Component-free notation

A component-free treatment of tensors uses notation that emphasises that tensors do not rely on any basis, and is defined in terms of the tensor product of vector spaces.

Operations

There are several operations on tensors that again produce a tensor. The linear nature of tensor implies that two tensors of the same type may be added together, and that tensors may be multiplied by a scalar with results analogous to the scaling of a vector. On components, these operations are simply performed component-wise. These operations do not change the type of the tensor; but there are also operations that produce a tensor of different type.

Tensor product

Main article: Tensor product

The tensor product takes two tensors, S and T, and produces a new tensor, S ⊗ T, whose order is the sum of the orders of the original tensors. When described as multilinear maps, the tensor product simply multiplies the two tensors, i.e.

${\displaystyle (S\otimes T)(v_{1},\ldots ,v_{n},v_{n+1},\ldots ,v_{n+m})=S(v_{1},\ldots ,v_{n})T(v_{n+1},\ldots ,v_{n+m}),}$

which again produces a map that is linear in all its arguments. On components, the effect is to multiply the components of the two input tensors pairwise, i.e.

${\displaystyle (S\otimes T)_{j_{1}\ldots j_{k}j_{k+1}\ldots j_{k+m}}^{i_{1}\ldots i_{l}i_{l+1}\ldots i_{l+n}}=S_{j_{1}\ldots j_{k}}^{i_{1}\ldots i_{l}}T_{j_{k+1}\ldots j_{k+m}}^{i_{l+1}\ldots i_{l+n}},}$

If S is of type (l, k) and T is of type (n, m), then the tensor product S ⊗ T has type (l + n, k + m).

Contraction

Main article: Tensor contraction

Tensor contraction is an operation that reduces a type (n, m) tensor to a type (n − 1, m − 1) tensor, of which the trace is a special case. It thereby reduces the total order of a tensor by two. The operation is achieved by summing components for which one specified contravariant index is the same as one specified covariant index to produce a new component. Components for which those two indices are different are discarded. For example, a (1, 1)-tensor ${\displaystyle T_{i}^{j}}$ can be contracted to a scalar through ${\displaystyle T_{i}^{i}}$. Where the summation is again implied. When the (1, 1)-tensor is interpreted as a linear map, this operation is known as the trace.

The contraction is often used in conjunction with the tensor product to contract an index from each tensor.

The contraction can also be understood using the definition of a tensor as an element of a tensor product of copies of the space V with the space V^∗ by first decomposing the tensor into a linear combination of simple tensors, and then applying a factor from V^∗ to a factor from V. For example, a tensor ${\displaystyle T\in V\otimes V\otimes V^{*}}$ can be written as a linear combination

${\displaystyle T=v_{1}\otimes w_{1}\otimes \alpha _{1}+v_{2}\otimes w_{2}\otimes \alpha _{2}+\cdots +v_{N}\otimes w_{N}\otimes \alpha _{N}.}$

The contraction of T on the first and last slots is then the vector

${\displaystyle \alpha _{1}(v_{1})w_{1}+\alpha _{2}(v_{2})w_{2}+\cdots +\alpha _{N}(v_{N})w_{N}.}$

In a vector space with an inner product (also known as a metric) g, the term contraction is used for removing two contravariant or two covariant indices by forming a trace with the metric tensor or its inverse. For example, a (2, 0)-tensor ${\displaystyle T^{ij}}$ can be contracted to a scalar through ${\displaystyle T^{ij}g_{ij}}$ (yet again assuming the summation convention).

Raising or lowering an index

Main article: Raising and lowering indices

When a vector space is equipped with a nondegenerate bilinear form (or metric tensor as it is often called in this context), operations can be defined that convert a contravariant (upper) index into a covariant (lower) index and vice versa. A metric tensor is a (symmetric) (0, 2)-tensor; it is thus possible to contract an upper index of a tensor with one of the lower indices of the metric tensor in the product. This produces a new tensor with the same index structure as the previous tensor, but with lower index generally shown in the same position of the contracted upper index. This operation is quite graphically known as lowering an index.

Conversely, the inverse operation can be defined, and is called raising an index. This is equivalent to a similar contraction on the product with a (2, 0)-tensor. This inverse metric tensor has components that are the matrix inverse of those of the metric tensor.

Applications

Continuum mechanics

Important examples are provided by continuum mechanics. The stresses inside a solid body or fluid are described by a tensor field. The stress tensor and strain tensor are both second-order tensor fields, and are related in a general linear elastic material by a fourth-order elasticity tensor field. In detail, the tensor quantifying stress in a 3-dimensional solid object has components that can be conveniently represented as a 3 × 3 array. The three faces of a cube-shaped infinitesimal volume segment of the solid are each subject to some given force. The force's vector components are also three in number. Thus, 3 × 3, or 9 components are required to describe the stress at this cube-shaped infinitesimal segment. Within the bounds of this solid is a whole mass of varying stress quantities, each requiring 9 quantities to describe. Thus, a second-order tensor is needed.

If a particular surface element inside the material is singled out, the material on one side of the surface will apply a force on the other side. In general, this force will not be orthogonal to the surface, but it will depend on the orientation of the surface in a linear manner. This is described by a tensor of type (2, 0), in linear elasticity, or more precisely by a tensor field of type (2, 0), since the stresses may vary from point to point.

Other examples from physics

Common applications include:

• Electromagnetic tensor (or Faraday tensor) in electromagnetism
• Finite deformation tensors for describing deformations and strain tensor for strain in continuum mechanics
• Permittivity and electric susceptibility are tensors in anisotropic media
• Four-tensors in general relativity (e.g. stress–energy tensor), used to represent momentum fluxes
• Spherical tensor operators are the eigenfunctions of the quantum angular momentum operator in spherical coordinates
• Diffusion tensors, the basis of diffusion tensor imaging, represent rates of diffusion in biological environments
• Quantum mechanics and quantum computing utilize tensor products for combination of quantum states

Applications of tensors of order > 2

The concept of a tensor of order two is often conflated with that of a matrix. Tensors of higher order do however capture ideas important in science and engineering, as has been shown successively in numerous areas as they develop. This happens, for instance, in the field of computer vision, with the trifocal tensor generalizing the fundamental matrix.

The field of nonlinear optics studies the changes to material polarization density under extreme electric fields. The polarization waves generated are related to the generating electric fields through the nonlinear susceptibility tensor. If the polarization P is not linearly proportional to the electric field E, the medium is termed nonlinear. To a good approximation (for sufficiently weak fields, assuming no permanent dipole moments are present), P is given by a Taylor series in E whose coefficients are the nonlinear susceptibilities:

${\displaystyle {\frac {P_{i}}{\varepsilon _{0}}}=\sum _{j}\chi _{ij}^{(1)}E_{j}+\sum _{jk}\chi _{ijk}^{(2)}E_{j}E_{k}+\sum _{jk\ell }\chi _{ijk\ell }^{(3)}E_{j}E_{k}E_{\ell }+\cdots .\!}$

Here ${\displaystyle \chi ^{(1)}}$ is the linear susceptibility, ${\displaystyle \chi ^{(2)}}$ gives the Pockels effect and second harmonic generation, and ${\displaystyle \chi ^{(3)}}$ gives the Kerr effect. This expansion shows the way higher-order tensors arise naturally in the subject matter.

Generalizations

Tensor products of vector spaces

The vector spaces of a tensor product need not be the same, and sometimes the elements of such a more general tensor product are called "tensors". For example, an element of the tensor product space V ⊗ W is a second-order "tensor" in this more general sense, and an order-d tensor may likewise be defined as an element of a tensor product of d different vector spaces. A type (n, m) tensor, in the sense defined previously, is also a tensor of order n + m in this more general sense. The concept of tensor product can be extended to arbitrary modules over a ring.

Tensors in infinite dimensions

The notion of a tensor can be generalized in a variety of ways to infinite dimensions. One, for instance, is via the tensor product of Hilbert spaces. Another way of generalizing the idea of tensor, common in nonlinear analysis, is via the multilinear maps definition where instead of using finite-dimensional vector spaces and their algebraic duals, one uses infinite-dimensional Banach spaces and their continuous dual. Tensors thus live naturally on Banach manifolds and Fréchet manifolds.

Tensor densities

Main article: Tensor density

Suppose that a homogeneous medium fills R³, so that the density of the medium is described by a single scalar value ρ in kg m⁻³. The mass, in kg, of a region Ω is obtained by multiplying ρ by the volume of the region Ω, or equivalently integrating the constant ρ over the region:

${\displaystyle m=\int _{\Omega }\rho \,dx\,dy\,dz}$

where the Cartesian coordinates xyz are measured in m. If the units of length are changed into cm, then the numerical values of the coordinate functions must be rescaled by a factor of 100:

${\displaystyle x'=100x,\quad y'=100y,\quad z'=100z}$

The numerical value of the density ρ must then also transform by ${\displaystyle 100^{-3}\mathrm {m^{3}/cm^{3}} }$ to compensate, so that the numerical value of the mass in kg is still given by integral of ${\displaystyle \rho \,dx\,dy\,dz}$. Thus ${\displaystyle \rho '=100^{-3}\rho }$ (in units of kg cm⁻³).

More generally, if the Cartesian coordinates xyz undergo a linear transformation, then the numerical value of the density ρ must change by a factor of the reciprocal of the absolute value of the determinant of the coordinate transformation, so that the integral remains invariant, by the change of variables formula for integration. Such a quantity that scales by the reciprocal of the absolute value of the determinant of the coordinate transition map is called a scalar density. To model a non-constant density, ρ is a function of the variables xyz (a scalar field), and under a curvilinear change of coordinates, it transforms by the reciprocal of the Jacobian of the coordinate change. For more on the intrinsic meaning, see Density on a manifold.

A tensor density transforms like a tensor under a coordinate change, except that it in addition picks up a factor of the absolute value of the determinant of the coordinate transition:

${\displaystyle T_{j'_{1}\dots j'_{q}}^{i'_{1}\dots i'_{p}}[\mathbf {f} \cdot R]=|\det R|^{-w}\left(R^{-1}\right)_{i_{1}}^{i'_{1}}\cdots \left(R^{-1}\right)_{i_{p}}^{i'_{p}}}$ ${\displaystyle T_{j_{1},\ldots ,j_{q}}^{i_{1},\ldots ,i_{p}}[\mathbf {f} ]}$ ${\displaystyle R_{j'_{1}}^{j_{1}}\cdots R_{j'_{q}}^{j_{q}}.}$

Here w is called the weight. In general, any tensor multiplied by a power of this function or its absolute value is called a tensor density, or a weighted tensor. An example of a tensor density is the current density of electromagnetism.

Under an affine transformation of the coordinates, a tensor transforms by the linear part of the transformation itself (or its inverse) on each index. These come from the rational representations of the general linear group. But this is not quite the most general linear transformation law that such an object may have: tensor densities are non-rational, but are still semisimple representations. A further class of transformations come from the logarithmic representation of the general linear group, a reducible but not semisimple representation, consisting of an (x,y) ∈ R² with the transformation law

${\displaystyle (x,y)\mapsto (x+y\log \left|\det R\right|,y).}$

Geometric objects

The transformation law for a tensor behaves as a functor on the category of admissible coordinate systems, under general linear transformations (or, other transformations within some class, such as local diffeomorphisms.) This makes a tensor a special case of a geometrical object, in the technical sense that it is a function of the coordinate system transforming functorially under coordinate changes. Examples of objects obeying more general kinds of transformation laws are jets and, more generally still, natural bundles.

Spinors

Main article: Spinor

When changing from one orthonormal basis (called a frame) to another by a rotation, the components of a tensor transform by that same rotation. This transformation does not depend on the path taken through the space of frames. However, the space of frames is not simply connected (see orientation entanglement and plate trick): there are continuous paths in the space of frames with the same beginning and ending configurations that are not deformable one into the other. It is possible to attach an additional discrete invariant to each frame that incorporates this path dependence, and which turns out (locally) to have values of ±1. A spinor is an object that transforms like a tensor under rotations in the frame, apart from a possible sign that is determined by the value of this discrete invariant.

Succinctly, spinors are elements of the spin representation of the rotation group, while tensors are elements of its tensor representations. Other classical groups have tensor representations, and so also tensors that are compatible with the group, but all non-compact classical groups have infinite-dimensional unitary representations as well.

History

The concepts of later tensor analysis arose from the work of Carl Friedrich Gauss in differential geometry, and the formulation was much influenced by the theory of algebraic forms and invariants developed during the middle of the nineteenth century. The word "tensor" itself was introduced in 1846 by William Rowan Hamilton to describe something different from what is now meant by a tensor. The contemporary usage was introduced by Woldemar Voigt in 1898.

Tensor calculus was developed around 1890 by Gregorio Ricci-Curbastro under the title absolute differential calculus, and originally presented by Ricci-Curbastro in 1892. It was made accessible to many mathematicians by the publication of Ricci-Curbastro and Tullio Levi-Civita's 1900 classic text Méthodes de calcul différentiel absolu et leurs applications (Methods of absolute differential calculus and their applications).

In the 20th century, the subject came to be known as tensor analysis, and achieved broader acceptance with the introduction of Einstein's theory of general relativity, around 1915. General relativity is formulated completely in the language of tensors. Einstein had learned about them, with great difficulty, from the geometer Marcel Grossmann. Levi-Civita then initiated a correspondence with Einstein to correct mistakes Einstein had made in his use of tensor analysis. The correspondence lasted 1915–17, and was characterized by mutual respect:

I admire the elegance of your method of computation; it must be nice to ride through these fields upon the horse of true mathematics while the like of us have to make our way laboriously on foot.

— Albert Einstein

Tensors were also found to be useful in other fields such as continuum mechanics. Some well-known examples of tensors in differential geometry are quadratic forms such as metric tensors, and the Riemann curvature tensor. The exterior algebra of Hermann Grassmann, from the middle of the nineteenth century, is itself a tensor theory, and highly geometric, but it was some time before it was seen, with the theory of differential forms, as naturally unified with tensor calculus. The work of Élie Cartan made differential forms one of the basic kinds of tensors used in mathematics.

From about the 1920s onwards, it was realised that tensors play a basic role in algebraic topology (for example in the Künneth theorem). Correspondingly there are types of tensors at work in many branches of abstract algebra, particularly in homological algebra and representation theory. Multilinear algebra can be developed in greater generality than for scalars coming from a field. For example, scalars can come from a ring. But the theory is then less geometric and computations more technical and less algorithmic. Tensors are generalized within category theory by means of the concept of monoidal category, from the 1960s.

Introduction to the mathematics of general relativity

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Introduction_to_the_mathematics_of_general_relativity 

The mathematics of general relativity is complex. In Newton's theories of motion, an object's length and the rate at which time passes remain constant while the object accelerates, meaning that many problems in Newtonian mechanics may be solved by algebra alone. In relativity, however, an object's length and the rate at which time passes both change appreciably as the object's speed approaches the speed of light, meaning that more variables and more complicated mathematics are required to calculate the object's motion. As a result, relativity requires the use of concepts such as vectors, tensors, pseudotensors and curvilinear coordinates.

For an introduction based on the example of particles following circular orbits about a large mass, nonrelativistic and relativistic treatments are given in, respectively, Newtonian motivations for general relativity and Theoretical motivation for general relativity.

Vectors and tensors

Main articles: Euclidean vector and Tensor

Vectors

Illustration of a typical vector.

In mathematics, physics, and engineering, a Euclidean vector (sometimes called a geometric or spatial vector, or – as here – simply a vector) is a geometric object that has both a magnitude (or length) and direction. A vector is what is needed to "carry" the point A to the point B; the Latin word vector means "one who carries". The magnitude of the vector is the distance between the two points and the direction refers to the direction of displacement from A to B. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operations which obey the familiar algebraic laws of commutativity, associativity, and distributivity.

Tensors

Stress is a second-order tensor that represents the response of a material to force applied at an angle. The two directions of the tensor represent the "normal" (at right angles to the surface) force, and "shear" (parallel to the surface) force.

A tensor extends the concept of a vector to additional directions. A scalar, that is, a simple number without a direction, would be shown on a graph as a point, a zero-dimensional object. A vector, which has a magnitude and direction, would appear on a graph as a line, which is a one-dimensional object. A vector is a first-order tensor, since it holds one direction. A second-order tensor has two magnitudes and two directions, and would appear on a graph as two lines similar to the hands of a clock. The "order" of a tensor is the number of directions contained within, which is separate from the dimensions of the individual directions. A second-order tensor in two dimensions might be represented mathematically by a 2-by-2 matrix, and in three dimensions by a 3-by-3 matrix, but in both cases the matrix is "square" for a second-order tensor. A third-order tensor has three magnitudes and directions, and would be represented by a cube of numbers, 3-by-3-by-3 for directions in three dimensions, and so on.

Applications

Vectors are fundamental in the physical sciences. They can be used to represent any quantity that has both a magnitude and direction, such as velocity, the magnitude of which is speed. For example, the velocity 5 meters per second upward could be represented by the vector (0, 5) (in 2 dimensions with the positive y axis as 'up'). Another quantity represented by a vector is force, since it has a magnitude and direction. Vectors also describe many other physical quantities, such as displacement, acceleration, momentum, and angular momentum. Other physical vectors, such as the electric and magnetic field, are represented as a system of vectors at each point of a physical space; that is, a vector field.

Tensors also have extensive applications in physics:

• Electromagnetic tensor (or Faraday's tensor) in electromagnetism
• Finite deformation tensors for describing deformations and strain tensor for strain in continuum mechanics
• Permittivity and electric susceptibility are tensors in anisotropic media
• Stress–energy tensor in general relativity, used to represent momentum fluxes
• Spherical tensor operators are the eigenfunctions of the quantum angular momentum operator in spherical coordinates
• Diffusion tensors, the basis of diffusion tensor imaging, represent rates of diffusion in biologic environments

Dimensions

In general relativity, four-dimensional vectors, or four-vectors, are required. These four dimensions are length, height, width and time. A "point" in this context would be an event, as it has both a location and a time. Similar to vectors, tensors in relativity require four dimensions. One example is the Riemann curvature tensor.

Coordinate transformation

• 

  A vector v, is shown with two coordinate grids, e_x and e_r. In space, there is no clear coordinate grid to use. This means that the coordinate system changes based on the location and orientation of the observer. Observer e_x and e_r in this image are facing different directions.

• 

  Here we see that e_x and e_r see the vector differently. The direction of the vector is the same. But to e_x, the vector is moving to its left. To e_r, the vector is moving to its right.

In physics, as well as mathematics, a vector is often identified with a tuple, or list of numbers, which depend on some auxiliary coordinate system or reference frame. When the coordinates are transformed, for example by rotation or stretching of the coordinate system, then the components of the vector also transform. The vector itself has not changed, but the reference frame has, so the components of the vector (or measurements taken with respect to the reference frame) must change to compensate.

The vector is called covariant or contravariant depending on how the transformation of the vector's components is related to the transformation of coordinates.

• Contravariant vectors have units of distance (such as a displacement) or distance times some other unit (such as velocity or acceleration) and transform in the opposite way as the coordinate system. For example, in changing units from meters to millimeters the coordinate units get smaller, but the numbers in a vector become larger: 1 m becomes 1000 mm.
• Covariant vectors, on the other hand, have units of one-over-distance (such as a gradient) and transform in the same way as the coordinate system. For example, in changing from meters to millimeters, the coordinate units become smaller and the number measuring a gradient will also become smaller: 1 K/m becomes 0.001 K/mm.

In Einstein notation, contravariant vectors and components of tensors are shown with superscripts, e.g. xⁱ, and covariant vectors and components of tensors with subscripts, e.g. x_i. Indices are "raised" or "lowered" by multiplication by an appropriate matrix, often the identity matrix.

Coordinate transformation is important because relativity states that there is not one reference point (or perspective) in the universe that is more favored than another. On earth, we use dimensions like north, east, and elevation, which are used throughout the entire planet. There is no such system for space. Without a clear reference grid, it becomes more accurate to describe the four dimensions as towards/away, left/right, up/down and past/future. As an example event, assume that Earth is a motionless object, and consider the signing of the Declaration of Independence. To a modern observer on Mount Rainier looking east, the event is ahead, to the right, below, and in the past. However, to an observer in medieval England looking north, the event is behind, to the left, neither up nor down, and in the future. The event itself has not changed, the location of the observer has.

Oblique axes

An oblique coordinate system is one in which the axes are not necessarily orthogonal to each other; that is, they meet at angles other than right angles. When using coordinate transformations as described above, the new coordinate system will often appear to have oblique axes compared to the old system.

Nontensors

See also: Pseudotensor

A nontensor is a tensor-like quantity that behaves like a tensor in the raising and lowering of indices, but that does not transform like a tensor under a coordinate transformation. For example, Christoffel symbols cannot be tensors themselves if the coordinates don't change in a linear way.

In general relativity, one cannot describe the energy and momentum of the gravitational field by an energy–momentum tensor. Instead, one introduces objects that behave as tensors only with respect to restricted coordinate transformations. Strictly speaking, such objects are not tensors at all. A famous example of such a pseudotensor is the Landau–Lifshitz pseudotensor.

Curvilinear coordinates and curved spacetime

High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of space and time (blue lines) due to the Sun's mass. That is, the Sun's mass causes the regular grid coordinate system (in blue) to distort and have curvature. The radio wave then follows this curvature and moves toward the Sun.

Curvilinear coordinates are coordinates in which the angles between axes can change from point to point. This means that rather than having a grid of straight lines, the grid instead has curvature.

A good example of this is the surface of the Earth. While maps frequently portray north, south, east and west as a simple square grid, that is not in fact the case. Instead, the longitude lines running north and south are curved and meet at the north pole. This is because the Earth is not flat, but instead round.

In general relativity, energy and mass have curvature effects on the four dimensions of the universe (= spacetime). This curvature gives rise to the gravitational force. A common analogy is placing a heavy object on a stretched out rubber sheet, causing the sheet to bend downward. This curves the coordinate system around the object, much like an object in the universe curves the coordinate system it sits in. The mathematics here are conceptually more complex than on Earth, as it results in four dimensions of curved coordinates instead of three as used to describe a curved 2D surface.

Parallel transport

Main article: Parallel transport

Example: Parallel displacement along a circle of a three-dimensional ball embedded in two dimensions. The circle of radius r is embedded in a two-dimensional space characterized by the coordinates z¹ and z². The circle itself is characterized by coordinates y¹ and y² in the two-dimensional space. The circle itself is one-dimensional and can be characterized by its arc length x. The coordinate y is related to the coordinate x through the relation y¹ = r cos x/r and y² = r sin x/r. This gives ∂y¹/∂x = −sin x/r and ∂y²/∂x = cos x/r In this case the metric is a scalar and is given by g = cos² x/r + sin² x/r = 1. The interval is then ds² = g dx² = dx². The interval is just equal to the arc length as expected.

The interval in a high-dimensional space

In a Euclidean space, the separation between two points is measured by the distance between the two points. The distance is purely spatial, and is always positive. In spacetime, the separation between two events is measured by the invariant interval between the two events, which takes into account not only the spatial separation between the events, but also their separation in time. The interval, s², between two events is defined as:

${\displaystyle s^{2}=\Delta r^{2}-c^{2}\Delta t^{2}\,}$     (spacetime interval),

where c is the speed of light, and Δr and Δt denote differences of the space and time coordinates, respectively, between the events. The choice of signs for s² above follows the space-like convention (−+++). A notation like Δr² means (Δr)². The reason s² is called the interval and not s is that s² can be positive, zero or negative.

Spacetime intervals may be classified into three distinct types, based on whether the temporal separation (c²Δt²) or the spatial separation (Δr²) of the two events is greater: time-like, light-like or space-like.

Certain types of world lines are called geodesics of the spacetime – straight lines in the case of flat Minkowski spacetime and their closest equivalent in the curved spacetime of general relativity. In the case of purely time-like paths, geodesics are (locally) the paths of greatest separation (spacetime interval) as measured along the path between two events, whereas in Euclidean space and Riemannian manifolds, geodesics are paths of shortest distance between two points. The concept of geodesics becomes central in general relativity, since geodesic motion may be thought of as "pure motion" (inertial motion) in spacetime, that is, free from any external influences.

The covariant derivative

Main article: Covariant derivative

The covariant derivative is a generalization of the directional derivative from vector calculus. As with the directional derivative, the covariant derivative is a rule, which takes as its inputs: (1) a vector, u, (along which the derivative is taken) defined at a point P, and (2) a vector field, v, defined in a neighborhood of P. The output is a vector, also at the point P. The primary difference from the usual directional derivative is that the covariant derivative must, in a certain precise sense, be independent of the manner in which it is expressed in a coordinate system.

Parallel transport

Given the covariant derivative, one can define the parallel transport of a vector v at a point P along a curve γ starting at P. For each point x of γ, the parallel transport of v at x will be a function of x, and can be written as v(x), where v(0) = v. The function v is determined by the requirement that the covariant derivative of v(x) along γ is 0. This is similar to the fact that a constant function is one whose derivative is constantly 0.

Christoffel symbols

Main article: Christoffel symbol

The equation for the covariant derivative can be written in terms of Christoffel symbols. The Christoffel symbols find frequent use in Einstein's theory of general relativity, where spacetime is represented by a curved 4-dimensional Lorentz manifold with a Levi-Civita connection. The Einstein field equations – which determine the geometry of spacetime in the presence of matter – contain the Ricci tensor. Since the Ricci tensor is derived from the Riemann curvature tensor, which can be written in terms of Christoffel symbols, a calculation of the Christoffel symbols is essential. Once the geometry is determined, the paths of particles and light beams are calculated by solving the geodesic equations in which the Christoffel symbols explicitly appear.

Geodesics

Main article: Geodesics in general relativity

In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational force, is a particular type of geodesic. In other words, a freely moving or falling particle always moves along a geodesic.

In general relativity, gravity can be regarded as not a force but a consequence of a curved spacetime geometry where the source of curvature is the stress–energy tensor (representing matter, for instance). Thus, for example, the path of a planet orbiting around a star is the projection of a geodesic of the curved 4-dimensional spacetime geometry around the star onto 3-dimensional space.

A curve is a geodesic if the tangent vector of the curve at any point is equal to the parallel transport of the tangent vector of the base point.

Curvature tensor

Main article: Riemann curvature tensor

The Riemann curvature tensor tells us, mathematically, how much curvature there is in any given region of space. Contracting the tensor produces 2 more mathematical objects:

1. The Riemann curvature tensor: R^ρ_σμν, which gives the most information on the curvature of a space and is derived from derivatives of the metric tensor. In flat space this tensor is zero.
2. The Ricci tensor: R_σν, comes from the need in Einstein's theory for a curvature tensor with only 2 indices. It is obtained by averaging certain portions of the Riemann curvature tensor.
3. The scalar curvature: R, the simplest measure of curvature, assigns a single scalar value to each point in a space. It is obtained by averaging the Ricci tensor.

The Riemann curvature tensor can be expressed in terms of the covariant derivative.

The Einstein tensor G is a rank-2 tensor defined over pseudo-Riemannian manifolds. In index-free notation it is defined as

${\displaystyle \mathbf {G} =\mathbf {R} -{\tfrac {1}{2}}\mathbf {g} R,}$

where R is the Ricci tensor, g is the metric tensor and R is the scalar curvature. It is used in the Einstein field equations.

Stress–energy tensor

Main article: Stress–energy tensor

Contravariant components of the stress–energy tensor.

The stress–energy tensor (sometimes stress–energy–momentum tensor or energy–momentum tensor) is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields. The stress–energy tensor is the source of the gravitational field in the Einstein field equations of general relativity, just as mass density is the source of such a field in Newtonian gravity. Because this tensor has 2 indices (see next section) the Riemann curvature tensor has to be contracted into the Ricci tensor, also with 2 indices.

Einstein equation

Main article: Einstein field equations

The Einstein field equations (EFE) or Einstein's equations are a set of 10 equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy. First published by Einstein in 1915 as a tensor equation, the EFE equate local spacetime curvature (expressed by the Einstein tensor) with the local energy and momentum within that spacetime (expressed by the stress–energy tensor).

The Einstein Field Equations can be written as

${\displaystyle G_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu },}$

where G_μν is the Einstein tensor and T_μν is the stress–energy tensor.

This implies that the curvature of space (represented by the Einstein tensor) is directly connected to the presence of matter and energy (represented by the stress–energy tensor).

Schwarzschild solution and black holes

Main article: Schwarzschild metric

In Einstein's theory of general relativity, the Schwarzschild metric (also Schwarzschild vacuum or Schwarzschild solution), is a solution to the Einstein field equations which describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, the angular momentum of the mass, and the universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. The solution is named after Karl Schwarzschild, who first published the solution in 1916, just before his death.

According to Birkhoff's theorem, the Schwarzschild metric is the most general spherically symmetric, vacuum solution of the Einstein field equations. A Schwarzschild black hole or static black hole is a black hole that has no charge or angular momentum. A Schwarzschild black hole is described by the Schwarzschild metric, and cannot be distinguished from any other Schwarzschild black hole except by its mass.