Bell's theorem

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Bell's_theorem 

Bell's theorem is a term encompassing a number of closely-related results in physics, all of which determine that quantum mechanics is incompatible with local hidden-variable theories. The "local" in this case refers to the principle of locality, the idea that a particle can only be influenced by its immediate surroundings, and that interactions mediated by physical fields can only occur at speeds no greater than the speed of light. "Hidden variables" are hypothetical properties possessed by quantum particles, properties that are undetectable but still affect the outcome of experiments. In the words of physicist John Stewart Bell, for whom this family of results is named, "If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."

The term is broadly applied to a number of different derivations, the first of which was introduced by Bell in a 1964 paper titled "On the Einstein Podolsky Rosen Paradox". Bell's paper was a response to a 1935 thought experiment that Albert Einstein, Boris Podolsky and Nathan Rosen used to argue that quantum physics is an "incomplete" theory. By 1935, it was already recognized that the predictions of quantum physics are probabilistic. Einstein, Podolsky and Rosen presented a scenario that involves preparing a pair of particles such that the quantum state of the pair is entangled, and then separating the particles to an arbitrarily large distance. The experimenter has a choice of possible measurements that can be performed on one of the particles. When they choose a measurement and obtain a result, the quantum state of the other particle apparently collapses instantaneously into a new state depending upon that result, no matter how far away the other particle is. This suggests that either the measurement of the first particle somehow also interacted with the second particle at faster than the speed of light, or that the entangled particles had some unmeasured property which pre-determined their final quantum states before they were separated. Therefore, assuming locality, quantum mechanics must be incomplete, because it cannot give a complete description of the particle's true physical characteristics. In other words, quantum particles, like electrons and photons, must carry some property or attributes not included in quantum theory, and the uncertainties in quantum theory's predictions would then be due to ignorance or unknowability of these properties, later termed "hidden variables".

Bell carried the analysis of quantum entanglement much further. He deduced that if measurements are performed independently on the two separated particles of an entangled pair, then the assumption that the outcomes depend upon hidden variables within each half implies a mathematical constraint on how the outcomes on the two measurements are correlated. This constraint would later be named the Bell inequality. Bell then showed that quantum physics predicts correlations that violate this inequality. Consequently, the only way that hidden variables could explain the predictions of quantum physics is if they are "nonlocal", which is to say that somehow the two particles were able to interact instantaneously no matter how widely the two particles are separated.

Multiple variations on Bell's theorem were put forward in the following years, introducing other closely related conditions generally known as Bell (or "Bell-type") inequalities. The first rudimentary experiment designed to test Bell's theorem was performed in 1972 by John Clauser and Stuart Freedman; more advanced experiments, known collectively as Bell tests, have been performed many times since. Often, these experiments have had the goal of "closing loopholes", that is, ameliorating problems of experimental design or set-up that could in principle affect the validity of the findings of earlier Bell tests. To date, Bell tests have consistently found that physical systems obey quantum mechanics and violate Bell inequalities; which is to say that the results of these experiments are incompatible with any local hidden variable theory.

The exact nature of the assumptions required to prove a Bell-type constraint on correlations has been debated by physicists and by philosophers. While the significance of Bell's theorem is not in doubt, its full implications for the interpretation of quantum mechanics remain unresolved.

Theorem

There are many variations on the basic idea, some employing stronger mathematical assumptions than others. Significantly, Bell-type theorems do not refer to any particular theory of local hidden variables, but instead show that quantum physics violates general assumptions behind classical pictures of nature. The original theorem proved by Bell in 1964 is not the most amenable to experiment, and it is convenient to introduce the genre of Bell-type inequalities with a later example.

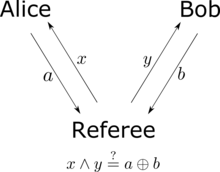
Alice and Bob stand in widely separated locations. Victor prepares a pair of particles and sends one to Alice and the other to Bob. When Alice receives her particle, she chooses to perform one of two possible measurements (perhaps by flipping a coin to decide which). Denote these measurements by ${\displaystyle A_{0}}$ and ${\displaystyle A_{1}}$. Both ${\displaystyle A_{0}}$ and ${\displaystyle A_{1}}$ are binary measurements: the result of ${\displaystyle A_{0}}$ is either ${\displaystyle +1}$ or ${\displaystyle -1}$, and likewise for ${\displaystyle A_{1}}$. When Bob receives his particle, he chooses one of two measurements, ${\displaystyle B_{0}}$ and ${\displaystyle B_{1}}$, which are also both binary.

Suppose that each measurement reveals a property that the particle already possessed. For instance, if Alice chooses to measure ${\displaystyle A_{0}}$ and obtains the result ${\displaystyle +1}$, then the particle she received carried a value of ${\displaystyle +1}$ for a property ${\displaystyle a_{0}}$. Consider the following combination:

$${\displaystyle a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}=(a_{0}+a_{1})b_{0}+(a_{0}-a_{1})b_{1}\,.}$$

Because both ${\displaystyle a_{0}}$ and ${\displaystyle a_{1}}$ take the values ${\displaystyle \pm 1}$, then either ${\displaystyle a_{0}=a_{1}}$ or ${\displaystyle a_{0}=-a_{1}}$. In the former case, ${\displaystyle (a_{0}-a_{1})b_{1}=0}$, while in the latter case, ${\displaystyle (a_{0}+a_{1})b_{0}=0}$. So, one of the terms on the right-hand side of the above expression will vanish, and the other will equal ${\displaystyle \pm 2}$. Consequently, if the experiment is repeated over many trials, with Victor preparing new pairs of particles, the average value of the combination ${\displaystyle a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}}$ across all the trials will be less than or equal to 2. No single trial can measure this quantity, because Alice and Bob can only choose one measurement each, but on the assumption that the underlying properties exist, the average value of the sum is just the sum of the averages for each term. Using angle brackets to denote averages,

$${\displaystyle \langle A_{0}B_{0}\rangle +\langle A_{0}B_{1}\rangle +\langle A_{1}B_{0}\rangle -\langle A_{1}B_{1}\rangle \leq 2\,.}$$

This is a Bell inequality, specifically, the CHSH inequality. Its derivation here depends upon two assumptions: first, that the underlying physical properties ${\displaystyle a_{0},a_{1},b_{0},}$ and ${\displaystyle b_{1}}$ exist independently of being observed or measured (sometimes called the assumption of realism); and second, that Alice's choice of action cannot influence Bob's result or vice versa (often called the assumption of locality).

Quantum mechanics can violate the CHSH inequality, as follows. Victor prepares a pair of qubits which he describes by the Bell state

$${\displaystyle |\psi \rangle ={\frac {|01\rangle -|10\rangle }{\sqrt {2}}}.}$$

Victor then passes the first qubit to Alice and the second to Bob. Alice and Bob's choices of possible measurements are defined by the Pauli matrices. Alice measures either of the two observables ${\displaystyle \sigma _{z}}$ and ${\displaystyle \sigma _{x}}$:

$${\displaystyle A_{0}=\sigma _{z}={\begin{pmatrix}1&0\\0&-1\end{pmatrix}},\ A_{1}=\sigma _{x}={\begin{pmatrix}0&1\\1&0\end{pmatrix}};}$$

and Bob measures either of the two observables

$${\displaystyle B_{0}=-{\frac {\sigma _{x}+\sigma _{z}}{\sqrt {2}}},\ B_{1}={\frac {\sigma _{x}-\sigma _{z}}{\sqrt {2}}}.}$$

Victor can calculate the quantum expectation values for pairs of these observables using the Born rule:

$${\displaystyle \langle A_{0}\otimes B_{0}\rangle ={\frac {1}{\sqrt {2}}},\langle A_{0}\otimes B_{1}\rangle ={\frac {1}{\sqrt {2}}},\langle A_{1}\otimes B_{0}\rangle ={\frac {1}{\sqrt {2}}},\langle A_{1}\otimes B_{1}\rangle =-{\frac {1}{\sqrt {2}}}\,.}$$

While only one of these four measurements can be made in a single trial of the experiment, the sum

$${\displaystyle \langle A_{0}\otimes B_{0}\rangle +\langle A_{0}\otimes B_{1}\rangle +\langle A_{1}\otimes B_{0}\rangle -\langle A_{1}\otimes B_{1}\rangle =2{\sqrt {2}}}$$

gives the sum of the average values that Victor expects to find across multiple trials. This value exceeds the classical upper bound of 2 that was deduced from the hypothesis of local hidden variables. The value ${\displaystyle 2{\sqrt {2}}}$ is in fact the largest that quantum physics permits for this combination of expectation values, making it a Tsirelson bound.

An illustration of the CHSH game: the referee, Victor, sends a bit each to Alice and to Bob, and Alice and Bob each send a bit back to the referee.

The CHSH inequality can also be thought of as a game in which Alice and Bob try to coordinate their actions. Victor prepares two bits, ${\displaystyle x}$ and ${\displaystyle y}$, independently and at random. He sends bit ${\displaystyle x}$ to Alice and bit ${\displaystyle y}$ to Bob. Alice and Bob win if they return answer bits ${\displaystyle a}$ and ${\displaystyle b}$ to Victor, satisfying

$${\displaystyle xy=a+b\mod 2\,.}$$

Or, equivalently, Alice and Bob win if the logical AND of ${\displaystyle x}$ and ${\displaystyle y}$ is the logical XOR of ${\displaystyle a}$ and ${\displaystyle b}$. Alice and Bob can agree upon any strategy they desire before the game, but they cannot communicate once the game begins. In any theory based on local hidden variables, Alice and Bob's probability of winning is no greater than ${\displaystyle 3/4}$, regardless of what strategy they agree upon beforehand. However, if they share an entangled quantum state, their probability of winning can be as large as

$${\displaystyle {\frac {2+{\sqrt {2}}}{4}}\approx 0.85\,.}$$

Variations and related results

Bell (1964)

Bell's 1964 paper points out that under restricted conditions, local hidden variable models can reproduce the predictions of quantum mechanics. He then demonstrates that this cannot hold true in general. Bell considers a refinement by David Bohm of the Einstein–Podolsky–Rosen (EPR) thought experiment. In this scenario, a pair of particles are formed together in such a way that they are described by a spin singlet state (which is an example of an entangled state). The particles then move apart in opposite directions. Each particle is measured by a Stern–Gerlach device, a measuring instrument that can be oriented in different directions and that reports one of two possible outcomes, representable by ${\displaystyle +1}$ and ${\displaystyle -1}$. The configuration of each measuring instrument is represented by a unit vector, and the quantum-mechanical prediction for the correlation between two detectors with settings ${\displaystyle {\vec {a}}}$ and ${\displaystyle {\vec {b}}}$ is

$${\displaystyle P({\vec {a}},{\vec {b}})=-{\vec {a}}\cdot {\vec {b}}\,.}$$

In particular, if the orientation of the two detectors is the same (${\displaystyle {\vec {a}}={\vec {b}}}$), then the outcome of one measurement is certain to be the negative of the outcome of the other, giving ${\displaystyle P({\vec {a}},{\vec {a}})=-1}$. And if the orientations of the two detectors are orthogonal (${\displaystyle {\vec {a}}\cdot {\vec {b}}=0}$), then the outcomes are uncorrelated, and ${\displaystyle P({\vec {a}},{\vec {b}})=0}$. Bell proves by example that these special cases can be explained in terms of hidden variables, then proceeds to show that the full range of possibilities involving intermediate angles cannot.

Bell posited that a local hidden variable model for these correlations would explain them in terms of an integral over the possible values of some hidden parameter ${\displaystyle \lambda }$:

$${\displaystyle P({\vec {a}},{\vec {b}})=\int d\lambda \,\rho (\lambda )A({\vec {a}},\lambda )B({\vec {b}},\lambda )\,,}$$

where ${\displaystyle \rho (\lambda )}$ is a probability density function. The two functions ${\displaystyle A({\vec {a}},\lambda )}$ and ${\displaystyle B({\vec {b}},\lambda )}$ provide the responses of the two detectors given the orientation vectors and the hidden variable:

$${\displaystyle A({\vec {a}},\lambda )=\pm 1,\,B({\vec {b}},\lambda )=\pm 1\,.}$$

Crucially, the outcome of detector ${\displaystyle A}$ does not depend upon ${\displaystyle {\vec {b}}}$, and likewise the outcome of ${\displaystyle B}$ does not depend upon ${\displaystyle {\vec {a}}}$, because the two detectors are physically separated. Now we suppose that the experimenter has a choice of settings for the second detector: it can be set either to ${\displaystyle {\vec {b}}}$ or to ${\displaystyle {\vec {c}}}$. Bell proves that the difference in correlation between these two choices of detector setting must satisfy the inequality

$${\displaystyle |P({\vec {a}},{\vec {b}})-P({\vec {a}},{\vec {c}})|\leq 1+P({\vec {b}},{\vec {c}})\,.}$$

However, it is easy to find situations where quantum mechanics violates the Bell inequality. For example, let the vectors ${\displaystyle {\vec {a}}}$ and ${\displaystyle {\vec {b}}}$ be orthogonal, and let ${\displaystyle {\vec {c}}}$ lie in their plane at a 45° angle from both of them. Then

$${\displaystyle P({\vec {a}},{\vec {b}})=0\,,}$$

while

$${\displaystyle P({\vec {a}},{\vec {c}})=P({\vec {b}},{\vec {c}})=-{\frac {\sqrt {2}}{2}}\,,}$$

but

$${\displaystyle {\frac {\sqrt {2}}{2}}\nleq 1-{\frac {\sqrt {2}}{2}}\,.}$$

Therefore, there is no local hidden variable model that can reproduce the predictions of quantum mechanics for all choices of ${\displaystyle {\vec {a}}}$, ${\displaystyle {\vec {b}}}$, and ${\displaystyle {\vec {c}}}$. Experimental results contradict the classical curves and match the curve predicted by quantum mechanics as long as experimental shortcomings are accounted for.

Bell's 1964 theorem requires the possibility of perfect anti-correlations: the ability to make a probability-1 prediction about the result from the second detector, knowing the result from the first. This is related to the "EPR criterion of reality", a concept introduced in the 1935 paper by Einstein, Podolsky, and Rosen. This paper posits, "If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of reality corresponding to that quantity."

GHZ–Mermin

Main article: GHZ experiment

Greenberger, Horne, and Zeilinger presented a four-particle thought experiment, which Mermin then simplified to use only three particles. In this thought experiment, Victor generates a set of three spin-1/2 particles described by the quantum state

$${\displaystyle |\psi \rangle ={\frac {1}{\sqrt {2}}}(|000\rangle -|111\rangle )\,,}$$

where as above, ${\displaystyle |0\rangle }$ and ${\displaystyle |1\rangle }$ are the eigenvectors of the Pauli matrix ${\displaystyle \sigma _{z}}$. Victor then sends a particle each to Alice, Bob, and Charlie, who wait at widely-separated locations. Alice measures either ${\displaystyle \sigma _{x}}$ or ${\displaystyle \sigma _{y}}$ on her particle, and so do Bob and Charlie. The result of each measurement is either ${\displaystyle +1}$ or ${\displaystyle -1}$. Applying the Born rule to the three-qubit state ${\displaystyle |\psi \rangle }$, Victor predicts that whenever the three measurements include one ${\displaystyle \sigma _{x}}$ and two ${\displaystyle \sigma _{y}}$'s, the product of the outcomes will always be ${\displaystyle +1}$. This follows because ${\displaystyle |\psi \rangle }$ is an eigenvector of ${\displaystyle \sigma _{x}\otimes \sigma _{y}\otimes \sigma _{y}}$ with eigenvalue ${\displaystyle +1}$, and likewise for ${\displaystyle \sigma _{y}\otimes \sigma _{x}\otimes \sigma _{y}}$ and ${\displaystyle \sigma _{y}\otimes \sigma _{y}\otimes \sigma _{x}}$. Therefore, knowing Alice's result for a ${\displaystyle \sigma _{x}}$ measurement and Bob's result for a ${\displaystyle \sigma _{y}}$ measurement, Victor can predict with probability 1 what result Charlie will return for a ${\displaystyle \sigma _{y}}$ measurement. According to the EPR criterion of reality, there would be an "element of reality" corresponding to the outcome of a ${\displaystyle \sigma _{y}}$ measurement upon Charlie's qubit. Indeed, this same logic applies to both measurements and all three qubits. Per the EPR criterion of reality, then, each particle contains an "instruction set" that determines the outcome of a ${\displaystyle \sigma _{x}}$ or ${\displaystyle \sigma _{y}}$ measurement upon it. The set of all three particles would then be described by the instruction set

$${\displaystyle (a_{x},a_{y},b_{x},b_{y},c_{x},c_{y})\,,}$$

with each entry being either ${\displaystyle -1}$ or ${\displaystyle +1}$, and each ${\displaystyle \sigma _{x}}$ or ${\displaystyle \sigma _{y}}$ measurement simply returning the appropriate value.

If Alice, Bob, and Charlie all perform the ${\displaystyle \sigma _{x}}$ measurement, then the product of their results would be ${\displaystyle a_{x}b_{x}c_{x}}$. This value can be deduced from

$${\displaystyle (a_{x}b_{y}c_{y})(a_{y}b_{x}c_{y})(a_{y}b_{y}c_{x})=a_{x}b_{x}c_{x}a_{y}^{2}b_{y}^{2}c_{y}^{2}=a_{x}b_{x}c_{x}\,,}$$

because the square of either ${\displaystyle -1}$ or ${\displaystyle +1}$ is ${\displaystyle 1}$. Each factor in parentheses equals ${\displaystyle +1}$, so

$${\displaystyle a_{x}b_{x}c_{x}=+1\,,}$$

and the product of Alice, Bob, and Charlie's results will be ${\displaystyle +1}$ with probability unity. But this is inconsistent with quantum physics: Victor can predict using the state ${\displaystyle |\psi \rangle }$ that the measurement ${\displaystyle \sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x}}$ will instead yield ${\displaystyle -1}$ with probability unity.

This thought experiment can also be recast as a traditional Bell inequality or, equivalently, as a nonlocal game in the same spirit as the CHSH game. In it, Alice, Bob, and Charlie receive bits ${\displaystyle x,y,z}$ from Victor, promised to always have an even number of ones, that is, ${\displaystyle x\oplus y\oplus z=0}$, and send him back bits ${\displaystyle a,b,c}$. They win the game if ${\displaystyle a,b,c}$ have an odd number of ones for all inputs except ${\displaystyle x=y=z=0}$, when they need to have an even number of ones. That is, they win the game iff ${\displaystyle a\oplus b\oplus c=x\lor y\lor z}$. With local hidden variables the highest probability of victory they can have is 3/4, whereas using the quantum strategy above they win it with certainty. This is an example of quantum pseudo-telepathy.

Kochen–Specker theorem

Main article: Kochen–Specker theorem

In quantum theory, orthonormal bases for a Hilbert space represent measurements than can be performed upon a system having that Hilbert space. Each vector in a basis represents a possible outcome of that measurement. Suppose that a hidden variable ${\displaystyle \lambda }$ exists, so that knowing the value of ${\displaystyle \lambda }$ would imply certainty about the outcome of any measurement. Given a value of ${\displaystyle \lambda }$, each measurement outcome — that is, each vector in the Hilbert space — is either impossible or guaranteed. A Kochen–Specker configuration is a finite set of vectors made of multiple interlocking bases, with the property that a vector in it will always be impossible when considered as belonging to one basis and guaranteed when taken as belonging to another. In other words, a Kochen–Specker configuration is an "uncolorable set" that demonstrates the inconsistency of assuming a hidden variable ${\displaystyle \lambda }$ can be controlling the measurement outcomes.

Free will theorem

Main article: Free will theorem

The Kochen–Specker type of argument, using configurations of interlocking bases, can be combined with the idea of measuring entangled pairs that underlies Bell-type inequalities. This was noted beginning in the 1970s by Kochen, Heywood and Redhead, Stairs, and Brown and Svetlichny. As EPR pointed out, obtaining a measurement outcome on one half of an entangled pair implies certainty about the outcome of a corresponding measurement on the other half. The "EPR criterion of reality" posits that because the second half of the pair was not disturbed, that certainty must be due to a physical property belonging to it. In other words, by this criterion, a hidden variable ${\displaystyle \lambda }$ must exist within the second, as-yet unmeasured half of the pair. No contradiction arises if only one measurement on the first half is considered. However, if the observer has a choice of multiple possible measurements, and the vectors defining those measurements form a Kochen–Specker configuration, then some outcome on the second half will be simultaneously impossible and guaranteed.

This type of argument gained attention when an instance of it was advanced by John Conway and Simon Kochen under the name of the free will theorem. The Conway–Kochen theorem uses a pair of entangled qutrits and a Kochen–Specker configuration discovered by Asher Peres.

Quasiclassical entanglement

Main articles: Spekkens toy model and Werner state

As Bell pointed out, some predictions of quantum mechanics can be replicated in local hidden variable models, including special cases of correlations produced from entanglement. This topic has been studied systematically in the years since Bell's theorem. In 1989, Reinhard Werner introduced what are now called Werner states, joint quantum states for a pair of systems that yield EPR-type correlations but also admit a hidden-variable model. Werner states are bipartite quantum states that are invariant under unitaries of symmetric tensor-product form:

$${\displaystyle \rho _{AB}=(U\otimes U)\rho _{AB}(U^{\dagger }\otimes U^{\dagger })\,.}$$

More recently, Robert Spekkens introduced a toy model that starts with the premise of local, discretized degrees of freedom and then imposes a "knowledge balance principle" that restricts how much an observer can know about those degrees of freedom, thereby making them into hidden variables. The allowed states of knowledge ("epistemic states") about the underlying variables ("ontic states") mimic some features of quantum states. Correlations in the toy model can emulate some aspects of entanglement, like monogamy, but by construction, the toy model can never violate a Bell inequality.

History

Background

Main articles: EPR paradox and History of quantum mechanics

The question of whether quantum mechanics can be "completed" by hidden variables dates to the early years of quantum theory. In his 1932 textbook on quantum mechanics, the Hungarian-born polymath John von Neumann presented what he claimed to be a proof that there could be no "hidden parameters". The validity and definitiveness of von Neumann's proof were questioned by Hans Reichenbach, in more detail by Grete Hermann, and possibly in conversation though not in print by Albert Einstein. (Simon Kochen and Ernst Specker rejected von Neumann's key assumption as early as 1961, but did not publish a criticism of it until 1967.)

Einstein argued persistently that quantum mechanics could not be a complete theory. His preferred argument relied on a principle of locality:

Consider a mechanical system constituted of two partial systems A and B which have interaction with each other only during limited time. Let the ψ function before their interaction be given. Then the Schrödinger equation will furnish the ψ function after their interaction has taken place. Let us now determine the physical condition of the partial system A as completely as possible by measurements. Then the quantum mechanics allows us to determine the ψ function of the partial system B from the measurements made, and from the ψ function of the total system. This determination, however, gives a result which depends upon which of the determining magnitudes specifying the condition of A has been measured (for instance coordinates or momenta). Since there can be only one physical condition of B after the interaction and which can reasonably not be considered as dependent on the particular measurement we perform on the system A separated from B it may be concluded that the ψ function is not unambiguously coordinated with the physical condition. This coordination of several ψ functions with the same physical condition of system B shows again that the ψ function cannot be interpreted as a (complete) description of a physical condition of a unit system.

The EPR thought experiment is similar, also considering two separated systems A and B described by a joint wave function. However, the EPR paper adds the idea later known as the EPR criterion of reality, according to which the ability to predict with probability 1 the outcome of a measurement upon B implies the existence of an "element of reality" within B.

In 1951, David Bohm proposed a variant of the EPR thought experiment in which the measurements have discrete ranges of possible outcomes, unlike the position and momentum measurements considered by EPR. The year before, Chien-Shiung Wu and Irving Shaknov had successfully measured polarizations of photons produced in entangled pairs, thereby making the Bohm version of the EPR thought experiment practically feasible.

By the late 1940s, the mathematician George Mackey had grown interested in the foundations of quantum physics, and in 1957 he drew up a list of postulates that he took to be a precise definition of quantum mechanics. Mackey conjectured that one of the postulates was redundant, and shortly thereafter, Andrew M. Gleason proved that it was indeed deducible from the other postulates. Gleason's theorem provided an argument that a broad class of hidden-variable theories are incompatible with quantum mechanics. More specifically, Gleason's theorem rules out hidden-variable models that are "noncontextual". Any hidden-variable model for quantum mechanics must, in order to avoid the implications of Gleason's theorem, involve hidden variables that are not properties belonging to the measured system alone but also dependent upon the external context in which the measurement is made. This type of dependence is often seen as contrived or undesirable; in some settings, it is inconsistent with special relativity. The Kochen–Specker theorem refines this statement by constructing a specific finite subset of rays on which no such probability measure can be defined.

Tsung-Dao Lee came close to deriving Bell's theorem in 1960. He considered events where two kaons were produced traveling in opposite directions, and came to the conclusion that hidden variables could not explain the correlations that could be obtained in such situations. However, complications arose due to the fact that kaons decay, and he did not go so far as to deduce a Bell-type inequality.

Bell's publications

Bell chose to publish his theorem in a comparatively obscure journal because it did not require page charges, and at the time it in fact paid the authors who published there. Because the journal did not provide free reprints of articles for the authors to distribute, however, Bell had to spend the money he received to buy copies that he could send to other physicists. While the articles printed in the journal themselves listed the publication's name simply as Physics, the covers carried the trilingual version Physics Physique Физика to reflect that it would print articles in English, French and Russian.

Prior to proving his 1964 result, Bell also proved a result equivalent to the Kochen–Specker theorem (hence why the latter is sometimes also known as the Bell–Kochen–Specker or Bell–KS theorem). However, publication of this theorem was inadvertently delayed until 1966. In that paper, Bell argued that because an explanation of quantum phenomena in terms of hidden variables would require nonlocality, the EPR paradox "is resolved in the way which Einstein would have liked least".

Experiments

Scheme of a "two-channel" Bell test
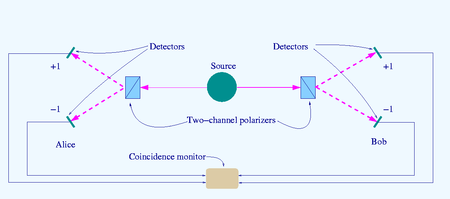
The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a two-channel polariser whose orientation (a or b) can be set by the experimenter. Emerging signals from each channel are detected and coincidences of four types (++, −−, +− and −+) counted by the coincidence monitor.

 

Main article: Bell test

In 1967, the unusual title Physics Physique Физика caught the attention of John Clauser, who then discovered Bell's paper and began to consider how to perform a Bell test in the laboratory. Clauser and Stuart Freedman would go on to perform a Bell test in 1972. This was only a limited test, because the choice of detector settings was made before the photons had left the source. In 1982, Alain Aspect and collaborators performed the first Bell test to remove this limitation. This began a trend of progressively more stringent Bell tests. The GHZ thought experiment was implemented in practice, using entangled triplets of photons, in 2000. By 2002, testing the CHSH inequality was feasible in undergraduate laboratory courses.

In Bell tests, there may be problems of experimental design or set-up that affect the validity of the experimental findings. These problems are often referred to as "loopholes". The purpose of the experiment is to test whether nature can be described by local hidden-variable theory, which would contradict the predictions of quantum mechanics.

The most prevalent loopholes in real experiments are the detection and locality loopholes. The detection loophole is opened when a small fraction of the particles (usually photons) are detected in the experiment, making it possible to explain the data with local hidden variables by assuming that the detected particles are an unrepresentative sample. The locality loophole is opened when the detections are not done with a spacelike separation, making it possible for the result of one measurement to influence the other without contradicting relativity. In some experiments there may be additional defects that make local-hidden-variable explanations of Bell test violations possible.

Although both the locality and detection loopholes had been closed in different experiments, a long-standing challenge was to close both simultaneously in the same experiment. This was finally achieved in three experiments in 2015. Regarding these results, Alain Aspect writes that "... no experiment ... can be said to be totally loophole-free," but he says the experiments "remove the last doubts that we should renounce" local hidden variables, and refers to examples of remaining loopholes as being "far fetched" and "foreign to the usual way of reasoning in physics."

Interpretations of Bell's theorem

The Copenhagen Interpretation

The Copenhagen interpretation is a collection of views about the meaning of quantum mechanics principally attributed to Niels Bohr and Werner Heisenberg. It is one of the oldest of numerous proposed interpretations of quantum mechanics, as features of it date to the development of quantum mechanics during 1925–1927, and it remains one of the most commonly taught. There is no definitive historical statement of what is the Copenhagen interpretation. In particular, there were fundamental disagreements between the views of Bohr and Heisenberg. Some basic principles generally accepted as part of the Copenhagen collection include the idea that quantum mechanics is intrinsically indeterministic, with probabilities calculated using the Born rule, and the complementarity principle: certain properties cannot be jointly defined for the same system at the same time. In order to talk about a specific property of a system, that system must be considered within the context of a specific laboratory arrangement. Observable quantities corresponding to mutually exclusive laboratory arrangements cannot be predicted together, but considering multiple such mutually exclusive experiments is necessary to characterize a system. Bohr himself used complementarity to argue that the EPR "paradox" was fallacious. Because measurements of position and of momentum are complementary, making the choice to measure one excludes the possibility of measuring the other. Consequently, he argued, a fact deduced regarding one arrangement of laboratory apparatus could not be combined with a fact deduced by means of the other, and so, the inference of predetermined position and momentum values for the second particle was not valid. Bohr concluded that EPR's "arguments do not justify their conclusion that the quantum description turns out to be essentially incomplete."

Copenhagen-type interpretations generally take the violation of Bell inequalities as grounds to reject the assumption often called counterfactual definiteness or "realism", which is not necessarily the same as abandoning realism in a broader philosophical sense. For example, Roland Omnès argues for the rejection of hidden variables and concludes that "quantum mechanics is probably as realistic as any theory of its scope and maturity ever will be." This is also the route taken by interpretations that descend from the Copenhagen tradition, such as consistent histories (often advertised as "Copenhagen done right"), as well as QBism.

Many-worlds interpretation of quantum mechanics

The Many-Worlds interpretation, also known as the Everett interpretation, is local and deterministic, as it consists of the unitary part of quantum mechanics without collapse. It can generate correlations that violate a Bell inequality because it violates an implicit assumption by Bell that measurements have a single outcome. In fact, Bell's theorem can be proven in the Many-Worlds framework from the assumption that a measurement has a single outcome. Therefore a violation of a Bell inequality can be interpreted as a demonstration that measurements have multiple outcomes.

The explanation it provides for the Bell correlations is that when Alice and Bob make their measurements, they split into local branches. From the point of view of each copy of Alice, there are multiple copies of Bob experiencing different results, so Bob cannot have a definite result, and the same is true from the point of view of each copy of Bob. They will obtain a mutually well-defined result only when their future light cones overlap. At this point we can say that the Bell correlation starts existing, but it was produced by a purely local mechanism. Therefore the violation of a Bell inequality cannot be interpreted as a proof of non-locality.

Non-local hidden variables

Most advocates of the hidden-variables idea believe that experiments have ruled out local hidden variables. They are ready to give up locality, explaining the violation of Bell's inequality by means of a non-local hidden variable theory, in which the particles exchange information about their states. This is the basis of the Bohm interpretation of quantum mechanics, which requires that all particles in the universe be able to instantaneously exchange information with all others. A 2007 experiment ruled out a large class of non-Bohmian non-local hidden variable theories, though not Bohmian mechanics itself.

The transactional interpretation, which postulates waves traveling both backwards and forwards in time, is likewise non-local.

Superdeterminism

Main article: Superdeterminism

A necessary assumption to derive Bell's theorem is that the hidden variables are not correlated with the measurement settings. This assumption has been justified on the grounds that the experimenter has "free will" to choose the settings, and that it is necessary to do science in the first place. A (hypothetical) theory where the choice of measurement is determined by the system being measured is known as superdeterministic.

A few advocates of deterministic models have not given up on local hidden variables. For example, Gerard 't Hooft has argued that superdeterminism cannot be dismissed.