Gaussian beam

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Gaussian_beam

Instantaneous absolute value of the real part of electric field amplitude of a TEM₀₀ gaussian beam, focal region. Showing ${\displaystyle |\mathcal{R}\mathcal{e}(E(t_1))|}$ thus with two peaks for each positive wavefront.

Top: transverse intensity profile of a Gaussian beam that is propagating out of the page. Blue curve: electric (or magnetic) field amplitude vs. radial position from the beam axis. The black curve is the corresponding intensity.

A 5 mW green laser pointer beam profile, showing the TEM₀₀ profile. Note the speckle pattern seen as granular noise here.

In optics, a Gaussian beam is a beam of electromagnetic radiation with high monochromaticity whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or TEM₀₀) transverse Gaussian mode describes the intended output of most (but not all) lasers, as such a beam can be focused into the most concentrated spot. When such a beam is refocused by a lens, the transverse phase dependence is altered; this results in a different Gaussian beam. The electric and magnetic field amplitude profiles along any such circular Gaussian beam (for a given wavelength and polarization) are determined by a single parameter: the so-called waist w₀. At any position z relative to the waist (focus) along a beam having a specified w₀, the field amplitudes and phases are thereby determined as detailed below.

The equations below assume a beam with a circular cross-section at all values of z; this can be seen by noting that a single transverse dimension, r, appears. Beams with elliptical cross-sections, or with waists at different positions in z for the two transverse dimensions (astigmatic beams) can also be described as Gaussian beams, but with distinct values of w₀ and of the z = 0 location for the two transverse dimensions x and y.

Arbitrary solutions of the paraxial Helmholtz equation can be expressed as combinations of Hermite–Gaussian modes (whose amplitude profiles are separable in x and y using Cartesian coordinates), Laguerre–Gaussian modes (whose amplitude profiles are separable in r and θ using cylindrical coordinates) or similarly as combinations of Ince–Gaussian modes (whose amplitude profiles are separable in ξ and η using elliptical coordinates). At any point along the beam z these modes include the same Gaussian factor as the fundamental Gaussian mode multiplying the additional geometrical factors for the specified mode. However different modes propagate with a different Gouy phase which is why the net transverse profile due to a superposition of modes evolves in z, whereas the propagation of any single Hermite–Gaussian (or Laguerre–Gaussian) mode retains the same form along a beam.

Although there are other possible modal decompositions, these families of solutions are the most useful for problems involving compact beams, that is, where the optical power is rather closely confined along an axis. Even when a laser is not operating in the fundamental Gaussian mode, its power will generally be found among the lowest-order modes using these decompositions, as the spatial extent of higher order modes will tend to exceed the bounds of a laser's resonator (cavity). "Gaussian beam" normally implies radiation confined to the fundamental (TEM₀₀) Gaussian mode.

Mathematical form

Gaussian beam intensity profile with w₀ = 2λ.

The Gaussian beam is a transverse electromagnetic (TEM) mode. The mathematical expression for the electric field amplitude is a solution to the paraxial Helmholtz equation. Assuming polarization in the x direction and propagation in the +z direction, the electric field in phasor (complex) notation is given by:

$${\displaystyle \mathbf{E}(r,z)=E_0\hat{\mathbf{x}}\frac{w_0}{w(z)}\exp \left(\frac{-r^2}{w(z{)}^2}\right)\exp \left(-i\left(kz+k\frac{r^2}{2R(z)}-\psi (z)\right)\right)}$$

where

• r is the radial distance from the center axis of the beam,
• z is the axial distance from the beam's focus (or "waist"),
• i is the imaginary unit,
• k = 2πn/λ is the wave number (in radians per meter) for a free-space wavelength λ, and n is the index of refraction of the medium in which the beam propagates,
• E₀ = E(0, 0), the electric field amplitude (and phase) at the origin (r = 0, z = 0),
• w(z) is the radius at which the field amplitudes fall to 1/e of their axial values (i.e., where the intensity values fall to 1/e² of their axial values), at the plane z along the beam,
• w₀ = w(0) is the waist radius,
• R(z) is the radius of curvature of the beam's wavefronts at z, and
• ψ(z) is the Gouy phase at z, an extra phase term beyond that attributable to the phase velocity of light.

The physical electric field is obtained from the phasor field amplitude given above by taking the real part of the amplitude times a time factor:

$${\displaystyle {\mathbf{E}}_{\text{phys}}(r,z,t)=\mathrm{Re}(\mathbf{E}(r,z)\cdot e^{i\omega t}),}$$

where $\omega$ is the angular frequency of the light and t is time. The time factor involves an arbitrary sign convention, as discussed at Mathematical descriptions of opacity § Complex conjugate ambiguity.

Since this solution relies on the paraxial approximation, it is not accurate for very strongly diverging beams. The above form is valid in most practical cases, where w₀ ≫ λ/n.

The corresponding intensity (or irradiance) distribution is given by

$${\displaystyle I(r,z)=\frac{|E(r,z){|}^2}{2\eta }=I_0{\left(\frac{w_0}{w(z)}\right)}^2\exp \left(\frac{-2r^2}{w(z{)}^2}\right),}$$

where the constant η is the wave impedance of the medium in which the beam is propagating. For free space, η = η₀ ≈ 377 Ω. I₀ = |E₀|²/2η is the intensity at the center of the beam at its waist.

If P₀ is the total power of the beam,

$${\displaystyle I_0=\frac{2P_0}{\pi w_0^2}.}$$

Evolving beam width

The Gaussian function has a 1/e² diameter (2w as used in the text) about 1.7 times the FWHM.

At a position z along the beam (measured from the focus), the spot size parameter w is given by a hyperbolic relation:

$${\displaystyle w(z)=w_0\sqrt{1+{\left(\frac{z}{z_{\mathrm{R}}}\right)}^2},}$$

where

$${\displaystyle z_{\mathrm{R}}=\frac{\pi w_0^{2}n}{\lambda }}$$

is called the Rayleigh range as further discussed below, and ${\displaystyle n}$ is the refractive index of the medium.

The radius of the beam w(z), at any position z along the beam, is related to the full width at half maximum (FWHM) of the intensity distribution at that position according to:

$${\displaystyle w(z)=\frac{\text{FWHM}(z)}{\sqrt{2\ln 2}}.}$$

Wavefront curvature

The curvature of the wavefronts is largest at the Rayleigh distance, z = ±z_R, on either side of the waist, crossing zero at the waist itself. Beyond the Rayleigh distance, |z| > z_R, it again decreases in magnitude, approaching zero as z → ±∞. The curvature is often expressed in terms of its reciprocal, R, the radius of curvature; for a fundamental Gaussian beam the curvature at position z is given by:

$${\displaystyle \frac{1}{R(z)}=\frac{z}{z^2+z_{\mathrm{R}}^2},}$$

so the radius of curvature R(z) is 

$${\displaystyle R(z)=z\left[1+{\left(\frac{z_{\mathrm{R}}}{z}\right)}^2\right].}$$

Being the reciprocal of the curvature, the radius of curvature reverses sign and is infinite at the beam waist where the curvature goes through zero.

Gouy phase

The Gouy phase is a phase shift gradually acquired by a beam around the focal region. At position z the Gouy phase of a fundamental Gaussian beam is given by

$${\displaystyle \psi (z)=\arctan \left(\frac{z}{z_{\mathrm{R}}}\right).}$$

Gouy phase.

The Gouy phase results in an increase in the apparent wavelength near the waist (z ≈ 0). Thus the phase velocity in that region formally exceeds the speed of light. That paradoxical behavior must be understood as a near-field phenomenon where the departure from the phase velocity of light (as would apply exactly to a plane wave) is very small except in the case of a beam with large numerical aperture, in which case the wavefronts' curvature (see previous section) changes substantially over the distance of a single wavelength. In all cases the wave equation is satisfied at every position.

The sign of the Gouy phase depends on the sign convention chosen for the electric field phasor. With e^iωt dependence, the Gouy phase changes from -π/2 to +π/2, while with e^-iωt dependence it changes from +π/2 to -π/2 along the axis.

For a fundamental Gaussian beam, the Gouy phase results in a net phase discrepancy with respect to the speed of light amounting to π radians (thus a phase reversal) as one moves from the far field on one side of the waist to the far field on the other side. This phase variation is not observable in most experiments. It is, however, of theoretical importance and takes on a greater range for higher-order Gaussian modes.

Elliptical and astigmatic beams

Many laser beams have an elliptical cross-section. Also common are beams with waist positions which are different for the two transverse dimensions, called astigmatic beams. These beams can be dealt with using the above two evolution equations, but with distinct values of each parameter for x and y and distinct definitions of the z = 0 point. The Gouy phase is a single value calculated correctly by summing the contribution from each dimension, with a Gouy phase within the range ±π/4 contributed by each dimension.

An elliptical beam will invert its ellipticity ratio as it propagates from the far field to the waist. The dimension which was the larger far from the waist, will be the smaller near the waist.

Beam parameters

The geometric dependence of the fields of a Gaussian beam are governed by the light's wavelength λ (in the dielectric medium, if not free space) and the following beam parameters, all of which are connected as detailed in the following sections.

Beam waist

See also: Beam diameter

Gaussian beam width w(z) as a function of the distance z along the beam, which forms a hyperbola. w₀: beam waist; b: depth of focus; z_R: Rayleigh range; Θ: total angular spread

The shape of a Gaussian beam of a given wavelength λ is governed solely by one parameter, the beam waist w₀. This is a measure of the beam size at the point of its focus (z = 0 in the above equations) where the beam width w(z) (as defined above) is the smallest (and likewise where the intensity on-axis (r = 0) is the largest). From this parameter the other parameters describing the beam geometry are determined. This includes the Rayleigh range z_R and asymptotic beam divergence θ, as detailed below.

Rayleigh range and confocal parameter

Main article: Rayleigh length

The Rayleigh distance or Rayleigh range z_R is determined given a Gaussian beam's waist size:

$${\displaystyle z_{\mathrm{R}}=\frac{\pi w_0^{2}n}{\lambda }.}$$

Here λ is the wavelength of the light, n is the index of refraction. At a distance from the waist equal to the Rayleigh range z_R, the width w of the beam is √2 larger than it is at the focus where w = w₀, the beam waist. That also implies that the on-axis (r = 0) intensity there is one half of the peak intensity (at z = 0). That point along the beam also happens to be where the wavefront curvature (1/R) is greatest.

The distance between the two points z = ±z_R is called the confocal parameter or depth of focus of the beam.

Beam divergence

Further information: Beam divergence

Although the tails of a Gaussian function never actually reach zero, for the purposes of the following discussion the "edge" of a beam is considered to be the radius where r = w(z). That is where the intensity has dropped to 1/e² of its on-axis value. Now, for z ≫ z_R the parameter w(z) increases linearly with z. This means that far from the waist, the beam "edge" (in the above sense) is cone-shaped. The angle between that cone (whose r = w(z)) and the beam axis (r = 0) defines the divergence of the beam:

$${\displaystyle \theta =\underset{z\to \mathrm{\infty }}{lim}\arctan \left(\frac{w(z)}{z}\right).}$$

In the paraxial case, as we have been considering, θ (in radians) is then approximately

$${\displaystyle \theta =\frac{\lambda }{\pi n{w}_0}}$$

where n is the refractive index of the medium the beam propagates through, and λ is the free-space wavelength. The total angular spread of the diverging beam, or apex angle of the above-described cone, is then given by

$${\displaystyle \mathrm{\Theta }=2\theta .}$$

That cone then contains 86% of the Gaussian beam's total power.

Because the divergence is inversely proportional to the spot size, for a given wavelength λ, a Gaussian beam that is focused to a small spot diverges rapidly as it propagates away from the focus. Conversely, to minimize the divergence of a laser beam in the far field (and increase its peak intensity at large distances) it must have a large cross-section (w₀) at the waist (and thus a large diameter where it is launched, since w(z) is never less than w₀). This relationship between beam width and divergence is a fundamental characteristic of diffraction, and of the Fourier transform which describes Fraunhofer diffraction. A beam with any specified amplitude profile also obeys this inverse relationship, but the fundamental Gaussian mode is a special case where the product of beam size at focus and far-field divergence is smaller than for any other case.

Since the Gaussian beam model uses the paraxial approximation, it fails when wavefronts are tilted by more than about 30° from the axis of the beam. From the above expression for divergence, this means the Gaussian beam model is only accurate for beams with waists larger than about 2λ/π.

Laser beam quality is quantified by the beam parameter product (BPP). For a Gaussian beam, the BPP is the product of the beam's divergence and waist size w₀. The BPP of a real beam is obtained by measuring the beam's minimum diameter and far-field divergence, and taking their product. The ratio of the BPP of the real beam to that of an ideal Gaussian beam at the same wavelength is known as M² ("M squared"). The M² for a Gaussian beam is one. All real laser beams have M² values greater than one, although very high quality beams can have values very close to one.

The numerical aperture of a Gaussian beam is defined to be NA = n sin θ, where n is the index of refraction of the medium through which the beam propagates. This means that the Rayleigh range is related to the numerical aperture by

$${\displaystyle z_{\mathrm{R}}=\frac{n{w}_0}{\mathrm{N}\mathrm{A}}.}$$

Power and intensity

Power through an aperture

With a beam centered on an aperture, the power P passing through a circle of radius r in the transverse plane at position z is

$${\displaystyle P(r,z)=P_0\left[1-e^{-2r^2/w^2(z)}\right],}$$

where

$${\displaystyle P_0=\frac{1}{2}\pi I_0{w}_0^2}$$

is the total power transmitted by the beam.

For a circle of radius r = w(z), the fraction of power transmitted through the circle is

$${\displaystyle \frac{P(z)}{P_0}=1-e^{-2}\approx \mathrm{0.865.}}$$

Similarly, about 90% of the beam's power will flow through a circle of radius r = 1.07 × w(z), 95% through a circle of radius r = 1.224 × w(z), and 99% through a circle of radius r = 1.52 × w(z).

Peak intensity

The peak intensity at an axial distance z from the beam waist can be calculated as the limit of the enclosed power within a circle of radius r, divided by the area of the circle πr² as the circle shrinks:

$${\displaystyle I(0,z)=\underset{r\to 0}{lim}\frac{P_0\left[1-e^{-2r^2/w^2(z)}\right]}{\pi r^2}.}$$

The limit can be evaluated using L'Hôpital's rule:

$${\displaystyle I(0,z)=\frac{P_0}{\pi }\underset{r\to 0}{lim}\frac{\left[-(-2)(2r)e^{-2r^2/w^2(z)}\right]}{w^2(z)(2r)}=\frac{2P_0}{\pi w^2(z)}.}$$

Complex beam parameter

Main article: Complex beam parameter

The spot size and curvature of a Gaussian beam as a function of z along the beam can also be encoded in the complex beam parameter q(z) given by:

$${\displaystyle q(z)=z+i{z}_{\mathrm{R}}.}$$

Introducing this complication leads to a simplification of the Gaussian beam field equation as shown below. It can be seen that the reciprocal of q(z) contains the wavefront curvature and relative on-axis intensity in its real and imaginary parts, respectively:

$${\displaystyle \frac{1}{q(z)}=\frac{1}{z+i{z}_{\mathrm{R}}}=\frac{z}{z^2+z_{\mathrm{R}}^2}-i\frac{z_{\mathrm{R}}}{z^2+z_{\mathrm{R}}^2}=\frac{1}{R(z)}-i\frac{\lambda }{n\pi w^2(z)}.}$$

The complex beam parameter simplifies the mathematical analysis of Gaussian beam propagation, and especially in the analysis of optical resonator cavities using ray transfer matrices.

Then using this form, the earlier equation for the electric (or magnetic) field is greatly simplified. If we call u the relative field strength of an elliptical Gaussian beam (with the elliptical axes in the x and y directions) then it can be separated in x and y according to:

$${\displaystyle u(x,y,z)=u_x(x,z)u_y(y,z),}$$

where

$${\displaystyle \begin{array}{rl}{u}_x(x,z)& =\frac{1}{\sqrt{q_x(z)}}\exp \left(-ik\frac{x^2}{2q_x(z)}\right),\\ u_y(y,z)& =\frac{1}{\sqrt{q_y(z)}}\exp \left(-ik\frac{y^2}{2q_y(z)}\right),\end{array}}$$

where q_x(z) and q_y(z) are the complex beam parameters in the x and y directions.

For the common case of a circular beam profile, q_x(z) = q_y(z) = q(z) and x² + y² = r², which yields

$${\displaystyle u(r,z)=\frac{1}{q(z)}\exp \left(-ik\frac{r^2}{2q(z)}\right).}$$

Beam optics

A diagram of a gaussian beam passing through a lens.

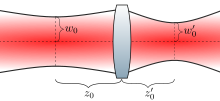
When a gaussian beam propagates through a thin lens, the outgoing beam is also a (different) gaussian beam, provided that the beam travels along the cylindrical symmetry axis of the lens. The focal length of the lens ${\displaystyle f}$, the beam waist radius ${\displaystyle w_0}$, and beam waist position ${\displaystyle z_0}$ of the incoming beam can be used to determine the beam waist radius ${\displaystyle w_0^{\prime }}$ and position ${\displaystyle z_0^{\prime }}$ of the outgoing beam.

Lens equation

As derived by Saleh and Teich, the relationship between the ingoing and outgoing beams can be found by considering the phase that is added to each point ${\displaystyle (x,y)}$ of the gaussian beam as it travels through the lens. An alternative approach due to Self is to consider the effect of a thin lens on the gaussian beam wavefronts.

The exact solution to the above problem is expressed simply in terms of the magnification ${\displaystyle M}$

${\displaystyle \begin{array}{rl}{w}_0^{\prime }& =M{w}_0\\ (z_0^{\prime }-f)& =M^2(z_0-f).\end{array}}$

The magnification, which depends on ${\displaystyle w_0}$ and ${\displaystyle z_0}$, is given by

${\displaystyle M=\frac{M_r}{\sqrt{1+r^2}}}$

where

${\displaystyle r=\frac{z_R}{z_0-f},M_r=\left|\frac{f}{z_0-f}\right|.}$

An equivalent expression for the beam position ${\displaystyle z_0^{\prime }}$ is

${\displaystyle \frac{1}{z_0+\frac{z_R^2}{(z_0-f)}}+\frac{1}{z_0^{\prime }}=\frac{1}{f}.}$

This last expression makes clear that the ray optics thin lens equation is recovered in the limit that ${\displaystyle \left|\left(\frac{z_R}{z_0}\right)\left(\frac{z_R}{z_0-f}\right)\right|\ll 1}$. It can also be noted that if ${\displaystyle \left|z_0+\frac{z_R^2}{z_0-f}\right|\gg f}$ then the incoming beam is "well collimated" so that ${\displaystyle z_0^{\prime }\approx f}$.

Beam focusing

In some applications it is desirable to use a converging lens to focus a laser beam to a very small spot. Mathematically, this implies minimization of the magnification ${\displaystyle M}$. If the beam size is constrained by the size of available optics, this is typically best achieved by sending the largest possible collimated beam through a small focal length lens, i.e. by maximizing ${\displaystyle z_R}$ and minimizing ${\displaystyle f}$. In this situation, it is justifiable to make the approximation ${\displaystyle z_R^2/(z_0-f{)}^2\gg 1}$, implying that ${\displaystyle M\approx f/z_R}$ and yielding the result ${\displaystyle w_0^{\prime }\approx f{w}_0/z_R}$. This result is often presented in the form

${\displaystyle \begin{array}{rl}2w_0^{\prime }& \approx \frac{4}{\pi }\lambda F_{\mathrm{\#}}\\ z_0^{\prime }& \approx f\end{array}}$

where

${\displaystyle F_{\mathrm{\#}}=\frac{f}{2w_0},}$

which is found after assuming that the medium has index of refraction ${\displaystyle n\approx 1}$ and substituting ${\displaystyle z_R=\pi w_0^2/\lambda }$. The factors of 2 are introduced because of a common preference to represent beam size by the beam waist diameters ${\displaystyle 2w_0^{\prime }}$ and ${\displaystyle 2w_0}$, rather than the waist radii ${\displaystyle w_0^{\prime }}$ and ${\displaystyle w_0}$.

Wave equation

As a special case of electromagnetic radiation, Gaussian beams (and the higher-order Gaussian modes detailed below) are solutions to the wave equation for an electromagnetic field in free space or in a homogeneous dielectric medium, obtained by combining Maxwell's equations for the curl of E and the curl of H, resulting in:

$${\displaystyle {\mathrm{\nabla }}^{2}U=\frac{1}{c^2}\frac{{\mathrm{\partial }}^{2}U}{\mathrm{\partial }{t}^2},}$$

where c is the speed of light in the medium, and U could either refer to the electric or magnetic field vector, as any specific solution for either determines the other. The Gaussian beam solution is valid only in the paraxial approximation, that is, where wave propagation is limited to directions within a small angle of an axis. Without loss of generality let us take that direction to be the +z direction in which case the solution U can generally be written in terms of u which has no time dependence and varies relatively smoothly in space, with the main variation spatially corresponding to the wavenumber k in the z direction:

$${\displaystyle U(x,y,z,t)=u(x,y,z)e^{-i(kz-\omega t)}\hat{\mathbf{x}}.}$$

Using this form along with the paraxial approximation, ∂²u/∂z² can then be essentially neglected. Since solutions of the electromagnetic wave equation only hold for polarizations which are orthogonal to the direction of propagation (z), we have without loss of generality considered the polarization to be in the x direction so that we now solve a scalar equation for u(x, y, z).

Substituting this solution into the wave equation above yields the paraxial approximation to the scalar wave equation:

$${\displaystyle \frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}+\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{y}^2}=2ik\frac{\mathrm{\partial }u}{\mathrm{\partial }z}.}$$

Writing the wave equations in the light-cone coordinates returns this equation without utilizing any approximation. Gaussian beams of any beam waist w₀ satisfy the paraxial approximation to the scalar wave equation; this is most easily verified by expressing the wave at z in terms of the complex beam parameter q(z) as defined above. There are many other solutions. As solutions to a linear system, any combination of solutions (using addition or multiplication by a constant) is also a solution. The fundamental Gaussian happens to be the one that minimizes the product of minimum spot size and far-field divergence, as noted above. In seeking paraxial solutions, and in particular ones that would describe laser radiation that is not in the fundamental Gaussian mode, we will look for families of solutions with gradually increasing products of their divergences and minimum spot sizes. Two important orthogonal decompositions of this sort are the Hermite–Gaussian or Laguerre-Gaussian modes, corresponding to rectangular and circular symmetry respectively, as detailed in the next section. With both of these, the fundamental Gaussian beam we have been considering is the lowest order mode.

Higher-order modes

See also: Transverse mode

Hermite-Gaussian modes

Twelve Hermite-Gaussian modes

It is possible to decompose a coherent paraxial beam using the orthogonal set of so-called Hermite-Gaussian modes, any of which are given by the product of a factor in x and a factor in y. Such a solution is possible due to the separability in x and y in the paraxial Helmholtz equation as written in Cartesian coordinates. Thus given a mode of order (l, m) referring to the x and y directions, the electric field amplitude at x, y, z may be given by:

$${\displaystyle E(x,y,z)=u_l(x,z)u_m(y,z)\exp (-ikz),}$$

where the factors for the x and y dependence are each given by:

$${\displaystyle u_J(x,z)={\left(\frac{\sqrt{2/\pi }}{2^{J}J!w_0}\right)}^{1/2}{\left(\frac{q_0}{q(z)}\right)}^{1/2}{\left(-\frac{q^{\ast }(z)}{q(z)}\right)}^{J/2}{H}_J\left(\frac{\sqrt{2}x}{w(z)}\right)\exp \left(-i\frac{k{x}^2}{2q(z)}\right),}$$

where we have employed the complex beam parameter q(z) (as defined above) for a beam of waist w₀ at z from the focus. In this form, the first factor is just a normalizing constant to make the set of u_J orthonormal. The second factor is an additional normalization dependent on z which compensates for the expansion of the spatial extent of the mode according to w(z)/w₀ (due to the last two factors). It also contains part of the Gouy phase. The third factor is a pure phase which enhances the Gouy phase shift for higher orders J.

The final two factors account for the spatial variation over x (or y). The fourth factor is the Hermite polynomial of order J ("physicists' form", i.e. H₁(x) = 2x), while the fifth accounts for the Gaussian amplitude fall-off exp(−x²/w(z)²), although this isn't obvious using the complex q in the exponent. Expansion of that exponential also produces a phase factor in x which accounts for the wavefront curvature (1/R(z)) at z along the beam.

Hermite-Gaussian modes are typically designated "TEM_lm"; the fundamental Gaussian beam may thus be referred to as TEM₀₀ (where TEM is transverse electro-magnetic). Multiplying u_l(x, z) and u_m(y, z) to get the 2-D mode profile, and removing the normalization so that the leading factor is just called E₀, we can write the (l, m) mode in the more accessible form:

$${\displaystyle \begin{array}{rl}{E}_{l,m}(x,y,z)=& E_0\frac{w_0}{w(z)}{H}_l(\frac{\sqrt{2}x}{w(z)})H_m(\frac{\sqrt{2}y}{w(z)})\times \\ & \exp \left(-\frac{x^2+y^2}{w^2(z)}\right)\exp \left(-i\frac{k(x^2+y^2)}{2R(z)}\right)\times \\ & \exp (i\psi (z))\exp (-ikz).\end{array}}$$

In this form, the parameter w₀, as before, determines the family of modes, in particular scaling the spatial extent of the fundamental mode's waist and all other mode patterns at z = 0. Given that w₀, w(z) and R(z) have the same definitions as for the fundamental Gaussian beam described above. It can be seen that with l = m = 0 we obtain the fundamental Gaussian beam described earlier (since H₀ = 1). The only specific difference in the x and y profiles at any z are due to the Hermite polynomial factors for the order numbers l and m. However, there is a change in the evolution of the modes' Gouy phase over z:

$${\displaystyle \psi (z)=(N+1)\arctan \left(\frac{z}{z_{\mathrm{R}}}\right),}$$

where the combined order of the mode N is defined as N = l + m. While the Gouy phase shift for the fundamental (0,0) Gaussian mode only changes by ±π/2 radians over all of z (and only by ±π/4 radians between ±z_R), this is increased by the factor N + 1 for the higher order modes.

Hermite Gaussian modes, with their rectangular symmetry, are especially suited for the modal analysis of radiation from lasers whose cavity design is asymmetric in a rectangular fashion. On the other hand, lasers and systems with circular symmetry can better be handled using the set of Laguerre-Gaussian modes introduced in the next section.

Laguerre-Gaussian modes

Intensity profiles of the first 12 Laguerre-Gaussian modes.

Beam profiles which are circularly symmetric (or lasers with cavities that are cylindrically symmetric) are often best solved using the Laguerre-Gaussian modal decomposition. These functions are written in cylindrical coordinates using generalized Laguerre polynomials. Each transverse mode is again labelled using two integers, in this case the radial index p ≥ 0 and the azimuthal index l which can be positive or negative (or zero):

$${\displaystyle \begin{array}{rl}u(r,\varphi ,z)=& C_{lp}^{LG}\frac{1}{w(z)}{\left(\frac{r\sqrt{2}}{w(z)}\right)}^{|l|}\exp \left(-\frac{r^2}{w^2(z)}\right)L_p^{|l|}\left(\frac{2r^2}{w^2(z)}\right)\times \\ & \exp \left(-ik\frac{r^2}{2R(z)}\right)\exp (-il\varphi )\exp (i\psi (z)),\end{array}}$$

where L_p^l are the generalized Laguerre polynomials. C^LG
_lp is a required normalization constant:

$${\displaystyle C_{lp}^{LG}=\sqrt{\frac{2p!}{\pi (p+|l|)!}}\Rightarrow {\int }_0^{2\pi }d\varphi {\int }_0^{\mathrm{\infty }}rdr|u(r,\varphi ,z){|}^2=1}$$

.

w(z) and R(z) have the same definitions as above. As with the higher-order Hermite-Gaussian modes the magnitude of the Laguerre-Gaussian modes' Gouy phase shift is exaggerated by the factor N + 1:

$${\displaystyle \psi (z)=(N+1)\arctan \left(\frac{z}{z_{\mathrm{R}}}\right),}$$

where in this case the combined mode number N = |l| + 2p. As before, the transverse amplitude variations are contained in the last two factors on the upper line of the equation, which again includes the basic Gaussian drop off in r but now multiplied by a Laguerre polynomial. The effect of the rotational mode number l, in addition to affecting the Laguerre polynomial, is mainly contained in the phase factor exp(−ilφ), in which the beam profile is advanced (or retarded) by l complete 2π phases in one rotation around the beam (in φ). This is an example of an optical vortex of topological charge l, and can be associated with the orbital angular momentum of light in that mode.

Ince-Gaussian modes

Transverse amplitude profile of the lowest order even Ince-Gaussian modes.

In elliptic coordinates, one can write the higher-order modes using Ince polynomials. The even and odd Ince-Gaussian modes are given by

$${\displaystyle u_{\epsilon }\left(\xi ,\eta ,z\right)=\frac{w_0}{w\left(z\right)}{\mathrm{C}}_p^m\left(i\xi ,\epsilon \right){\mathrm{C}}_p^m\left(\eta ,\epsilon \right)\exp \left[-ik\frac{r^2}{2q\left(z\right)}-\left(p+1\right)\zeta \left(z\right)\right],}$$

where ξ and η are the radial and angular elliptic coordinates defined by

$${\displaystyle \begin{array}{rl}x& =\sqrt{\epsilon /2}w(z)\cosh \xi \cos \eta ,\\ y& =\sqrt{\epsilon /2}w(z)\sinh \xi \sin \eta .\end{array}}$$

C^m
_p(η, ε) are the even Ince polynomials of order p and degree m where ε is the ellipticity parameter. The Hermite-Gaussian and Laguerre-Gaussian modes are a special case of the Ince-Gaussian modes for ε = ∞ and ε = 0 respectively.

Hypergeometric-Gaussian modes

There is another important class of paraxial wave modes in cylindrical coordinates in which the complex amplitude is proportional to a confluent hypergeometric function.

These modes have a singular phase profile and are eigenfunctions of the photon orbital angular momentum. Their intensity profiles are characterized by a single brilliant ring; like Laguerre–Gaussian modes, their intensities fall to zero at the center (on the optical axis) except for the fundamental (0,0) mode. A mode's complex amplitude can be written in terms of the normalized (dimensionless) radial coordinate ρ = r/w₀ and the normalized longitudinal coordinate Ζ = z/z_R as follows:

$${\displaystyle \begin{array}{rl}{u}_{\mathsf{p}m}(\rho ,\varphi ,\mathrm{Z})=& \sqrt{\frac{2^{\mathsf{p}+|m|+1}}{\pi \mathrm{\Gamma }(\mathsf{p}+|m|+1)}}\frac{\mathrm{\Gamma }\left(\frac{\mathsf{p}}{2}+|m|+1\right)}{\mathrm{\Gamma }(|m|+1)}{i}^{|m|+1}\times \\ & {\mathrm{Z}}^{\frac{\mathsf{p}}{2}}(\mathrm{Z}+i{)}^{-\left(\frac{\mathsf{p}}{2}+|m|+1\right)}{\rho }^{|m|}\times \\ & \exp \left(-\frac{i{\rho }^2}{\mathrm{Z}+i}\right)e^{im\varphi }{}_1{F}_1\left(-\frac{\mathsf{p}}{2},|m|+1;\frac{{\rho }^2}{\mathrm{Z}(\mathrm{Z}+i)}\right)\end{array}}$$

where the rotational index m is an integer, and ${\displaystyle \mathsf{p}\ge -|m|}$ is real-valued, Γ(x) is the gamma function and ₁F₁(a, b; x) is a confluent hypergeometric function.

Some subfamilies of hypergeometric-Gaussian (HyGG) modes can be listed as the modified Bessel-Gaussian modes, the modified exponential Gaussian modes, and the modified Laguerre–Gaussian modes.

The set of hypergeometric-Gaussian modes is overcomplete and is not an orthogonal set of modes. In spite of its complicated field profile, HyGG modes have a very simple profile at the beam waist (z = 0):

$${\displaystyle u(\rho ,\varphi ,0)\propto {\rho }^{\mathsf{p}+|m|}{e}^{-{\rho }^2+im\varphi }.}$$

Biological half-life

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Biological_half-life

Biological half-life (elimination half-life, pharmacological half-life) is the time taken for concentration of a biological substance (such as a medication) to decrease from its maximum concentration (C_max) to half of C_max in the blood plasma. It is denoted by the abbreviation ${\displaystyle t_{\frac{1}{2}}}$.

This is used to measure the removal of things such as metabolites, drugs, and signalling molecules from the body. Typically, the biological half-life refers to the body's natural detoxification (cleansing) through liver metabolism and through the excretion of the measured substance through the kidneys and intestines. This concept is used when the rate of removal is roughly exponential.

In a medical context, half-life explicitly describes the time it takes for the blood plasma concentration of a substance to halve (plasma half-life) its steady-state when circulating in the full blood of an organism. This measurement is useful in medicine, pharmacology and pharmacokinetics because it helps determine how much of a drug needs to be taken and how frequently it needs to be taken if a certain average amount is needed constantly. By contrast, the stability of a substance in plasma is described as plasma stability. This is essential to ensure accurate analysis of drugs in plasma and for drug discovery.

The relationship between the biological and plasma half-lives of a substance can be complex depending on the substance in question, due to factors including accumulation in tissues, protein binding, active metabolites, and receptor interactions.

Examples

Water

The biological half-life of water in a human is about 7 to 14 days. It can be altered by behavior. Drinking large amounts of alcohol will reduce the biological half-life of water in the body. This has been used to decontaminate patients who are internally contaminated with tritiated water. The basis of this decontamination method is to increase the rate at which the water in the body is replaced with new water.

Alcohol

The removal of ethanol (drinking alcohol) through oxidation by alcohol dehydrogenase in the liver from the human body is limited. Hence the removal of a large concentration of alcohol from blood may follow zero-order kinetics. Also the rate-limiting steps for one substance may be in common with other substances. For instance, the blood alcohol concentration can be used to modify the biochemistry of methanol and ethylene glycol. In this way the oxidation of methanol to the toxic formaldehyde and formic acid in the human body can be prevented by giving an appropriate amount of ethanol to a person who has ingested methanol. Methanol is very toxic and causes blindness and death. A person who has ingested ethylene glycol can be treated in the same way. Half life is also relative to the subjective metabolic rate of the individual in question.

Common prescription medications

Substance	Biological half-life
Adenosine	Less than 10 seconds (estimate)
Norepinephrine	2 minutes
Oxaliplatin	14 minutes
Zaleplon	1 hour
Morphine	1.5–4.5 hours
Flurazepam	2.3 hours Active metabolite (N-desalkylflurazepam): 47–100 hours
Methotrexate	3–10 hours (lower doses), 8–15 hours (higher doses)
Methadone	15–72 hours in rare cases up to 8 days
Diazepam	20–50 hours Active metabolite (nordazepam): 30–200 hours
Phenytoin	20–60 hours
Buprenorphine	28–35 hours
Clonazepam	30–40 hours
Donepezil	3 days (70 hours)
Fluoxetine	4–6 days (under continuous administration) Active lipophilic metabolite (norfluoxetine): 4–16 days
Amiodarone	14–107 days
Vandetanib	19 days
Dutasteride	21–35 days (under continuous administration)
Bedaquiline	165 days

Metals

The biological half-life of caesium in humans is between one and four months. This can be shortened by feeding the person prussian blue. The prussian blue in the digestive system acts as a solid ion exchanger which absorbs the caesium while releasing potassium ions.

For some substances, it is important to think of the human or animal body as being made up of several parts, each with their own affinity for the substance, and each part with a different biological half-life (physiologically-based pharmacokinetic modelling). Attempts to remove a substance from the whole organism may have the effect of increasing the burden present in one part of the organism. For instance, if a person who is contaminated with lead is given EDTA in a chelation therapy, then while the rate at which lead is lost from the body will be increased, the lead within the body tends to relocate into the brain where it can do the most harm.

• Polonium in the body has a biological half-life of about 30 to 50 days.
• Caesium in the body has a biological half-life of about one to four months.
• Mercury (as methylmercury) in the body has a half-life of about 65 days.
• Lead in the blood has a half life of 28–36 days.
• Lead in bone has a biological half-life of about ten years.
• Cadmium in bone has a biological half-life of about 30 years.
• Plutonium in bone has a biological half-life of about 100 years.
• Plutonium in the liver has a biological half-life of about 40 years.

Peripheral half-life

Some substances may have different half-lives in different parts of the body. For example, oxytocin has a half-life of typically about three minutes in the blood when given intravenously. Peripherally administered (e.g. intravenous) peptides like oxytocin cross the blood-brain-barrier very poorly, although very small amounts (< 1%) do appear to enter the central nervous system in humans when given via this route. In contrast to peripheral administration, when administered intranasally via a nasal spray, oxytocin reliably crosses the blood–brain barrier and exhibits psychoactive effects in humans. In addition, also unlike the case of peripheral administration, intranasal oxytocin has a central duration of at least 2.25 hours and as long as 4 hours. In likely relation to this fact, endogenous oxytocin concentrations in the brain have been found to be as much as 1000-fold higher than peripheral levels.

Rate equations

Main article: Rate equation

See also: Pharmacokinetics § Metrics

First-order elimination

Timeline of an exponential decay process

Time (t)	Percent of initial value	Percent completion
t½	50%	50%
t½ × 2	25%	75%
t½ × 3	12.5%	87.5%
t½ × 3.322	10.00%	90.00%
t½ × 4	6.25%	93.75%
t½ × 4.322	5.00%	95.00%
t½ × 5	3.125%	96.875%
t½ × 6	1.5625%	98.4375%
t½ × 7	0.78125%	99.21875%
t½ × 10	~0.09766%	~99.90234%

Half-times apply to processes where the elimination rate is exponential. If ${\displaystyle C(t)}$ is the concentration of a substance at time ${\displaystyle t}$, its time dependence is given by

${\displaystyle C(t)=C(0)e^{-kt}}$

where k is the reaction rate constant. Such a decay rate arises from a first-order reaction where the rate of elimination is proportional to the amount of the substance:

${\displaystyle \frac{dC}{dt}=-kC.}$

The half-life for this process is

${\displaystyle t_{\frac{1}{2}}=\frac{\ln 2}{k}.}$

Alternatively, half-life is given by

${\displaystyle t_{\frac{1}{2}}=\frac{\ln 2}{{\lambda }_z}}$

where λ_z is the slope of the terminal phase of the time–concentration curve for the substance on a semilogarithmic scale.

Half-life is determined by clearance (CL) and volume of distribution (V_D) and the relationship is described by the following equation:

${\displaystyle t_{\frac{1}{2}}=\frac{\ln 2\cdot V_D}{CL}}$

In clinical practice, this means that it takes 4 to 5 times the half-life for a drug's serum concentration to reach steady state after regular dosing is started, stopped, or the dose changed. So, for example, digoxin has a half-life (or t_½) of 24–36 h; this means that a change in the dose will take the best part of a week to take full effect. For this reason, drugs with a long half-life (e.g., amiodarone, elimination t_½ of about 58 days) are usually started with a loading dose to achieve their desired clinical effect more quickly.

Biphasic half-life

Many drugs follow a biphasic elimination curve — first a steep slope then a shallow slope:

STEEP (initial) part of curve —> initial distribution of the drug in the body.

SHALLOW part of curve —> ultimate excretion of drug, which is dependent on the release of the drug from tissue compartments into the blood.

The longer half-life is called the terminal half-life and the half-life of the largest component is called the dominant half-life. For a more detailed description see Pharmacokinetics § Multi-compartmental models.

Very-long-baseline interferometry

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Very-long-baseline_interferometry

Some of the Atacama Large Millimeter Array radio telescopes.

The eight radio telescopes of the Smithsonian Submillimeter Array, located at the Mauna Kea Observatory in Hawai'i.

VLBI was used to create the first image of a black hole, imaged by the Event Horizon Telescope and published in April 2019.

Very-long-baseline interferometry (VLBI) is a type of astronomical interferometry used in radio astronomy. In VLBI a signal from an astronomical radio source, such as a quasar, is collected at multiple radio telescopes on Earth or in space. The distance between the radio telescopes is then calculated using the time difference between the arrivals of the radio signal at different telescopes. This allows observations of an object that are made simultaneously by many radio telescopes to be combined, emulating a telescope with a size equal to the maximum separation between the telescopes.

Data received at each antenna in the array include arrival times from a local atomic clock, such as a hydrogen maser. At a later time, the data are correlated with data from other antennas that recorded the same radio signal, to produce the resulting image. The resolution achievable using interferometry is proportional to the observing frequency. The VLBI technique enables the distance between telescopes to be much greater than that possible with conventional interferometry, which requires antennas to be physically connected by coaxial cable, waveguide, optical fiber, or other type of transmission line. The greater telescope separations are possible in VLBI due to the development of the closure phase imaging technique by Roger Jennison in the 1950s, allowing VLBI to produce images with superior resolution.

VLBI is best known for imaging distant cosmic radio sources, spacecraft tracking, and for applications in astrometry. However, since the VLBI technique measures the time differences between the arrival of radio waves at separate antennas, it can also be used "in reverse" to perform Earth rotation studies, map movements of tectonic plates very precisely (within millimetres), and perform other types of geodesy. Using VLBI in this manner requires large numbers of time difference measurements from distant sources (such as quasars) observed with a global network of antennas over a period of time.

Method

Recording data at each of the telescopes in a VLBI array. Extremely accurate high-frequency clocks are recorded alongside the astronomical data in order to help get the synchronization correct

In VLBI, the digitized antenna data are usually recorded at each of the telescopes (in the past this was done on large magnetic tapes, but nowadays it is usually done on large arrays of computer disk drives). The antenna signal is sampled with an extremely precise and stable atomic clock (usually a hydrogen maser) that is additionally locked onto a GPS time standard. Alongside the astronomical data samples, the output of this clock is recorded. The recorded media are then transported to a central location. More recent experiments have been conducted with "electronic" VLBI (e-VLBI) where the data are sent by fibre-optics (e.g., 10 Gbit/s fiber-optic paths in the European GEANT2 research network) and not recorded at the telescopes, speeding up and simplifying the observing process significantly. Even though the data rates are very high, the data can be sent over normal Internet connections taking advantage of the fact that many of the international high speed networks have significant spare capacity at present.

At the location of the correlator, the data is played back. The timing of the playback is adjusted according to the atomic clock signals, and the estimated times of arrival of the radio signal at each of the telescopes. A range of playback timings over a range of nanoseconds are usually tested until the correct timing is found.

Playing back the data from each of the telescopes in a VLBI array. Great care must be taken to synchronize the play back of the data from different telescopes. Atomic clock signals recorded with the data help in getting the timing correct.

Each antenna will be a different distance from the radio source, and as with the short baseline radio interferometer the delays incurred by the extra distance to one antenna must be added artificially to the signals received at each of the other antennas. The approximate delay required can be calculated from the geometry of the problem. The tape playback is synchronized using the recorded signals from the atomic clocks as time references, as shown in the drawing on the right. If the position of the antennas is not known to sufficient accuracy or atmospheric effects are significant, fine adjustments to the delays must be made until interference fringes are detected. If the signal from antenna A is taken as the reference, inaccuracies in the delay will lead to errors ${\displaystyle {ϵ}_B}$ and ${\displaystyle {ϵ}_C}$ in the phases of the signals from tapes B and C respectively (see drawing on right). As a result of these errors the phase of the complex visibility cannot be measured with a very-long-baseline interferometer.

Temperature variations at VLBI sites can deform the structure of the antennas and affect the baseline measurements. Neglecting atmospheric pressure and hydrological loading corrections at the observation level can also contaminate the VLBI measurements by introducing annual and seasonal signals, like in the Global Navigation Satellite System time series.

The phase of the complex visibility depends on the symmetry of the source brightness distribution. Any brightness distribution can be written as the sum of a symmetric component and an anti-symmetric component. The symmetric component of the brightness distribution only contributes to the real part of the complex visibility, while the anti-symmetric component only contributes to the imaginary part. As the phase of each complex visibility measurement cannot be determined with a very-long-baseline interferometer the symmetry of the corresponding contribution to the source brightness distributions is not known.

Roger Clifton Jennison developed a novel technique for obtaining information about visibility phases when delay errors are present, using an observable called the closure phase. Although his initial laboratory measurements of closure phase had been done at optical wavelengths, he foresaw greater potential for his technique in radio interferometry. In 1958 he demonstrated its effectiveness with a radio interferometer, but it only became widely used for long-baseline radio interferometry in 1974. At least three antennas are required. This method was used for the first VLBI measurements, and a modified form of this approach ("Self-Calibration") is still used today.

Scientific results

Some of the scientific results derived from VLBI include:

• High resolution radio imaging of cosmic radio sources.
• Imaging the surfaces of nearby stars at radio wavelengths (see also interferometry) – similar techniques have also been used to make infrared and optical images of stellar surfaces.
• Definition of the celestial reference frame.
• Measurement of the acceleration of the Solar System toward the center of the Milky Way.
• Motion of the Earth's tectonic plates.
• Regional deformation and local uplift or subsidence.
• Earth's orientation parameters and fluctuations in the length of day.
• Maintenance of the terrestrial reference frame.
• Measurement of gravitational forces of the Sun and Moon on the Earth and the deep structure of the Earth.
• Improvement of atmospheric models.
• Measurement of the fundamental speed of gravity.
• The tracking of the Huygens probe as it passed through Titan's atmosphere, allowing wind velocity measurements.
• First imaging of a supermassive black hole.

VLBI arrays

There are several VLBI arrays located in Europe, Canada, the United States, Chile, Russia, China, South Korea, Japan, Mexico, Australia and Thailand. The most sensitive VLBI array in the world is the European VLBI Network (EVN). This is a part-time array that brings together the largest European radiotelescopes and some others outside of Europe for typically weeklong sessions, with the data being processed at the Joint Institute for VLBI in Europe (JIVE). The Very Long Baseline Array (VLBA), which uses ten dedicated, 25-meter telescopes spanning 5351 miles across the United States, is the largest VLBI array that operates all year round as both an astronomical and geodesy instrument. The combination of the EVN and VLBA is known as Global VLBI. When one or both of these arrays are combined with space-based VLBI antennas such as HALCA or Spektr-R, the resolution obtained is higher than any other astronomical instrument, capable of imaging the sky with a level of detail measured in microarcseconds. VLBI generally benefits from the longer baselines afforded by international collaboration, with a notable early example in 1976, when radio telescopes in the United States, USSR and Australia were linked to observe hydroxyl-maser sources. This technique is currently being used by the Event Horizon Telescope, whose goal is to observe the supermassive black holes at the centers of the Milky Way Galaxy and Messier 87.

e-VLBI

Image of the source IRC +10420. The lower resolution image on the left was taken with the UK's MERLIN array and shows the shell of maser emission produced by an expanding shell of gas with a diameter about 200 times that of the Solar System. The shell of gas was ejected from a supergiant star (10 times the mass of the Sun) at the centre of the emission about 900 years ago. The corresponding EVN e-VLBI image (right) shows the much finer structure of the masers made visible with the higher resolution of the VLBI array.

VLBI has traditionally operated by recording the signal at each telescope on magnetic tapes or disks, and shipping those to the correlation center for replay. In 2004 it became possible to connect VLBI radio telescopes in close to real-time, while still employing the local time references of the VLBI technique, in a technique known as e-VLBI. In Europe, six radio telescopes of the European VLBI Network (EVN) were connected with Gigabit per second links via their National Research Networks and the Pan-European research network GEANT2, and the first astronomical experiments using this new technique were successfully conducted.

The image to the right shows the first science produced by the European VLBI Network using e-VLBI. The data from each of the telescopes were routed through the GÉANT2 network and on through SURFnet to be the processed in real time at the European Data Processing centre at JIVE.

Space VLBI

In the quest for even greater angular resolution, dedicated VLBI satellites have been placed in Earth orbit to provide greatly extended baselines. Experiments incorporating such space-borne array elements are termed Space Very Long Baseline Interferometry (SVLBI). The first SVLBI experiment was carried out on Salyut-6 orbital station with KRT-10, a 10-meter radio telescope, which was launched in July 1978.

The first dedicated SVLBI satellite was HALCA, an 8-meter radio telescope, which was launched in February 1997 and made observations until October 2003. Due to the small size of the dish, only very strong radio sources could be observed with SVLBI arrays incorporating it.

Another SVLBI satellite, a 10-meter radio telescope Spektr-R, was launched in July 2011 and made observations until January 2019. It was placed into a highly elliptical orbit, ranging from a perigee of 10,652 km to an apogee of 338,541 km, making RadioAstron, the SVLBI program incorporating the satellite and ground arrays, the biggest radio interferometer to date. The resolution of the system reached 8 microarcseconds.

International VLBI Service for Geodesy and Astrometry

The International VLBI Service for Geodesy and Astrometry (IVS) is an international collaboration whose purpose is to use the observation of astronomical radio sources using VLBI to precisely determine earth orientation parameters (EOP) and celestial reference frames (CRF) and terrestrial reference frames (TRF). IVS is a service operating under the International Astronomical Union (IAU) and the International Association of Geodesy (IAG).