Coriolis force

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Coriolis_force

 

In the inertial frame of reference (upper part of the picture), the black ball moves in a straight line. However, the observer (red dot) who is standing in the rotating/non-inertial frame of reference (lower part of the picture) sees the object as following a curved path due to the Coriolis and centrifugal forces present in this frame.

In physics, the Coriolis force is an inertial or fictitious force that acts on objects that are in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise (or counterclockwise) rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology.

Newton's laws of motion describe the motion of an object in an inertial (non-accelerating) frame of reference. When Newton's laws are transformed to a rotating frame of reference, the Coriolis and centrifugal accelerations appear. When applied to massive objects, the respective forces are proportional to the masses of them. The Coriolis force is proportional to the rotation rate and the centrifugal force is proportional to the square of the rotation rate. The Coriolis force acts in a direction perpendicular to the rotation axis and to the velocity of the body in the rotating frame and is proportional to the object's speed in the rotating frame (more precisely, to the component of its velocity that is perpendicular to the axis of rotation). The centrifugal force acts outwards in the radial direction and is proportional to the distance of the body from the axis of the rotating frame. These additional forces are termed inertial forces, fictitious forces or pseudo forces. By accounting for the rotation by addition of these fictitious forces, Newton's laws of motion can be applied to a rotating system as though it was an inertial system. They are correction factors which are not required in a non-rotating system.

In popular (non-technical) usage of the term "Coriolis effect", the rotating reference frame implied is almost always the Earth. Because the Earth spins, Earth-bound observers need to account for the Coriolis force to correctly analyze the motion of objects. The Earth completes one rotation for each day/night cycle, so for motions of everyday objects the Coriolis force is usually quite small compared with other forces; its effects generally become noticeable only for motions occurring over large distances and long periods of time, such as large-scale movement of air in the atmosphere or water in the ocean; or where high precision is important, such as long-range artillery or missile trajectories. Such motions are constrained by the surface of the Earth, so only the horizontal component of the Coriolis force is generally important. This force causes moving objects on the surface of the Earth to be deflected to the right (with respect to the direction of travel) in the Northern Hemisphere and to the left in the Southern Hemisphere. The horizontal deflection effect is greater near the poles, since the effective rotation rate about a local vertical axis is largest there, and decreases to zero at the equator. Rather than flowing directly from areas of high pressure to low pressure, as they would in a non-rotating system, winds and currents tend to flow to the right of this direction north of the equator (anticlockwise) and to the left of this direction south of it (clockwise). This effect is responsible for the rotation and thus formation of cyclones.

For an intuitive explanation of the origin of the Coriolis force, consider an object, constrained to follow the Earth's surface and moving northward in the northern hemisphere. Viewed from outer space, the object does not appear to go due north, but has an eastward motion (it rotates around toward the right along with the surface of the Earth). The further north it travels, the smaller the "diameter of its parallel" (the minimum distance from the surface point to the axis of rotation, which is in a plane orthogonal to the axis), and so the slower the eastward motion of its surface. As the object moves north, to higher latitudes, it has a tendency to maintain the eastward speed it started with (rather than slowing down to match the reduced eastward speed of local objects on the Earth's surface), so it veers east (i.e. to the right of its initial motion).

Though not obvious from this example, which considers northward motion, the horizontal deflection occurs equally for objects moving eastward or westward (or in any other direction). However, the theory that the effect determines the rotation of draining water in a typical size household bathtub, sink or toilet has been repeatedly disproven by modern-day scientists; the force is negligibly small compared to the many other influences on the rotation.

History

Image from Cursus seu Mundus Mathematicus (1674) of C.F.M. Dechales, showing how a cannonball should deflect to the right of its target on a rotating Earth, because the rightward motion of the ball is faster than that of the tower.

 

Image from Cursus seu Mundus Mathematicus (1674) of C.F.M. Dechales, showing how a ball should fall from a tower on a rotating Earth. The ball is released from F. The top of the tower moves faster than its base, so while the ball falls, the base of the tower moves to I, but the ball, which has the eastward speed of the tower's top, outruns the tower's base and lands further to the east at L.

Italian scientist Giovanni Battista Riccioli and his assistant Francesco Maria Grimaldi described the effect in connection with artillery in the 1651 Almagestum Novum, writing that rotation of the Earth should cause a cannonball fired to the north to deflect to the east. In 1674 Claude François Milliet Dechales described in his Cursus seu Mundus Mathematicus how the rotation of the Earth should cause a deflection in the trajectories of both falling bodies and projectiles aimed toward one of the planet's poles. Riccioli, Grimaldi, and Dechales all described the effect as part of an argument against the heliocentric system of Copernicus. In other words, they argued that the Earth's rotation should create the effect, and so failure to detect the effect was evidence for an immobile Earth. The Coriolis acceleration equation was derived by Euler in 1749, and the effect was described in the tidal equations of Pierre-Simon Laplace in 1778.

Gaspard-Gustave Coriolis published a paper in 1835 on the energy yield of machines with rotating parts, such as waterwheels. That paper considered the supplementary forces that are detected in a rotating frame of reference. Coriolis divided these supplementary forces into two categories. The second category contained a force that arises from the cross product of the angular velocity of a coordinate system and the projection of a particle's velocity into a plane perpendicular to the system's axis of rotation. Coriolis referred to this force as the "compound centrifugal force" due to its analogies with the centrifugal force already considered in category one. The effect was known in the early 20th century as the "acceleration of Coriolis", and by 1920 as "Coriolis force".

In 1856, William Ferrel proposed the existence of a circulation cell in the mid-latitudes with air being deflected by the Coriolis force to create the prevailing westerly winds.

The understanding of the kinematics of how exactly the rotation of the Earth affects airflow was partial at first. Late in the 19th century, the full extent of the large scale interaction of pressure-gradient force and deflecting force that in the end causes air masses to move along isobars was understood.

Formula

In Newtonian mechanics, the equation of motion for an object in an inertial reference frame is

${\displaystyle {\boldsymbol {F}}=m{\boldsymbol {a}}}$

where ${\displaystyle {\boldsymbol {F}}}$ is the vector sum of the physical forces acting on the object, ${\displaystyle m}$ is the mass of the object, and ${\displaystyle {\boldsymbol {a}}}$ is the acceleration of the object relative to the inertial reference frame.

Transforming this equation to a reference frame rotating about a fixed axis through the origin with angular velocity ${\displaystyle {\boldsymbol {\omega }}}$ having variable rotation rate, the equation takes the form

${\displaystyle {\boldsymbol {F}}-m{\frac {\operatorname {d} {\boldsymbol {\omega }}}{\operatorname {d} t}}\times {\boldsymbol {r'}}-2m{\boldsymbol {\omega }}\times {\boldsymbol {v'}}-m{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {r'}})}$ ${\displaystyle =m{\boldsymbol {a'}}}$

where

${\displaystyle {\boldsymbol {F}}}$ is the vector sum of the physical forces acting on the object

${\displaystyle {\boldsymbol {\omega }}}$ is the angular velocity, of the rotating reference frame relative to the inertial frame

${\displaystyle {\boldsymbol {v'}}}$ is the velocity relative to the rotating reference frame

${\displaystyle {\boldsymbol {r'}}}$ is the position vector of the object relative to the rotating reference frame

${\displaystyle {\boldsymbol {a'}}}$ is the acceleration relative to the rotating reference frame

The fictitious forces as they are perceived in the rotating frame act as additional forces that contribute to the apparent acceleration just like the real external forces. The fictitious force terms of the equation are, reading from left to right:

• Euler force ${\displaystyle -m{\frac {\operatorname {d} {\boldsymbol {\omega }}}{\operatorname {d} t}}\times {\boldsymbol {r'}}}$
• Coriolis force ${\displaystyle -2m({\boldsymbol {\omega }}\times {\boldsymbol {v'}})}$
• centrifugal force ${\displaystyle -m{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {r'}})}$

Notice the Euler and centrifugal forces depend on the position vector ${\displaystyle {\boldsymbol {r'}}}$ of the object, while the Coriolis force depends on the object's velocity ${\displaystyle {\boldsymbol {v'}}}$ as measured in the rotating reference frame. As expected, for a non-rotating inertial frame of reference ${\displaystyle ({\boldsymbol {\omega }}=0)}$ the Coriolis force and all other fictitious forces disappear. The forces also disappear for zero mass ${\displaystyle (m=0)}$.

As the Coriolis force is proportional to a cross product of two vectors, it is perpendicular to both vectors, in this case the object's velocity and the frame's rotation vector. It therefore follows that:

• if the velocity is parallel to the rotation axis, the Coriolis force is zero. (For example, on Earth, this situation occurs for a body on the equator moving north or south relative to Earth's surface.)
• if the velocity is straight inward to the axis, the Coriolis force is in the direction of local rotation. (For example, on Earth, this situation occurs for a body on the equator falling downward, as in the Dechales illustration above, where the falling ball travels further to the east than does the tower.)
• if the velocity is straight outward from the axis, the Coriolis force is against the direction of local rotation. (In the tower example, a ball launched upward would move toward the west.)
• if the velocity is in the direction of rotation, the Coriolis force is outward from the axis. (For example, on Earth, this situation occurs for a body on the equator moving east relative to Earth's surface. It would move upward as seen by an observer on the surface. This effect (see Eötvös effect below) was discussed by Galileo Galilei in 1632 and by Riccioli in 1651.)
• if the velocity is against the direction of rotation, the Coriolis force is inward to the axis. (On Earth, this situation occurs for a body on the equator moving west, which would deflect downward as seen by an observer.)

Length scales and the Rossby number

The time, space and velocity scales are important in determining the importance of the Coriolis force. Whether rotation is important in a system can be determined by its Rossby number, which is the ratio of the velocity, U, of a system to the product of the Coriolis parameter,${\displaystyle f=2\omega \sin \varphi \,}$, and the length scale, L, of the motion:

${\displaystyle Ro={\frac {U}{fL}}.}$

The Rossby number is the ratio of inertial to Coriolis forces. A small Rossby number indicates a system is strongly affected by Coriolis forces, and a large Rossby number indicates a system in which inertial forces dominate. For example, in tornadoes, the Rossby number is large, in low-pressure systems it is low, and in oceanic systems it is around 1. As a result, in tornadoes the Coriolis force is negligible, and balance is between pressure and centrifugal forces. In low-pressure systems, centrifugal force is negligible and balance is between Coriolis and pressure forces. In the oceans all three forces are comparable.

An atmospheric system moving at U = 10 m/s (22 mph) occupying a spatial distance of L = 1,000 km (621 mi), has a Rossby number of approximately 0.1.

A baseball pitcher may throw the ball at U = 45 m/s (100 mph) for a distance of L = 18.3 m (60 ft). The Rossby number in this case would be 32,000.

Baseball players don't care about which hemisphere they're playing in. However, an unguided missile obeys exactly the same physics as a baseball, but can travel far enough and be in the air long enough to experience the effect of Coriolis force. Long-range shells in the Northern Hemisphere landed close to, but to the right of, where they were aimed until this was noted. (Those fired in the Southern Hemisphere landed to the left.) In fact, it was this effect that first got the attention of Coriolis himself.

Simple cases

Tossed ball on a rotating carousel

A carousel is rotating counter-clockwise. Left panel: a ball is tossed by a thrower at 12:00 o'clock and travels in a straight line to the center of the carousel. While it travels, the thrower circles in a counter-clockwise direction. Right panel: The ball's motion as seen by the thrower, who now remains at 12:00 o'clock, because there is no rotation from their viewpoint.

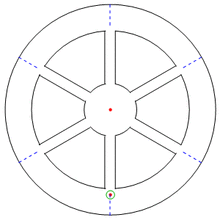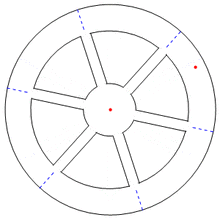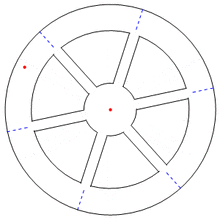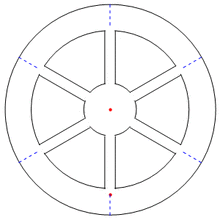
The figure illustrates a ball tossed from 12:00 o'clock toward the center of a counter-clockwise rotating carousel. On the left, the ball is seen by a stationary observer above the carousel, and the ball travels in a straight line to the center, while the ball-thrower rotates counter-clockwise with the carousel. On the right the ball is seen by an observer rotating with the carousel, so the ball-thrower appears to stay at 12:00 o'clock. The figure shows how the trajectory of the ball as seen by the rotating observer can be constructed.

On the left, two arrows locate the ball relative to the ball-thrower. One of these arrows is from the thrower to the center of the carousel (providing the ball-thrower's line of sight), and the other points from the center of the carousel to the ball. (This arrow gets shorter as the ball approaches the center.) A shifted version of the two arrows is shown dotted.

On the right is shown this same dotted pair of arrows, but now the pair are rigidly rotated so the arrow corresponding to the line of sight of the ball-thrower toward the center of the carousel is aligned with 12:00 o'clock. The other arrow of the pair locates the ball relative to the center of the carousel, providing the position of the ball as seen by the rotating observer. By following this procedure for several positions, the trajectory in the rotating frame of reference is established as shown by the curved path in the right-hand panel.

The ball travels in the air, and there is no net force upon it. To the stationary observer, the ball follows a straight-line path, so there is no problem squaring this trajectory with zero net force. However, the rotating observer sees a curved path. Kinematics insists that a force (pushing to the right of the instantaneous direction of travel for a counter-clockwise rotation) must be present to cause this curvature, so the rotating observer is forced to invoke a combination of centrifugal and Coriolis forces to provide the net force required to cause the curved trajectory.

Bounced ball

Bird's-eye view of carousel. The carousel rotates clockwise. Two viewpoints are illustrated: that of the camera at the center of rotation rotating with the carousel (left panel) and that of the inertial (stationary) observer (right panel). Both observers agree at any given time just how far the ball is from the center of the carousel, but not on its orientation. Time intervals are 1/10 of time from launch to bounce.

The figure describes a more complex situation where the tossed ball on a turntable bounces off the edge of the carousel and then returns to the tosser, who catches the ball. The effect of Coriolis force on its trajectory is shown again as seen by two observers: an observer (referred to as the "camera") that rotates with the carousel, and an inertial observer. The figure shows a bird's-eye view based upon the same ball speed on forward and return paths. Within each circle, plotted dots show the same time points. In the left panel, from the camera's viewpoint at the center of rotation, the tosser (smiley face) and the rail both are at fixed locations, and the ball makes a very considerable arc on its travel toward the rail, and takes a more direct route on the way back. From the ball tosser's viewpoint, the ball seems to return more quickly than it went (because the tosser is rotating toward the ball on the return flight).

On the carousel, instead of tossing the ball straight at a rail to bounce back, the tosser must throw the ball toward the right of the target and the ball then seems to the camera to bear continuously to the left of its direction of travel to hit the rail (left because the carousel is turning clockwise). The ball appears to bear to the left from direction of travel on both inward and return trajectories. The curved path demands this observer to recognize a leftward net force on the ball. (This force is "fictitious" because it disappears for a stationary observer, as is discussed shortly.) For some angles of launch, a path has portions where the trajectory is approximately radial, and Coriolis force is primarily responsible for the apparent deflection of the ball (centrifugal force is radial from the center of rotation, and causes little deflection on these segments). When a path curves away from radial, however, centrifugal force contributes significantly to deflection.

The ball's path through the air is straight when viewed by observers standing on the ground (right panel). In the right panel (stationary observer), the ball tosser (smiley face) is at 12 o'clock and the rail the ball bounces from is at position 1. From the inertial viewer's standpoint, positions 1, 2, and 3 are occupied in sequence. At position 2 the ball strikes the rail, and at position 3 the ball returns to the tosser. Straight-line paths are followed because the ball is in free flight, so this observer requires that no net force is applied.

Applied to the Earth

The force affecting the motion of air "sliding" over the Earth's surface is the horizontal component of the Coriolis term

${\displaystyle -2\,{\boldsymbol {\Omega \times v}}}$

This component is orthogonal to the velocity over the Earth surface and is given by the expression

${\displaystyle \omega \,v\ 2\,\sin \phi }$

where

${\displaystyle \omega }$ is the spin rate of the Earth

${\displaystyle \phi }$ is the latitude, positive in northern hemisphere and negative in the southern hemisphere

In the northern hemisphere where the sign is positive this force/acceleration, as viewed from above, is to the right of the direction of motion, in the southern hemisphere where the sign is negative this force/acceleration is to the left of the direction of motion

Rotating sphere

Coordinate system at latitude φ with x-axis east, y-axis north and z-axis upward (that is, radially outward from center of sphere).

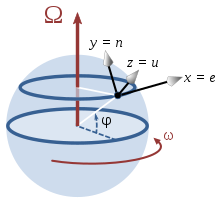
Consider a location with latitude φ on a sphere that is rotating around the north–south axis. A local coordinate system is set up with the x axis horizontally due east, the y axis horizontally due north and the z axis vertically upwards. The rotation vector, velocity of movement and Coriolis acceleration expressed in this local coordinate system (listing components in the order east (e), north (n) and upward (u)) are:

${\displaystyle {\boldsymbol {\Omega }}=\omega {\begin{pmatrix}0\\\cos \varphi \\\sin \varphi \end{pmatrix}}\ ,}$     ${\displaystyle {\boldsymbol {v}}={\begin{pmatrix}v_{e}\\v_{n}\\v_{u}\end{pmatrix}}\ ,}$

${\displaystyle {\boldsymbol {a}}_{C}=-2{\boldsymbol {\Omega \times v}}=2\,\omega \,{\begin{pmatrix}v_{n}\sin \varphi -v_{u}\cos \varphi \\-v_{e}\sin \varphi \\v_{e}\cos \varphi \end{pmatrix}}\ .}$

When considering atmospheric or oceanic dynamics, the vertical velocity is small, and the vertical component of the Coriolis acceleration is small compared with the acceleration due to gravity. For such cases, only the horizontal (east and north) components matter. The restriction of the above to the horizontal plane is (setting v_u = 0):

${\displaystyle {\boldsymbol {v}}={\begin{pmatrix}v_{e}\\v_{n}\end{pmatrix}}\ ,}$     ${\displaystyle {\boldsymbol {a}}_{c}={\begin{pmatrix}v_{n}\\-v_{e}\end{pmatrix}}\ f\ ,}$

where ${\displaystyle f=2\omega \sin \varphi \,}$ is called the Coriolis parameter.

By setting v_n = 0, it can be seen immediately that (for positive φ and ω) a movement due east results in an acceleration due south. Similarly, setting v_e = 0, it is seen that a movement due north results in an acceleration due east. In general, observed horizontally, looking along the direction of the movement causing the acceleration, the acceleration always is turned 90° to the right and of the same size regardless of the horizontal orientation.

As a different case, consider equatorial motion setting φ = 0°. In this case, Ω is parallel to the north or n-axis, and:

${\displaystyle {\boldsymbol {\Omega }}=\omega {\begin{pmatrix}0\\1\\0\end{pmatrix}}\ ,}$     ${\displaystyle {\boldsymbol {v}}={\begin{pmatrix}v_{e}\\v_{n}\\v_{u}\end{pmatrix}}\ ,}$  ${\displaystyle {\boldsymbol {a}}_{C}=-2{\boldsymbol {\Omega \times v}}=2\,\omega \,{\begin{pmatrix}-v_{u}\\0\\v_{e}\end{pmatrix}}\ .}$

Accordingly, an eastward motion (that is, in the same direction as the rotation of the sphere) provides an upward acceleration known as the Eötvös effect, and an upward motion produces an acceleration due west.

For additional examples in other articles, see rotating spheres, apparent motion of stationary objects, and carousel.

Meteorology

This low-pressure system over Iceland spins counterclockwise due to balance between the Coriolis force and the pressure gradient force.

 

Schematic representation of flow around a low-pressure area in the Northern Hemisphere. The Rossby number is low, so the centrifugal force is virtually negligible. The pressure-gradient force is represented by blue arrows, the Coriolis acceleration (always perpendicular to the velocity) by red arrows

 

Schematic representation of inertial circles of air masses in the absence of other forces, calculated for a wind speed of approximately 50 to 70 m/s (110 to 160 mph).

 

Cloud formations in a famous image of Earth from Apollo 17, makes similar circulation directly visible

Perhaps the most important impact of the Coriolis effect is in the large-scale dynamics of the oceans and the atmosphere. In meteorology and oceanography, it is convenient to postulate a rotating frame of reference wherein the Earth is stationary. In accommodation of that provisional postulation, the centrifugal and Coriolis forces are introduced. Their relative importance is determined by the applicable Rossby numbers. Tornadoes have high Rossby numbers, so, while tornado-associated centrifugal forces are quite substantial, Coriolis forces associated with tornadoes are for practical purposes negligible.

Because surface ocean currents are driven by the movement of wind over the water's surface, the Coriolis force also affects the movement of ocean currents and cyclones as well. Many of the ocean's largest currents circulate around warm, high-pressure areas called gyres. Though the circulation is not as significant as that in the air, the deflection caused by the Coriolis effect is what creates the spiralling pattern in these gyres. The spiralling wind pattern helps the hurricane form. The stronger the force from the Coriolis effect, the faster the wind spins and picks up additional energy, increasing the strength of the hurricane.

Air within high-pressure systems rotates in a direction such that the Coriolis force is directed radially inwards, and nearly balanced by the outwardly radial pressure gradient. As a result, air travels clockwise around high pressure in the Northern Hemisphere and anticlockwise in the Southern Hemisphere. Air around low-pressure rotates in the opposite direction, so that the Coriolis force is directed radially outward and nearly balances an inwardly radial pressure gradient.

Flow around a low-pressure area

If a low-pressure area forms in the atmosphere, air tends to flow in towards it, but is deflected perpendicular to its velocity by the Coriolis force. A system of equilibrium can then establish itself creating circular movement, or a cyclonic flow. Because the Rossby number is low, the force balance is largely between the pressure-gradient force acting towards the low-pressure area and the Coriolis force acting away from the center of the low pressure.

Instead of flowing down the gradient, large scale motions in the atmosphere and ocean tend to occur perpendicular to the pressure gradient. This is known as geostrophic flow. On a non-rotating planet, fluid would flow along the straightest possible line, quickly eliminating pressure gradients. The geostrophic balance is thus very different from the case of "inertial motions" (see below), which explains why mid-latitude cyclones are larger by an order of magnitude than inertial circle flow would be.

This pattern of deflection, and the direction of movement, is called Buys-Ballot's law. In the atmosphere, the pattern of flow is called a cyclone. In the Northern Hemisphere the direction of movement around a low-pressure area is anticlockwise. In the Southern Hemisphere, the direction of movement is clockwise because the rotational dynamics is a mirror image there. At high altitudes, outward-spreading air rotates in the opposite direction. Cyclones rarely form along the equator due to the weak Coriolis effect present in this region.

Inertial circles

An air or water mass moving with speed ${\displaystyle v\,}$ subject only to the Coriolis force travels in a circular trajectory called an 'inertial circle'. Since the force is directed at right angles to the motion of the particle, it moves with a constant speed around a circle whose radius ${\displaystyle R}$ is given by:

${\displaystyle R={\frac {v}{f}}\,}$

where ${\displaystyle f}$ is the Coriolis parameter ${\displaystyle 2\Omega \sin \varphi }$, introduced above (where ${\displaystyle \varphi }$ is the latitude). The time taken for the mass to complete a full circle is therefore ${\displaystyle 2\pi /f}$. The Coriolis parameter typically has a mid-latitude value of about 10⁻⁴ s⁻¹; hence for a typical atmospheric speed of 10 m/s (22 mph) the radius is 100 km (62 mi), with a period of about 17 hours. For an ocean current with a typical speed of 10 cm/s (0.22 mph), the radius of an inertial circle is 1 km (0.6 mi). These inertial circles are clockwise in the Northern Hemisphere (where trajectories are bent to the right) and anticlockwise in the Southern Hemisphere.

If the rotating system is a parabolic turntable, then ${\displaystyle f}$ is constant and the trajectories are exact circles. On a rotating planet, ${\displaystyle f}$ varies with latitude and the paths of particles do not form exact circles. Since the parameter ${\displaystyle f}$ varies as the sine of the latitude, the radius of the oscillations associated with a given speed are smallest at the poles (latitude = ±90°), and increase toward the equator.

Other terrestrial effects

The Coriolis effect strongly affects the large-scale oceanic and atmospheric circulation, leading to the formation of robust features like jet streams and western boundary currents. Such features are in geostrophic balance, meaning that the Coriolis and pressure gradient forces balance each other. Coriolis acceleration is also responsible for the propagation of many types of waves in the ocean and atmosphere, including Rossby waves and Kelvin waves. It is also instrumental in the so-called Ekman dynamics in the ocean, and in the establishment of the large-scale ocean flow pattern called the Sverdrup balance.

Eötvös effect

The practical impact of the "Coriolis effect" is mostly caused by the horizontal acceleration component produced by horizontal motion.

There are other components of the Coriolis effect. Westward-travelling objects are deflected downwards, while Eastward-travelling objects are deflected upwards. This is known as the Eötvös effect. This aspect of the Coriolis effect is greatest near the equator. The force produced by the Eötvös effect is similar to the horizontal component, but the much larger vertical forces due to gravity and pressure suggest that it is unimportant in the hydrostatic equilibrium. However, in the atmosphere, winds are associated with small deviations of pressure from the hydrostatic equilibrium. In the tropical atmosphere, the order of magnitude of the pressure deviations is so small that the contribution of the Eötvös effect to the pressure deviations is considerable.

In addition, objects travelling upwards (i.e., out) or downwards (i.e., in) are deflected to the west or east respectively. This effect is also the greatest near the equator. Since vertical movement is usually of limited extent and duration, the size of the effect is smaller and requires precise instruments to detect. For example, idealized numerical modeling studies suggest that this effect can directly affect tropical large-scale wind field by roughly 10% given long-duration (2 weeks or more) heating or cooling in the atmosphere. Moreover, in the case of large changes of momentum, such as a spacecraft being launched into orbit, the effect becomes significant. The fastest and most fuel-efficient path to orbit is a launch from the equator that curves to a directly eastward heading.

Intuitive example

Imagine a train that travels through a frictionless railway line along the equator. Assume that, when in motion, it moves at the necessary speed to complete a trip around the world in one day (465 m/s). The Coriolis effect can be considered in three cases: when the train travels west, when it is at rest, and when it travels east. In each case, the Coriolis effect can be calculated from the rotating frame of reference on Earth first, and then checked against a fixed inertial frame. The image below illustrates the three cases as viewed by an observer at rest in a (near) inertial frame from a fixed point above the North Pole along the Earth's axis of rotation; the train is denoted by a few red pixels, fixed at the left side in the leftmost picture, moving in the others ${\displaystyle (1{\text{day}}\;{\overset {\land }{=}}\;8{\text{s}}):}$

1. The train travels toward the west: In that case, it moves against the direction of rotation. Therefore, on the Earth's rotating frame the Coriolis term is pointed inwards towards the axis of rotation (down). This additional force downwards should cause the train to be heavier while moving in that direction.

• If one looks at this train from the fixed non-rotating frame on top of the center of the Earth, at that speed it remains stationary as the Earth spins beneath it. Hence, the only force acting on it is gravity and the reaction from the track. This force is greater (by 0.34%) than the force that the passengers and the train experience when at rest (rotating along with Earth). This difference is what the Coriolis effect accounts for in the rotating frame of reference.

2. The train comes to a stop: From the point of view on the Earth's rotating frame, the velocity of the train is zero, thus the Coriolis force is also zero and the train and its passengers recuperate their usual weight.

• From the fixed inertial frame of reference above Earth, the train now rotates along with the rest of the Earth. 0.34% of the force of gravity provides the centripetal force needed to achieve the circular motion on that frame of reference. The remaining force, as measured by a scale, makes the train and passengers "lighter" than in the previous case.

3. The train travels east. In this case, because it moves in the direction of Earth's rotating frame, the Coriolis term is directed outward from the axis of rotation (up). This upward force makes the train seem lighter still than when at rest.

Graph of the force experienced by a 10-kilogram object as a function of its speed moving along Earth's equator (as measured within the rotating frame). (Positive force in the graph is directed upward. Positive speed is directed eastward and negative speed is directed westward).

• From the fixed inertial frame of reference above Earth, the train travelling east now rotates at twice the rate as when it was at rest—so the amount of centripetal force needed to cause that circular path increases leaving less force from gravity to act on the track. This is what the Coriolis term accounts for on the previous paragraph.
• As a final check one can imagine a frame of reference rotating along with the train. Such frame would be rotating at twice the angular velocity as Earth's rotating frame. The resulting centrifugal force component for that imaginary frame would be greater. Since the train and its passengers are at rest, that would be the only component in that frame explaining again why the train and the passengers are lighter than in the previous two cases.

This also explains why high-speed projectiles that travel west are deflected down, and those that travel east are deflected up. This vertical component of the Coriolis effect is called the Eötvös effect.

The above example can be used to explain why the Eötvös effect starts diminishing when an object is travelling westward as its tangential speed increases above Earth's rotation (465 m/s). If the westward train in the above example increases speed, part of the force of gravity that pushes against the track accounts for the centripetal force needed to keep it in circular motion on the inertial frame. Once the train doubles its westward speed at 930 m/s that centripetal force becomes equal to the force the train experiences when it stops. From the inertial frame, in both cases it rotates at the same speed but in the opposite directions. Thus, the force is the same cancelling completely the Eötvös effect. Any object that moves westward at a speed above 930 m/s experiences an upward force instead. In the figure, the Eötvös effect is illustrated for a 10 kilogram object on the train at different speeds. The parabolic shape is because the centripetal force is proportional to the square of the tangential speed. On the inertial frame, the bottom of the parabola is centered at the origin. The offset is because this argument uses the Earth's rotating frame of reference. The graph shows that the Eötvös effect is not symmetrical, and that the resulting downward force experienced by an object that travels west at high velocity is less than the resulting upward force when it travels east at the same speed.

Draining in bathtubs and toilets

Contrary to popular misconception, bathtubs, toilets, and other water receptacles do not drain in opposite directions in the northern and southern hemispheres. This is because the magnitude of the Coriolis force is negligible at this scale. Forces determined by the initial conditions of the water (e.g. the geometry of the drain, the geometry of the receptacle, pre-existing momentum of the water, etc.) are likely to be orders of magnitude greater than the Coriolis force and hence will determine the direction of water rotation, if any. For example, identical toilets flushed in both hemispheres drain in the same direction, and this direction is determined mostly by the shape of the toilet bowl.

Under real-world conditions, the Coriolis force does not influence the direction of water flow perceptibly. Only if the water is so still that the effective rotation rate of the Earth is faster than that of the water relative to its container, and if externally applied torques (such as might be caused by flow over an uneven bottom surface) are small enough, the Coriolis effect may indeed determine the direction of the vortex. Without such careful preparation, the Coriolis effect will to be much smaller than various other influences on drain direction such as any residual rotation of the water and the geometry of the container.

Laboratory testing of draining water under atypical conditions

In 1962, Prof. Ascher Shapiro performed an experiment at MIT to test the Coriolis force on a large basin of water, 2 metres across, with a small wooden cross above the plug hole to display the direction of rotation, covering it and waiting for at least 24 hours for the water to settle. Under these precise laboratory conditions, he demonstrated the effect and consistent counterclockwise rotation. Consistent clockwise rotation in the southern hemisphere was confirmed in 1965 by Dr Lloyd Trefethen at the University of Sydney. See the article "Bath-Tub Vortex" by Shapiro in the journal Nature (15 December 1962, vol. 196, p. 1080–1081) and the follow-up article "The Bath-Tub Vortex in the Southern Hemisphere" by Dr Trefethen in the same journal (4 September 1965, vol.207, p. 1084-1085).

Shapiro reported that,

Both schools of thought are in some sense correct. For the everyday observations of the kitchen sink and bath-tub variety, the direction of the vortex seems to vary in an unpredictable manner with the date, the time of day, and the particular household of the experimenter. But under well-controlled conditions of experimentation, the observer looking downward at a drain in the northern hemisphere will always see a counter-clockwise vortex, while one in the southern hemisphere will always see a clockwise vortex. In a properly designed experiment, the vortex is produced by Coriolis forces, which are counter-clockwise in the northern hemisphere.

Trefethen reported that, "Clockwise rotation was observed in all five of the later tests that had settling times of 18 h or more."

Ballistic trajectories

The Coriolis force is important in external ballistics for calculating the trajectories of very long-range artillery shells. The most famous historical example was the Paris gun, used by the Germans during World War I to bombard Paris from a range of about 120 km (75 mi). The Coriolis force minutely changes the trajectory of a bullet, affecting accuracy at extremely long distances. It is adjusted for by accurate long-distance shooters, such as snipers. At the latitude of Sacramento, California, a 1,000 yd (910 m) northward shot would be deflected 2.8 in (71 mm) to the right. There is also a vertical component, explained in the Eötvös effect section above, which causes westward shots to hit low, and eastward shots to hit high.

The effects of the Coriolis force on ballistic trajectories should not be confused with the curvature of the paths of missiles, satellites, and similar objects when the paths are plotted on two-dimensional (flat) maps, such as the Mercator projection. The projections of the three-dimensional curved surface of the Earth to a two-dimensional surface (the map) necessarily results in distorted features. The apparent curvature of the path is a consequence of the sphericity of the Earth and would occur even in a non-rotating frame.

Trajectory, ground track, and drift of a typical projectile. The axes are not to scale.

The Coriolis force on a moving projectile depends on velocity components in all three directions, latitude and azimuth. The directions are typically downrange (the direction that the gun is initially pointing), vertical, and cross-range.

${\displaystyle A_{\mathrm {X} }=-2\omega (V_{\mathrm {Y} }\cos \theta _{\mathrm {lat} }\sin \phi _{\mathrm {az} }+V_{\mathrm {Z} }\sin \theta _{\mathrm {lat} })}$

${\displaystyle A_{\mathrm {Y} }=2\omega (V_{\mathrm {X} }\cos \theta _{\mathrm {lat} }\sin \phi _{\mathrm {az} }+V_{\mathrm {Z} }\cos \theta _{\mathrm {lat} }\cos \phi _{\mathrm {az} })}$

${\displaystyle A_{\mathrm {Z} }=2\omega (V_{\mathrm {X} }\sin \theta _{\mathrm {lat} }-V_{\mathrm {Y} }\cos \theta _{\mathrm {lat} }\cos \phi _{\mathrm {az} })}$

where

${\displaystyle A_{\mathrm {X} }}$ = down-range acceleration.

${\displaystyle A_{\mathrm {Y} }}$ = vertical acceleration with positive indicating acceleration upward.

${\displaystyle A_{\mathrm {Z} }}$ = cross-range acceleration with positive indicating acceleration to the right.

${\displaystyle V_{\mathrm {X} }}$ = down-range velocity.

${\displaystyle V_{\mathrm {Y} }}$ = vertical velocity with positive indicating upward.

${\displaystyle V_{\mathrm {Z} }}$ = cross-range velocity with positive indicating velocity to the right.

${\displaystyle \omega }$ = angular velocity of the earth = 0.00007292 rad/sec (based on a sidereal day).

${\displaystyle \theta _{\mathrm {lat} }}$ = latitude with positive indicating Northern hemisphere.

${\displaystyle \phi _{\mathrm {az} }}$ = azimuth measured clockwise from due North.

Visualization of the Coriolis effect

Fluid assuming a parabolic shape as it is rotating

 

Object moving frictionlessly over the surface of a very shallow parabolic dish. The object has been released in such a way that it follows an elliptical trajectory.
Left: The inertial point of view.
Right: The co-rotating point of view.

The forces at play in the case of a curved surface.
Red: gravity
Green: the normal force
Blue: the net resultant centripetal force.

To demonstrate the Coriolis effect, a parabolic turntable can be used. On a flat turntable, the inertia of a co-rotating object forces it off the edge. However, if the turntable surface has the correct paraboloid (parabolic bowl) shape (see the figure) and rotates at the corresponding rate, the force components shown in the figure make the component of gravity tangential to the bowl surface exactly equal to the centripetal force necessary to keep the object rotating at its velocity and radius of curvature (assuming no friction). (See banked turn.) This carefully contoured surface allows the Coriolis force to be displayed in isolation.

Discs cut from cylinders of dry ice can be used as pucks, moving around almost frictionlessly over the surface of the parabolic turntable, allowing effects of Coriolis on dynamic phenomena to show themselves. To get a view of the motions as seen from the reference frame rotating with the turntable, a video camera is attached to the turntable so as to co-rotate with the turntable, with results as shown in the figure. In the left panel of the figure, which is the viewpoint of a stationary observer, the gravitational force in the inertial frame pulling the object toward the center (bottom ) of the dish is proportional to the distance of the object from the center. A centripetal force of this form causes the elliptical motion. In the right panel, which shows the viewpoint of the rotating frame, the inward gravitational force in the rotating frame (the same force as in the inertial frame) is balanced by the outward centrifugal force (present only in the rotating frame). With these two forces balanced, in the rotating frame the only unbalanced force is Coriolis (also present only in the rotating frame), and the motion is an inertial circle. Analysis and observation of circular motion in the rotating frame is a simplification compared with analysis and observation of elliptical motion in the inertial frame.

Because this reference frame rotates several times a minute rather than only once a day like the Earth, the Coriolis acceleration produced is many times larger and so easier to observe on small time and spatial scales than is the Coriolis acceleration caused by the rotation of the Earth.

In a manner of speaking, the Earth is analogous to such a turntable. The rotation has caused the planet to settle on a spheroid shape, such that the normal force, the gravitational force and the centrifugal force exactly balance each other on a "horizontal" surface.

The Coriolis effect caused by the rotation of the Earth can be seen indirectly through the motion of a Foucault pendulum.

Coriolis effects in other areas

Coriolis flow meter

A practical application of the Coriolis effect is the mass flow meter, an instrument that measures the mass flow rate and density of a fluid flowing through a tube. The operating principle involves inducing a vibration of the tube through which the fluid passes. The vibration, though not completely circular, provides the rotating reference frame that gives rise to the Coriolis effect. While specific methods vary according to the design of the flow meter, sensors monitor and analyze changes in frequency, phase shift, and amplitude of the vibrating flow tubes. The changes observed represent the mass flow rate and density of the fluid.

Molecular physics

In polyatomic molecules, the molecule motion can be described by a rigid body rotation and internal vibration of atoms about their equilibrium position. As a result of the vibrations of the atoms, the atoms are in motion relative to the rotating coordinate system of the molecule. Coriolis effects are therefore present, and make the atoms move in a direction perpendicular to the original oscillations. This leads to a mixing in molecular spectra between the rotational and vibrational levels, from which Coriolis coupling constants can be determined.

Gyroscopic precession

When an external torque is applied to a spinning gyroscope along an axis that is at right angles to the spin axis, the rim velocity that is associated with the spin becomes radially directed in relation to the external torque axis. This causes a Torque Induced force to act on the rim in such a way as to tilt the gyroscope at right angles to the direction that the external torque would have tilted it. This tendency has the effect of keeping spinning bodies in their rotational frame.

Insect flight

Flies (Diptera) and some moths (Lepidoptera) exploit the Coriolis effect in flight with specialized appendages and organs that relay information about the angular velocity of their bodies.

Coriolis forces resulting from linear motion of these appendages are detected within the rotating frame of reference of the insects' bodies. In the case of flies, their specialized appendages are dumbbell shaped organs located just behind their wings called "halteres".

The fly's halteres oscillate in a plane at the same beat frequency as the main wings so that any body rotation results in lateral deviation of the halteres from their plane of motion.

In moths, their antennae are known to be responsible for the sensing of Coriolis forces in the similar manner as with the halteres in flies. In both flies and moths, a collection of mechanosensors at the base of the appendage are sensitive to deviations at the beat frequency, correlating to rotation in the pitch and roll planes, and at twice the beat frequency, correlating to rotation in the yaw plane.

Lagrangian point stability

In astronomy, Lagrangian points are five positions in the orbital plane of two large orbiting bodies where a small object affected only by gravity can maintain a stable position relative to the two large bodies. The first three Lagrangian points (L₁, L₂, L₃) lie along the line connecting the two large bodies, while the last two points (L₄ and L₅) each form an equilateral triangle with the two large bodies. The L₄ and L₅ points, although they correspond to maxima of the effective potential in the coordinate frame that rotates with the two large bodies, are stable due to the Coriolis effect. The stability can result in orbits around just L₄ or L₅, known as tadpole orbits, where trojans can be found. It can also result in orbits that encircle L₃, L₄, and L₅, known as horseshoe orbits.

Artificial gravity

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Artificial_gravity 

 

Gemini 11 Agena tethered operations

 

Proposed Nautilus-X International space station centrifuge demo concept, 2011.

Artificial gravity (sometimes referred to as pseudogravity) is the creation of an inertial force that mimics the effects of a gravitational force, usually by rotation. Artificial gravity, or rotational gravity, is thus the appearance of a centrifugal force in a rotating frame of reference (the transmission of centripetal acceleration via normal force in the non-rotating frame of reference), as opposed to the force experienced in linear acceleration, which by the equivalence principle is indistinguishable from gravity. In a more general sense, "artificial gravity" may also refer to the effect of linear acceleration, e.g. by means of a rocket engine.

Rotational simulated gravity has been used in simulations to help astronauts train for extreme conditions. Rotational simulated gravity has been proposed as a solution in human spaceflight to the adverse health effects caused by prolonged weightlessness. However, there are no current practical outer space applications of artificial gravity for humans due to concerns about the size and cost of a spacecraft necessary to produce a useful centripetal force comparable to the gravitational field strength on Earth (g). Scientists are concerned about the effect of such a system on the inner ear of the occupants. The concern is that using centripetal force to create artificial gravity will cause disturbances in the inner ear leading to nausea and disorientation. The adverse effects may prove intolerable for the occupants.

Centripetal force

Artificial gravity space station. 1969 NASA concept. A drawback is that the astronauts would be walking back and forth between higher gravity near the ends and lower gravity near the center.

Artificial gravity can be created using a centripetal force. A centripetal force directed towards the center of the turn is required for any object to move in a circular path.

In the context of a rotating space station it is the normal force provided by the spacecraft's hull that acts as centripetal force. Thus, the "gravity" force felt by an object is the centrifugal force perceived in the rotating frame of reference as pointing "downwards" towards the hull. In accordance with Newton's Third Law the value of little g (the perceived "downward" acceleration) is equal in magnitude and opposite in direction to the centripetal acceleration.

Mechanism

Balls in a rotating spacecraft

From the point of view of people rotating with the habitat, artificial gravity by rotation behaves in some ways similarly to normal gravity but with the following differences:

• Centrifugal force varies with distance: Unlike real gravity, which pulls towards a center of the planet, the apparent centrifugal force felt by observers in the habitat pushes radially outward from the center, and assuming a fixed rotation rate (constant angular velocity), the centrifugal force is directly proportional to the distance from the center of the habitat. With a small radius of rotation, the amount of gravity felt at one's head would be significantly different from the amount felt at one's feet. This could make movement and changing body position awkward. In accordance with the physics involved, slower rotations or larger rotational radii would reduce or eliminate this problem. Similarly the linear velocity of the habitat should be significantly higher than the relative velocities with which an astronaut will change position within it. Otherwise moving in the direction of the rotation will increase the felt gravity (while moving in the opposite direction will decrease it) to the point that it should cause problems.
• The Coriolis effect gives an apparent force that acts on objects that move relative to a rotating reference frame. This apparent force acts at right angles to the motion and the rotation axis and tends to curve the motion in the opposite sense to the habitat's spin. If an astronaut inside a rotating artificial gravity environment moves towards or away from the axis of rotation, they will feel a force pushing them towards or away from the direction of spin. These forces act on the semicircular canals of the inner ear and can cause dizziness, nausea and disorientation. Lengthening the period of rotation (slower spin rate) reduces the Coriolis force and its effects. It is generally believed that at 2 rpm or less, no adverse effects from the Coriolis forces will occur, although humans have been shown to adapt to rates as high as 23 rpm. It is not yet known whether very long exposures to high levels of Coriolis forces can increase the likelihood of becoming accustomed. The nausea-inducing effects of Coriolis forces can also be mitigated by restraining movement of the head.

This form of artificial gravity has additional engineering issues:

• Kinetic energy and angular momentum: Spinning up (or down) parts or all of the habitat requires energy, while angular momentum must be conserved. This would require a propulsion system and expendable propellant, or could be achieved without expending mass, by an electric motor and a counterweight, such as a reaction wheel or possibly another living area spinning in the opposite direction.
• Extra strength is needed in the structure to keep it from flying apart because of the rotation. However, the amount of structure needed over and above that to hold a breathable atmosphere (10 tons force per square meter at 1 atmosphere) is relatively modest for most structures.
• If parts of the structure are intentionally not spinning, friction and similar torques will cause the rates of spin to converge (as well as causing the otherwise stationary parts to spin), requiring motors and power to be used to compensate for the losses due to friction.
• Depending upon the spacecraft's configuration a pressure seal between stationary and rotating sections might be required.

Formulae
${\displaystyle R=a\left({\frac {T}{2\pi }}\right)^{2},}$ ${\displaystyle a=R\left({\frac {2\pi }{T}}\right)^{2}\quad (T>0),}$ ${\displaystyle T=2\pi {\sqrt {\frac {R}{a}}}\quad (a>0),}$ where: R = Radius from center of rotation a = Artificial gravity T = Rotating spacecraft period

Speed in rpm for a centrifuge of a given radius to achieve a given g-force

Human spaceflight

The engineering challenges of creating a rotating spacecraft are comparatively modest to any other proposed approach. Theoretical spacecraft designs using artificial gravity have a great number of variants with intrinsic problems and advantages. The formula for the centripetal force implies that the radius of rotation grows with the square of the rotating spacecraft period, so a doubling of the period requires a fourfold increase in the radius of rotation. For example, to produce standard gravity, ɡ₀ = 9.8 m/s² with a rotating spacecraft period of 15 s, the radius of rotation would have to be 56 m (184 ft), while a period of 30 s would require it to be 224 m (735 ft). To reduce mass, the support along the diameter could consist of nothing but a cable connecting two sections of the spaceship. Among the possible solutions include a habitat module and a counterweight consisting of every other part of the spacecraft, alternatively two habitable modules of similar weight could be attached.

Whatever design is chosen, it would be necessary for the spacecraft to possess some means to quickly transfer ballast from one section to another, otherwise, even small shifts in mass could cause a substantial shift in the spacecraft's axis, which would result in a dangerous "wobble." One possible solution would be to engineer the spacecraft's plumbing system to serve this purpose, using drinking water and/or wastewater as the ballast.

It is not yet known whether exposure to high gravity for short periods is as beneficial to health as continuous exposure to normal gravity. It is also not known how effective low levels of gravity would be at countering the adverse effects on the health of weightlessness. Artificial gravity at 0.1g and a rotating spacecraft period of 30 s would require a radius of only 22 m (72 ft). Likewise, at a radius of 10 m, a period of just over 6 s would be required to produce standard gravity (at the hips; gravity would be 11% higher at the feet), while 4.5 s would produce 2g. If brief exposure to high gravity can negate the harmful effects of weightlessness, then a small centrifuge could be used as an exercise area.

Gemini missions

The Gemini 11 mission attempted to produce artificial gravity by rotating the capsule around the Agena Target Vehicle to which it was attached by a 36-meter tether. They were able to generate a small amount of artificial gravity, about 0.00015 g, by firing their side thrusters to slowly rotate the combined craft like a slow-motion pair of bolas. The resultant force was too small to be felt by either astronaut, but objects were observed moving towards the "floor" of the capsule. The Gemini 8 mission achieved artificial gravity for a few minutes. This, however, was due to an electrical fault causing continuous firing of one thruster. The acceleration forces upon the crew were high (around 4 g), and the mission had to be urgently terminated.

Health benefits

Artificial gravity has been suggested for interplanetary journeys to Mars

Artificial gravity has been suggested as a solution to the various health risks associated with spaceflight. In 1964, the Soviet space program believed that a human could not survive more than 14 days in space due to a fear that the heart and blood vessels would be unable to adapt to the weightless conditions. This fear was eventually discovered to be unfounded as spaceflights have now lasted up to 437 consecutive days, with missions aboard the International Space Station commonly lasting 6 months. However, the question of human safety in space did launch an investigation into the physical effects of prolonged exposure to weightlessness. In June 1991, a Spacelab Life Sciences 1 flight performed 18 experiments on two men and two women over a period of nine days. In an environment without gravity, it was concluded that the response of white blood cells and muscle mass decreased. Additionally, within the first 24 hours spent in a weightless environment, blood volume decreased by 10%. Long weightless periods can cause brain-swelling and eyesight problems. Upon return to earth, the effects of prolonged weightlessness continue to affect the human body as fluids pool back to the lower body, the heart rate rises, a drop in blood pressure occurs and there is a reduced ability to exercise.

Artificial gravity, due to its ability to mimic the behavior of gravity on the human body has been suggested as one of the most encompassing manners of combating the physical effects inherent with weightless environments. Other measures that have been suggested as symptomatic treatments include exercise, diet and penguin suits. However, criticism of those methods lies in the fact that they do not fully eliminate the health problems and require a variety of solutions to address all issues. Artificial gravity, in contrast, would remove the weightlessness inherent with space travel. By implementing artificial gravity, space travelers would never have to experience weightlessness or the associated side effects. Especially in a modern-day six-month journey to Mars, exposure to artificial gravity is suggested in either a continuous or intermittent form to prevent extreme debilitation to the astronauts during travel.

Proposals

Rotating Mars spacecraft - 1989 NASA concept.

A number of proposals have incorporated artificial gravity into their design:

• Discovery II: a 2005 vehicle proposal capable of delivering a 172-metric-ton crew to Jupiter's orbit in 118 days. A very small portion of the 1,690 metric-ton craft would incorporate a centrifugal crew station.
• Multi-Mission Space Exploration Vehicle (MMSEV): a 2011 NASA proposal for a long-duration crewed space transport vehicle; it included a rotational artificial gravity space habitat intended to promote crew-health for a crew of up to six persons on missions of up to two years in duration. The torus-ring centrifuge would utilize both standard metal-frame and inflatable spacecraft structures and would provide 0.11 to 0.69g if built with the 40 feet (12 m) diameter option.
• ISS Centrifuge Demo: a 2011 NASA proposal for a demonstration project preparatory to the final design of the larger torus centrifuge space habitat for the Multi-Mission Space Exploration Vehicle. The structure would have an outside diameter of 30 feet (9.1 m) with a ring interior cross-section diameter of 30 inches (760 mm). It would provide 0.08 to 0.51g partial gravity. This test and evaluation centrifuge would have the capability to become a Sleep Module for ISS crew.

Artist view of TEMPO³ in orbit.

• Mars Direct: A plan for a manned Mars mission created by NASA engineers Robert Zubrin and David Baker in 1990, later expanded upon in Zubrin's 1996 book The Case for Mars. The "Mars Habitat Unit", which would carry astronauts to Mars to join the previously launched "Earth Return Vehicle", would have had artificial gravity generated during flight by tying the spent upper stage of the booster to the Habitat Unit, and setting them both rotating about a common axis.
• The proposed Tempo3 mission rotates two halves of a spacecraft connected by a tether to test the feasibility of simulating gravity on a crewed mission to Mars.
• The Mars Gravity Biosatellite was a proposed mission meant to study the effect of artificial gravity on mammals. An artificial gravity field of 0.38 g (equivalent to Mars's surface gravity) was to be produced by rotation (32 rpm, radius of ca. 30 cm). Fifteen mice would have orbited Earth (Low Earth orbit) for five weeks and then land alive. However, the program was canceled on 24 June 2009, due to lack of funding and shifting priorities at NASA.

Issues with implementation

Some of the reasons that artificial gravity remains unused today in spaceflight trace back to the problems inherent in implementation. One of the realistic methods of creating artificial gravity is a centripetal force pulling a person towards a relative floor. In that model, however, issues arise in the size of the spacecraft. As expressed by John Page and Matthew Francis, the smaller a spacecraft (the shorter the radius of rotation), the more rapid the rotation that is required. As such, to simulate gravity, it would be better to utilize a larger spacecraft that rotates slowly. The requirements on size with regard to rotation are due to the differing forces on parts of the body at different distances from the center of rotation. If parts of the body closer to the rotational center experience a force significantly different from parts farther from the center, then this could have adverse effects. Additionally, questions remain as to what the best way is to initially set the rotating motion in place without disturbing the stability of the whole spacecraft's orbit. At the moment, there is not a ship massive enough to meet the rotation requirements, and the costs associated with building, maintaining, and launching such a craft are extensive.

In general, with the limited health effects present in shorter spaceflights, as well as the high cost of research, application of artificial gravity is often stunted and sporadic.

In science fiction

Several science fiction novels, films and series have featured artificial gravity production. In the movie 2001: A Space Odyssey, a rotating centrifuge in the Discovery spacecraft provides artificial gravity. In the novel The Martian, the Hermes spacecraft achieves artificial gravity by design; it employs a ringed structure, at whose periphery forces around 40% of Earth's gravity are experienced, similar to Mars' gravity. The movie Interstellar features a spacecraft called the Endurance that can rotate on its center axis to create artificial gravity, controlled by retro thrusters on the ship. The 2021 film Stowaway features the upper stage of launch vehicle is connected by 450 meter long tethers to the ship's main hull, acting as a counterweight for inertia-based artificial gravity.

Centrifuges

High-G training is done by aviators and astronauts who are subject to high levels of acceleration ('G') in large-radius centrifuges. It is designed to prevent a g-induced loss Of consciousness (abbreviated G-LOC), a situation when g-forces move the blood away from the brain to the extent that consciousness is lost. Incidents of acceleration-induced loss of consciousness have caused fatal accidents in aircraft capable of sustaining high-g for considerable periods.

In amusement parks, pendulum rides and centrifuges provide rotational force. Roller coasters also do, whenever they go over dips, humps, or loops. When going over a hill, time in which zero or negative gravity is felt is called air time, or "airtime", which can be divided into "floater air time" (for zero gravity) and "ejector air time" (for negative gravity).

Linear acceleration

Linear acceleration is another method of generating artificial gravity, by using the thrust from a spacecraft's engines to create the illusion of being under a gravitational pull. A spacecraft under constant acceleration in a straight line would have the appearance of a gravitational pull in the direction opposite of the acceleration, as the thrust from the engines would cause the spacecraft to "push" itself up into the objects and persons inside of the vessel, thus creating the feeling of weight. This is because of Newton's third law: the weight that one would feel standing in a linearly accelerating spacecraft would not be a true gravitational pull, but simply the reaction of oneself pushing against the craft's hull as it pushes back. Similarly, objects that would otherwise be free-floating within the spacecraft if it were not accelerating would "fall" towards the engines when it started accelerating, as a consequence of Newton's first law: the floating object would remain at rest, while the spacecraft would accelerate towards it, and appear to an observer within that the object was "falling".

To emulate artificial gravity on Earth, spacecraft using linear acceleration gravity may be built similar to a skyscraper, with its engines as the bottom "floor". If the spacecraft were to accelerate at the rate of 1g—Earth's gravitational pull—the individuals inside would be pressed into the hull at the same force, and thus be able to walk and behave as if they were on Earth.

This form of artificial gravity is desirable because it could functionally create the illusion of a gravity field that is uniform and unidirectional throughout a spacecraft, without the need for large, spinning rings, whose fields may not be uniform, not unidirectional with respect to the spacecraft, and require constant rotation. This would also have the advantage of relatively high speed: a spaceship accelerating at 1g, 9.8 m/s², for the first half of the journey, and then decelerating for the other half, could reach Mars within a few days. Similarly, a hypothetical space travel using constant acceleration of 1g for one year would reach relativistic speeds and allow for a round trip to the nearest star, Proxima Centauri. As such, low-impulse but long-term linear acceleration has been proposed for various interplanetary missions. For example, even heavy (100 ton) cargo payloads to Mars could be transported to Mars in 27 months and retain approximately 55 percent of the LEO vehicle mass upon arrival into a Mars orbit, providing a low-gravity gradient to the spacecraft during the entire journey.

This form of gravity is not without challenges, however. At present, the only practical engines that could propel a vessel fast enough to reach speeds comparable to Earth's gravitational pull require chemical reaction rockets, which expel reaction mass to achieve thrust, and thus the acceleration could only last for as long as a vessel had fuel. The vessel would also need to be constantly accelerating and at a constant speed to maintain the gravitational effect, and thus would not have gravity while stationary, and could experience significant swings in g-forces if the vessel were to accelerate above or below 1g. Further, for point-to-point journeys, such as Earth-Mars transits, vessels would need to constantly accelerate for half the journey, turn off their engines, perform a 180° flip, reactivate their engines, and then begin decelerating towards the target destination, requiring everything inside the vessel to experience weightlessness and possibly be secured down for the duration of the flip.

A propulsion system with a very high specific impulse (that is, good efficiency in the use of reaction mass that must be carried along and used for propulsion on the journey) could accelerate more slowly producing useful levels of artificial gravity for long periods of time. A variety of electric propulsion systems provide examples. Two examples of this long-duration, low-thrust, high-impulse propulsion that have either been practically used on spacecraft or are planned in for near-term in-space use are Hall effect thrusters and Variable Specific Impulse Magnetoplasma Rockets (VASIMR). Both provide very high specific impulse but relatively low thrust, compared to the more typical chemical reaction rockets. They are thus ideally suited for long-duration firings which would provide limited amounts of, but long-term, milli-g levels of artificial gravity in spacecraft.

In a number of science fiction plots, acceleration is used to produce artificial gravity for interstellar spacecraft, propelled by as yet theoretical or hypothetical means.

This effect of linear acceleration is well understood, and is routinely used for 0g cryogenic fluid management for post-launch (subsequent) in-space firings of upper stage rockets.

Roller coasters, especially launched roller coasters or those that rely on electromagnetic propulsion, can provide linear acceleration "gravity", and so can relatively high acceleration vehicles, such as sports cars. Linear acceleration can be used to provide air-time on roller coasters and other thrill rides.

Simulating microgravity

Parabolic flight

Weightless Wonder is the nickname for the NASA aircraft that flies parabolic trajectories and briefly provides a nearly weightless environment in which to train astronauts, conduct research, and film motion pictures. The parabolic trajectory creates a vertical linear acceleration which matches that of gravity, giving zero-g for a short time, usually 20–30 seconds, followed by approximately 1.8g for a similar period. The nickname Vomit Comet is also used to refer to motion sickness that is often experienced by the aircraft passengers during these parabolic trajectories. Such reduced gravity aircraft are nowadays operated by several organizations worldwide.

Neutral buoyancy

The Neutral Buoyancy Laboratory (NBL) is an astronaut training facility at the Sonny Carter Training Facility at the NASA Johnson Space Center in Houston, Texas. The NBL is a large indoor pool of water, the largest in the world, in which astronauts may perform simulated EVA tasks in preparation for space missions. The NBL contains full-sized mock-ups of the Space Shuttle cargo bay, flight payloads, and the International Space Station (ISS).

The principle of neutral buoyancy is used to simulate the weightless environment of space. The suited astronauts are lowered into the pool using an overhead crane and their weight is adjusted by support divers so that they experience no buoyant force and no rotational moment about their center of mass. The suits worn in the NBL are down-rated from fully flight-rated EMU suits like those in use on the space shuttle and International Space Station.

The NBL tank is 202 feet (62 m) in length, 102 feet (31 m) wide, and 40 feet 6 inches (12.34 m) deep, and contains 6.2 million gallons (23.5 million litres) of water. Divers breathe nitrox while working in the tank.

Neutral buoyancy in a pool is not weightlessness, since the balance organs in the inner ear still sense the up-down direction of gravity. Also, there is a significant amount of drag presented by water. Generally, drag effects are minimized by doing tasks slowly in the water. Another difference between neutral buoyancy simulation in a pool and actual EVA during spaceflight is that the temperature of the pool and the lighting conditions are maintained constant.

Speculative or fictional mechanisms

In science fiction, artificial gravity (or cancellation of gravity) or "paragravity" is sometimes present in spacecraft that are neither rotating nor accelerating. At present, there is no confirmed technique that can simulate gravity other than actual mass or acceleration. There have been many claims over the years of such a device. Eugene Podkletnov, a Russian engineer, has claimed since the early 1990s to have made such a device consisting of a spinning superconductor producing a powerful "gravitomagnetic field", but there has been no verification or even negative results from third parties. In 2006, a research group funded by ESA claimed to have created a similar device that demonstrated positive results for the production of gravitomagnetism, although it produced only 0.0001g. This result has not been replicated.

Anti-gravity

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Anti-gravity 

Anti-gravity (also known as non-gravitational field) is a hypothetical phenomenon of creating a place or object that is free from the force of gravity. It does not refer to the lack of weight under gravity experienced in free fall or orbit, or to balancing the force of gravity with some other force, such as electromagnetism or aerodynamic lift. Anti-gravity is a recurring concept in science fiction, particularly in the context of spacecraft propulsion. Examples are the gravity blocking substance "Cavorite" in H. G. Wells's The First Men in the Moon and the Spindizzy machines in James Blish's Cities in Flight.

"Anti-gravity" is often used to refer to devices that look as if they reverse gravity even though they operate through other means, such as lifters, which fly in the air by moving air with electromagnetic fields.

What is commonly misconstrued is that while anti-gravity is the nullification of gravity, it is not repulsive gravity or negative gravity. Gravity plates and compensators as envisioned in contemporary science fiction also are not anti-gravity.

Historical attempts at understanding gravity

The possibility of creating anti-gravity depends upon a complete understanding and description of gravity and its interactions with other physical theories, such as general relativity and quantum mechanics; as of 2020 physicists have yet to discover a quantum theory of gravity.

During the summer of 1666, Isaac Newton observed an apple (variety Flower of Kent) falling from the tree in his garden, thus realizing the principle of universal gravitation. Albert Einstein in 1915 considered the physical interaction between matter and space, where gravity occurs as a consequence of matter causing a geometric deformation of space which is otherwise flat. Einstein, both independently and with Walther Mayer, attempted to unify his theory of gravity with electromagnetism using the work of Theodor Kaluza and James Clerk Maxwell to link gravity and quantum field theory.

Theoretical quantum physicists have postulated the existence of a quantum gravity particle, the graviton. Various theoretical explanations of quantum gravity have been created, these include superstring theory, loop quantum gravity, E8 theory and asymptotic safety theory among many others.

Hypothetical solutions

In Newton's law of universal gravitation, gravity was an external force transmitted by unknown means. In the 20th century, Newton's model was replaced by general relativity where gravity is not a force but the result of the geometry of spacetime. Under general relativity, anti-gravity is impossible except under contrived circumstances.

Gravity shields

A monument at Babson College dedicated to Roger Babson for research into anti-gravity and partial gravity insulators

In 1948 businessman Roger Babson (founder of Babson College) formed the Gravity Research Foundation to study ways to reduce the effects of gravity. Their efforts were initially somewhat "crankish", but they held occasional conferences that drew such people as Clarence Birdseye, known for his frozen-food products, and Igor Sikorsky, inventor of the helicopter. Over time the Foundation turned its attention away from trying to control gravity, to simply better understanding it. The Foundation nearly disappeared after Babson's death in 1967. However, it continues to run an essay award, offering prizes of up to $4,000. As of 2017, it is still administered out of Wellesley, Massachusetts, by George Rideout Jr., son of the foundation's original director. Winners include California astrophysicist George F. Smoot (1993), who later won the 2006 Nobel Prize in physics, and Gerard 't Hooft (2015) who previously won the 1999 Nobel Prize in physics.

General relativity research in the 1950s

General relativity was introduced in the 1910s, but development of the theory was greatly slowed by a lack of suitable mathematical tools. It appeared that anti-gravity was outlawed under general relativity.

It is claimed the US Air Force also ran a study effort throughout the 1950s and into the 1960s. Former Lieutenant Colonel Ansel Talbert wrote two series of newspaper articles claiming that most of the major aviation firms had started gravity control propulsion research in the 1950s. However, there is little outside confirmation of these stories, and since they take place in the midst of the policy by press release era, it is not clear how much weight these stories should be given.

It is known that there were serious efforts underway at the Glenn L. Martin Company, who formed the Research Institute for Advanced Study. Major newspapers announced the contract that had been made between theoretical physicist Burkhard Heim and the Glenn L. Martin Company. Another effort in the private sector to master understanding of gravitation was the creation of the Institute for Field Physics, University of North Carolina at Chapel Hill in 1956, by Gravity Research Foundation trustee Agnew H. Bahnson.

Military support for anti-gravity projects was terminated by the Mansfield Amendment of 1973, which restricted Department of Defense spending to only the areas of scientific research with explicit military applications. The Mansfield Amendment was passed specifically to end long-running projects that had little to show for their efforts.

Under general relativity, gravity is the result of following spatial geometry (change in the normal shape of space) caused by local mass-energy. This theory holds that it is the altered shape of space, deformed by massive objects, that causes gravity, which is actually a property of deformed space rather than being a true force. Although the equations cannot normally produce a "negative geometry", it is possible to do so by using "negative mass". The same equations do not, of themselves, rule out the existence of negative mass.

Both general relativity and Newtonian gravity appear to predict that negative mass would produce a repulsive gravitational field. In particular, Sir Hermann Bondi proposed in 1957 that negative gravitational mass, combined with negative inertial mass, would comply with the strong equivalence principle of general relativity theory and the Newtonian laws of conservation of linear momentum and energy. Bondi's proof yielded singularity-free solutions for the relativity equations. In July 1988, Robert L. Forward presented a paper at the AIAA/ASME/SAE/ASEE 24th Joint Propulsion Conference that proposed a Bondi negative gravitational mass propulsion system.

Bondi pointed out that a negative mass will fall toward (and not away from) "normal" matter, since although the gravitational force is repulsive, the negative mass (according to Newton's law, F=ma) responds by accelerating in the opposite of the direction of the force. Normal mass, on the other hand, will fall away from the negative matter. He noted that two identical masses, one positive and one negative, placed near each other will therefore self-accelerate in the direction of the line between them, with the negative mass chasing after the positive mass. Notice that because the negative mass acquires negative kinetic energy, the total energy of the accelerating masses remains at zero. Forward pointed out that the self-acceleration effect is due to the negative inertial mass, and could be seen induced without the gravitational forces between the particles.

The Standard Model of particle physics, which describes all currently known forms of matter, does not include negative mass. Although cosmological dark matter may consist of particles outside the Standard Model whose nature is unknown, their mass is ostensibly known – since they were postulated from their gravitational effects on surrounding objects, which implies their mass is positive. The proposed cosmological dark energy, on the other hand, is more complicated, since according to general relativity the effects of both its energy density and its negative pressure contribute to its gravitational effect.

Unique force

Under general relativity any form of energy couples with spacetime to create the geometries that cause gravity. A longstanding question was whether or not these same equations applied to antimatter. The issue was considered solved in 1960 with the development of CPT symmetry, which demonstrated that antimatter follows the same laws of physics as "normal" matter, and therefore has positive energy content and also causes (and reacts to) gravity like normal matter.

For much of the last quarter of the 20th century, the physics community was involved in attempts to produce a unified field theory, a single physical theory that explains the four fundamental forces: gravity, electromagnetism, and the strong and weak nuclear forces. Scientists have made progress in unifying the three quantum forces, but gravity has remained "the problem" in every attempt. This has not stopped any number of such attempts from being made, however.

Generally these attempts tried to "quantize gravity" by positing a particle, the graviton, that carried gravity in the same way that photons (light) carry electromagnetism. Simple attempts along this direction all failed, however, leading to more complex examples that attempted to account for these problems. Two of these, supersymmetry and the relativity related supergravity, both required the existence of an extremely weak "fifth force" carried by a graviphoton, which coupled together several "loose ends" in quantum field theory, in an organized manner. As a side effect, both theories also all but required that antimatter be affected by this fifth force in a way similar to anti-gravity, dictating repulsion away from mass. Several experiments were carried out in the 1990s to measure this effect, but none yielded positive results.

In 2013 CERN looked for an antigravity effect in an experiment designed to study the energy levels within antihydrogen. The antigravity measurement was just an "interesting sideshow" and was inconclusive.

Breakthrough Propulsion Physics Program

During the close of the twentieth century NASA provided funding for the Breakthrough Propulsion Physics Program (BPP) from 1996 through 2002. This program studied a number of "far out" designs for space propulsion that were not receiving funding through normal university or commercial channels. Anti-gravity-like concepts were investigated under the name "diametric drive". The work of the BPP program continues in the independent, non-NASA affiliated Tau Zero Foundation.

Empirical claims and commercial efforts

There have been a number of attempts to build anti-gravity devices, and a small number of reports of anti-gravity-like effects in the scientific literature. None of the examples that follow are accepted as reproducible examples of anti-gravity.

Gyroscopic devices

A "kinemassic field" generator from U.S. Patent 3,626,605: Method and apparatus for generating a secondary gravitational force field

Gyroscopes produce a force when twisted that operates "out of plane" and can appear to lift themselves against gravity. Although this force is well understood to be illusory, even under Newtonian models, it has nevertheless generated numerous claims of anti-gravity devices and any number of patented devices. None of these devices have ever been demonstrated to work under controlled conditions, and have often become the subject of conspiracy theories as a result.

Another "rotating device" example is shown in a series of patents granted to Henry Wallace between 1968 and 1974. His devices consist of rapidly spinning disks of brass, a material made up largely of elements with a total half-integer nuclear spin. He claimed that by rapidly rotating a disk of such material, the nuclear spin became aligned, and as a result created a "gravitomagnetic" field in a fashion similar to the magnetic field created by the Barnett effect. No independent testing or public demonstration of these devices is known.

In 1989, it was reported that a weight decreases along the axis of a right spinning gyroscope. A test of this claim a year later yielded null results. A recommendation was made to conduct further tests at a 1999 AIP conference.

Thomas Townsend Brown's gravitator

In 1921, while still in high school, Thomas Townsend Brown found that a high-voltage Coolidge tube seemed to change mass depending on its orientation on a balance scale. Through the 1920s Brown developed this into devices that combined high voltages with materials with high dielectric constants (essentially large capacitors); he called such a device a "gravitator". Brown made the claim to observers and in the media that his experiments were showing anti-gravity effects. Brown would continue his work and produced a series of high-voltage devices in the following years in attempts to sell his ideas to aircraft companies and the military. He coined the names Biefeld–Brown effect and electrogravitics in conjunction with his devices. Brown tested his asymmetrical capacitor devices in a vacuum, supposedly showing it was not a more down-to-earth electrohydrodynamic effect generated by high voltage ion flow in air.

Electrogravitics is a popular topic in ufology, anti-gravity, free energy, with government conspiracy theorists and related websites, in books and publications with claims that the technology became highly classified in the early 1960s and that it is used to power UFOs and the B-2 bomber. There is also research and videos on the internet purported to show lifter-style capacitor devices working in a vacuum, therefore not receiving propulsion from ion drift or ion wind being generated in air.

Follow-up studies on Brown's work and other claims have been conducted by R. L. Talley in a 1990 US Air Force study, NASA scientist Jonathan Campbell in a 2003 experiment, and Martin Tajmar in a 2004 paper. They have found that no thrust could be observed in a vacuum and that Brown's and other ion lifter devices produce thrust along their axis regardless of the direction of gravity consistent with electrohydrodynamic effects.

Gravitoelectric coupling

In 1992, the Russian researcher Eugene Podkletnov claimed to have discovered, whilst experimenting with superconductors, that a fast rotating superconductor reduces the gravitational effect. Many studies have attempted to reproduce Podkletnov's experiment, always to negative results.

Ning Li and Douglas Torr, of the University of Alabama in Huntsville proposed how a time dependent magnetic field could cause the spins of the lattice ions in a superconductor to generate detectable gravitomagnetic and gravitoelectric fields in a series of papers published between 1991 and 1993. In 1999, Li and her team appeared in Popular Mechanics, claiming to have constructed a working prototype to generate what she described as "AC Gravity." No further evidence of this prototype has been offered.

Douglas Torr and Timir Datta were involved in the development of a "gravity generator" at the University of South Carolina. According to a leaked document from the Office of Technology Transfer at the University of South Carolina and confirmed to Wired reporter Charles Platt in 1998, the device would create a "force beam" in any desired direction and that the university planned to patent and license this device. No further information about this university research project or the "Gravity Generator" device was ever made public.

Göde Award

The Institute for Gravity Research of the Göde Scientific Foundation has tried to reproduce many of the different experiments which claim any "anti-gravity" effects. All attempts by this group to observe an anti-gravity effect by reproducing past experiments have been unsuccessful thus far. The foundation has offered a reward of one million euros for a reproducible anti-gravity experiment.

In fiction

The existence of anti-gravity is a common theme in fantasy and science fiction.

Apergy

Apergy is a fictitious form of anti-gravitational energy first described by Percy Greg in his 1880 sword and planet novel Across the Zodiac.

It is also used by John Jacob Astor IV in his 1894 science fiction novel, A Journey in Other Worlds.

Apergy can also be found in an 1896 article by Clara Jessup Bloomfield-Moore, called "Some Truths About Keely". In it, apergy is used to describe the latent force John Keely harnessed, by using frequency to release the latent force found within all atomic matter.

In an 1897, ostensibly non-fictitious, article in The San Francisco Call titled "The Secret of Aerial Flight Revealed", science correspondent Frank M. Close, D. Sc., visits an unnamed Hindu man masquerading as a viticulturist somewhere on the Pacific coast who claims to have invented a flying boat that uses an "apergent"—a rare metal called "radlum"—to produce controlled apergic force, allowing the vessel to ascend and descend. The inventor describes apergy as "a force obtained by blending positive and negative electricity with ultheic, the third element or state of electric energy" and calls apergy a "second phase of gravity", hinting at a third phase as well.

In S. P. Meek's short story "Cold Light", which appeared in Astounding Stories of Super-Science, March 1930, apergy is mentioned as the opposite force of gravity.

In Chris Roberson's short story "Annus Mirabilis" from the 2006 second volume of Tales of the Shadowmen, Doctor Omega and Albert Einstein investigate apergy. Apergy is also mentioned in the Warren Ellis comic Aetheric Mechanics, as being generated by Cavorite technology from The First Men in the Moon.