Turing machine

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Turing_machine 

Turing machines
Machine
Turing machine equivalents Turing machine examples Turing machine gallery
Variants
Alternating Turing machine Neural Turing machine Nondeterministic Turing machine Quantum Turing machine Post–Turing machine Probabilistic Turing machine Multitape Turing machine Multi-track Turing machine Symmetric Turing machine Total Turing machine Unambiguous Turing machine Universal Turing machine Zeno machine
Science
Alan Turing Category:Turing machine

A physical Turing machine model. A true Turing machine would have unlimited tape on both sides, however, physical models can only have a finite amount of tape.

A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algorithm.

The machine operates on an infinite memory tape divided into discrete cells, each of which can hold a single symbol drawn from a finite set of symbols called the alphabet of the machine. It has a "head" that, at any point in the machine's operation, is positioned over one of these cells, and a "state" selected from a finite set of states. At each step of its operation, the head reads the symbol in its cell. Then, based on the symbol and the machine's own present state, the machine writes a symbol into the same cell, and moves the head one step to the left or the right, or halts the computation. The choice of which replacement symbol to write and which direction to move is based on a finite table that specifies what to do for each combination of the current state and the symbol that is read.

The Turing machine was invented in 1936 by Alan Turing, who called it an "a-machine" (automatic machine). It was Turing's Doctoral advisor, Alonzo Church, who later coined the term "Turing machine" in a review. With this model, Turing was able to answer two questions in the negative:

• Does a machine exist that can determine whether any arbitrary machine on its tape is "circular" (e.g., freezes, or fails to continue its computational task)?
• Does a machine exist that can determine whether any arbitrary machine on its tape ever prints a given symbol?

Thus by providing a mathematical description of a very simple device capable of arbitrary computations, he was able to prove properties of computation in general—and in particular, the uncomputability of the Entscheidungsproblem ('decision problem').

Turing machines proved the existence of fundamental limitations on the power of mechanical computation. While they can express arbitrary computations, their minimalist design makes them unsuitable for computation in practice: real-world computers are based on different designs that, unlike Turing machines, use random-access memory.

Turing completeness is the ability for a system of instructions to simulate a Turing machine. A programming language that is Turing complete is theoretically capable of expressing all tasks accomplishable by computers; nearly all programming languages are Turing complete if the limitations of finite memory are ignored.

Overview

A Turing machine is a general example of a central processing unit (CPU) that controls all data manipulation done by a computer, with the canonical machine using sequential memory to store data. More specifically, it is a machine (automaton) capable of enumerating some arbitrary subset of valid strings of an alphabet; these strings are part of a recursively enumerable set. A Turing machine has a tape of infinite length on which it can perform read and write operations.

Assuming a black box, the Turing machine cannot know whether it will eventually enumerate any one specific string of the subset with a given program. This is due to the fact that the halting problem is unsolvable, which has major implications for the theoretical limits of computing.

The Turing machine is capable of processing an unrestricted grammar, which further implies that it is capable of robustly evaluating first-order logic in an infinite number of ways. This is famously demonstrated through lambda calculus.

A Turing machine that is able to simulate any other Turing machine is called a universal Turing machine (UTM, or simply a universal machine). A more mathematically oriented definition with a similar "universal" nature was introduced by Alonzo Church, whose work on lambda calculus intertwined with Turing's in a formal theory of computation known as the Church–Turing thesis. The thesis states that Turing machines indeed capture the informal notion of effective methods in logic and mathematics, and provide a precise definition of an algorithm or "mechanical procedure". Studying their abstract properties yields many insights into computer science and complexity theory.

Physical description

In his 1948 essay, "Intelligent Machinery", Turing wrote that his machine consisted of:

...an unlimited memory capacity obtained in the form of an infinite tape marked out into squares, on each of which a symbol could be printed. At any moment there is one symbol in the machine; it is called the scanned symbol. The machine can alter the scanned symbol, and its behavior is in part determined by that symbol, but the symbols on the tape elsewhere do not affect the behavior of the machine. However, the tape can be moved back and forth through the machine, this being one of the elementary operations of the machine. Any symbol on the tape may therefore eventually have an innings.

— Turing 1948, p. 3

Description

For visualizations of Turing machines, see Turing machine gallery.

The Turing machine mathematically models a machine that mechanically operates on a tape. On this tape are symbols, which the machine can read and write, one at a time, using a tape head. Operation is fully determined by a finite set of elementary instructions such as "in state 42, if the symbol seen is 0, write a 1; if the symbol seen is 1, change into state 17; in state 17, if the symbol seen is 0, write a 1 and change to state 6;" etc. In the original article ("On Computable Numbers, with an Application to the Entscheidungsproblem", see also references below), Turing imagines not a mechanism, but a person whom he calls the "computer", who executes these deterministic mechanical rules slavishly (or as Turing puts it, "in a desultory manner").

The head is always over a particular square of the tape; only a finite stretch of squares is shown. The instruction to be performed (q₄) is shown over the scanned square. (Drawing after Kleene (1952) p. 375.)

 

Here, the internal state (q₁) is shown inside the head, and the illustration describes the tape as being infinite and pre-filled with "0", the symbol serving as blank. The system's full state (its "complete configuration") consists of the internal state, any non-blank symbols on the tape (in this illustration "11B"), and the position of the head relative to those symbols including blanks, i.e. "011B". (Drawing after Minsky (1967) p. 121.)

More explicitly, a Turing machine consists of:

• A tape divided into cells, one next to the other. Each cell contains a symbol from some finite alphabet. The alphabet contains a special blank symbol (here written as '0') and one or more other symbols. The tape is assumed to be arbitrarily extendable to the left and to the right, so that the Turing machine is always supplied with as much tape as it needs for its computation. Cells that have not been written before are assumed to be filled with the blank symbol. In some models the tape has a left end marked with a special symbol; the tape extends or is indefinitely extensible to the right.
• A head that can read and write symbols on the tape and move the tape left and right one (and only one) cell at a time. In some models the head moves and the tape is stationary.
• A state register that stores the state of the Turing machine, one of finitely many. Among these is the special start state with which the state register is initialized. These states, writes Turing, replace the "state of mind" a person performing computations would ordinarily be in.
• A finite table of instructions that, given the state(q_i) the machine is currently in and the symbol(a_j) it is reading on the tape (symbol currently under the head), tells the machine to do the following in sequence (for the 5-tuple models):

1. Either erase or write a symbol (replacing a_j with a_j1).
2. Move the head (which is described by d_k and can have values: 'L' for one step left or 'R' for one step right or 'N' for staying in the same place).
3. Assume the same or a new state as prescribed (go to state q_i1).

In the 4-tuple models, erasing or writing a symbol (a_j1) and moving the head left or right (d_k) are specified as separate instructions. The table tells the machine to (ia) erase or write a symbol or (ib) move the head left or right, and then (ii) assume the same or a new state as prescribed, but not both actions (ia) and (ib) in the same instruction. In some models, if there is no entry in the table for the current combination of symbol and state, then the machine will halt; other models require all entries to be filled.

Every part of the machine (i.e. its state, symbol-collections, and used tape at any given time) and its actions (such as printing, erasing and tape motion) is finite, discrete and distinguishable; it is the unlimited amount of tape and runtime that gives it an unbounded amount of storage space.

Formal definition

Following Hopcroft & Ullman (1979, p. 148), a (one-tape) Turing machine can be formally defined as a 7-tuple ${\displaystyle M=\langle Q,\Gamma ,b,\Sigma ,\delta ,q_{0},F\rangle }$ where

• ${\displaystyle \Gamma }$ is a finite, non-empty set of tape alphabet symbols;
• ${\displaystyle b\in \Gamma }$ is the blank symbol (the only symbol allowed to occur on the tape infinitely often at any step during the computation);
• ${\displaystyle \Sigma \subseteq \Gamma \setminus \{b\}}$ is the set of input symbols, that is, the set of symbols allowed to appear in the initial tape contents;
• ${\displaystyle Q}$ is a finite, non-empty set of states;
• ${\displaystyle q_{0}\in Q}$ is the initial state;
• ${\displaystyle F\subseteq Q}$ is the set of final states or accepting states. The initial tape contents is said to be accepted by ${\displaystyle M}$ if it eventually halts in a state from ${\displaystyle F}$.
• ${\displaystyle \delta :(Q\setminus F)\times \Gamma \not \to Q\times \Gamma \times \{L,R\}}$ is a partial function called the transition function, where L is left shift, R is right shift. If ${\displaystyle \delta }$ is not defined on the current state and the current tape symbol, then the machine halts; intuitively, the transition function specifies the next state transited from the current state, which symbol to overwrite the current symbol pointed by the head, and the next head movement.

3-state Busy Beaver. Black icons represent location and state of head; square colors represent 1s (orange) and 0s (white); time progresses vertically from the top until the HALT state at the bottom.

In addition, the Turing machine can also have a reject state to make rejection more explicit. In that case there are three possibilities: accepting, rejecting, and running forever. Another possibility is to regard the final values on the tape as the output. However, if the only output is the final state the machine ends up in (or never halting), the machine can still effectively output a longer string by taking in an integer that tells it which bit of the string to output.

A relatively uncommon variant allows "no shift", say N, as a third element of the set of directions ${\displaystyle \{L,R\}}$.

The 7-tuple for the 3-state busy beaver looks like this (see more about this busy beaver at Turing machine examples):

• ${\displaystyle Q=\{{\mbox{A}},{\mbox{B}},{\mbox{C}},{\mbox{HALT}}\}}$ (states);
• ${\displaystyle \Gamma =\{0,1\}}$ (tape alphabet symbols);
• ${\displaystyle b=0}$ (blank symbol);
• ${\displaystyle \Sigma =\{1\}}$ (input symbols);
• ${\displaystyle q_{0}={\mbox{A}}}$ (initial state);
• ${\displaystyle F=\{{\mbox{HALT}}\}}$ (final states);
• ${\displaystyle \delta =}$ see state-table below (transition function).

Initially all tape cells are marked with ${\displaystyle 0}$.

State table for 3-state, 2-symbol busy beaver

Tape symbol	Current state A			Current state B			Current state C
	Write symbol	Move tape	Next state	Write symbol	Move tape	Next state	Write symbol	Move tape	Next state
0	1	R	B	1	L	A	1	L	B
1	1	L	C	1	R	B	1	R	HALT

Additional details required to visualize or implement Turing machines

In the words of van Emde Boas (1990), p. 6: "The set-theoretical object [his formal seven-tuple description similar to the above] provides only partial information on how the machine will behave and what its computations will look like."

For instance,

• There will need to be many decisions on what the symbols actually look like, and a failproof way of reading and writing symbols indefinitely.
• The shift left and shift right operations may shift the tape head across the tape, but when actually building a Turing machine it is more practical to make the tape slide back and forth under the head instead.
• The tape can be finite, and automatically extended with blanks as needed (which is closest to the mathematical definition), but it is more common to think of it as stretching infinitely at one or both ends and being pre-filled with blanks except on the explicitly given finite fragment the tape head is on. (This is, of course, not implementable in practice.) The tape cannot be fixed in length, since that would not correspond to the given definition and would seriously limit the range of computations the machine can perform to those of a linear bounded automaton if the tape was proportional to the input size, or finite-state machine if it was strictly fixed-length.

Alternative definitions

Definitions in literature sometimes differ slightly, to make arguments or proofs easier or clearer, but this is always done in such a way that the resulting machine has the same computational power. For example, the set could be changed from ${\displaystyle \{L,R\}}$ to ${\displaystyle \{L,R,N\}}$, where N ("None" or "No-operation") would allow the machine to stay on the same tape cell instead of moving left or right. This would not increase the machine's computational power.

The most common convention represents each "Turing instruction" in a "Turing table" by one of nine 5-tuples, per the convention of Turing/Davis (Turing (1936) in The Undecidable, p. 126-127 and Davis (2000) p. 152):

(definition 1): (q_i, S_j, S_k/E/N, L/R/N, q_m)

( current state q_i , symbol scanned S_j , print symbol S_k/erase E/none N , move_tape_one_square left L/right R/none N , new state q_m )

Other authors (Minsky (1967) p. 119, Hopcroft and Ullman (1979) p. 158, Stone (1972) p. 9) adopt a different convention, with new state q_m listed immediately after the scanned symbol S_j:

(definition 2): (q_i, S_j, q_m, S_k/E/N, L/R/N)

( current state q_i , symbol scanned S_j , new state q_m , print symbol S_k/erase E/none N , move_tape_one_square left L/right R/none N )

For the remainder of this article "definition 1" (the Turing/Davis convention) will be used.

Example: state table for the 3-state 2-symbol busy beaver reduced to 5-tuples

Current state	Scanned symbol		Print symbol	Move tape	Final (i.e. next) state	5-tuples
A	0		1	R	B	(A, 0, 1, R, B)
A	1		1	L	C	(A, 1, 1, L, C)
B	0		1	L	A	(B, 0, 1, L, A)
B	1		1	R	B	(B, 1, 1, R, B)
C	0		1	L	B	(C, 0, 1, L, B)
C	1		1	N	H	(C, 1, 1, N, H)

In the following table, Turing's original model allowed only the first three lines that he called N1, N2, N3 (cf. Turing in The Undecidable, p. 126). He allowed for erasure of the "scanned square" by naming a 0th symbol S₀ = "erase" or "blank", etc. However, he did not allow for non-printing, so every instruction-line includes "print symbol S_k" or "erase" (cf. footnote 12 in Post (1947), The Undecidable, p. 300). The abbreviations are Turing's (The Undecidable, p. 119). Subsequent to Turing's original paper in 1936–1937, machine-models have allowed all nine possible types of five-tuples:

	Current m-configuration (Turing state)	Tape symbol	Print-operation	Tape-motion	Final m-configuration (Turing state)	5-tuple	5-tuple comments	4-tuple
N1	qi	Sj	Print(Sk)	Left L	qm	(qi, Sj, Sk, L, qm)	"blank" = S0, 1=S1, etc.
N2	qi	Sj	Print(Sk)	Right R	qm	(qi, Sj, Sk, R, qm)	"blank" = S0, 1=S1, etc.
N3	qi	Sj	Print(Sk)	None N	qm	(qi, Sj, Sk, N, qm)	"blank" = S0, 1=S1, etc.	(qi, Sj, Sk, qm)
4	qi	Sj	None N	Left L	qm	(qi, Sj, N, L, qm)		(qi, Sj, L, qm)
5	qi	Sj	None N	Right R	qm	(qi, Sj, N, R, qm)		(qi, Sj, R, qm)
6	qi	Sj	None N	None N	qm	(qi, Sj, N, N, qm)	Direct "jump"	(qi, Sj, N, qm)
7	qi	Sj	Erase	Left L	qm	(qi, Sj, E, L, qm)
8	qi	Sj	Erase	Right R	qm	(qi, Sj, E, R, qm)
9	qi	Sj	Erase	None N	qm	(qi, Sj, E, N, qm)		(qi, Sj, E, qm)

Any Turing table (list of instructions) can be constructed from the above nine 5-tuples. For technical reasons, the three non-printing or "N" instructions (4, 5, 6) can usually be dispensed with. For examples see Turing machine examples.

Less frequently the use of 4-tuples are encountered: these represent a further atomization of the Turing instructions (cf. Post (1947), Boolos & Jeffrey (1974, 1999), Davis-Sigal-Weyuker (1994)); also see more at Post–Turing machine.

The "state"

The word "state" used in context of Turing machines can be a source of confusion, as it can mean two things. Most commentators after Turing have used "state" to mean the name/designator of the current instruction to be performed—i.e. the contents of the state register. But Turing (1936) made a strong distinction between a record of what he called the machine's "m-configuration", and the machine's (or person's) "state of progress" through the computation—the current state of the total system. What Turing called "the state formula" includes both the current instruction and all the symbols on the tape:

Thus the state of progress of the computation at any stage is completely determined by the note of instructions and the symbols on the tape. That is, the state of the system may be described by a single expression (sequence of symbols) consisting of the symbols on the tape followed by Δ (which is supposed to not to appear elsewhere) and then by the note of instructions. This expression is called the "state formula".

— The Undecidable, pp. 139–140, emphasis added

Earlier in his paper Turing carried this even further: he gives an example where he placed a symbol of the current "m-configuration"—the instruction's label—beneath the scanned square, together with all the symbols on the tape (The Undecidable, p. 121); this he calls "the complete configuration" (The Undecidable, p. 118). To print the "complete configuration" on one line, he places the state-label/m-configuration to the left of the scanned symbol.

A variant of this is seen in Kleene (1952) where Kleene shows how to write the Gödel number of a machine's "situation": he places the "m-configuration" symbol q₄ over the scanned square in roughly the center of the 6 non-blank squares on the tape (see the Turing-tape figure in this article) and puts it to the right of the scanned square. But Kleene refers to "q₄" itself as "the machine state" (Kleene, p. 374-375). Hopcroft and Ullman call this composite the "instantaneous description" and follow the Turing convention of putting the "current state" (instruction-label, m-configuration) to the left of the scanned symbol (p. 149), that is, the instantaneous description is the composite of non-blank symbols to the left, state of the machine, the current symbol scanned by the head, and the non-blank symbols to the right.

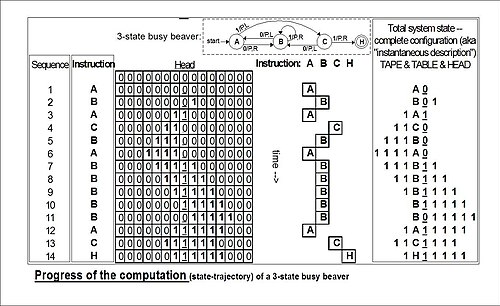
Example: total state of 3-state 2-symbol busy beaver after 3 "moves" (taken from example "run" in the figure below):

1A1

This means: after three moves the tape has ... 000110000 ... on it, the head is scanning the right-most 1, and the state is A. Blanks (in this case represented by "0"s) can be part of the total state as shown here: B01; the tape has a single 1 on it, but the head is scanning the 0 ("blank") to its left and the state is B.

"State" in the context of Turing machines should be clarified as to which is being described: the current instruction, or the list of symbols on the tape together with the current instruction, or the list of symbols on the tape together with the current instruction placed to the left of the scanned symbol or to the right of the scanned symbol.

Turing's biographer Andrew Hodges (1983: 107) has noted and discussed this confusion.

"State" diagrams

The table for the 3-state busy beaver ("P" = print/write a "1")

Tape symbol	Current state A			Current state B			Current state C
	Write symbol	Move tape	Next state	Write symbol	Move tape	Next state	Write symbol	Move tape	Next state
0	P	R	B	P	L	A	P	L	B
1	P	L	C	P	R	B	P	R	HALT

The "3-state busy beaver" Turing machine in a finite-state representation. Each circle represents a "state" of the table—an "m-configuration" or "instruction". "Direction" of a state transition is shown by an arrow. The label (e.g. 0/P,R) near the outgoing state (at the "tail" of the arrow) specifies the scanned symbol that causes a particular transition (e.g. 0) followed by a slash /, followed by the subsequent "behaviors" of the machine, e.g. "P print" then move tape "R right". No general accepted format exists. The convention shown is after McClusky (1965), Booth (1967), Hill, and Peterson (1974).

To the right: the above table as expressed as a "state transition" diagram.

Usually large tables are better left as tables (Booth, p. 74). They are more readily simulated by computer in tabular form (Booth, p. 74). However, certain concepts—e.g. machines with "reset" states and machines with repeating patterns (cf. Hill and Peterson p. 244ff)—can be more readily seen when viewed as a drawing.

Whether a drawing represents an improvement on its table must be decided by the reader for the particular context.

The evolution of the busy beaver's computation starts at the top and proceeds to the bottom.

The reader should again be cautioned that such diagrams represent a snapshot of their table frozen in time, not the course ("trajectory") of a computation through time and space. While every time the busy beaver machine "runs" it will always follow the same state-trajectory, this is not true for the "copy" machine that can be provided with variable input "parameters".

The diagram "progress of the computation" shows the three-state busy beaver's "state" (instruction) progress through its computation from start to finish. On the far right is the Turing "complete configuration" (Kleene "situation", Hopcroft–Ullman "instantaneous description") at each step. If the machine were to be stopped and cleared to blank both the "state register" and entire tape, these "configurations" could be used to rekindle a computation anywhere in its progress (cf. Turing (1936) The Undecidable, pp. 139–140).

Equivalent models

See also: Turing machine equivalents, Register machine, and Post–Turing machine

Many machines that might be thought to have more computational capability than a simple universal Turing machine can be shown to have no more power (Hopcroft and Ullman p. 159, cf. Minsky (1967)). They might compute faster, perhaps, or use less memory, or their instruction set might be smaller, but they cannot compute more powerfully (i.e. more mathematical functions). (The Church–Turing thesis hypothesizes this to be true for any kind of machine: that anything that can be "computed" can be computed by some Turing machine.)

A Turing machine is equivalent to a single-stack pushdown automaton (PDA) that has been made more flexible and concise by relaxing the last-in-first-out (LIFO) requirement of its stack. In addition, a Turing machine is also equivalent to a two-stack PDA with standard LIFO semantics, by using one stack to model the tape left of the head and the other stack for the tape to the right.

At the other extreme, some very simple models turn out to be Turing-equivalent, i.e. to have the same computational power as the Turing machine model.

Common equivalent models are the multi-tape Turing machine, multi-track Turing machine, machines with input and output, and the non-deterministic Turing machine (NDTM) as opposed to the deterministic Turing machine (DTM) for which the action table has at most one entry for each combination of symbol and state.

Read-only, right-moving Turing machines are equivalent to DFAs (as well as NFAs by conversion using the NDFA to DFA conversion algorithm).

For practical and didactical intentions the equivalent register machine can be used as a usual assembly programming language.

A relevant question is whether or not the computation model represented by concrete programming languages is Turing equivalent. While the computation of a real computer is based on finite states and thus not capable to simulate a Turing machine, programming languages themselves do not necessarily have this limitation. Kirner et al., 2009 have shown that among the general-purpose programming languages some are Turing complete while others are not. For example, ANSI C is not Turing-equivalent, as all instantiations of ANSI C (different instantiations are possible as the standard deliberately leaves certain behaviour undefined for legacy reasons) imply a finite-space memory. This is because the size of memory reference data types, called pointers, is accessible inside the language. However, other programming languages like Pascal do not have this feature, which allows them to be Turing complete in principle. It is just Turing complete in principle, as memory allocation in a programming language is allowed to fail, which means the programming language can be Turing complete when ignoring failed memory allocations, but the compiled programs executable on a real computer cannot.

Choice c-machines, oracle o-machines

Early in his paper (1936) Turing makes a distinction between an "automatic machine"—its "motion ... completely determined by the configuration" and a "choice machine":

...whose motion is only partially determined by the configuration ... When such a machine reaches one of these ambiguous configurations, it cannot go on until some arbitrary choice has been made by an external operator. This would be the case if we were using machines to deal with axiomatic systems.

— The Undecidable, p. 118

Turing (1936) does not elaborate further except in a footnote in which he describes how to use an a-machine to "find all the provable formulae of the [Hilbert] calculus" rather than use a choice machine. He "suppose[s] that the choices are always between two possibilities 0 and 1. Each proof will then be determined by a sequence of choices i₁, i₂, ..., i_n (i₁ = 0 or 1, i₂ = 0 or 1, ..., i_n = 0 or 1), and hence the number 2ⁿ + i₁2^n-1 + i₂2^n-2 + ... +i_n completely determines the proof. The automatic machine carries out successively proof 1, proof 2, proof 3, ..." (Footnote ‡, The Undecidable, p. 138)

This is indeed the technique by which a deterministic (i.e., a-) Turing machine can be used to mimic the action of a nondeterministic Turing machine; Turing solved the matter in a footnote and appears to dismiss it from further consideration.

An oracle machine or o-machine is a Turing a-machine that pauses its computation at state "o" while, to complete its calculation, it "awaits the decision" of "the oracle"—an unspecified entity "apart from saying that it cannot be a machine" (Turing (1939), The Undecidable, p. 166–168).

Universal Turing machines

Main article: Universal Turing machine

 

An implementation of a Turing machine

As Turing wrote in The Undecidable, p. 128 (italics added):

It is possible to invent a single machine which can be used to compute any computable sequence. If this machine U is supplied with the tape on the beginning of which is written the string of quintuples separated by semicolons of some computing machine M, then U will compute the same sequence as M.

This finding is now taken for granted, but at the time (1936) it was considered astonishing.^{[citation needed]} The model of computation that Turing called his "universal machine"—"U" for short—is considered by some (cf. Davis (2000)) to have been the fundamental theoretical breakthrough that led to the notion of the stored-program computer.

Turing's paper ... contains, in essence, the invention of the modern computer and some of the programming techniques that accompanied it.

— Minsky (1967), p. 104

In terms of computational complexity, a multi-tape universal Turing machine need only be slower by logarithmic factor compared to the machines it simulates. This result was obtained in 1966 by F. C. Hennie and R. E. Stearns. (Arora and Barak, 2009, theorem 1.9)

Comparison with real machines

A Turing machine realization using Lego pieces

It is often believed that Turing machines, unlike simpler automata, are as powerful as real machines, and are able to execute any operation that a real program can. What is neglected in this statement is that, because a real machine can only have a finite number of configurations, it is nothing but a finite-state machine, whereas a Turing machine has an unlimited amount of storage space available for its computations.

There are a number of ways to explain why Turing machines are useful models of real computers:

• Anything a real computer can compute, a Turing machine can also compute. For example: "A Turing machine can simulate any type of subroutine found in programming languages, including recursive procedures and any of the known parameter-passing mechanisms" (Hopcroft and Ullman p. 157). A large enough FSA can also model any real computer, disregarding IO. Thus, a statement about the limitations of Turing machines will also apply to real computers.
• The difference lies only with the ability of a Turing machine to manipulate an unbounded amount of data. However, given a finite amount of time, a Turing machine (like a real machine) can only manipulate a finite amount of data.
• Like a Turing machine, a real machine can have its storage space enlarged as needed, by acquiring more disks or other storage media.
• Descriptions of real machine programs using simpler abstract models are often much more complex than descriptions using Turing machines. For example, a Turing machine describing an algorithm may have a few hundred states, while the equivalent deterministic finite automaton (DFA) on a given real machine has quadrillions. This makes the DFA representation infeasible to analyze.
• Turing machines describe algorithms independent of how much memory they use. There is a limit to the memory possessed by any current machine, but this limit can rise arbitrarily in time. Turing machines allow us to make statements about algorithms which will (theoretically) hold forever, regardless of advances in conventional computing machine architecture.
• Turing machines simplify the statement of algorithms. Algorithms running on Turing-equivalent abstract machines are usually more general than their counterparts running on real machines, because they have arbitrary-precision data types available and never have to deal with unexpected conditions (including, but not limited to, running out of memory).

Another Turing machine realization

Limitations

Computational complexity theory

Further information: Computational complexity theory

A limitation of Turing machines is that they do not model the strengths of a particular arrangement well. For instance, modern stored-program computers are actually instances of a more specific form of abstract machine known as the random-access stored-program machine or RASP machine model. Like the universal Turing machine, the RASP stores its "program" in "memory" external to its finite-state machine's "instructions". Unlike the universal Turing machine, the RASP has an infinite number of distinguishable, numbered but unbounded "registers"—memory "cells" that can contain any integer (cf. Elgot and Robinson (1964), Hartmanis (1971), and in particular Cook-Rechow (1973); references at random-access machine). The RASP's finite-state machine is equipped with the capability for indirect addressing (e.g., the contents of one register can be used as an address to specify another register); thus the RASP's "program" can address any register in the register-sequence. The upshot of this distinction is that there are computational optimizations that can be performed based on the memory indices, which are not possible in a general Turing machine; thus when Turing machines are used as the basis for bounding running times, a "false lower bound" can be proven on certain algorithms' running times (due to the false simplifying assumption of a Turing machine). An example of this is binary search, an algorithm that can be shown to perform more quickly when using the RASP model of computation rather than the Turing machine model.

Concurrency

Another limitation of Turing machines is that they do not model concurrency well. For example, there is a bound on the size of integer that can be computed by an always-halting nondeterministic Turing machine starting on a blank tape. (See article on unbounded nondeterminism.) By contrast, there are always-halting concurrent systems with no inputs that can compute an integer of unbounded size. (A process can be created with local storage that is initialized with a count of 0 that concurrently sends itself both a stop and a go message. When it receives a go message, it increments its count by 1 and sends itself a go message. When it receives a stop message, it stops with an unbounded number in its local storage.)

Interaction

In the early days of computing, computer use was typically limited to batch processing, i.e., non-interactive tasks, each producing output data from given input data. Computability theory, which studies computability of functions from inputs to outputs, and for which Turing machines were invented, reflects this practice.

Since the 1970s, interactive use of computers became much more common. In principle, it is possible to model this by having an external agent read from the tape and write to it at the same time as a Turing machine, but this rarely matches how interaction actually happens; therefore, when describing interactivity, alternatives such as I/O automata are usually preferred.

History

See also: Algorithm and Church–Turing thesis

They were described in 1936 by Alan Turing.

Historical background: computational machinery

Robin Gandy (1919–1995)—a student of Alan Turing (1912–1954), and his lifelong friend—traces the lineage of the notion of "calculating machine" back to Charles Babbage (circa 1834) and actually proposes "Babbage's Thesis":

That the whole of development and operations of analysis are now capable of being executed by machinery.

— (italics in Babbage as cited by Gandy, p. 54)

Gandy's analysis of Babbage's analytical engine describes the following five operations (cf. p. 52–53):

• The arithmetic functions +, −, ×, where − indicates "proper" subtraction x − y = 0 if y ≥ x.
• Any sequence of operations is an operation.
• Iteration of an operation (repeating n times an operation P).
• Conditional iteration (repeating n times an operation P conditional on the "success" of test T).
• Conditional transfer (i.e., conditional "goto").

Gandy states that "the functions which can be calculated by (1), (2), and (4) are precisely those which are Turing computable." (p. 53). He cites other proposals for "universal calculating machines" including those of Percy Ludgate (1909), Leonardo Torres y Quevedo (1914), Maurice d'Ocagne (1922), Louis Couffignal (1933), Vannevar Bush (1936), Howard Aiken (1937). However:

… the emphasis is on programming a fixed iterable sequence of arithmetical operations. The fundamental importance of conditional iteration and conditional transfer for a general theory of calculating machines is not recognized…

— Gandy p. 55

The Entscheidungsproblem (the "decision problem"): Hilbert's tenth question of 1900

With regard to Hilbert's problems posed by the famous mathematician David Hilbert in 1900, an aspect of problem #10 had been floating about for almost 30 years before it was framed precisely. Hilbert's original expression for No. 10 is as follows:

10. Determination of the solvability of a Diophantine equation. Given a Diophantine equation with any number of unknown quantities and with rational integral coefficients: To devise a process according to which it can be determined in a finite number of operations whether the equation is solvable in rational integers. The Entscheidungsproblem [decision problem for first-order logic] is solved when we know a procedure that allows for any given logical expression to decide by finitely many operations its validity or satisfiability ... The Entscheidungsproblem must be considered the main problem of mathematical logic.

— quoted, with this translation and the original German, in Dershowitz and Gurevich, 2008

By 1922, this notion of "Entscheidungsproblem" had developed a bit, and H. Behmann stated that

... most general form of the Entscheidungsproblem [is] as follows:

A quite definite generally applicable prescription is required which will allow one to decide in a finite number of steps the truth or falsity of a given purely logical assertion ...

— Gandy p. 57, quoting Behmann

Behmann remarks that ... the general problem is equivalent to the problem of deciding which mathematical propositions are true.

— ibid.

If one were able to solve the Entscheidungsproblem then one would have a "procedure for solving many (or even all) mathematical problems".

— ibid., p. 92

By the 1928 international congress of mathematicians, Hilbert "made his questions quite precise. First, was mathematics complete ... Second, was mathematics consistent ... And thirdly, was mathematics decidable?" (Hodges p. 91, Hawking p. 1121). The first two questions were answered in 1930 by Kurt Gödel at the very same meeting where Hilbert delivered his retirement speech (much to the chagrin of Hilbert); the third—the Entscheidungsproblem—had to wait until the mid-1930s.

The problem was that an answer first required a precise definition of "definite general applicable prescription", which Princeton professor Alonzo Church would come to call "effective calculability", and in 1928 no such definition existed. But over the next 6–7 years Emil Post developed his definition of a worker moving from room to room writing and erasing marks per a list of instructions (Post 1936), as did Church and his two students Stephen Kleene and J. B. Rosser by use of Church's lambda-calculus and Gödel's recursion theory (1934). Church's paper (published 15 April 1936) showed that the Entscheidungsproblem was indeed "undecidable" and beat Turing to the punch by almost a year (Turing's paper submitted 28 May 1936, published January 1937). In the meantime, Emil Post submitted a brief paper in the fall of 1936, so Turing at least had priority over Post. While Church refereed Turing's paper, Turing had time to study Church's paper and add an Appendix where he sketched a proof that Church's lambda-calculus and his machines would compute the same functions.

But what Church had done was something rather different, and in a certain sense weaker. ... the Turing construction was more direct, and provided an argument from first principles, closing the gap in Church's demonstration.

— Hodges p. 112

And Post had only proposed a definition of calculability and criticized Church's "definition", but had proved nothing.

Alan Turing's a-machine

In the spring of 1935, Turing as a young Master's student at King's College, Cambridge, took on the challenge; he had been stimulated by the lectures of the logician M. H. A. Newman "and learned from them of Gödel's work and the Entscheidungsproblem ... Newman used the word 'mechanical' ... In his obituary of Turing 1955 Newman writes:

To the question 'what is a "mechanical" process?' Turing returned the characteristic answer 'Something that can be done by a machine' and he embarked on the highly congenial task of analysing the general notion of a computing machine.

— Gandy, p. 74

Gandy states that:

I suppose, but do not know, that Turing, right from the start of his work, had as his goal a proof of the undecidability of the Entscheidungsproblem. He told me that the 'main idea' of the paper came to him when he was lying in Grantchester meadows in the summer of 1935. The 'main idea' might have either been his analysis of computation or his realization that there was a universal machine, and so a diagonal argument to prove unsolvability.

— ibid., p. 76

While Gandy believed that Newman's statement above is "misleading", this opinion is not shared by all. Turing had a lifelong interest in machines: "Alan had dreamt of inventing typewriters as a boy; [his mother] Mrs. Turing had a typewriter; and he could well have begun by asking himself what was meant by calling a typewriter 'mechanical'" (Hodges p. 96). While at Princeton pursuing his PhD, Turing built a Boolean-logic multiplier (see below). His PhD thesis, titled "Systems of Logic Based on Ordinals", contains the following definition of "a computable function":

It was stated above that 'a function is effectively calculable if its values can be found by some purely mechanical process'. We may take this statement literally, understanding by a purely mechanical process one which could be carried out by a machine. It is possible to give a mathematical description, in a certain normal form, of the structures of these machines. The development of these ideas leads to the author's definition of a computable function, and to an identification of computability with effective calculability. It is not difficult, though somewhat laborious, to prove that these three definitions [the 3rd is the λ-calculus] are equivalent.

— Turing (1939) in The Undecidable, p. 160

When Turing returned to the UK he ultimately became jointly responsible for breaking the German secret codes created by encryption machines called "The Enigma"; he also became involved in the design of the ACE (Automatic Computing Engine), "[Turing's] ACE proposal was effectively self-contained, and its roots lay not in the EDVAC [the USA's initiative], but in his own universal machine" (Hodges p. 318). Arguments still continue concerning the origin and nature of what has been named by Kleene (1952) Turing's Thesis. But what Turing did prove with his computational-machine model appears in his paper "On Computable Numbers, with an Application to the Entscheidungsproblem" (1937):

[that] the Hilbert Entscheidungsproblem can have no solution ... I propose, therefore to show that there can be no general process for determining whether a given formula U of the functional calculus K is provable, i.e. that there can be no machine which, supplied with any one U of these formulae, will eventually say whether U is provable.

— from Turing's paper as reprinted in The Undecidable, p. 145

Turing's example (his second proof): If one is to ask for a general procedure to tell us: "Does this machine ever print 0", the question is "undecidable".

1937–1970: The "digital computer", the birth of "computer science"

In 1937, while at Princeton working on his PhD thesis, Turing built a digital (Boolean-logic) multiplier from scratch, making his own electromechanical relays (Hodges p. 138). "Alan's task was to embody the logical design of a Turing machine in a network of relay-operated switches ..." (Hodges p. 138). While Turing might have been just initially curious and experimenting, quite-earnest work in the same direction was going in Germany (Konrad Zuse (1938)), and in the United States (Howard Aiken) and George Stibitz (1937); the fruits of their labors were used by both the Axis and Allied militaries in World War II (cf. Hodges p. 298–299). In the early to mid-1950s Hao Wang and Marvin Minsky reduced the Turing machine to a simpler form (a precursor to the Post–Turing machine of Martin Davis); simultaneously European researchers were reducing the new-fangled electronic computer to a computer-like theoretical object equivalent to what was now being called a "Turing machine". In the late 1950s and early 1960s, the coincidentally parallel developments of Melzak and Lambek (1961), Minsky (1961), and Shepherdson and Sturgis (1961) carried the European work further and reduced the Turing machine to a more friendly, computer-like abstract model called the counter machine; Elgot and Robinson (1964), Hartmanis (1971), Cook and Reckhow (1973) carried this work even further with the register machine and random-access machine models—but basically all are just multi-tape Turing machines with an arithmetic-like instruction set.

1970–present: as a model of computation

Today, the counter, register and random-access machines and their sire the Turing machine continue to be the models of choice for theorists investigating questions in the theory of computation. In particular, computational complexity theory makes use of the Turing machine:

Depending on the objects one likes to manipulate in the computations (numbers like nonnegative integers or alphanumeric strings), two models have obtained a dominant position in machine-based complexity theory:

the off-line multitape Turing machine..., which represents the standard model for string-oriented computation, and the random access machine (RAM) as introduced by Cook and Reckhow ..., which models the idealized Von Neumann-style computer.

— van Emde Boas 1990:4

Only in the related area of analysis of algorithms this role is taken over by the RAM model.

— van Emde Boas 1990:16

Homo habilis

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Homo_habilis 

 

Homo habilis Temporal range: 2.3–1.65 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓
Reconstruction of KNM-ER 1813 at the Naturmuseum Senckenberg, Germany
Scientific classification
Kingdom:	Animalia
Phylum:	Chordata
Class:	Mammalia
Order:	Primates
Suborder:	Haplorhini
Infraorder:	Simiiformes
Family:	Hominidae
Subfamily:	Homininae
Tribe:	Hominini
Genus:	Homo
Species:	†H. habilis
Binomial name
†Homo habilis Leakey et al., 1964
Synonyms
Australopithecus habilis Wood and Collard, 1999 Homo microcranous Ferguson, 1995 Homo gautengensis? Curnoe, 2010 Homo rudolfensis? Alexeev, 1986

Homo habilis ("handy man") is an extinct species of archaic human from the Early Pleistocene of East and South Africa about 2.31 million years ago to 1.65 million years ago (mya). Upon species description in 1964, H. habilis was highly contested, with many researchers recommending it be synonymised with Australopithecus africanus, the only other early hominin known at the time, but H. habilis received more recognition as time went on and more relevant discoveries were made. By the 1980s, H. habilis was proposed to have been a human ancestor, directly evolving into Homo erectus which directly led to modern humans. This viewpoint is now debated. Several specimens with insecure species identification were assigned to H. habilis, leading to arguments for splitting, namely into "H. rudolfensis" and "H. gautengensis" of which only the former has received wide support.

Like contemporary Homo, H. habilis brain size generally varied from 500–900 cm³ (31–55 cu in). The body proportions of H. habilis are only known from two highly fragmentary skeletons, and is based largely on assuming a similar anatomy to the earlier australopithecines. Because of this, it has also been proposed H. habilis be moved to the genus Australopithecus as Australopithecus habilis. However, the interpretation of H. habilis as a small-statured human with inefficient long distance travel capabilities has been challenged. The presumed female specimen OH 62 is traditionally interpreted as having been 100–120 cm (3 ft 3 in – 3 ft 11 in) in height and 20–37 kg (44–82 lb) in weight assuming australopithecine-like proportions, but assuming humanlike proportions she would have been about 148 cm (4 ft 10 in) and 35 kg (77 lb). Nonetheless, H. habilis may have been at least partially arboreal like what is postulated for australopithecines. Early hominins are typically reconstructed as having thick hair and marked sexual dimorphism with males much larger than females, though relative male and female size is not definitively known.

H. habilis manufactured the Oldowan stone-tool industry and mainly used tools in butchering. Early Homo, compared to australopithecines, are generally thought to have consumed high quantities of meat and, in the case of H. habilis, scavenged meat. Typically, early hominins are interpreted as having lived in polygynous societies, though this is highly speculative. Assuming H. habilis society was similar to that of modern savanna chimpanzees and baboons, groups may have numbered 70–85 members, with multiple males to defend against open savanna predators, such as big cats, hyenas and crocodiles. H. habilis coexisted with H. rudolfensis, H. ergaster / H. erectus and Paranthropus boisei.

Taxonomy

Research history

KNM-ER 1813 reconstructed skull and jaw

The first recognised remains—OH 7, partial juvenile skull, hand, and foot bones dating to 1.75 million years ago (mya)—were discovered in Olduvai Gorge, Tanzania, in 1960 by Jonathan Leakey. However, the actual first remains—OH 4, a molar—were discovered by the senior assistant of Louis and Mary Leakey (Jonathan's parents), Heselon Mukiri, in 1959, but this was not realised at the time. By this time, the Leakeys had spent 29 years excavating in Olduvai Gorge for early hominin remains, but had instead recovered mainly other animal remains as well as the Oldowan stone-tool industry. The industry had been ascribed to Paranthropus boisei (at the time "Zinjanthropus") in 1959 as it was the first and only hominin recovered in the area, but this was revised upon OH 7's discovery. In 1964, Louis, South African palaeoanthropologist Phillip V. Tobias, and British primatologist John R. Napier officially assigned the remains into the genus Homo as, on recommendation by Australian anthropologist Raymond Dart, H. habilis, the specific name meaning "able, handy, mentally skillful, vigorous" in Latin. The specimen's association with the Oldowan (then considered evidence of advanced cognitive ability) was also used as justification for classifying it into Homo. OH 7 was designated the holotype specimen.

After description, it was hotly debated if H. habilis should be reclassified into Australopithecus africanus (the only other early hominin known at the time), in part because the remains were so old and at the time Homo was presumed to have evolved in Asia (with the australopithecines having no living descendants). Also, the brain size was smaller than what Wilfrid Le Gros Clark proposed in 1955 when considering Homo. The classification H. habilis began to receive wider acceptance as more fossil elements and species were unearthed. In 1983, Tobias proposed that A. africanus was a direct ancestor of Paranthropus and Homo (the two were sister taxa), and that A. africanus evolved into H. habilis which evolved into H. erectus which evolved into modern humans (by a process of cladogenesis). He further said that there was a major evolutionary leap between A. africanus and H. habilis, and thereupon human evolution progressed gradually because H. habilis brain size had nearly doubled compared to australopithecine predecessors.

Australopithecus

 

H. habilis

 

H. ergaster / H. erectus

 

H. sapiens

 

Human evolution according to Tobias, 1983

 

Cast of the type specimen OH 7

Many had accepted Tobias' model and assigned Late Pliocene to Early Pleistocene hominin remains outside the range of Paranthropus and H. erectus into H. habilis. For non-skull elements, this was done on the basis of size as there was a lack of clear diagnostic characteristics. Because of these practices, the range of variation for the species became quite wide, and the terms H. habilis sensu stricto ("in the strict sense") and H. habilis sensu lato ("in the broad sense") were in use to include and exclude, respectively, more discrepant morphs. To address this, in 1985, English palaeoanthropologist Bernard Wood proposed that the comparatively massive skull KNM-ER 1470 from Lake Turkana, Kenya, discovered in 1972 and assigned to H. habilis, actually represented a different species, now referred to as Homo rudolfensis. It is also argued that instead it represents a male specimen whereas other H. habilis specimens are female. Early Homo from South Africa have variously been assigned to H. habilis or H. ergaster / H. erectus, but species designation has largely been unclear. In 2010, Australian archaeologist Darren Curoe proposed splitting off South African early Homo into a new species, "Homo gautengensis".

In 1986, OH 62, a fragmentary skeleton, was discovered by American anthropologist Tim D. White in association with H. habilis skull fragments, definitively establishing aspects of H. habilis skeletal anatomy for the first time, and revealing more Australopithecus-like than Homo-like features. Because of this, as well as similarities in dental adaptations, Wood and biological anthropologist Mark Collard suggested moving the species to Australopithecus in 1999. However, reevaluation of OH 62 to a more humanlike physiology, if correct, would cast doubt on this. The discovery of the 1.8 Ma Georgian Dmanisi skulls in the early 2000s, which exhibit several similarities with early Homo, has led to suggestions that all contemporary groups of early Homo in Africa, including H. habilis and H. rudolfensis, are the same species and should be assigned to H. erectus.

Classification

There is still no wide consensus as to whether or not H. habilis is ancestral to H. ergaster / H. erectus or is an offshoot of the human line, and whether or not all specimens assigned to H. habilis are correctly assigned or the species is an assemblage of different Australopithecus and Homo species. Nonetheless, H. habilis and H. rudolfensis generally are recognised members of the genus at the base of the family tree, with arguments for synonymisation or removal from the genus not widely adopted.

Though it is now largely agreed upon that Homo evolved from Australopithecus, the timing and placement of this split has been much debated, with many Australopithecus species having been proposed as the ancestor. The discovery of LD 350-1, the oldest Homo specimen, dating to 2.8 mya, in the Afar Region of Ethiopia may indicate that the genus evolved from A. afarensis around this time. The species LD 350-1 belongs to could be the ancestor of H. habilis, but this is unclear. The oldest H. habilis specimen, A.L. 666-1, dates to 2.3 mya, but is anatomically more derived (has less ancestral, or basal, traits) than the younger OH 7, suggesting derived and basal morphs lived concurrently, and that the H. habilis lineage began before 2.3 mya. Based on 2.1-million-year-old stone tools from Shangchen, China, H. habilis or an ancestral species may have dispersed across Asia. The youngest H. habilis specimen, OH 13, dates to about 1.65 mya.

African hominin timeline (in mya)
View references

Anatomy

Skull

It has generally been thought that brain size increased along the human line especially rapidly at the transition between species, with H. habilis brain size smaller than that of H. ergaster / H. erectus, jumping from about 600–650 cc (37–40 cu in) in H. habilis to about 900–1,000 cc (55–61 cu in) in H. ergaster and H. erectus. However, a 2015 study showed that the brain sizes of H. habilis, H. rudolfensis, and H. ergaster generally ranged between 500–900 cc (31–55 cu in) after reappraising the brain volume of OH 7 from 647–687 cc (39.5–41.9 cu in) to 729–824 cc (44.5–50.3 cu in). This does, nonetheless, indicate a jump from australopithecine brain size which generally ranged from 400–500 cc (24–31 cu in).

The brain anatomy of all Homo features an expanded cerebrum in comparison to australopithecines. The pattern of striations on the teeth of OH 65 slanting right, which may have been accidentally self-inflicted when the individual was pulling a piece of meat with its teeth and the left hand while trying to cut it with a stone tool using the right hand. If correct, this could indicate right handedness, and handedness is associated with major reorganisation of the brain and the lateralisation of brain function between the left and right hemispheres. This scenario has also been hypothesised for some Neanderthal specimens. Lateralisation could be implicated in tool use. In modern humans, lateralisation is weakly associated with language.

The tooth rows of H. habilis were V-shaped as opposed to U-shaped in later Homo, and the mouth jutted outwards (was prognathic), though the face was flat from the nose up.

Build

Based on the fragmentary skeletons OH 62 (presumed female) and KNM-ER 3735 (presumed male), H. habilis body anatomy has generally been considered to have been more apelike than even that of the earlier A. afarensis and consistent with an at least partially arboreal lifestyle in the trees as is assumed in australopithecines. Based on OH 62 and assuming comparable body dimensions to australopithecines, H. habilis has generally been interpreted as having been small-bodied like australopithecines, with OH 62 generally estimated at about 100–120 cm (3 ft 3 in – 3 ft 11 in) in height and 20–37 kg (44–82 lb) in weight. However, assuming longer, modern humanlike legs, OH 62 would have been about 148 cm (4 ft 10 in) and 35 kg (77 lb), and KNM-ER 3735 about the same size. For comparison, modern human men and women in the year 1900 averaged 163 cm (5 ft 4 in) and 152.7 cm (5.01 ft), respectively. It is generally assumed that pre-H. ergaster hominins, including H. habilis, exhibited notable sexual dimorphism with males markedly bigger than females. However, relative female body mass is unknown in this species.

Early hominins, including H. habilis, are thought to have had thick body hair coverage like modern non-human apes because they appear to have inhabited colder regions and are thought to have had a less active lifestyle than (presumed hairless) post-ergaster species. Consequently, they probably required thick body hair to stay warm. Based on dental development rates, H. habilis is assumed to have had an accelerated growth rate compared to modern humans, more like that of modern non-human apes.

Limbs

The arms of H. habilis and australopithecines have generally been considered to have been proportionally long and so adapted for climbing and swinging. In 2004, anthropologists Martin Haeusler and Henry McHenry argued that, because the humerus to femur ratio of OH 62 is within the range of variation for modern humans, and KNM-ER 3735 is close to the modern human average, it is unsafe to assume apelike proportions. Nonetheless, the humerus of OH 62 measured 258–270 mm (10.2–10.6 in) long and the ulna (forearm) 245–255 mm (9.6–10.0 in), which is closer to the proportion seen in chimpanzees. The hand bones of OH 7 suggest precision gripping, important in dexterity, as well as adaptations for climbing. In regard to the femur, traditionally comparisons with the A. afarensis specimen AL 288-1 have been used to reconstruct stout legs for H. habilis, but Haeusler and McHenry suggested the more gracile OH 24 femur (either belonging to H. ergaster / H. erectus or P. boisei) may be a more apt comparison. In this instance, H. habilis would have had longer, humanlike legs and have been effective long-distance travellers as is assumed to have been the case in H. ergaster. However, estimating the unpreserved length of a fossil is highly problematic. The thickness of the limb bones in OH 62 is more similar to chimpanzees than H. ergaster / H. erectus and modern humans, which may indicate different load bearing capabilities more suitable for arboreality in H. habilis. The strong fibula of OH 35 (though this may belong to P. boisei) is more like that of non-human apes, and consistent with arboreality and vertical climbing.

OH 8, bearing crocodile tooth marks

OH 8, a foot, is better suited for terrestrial movement than the foot of A. afarensis, though still retains many apelike features consistent with climbing. However, the foot has projected toe bone and compacted mid-foot joint structures, which restrict rotation between the foot and ankle as well as at the front foot. Foot stability enhances the efficiency of force transfer between the leg and the foot and vice versa, and is implicated in the plantar arch elastic spring mechanism which generates energy while running (but not walking). This could possibly indicate H. habilis was capable of some degree of endurance running, which is typically thought to have evolved later in H. ergaster / H. erectus.

Culture

Society

Typically, H. ergaster / H. erectus is considered to have been the first human to have lived in a monogamous society, and all preceding hominins were polygynous. However, it is highly difficult to speculate with any confidence the group dynamics of early hominins. The degree of sexual dimorphism and the size disparity between males and females is often used to correlate between polygyny with high disparity and monogamy with low disparity based on general trends (though not without exceptions) seen in modern primates. Rates of sexual dimorphism are difficult to determine as early hominin anatomy is poorly known, and are largely based on few specimens like. In some cases, sex is arbitrarily determined in large part based on perceived size and apparent robustness in the absence of more reliable elements in sex identification (namely the pelvis). Mating systems are also based on dental anatomy, but early hominins possess a mosaic anatomy of different traits not seen together in modern primates; the enlarged cheek teeth would suggest marked size-related dimorphism and thus intense male–male conflict over mates and a polygynous society, but the small canines should indicate the opposite. Other selective pressures, including diet, can also dramatically impact dental anatomy. The spatial distribution of tools and processed animal bones at the FLK Zinj and PTK sites in Olduvai Gorge indicate the inhabitants used this area as a communal butchering and eating grounds, as opposed to the nuclear family system of modern hunter gatherers where the group is subdivided into smaller units each with their own butchering and eating grounds.

The behaviour of early Homo, including H. habilis, is sometimes modelled on that of savanna chimps and baboons. These communities consist of several males (as opposed to a harem society) in order to defend the group on the dangerous and exposed habitat, sometimes engaging in a group display of throwing sticks and stones against enemies and predators. The left foot OH 8 seems to have been bitten off by a crocodile, possibly Crocodylus anthropophagus, and the leg OH 35, which either belongs to P. boisei or H. habilis, shows evidence of leopard predation. H. habilis and contemporary hominins were likely predated upon by other large carnivores of the time, such as (in Olduvai Gorge) the hunting hyena Chasmaporthetes nitidula, and the saber-toothed cats Dinofelis and Megantereon. In 1993, American palaeoanthropologist Leslie C. Aiello and British evolutionary psychologist Robin Dunbar estimated that H. habilis group size ranged from 70–85 members—on the upper end of chimp and baboon group size—based on trends seen in neocortex size and group size in modern non-human primates.

H. habilis coexisted with H. rudolfensis, H. ergaster / H. erectus, and P. boisei. It is unclear how all of these species interacted. To explain why P. boisei was associated with Olduwan tools despite not being the knapper (the one who made the tools), Leakey and colleagues, when describing H. habilis, suggested that one possibility was P. boisei was killed by H. habilis, perhaps as food. However, when describing P. boisei five years earlier, Louis Leakey said, "There is no reason whatever, in this case, to believe that the skull represents the victim of a cannibalistic feast by some hypothetical more advanced type of man."

Diet

OH 13 mandible compared to other hominin species

It is thought H. habilis derived meat from scavenging rather than hunting (scavenger hypothesis), acting as a confrontational scavenger and stealing kills from smaller predators such as jackals or cheetahs. Fruit was likely also an important dietary component, indicated by dental erosion consistent with repetitive exposure to acidity. Based on dental microwear-texture analysis, H. habilis (like other early Homo) likely did not regularly consume tough foods. Microwear-texture complexity is, on average, somewhere between that of tough-food eaters and leaf eaters (folivores), and points to an increasingly generalised and omnivorous diet.

It is typically thought that the diets of H. habilis and other early Homo had a greater proportion of meat than Australopithecus, and that this led to brain growth. The main hypotheses regarding this are: meat is energy- and nutrient-rich and put evolutionary pressure on developing enhanced cognitive skills to facilitate strategic scavenging and monopolise fresh carcasses, or meat allowed the large and calorie-expensive ape gut to decrease in size allowing this energy to be diverted to brain growth. Alternatively, it is also suggested that early Homo, in a drying climate with scarcer food options, relied primarily on underground storage organs (such as tubers) and food sharing, which facilitated social bonding among both male and female group members. However, unlike what is presumed for H. ergaster and later Homo, short-statured early Homo are generally considered to have been incapable of endurance running and hunting, and the long and Australopithecus-like forearm of H. habilis could indicate early Homo were still arboreal to a degree. Also, organised hunting and gathering is thought to have emerged in H. ergaster. Nonetheless, the proposed food-gathering models to explain large brain growth necessitate increased daily travel distance. It has also been argued that H. habilis instead had long, modern humanlike legs and was fully capable of effective long distance travel, while still remaining at least partially arboreal.

Large incisor size in H. habilis compared to Australopithecus predecessors implies this species relied on incisors more. The bodies of the mandibles of H. habilis and other early Homo are thicker than those of modern humans and all living apes, more comparable to Australopithecus. The mandibular body resists torsion from the bite force or chewing, meaning their jaws could produce unusually powerful stresses while eating. The greater molar cusp relief in H. habilis compared to Australopithecus suggests the former used tools to fracture tough foods (such as pliable plant parts or meat), otherwise the cusps would have been more worn down. Nonetheless, the jaw adaptations for processing mechanically challenging food indicates technological advancement did not greatly affect diet.

Technology

Oldowan chopper

H. habilis is associated with the Early Stone Age Oldowan stone tool industry. Individuals likely used these tools primarily to butcher and skin animals and crush bones, but also sometimes to saw and scrape wood and cut soft plants. Knappers - individuals shaping stones, appear to have carefully selected lithic cores and knew that certain rocks would break in a specific way when struck hard enough and on the right spot, and they produced several different types, including choppers, polyhedrons, and discoids. Nonetheless, specific shapes were likely not thought of in advance, and probably stem from a lack of standardisation in producing such tools as well as the types of raw materials at the knappers' disposal. For example, spheroids are common at Olduvai which features an abundance of large and soft quartz and quartzite pieces, whereas Koobi Fora lacks spheroids and provides predominantly hard basalt lava rocks. Unlike the later Acheulean culture invented by H. ergaster / H. erectus, Oldowan technology does not require planning and foresight to manufacture, and thus does not indicate high cognition in Oldowan knappers, though it does require a degree of coordination and some knowledge of mechanics. Oldowan tools infrequently exhibit retouching and were probably discarded immediately after use most of the time.

The Olduwan was first reported in 1934, but it was not until the 1960s that it become widely accepted as the earliest culture, dating to 1.8 mya, and as having been manufactured by H. habilis. Since then, more discoveries have placed the origins of material culture substantially backwards in time, with the Oldowan being discovered in Ledi-Geraru and Gona in Ethiopia dating to 2.6 mya, perhaps associated with the evolution of the genus. Australopithecines are also known to have manufactured tools, such as the 3.3 Ma Lomekwi stone tool industry, and some evidence of butchering from about 3.4 mya. Nonetheless, the comparatively sharp-edged Oldowan culture was a major innovation from australopithecine technology, and it would have allowed different feeding strategies and the ability to process a wider range of foods, which would have been advantageous in the changing climate of the time. It is unclear if the Oldowan was independently invented or if it was the result of hominin experimentation with rocks over hundreds of thousands of years across multiple species.

In 1962, a 366 cm × 427 cm × 30 cm (12 ft × 14 ft × 1 ft) circle made with volcanic rocks was discovered in Olduvai Gorge. At 61–76 cm (2–2.5 ft) intervals, rocks were piled up to 15–23 cm (6–9 in) high. Mary Leakey suggested the rock piles were used to support poles stuck into the ground, possibly to support a windbreak or a rough hut. Some modern-day nomadic tribes build similar low-lying rock walls to build temporary shelters upon, bending upright branches as poles and using grasses or animal hide as a screen. Dating to 1.75 mya, it is attributed to some early Homo, and is the oldest-claimed evidence of architecture.