Crystal structure

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Crystal_structure 

 

Crystal structure of table salt (sodium in purple, chloride in green)

In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions or molecules in a crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.

The smallest group of particles in the material that constitutes this repeating pattern is the unit cell of the structure. The unit cell completely reflects the symmetry and structure of the entire crystal, which is built up by repetitive translation of the unit cell along its principal axes. The translation vectors define the nodes of the Bravais lattice.

The lengths of the principal axes, or edges, of the unit cell and the angles between them are the lattice constants, also called lattice parameters or cell parameters. The symmetry properties of the crystal are described by the concept of space groups. All possible symmetric arrangements of particles in three-dimensional space may be described by the 230 space groups.

The crystal structure and symmetry play a critical role in determining many physical properties, such as cleavage, electronic band structure, and optical transparency.

Unit cell

Main article: Unit cell

Crystal structure is described in terms of the geometry of arrangement of particles in the unit cells. The unit cell is defined as the smallest repeating unit having the full symmetry of the crystal structure. The geometry of the unit cell is defined as a parallelepiped, providing six lattice parameters taken as the lengths of the cell edges (a, b, c) and the angles between them (α, β, γ). The positions of particles inside the unit cell are described by the fractional coordinates (x_i, y_i, z_i) along the cell edges, measured from a reference point. It is only necessary to report the coordinates of a smallest asymmetric subset of particles. This group of particles may be chosen so that it occupies the smallest physical space, which means that not all particles need to be physically located inside the boundaries given by the lattice parameters. All other particles of the unit cell are generated by the symmetry operations that characterize the symmetry of the unit cell. The collection of symmetry operations of the unit cell is expressed formally as the space group of the crystal structure.

• 

  Simple cubic (P)

• 

  Body-centered cubic (I)

• 

  Face-centered cubic (F)

Miller indices

Planes with different Miller indices in cubic crystals

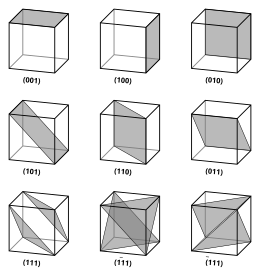
Vectors and planes in a crystal lattice are described by the three-value Miller index notation. This syntax uses the indices ℓ, m, and n as directional parameters.

By definition, the syntax (ℓmn) denotes a plane that intercepts the three points a₁/ℓ, a₂/m, and a₃/n, or some multiple thereof. That is, the Miller indices are proportional to the inverses of the intercepts of the plane with the unit cell (in the basis of the lattice vectors). If one or more of the indices is zero, it means that the planes do not intersect that axis (i.e., the intercept is "at infinity"). A plane containing a coordinate axis is translated so that it no longer contains that axis before its Miller indices are determined. The Miller indices for a plane are integers with no common factors. Negative indices are indicated with horizontal bars, as in (123). In an orthogonal coordinate system for a cubic cell, the Miller indices of a plane are the Cartesian components of a vector normal to the plane.

Considering only (ℓmn) planes intersecting one or more lattice points (the lattice planes), the distance d between adjacent lattice planes is related to the (shortest) reciprocal lattice vector orthogonal to the planes by the formula

${\displaystyle d={\frac {2\pi }{|\mathbf {g} _{\ell mn}|}}}$

Planes and directions

The crystallographic directions are geometric lines linking nodes (atoms, ions or molecules) of a crystal. Likewise, the crystallographic planes are geometric planes linking nodes. Some directions and planes have a higher density of nodes. These high density planes have an influence on the behavior of the crystal as follows:

• Optical properties: Refractive index is directly related to density (or periodic density fluctuations).
• Adsorption and reactivity: Physical adsorption and chemical reactions occur at or near surface atoms or molecules. These phenomena are thus sensitive to the density of nodes.
• Surface tension: The condensation of a material means that the atoms, ions or molecules are more stable if they are surrounded by other similar species. The surface tension of an interface thus varies according to the density on the surface.

Dense crystallographic planes

• Microstructural defects: Pores and crystallites tend to have straight grain boundaries following higher density planes.
• Cleavage: This typically occurs preferentially parallel to higher density planes.
• Plastic deformation: Dislocation glide occurs preferentially parallel to higher density planes. The perturbation carried by the dislocation (Burgers vector) is along a dense direction. The shift of one node in a more dense direction requires a lesser distortion of the crystal lattice.

Some directions and planes are defined by symmetry of the crystal system. In monoclinic, rhombohedral, tetragonal, and trigonal/hexagonal systems there is one unique axis (sometimes called the principal axis) which has higher rotational symmetry than the other two axes. The basal plane is the plane perpendicular to the principal axis in these crystal systems. For triclinic, orthorhombic, and cubic crystal systems the axis designation is arbitrary and there is no principal axis.

Cubic structures

For the special case of simple cubic crystals, the lattice vectors are orthogonal and of equal length (usually denoted a); similarly for the reciprocal lattice. So, in this common case, the Miller indices (ℓmn) and [ℓmn] both simply denote normals/directions in Cartesian coordinates. For cubic crystals with lattice constant a, the spacing d between adjacent (ℓmn) lattice planes is (from above):

${\displaystyle d_{\ell mn}={\frac {a}{\sqrt {\ell ^{2}+m^{2}+n^{2}}}}}$

Because of the symmetry of cubic crystals, it is possible to change the place and sign of the integers and have equivalent directions and planes:

• Coordinates in angle brackets such as ⟨100⟩ denote a family of directions that are equivalent due to symmetry operations, such as [100], [010], [001] or the negative of any of those directions.
• Coordinates in curly brackets or braces such as {100} denote a family of plane normals that are equivalent due to symmetry operations, much the way angle brackets denote a family of directions.

For face-centered cubic (fcc) and body-centered cubic (bcc) lattices, the primitive lattice vectors are not orthogonal. However, in these cases the Miller indices are conventionally defined relative to the lattice vectors of the cubic supercell and hence are again simply the Cartesian directions.

Interplanar spacing

The spacing d between adjacent (hkℓ) lattice planes is given by:

• Cubic:

  ${\displaystyle {\frac {1}{d^{2}}}={\frac {h^{2}+k^{2}+\ell ^{2}}{a^{2}}}}$

• Tetragonal:

  ${\displaystyle {\frac {1}{d^{2}}}={\frac {h^{2}+k^{2}}{a^{2}}}+{\frac {\ell ^{2}}{c^{2}}}}$

• Hexagonal:

  ${\displaystyle {\frac {1}{d^{2}}}={\frac {4}{3}}\left({\frac {h^{2}+hk+k^{2}}{a^{2}}}\right)+{\frac {\ell ^{2}}{c^{2}}}}$

• Rhombohedral:

  ${\displaystyle {\frac {1}{d^{2}}}={\frac {(h^{2}+k^{2}+\ell ^{2})\sin ^{2}\alpha +2(hk+k\ell +h\ell )(\cos ^{2}\alpha -\cos \alpha )}{a^{2}(1-3\cos ^{2}\alpha +2\cos ^{3}\alpha )}}}$

• Orthorhombic:

  ${\displaystyle {\frac {1}{d^{2}}}={\frac {h^{2}}{a^{2}}}+{\frac {k^{2}}{b^{2}}}+{\frac {\ell ^{2}}{c^{2}}}}$

• Monoclinic:

  ${\displaystyle {\frac {1}{d^{2}}}=\left({\frac {h^{2}}{a^{2}}}+{\frac {k^{2}\sin ^{2}\beta }{b^{2}}}+{\frac {\ell ^{2}}{c^{2}}}-{\frac {2h\ell \cos \beta }{ac}}\right)\csc ^{2}\beta }$

• Triclinic:

  ${\displaystyle {\frac {1}{d^{2}}}={\frac {{\frac {h^{2}}{a^{2}}}\sin ^{2}\alpha +{\frac {k^{2}}{b^{2}}}\sin ^{2}\beta +{\frac {\ell ^{2}}{c^{2}}}\sin ^{2}\gamma +{\frac {2k\ell }{bc}}(\cos \beta \cos \gamma -\cos \alpha )+{\frac {2h\ell }{ac}}(\cos \gamma \cos \alpha -\cos \beta )+{\frac {2hk}{ab}}(\cos \alpha \cos \beta -\cos \gamma )}{1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}}$

Classification by symmetry

Main article: Crystal system

The defining property of a crystal is its inherent symmetry. Performing certain symmetry operations on the crystal lattice leaves it unchanged. All crystals have translational symmetry in three directions, but some have other symmetry elements as well. For example, rotating the crystal 180° about a certain axis may result in an atomic configuration that is identical to the original configuration; the crystal has twofold rotational symmetry about this axis. In addition to rotational symmetry, a crystal may have symmetry in the form of mirror planes, and also the so-called compound symmetries, which are a combination of translation and rotation or mirror symmetries. A full classification of a crystal is achieved when all inherent symmetries of the crystal are identified.

Lattice systems

Lattice systems are a grouping of crystal structures according to the axial system used to describe their lattice. Each lattice system consists of a set of three axes in a particular geometric arrangement. All crystals fall into one of seven lattice systems. They are similar to, but not quite the same as the seven crystal systems.

Crystal family	Lattice system	Point group (Schönflies notation)	14 Bravais lattices
			Primitive (P)	Base-centered (S)	Body-centered (I)	Face-centered (F)
Triclinic (a)		Ci	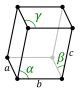aP
Monoclinic (m)		C2h	mP	mS
Orthorhombic (o)		D2h	oP	oS	oI	oF
Tetragonal (t)		D4h	tP		tI
Hexagonal (h)	Rhombohedral	D3d	hR
	Hexagonal	D6h	hP
Cubic (c)		Oh	cP		cI	cF

The simplest and most symmetric, the cubic or isometric system, has the symmetry of a cube, that is, it exhibits four threefold rotational axes oriented at 109.5° (the tetrahedral angle) with respect to each other. These threefold axes lie along the body diagonals of the cube. The other six lattice systems, are hexagonal, tetragonal, rhombohedral (often confused with the trigonal crystal system), orthorhombic, monoclinic and triclinic.

Bravais lattices

Bravais lattices, also referred to as space lattices, describe the geometric arrangement of the lattice points, and therefore the translational symmetry of the crystal. The three dimensions of space afford 14 distinct Bravais lattices describing the translational symmetry. All crystalline materials recognized today, not including quasicrystals, fit in one of these arrangements. The fourteen three-dimensional lattices, classified by lattice system, are shown above.

The crystal structure consists of the same group of atoms, the basis, positioned around each and every lattice point. This group of atoms therefore repeats indefinitely in three dimensions according to the arrangement of one of the Bravais lattices. The characteristic rotation and mirror symmetries of the unit cell is described by its crystallographic point group.

Crystal systems

See also: Crystallographic point group § Isomorphisms

A crystal system is a set of point groups in which the point groups themselves and their corresponding space groups are assigned to a lattice system. Of the 32 point groups that exist in three dimensions, most are assigned to only one lattice system, in which case the crystal system and lattice system both have the same name. However, five point groups are assigned to two lattice systems, rhombohedral and hexagonal, because both lattice systems exhibit threefold rotational symmetry. These point groups are assigned to the trigonal crystal system.

Crystal family	Crystal system	Point group / Crystal class	Schönflies	Point symmetry	Order	Abstract group
triclinic		pedial	C1	enantiomorphic polar	1	trivial ${\displaystyle \mathbb {Z} _{1}}$
		pinacoidal	Ci (S2)	centrosymmetric	2	cyclic ${\displaystyle \mathbb {Z} _{2}}$
monoclinic		sphenoidal	C2	enantiomorphic polar	2	cyclic ${\displaystyle \mathbb {Z} _{2}}$
		domatic	Cs (C1h)	polar	2	cyclic ${\displaystyle \mathbb {Z} _{2}}$
		prismatic	C2h	centrosymmetric	4	Klein four ${\displaystyle \mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}}$
orthorhombic		rhombic-disphenoidal	D2 (V)	enantiomorphic	4	Klein four ${\displaystyle \mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}}$
		rhombic-pyramidal	C2v	polar	4	Klein four ${\displaystyle \mathbb {V} =\mathbb {Z} _{2}\times \mathbb {Z} _{2}}$
		rhombic-dipyramidal	D2h (Vh)	centrosymmetric	8	${\displaystyle \mathbb {V} \times \mathbb {Z} _{2}}$
tetragonal		tetragonal-pyramidal	C4	enantiomorphic polar	4	cyclic ${\displaystyle \mathbb {Z} _{4}}$
		tetragonal-disphenoidal	S4	non-centrosymmetric	4	cyclic ${\displaystyle \mathbb {Z} _{4}}$
		tetragonal-dipyramidal	C4h	centrosymmetric	8	${\displaystyle \mathbb {Z} _{4}\times \mathbb {Z} _{2}}$
		tetragonal-trapezohedral	D4	enantiomorphic	8	dihedral ${\displaystyle \mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}}$
		ditetragonal-pyramidal	C4v	polar	8	dihedral ${\displaystyle \mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}}$
		tetragonal-scalenohedral	D2d (Vd)	non-centrosymmetric	8	dihedral ${\displaystyle \mathbb {D} _{8}=\mathbb {Z} _{4}\rtimes \mathbb {Z} _{2}}$
		ditetragonal-dipyramidal	D4h	centrosymmetric	16	${\displaystyle \mathbb {D} _{8}\times \mathbb {Z} _{2}}$
hexagonal	trigonal	trigonal-pyramidal	C3	enantiomorphic polar	3	cyclic ${\displaystyle \mathbb {Z} _{3}}$
		rhombohedral	C3i (S6)	centrosymmetric	6	cyclic ${\displaystyle \mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}}$
		trigonal-trapezohedral	D3	enantiomorphic	6	dihedral ${\displaystyle \mathbb {D} _{6}=\mathbb {Z} _{3}\rtimes \mathbb {Z} _{2}}$
		ditrigonal-pyramidal	C3v	polar	6	dihedral ${\displaystyle \mathbb {D} _{6}=\mathbb {Z} _{3}\rtimes \mathbb {Z} _{2}}$
		ditrigonal-scalenohedral	D3d	centrosymmetric	12	dihedral ${\displaystyle \mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}}$
	hexagonal	hexagonal-pyramidal	C6	enantiomorphic polar	6	cyclic ${\displaystyle \mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}}$
		trigonal-dipyramidal	C3h	non-centrosymmetric	6	cyclic ${\displaystyle \mathbb {Z} _{6}=\mathbb {Z} _{3}\times \mathbb {Z} _{2}}$
		hexagonal-dipyramidal	C6h	centrosymmetric	12	${\displaystyle \mathbb {Z} _{6}\times \mathbb {Z} _{2}}$
		hexagonal-trapezohedral	D6	enantiomorphic	12	dihedral ${\displaystyle \mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}}$
		dihexagonal-pyramidal	C6v	polar	12	dihedral ${\displaystyle \mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}}$
		ditrigonal-dipyramidal	D3h	non-centrosymmetric	12	dihedral ${\displaystyle \mathbb {D} _{12}=\mathbb {Z} _{6}\rtimes \mathbb {Z} _{2}}$
		dihexagonal-dipyramidal	D6h	centrosymmetric	24	${\displaystyle \mathbb {D} _{12}\times \mathbb {Z} _{2}}$
cubic		tetartoidal	T	enantiomorphic	12	alternating ${\displaystyle \mathbb {A} _{4}}$
		diploidal	Th	centrosymmetric	24	${\displaystyle \mathbb {A} _{4}\times \mathbb {Z} _{2}}$
		gyroidal	O	enantiomorphic	24	symmetric ${\displaystyle \mathbb {S} _{4}}$
		hextetrahedral	Td	non-centrosymmetric	24	symmetric ${\displaystyle \mathbb {S} _{4}}$
		hexoctahedral	Oh	centrosymmetric	48	${\displaystyle \mathbb {S} _{4}\times \mathbb {Z} _{2}}$

In total there are seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic.

Point groups

The crystallographic point group or crystal class is the mathematical group comprising the symmetry operations that leave at least one point unmoved and that leave the appearance of the crystal structure unchanged. These symmetry operations include

• Reflection, which reflects the structure across a reflection plane
• Rotation, which rotates the structure a specified portion of a circle about a rotation axis
• Inversion, which changes the sign of the coordinate of each point with respect to a center of symmetry or inversion point
• Improper rotation, which consists of a rotation about an axis followed by an inversion.

Rotation axes (proper and improper), reflection planes, and centers of symmetry are collectively called symmetry elements. There are 32 possible crystal classes. Each one can be classified into one of the seven crystal systems.

Space groups

In addition to the operations of the point group, the space group of the crystal structure contains translational symmetry operations. These include:

• Pure translations, which move a point along a vector
• Screw axes, which rotate a point around an axis while translating parallel to the axis.
• Glide planes, which reflect a point through a plane while translating it parallel to the plane.

There are 230 distinct space groups.

Atomic coordination

By considering the arrangement of atoms relative to each other, their coordination numbers, interatomic distances, types of bonding, etc., it is possible to form a general view of the structures and alternative ways of visualizing them.

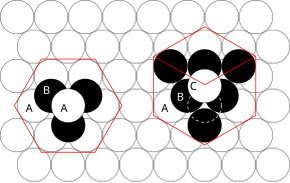
Close packing

Main article: Close-packing of equal spheres

 

The hcp lattice (left) and the fcc lattice (right)

The principles involved can be understood by considering the most efficient way of packing together equal-sized spheres and stacking close-packed atomic planes in three dimensions. For example, if plane A lies beneath plane B, there are two possible ways of placing an additional atom on top of layer B. If an additional layer was placed directly over plane A, this would give rise to the following series:

...ABABABAB...

This arrangement of atoms in a crystal structure is known as hexagonal close packing (hcp).

If, however, all three planes are staggered relative to each other and it is not until the fourth layer is positioned directly over plane A that the sequence is repeated, then the following sequence arises:

...ABCABCABC...

This type of structural arrangement is known as cubic close packing (ccp).

The unit cell of a ccp arrangement of atoms is the face-centered cubic (fcc) unit cell. This is not immediately obvious as the closely packed layers are parallel to the {111} planes of the fcc unit cell. There are four different orientations of the close-packed layers.

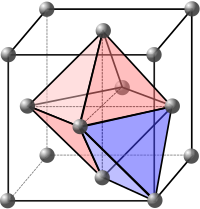
APF and CN

Main articles: Atomic packing factor and Coordination number

One important characteristic of a crystalline structure is its atomic packing factor (APF). This is calculated by assuming that all the atoms are identical spheres, with a radius large enough that each sphere abuts on the next. The atomic packing factor is the proportion of space filled by these spheres which can be worked out by calculating the total volume of the spheres and dividing by the volume of the cell as follows:

${\displaystyle \mathrm {APF} ={\frac {N_{\mathrm {particle} }V_{\mathrm {particle} }}{V_{\text{unit cell}}}}}$

Another important characteristic of a crystalline structure is its coordination number (CN). This is the number of nearest neighbours of a central atom in the structure.

The APFs and CNs of the most common crystal structures are shown below:

Crystal structure	Atomic packing factor	Coordination number (Geometry)
Diamond cubic	0.34	4 (Tetrahedron)
Simple cubic	0.52	6 (Octahedron)
Body-centered cubic (BCC)	0.68	8 (Cube)
Face-centered cubic (FCC)	0.74	12 (Cuboctahedron)
Hexagonal close-packed (HCP)	0.74	12 (Triangular orthobicupola)

The 74% packing efficiency of the FCC and HCP is the maximum density possible in unit cells constructed of spheres of only one size.

Interstitial sites

Main article: Interstitial site

 

Octahedral (red) and tetrahedral (blue) interstitial sites in a face-centered cubic lattice.

Interstitial sites refer to the empty spaces in between the atoms in the crystal lattice. These spaces can be filled by oppositely charged ions to form multi-element structures. They can also be filled by impurity atoms or self-interstitials to form interstitial defects.

Defects and impurities

Main article: Crystallographic defect

Real crystals feature defects or irregularities in the ideal arrangements described above and it is these defects that critically determine many of the electrical and mechanical properties of real materials.

Impurities

When one atom substitutes for one of the principal atomic components within the crystal structure, alteration in the electrical and thermal properties of the material may ensue. Impurities may also manifest as electron spin impurities in certain materials. Research on magnetic impurities demonstrates that substantial alteration of certain properties such as specific heat may be affected by small concentrations of an impurity, as for example impurities in semiconducting ferromagnetic alloys may lead to different properties as first predicted in the late 1960s.

Dislocations

Main article: Dislocation

Dislocations in the crystal lattice allow shear at lower stress than that needed for a perfect crystal structure.

Grain boundaries

Main article: Grain boundary

Grain boundaries are interfaces where crystals of different orientations meet. A grain boundary is a single-phase interface, with crystals on each side of the boundary being identical except in orientation. The term "crystallite boundary" is sometimes, though rarely, used. Grain boundary areas contain those atoms that have been perturbed from their original lattice sites, dislocations, and impurities that have migrated to the lower energy grain boundary.

Treating a grain boundary geometrically as an interface of a single crystal cut into two parts, one of which is rotated, we see that there are five variables required to define a grain boundary. The first two numbers come from the unit vector that specifies a rotation axis. The third number designates the angle of rotation of the grain. The final two numbers specify the plane of the grain boundary (or a unit vector that is normal to this plane).

Grain boundaries disrupt the motion of dislocations through a material, so reducing crystallite size is a common way to improve strength, as described by the Hall–Petch relationship. Since grain boundaries are defects in the crystal structure they tend to decrease the electrical and thermal conductivity of the material. The high interfacial energy and relatively weak bonding in most grain boundaries often makes them preferred sites for the onset of corrosion and for the precipitation of new phases from the solid. They are also important to many of the mechanisms of creep.

Grain boundaries are in general only a few nanometers wide. In common materials, crystallites are large enough that grain boundaries account for a small fraction of the material. However, very small grain sizes are achievable. In nanocrystalline solids, grain boundaries become a significant volume fraction of the material, with profound effects on such properties as diffusion and plasticity. In the limit of small crystallites, as the volume fraction of grain boundaries approaches 100%, the material ceases to have any crystalline character, and thus becomes an amorphous solid.

Prediction of structure

Main article: Crystal structure prediction

The difficulty of predicting stable crystal structures based on the knowledge of only the chemical composition has long been a stumbling block on the way to fully computational materials design. Now, with more powerful algorithms and high-performance computing, structures of medium complexity can be predicted using such approaches as evolutionary algorithms, random sampling, or metadynamics.

The crystal structures of simple ionic solids (e.g., NaCl or table salt) have long been rationalized in terms of Pauling's rules, first set out in 1929 by Linus Pauling, referred to by many since as the "father of the chemical bond". Pauling also considered the nature of the interatomic forces in metals, and concluded that about half of the five d-orbitals in the transition metals are involved in bonding, with the remaining nonbonding d-orbitals being responsible for the magnetic properties. He, therefore, was able to correlate the number of d-orbitals in bond formation with the bond length as well as many of the physical properties of the substance. He subsequently introduced the metallic orbital, an extra orbital necessary to permit uninhibited resonance of valence bonds among various electronic structures.

In the resonating valence bond theory, the factors that determine the choice of one from among alternative crystal structures of a metal or intermetallic compound revolve around the energy of resonance of bonds among interatomic positions. It is clear that some modes of resonance would make larger contributions (be more mechanically stable than others), and that in particular a simple ratio of number of bonds to number of positions would be exceptional. The resulting principle is that a special stability is associated with the simplest ratios or "bond numbers": 1⁄2, 1⁄3, 2⁄3, 1⁄4, 3⁄4, etc. The choice of structure and the value of the axial ratio (which determines the relative bond lengths) are thus a result of the effort of an atom to use its valency in the formation of stable bonds with simple fractional bond numbers.

After postulating a direct correlation between electron concentration and crystal structure in beta-phase alloys, Hume-Rothery analyzed the trends in melting points, compressibilities and bond lengths as a function of group number in the periodic table in order to establish a system of valencies of the transition elements in the metallic state. This treatment thus emphasized the increasing bond strength as a function of group number. The operation of directional forces were emphasized in one article on the relation between bond hybrids and the metallic structures. The resulting correlation between electronic and crystalline structures is summarized by a single parameter, the weight of the d-electrons per hybridized metallic orbital. The "d-weight" calculates out to 0.5, 0.7 and 0.9 for the fcc, hcp and bcc structures respectively. The relationship between d-electrons and crystal structure thus becomes apparent.

In crystal structure predictions/simulations, the periodicity is usually applied, since the system is imagined as unlimited big in all directions. Starting from a triclinic structure with no further symmetry property assumed, the system may be driven to show some additional symmetry properties by applying Newton's Second Law on particles in the unit cell and a recently developed dynamical equation for the system period vectors  (lattice parameters including angles), even if the system is subject to external stress.

Polymorphism

Quartz is one of the several crystalline forms of silica, SiO₂. The most important forms of silica include: α-quartz, β-quartz, tridymite, cristobalite, coesite, and stishovite.

Polymorphism is the occurrence of multiple crystalline forms of a material. It is found in many crystalline materials including polymers, minerals, and metals. According to Gibbs' rules of phase equilibria, these unique crystalline phases are dependent on intensive variables such as pressure and temperature. Polymorphism is related to allotropy, which refers to elemental solids. The complete morphology of a material is described by polymorphism and other variables such as crystal habit, amorphous fraction or crystallographic defects. Polymorphs have different stabilities and may spontaneously and irreversibly transform from a metastable form (or thermodynamically unstable form) to the stable form at a particular temperature. They also exhibit different melting points, solubilities, and X-ray diffraction patterns.

One good example of this is the quartz form of silicon dioxide, or SiO₂. In the vast majority of silicates, the Si atom shows tetrahedral coordination by 4 oxygens. All but one of the crystalline forms involve tetrahedral {SiO₄} units linked together by shared vertices in different arrangements. In different minerals the tetrahedra show different degrees of networking and polymerization. For example, they occur singly, joined together in pairs, in larger finite clusters including rings, in chains, double chains, sheets, and three-dimensional frameworks. The minerals are classified into groups based on these structures. In each of the 7 thermodynamically stable crystalline forms or polymorphs of crystalline quartz, only 2 out of 4 of each the edges of the {SiO₄} tetrahedra are shared with others, yielding the net chemical formula for silica: SiO₂.

Another example is elemental tin (Sn), which is malleable near ambient temperatures but is brittle when cooled. This change in mechanical properties due to existence of its two major allotropes, α- and β-tin. The two allotropes that are encountered at normal pressure and temperature, α-tin and β-tin, are more commonly known as gray tin and white tin respectively. Two more allotropes, γ and σ, exist at temperatures above 161 °C and pressures above several GPa. White tin is metallic, and is the stable crystalline form at or above room temperature. Below 13.2 °C, tin exists in the gray form, which has a diamond cubic crystal structure, similar to diamond, silicon or germanium. Gray tin has no metallic properties at all, is a dull gray powdery material, and has few uses, other than a few specialized semiconductor applications. Although the α–β transformation temperature of tin is nominally 13.2 °C, impurities (e.g. Al, Zn, etc.) lower the transition temperature well below 0 °C, and upon addition of Sb or Bi the transformation may not occur at all.

Physical properties

Twenty of the 32 crystal classes are piezoelectric, and crystals belonging to one of these classes (point groups) display piezoelectricity. All piezoelectric classes lack inversion symmetry. Any material develops a dielectric polarization when an electric field is applied, but a substance that has such a natural charge separation even in the absence of a field is called a polar material. Whether or not a material is polar is determined solely by its crystal structure. Only 10 of the 32 point groups are polar. All polar crystals are pyroelectric, so the 10 polar crystal classes are sometimes referred to as the pyroelectric classes.

There are a few crystal structures, notably the perovskite structure, which exhibit ferroelectric behavior. This is analogous to ferromagnetism, in that, in the absence of an electric field during production, the ferroelectric crystal does not exhibit a polarization. Upon the application of an electric field of sufficient magnitude, the crystal becomes permanently polarized. This polarization can be reversed by a sufficiently large counter-charge, in the same way that a ferromagnet can be reversed. However, although they are called ferroelectrics, the effect is due to the crystal structure (not the presence of a ferrous metal).

Alice's Restaurant

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Alice%27s_Restaurant 

"Alice's Restaurant Massacree"
Song by Arlo Guthrie
from the album Alice's Restaurant
Released	October 1967
Recorded	1967
Genre	Talking blues folk rock
Length	18:34
Label	Warner Bros.
Songwriter(s)	Arlo Guthrie
Producer(s)	Fred Hellerman

"Alice's Restaurant Massacree", commonly known as "Alice's Restaurant", is a satirical talking blues song by singer-songwriter Arlo Guthrie, released as the title track to his 1967 debut album Alice's Restaurant. The song is a deadpan protest against the Vietnam War draft, in the form of a comically exaggerated but largely true story from Guthrie's own life: he is arrested and convicted of dumping trash illegally, which later endangers his suitability for the military draft. The title refers to a restaurant owned by one of Guthrie's friends; although she is a minor character in the story, the restaurant plays no role in it aside from being the subject of the chorus.

The song was an inspiration for the 1969 film also named Alice's Restaurant. The work has become Guthrie's signature song and he has periodically re-released it with updated lyrics. In 2017, it was selected for preservation in the National Recording Registry by the Library of Congress as being "culturally, historically, or artistically significant".

Characteristics

The song consists of a protracted spoken monologue, with a constantly repeated fingerstyle ragtime guitar (Piedmont style) backing and light brush-on-snare drum percussion (the drummer on the record is uncredited), bookended by a short chorus about the titular diner. (Guthrie has used the brief "Alice's Restaurant" bookends and guitar backing for other monologues bearing the Alice's Restaurant name.) The track lasts 18 minutes and 34 seconds, occupying the entire A-side of the Alice's Restaurant album. Due to Guthrie's rambling and circuitous telling with unimportant details, it has been described as a shaggy dog story.

Guthrie refers to the incident as a "massacree", a colloquialism originating in the Ozark Mountains that describes "an event so wildly and improbably and baroquely messed up that the results are almost impossible to believe". It is a corruption of the word massacre, but carries a much lighter and more sarcastic connotation, rather than describing anything involving actual death.

Story

Prologue

Guthrie states that the song is entitled "Alice's Restaurant" but clarifies that this is only the name of the song, not the business owned by his friend Alice. He then sings the chorus, which is in the form of a jingle for the restaurant, beginning "You can get anything you want at Alice's restaurant", and continuing with directions to it.

Part One

Alice Brock, the titular host of the Thanksgiving dinner who bailed Arlo and his friend out of jail

Guthrie recounts events that took place in 1965 (two years prior at the time of the original recording), when he and a friend spent Thanksgiving Day at a deconsecrated church on the outskirts of Stockbridge, Massachusetts, which their friends Alice and Ray had been using as a home. As a favor to them, Guthrie and the friend volunteered to take their large accumulation of garbage to the local dump in their VW Microbus, not realizing until they arrived there that the dump would be closed for the holiday. They eventually noticed a pile of other trash that had previously been dumped off a cliff near a side road, and added theirs to the accumulation.

The next morning, the church received a phone call from the local policeman, Officer Obie, saying that an envelope in the garbage pile had been traced back to them. Guthrie, stating "I cannot tell a lie" and with tongue in cheek, confessed that he "put that envelope underneath" the garbage. He and his friend drove to the police station, expecting a verbal reprimand and to be required to clean up the garbage, but they were instead arrested, handcuffed, and taken to the scene of the crime. There, Obie and a crew of police officers from the surrounding areas collected extensive forensic evidence of the litter, including "twenty-seven 8-by-10 color glossy pictures with circles and arrows and a paragraph on the back of each one explaining what each one was, to be used as evidence against us" amid a media circus of local media trying to get news stories on the littering. The young men were briefly jailed, with Obie taking drastic precautions to prevent Guthrie from escaping or committing suicide. After a few hours, Alice bailed them out.

Guthrie and his friend stood trial the next day. When Obie saw that the judge relied upon a seeing-eye dog, he realized that the officers' meticulous work had been foiled by a literal "case of American blind justice". Guthrie and his friend paid a $50 fine to the court and were ordered to pick up the garbage.

Part Two

The Army Building where Guthrie had his physical examination

Guthrie then states that the littering incident was "not what I came to tell you about" and shifts to another story, this one based at the Army Building on Whitehall Street in New York City as Guthrie appeared for a physical exam related to the Vietnam War draft. He tried various strategies to be found unfit for military service, including getting drunk the night before so he was hung over, and attempting to convince the psychiatrist that he was homicidal, which only earned him praise.

After several hours, Guthrie was asked whether he had ever been convicted of a crime. He nodded, began to tell his story, and was sent to the "Group W" bench to file for a moral waiver. The other convicts ("mother-rapers... father-stabbers... father-rapers") were initially put off that his conviction had been for littering, but accepted him when he added "and creating a nuisance". When Guthrie noticed one of the questions on the paperwork asked whether he had rehabilitated himself since the crime, he noted the irony of having to prove himself reformed from a crime of littering when the realities of war were often far more brutal. The officer in charge of the induction process commented, "We don't like your kind", rejecting Guthrie and sending his fingerprints to the federal government to be put on file.

Epilogue

In the final part of the song, Guthrie explains to the live audience that anyone finding themselves in a similar situation should walk into the military psychiatrist's office, sing the opening line from the chorus and walk out. He predicts that a single person doing it would be rejected as "sick" and that two people doing it, in harmony, would be rejected as "faggots", but that once three people started doing it they would begin to suspect "an organization" and 50 people a day would be recognized as "the Alice's Restaurant Anti-Massacree Movement". As he continues fingerpicking, he invites the audience to sing the chorus along with him "the next time it comes around on the guitar". When they do so, Guthrie claims that their singing "was horrible", and challenges them to sing it with him "with four-part harmony and feeling". Guthrie and the crowd then sing the chorus, and he wraps it up.

Development

Guthrie cited the long-form monologues of Lord Buckley and Bill Cosby as inspirations for the song's lyrics, and a number of different musicians (in particular Mississippi John Hurt) as inspirations for the Piedmont fingerstyle guitar accompaniment. The song was written as the events happened over the course of approximately one year; it grew out of a simple joke riff Guthrie had been working on in 1965 and 1966 before he appeared before the draft board (the opening was originally written as "you can hide from Obanhein at Alice's restaurant", which is how the restaurant got tied into the original story), and he later added his experience before the draft board to create the song as it is known today. Additional portions of the song were written during one of Guthrie's many stays with the English songwriter and music journalist Karl Dallas and his family in London. Guthrie sent a demo recording of the song to his father Woody Guthrie on his deathbed; it was, according to a "family joke", the last thing Woody heard before he died in October 1967. Because of the song's length, Guthrie never expected it to be released, because such extended monologues were extremely rare in an era when singles were typically less than three minutes.

Response

Arlo Guthrie performing during his 2005 Alice's Restaurant Massacree 40th Anniversary tour

1960s

"Alice's Restaurant" was first performed publicly with Guthrie singing live on Radio Unnameable, the overnight program hosted by Bob Fass that aired on New York radio station WBAI, one evening in 1966. The initial performance was part of an impromptu supergroup at the WBAI studios that included David Bromberg, Jerry Jeff Walker and Ramblin' Jack Elliot. Guthrie performed the song several times live on WBAI in 1966 and 1967 before its commercial release. The song proved so popular that at one point Fass (who was known for playing songs he liked over and over again in his graveyard slot) started playing a recording of one of Guthrie's live performances of the song repeatedly; eventually the non-commercial station rebroadcast it only when listeners pledged to donate a large amount of money. (Fass subverted it and occasionally asked for donations to get him to stop playing the recording.)

"Alice's Restaurant" was performed on July 17, 1967, at the Newport Folk Festival in a workshop or breakout section on "topical songs", where it was such a hit that he was called upon to perform it for the entire festival audience. The song's success at Newport and on WBAI led Guthrie to record it in front of a studio audience in New York City and release it as side one of the album Alice's Restaurant in October 1967.

The original album spent 16 weeks on the Billboard 200 album chart, peaking at #29 during the week of March 2, 1968, then reentered the chart on December 27, 1969, after the film version was released, peaking that time at #63. In the wake of the film version, Guthrie recorded a more single-friendly edit of the chorus in 1969. Titled "Alice's Rock & Roll Restaurant", it included three verses, all of which advertise the restaurant, and a fiddle solo by country singer Doug Kershaw; to fit the song on a record, the monologue was removed, bringing the song's length to 4:43. This version, backed with "Ring Around the Rosy Rag" (a cut from the Alice's Restaurant album), peaked at #97 on the Billboard Hot 100. Because the single did not reach the popularity of the full version, which did not qualify for the Hot 100 because of its length, Billboard officially classifies Guthrie as a one-hit wonder for his later hit "City of New Orleans".

After the release of the original album, Guthrie continued to perform the song in concert, regularly revising and updating the lyrics. In 1969, for instance, he performed a 20-minute rendition of the song that, instead of the original narrative, told a fictional story of how Russian and Chinese military operatives attempted to weaponize "multicolored rainbow roaches" they had found at Alice's restaurant, and the Lyndon Johnson administration orchestrated a plan for the nation to defend itself. A recording of this version titled "Alice: Before Time Began" was released in 2009 on a CD distributed by Guthrie's Rising Son Records label; another recording of this version, titled "The Alice's Restaurant Multicolored Rainbow Roach Affair", was also released on that label.

Developing tradition

It has become a tradition for many classic rock and adult album alternative radio stations to play the song each Thanksgiving. Despite its use of the slur "faggots", radio stations generally present the song as originally recorded, and the Federal Communications Commission has never punished a station for playing it. When performing the song in later years, Guthrie began to change the line to something less offensive and often topical: during the 1990s and 2000s, the song alluded to the Seinfeld episode "The Outing" by saying "They'll think you're gay—not that there's anything wrong with that," and in 2015, Guthrie used the line "They'll think they're trying to get married in some parts of Kentucky", a nod to the controversy of the time surrounding county clerk Kim Davis.

By the late 1970s, Guthrie had removed the song from his regular concert repertoire. In 1984, Guthrie, who was supporting George McGovern's ultimately unsuccessful comeback bid for the Democratic presidential nomination, revived "Alice's Restaurant" to protest the Reagan Administration's reactivation of the Selective Service System registrations. That version has not been released on a commercial recording; at least one bootleg of it from one of Guthrie's performances exists. It was this tour, which occurred near the 20th anniversary of the song (and continued as a general tour after McGovern dropped out of the race), that prompted Guthrie to return the song to his playlist every ten years, usually coinciding with the anniversary of either the song or the incident. The 30th anniversary version of the song includes a follow-up recounting how he learned that Richard Nixon had owned a copy of the song, and he jokingly suggested that this explained the famous 18½-minute gap in the Watergate tapes.

Guthrie rerecorded his entire debut album for his 1997 CD Alice's Restaurant: The Massacree Revisited, on the Rising Son label, which includes this expanded version. The 40th anniversary edition, performed at and released as a recording by the Kerrville Folk Festival, made note of some parallels between the 1960s and the Iraq War and George W. Bush administration. Guthrie revived the song for the 50th anniversary edition in 2015, which he expected would be the last time he would do so. In 2018, Guthrie began the "Alice's Restaurant: Back by Popular Demand" Tour, reuniting with members of his 1970s backing band Shenandoah. The tour, which features Guthrie's daughter Sarah Lee Guthrie as the opening act, was scheduled to wrap up in 2020. To justify bringing the song back out of its usual ten-year sequence, he stated that he was doing so to commemorate the 50th anniversary of the film version of the song. The tour ended in 2019 and was later confirmed to have been Guthrie's last; he suffered a career-ending stroke in November of that year and announced his retirement in October 2020.

Artist's reflections

In a 2014 interview with Rolling Stone, Guthrie said he believed there are such things as just wars, and that the message of this song was targeted at the Vietnam War in particular. Interviews with Ron Bennington in 2009 and NPR in 2005 describe the song not so much as anti-war but as "anti-stupidity". Guthrie considered the song as relevant as in 1965.

Historicity

Most of the events of the story are true; the littering incident was recorded in the local newspaper at the time it happened, and although Guthrie made some minor embellishments, the persons mentioned in the first half of the story all granted interviews on the subject, mostly verifying that part of the story. The second half of the story does not have as much specific corroborating evidence to support it; the public exposure of COINTELPRO in 1971 confirmed that the federal government was collecting personal information on anti-war protesters as Guthrie alleged.

Alice, Ray and the restaurant

The Alice in the song was restaurant-owner Alice May Brock (born c. 1941). In 1964, shortly after graduating from Sarah Lawrence College, Alice used $2,000 supplied by her mother to purchase a deconsecrated church in Great Barrington, Massachusetts, where Alice and her husband, Ray Brock (c. 1928–1979), would live. Alice was a painter and designer, while Ray was an architect and woodworker who originally was from Virginia; the two had met while in Greenwich Village in 1962. Both worked at a nearby private academy, the music and art-oriented Stockbridge School, from which Guthrie (then of Howard Beach, a neighborhood in Queens, New York City) had graduated.

Sign to restaurant

Alice Brock operated a restaurant called "The Back Room" in 1966, at 40 Main Street in Stockbridge, located behind a grocery store and directly underneath the studios of Norman Rockwell. The Back Room was already closed by the time the song was released; it ceased operations in April 1966. (Theresa's Stockbridge Café was last known to occupy the site; the café's sign makes note that the space was "formerly Alice's Restaurant".) After a breakup and abortive reconciliation, Alice divorced Ray in 1968; she went on to launch two more restaurants (a take-out window in Housatonic in 1971 and a much larger establishment in Lenox in the late 1970s) before leaving the restaurant business in 1979. Ray returned to Virginia after the divorce and took on various projects until his death in 1979.

Alice owned an art studio and gallery in Provincetown, Massachusetts, until 2016. She illustrated the 2004 children's book Mooses Come Walking, written by Guthrie, and authored and illustrated another, How to Massage Your Cat.

In 1969, Random House published The Alice's Restaurant Cookbook (ISBN 039440100X) which featured recipes and hippie wisdom from Alice Brock, as well as photos of Alice and Guthrie, and publicity stills from the movie. A tear-out record was included in the book with Brock and Guthrie bantering on two tracks, "Italian-Type Meatballs" and "My Granma's Beet Jam".

The church

The former church where the story begins, located at 4 Van Deusenville Road in Great Barrington, Massachusetts; the building later became the Guthrie Center.

The church, originally built as the St. James Chapel in 1829, was enlarged in 1866 and renamed Trinity Church. Ray and Alice Brock purchased the property in 1964 and made it their home. Alice sold the building shortly after the film adaptation was released, commenting that the song and film had brought a great deal of unwanted publicity. The building changed ownership several times in the 1970s and 1980s until Guthrie bought the facility in 1991 and converted it to the Guthrie Center, a nondenominational, interfaith meeting place.

In the main chapel area is a stage on which Officer Obie's chair sits as a reminder of the arrest. A set of private rooms in which Alice and Ray once lived remains.

In later years, the Guthrie Center became a folk music venue, hosting a Thursday evening hootenanny as well as the Troubadour Concert series annually from Memorial Day to Labor Day. Musical guests have included John Gorka, Tom Paxton, Ellis Paul, Tom Rush, The Highwaymen folk group and Arlo Guthrie. The Troubadour series helps to support the church's free community lunch program which is held at the church every Wednesday at noon. On Thanksgiving, the church hosts a "Thanksgiving dinner that can't be beat" for the local community. The annual "Garbage Trail Walk", retracing the steps of Arlo and folksinger Rick Robbins (as told in the song), raises money for Huntington's disease research.

The littering incident

The incident which Guthrie recounts in the first half of the song was reported in The Berkshire Eagle on November 29, 1965. It describes the conviction of Richard J. Robbins, age 19, and Arlo Guthrie, age 18, for illegally disposing of rubbish, and a fine of $25 each, plus an order to remove the trash. The arresting officer was Stockbridge police chief William J. Obanhein ("Officer Obie"), and the trial was presided over by Special Judge James E. Hannon. It identifies the incriminating evidence as an envelope addressed to a male resident of Great Barrington (presumably Ray Brock) rather than Guthrie. In a 1972 interview with Playboy's Music Scene, Obanhein denied handcuffing Guthrie and Robbins. He also said the real reason there was no toilet seat in the jail cell was to prevent such items from being stolen, not as a suicide deterrent as Guthrie had joked. Guthrie also admitted in 2020 that the police photographs were in black-and-white, not in color. The Microbus that Guthrie and Robbins used to dispose of the garbage was eventually scrapped; the Guthrie Center later acquired a replica that Guthrie occasionally drives.

The draft

The Armed Forces Examination and Entrance Station was part of a large complex at 39 Whitehall Street in New York City from 1884 to 1969. By the late 1960s, the building had become a target for anti-war protesters, and two bombings left minor damage to the building, prompting the building to be vacated. The building has since been repurposed as a mixed-use development and its address changed (it is now 3 New York Plaza).

The brief mention of "faggots" being rejected for military service in the song's epilogue was based on military policy at the time, which rejected all homosexuals and expelled anyone caught engaging in homosexual behavior with a section 8 dishonorable discharge. The policy was modified in 1993 and fully repealed in 2012.

Guthrie acknowledged that he was never in danger of being drafted because he had been given a high draft number. A fellow friend commented that he and Guthrie were "not going to get called unless there's a squirrel invasion in New Hampshire."

Legacy

Alice's Restaurant in Sky Londa, California

Alice's Restaurant of Sky Londa, California, founded in the 1960s, was originally founded by Alice Taylor with no direct connection to Alice Brock. Subsequent owners of the restaurant kept the original name as a homage to the song, eventually adding a "Group W bench," because the name had made the restaurant a tourist attraction that was "good for business."

Feature film

Main article: Alice's Restaurant (film)

The song was adapted into the 1969 movie Alice's Restaurant, directed and co-written by Arthur Penn, who had heard the song in 1967 while living in Stockbridge and immediately wanted to make the song into a movie. Guthrie appears as himself, with Pat Quinn as Alice Brock and James Broderick as Ray Brock, William Obanhein and James Hannon appearing as themselves, and Alice Brock making a cameo appearance.

The movie was released in August 1969, a few days after Guthrie appeared at the Woodstock Festival. A soundtrack album for the film was also released by United Artists Records. The soundtrack includes a studio version of the song, which was originally divided into two parts (one for each album side); a compact disc reissue on the Rykodisc label presents this version in full and adds several bonus tracks to the original LP.