Kerr metric

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Kerr_metric

 

General relativity
${\displaystyle G_{\mu \nu }+\mathrm{\Lambda }{g}_{\mu \nu }=\kappa T_{\mu \nu }}$

The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find.

Overview

The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a charged, spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, rotating black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr. The natural extension to a charged, rotating black hole, the Kerr–Newman metric, was discovered shortly thereafter in 1965. These four related solutions may be summarized by the following table, where Q represents the body's electric charge and J represents its spin angular momentum:

	Non-rotating (J = 0)	Rotating (J ≠ 0)
Uncharged (Q = 0)	Schwarzschild	Kerr
Charged (Q ≠ 0)	Reissner–Nordström	Kerr–Newman

According to the Kerr metric, a rotating body should exhibit frame-dragging (also known as Lense–Thirring precession), a distinctive prediction of general relativity. The first measurement of this frame dragging effect was done in 2011 by the Gravity Probe B experiment. Roughly speaking, this effect predicts that objects coming close to a rotating mass will be entrained to participate in its rotation, not because of any applied force or torque that can be felt, but rather because of the swirling curvature of spacetime itself associated with rotating bodies. In the case of a rotating black hole, at close enough distances, all objects – even light – must rotate with the black hole; the region where this holds is called the ergosphere.

The light from distant sources can travel around the event horizon several times (if close enough); creating multiple images of the same object. To a distant viewer, the apparent perpendicular distance between images decreases at a factor of e^2π (about 500). However, fast spinning black holes have less distance between multiplicity images.

Rotating black holes have surfaces where the metric seems to have apparent singularities; the size and shape of these surfaces depends on the black hole's mass and angular momentum. The outer surface encloses the ergosphere and has a shape similar to a flattened sphere. The inner surface marks the event horizon; objects passing into the interior of this horizon can never again communicate with the world outside that horizon. However, neither surface is a true singularity, since their apparent singularity can be eliminated in a different coordinate system. A similar situation obtains when considering the Schwarzschild metric which also appears to result in a singularity at ⁠${\displaystyle r=r_{\text{s}}}$⁠ dividing the space above and below r_s into two disconnected patches; using a different coordinate transformation one can then relate the extended external patch to the inner patch (see Schwarzschild metric § Singularities and black holes) – such a coordinate transformation eliminates the apparent singularity where the inner and outer surfaces meet. Objects between these two surfaces must co-rotate with the rotating black hole, as noted above; this feature can in principle be used to extract energy from a rotating black hole, up to its invariant mass energy, Mc².

The LIGO experiment that first detected gravitational waves, announced in 2016, also provided the first direct observation of a pair of Kerr black holes.

Metric

The Kerr metric is commonly expressed in one of two forms, the Boyer–Lindquist form and the Kerr–Schild form. It can be readily derived from the Schwarzschild metric, using the Newman–Janis algorithm by Newman–Penrose formalism (also known as the spin–coefficient formalism), Ernst equation, or Ellipsoid coordinate transformation.

Boyer–Lindquist coordinates

Main article: Boyer–Lindquist coordinates

The Kerr metric describes the geometry of spacetime in the vicinity of a mass ⁠${\displaystyle M}$⁠ rotating with angular momentum ⁠${\displaystyle J}$⁠. The metric (or equivalently its line element for proper time) in Boyer–Lindquist coordinates is

${\displaystyle \begin{array}{rl}d{s}^2& =-c^{2}d{\tau }^2\\ & =-\left(1-\frac{r_{\text{s}}r}{\mathrm{\Sigma }}\right)c^{2}d{t}^2+\frac{\mathrm{\Sigma }}{\mathrm{\Delta }}d{r}^2+\mathrm{\Sigma }d{\theta }^2+\left(r^2+a^2+\frac{r_{\text{s}}r{a}^2}{\mathrm{\Sigma }}{\sin }^2\theta \right){\sin }^2\theta d{\varphi }^2-\frac{2r_{\text{s}}ra{\sin }^2\theta }{\mathrm{\Sigma }}cdtd\varphi \end{array}}$

(1)

where the coordinates ⁠${\displaystyle r,\theta ,\varphi }$⁠ are standard oblate spheroidal coordinates, which are equivalent to the cartesian coordinates

${\displaystyle x=\sqrt{r^2+a^2}\sin \theta \cos \varphi }$

(2)

${\displaystyle y=\sqrt{r^2+a^2}\sin \theta \sin \varphi }$

(3)

${\displaystyle z=r\cos \theta ,}$

(4)

where ${\displaystyle r_{\text{s}}}$ is the Schwarzschild radius

${\displaystyle r_{\text{s}}=\frac{2GM}{c^2},}$

(5)

and where for brevity, the length scales ⁠${\displaystyle a,\mathrm{\Sigma }}$⁠ and ⁠${\displaystyle \mathrm{\Delta }}$⁠ have been introduced as

${\displaystyle a=\frac{J}{Mc},}$

(6)

${\displaystyle \mathrm{\Sigma }=r^2+a^2{\cos }^2\theta ,}$

(7)

${\displaystyle \mathrm{\Delta }=r^2-r_{\text{s}}r+a^2.}$

(8)

A key feature to note in the above metric is the cross-term ⁠${\displaystyle dtd\varphi }$⁠. This implies that there is coupling between time and motion in the plane of rotation that disappears when the black hole's angular momentum goes to zero.

In the non-relativistic limit where ⁠${\displaystyle M}$⁠ (or, equivalently, ⁠${\displaystyle r_{\text{s}}}$⁠) goes to zero, the Kerr metric becomes the orthogonal metric for the oblate spheroidal coordinates

${\displaystyle g\underset{M\to 0}{⟶}-c^{2}d{t}^2+\frac{\mathrm{\Sigma }}{r^2+a^2}d{r}^2+\mathrm{\Sigma }d{\theta }^2+\left(r^2+a^2\right){\sin }^2\theta d{\varphi }^2}$

(9)

Kerr–Schild coordinates

The Kerr metric can be expressed in "Kerr–Schild" form, using a particular set of Cartesian coordinates as follows. These solutions were proposed by Kerr and Schild in 1965.

${\displaystyle g_{\mu \nu }={\eta }_{\mu \nu }+f{k}_{\mu }{k}_{\nu }}$

(10)

${\displaystyle f=\frac{2GM{r}^3}{r^4+a^2{z}^2}}$

(11)

${\displaystyle \mathbf{k}=(k_x,k_y,k_z)=\left(\frac{rx+ay}{r^2+a^2},\frac{ry-ax}{r^2+a^2},\frac{z}{r}\right)}$

(12)

${\displaystyle k_0=1.}$

(13)

Notice that k is a unit 3-vector, making the 4-vector a null vector, with respect to both g and η. Here M is the constant mass of the spinning object, η is the Minkowski tensor, and a is a constant rotational parameter of the spinning object. It is understood that the vector ⁠${\displaystyle \overrightarrow{a}}$⁠ is directed along the positive z-axis. The quantity r is not the radius, but rather is implicitly defined by

${\displaystyle \frac{x^2+y^2}{r^2+a^2}+\frac{z^2}{r^2}=1}$

(14)

Notice that the quantity r becomes the usual radius R

${\displaystyle r\to R=\sqrt{x^2+y^2+z^2}}$

when the rotational parameter ⁠${\displaystyle a}$⁠ approaches zero. In this form of solution, units are selected so that the speed of light is unity (⁠${\displaystyle c=1}$⁠). At large distances from the source (R ≫ a), these equations reduce to the Eddington–Finkelstein form of the Schwarzschild metric.

In the Kerr–Schild form of the Kerr metric, the determinant of the metric tensor is everywhere equal to negative one, even near the source.

Soliton coordinates

As the Kerr metric (along with the Kerr–NUT metric) is axially symmetric, it can be cast into a form to which the Belinski–Zakharov transform can be applied. This implies that the Kerr black hole has the form of a gravitational soliton.

Mass of rotational energy

If the complete rotational energy ⁠${\displaystyle E_{\mathrm{r}\mathrm{o}\mathrm{t}}=c^2\left(M-M_{\mathrm{i}\mathrm{r}\mathrm{r}}\right)}$⁠ of a black hole is extracted, for example with the Penrose process, the remaining mass cannot shrink below the irreducible mass. Therefore, if a black hole rotates with the spin ⁠${\displaystyle a=M}$⁠, its total mass-equivalent ⁠${\displaystyle M}$⁠ is higher by a factor of ⁠${\displaystyle \sqrt{2}}$⁠ in comparison with a corresponding Schwarzschild black hole where ⁠${\displaystyle M}$⁠ is equal to ⁠${\displaystyle M_{\text{irr}}}$⁠. The reason for this is that in order to get a static body to spin, energy needs to be applied to the system. Because of the mass–energy equivalence this energy also has a mass-equivalent, which adds to the total mass–energy of the system, ⁠${\displaystyle M}$⁠.

The total mass equivalent ⁠${\displaystyle M}$⁠ (the gravitating mass) of the body (including its rotational energy) and its irreducible mass ⁠${\displaystyle M_{\text{irr}}}$⁠ are related by

${\displaystyle 2M_{\mathrm{i}\mathrm{r}\mathrm{r}}^2=M^2+\sqrt{M^4-J^2{c}^2/G^2}⟹M^2=M_{\mathrm{i}\mathrm{r}\mathrm{r}}^2+\frac{J^2{c}^2}{4M_{\mathrm{i}\mathrm{r}\mathrm{r}}^2{G}^2}.}$

Wave operator

Since even a direct check on the Kerr metric involves cumbersome calculations, the contravariant components ⁠${\displaystyle g^{ik}}$⁠ of the metric tensor in Boyer–Lindquist coordinates are shown below in the expression for the square of the four-gradient operator:

${\displaystyle g^{\mu \nu }\frac{\mathrm{\partial }}{\mathrm{\partial }{x}^{\mu }}\frac{\mathrm{\partial }}{\mathrm{\partial }{x}^{\nu }}=-\frac{1}{c^2\mathrm{\Delta }}\left(r^2+a^2+\frac{r_{\text{s}}r{a}^2}{\mathrm{\Sigma }}{\sin }^2\theta \right){\left(\frac{\mathrm{\partial }}{\mathrm{\partial }t}\right)}^2-\frac{2r_{\text{s}}ra}{c\mathrm{\Sigma }\mathrm{\Delta }}\frac{\mathrm{\partial }}{\mathrm{\partial }\varphi }\frac{\mathrm{\partial }}{\mathrm{\partial }t}+\frac{1}{\mathrm{\Delta }{\sin }^2\theta }\left(1-\frac{r_{\text{s}}r}{\mathrm{\Sigma }}\right){\left(\frac{\mathrm{\partial }}{\mathrm{\partial }\varphi }\right)}^2+\frac{\mathrm{\Delta }}{\mathrm{\Sigma }}{\left(\frac{\mathrm{\partial }}{\mathrm{\partial }r}\right)}^2+\frac{1}{\mathrm{\Sigma }}{\left(\frac{\mathrm{\partial }}{\mathrm{\partial }\theta }\right)}^2}$

(15)

Frame dragging

We may rewrite the Kerr metric (1) in the following form:

${\displaystyle c^{2}d{\tau }^2=\left(g_{tt}-\frac{g_{t\varphi }^2}{g_{\varphi \varphi }}\right)d{t}^2+g_{\mathrm{r}\mathrm{r}}d{r}^2+g_{\theta \theta }d{\theta }^2+g_{\varphi \varphi }{\left(d\varphi +\frac{g_{t\varphi }}{g_{\varphi \varphi }}dt\right)}^2.}$

(16)

This metric is equivalent to a co-rotating reference frame that is rotating with angular speed Ω that depends on both the radius r and the colatitude θ, where Ω is called the Killing horizon.

${\displaystyle \mathrm{\Omega }=-\frac{g_{t\varphi }}{g_{\varphi \varphi }}=\frac{r_{\text{s}}rac}{\mathrm{\Sigma }\left(r^2+a^2\right)+r_{\text{s}}r{a}^2{\sin }^2\theta }.}$

(17)

Thus, an inertial reference frame is entrained by the rotating central mass to participate in the latter's rotation; this is called frame-dragging, and has been tested experimentally. Qualitatively, frame-dragging can be viewed as the gravitational analog of electromagnetic induction. An "ice skater", in orbit over the equator and rotationally at rest with respect to the stars, extends her arms. The arm extended toward the black hole will be torqued spinward. The arm extended away from the black hole will be torqued anti-spinward. She will therefore be rotationally sped up, in a counter-rotating sense to the black hole. This is the opposite of what happens in everyday experience. If she is already rotating at a certain speed when she extends her arms, inertial effects and frame-dragging effects will balance and her spin will not change. Due to the equivalence principle, gravitational effects are locally indistinguishable from inertial effects, so this rotation rate, at which when she extends her arms nothing happens, is her local reference for non-rotation. This frame is rotating with respect to the fixed stars and counter-rotating with respect to the black hole. A useful metaphor is a planetary gear system with the black hole being the sun gear, the ice skater being a planetary gear and the outside universe being the ring gear. This can also be interpreted through Mach's principle.

Important surfaces

Location of the horizons, ergospheres and the ring singularity of the Kerr spacetime in Cartesian Kerr–Schild coordinates.

Comparison of the shadow (black) and the important surfaces (white) of a black hole. The spin parameter ⁠${\displaystyle a}$⁠ is animated from ⁠${\displaystyle 0}$⁠ to ⁠${\displaystyle M}$⁠, while the left side of the black hole is rotating towards the observer.

There are several important surfaces in the Kerr metric (1). The inner surface corresponds to an event horizon similar to that observed in the Schwarzschild metric; this occurs where the purely radial component g_rr of the metric goes to infinity. Solving the quadratic equation ⁠1/g_rr⁠ = 0 yields the solution:

${\displaystyle r_{\mathrm{H}}^{\pm }=\frac{r_{\text{s}}\pm \sqrt{r_{\text{s}}^2-4a^2}}{2}}$

which in natural units (that give ⁠${\displaystyle G=M=c=1}$⁠) simplifies to:

${\displaystyle r_{\mathrm{H}}^{\pm }=1\pm \sqrt{1-a^2}}$

While in the Schwarzschild metric the event horizon is also the place where the purely temporal component g_tt of the metric changes sign from positive to negative, in Kerr metric that happens at a different distance. Again solving a quadratic equation g_tt = 0 yields the solution:

${\displaystyle r_{\mathrm{E}}^{\pm }=\frac{r_{\text{s}}\pm \sqrt{r_{\text{s}}^2-4a^2{\cos }^2\theta }}{2}}$

or in natural units:

${\displaystyle r_{\mathrm{E}}^{\pm }=1\pm \sqrt{1-a^2{\cos }^2\theta }}$

Due to the cos²θ term in the square root, this outer surface resembles a flattened sphere that touches the inner surface at the poles of the rotation axis, where the colatitude θ equals 0 or π; the space between these two surfaces is called the ergosphere. Within this volume, the purely temporal component g_tt is negative, i.e., acts like a purely spatial metric component. Consequently, particles within this ergosphere must co-rotate with the inner mass, if they are to retain their time-like character. A moving particle experiences a positive proper time along its worldline, its path through spacetime. However, this is impossible within the ergosphere, where g_tt is negative, unless the particle is co-rotating around the interior mass ⁠${\displaystyle M}$⁠ with an angular speed at least of ⁠${\displaystyle \mathrm{\Omega }}$⁠. Thus, no particle can move in the direction opposite to central mass's rotation within the ergosphere.

As with the event horizon in the Schwarzschild metric, the apparent singularity at r_H is due to the choice of coordinates (i.e., it is a coordinate singularity). In fact, the spacetime can be smoothly continued through it by an appropriate choice of coordinates. In turn, the outer boundary of the ergosphere at r_E is not singular by itself even in Kerr coordinates due to non-zero ⁠${\displaystyle dtd\varphi }$⁠ term.

Ergosphere and the Penrose process

Main article: Penrose process

A black hole in general is surrounded by a surface, called the event horizon and situated at the Schwarzschild radius for a nonrotating black hole, where the escape velocity is equal to the velocity of light. Within this surface, no observer/particle can maintain itself at a constant radius. It is forced to fall inwards, and so this is sometimes called the static limit.

A rotating black hole has the same static limit at its event horizon but there is an additional surface outside the event horizon named the "ergosurface" given by

${\displaystyle (r-M{)}^2=M^2-J^2{\cos }^2\theta }$

in Boyer–Lindquist coordinates, which can be intuitively characterized as the sphere where "the rotational velocity of the surrounding space" is dragged along with the velocity of light. Within this sphere the dragging is greater than the speed of light, and any observer/particle is forced to co-rotate.

The region outside the event horizon but inside the surface where the rotational velocity is the speed of light, is called the ergosphere (from Greek ergon meaning work). Particles falling within the ergosphere are forced to rotate faster and thereby gain energy. Because they are still outside the event horizon, they may escape the black hole. The net process is that the rotating black hole emits energetic particles at the cost of its own total energy. The possibility of extracting spin energy from a rotating black hole was first proposed by the mathematician Roger Penrose in 1969 and is thus called the Penrose process. Rotating black holes in astrophysics are a potential source of large amounts of energy and are used to explain energetic phenomena, such as gamma-ray bursts.

Features of the Kerr geometry

The Kerr geometry exhibits many noteworthy features: the maximal analytic extension includes a sequence of asymptotically flat exterior regions, each associated with an ergosphere, stationary limit surfaces, event horizons, Cauchy horizons, closed timelike curves, and a ring-shaped curvature singularity. The geodesic equation can be solved exactly in closed form. In addition to two Killing vector fields (corresponding to time translation and axisymmetry), the Kerr geometry admits a remarkable Killing tensor. There is a pair of principal null congruences (one ingoing and one outgoing). The Weyl tensor is algebraically special, in fact it has Petrov type D. The global structure is known. Topologically, the homotopy type of the Kerr spacetime can be simply characterized as a line with circles attached at each integer point.

Note that the inner Kerr geometry is unstable with regard to perturbations in the interior region. This instability means that although the Kerr metric is axis-symmetric, a black hole created through gravitational collapse may not be so. This instability also implies that many of the features of the Kerr geometry described above may not be present inside such a black hole.

A surface on which light can orbit a black hole is called a photon sphere. The Kerr solution has infinitely many photon spheres, lying between an inner one and an outer one. In the nonrotating, Schwarzschild solution, with ⁠${\displaystyle a=0}$⁠, the inner and outer photon spheres degenerate, so that there is only one photon sphere at a single radius. The greater the spin of a black hole, the farther from each other the inner and outer photon spheres move. A beam of light traveling in a direction opposite to the spin of the black hole will circularly orbit the hole at the outer photon sphere. A beam of light traveling in the same direction as the black hole's spin will circularly orbit at the inner photon sphere. Orbiting geodesics with some angular momentum perpendicular to the axis of rotation of the black hole will orbit on photon spheres between these two extremes. Because the spacetime is rotating, such orbits exhibit a precession, since there is a shift in the ⁠${\displaystyle \varphi }$⁠ variable after completing one period in the ⁠${\displaystyle \theta }$⁠ variable.

Trajectory equations

Animation of a test-particle's orbit around a spinning black hole. Left: top view, right: side view.

Another trajectory of a test mass around a spinning (Kerr) black hole. Unlike orbits around a Schwarzschild black hole, the orbit is not confined to a single plane, but will ergodically fill a toruslike region around the equator.

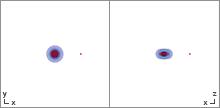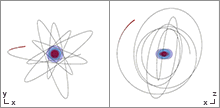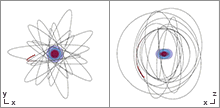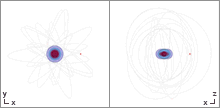
The equations of motion for test particles in the Kerr spacetime are governed by four constants of motion. The first is the invariant mass ⁠${\displaystyle \mu }$⁠ of the test particle, defined by the relation $${\displaystyle -{\mu }^2=p^{\alpha }{g}_{\alpha \beta }{p}^{\beta },}$$ where ⁠${\displaystyle p^{\alpha }}$⁠ is the four-momentum of the particle. Furthermore, there are two constants of motion given by the time translation and rotation symmetries of Kerr spacetime, the energy ⁠${\displaystyle E}$⁠, and the component of the orbital angular momentum parallel to the spin of the black hole ⁠${\displaystyle L_z}$⁠.$${\displaystyle E=-p_t,}$$ and $${\displaystyle L_z=p_{\varphi }}$$

Using Hamilton–Jacobi theory, Brandon Carter showed that there exists a fourth constant of motion, ⁠${\displaystyle Q}$⁠, now referred to as the Carter constant. It is related to the total angular momentum of the particle and is given by $${\displaystyle Q=p_{\theta }^2+{\cos }^2\theta \left(a^2\left({\mu }^2-E^2\right)+{\left(\frac{L_z}{\sin \theta }\right)}^2\right).}$$

Since there are four (independent) constants of motion for degrees of freedom, the equations of motion for a test particle in Kerr spacetime are integrable.

Using these constants of motion, the trajectory equations for a test particle can be written (using natural units of ⁠${\displaystyle G=M=c=1}$⁠), $${\displaystyle \begin{array}{rl}\mathrm{\Sigma }\frac{dr}{d\lambda }& =\pm \sqrt{R(r)}\\ \mathrm{\Sigma }\frac{d\theta }{d\lambda }& =\pm \sqrt{\mathrm{\Theta }(\theta )}\\ \mathrm{\Sigma }\frac{d\varphi }{d\lambda }& =-\left(aE-\frac{L_z}{{\sin }^2\theta }\right)+\frac{a}{\mathrm{\Delta }}P(r)\\ \mathrm{\Sigma }\frac{dt}{d\lambda }& =-a\left(aE{\sin }^2\theta -L_z\right)+\frac{r^2+a^2}{\mathrm{\Delta }}P(r)\end{array}}$$ with

• ${\displaystyle \mathrm{\Theta }(\theta )=Q-{\cos }^2\theta \left(a^2\left({\mu }^2-E^2\right)+\frac{L_z^2}{{\sin }^2\theta }\right)}$
• ${\displaystyle P(r)=E\left(r^2+a^2\right)-a{L}_z}$
• ${\displaystyle R(r)=P(r{)}^2-\mathrm{\Delta }\left({\mu }^2{r}^2+(L_z-aE{)}^2+Q\right)}$

where ⁠${\displaystyle \lambda }$⁠ is an affine parameter such that ⁠${\displaystyle \frac{d{x}^{\alpha }}{d\lambda }=p^{\alpha }}$⁠. In particular, when ⁠${\displaystyle \mu >0}$⁠ the affine parameter ⁠${\displaystyle \lambda }$⁠, is related to the proper time ⁠${\displaystyle \tau }$⁠ through ⁠${\displaystyle \lambda =\tau /\mu }$⁠.

Because of the frame-dragging-effect, a zero-angular-momentum observer (ZAMO) is corotating with the angular velocity ⁠${\displaystyle \mathrm{\Omega }}$⁠ which is defined with respect to the bookkeeper's coordinate time ⁠${\displaystyle t}$⁠. The local velocity ⁠${\displaystyle v}$⁠ of the test-particle is measured relative to a probe corotating with ⁠${\displaystyle \mathrm{\Omega }}$⁠. The gravitational time-dilation between a ZAMO at fixed ⁠${\displaystyle r}$⁠ and a stationary observer far away from the mass is $${\displaystyle \frac{t}{\tau }=\sqrt{\frac{{\left(a^2+r^2\right)}^2-a^2\mathrm{\Delta }{\sin }^2\theta }{\mathrm{\Delta }\mathrm{\Sigma }}}.}$$ In Cartesian Kerr–Schild coordinates, the equations for a photon are^[32] $${\displaystyle \ddot{x}+i\ddot{y}=4iMa\frac{r}{{\mathrm{\Sigma }}^2}W\left[\dot{x}+i\dot{y}-\frac{x+iy}{r}\dot{r}\right]-M(x+iy)\left(\frac{4r^2}{\mathrm{\Sigma }}-1\right)\frac{C-a^2{W}^2}{r{\mathrm{\Sigma }}^2}}$$ $${\displaystyle \ddot{z}=-Mz\left(\frac{4r^2}{\mathrm{\Sigma }}-1\right)\frac{C}{r{\mathrm{\Sigma }}^2}}$$ where ⁠${\displaystyle C}$⁠ is analogous to Carter's constant and ⁠${\displaystyle W}$⁠ is a useful quantity $${\displaystyle C=p_{\theta }^2+{\left(aE\sin \theta -\frac{L_z}{\sin \theta }\right)}^2}$$ $${\displaystyle W=\dot{t}-a{\sin }^2\theta \dot{\varphi }}$$

If we set ⁠${\displaystyle a=0}$⁠, the Schwarzschild geodesics are restored.

Symmetries

The group of isometries of the Kerr metric is the subgroup of the ten-dimensional Poincaré group which takes the two-dimensional locus of the singularity to itself. It retains the time translations (one dimension) and rotations around its axis of rotation (one dimension). Thus it has two dimensions. Like the Poincaré group, it has four connected components: the component of the identity; the component which reverses time and longitude; the component which reflects through the equatorial plane; and the component that does both.

In physics, symmetries are typically associated with conserved constants of motion, in accordance with Noether's theorem. As shown above, the geodesic equations have four conserved quantities: one of which comes from the definition of a geodesic, and two of which arise from the time translation and rotation symmetry of the Kerr geometry. The fourth conserved quantity does not arise from a symmetry in the standard sense and is commonly referred to as a hidden symmetry.

Overextreme Kerr solutions

The location of the event horizon is determined by the larger root of ⁠${\displaystyle \mathrm{\Delta }=0}$⁠. When ⁠${\displaystyle r_{\text{s}}/2<a}$⁠ (i.e. ⁠${\displaystyle G{M}^2<Jc}$⁠), there are no (real valued) solutions to this equation, and there is no event horizon. With no event horizons to hide it from the rest of the universe, the black hole ceases to be a black hole and will instead be a naked singularity.

Kerr black holes as wormholes

Although the Kerr solution appears to be singular at the roots of ⁠${\displaystyle \mathrm{\Delta }=0}$⁠, these are actually coordinate singularities, and, with an appropriate choice of new coordinates, the Kerr solution can be smoothly extended through the values of ⁠${\displaystyle r}$⁠ corresponding to these roots. The larger of these roots determines the location of the event horizon, and the smaller determines the location of a Cauchy horizon. A (future-directed, time-like) curve can start in the exterior and pass through the event horizon. Once having passed through the event horizon, the ⁠${\displaystyle r}$⁠ coordinate now behaves like a time coordinate, so it must decrease until the curve passes through the Cauchy horizon.

The region beyond the Cauchy horizon has several surprising features. The ⁠${\displaystyle r}$⁠ coordinate again behaves like a spatial coordinate and can vary freely. The interior region has a reflection symmetry, so that a (future-directed time-like) curve may continue along a symmetric path, which continues through a second Cauchy horizon, through a second event horizon, and out into a new exterior region which is isometric to the original exterior region of the Kerr solution. The curve could then escape to infinity in the new region or enter the future event horizon of the new exterior region and repeat the process. This second exterior is sometimes thought of as another universe. On the other hand, in the Kerr solution, the singularity is a ring, and the curve may pass through the center of this ring. The region beyond permits closed time-like curves. Since the trajectory of observers and particles in general relativity are described by time-like curves, it is possible for observers in this region to return to their past. This interior solution is not likely to be physical and considered as a purely mathematical artefact.

While it is expected that the exterior region of the Kerr solution is stable, and that all rotating black holes will eventually approach a Kerr metric, the interior region of the solution appears to be unstable, much like a pencil balanced on its point. This is related to the idea of cosmic censorship.

Relation to other exact solutions

The Kerr geometry is a particular example of a stationary axially symmetric vacuum solution to the Einstein field equation. The family of all stationary axially symmetric vacuum solutions to the Einstein field equation are the Ernst vacuums.

The Kerr solution is also related to various non-vacuum solutions which model black holes. For example, the Kerr–Newman electrovacuum models a (rotating) black hole endowed with an electric charge, while the Kerr–Vaidya null dust models a (rotating) hole with infalling electromagnetic radiation.

The special case ⁠${\displaystyle a=0}$⁠ of the Kerr metric yields the Schwarzschild metric, which models a nonrotating black hole which is static and spherically symmetric, in the Schwarzschild coordinates. (In this case, every Geroch moment but the mass vanishes.)

The interior of the Kerr geometry, or rather a portion of it, is locally isometric to the Chandrasekhar–Ferrari CPW vacuum, an example of a colliding plane wave model. This is particularly interesting, because the global structure of this CPW solution is quite different from that of the Kerr geometry, and in principle, an experimenter could hope to study the geometry of (the outer portion of) the Kerr interior by arranging the collision of two suitable gravitational plane waves.

Multipole moments

Each asymptotically flat Ernst vacuum can be characterized by giving the infinite sequence of relativistic multipole moments, the first two of which can be interpreted as the mass and angular momentum of the source of the field. There are alternative formulations of relativistic multipole moments due to Hansen, Thorne, and Geroch, which turn out to agree with each other. The relativistic multipole moments of the Kerr geometry were computed by Hansen; they turn out to be

${\displaystyle M_n=M[ia{]}^n}$

Thus, the special case of the Schwarzschild vacuum (⁠${\displaystyle a=0}$⁠) gives the "monopole point source" of general relativity.

Weyl multipole moments arise from treating a certain metric function (formally corresponding to Newtonian gravitational potential) which appears the Weyl–Papapetrou chart for the Ernst family of all stationary axisymmetric vacuum solutions using the standard euclidean scalar multipole moments. They are distinct from the moments computed by Hansen, above. In a sense, the Weyl moments only (indirectly) characterize the "mass distribution" of an isolated source, and they turn out to depend only on the even order relativistic moments. In the case of solutions symmetric across the equatorial plane the odd order Weyl moments vanish. For the Kerr vacuum solutions, the first few Weyl moments are given by

${\displaystyle a_0=M,a_1=0,a_2=M\left(\frac{M^2}{3}-a^2\right)}$

In particular, we see that the Schwarzschild vacuum has nonzero second order Weyl moment, corresponding to the fact that the "Weyl monopole" is the Chazy–Curzon vacuum solution, not the Schwarzschild vacuum solution, which arises from the Newtonian potential of a certain finite length uniform density thin rod.

In weak field general relativity, it is convenient to treat isolated sources using another type of multipole, which generalize the Weyl moments to mass multipole moments and momentum multipole moments, characterizing respectively the distribution of mass and of momentum of the source. These are multi-indexed quantities whose suitably symmetrized and anti-symmetrized parts can be related to the real and imaginary parts of the relativistic moments for the full nonlinear theory in a rather complicated manner.

Perez and Moreschi have given an alternative notion of "monopole solutions" by expanding the standard NP tetrad of the Ernst vacuums in powers of ⁠${\displaystyle r}$⁠ (the radial coordinate in the Weyl–Papapetrou chart). According to this formulation:

• the isolated mass monopole source with zero angular momentum is the Schwarzschild vacuum family (one parameter),
• the isolated mass monopole source with radial angular momentum is the Taub–NUT vacuum family (two parameters; not quite asymptotically flat),
• the isolated mass monopole source with axial angular momentum is the Kerr vacuum family (two parameters).

In this sense, the Kerr vacuums are the simplest stationary axisymmetric asymptotically flat vacuum solutions in general relativity.

Open problems

The Kerr geometry is often used as a model of a rotating black hole but if the solution is held to be valid only outside some compact region (subject to certain restrictions), in principle, it should be able to be used as an exterior solution to model the gravitational field around a rotating massive object other than a black hole such as a neutron star, or the Earth. This works out very nicely for the non-rotating case, where the Schwarzschild vacuum exterior can be matched to a Schwarzschild fluid interior, and indeed to more general static spherically symmetric perfect fluid solutions. However, the problem of finding a rotating perfect-fluid interior which can be matched to a Kerr exterior, or indeed to any asymptotically flat vacuum exterior solution, has proven very difficult. In particular, the Wahlquist fluid, which was once thought to be a candidate for matching to a Kerr exterior, is now known not to admit any such matching. At present, it seems that only approximate solutions modeling slowly rotating fluid balls are known (These are the relativistic analog of oblate spheroidal balls with nonzero mass and angular momentum but vanishing higher multipole moments). However, the exterior of the Neugebauer–Meinel disk, an exact dust solution which models a rotating thin disk, approaches in a limiting case the ⁠${\displaystyle G{M}^2=cJ}$⁠ Kerr geometry. Physical thin-disk solutions obtained by identifying parts of the Kerr spacetime are also known.

Chandra X-ray Observatory

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Chandra_X-ray_Observatory

 

Chandra X-ray Observatory

Illustration of Chandra

Instruments

NASA Great Observatories ← Compton Spitzer → Large Strategic Science Missions Astrophysics Division ← Compton Webb →

The Chandra X-ray Observatory (CXO), previously known as the Advanced X-ray Astrophysics Facility (AXAF), is a Flagship-class space telescope launched aboard the Space Shuttle Columbia during STS-93 by NASA on July 23, 1999. Chandra was sensitive to X-ray sources 100 times fainter than any previous X-ray telescope, enabled by the high angular resolution of its mirrors. Since the Earth's atmosphere absorbs the vast majority of X-rays, they are not detectable from Earth-based telescopes; therefore space-based telescopes are required to make these observations. Chandra is an Earth satellite in a 64-hour orbit, and its mission is ongoing as of 2024.

Chandra is one of the Great Observatories, along with the Hubble Space Telescope, Compton Gamma Ray Observatory (1991–2000), and the Spitzer Space Telescope (2003–2020). The telescope is named after the Nobel Prize-winning Indian astrophysicist Subrahmanyan Chandrasekhar. Its mission is similar to that of ESA's XMM-Newton spacecraft, also launched in 1999 but the two telescopes have different design foci, as Chandra has a much higher angular resolution and XMM-Newton higher spectroscopy throughput.

In response to a decrease in NASA funding in 2024 by the US Congress, Chandra is threatened with an early cancellation despite having more than a decade of operation left. The cancellation has been referred to as a potential "extinction-level" event for X-ray astronomy in the US. A group of astronomers have put together a public outreach project to try to get enough American citizens to persuade the US Congress to provide enough funding to avoid early termination of the observatory.

History

In 1976, the Chandra X-ray Observatory (called AXAF at the time) was proposed to NASA by Riccardo Giacconi and Harvey Tananbaum. Preliminary work began the following year at Marshall Space Flight Center (MSFC) and the Smithsonian Astrophysical Observatory (SAO), where the telescope is now operated for NASA at the Chandra X-ray Center in the Center for Astrophysics | Harvard & Smithsonian. In the meantime, in 1978, NASA launched the first imaging X-ray telescope, Einstein (HEAO-2), into orbit. Work continued on the AXAF project throughout the 1980s and 1990s. In 1992, to reduce costs, the spacecraft was redesigned. Four of the twelve planned mirrors were eliminated, as were two of the six scientific instruments. AXAF's planned orbit was changed to an elliptical one, reaching one third of the way to the Moon's at its farthest point. This eliminated the possibility of improvement or repair by the Space Shuttle but put the observatory above the Earth's radiation belts for most of its orbit. AXAF was assembled and tested by TRW (now Northrop Grumman Aerospace Systems) in Redondo Beach, California.

Space Shuttle Columbia, STS-93 launches in 1999

AXAF was renamed Chandra as part of a contest held by NASA in 1998, which drew more than 6,000 submissions worldwide. The contest winners, Jatila van der Veen and Tyrel Johnson (then a high school teacher and high school student, respectively), suggested the name in honor of Nobel Prize–winning Indian-American astrophysicist Subrahmanyan Chandrasekhar. He is known for his work in determining the maximum mass of white dwarf stars, leading to greater understanding of high energy astronomical phenomena such as neutron stars and black holes. Fittingly, the name Chandra means "moon" in Sanskrit.

Originally scheduled to be launched in December 1998, the spacecraft was delayed several months, eventually being launched on July 23, 1999, at 04:31 UTC by Space Shuttle Columbia during STS-93. Chandra was deployed by Cady Coleman from Columbia at 11:47 UTC. The Inertial Upper Stage's first stage motor ignited at 12:48 UTC, and after burning for 125 seconds and separating, the second stage ignited at 12:51 UTC and burned for 117 seconds. At 22,753 kilograms (50,162 lb), it was the heaviest payload ever launched by the shuttle, a consequence of the two-stage Inertial Upper Stage booster rocket system needed to transport the spacecraft to its high orbit.

Chandra has been returning data since the month after it launched. It is operated by the SAO at the Chandra X-ray Center in Cambridge, Massachusetts, with assistance from MIT and Northrop Grumman Space Technology. The ACIS CCDs suffered particle damage during early radiation belt passages. To prevent further damage, the instrument is now removed from the telescope's focal plane during passages.

Although Chandra was initially given an expected lifetime of 5 years, on September 4, 2001, NASA extended its lifetime to 10 years "based on the observatory's outstanding results." Physically Chandra could last much longer. A 2004 study performed at the Chandra X-ray Center indicated that the observatory could last at least 15 years. It is active as of 2024 and has an upcoming schedule of observations published by the Chandra X-ray Center.

In July 2008, the International X-ray Observatory, a joint project between ESA, NASA and JAXA, was proposed as the next major X-ray observatory but was later canceled. ESA later resurrected a downsized version of the project as the Advanced Telescope for High Energy Astrophysics (ATHENA), with a proposed launch in 2028.

On October 10, 2018, Chandra entered safe mode operations, due to a gyroscope glitch. NASA reported that all science instruments were safe. Within days, the 3-second error in data from one gyro was understood, and plans were made to return Chandra to full service. The gyroscope that experienced the glitch was placed in reserve and is otherwise healthy.

In March 2024, Congress decided to reduce funding for NASA and its missions. This may lead to the premature end of this mission. In June 2024, Senators urged NASA to reconsider the cuts to Chandra.

Example discoveries

Crew of STS-93 with a scale model

The data gathered by Chandra has greatly advanced the field of X-ray astronomy. Here are some examples of discoveries supported by observations from Chandra:

• The first light image, of supernova remnant Cassiopeia A, gave astronomers their first glimpse of the compact object at the center of the remnant, probably a neutron star or black hole.
• In the Crab Nebula, another supernova remnant, Chandra showed a never-before-seen ring around the central pulsar and jets that had only been partially seen by earlier telescopes.
• The first X-ray emission was seen from the supermassive black hole, Sagittarius A*, at the center of the Milky Way.
• Chandra found much more cool gas than expected spiraling into the center of the Andromeda Galaxy.
• Pressure fronts were observed in detail for the first time in Abell 2142, where clusters of galaxies are merging.
• The earliest images in X-rays of the shock wave of a supernova were taken of SN 1987A.
• Chandra showed for the first time the shadow of a small galaxy as it is being cannibalized by a larger one, in an image of Perseus A.
• Anew type of black hole was discovered in galaxy M82, mid-mass objects purported to be the missing link between stellar-sized black holes and super massive black holes.
• X-ray emission lines were associated for the first time with a gamma-ray burst, Beethoven Burst GRB 991216.
• High school students, using Chandra data, discovered a neutron star in supernova remnant IC 443.
• Observations by Chandra and BeppoSAX suggest that gamma-ray bursts occur in star-forming regions.
• Chandra data suggested that RX J1856.5-3754 and 3C58, previously thought to be pulsars, might be even denser objects: quark stars. These results are still debated.
• Sound waves from violent activity around a super massive black hole were observed in the Perseus Cluster (2003).

• 

  CXO image of the brown dwarf TWA 5B

  TWA 5B, a brown dwarf, was seen orbiting a binary system of Sun-like stars.
• Nearly all stars on the main sequence are X-ray emitters.
• The X-ray shadow of Titan was seen when it transited the Crab Nebula.
• X-ray emissions from materials falling from a protoplanetary disc into a star.
• Hubble constant measured to be 76.9 km/s/Mpc using Sunyaev-Zel'dovich effect.
• 2006 Chandra found strong evidence that dark matter exists by observing super cluster collision.
• 2006 X-ray emitting loops, rings and filaments discovered around a super massive black hole within Messier 87 imply the presence of pressure waves, shock waves and sound waves. The evolution of Messier 87 may have been dramatically affected.
• Observations of the Bullet cluster put limits on the cross-section of the self-interaction of dark matter.
• "The Hand of God" photograph of PSR B1509-58.
• Jupiter's x-rays coming from poles, not auroral ring.
• A large halo of hot gas was found surrounding the Milky Way.
• Extremely dense and luminous dwarf galaxy M60-UCD1 observed.
• On January 5, 2015, NASA reported that CXO observed an X-ray flare 400 times brighter than usual, a record-breaker, from Sagittarius A*, the supermassive black hole in the center of the Milky Way galaxy. The unusual event may have been caused by the breaking apart of an asteroid falling into the black hole or by the entanglement of magnetic field lines within gas flowing into Sagittarius A*, according to astronomers.
• In September 2016, it was announced that Chandra had detected X-ray emissions from Pluto, the first detection of X-rays from a Kuiper belt object. Chandra had made the observations in 2014 and 2015, supporting the New Horizons spacecraft for its July 2015 encounter.
• In September 2020, Chandra reportedly may have made an observation of an exoplanet in the Whirlpool Galaxy, which would be the first planet discovered beyond the Milky Way.
• In April 2021, NASA announced findings from the observatory in a tweet saying "Uranus gives off X-rays, astronomers find". The discovery would have "intriguing implications for understanding Uranus" if it is confirmed that the X-rays originate from the planet and are not emitted by the Sun.

Technical description

Assembly of the telescope

The main mirror of AXAF (Chandra)

HRC flight unit of Chandra

Unlike optical telescopes which possess simple aluminized parabolic surfaces (mirrors), X-ray telescopes generally use a Wolter telescope consisting of nested cylindrical paraboloid and hyperboloid surfaces coated with iridium or gold. X-ray photons would be absorbed by normal mirror surfaces, so mirrors with a low grazing angle are necessary to reflect them. Chandra uses four pairs of nested mirrors, together with their support structure, called the High Resolution Mirror Assembly (HRMA); the mirror substrate is 2 cm-thick glass, with the reflecting surface a 33 nm iridium coating, and the diameters are 65 cm, 87 cm, 99 cm and 123 cm. The thick substrate and particularly careful polishing allowed a very precise optical surface, which is responsible for Chandra's unmatched resolution: between 80% and 95% of the incoming X-ray energy is focused into a one-arcsecond circle. However, the thickness of the substrate limits the proportion of the aperture which is filled, leading to the low collecting area compared to XMM-Newton.

Chandra's highly elliptical orbit allows it to observe continuously for up to 55 hours of its 65-hour orbital period. At its furthest orbital point from Earth, Chandra is one of the most distant Earth-orbiting satellites. This orbit takes it beyond the geostationary satellites and beyond the outer Van Allen belt.

With an angular resolution of 0.5 arcsecond (2.4 μrad), Chandra possesses a resolution over 1000 times better than that of the first orbiting X-ray telescope.

CXO uses mechanical gyroscopes, which are sensors that help determine what direction the telescope is pointed. Other navigation and orientation systems on board CXO include an aspect camera, Earth and Sun sensors, and reaction wheels. It also has two sets of thrusters, one for movement and another for offloading momentum.

Instruments

The Science Instrument Module (SIM) holds the two focal plane instruments, the Advanced CCD Imaging Spectrometer (ACIS) and the High Resolution Camera (HRC), moving whichever is called for into position during an observation.

ACIS consists of 10 CCD chips and provides images as well as spectral information of the object observed. It operates in the photon energy range of 0.2–10 keV. The HRC has two micro-channel plate components and images over the range of 0.1–10 keV. It also has a time resolution of 16 microseconds. Both of these instruments can be used on their own or in conjunction with one of the observatory's two transmission gratings.

The transmission gratings, which swing into the optical path behind the mirrors, provide Chandra with high resolution spectroscopy. The High Energy Transmission Grating Spectrometer (HETGS) works over 0.4–10 keV and has a spectral resolution of 60–1000. The Low Energy Transmission Grating Spectrometer (LETGS) has a range of 0.09–3 keV and a resolution of 40–2000.

Summary:

• High Resolution Camera (HRC)
• Advanced CCD Imaging Spectrometer (ACIS)
• High Energy Transmission Grating Spectrometer (HETGS)
• Low Energy Transmission Grating Spectrometer (LETGS)

Direct collapse black hole

From Wikipedia, the free encyclopedia

Artist's impression for the formation of a massive black hole seed via the direct black hole channel.

Direct collapse black holes (DCBHs) are high-mass black hole seeds that form from the direct collapse of a large amount of material. They putatively formed within the redshift range z=15–30, when the Universe was about 100–250 million years old. Unlike seeds formed from the first population of stars (also known as Population III stars), direct collapse black hole seeds are formed by a direct, general relativistic instability. They are very massive, with a typical mass at formation of ~10⁵ M_☉. This category of black hole seeds was originally proposed theoretically to alleviate the challenge in building supermassive black holes already at redshift z~7, as numerous observations to date have confirmed.

Formation

Direct collapse black holes (DCBHs) are massive black hole seeds theorized to have formed in the high-redshift Universe and with typical masses at formation of ~10⁵ M_☉, but spanning between 10⁴ M_☉ and 10⁶ M_☉. The environmental physical conditions to form a DCBH (as opposed to a cluster of stars) are the following:

1. Metal-free gas (gas containing only hydrogen and helium).
2. Atomic-cooling gas.
3. Sufficiently large flux of Lyman–Werner photons, in order to destroy hydrogen molecules, which are very efficient gas coolants.

The previous conditions are necessary to avoid gas cooling and, hence, fragmentation of the primordial gas cloud. Unable to fragment and form stars, the gas cloud undergoes a gravitational collapse of the entire structure, reaching extremely high matter density at its core, on the order of ~10⁷ g/cm³. At this density, the object undergoes a general relativistic instability, which leads to the formation of a black hole of a typical mass ~10⁵ M_☉, and up to 1 million M_☉. The occurrence of the general relativistic instability, as well as the absence of the intermediate stellar phase, led to the denomination of direct collapse black hole. In other words, these objects collapse directly from the primordial gas cloud, not from a stellar progenitor as prescribed in standard black hole models.

A computer simulation reported in July 2022 showed that a halo at the rare convergence of strong, cold accretion flows can create massive black holes seeds without the need for ultraviolet backgrounds, supersonic streaming motions or even atomic cooling. Cold flows produced turbulence in the halo, which suppressed star formation. In the simulation, no stars formed in the halo until it had grown to 40 million solar masses at a redshift of 25.7 when the halo's gravity was finally able to overcome the turbulence; the halo then collapsed and formed two supermassive stars that died as DCBHs of 31,000 and 40,000 M_☉.

Demography

Direct collapse black holes are generally thought to be extremely rare objects in the high-redshift Universe, because the three fundamental conditions for their formation (see above in section Formation) are challenging to be met all together in the same gas cloud. Current cosmological simulations suggest that DCBHs could be as rare as only about 1 per cubic gigaparsec at redshift 15. The prediction on their number density is highly dependent on the minimum flux of Lyman–Werner photons required for their formation and can be as large as ~10⁷ DCBHs per cubic gigaparsec in the most optimistic scenarios.

Detection

In 2016, a team led by Harvard University astrophysicist Fabio Pacucci identified the first two candidate direct collapse black holes, using data from the Hubble Space Telescope and the Chandra X-ray Observatory. The two candidates, both at redshift ${\displaystyle z>6}$, were found in the CANDELS GOODS-S field and matched the spectral properties predicted for this type of astrophysical sources. In particular, these sources are predicted to have a significant excess of infrared radiation, when compared to other categories of sources at high redshift. Additional observations, in particular with the James Webb Space Telescope, will be crucial to investigate the properties of these sources and confirm their nature.

Difference from primordial and stellar collapse black holes

A primordial black hole is the result of the direct collapse of energy, ionized matter, or both, during the inflationary or radiation-dominated eras, while a direct collapse black hole is the result of the collapse of unusually dense and large regions of gas. Note that a black hole formed by the collapse of a Population III star is not considered "direct" collapse.