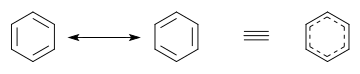
Two different resonance forms of benzene (top) combine to produce an average structure (bottom)
In organic chemistry, the term aromaticity is used to describe a cyclic (ring-shaped), planar (flat) molecule with a ring of resonance bonds that exhibits more stability than other geometric or connective arrangements with the same set of atoms. Aromatic molecules are very stable, and do not break apart easily to react with other substances. Organic compounds that are not aromatic are classified as aliphatic compounds—they might be cyclic, but only aromatic rings have special stability (low reactivity).
Since the most common aromatic compounds are derivatives of benzene (an aromatic hydrocarbon common in petroleum and its distillates), the word “aromatic” occasionally refers informally to benzene derivatives, and so it was first defined. Nevertheless, many non-benzene aromatic compounds exist. In living organisms, for example, the most common aromatic rings are the double-ringed bases in RNA and DNA. An aromatic functional group or other substituent is called an aryl group.
The earliest use of the term "aromatic" was in an article by August Wilhelm Hofmann in 1855.[1] Hofmann used the term for a class of benzene compounds, many of which have odors (aromas), unlike pure saturated hydrocarbons. Aromaticity as a chemical property bears no general relationship with the olfactory properties of such compounds (how they smell), although in 1855, before the structure of benzene or organic compounds was understood, chemists like Hofmann were beginning to understand that odiferous molecules from plants, such as terpenes, had chemical properties that we recognize today are similar to unsaturated petroleum hydrocarbons like benzene.
In terms of the electronic nature of the molecule, aromaticity describes a conjugated system often made of alternating single and double bonds in a ring. This configuration allows for the electrons in the molecule's pi system to be delocalized around the ring, increasing the molecule's stability. The molecule cannot be represented by one structure, but rather a resonance hybrid of different structures, such as with the two resonance structures of benzene. These molecules cannot be found in either one of these representations, with the longer single bonds in one location and the shorter double bond in another (see Theory below). Rather, the molecule exhibits bond lengths in between those of single and double bonds. This commonly seen model of aromatic rings, namely the idea that benzene was formed from a six-membered carbon ring with alternating single and double bonds (cyclohexatriene), was developed by August Kekulé (see History below). The model for benzene consists of two resonance forms, which corresponds to the double and single bonds superimposing to produce six one-and-a-half bonds. Benzene is a more stable molecule than would be expected without accounting for charge delocalization.
Theory
As is standard for resonance diagrams, the use of a double-headed arrow indicates that two structures are not distinct entities but merely hypothetical possibilities. Neither is an accurate representation of the actual compound, which is best represented by a hybrid (average) of these structures. A C=C bond is shorter than a C−C bond. Benzene is a regular hexagon—it is planar and all six carbon–carbon bonds have the same length, which is intermediate between that of a single and that of a double bond.
In a cyclic molecule with three alternating double bonds, cyclohexatriene, the bond length of the single bond would be 1.54 Å and that of the double bond would be 1.34 Å. However, in a molecule of benzene, the length of each of the bonds is 1.40 Å, indicating it to be the average of single and double bond.[2][3]
A better representation is that of the circular π-bond (Armstrong's inner cycle), in which the electron density is evenly distributed through a π-bond above and below the ring. This model more correctly represents the location of electron density within the aromatic ring.
The single bonds are formed from overlap of hybridized atomic sp2-orbitals in line between the carbon nuclei—these are called σ-bonds. Double bonds consist of a σ-bond and a π-bond. The π-bonds are formed from overlap of atomic p-orbitals above and below the plane of the ring. The following diagram shows the positions of these p-orbitals:
Since they are out of the plane of the atoms, these orbitals can interact with each other freely, and become delocalized. This means that, instead of being tied to one atom of carbon, each electron is shared by all six in the ring. Thus, there are not enough electrons to form double bonds on all the carbon atoms, but the "extra" electrons strengthen all of the bonds on the ring equally. The resulting molecular orbital is considered to have π symmetry.
History
The term "aromatic"
The first known use of the word "aromatic" as a chemical term—namely, to apply to compounds that contain the phenyl group—occurs in an article by August Wilhelm Hofmann in 1855.[1][4] If this is indeed the earliest introduction of the term, it is curious that Hofmann says nothing about why he introduced an adjective indicating olfactory character to apply to a group of chemical substances only some of which have notable aromas. Also, many of the most odoriferous organic substances known are terpenes, which are not aromatic in the chemical sense. But terpenes and benzenoid substances do have a chemical characteristic in common, namely higher unsaturation than many aliphatic compounds, and Hofmann may not have been making a distinction between the two categories. Many of the earliest-known examples of aromatic compounds, such as benzene and toluene, have distinctive pleasant smells. This property led to the term "aromatic" for this class of compounds, and hence the term "aromaticity" for the eventually discovered electronic property.[5]The structure of the benzene ring
Historic benzene formulae as proposed by August Kekulé in 1865.[6]
In the 19th century chemists found it puzzling that benzene could be so unreactive toward addition reactions, given its presumed high degree of unsaturation. The cyclohexatriene structure for benzene was first proposed by August Kekulé in 1865.[7][8] Most chemists were quick to accept this structure, since it accounted for most of the known isomeric relationships of aromatic chemistry. The hexagonal structure explains why only one isomer of benzene exists and why disubstituted compounds have three isomers.[4]
Between 1897 and 1906, J. J. Thomson, the discoverer of the electron, proposed three equivalent electrons between each pair of carbon atoms in benzene. An explanation for the exceptional stability of benzene is conventionally attributed to Sir Robert Robinson, who was apparently the first (in 1925)[9] to coin the term aromatic sextet as a group of six electrons that resists disruption.
In fact, this concept can be traced further back, via Ernest Crocker in 1922,[10] to Henry Edward Armstrong, who in 1890 wrote "the (six) centric affinities act within a cycle...benzene may be represented by a double ring (sic) ... and when an additive compound is formed, the inner cycle of affinity suffers disruption, the contiguous carbon-atoms to which nothing has been attached of necessity acquire the ethylenic condition".[11][verification needed]
Here, Armstrong is describing at least four modern concepts.[verification needed] First, his "affinity" is better known nowadays as the electron, which was to be discovered only seven years later by J. J. Thomson. Second, he is describing electrophilic aromatic substitution, proceeding (third) through a Wheland intermediate, in which (fourth) the conjugation of the ring is broken. He introduced the symbol C centered on the ring as a shorthand for the inner cycle, thus anticipating Erich Clar's notation. It is argued that he also anticipated the nature of wave mechanics, since he recognized that his affinities had direction, not merely being point particles, and collectively having a distribution that could be altered by introducing substituents onto the benzene ring (much as the distribution of the electric charge in a body is altered by bringing it near to another body).
The quantum mechanical origins of this stability, or aromaticity, were first modelled by Hückel in 1931. He was the first to separate the bonding electrons into sigma and pi electrons.
Aromaticity of an arbitrary aromatic compound can be measured quantitatively by the nucleus-independent chemical shift (NICS) computational method[12] and aromaticity percentage[13] methods.
Characteristics of aromatic (aryl) compounds
An aromatic (or aryl) compound contains a set of covalently bound atoms with specific characteristics:- A delocalized conjugated π system, most commonly an arrangement of alternating single and double bonds
- Coplanar structure, with all the contributing atoms in the same plane
- Contributing atoms arranged in one or more rings
- A number of π delocalized electrons that is even, but not a multiple of 4. That is, 4n + 2 π-electrons, where n = 0, 1, 2, 3, and so on. This is known as Hückel's rule.
Aromatic molecules typically display enhanced chemical stability, compared to similar non-aromatic molecules. A molecule that can be aromatic will tend to change toward aromaticity, and the added stability changes the chemistry of the molecule. Aromatic compounds undergo electrophilic aromatic substitution and nucleophilic aromatic substitution reactions, but not electrophilic addition reactions as happens with carbon–carbon double bonds.
In the presence of a magnetic field, the circulating π-electrons in an aromatic molecule produce an aromatic ring current that induces an additional magnetic field, an important effect in nuclear magnetic resonance.[14] The NMR signal of protons in the plane of an aromatic ring are shifted substantially further down-field than those on non-aromatic sp2 carbons. This is an important way of detecting aromaticity. By the same mechanism, the signals of protons located near the ring axis are shifted upfield.
Aromatic molecules are able to interact with each other in so-called π–π stacking: The π systems form two parallel rings overlap in a "face-to-face" orientation. Aromatic molecules are also able to interact with each other in an "edge-to-face" orientation: The slight positive charge of the substituents on the ring atoms of one molecule are attracted to the slight negative charge of the aromatic system on another molecule.
Planar monocyclic molecules containing 4n π-electrons are called antiaromatic and are, in general, unstable. Molecules that could be antiaromatic will tend to change from this electronic or conformation, thereby becoming non-aromatic. For example, cyclooctatetraene (COT) distorts out of planarity, breaking π overlap between adjacent double bonds. Recent studies have determined that cyclobutadiene adopts an asymmetric, rectangular configuration in which single and double bonds indeed alternate, with no resonance; the single bonds are markedly longer than the double bonds, reducing unfavorable p-orbital overlap. This reduction of symmetry lifts the degeneracy of the two formerly non-bonding molecular orbitals, which by Hund's rule forces the two unpaired electrons into a new, weakly bonding orbital (and also creates a weakly antibonding orbital). Hence, cyclobutadiene is non-aromatic; the strain of the asymmetric configuration outweighs the anti-aromatic destabilization that would afflict the symmetric, square configuration.
Importance of aromatic compounds
Aromatic compounds play key roles in the biochemistry of all living things. The four aromatic amino acids histidine, phenylalanine, tryptophan, and tyrosine each serve as one of the 20 basic building-blocks of proteins. Further, all 5 nucleotides (adenine, thymine, cytosine, guanine, and uracil) that make up the sequence of the genetic code in DNA and RNA are aromatic purines or pyrimidines. The molecule heme contains an aromatic system with 22 π-electrons. Chlorophyll also has a similar aromatic system.Aromatic compounds are important in industry. Key aromatic hydrocarbons of commercial interest are benzene, toluene, ortho-xylene and para-xylene. About 35 million tonnes are produced worldwide every year. They are extracted from complex mixtures obtained by the refining of oil or by distillation of coal tar, and are used to produce a range of important chemicals and polymers, including styrene, phenol, aniline, polyester and nylon.
Types of aromatic compounds
The overwhelming majority of aromatic compounds are compounds of carbon, but they need not be hydrocarbons.Neutral homocyclics
Benzene, as well as most other annulenes (cyclodecapentaene excepted) with the formula CnHn where n is an even number, such as cyclotetradecaheptaene.Heterocyclics
In heterocyclic aromatics (heteroaromatics), one or more of the atoms in the aromatic ring is of an element other than carbon. This can lessen the ring's aromaticity, and thus (as in the case of furan) increase its reactivity. Other examples include pyridine, pyrazine, pyrrole, imidazole, pyrazole, oxazole, thiophene, and their benzannulated analogs (benzimidazole, for example). In all these examples, the number of π-electrons is 6, due to the π-electrons from the double bonds as well as the two electrons from any lone pair that is in the p-orbital that is in the plane of the aromatic π system. For example, in pyridine, the five sp2-hybridized carbons each have a p-orbital that is perpendicular to the plane of the ring, and each of these p-orbitals contains one π-electron. Additionally, the nitrogen atom is also sp2-hybridized and has one electron in a p-orbital, which adds up to 6 p-electrons, thus making pyridine aromatic. The lone pair on the nitrogen is not part of the aromatic π system. Pyrrole and imidazole are both five membered aromatic rings that contain heteroatoms. In pyrrole, each of the four sp2-hybridized carbons contributes one π-electron, and the nitrogen atom is also sp2-hybridized and contributes two π-electrons from its lone pair, which occupies a p-orbital. In imidazole, both nitrogens are sp2-hybridized; the one in the double bond contributes one electron and the one which is not in the double bond and is in a lone pair contributes two electrons to the π system.[15]Fused aromatics and polycyclics
Polycyclic aromatic hydrocarbons are molecules containing two or more simple aromatic rings fused together by sharing two neighboring carbon atoms (see also simple aromatic rings). Examples are naphthalene, anthracene, and phenanthrene. In fused aromatics, not all carbon–carbon bonds are necessarily equivalent, as the electrons are not delocalized over the entire molecule. The aromaticity of these molecules can be explained using their orbital picture. Like benzene and other monocyclic aromatic molecules, polycyclics have a cyclic conjugated pi system with p-orbital overlap above and below the plane of the ring.[15]Substituted aromatics
Many chemical compounds are aromatic rings with other functional groups attached. Examples include trinitrotoluene (TNT), acetylsalicylic acid (aspirin), paracetamol, and the nucleotides of DNA.Aromatic ions
Aromatic molecules need not be neutral molecules. Ions that satisfy Huckel’s rule of 4n + 2 π-electrons in a planar, cyclic, conjugated molecule are considered to be aromatic ions. For example, the cyclopentadienyl anion and the cycloheptatrienylium cation are both considered to be aromatic ions, and the azulene molecule can be approximated as a combination of both.In order to convert the atom from sp3 to sp2, a carbocation, carbanion, or carbon radical must be formed. These leave sp2-hybridized carbons that can partake in the π system of an aromatic molecule. Like neutral aromatic compounds, these compounds are stable and form easily. The cyclopentadienyl anion is formed very easily and thus 1,3-cyclopentadiene is a very acidic hydrocarbon with a pKa of 16.[15] Other examples of aromatic ions include the cyclopropenium cation (2 π-electrons) and cyclooctatetraenyl dianion (10 pi electrons).
Atypical aromatic compounds
Aromaticity also occurs in compounds that are not carbocyclic or heterocyclic; inorganic six-membered-ring compounds analogous to benzene have been synthesized. For example, borazine is a six-membered ring composed of alternating boron and nitrogen atoms, each with one hydrogen attached. It has a delocalized π system and undergoes electrophilic substitution reactions appropriate to aromatic rings rather than reactions expected of non-aromatic molecules.[16]Quite recently, the aromaticity of planar Si6−
5 rings occurring in the Zintl phase Li12Si7 was experimentally evinced by Li solid-state NMR.[17][non-primary source needed] Metal aromaticity is believed to exist in certain clusters of aluminium, for example.[citation needed]
Homoaromaticity is the term used to describe systems where conjugation is interrupted by a single sp3 hybridized carbon atom.[18]
Möbius aromaticity occurs when a cyclic system of molecular orbitals, formed from pπ atomic orbitals and populated in a closed shell by 4n (n is an integer) electrons, is given a single half-twist to form a Möbius strip. A π system with 4n electrons in a flat (non-twisted) ring would be antiaromatic, and therefore highly unstable, due to the symmetry of the combinations of p atomic orbitals. By twisting the ring, the symmetry of the system changes and becomes allowed (see also Möbius–Hückel concept for details). Because the twist can be left-handed or right-handed, the resulting Möbius aromatics are dissymmetric or chiral. But as of 2012, no Möbius aromatic molecules had been synthesized.[19][20] Aromatics with two half-twists corresponding to the paradromic topologies were first suggested by Johann Listing.[21] In carbo-benzene the ring bonds are extended with alkyne and allene groups.
Y-aromaticity is a concept developed to explain the extraordinary stability and high basicity of the guanidinium cation. Guanidinium is not a ring molecule, and is cross-conjugated rather than a linear π system, but is reported to have its six π-electrons delocalized over the whole molecule. The concept is controversial and some authors emphasize different effects.[22][23][24]
σ-aromaticity refers to stabilization arising from the delocalization of sigma bonds. It is often invoked in cluster chemistry and is closely related to Wade's Rule.



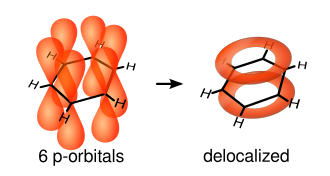







![{\displaystyle {\ce {[{\mathsf {F-XeF^{-}<->F^{-}Xe-F}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6841f8221ad24ec2c691c3280284c43996ad1ffb)