Boolean algebra

From Wikipedia, the free encyclopedia

In mathematics and mathematical logic, Boolean algebra is the branch of algebra in which the values of the variables are the truth values true and false, usually denoted 1 and 0 respectively. Instead of elementary algebra where the values of the variables are numbers, and the prime operations are addition and multiplication, the main operations of Boolean algebra are the conjunction and denoted as ∧, the disjunction or denoted as ∨, and the negation not denoted as ¬. It is thus a formalism for describing logical relations in the same way that ordinary algebra describes numeric relations.

Boolean algebra was introduced by George Boole in his first book The Mathematical Analysis of Logic (1847), and set forth more fully in his An Investigation of the Laws of Thought (1854).^[1] According to Huntington, the term "Boolean algebra" was first suggested by Sheffer in 1913,^[2] although Charles Sanders Peirce in 1880 gave the title "A Boolian Algebra with One Constant" to the first chapter of his "The Simplest Mathematics".^[3] Boolean algebra has been fundamental in the development of digital electronics, and is provided for in all modern programming languages. It is also used in set theory and statistics.^[4]

History

Boole's algebra predated the modern developments in abstract algebra and mathematical logic; it is however seen as connected to the origins of both fields.^[5] In an abstract setting, Boolean algebra was perfected in the late 19th century by Jevons, Schröder, Huntington, and others until it reached the modern conception of an (abstract) mathematical structure.^[5] For example, the empirical observation that one can manipulate expressions in the algebra of sets by translating them into expressions in Boole's algebra is explained in modern terms by saying that the algebra of sets is a Boolean algebra (note the indefinite article). In fact, M. H. Stone proved in 1936 that every Boolean algebra is isomorphic to a field of sets.

In the 1930s, while studying switching circuits, Claude Shannon observed that one could also apply the rules of Boole's algebra in this setting, and he introduced switching algebra as a way to analyze and design circuits by algebraic means in terms of logic gates. Shannon already had at his disposal the abstract mathematical apparatus, thus he cast his switching algebra as the two-element Boolean algebra. In circuit engineering settings today, there is little need to consider other Boolean algebras, thus "switching algebra" and "Boolean algebra" are often used interchangeably.^[6][7][8] Efficient implementation of Boolean functions is a fundamental problem in the design of combinational logic circuits. Modern electronic design automation tools for VLSI circuits often rely on an efficient representation of Boolean functions known as (reduced ordered) binary decision diagrams (BDD) for logic synthesis and formal verification.^[9]

Logic sentences that can be expressed in classical propositional calculus have an equivalent expression in Boolean algebra. Thus, Boolean logic is sometimes used to denote propositional calculus performed in this way.^[10][11][12] Boolean algebra is not sufficient to capture logic formulas using quantifiers, like those from first order logic. Although the development of mathematical logic did not follow Boole's program, the connection between his algebra and logic was later put on firm ground in the setting of algebraic logic, which also studies the algebraic systems of many other logics.^[5] The problem of determining whether the variables of a given Boolean (propositional) formula can be assigned in such a way as to make the formula evaluate to true is called the Boolean satisfiability problem (SAT), and is of importance to theoretical computer science, being the first problem shown to be NP-complete. The closely related model of computation known as a Boolean circuit relates time complexity (of an algorithm) to circuit complexity.

Values

Whereas in elementary algebra expressions denote mainly numbers, in Boolean algebra they denote the truth values false and true. These values are represented with the bits (or binary digits), namely 0 and 1. They do not behave like the integers 0 and 1, for which 1 + 1 = 2, but may be identified with the elements of the two-element field GF(2), that is, integer arithmetic modulo 2, for which 1 + 1 = 0. Addition and multiplication then play the Boolean roles of XOR (exclusive-or) and AND (conjunction) respectively, with disjunction x∨y (inclusive-or) definable as x + y - xy.

Boolean algebra also deals with functions which have their values in the set {0, 1}. A sequence of bits is a commonly used such function. Another common example is the subsets of a set E: to a subset F of E is associated the indicator function that takes the value 1 on F and 0 outside F. The most general example is the elements of a Boolean algebra, with all of the foregoing being instances thereof.

As with elementary algebra, the purely equational part of the theory may be developed without considering explicit values for the variables.^[13]

Operations

Basic operations

The basic operations of Boolean algebra are as follows:

• AND (conjunction), denoted x∧y (sometimes x AND y or Kxy), satisfies x∧y = 1 if x = y = 1 and x∧y = 0 otherwise.
• OR (disjunction), denoted x∨y (sometimes x OR y or Axy), satisfies x∨y = 0 if x = y = 0 and x∨y = 1 otherwise.
• NOT (negation), denoted ¬x (sometimes NOT x, Nx or !x), satisfies ¬x = 0 if x = 1 and ¬x = 1 if x = 0.

Alternatively the values of x∧y, x∨y, and ¬x can be expressed by tabulating their values with truth tables as follows.

${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x\wedge y}$ ${\displaystyle x\vee y}$ 0 0 0 0 1 0 0 1 0 1 0 1 1 1 1 1

${\displaystyle x}$ ${\displaystyle \neg x}$ 0 1 1 0

If the truth values 0 and 1 are interpreted as integers, these operations may be expressed with the ordinary operations of arithmetic (where x + y uses addition and xy uses multiplication), or by the minimum/maximum functions:

${\displaystyle {\begin{aligned}x\wedge y&=xy=\min(x,y)\\x\vee y&=x+y-xy=\max(x,y)\\\neg x&=1-x\end{aligned}}}$

One may consider that only the negation and one of the two other operations are basic, because of the following identities that allow to define the conjunction in terms of the negation and the disjunction, and vice versa:

${\displaystyle {\begin{aligned}x\wedge y&=\neg (\neg x\vee \neg y)\\x\vee y&=\neg (\neg x\wedge \neg y)\end{aligned}}}$

Secondary operations

The three Boolean operations described above are referred to as basic, meaning that they can be taken as a basis for other Boolean operations that can be built up from them by composition, the manner in which operations are combined or compounded. Operations composed from the basic operations include the following examples:

${\displaystyle x\rightarrow y=\neg {x}\vee y}$

${\displaystyle x\oplus y=(x\vee y)\wedge \neg {(x\wedge y)}}$

${\displaystyle x\equiv y=\neg {(x\oplus y)}}$

These definitions give rise to the following truth tables giving the values of these operations for all four possible inputs.

${\displaystyle x}$	${\displaystyle y}$	${\displaystyle x\rightarrow y}$	${\displaystyle x\oplus y}$	${\displaystyle x\equiv y}$
0	0	1	0	1
1	0	0	1	0
0	1	1	1	0
1	1	1	0	1

The first operation, x → y, or Cxy, is called material implication. If x is true then the value of x → y is taken to be that of y. But if x is false then the value of y can be ignored; however the operation must return some boolean value and there are only two choices. So by definition, x → y is true when x is false. (Relevance logic suggests this definition by viewing an implication with a false premise as something other than either true or false.)

The second operation, x ⊕ y, or Jxy, is called exclusive or (often abbreviated as XOR) to distinguish it from disjunction as the inclusive kind. It excludes the possibility of both x and y. Defined in terms of arithmetic it is addition mod 2 where 1 + 1 = 0.

The third operation, the complement of exclusive or, is equivalence or Boolean equality: x ≡ y, or Exy, is true just when x and y have the same value. Hence x ⊕ y as its complement can be understood as x ≠ y, being true just when x and y are different. Equivalence's counterpart in arithmetic mod 2 is x + y + 1.

Given two operands, each with two possible values, there are 2² = 4 possible combinations of inputs. Because each output can have two possible values, there are a total of 2⁴ = 16 possible binary Boolean operations.

Laws

A law of Boolean algebra is an identity such as x∨(y∨z) = (x∨y)∨z between two Boolean terms, where a Boolean term is defined as an expression built up from variables and the constants 0 and 1 using the operations ∧, ∨, and ¬. The concept can be extended to terms involving other Boolean operations such as ⊕, →, and ≡, but such extensions are unnecessary for the purposes to which the laws are put. Such purposes include the definition of a Boolean algebra as any model of the Boolean laws, and as a means for deriving new laws from old as in the derivation of x∨(y∧z) = x∨(z∧y) from y∧z = z∧y as treated in the section on axiomatization.

Monotone laws

Boolean algebra satisfies many of the same laws as ordinary algebra when one matches up ∨ with addition and ∧ with multiplication. In particular the following laws are common to both kinds of algebra:^[14]

Associativity of ${\displaystyle \vee }$:		${\displaystyle x\vee (y\vee z)}$	${\displaystyle =(x\vee y)\vee z}$
Associativity of ${\displaystyle \wedge }$:		${\displaystyle x\wedge (y\wedge z)}$	${\displaystyle =(x\wedge y)\wedge z}$
Commutativity of ${\displaystyle \vee }$:		${\displaystyle x\vee y}$	${\displaystyle =y\vee x}$
Commutativity of ${\displaystyle \wedge }$:		${\displaystyle x\wedge y}$	${\displaystyle =y\wedge x}$
Distributivity of ${\displaystyle \wedge }$ over ${\displaystyle \vee }$:		${\displaystyle x\wedge (y\vee z)}$	${\displaystyle =(x\wedge y)\vee (x\wedge z)}$
Identity for ${\displaystyle \vee }$:		${\displaystyle x\vee 0}$	${\displaystyle =x}$
Identity for ${\displaystyle \wedge }$:		${\displaystyle x\wedge 1}$	${\displaystyle =x}$
Annihilator for ${\displaystyle \wedge }$:		${\displaystyle x\wedge 0}$	${\displaystyle =0}$

The following laws hold in Boolean Algebra, but not in ordinary algebra:

Annihilator for ${\displaystyle \vee }$:		${\displaystyle x\vee 1}$	${\displaystyle =1}$
Idempotence of ${\displaystyle \vee }$:		${\displaystyle x\vee x}$	${\displaystyle =x}$
Idempotence of ${\displaystyle \wedge }$:		${\displaystyle x\wedge x}$	${\displaystyle =x}$
Absorption 1:		${\displaystyle x\wedge (x\vee y)}$	${\displaystyle =x}$
Absorption 2:		${\displaystyle x\vee (x\wedge y)}$	${\displaystyle =x}$
Distributivity of ${\displaystyle \vee }$ over ${\displaystyle \wedge }$:		${\displaystyle x\vee (y\wedge z)}$	${\displaystyle =(x\vee y)\wedge (x\vee z)}$

Taking x = 2 in the third law above shows that it is not an ordinary algebra law, since 2×2 = 4. The remaining five laws can be falsified in ordinary algebra by taking all variables to be 1, for example in Absorption Law 1 the left hand side would be 1(1+1) = 2 while the right hand side would be 1, and so on.

All of the laws treated so far have been for conjunction and disjunction. These operations have the property that changing either argument either leaves the output unchanged or the output changes in the same way as the input. Equivalently, changing any variable from 0 to 1 never results in the output changing from 1 to 0. Operations with this property are said to be monotone. Thus the axioms so far have all been for monotonic Boolean logic. Nonmonotonicity enters via complement ¬ as follows.^[4]

Nonmonotone laws

The complement operation is defined by the following two laws.

${\displaystyle {\begin{aligned}&{\text{Complementation 1}}&x\wedge \neg x&=0\\&{\text{Complementation 2}}&x\vee \neg x&=1\end{aligned}}}$

All properties of negation including the laws below follow from the above two laws alone.^[4]

In both ordinary and Boolean algebra, negation works by exchanging pairs of elements, whence in both algebras it satisfies the double negation law (also called involution law):

${\displaystyle {\begin{aligned}&{\text{Double negation}}&\neg {(\neg {x})}&=x\end{aligned}}}$

But whereas ordinary algebra satisfies the two laws

${\displaystyle {\begin{aligned}(-x)(-y)&=xy\\(-x)+(-y)&=-(x+y)\end{aligned}}}$

Boolean algebra satisfies De Morgan's laws:

${\displaystyle {\begin{aligned}&{\text{De Morgan 1}}&\neg x\wedge \neg y&=\neg {(x\vee y)}\\&{\text{De Morgan 2}}&\neg x\vee \neg y&=\neg {(x\wedge y)}\end{aligned}}}$

Completeness

The laws listed above define Boolean algebra, in the sense that they entail the rest of the subject. The laws Complementation 1 and 2, together with the monotone laws, suffice for this purpose and can therefore be taken as one possible complete set of laws or axiomatization of Boolean algebra. Every law of Boolean algebra follows logically from these axioms. Furthermore, Boolean algebras can then be defined as the models of these axioms as treated in the section thereon.

To clarify, writing down further laws of Boolean algebra cannot give rise to any new consequences of these axioms, nor can it rule out any model of them. In contrast, in a list of some but not all of the same laws, there could have been Boolean laws that did not follow from those on the list, and moreover there would have been models of the listed laws that were not Boolean algebras.

This axiomatization is by no means the only one, or even necessarily the most natural given that we did not pay attention to whether some of the axioms followed from others but simply chose to stop when we noticed we had enough laws, treated further in the section on axiomatizations. Or the intermediate notion of axiom can be sidestepped altogether by defining a Boolean law directly as any tautology, understood as an equation that holds for all values of its variables over 0 and 1. All these definitions of Boolean algebra can be shown to be equivalent.

Duality principle

Principle: If {X, R} is a poset, then {X, R(inverse)} is also a poset.

There is nothing magical about the choice of symbols for the values of Boolean algebra. We could rename 0 and 1 to say α and β, and as long as we did so consistently throughout it would still be Boolean algebra, albeit with some obvious cosmetic differences.

But suppose we rename 0 and 1 to 1 and 0 respectively. Then it would still be Boolean algebra, and moreover operating on the same values. However it would not be identical to our original Boolean algebra because now we find ∨ behaving the way ∧ used to do and vice versa. So there are still some cosmetic differences to show that we've been fiddling with the notation, despite the fact that we're still using 0s and 1s.

But if in addition to interchanging the names of the values we also interchange the names of the two binary operations, now there is no trace of what we have done. The end product is completely indistinguishable from what we started with. We might notice that the columns for x∧y and x∨y in the truth tables had changed places, but that switch is immaterial.

When values and operations can be paired up in a way that leaves everything important unchanged when all pairs are switched simultaneously, we call the members of each pair dual to each other. Thus 0 and 1 are dual, and ∧ and ∨ are dual. The Duality Principle, also called De Morgan duality, asserts that Boolean algebra is unchanged when all dual pairs are interchanged.

One change we did not need to make as part of this interchange was to complement. We say that complement is a self-dual operation. The identity or do-nothing operation x (copy the input to the output) is also self-dual. A more complicated example of a self-dual operation is (x∧y) ∨ (y∧z) ∨ (z∧x). There is no self-dual binary operation that depends on both its arguments. A composition of self-dual operations is a self-dual operation. For example, if f(x, y, z) = (x∧y) ∨ (y∧z) ∨ (z∧x), then f(f(x, y, z), x, t) is a self-dual operation of four arguments x,y,z,t.

The principle of duality can be explained from a group theory perspective by the fact that there are exactly four functions that are one-to-one mappings (automorphisms) of the set of Boolean polynomials back to itself: the identity function, the complement function, the dual function and the contradual function (complemented dual). These four functions form a group under function composition, isomorphic to the Klein four-group, acting on the set of Boolean polynomials. Walter Gottschalk remarked that consequently a more appropriate name for the phenomenon would be the principle (or square) of quaternality.^[15]

Diagrammatic representations

Venn diagrams

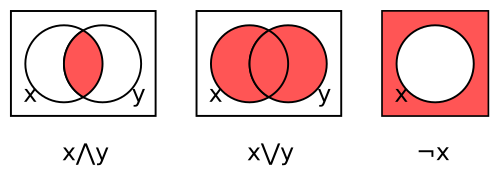
A Venn diagram^[16] is a representation of a Boolean operation using shaded overlapping regions. There is one region for each variable, all circular in the examples here. The interior and exterior of region x corresponds respectively to the values 1 (true) and 0 (false) for variable x. The shading indicates the value of the operation for each combination of regions, with dark denoting 1 and light 0 (some authors use the opposite convention).

The three Venn diagrams in the figure below represent respectively conjunction x∧y, disjunction x∨y, and complement ¬x.

Figure 2. Venn diagrams for conjunction, disjunction, and complement

For conjunction, the region inside both circles is shaded to indicate that x∧y is 1 when both variables are 1. The other regions are left unshaded to indicate that x∧y is 0 for the other three combinations.

The second diagram represents disjunction x∨y by shading those regions that lie inside either or both circles. The third diagram represents complement ¬x by shading the region not inside the circle.

While we have not shown the Venn diagrams for the constants 0 and 1, they are trivial, being respectively a white box and a dark box, neither one containing a circle. However we could put a circle for x in those boxes, in which case each would denote a function of one argument, x, which returns the same value independently of x, called a constant function. As far as their outputs are concerned, constants and constant functions are indistinguishable; the difference is that a constant takes no arguments, called a zeroary or nullary operation, while a constant function takes one argument, which it ignores, and is a unary operation.

Venn diagrams are helpful in visualizing laws. The commutativity laws for ∧ and ∨ can be seen from the symmetry of the diagrams: a binary operation that was not commutative would not have a symmetric diagram because interchanging x and y would have the effect of reflecting the diagram horizontally and any failure of commutativity would then appear as a failure of symmetry.
Idempotence of ∧ and ∨ can be visualized by sliding the two circles together and noting that the shaded area then becomes the whole circle, for both ∧ and ∨.

To see the first absorption law, x∧(x∨y) = x, start with the diagram in the middle for x∨y and note that the portion of the shaded area in common with the x circle is the whole of the x circle. For the second absorption law, x∨(x∧y) = x, start with the left diagram for x∧y and note that shading the whole of the x circle results in just the x circle being shaded, since the previous shading was inside the x circle.

The double negation law can be seen by complementing the shading in the third diagram for ¬x, which shades the x circle.

To visualize the first De Morgan's law, (¬x)∧(¬y) = ¬(x∨y), start with the middle diagram for x∨y and complement its shading so that only the region outside both circles is shaded, which is what the right hand side of the law describes. The result is the same as if we shaded that region which is both outside the x circle and outside the y circle, i.e. the conjunction of their exteriors, which is what the left hand side of the law describes.

The second De Morgan's law, (¬x)∨(¬y) = ¬(x∧y), works the same way with the two diagrams interchanged.

The first complement law, x∧¬x = 0, says that the interior and exterior of the x circle have no overlap. The second complement law, x∨¬x = 1, says that everything is either inside or outside the x circle.

Digital logic gates

Digital logic is the application of the Boolean algebra of 0 and 1 to electronic hardware consisting of logic gates connected to form a circuit diagram. Each gate implements a Boolean operation, and is depicted schematically by a shape indicating the operation. The shapes associated with the gates for conjunction (AND-gates), disjunction (OR-gates), and complement (inverters) are as follows.

The lines on the left of each gate represent input wires or ports. The value of the input is represented by a voltage on the lead. For so-called "active-high" logic, 0 is represented by a voltage close to zero or "ground", while 1 is represented by a voltage close to the supply voltage; active-low reverses this. The line on the right of each gate represents the output port, which normally follows the same voltage conventions as the input ports.

Complement is implemented with an inverter gate. The triangle denotes the operation that simply copies the input to the output; the small circle on the output denotes the actual inversion complementing the input. The convention of putting such a circle on any port means that the signal passing through this port is complemented on the way through, whether it is an input or output port.

The Duality Principle, or De Morgan's laws, can be understood as asserting that complementing all three ports of an AND gate converts it to an OR gate and vice versa, as shown in Figure 4 below. Complementing both ports of an inverter however leaves the operation unchanged.

More generally one may complement any of the eight subsets of the three ports of either an AND or OR gate. The resulting sixteen possibilities give rise to only eight Boolean operations, namely those with an odd number of 1's in their truth table. There are eight such because the "odd-bit-out" can be either 0 or 1 and can go in any of four positions in the truth table. There being sixteen binary Boolean operations, this must leave eight operations with an even number of 1's in their truth tables. Two of these are the constants 0 and 1 (as binary operations that ignore both their inputs); four are the operations that depend nontrivially on exactly one of their two inputs, namely x, y, ¬x, and ¬y; and the remaining two are x⊕y (XOR) and its complement x≡y.

Boolean algebras

The term "algebra" denotes both a subject, namely the subject of algebra, and an object, namely an algebraic structure. Whereas the foregoing has addressed the subject of Boolean algebra, this section deals with mathematical objects called Boolean algebras, defined in full generality as any model of the Boolean laws. We begin with a special case of the notion definable without reference to the laws, namely concrete Boolean algebras, and then give the formal definition of the general notion.

Concrete Boolean algebras

A concrete Boolean algebra or field of sets is any nonempty set of subsets of a given set X closed under the set operations of union, intersection, and complement relative to X.^[4]

(As an aside, historically X itself was required to be nonempty as well to exclude the degenerate or one-element Boolean algebra, which is the one exception to the rule that all Boolean algebras satisfy the same equations since the degenerate algebra satisfies every equation. However this exclusion conflicts with the preferred purely equational definition of "Boolean algebra," there being no way to rule out the one-element algebra using only equations— 0 ≠ 1 does not count, being a negated equation. Hence modern authors allow the degenerate Boolean algebra and let X be empty.)

Example 1. The power set 2^X of X, consisting of all subsets of X. Here X may be any set: empty, finite, infinite, or even uncountable.

Example 2. The empty set and X. This two-element algebra shows that a concrete Boolean algebra can be finite even when it consists of subsets of an infinite set. It can be seen that every field of subsets of X must contain the empty set and X. Hence no smaller example is possible, other than the degenerate algebra obtained by taking X to be empty so as to make the empty set and X coincide.

Example 3. The set of finite and cofinite sets of integers, where a cofinite set is one omitting only finitely many integers. This is clearly closed under complement, and is closed under union because the union of a cofinite set with any set is cofinite, while the union of two finite sets is finite. Intersection behaves like union with "finite" and "cofinite" interchanged.

Example 4. For a less trivial example of the point made by Example 2, consider a Venn diagram formed by n closed curves partitioning the diagram into 2ⁿ regions, and let X be the (infinite) set of all points in the plane not on any curve but somewhere within the diagram. The interior of each region is thus an infinite subset of X, and every point in X is in exactly one region. Then the set of all 2²ⁿ possible unions of regions (including the empty set obtained as the union of the empty set of regions and X obtained as the union of all 2ⁿ regions) is closed under union, intersection, and complement relative to X and therefore forms a concrete Boolean algebra. Again we have finitely many subsets of an infinite set forming a concrete Boolean algebra, with Example 2 arising as the case n = 0 of no curves.

Subsets as bit vectors

A subset Y of X can be identified with an indexed family of bits with index set X, with the bit indexed by x ∈ X being 1 or 0 according to whether or not x ∈ Y. (This is the so-called characteristic function notion of a subset.) For example, a 32-bit computer word consists of 32 bits indexed by the set {0,1,2,…,31}, with 0 and 31 indexing the low and high order bits respectively. For a smaller example, if X = {a,b,c} where a, b, c are viewed as bit positions in that order from left to right, the eight subsets {}, {c}, {b}, {b,c}, {a}, {a,c}, {a,b}, and {a,b,c} of X can be identified with the respective bit vectors 000, 001, 010, 011, 100, 101, 110, and 111. Bit vectors indexed by the set of natural numbers are infinite sequences of bits, while those indexed by the reals in the unit interval [0,1] are packed too densely to be able to write conventionally but nonetheless form well-defined indexed families (imagine coloring every point of the interval [0,1] either black or white independently; the black points then form an arbitrary subset of [0,1]).

From this bit vector viewpoint, a concrete Boolean algebra can be defined equivalently as a nonempty set of bit vectors all of the same length (more generally, indexed by the same set) and closed under the bit vector operations of bitwise ∧, ∨, and ¬, as in 1010∧0110 = 0010, 1010∨0110 = 1110, and ¬1010 = 0101, the bit vector realizations of intersection, union, and complement respectively.

The prototypical Boolean algebra

The set {0,1} and its Boolean operations as treated above can be understood as the special case of bit vectors of length one, which by the identification of bit vectors with subsets can also be understood as the two subsets of a one-element set. We call this the prototypical Boolean algebra, justified by the following observation.

The laws satisfied by all nondegenerate concrete Boolean algebras coincide with those satisfied by the prototypical Boolean algebra.

This observation is easily proved as follows. Certainly any law satisfied by all concrete Boolean algebras is satisfied by the prototypical one since it is concrete. Conversely any law that fails for some concrete Boolean algebra must have failed at a particular bit position, in which case that position by itself furnishes a one-bit counterexample to that law. Nondegeneracy ensures the existence of at least one bit position because there is only one empty bit vector.

The final goal of the next section can be understood as eliminating "concrete" from the above observation. We shall however reach that goal via the surprisingly stronger observation that, up to isomorphism, all Boolean algebras are concrete.

Boolean algebras: the definition

The Boolean algebras we have seen so far have all been concrete, consisting of bit vectors or equivalently of subsets of some set. Such a Boolean algebra consists of a set and operations on that set which can be shown to satisfy the laws of Boolean algebra.

Instead of showing that the Boolean laws are satisfied, we can instead postulate a set X, two binary operations on X, and one unary operation, and require that those operations satisfy the laws of Boolean algebra. The elements of X need not be bit vectors or subsets but can be anything at all. This leads to the more general abstract definition.

A Boolean algebra is any set with binary operations ∧ and ∨ and a unary operation ¬ thereon satisfying the Boolean laws.^[18]

For the purposes of this definition it is irrelevant how the operations came to satisfy the laws, whether by fiat or proof. All concrete Boolean algebras satisfy the laws (by proof rather than fiat), whence every concrete Boolean algebra is a Boolean algebra according to our definitions. This axiomatic definition of a Boolean algebra as a set and certain operations satisfying certain laws or axioms by fiat is entirely analogous to the abstract definitions of group, ring, field etc. characteristic of modern or abstract algebra.

Given any complete axiomatization of Boolean algebra, such as the axioms for a complemented distributive lattice, a sufficient condition for an algebraic structure of this kind to satisfy all the Boolean laws is that it satisfy just those axioms. The following is therefore an equivalent definition.

A Boolean algebra is a complemented distributive lattice.

The section on axiomatization lists other axiomatizations, any of which can be made the basis of an equivalent definition.

Representable Boolean algebras

Although every concrete Boolean algebra is a Boolean algebra, not every Boolean algebra need be concrete. Let n be a square-free positive integer, one not divisible by the square of an integer, for example 30 but not 12. The operations of greatest common divisor, least common multiple, and division into n (that is, ¬x = n/x), can be shown to satisfy all the Boolean laws when their arguments range over the positive divisors of n. Hence those divisors form a Boolean algebra. These divisors are not subsets of a set, making the divisors of n a Boolean algebra that is not concrete according to our definitions.

However, if we represent each divisor of n by the set of its prime factors, we find that this nonconcrete Boolean algebra is isomorphic to the concrete Boolean algebra consisting of all sets of prime factors of n, with union corresponding to least common multiple, intersection to greatest common divisor, and complement to division into n. So this example while not technically concrete is at least "morally" concrete via this representation, called an isomorphism. This example is an instance of the following notion.

A Boolean algebra is called representable when it is isomorphic to a concrete Boolean algebra.

The obvious next question is answered positively as follows.

Every Boolean algebra is representable.

That is, up to isomorphism, abstract and concrete Boolean algebras are the same thing. This quite nontrivial result depends on the Boolean prime ideal theorem, a choice principle slightly weaker than the axiom of choice, and is treated in more detail in the article Stone's representation theorem for Boolean algebras. This strong relationship implies a weaker result strengthening the observation in the previous subsection to the following easy consequence of representability.

The laws satisfied by all Boolean algebras coincide with those satisfied by the prototypical Boolean algebra.

It is weaker in the sense that it does not of itself imply representability. Boolean algebras are special here, for example a relation algebra is a Boolean algebra with additional structure but it is not the case that every relation algebra is representable in the sense appropriate to relation algebras.

Axiomatizing Boolean algebra

The above definition of an abstract Boolean algebra as a set and operations satisfying "the" Boolean laws raises the question, what are those laws? A simple-minded answer is "all Boolean laws," which can be defined as all equations that hold for the Boolean algebra of 0 and 1. Since there are infinitely many such laws this is not a terribly satisfactory answer in practice, leading to the next question: does it suffice to require only finitely many laws to hold?
In the case of Boolean algebras the answer is yes. In particular the finitely many equations we have listed above suffice. We say that Boolean algebra is finitely axiomatizable or finitely based.

Can this list be made shorter yet? Again the answer is yes. To begin with, some of the above laws are implied by some of the others. A sufficient subset of the above laws consists of the pairs of associativity, commutativity, and absorption laws, distributivity of ∧ over ∨ (or the other distributivity law—one suffices), and the two complement laws. In fact this is the traditional axiomatization of Boolean algebra as a complemented distributive lattice.

By introducing additional laws not listed above it becomes possible to shorten the list yet further. In 1933 Edward Huntington showed that if the basic operations are taken to be x∨y and ¬x, with x∧y considered a derived operation (e.g. via De Morgan's law in the form x∧y = ¬(¬x∨¬y)), then the equation ¬(¬x∨¬y)∨¬(¬x∨y) = x along with the two equations expressing associativity and commutativity of ∨ completely axiomatized Boolean algebra. When the only basic operation is the binary NAND operation ¬(x∧y), Stephen Wolfram has proposed in his book A New Kind of Science the single axiom (((xy)z)(x((xz)x))) = z as a one-equation axiomatization of Boolean algebra, where for convenience here xy denotes the NAND rather than the AND of x and y.

Propositional logic

Propositional logic is a logical system that is intimately connected to Boolean algebra.^[4] Many syntactic concepts of Boolean algebra carry over to propositional logic with only minor changes in notation and terminology, while the semantics of propositional logic are defined via Boolean algebras in a way that the tautologies (theorems) of propositional logic correspond to equational theorems of Boolean algebra.
Syntactically, every Boolean term corresponds to a propositional formula of propositional logic. In this translation between Boolean algebra and propositional logic, Boolean variables x,y… become propositional variables (or atoms) P,Q,…, Boolean terms such as x∨y become propositional formulas P∨Q, 0 becomes false or ⊥, and 1 becomes true or T. It is convenient when referring to generic propositions to use Greek letters Φ, Ψ,… as metavariables (variables outside the language of propositional calculus, used when talking about propositional calculus) to denote propositions.

The semantics of propositional logic rely on truth assignments. The essential idea of a truth assignment is that the propositional variables are mapped to elements of a fixed Boolean algebra, and then the truth value of a propositional formula using these letters is the element of the Boolean algebra that is obtained by computing the value of the Boolean term corresponding to the formula. In classical semantics, only the two-element Boolean algebra is used, while in Boolean-valued semantics arbitrary Boolean algebras are considered. A tautology is a propositional formula that is assigned truth value 1 by every truth assignment of its propositional variables to an arbitrary Boolean algebra (or, equivalently, every truth assignment to the two element Boolean algebra).

These semantics permit a translation between tautologies of propositional logic and equational theorems of Boolean algebra. Every tautology Φ of propositional logic can be expressed as the Boolean equation Φ = 1, which will be a theorem of Boolean algebra. Conversely every theorem Φ = Ψ of Boolean algebra corresponds to the tautologies (Φ∨¬Ψ) ∧ (¬Φ∨Ψ) and (Φ∧Ψ) ∨ (¬Φ∧¬Ψ). If → is in the language these last tautologies can also be written as (Φ→Ψ) ∧ (Ψ→Φ), or as two separate theorems Φ→Ψ and Ψ→Φ; if ≡ is available then the single tautology Φ ≡ Ψ can be used.

Applications

One motivating application of propositional calculus is the analysis of propositions and deductive arguments in natural language. Whereas the proposition "if x = 3 then x+1 = 4" depends on the meanings of such symbols as + and 1, the proposition "if x = 3 then x = 3" does not; it is true merely by virtue of its structure, and remains true whether "x = 3" is replaced by "x = 4" or "the moon is made of green cheese." The generic or abstract form of this tautology is "if P then P", or in the language of Boolean algebra, "P → P".

Replacing P by x = 3 or any other proposition is called instantiation of P by that proposition. The result of instantiating P in an abstract proposition is called an instance of the proposition. Thus "x = 3 → x = 3" is a tautology by virtue of being an instance of the abstract tautology "P → P". All occurrences of the instantiated variable must be instantiated with the same proposition, to avoid such nonsense as P → x = 3 or x = 3 → x = 4.

Propositional calculus restricts attention to abstract propositions, those built up from propositional variables using Boolean operations. Instantiation is still possible within propositional calculus, but only by instantiating propositional variables by abstract propositions, such as instantiating Q by Q→P in P→(Q→P) to yield the instance P→((Q→P)→P).

(The availability of instantiation as part of the machinery of propositional calculus avoids the need for metavariables within the language of propositional calculus, since ordinary propositional variables can be considered within the language to denote arbitrary propositions. The metavariables themselves are outside the reach of instantiation, not being part of the language of propositional calculus but rather part of the same language for talking about it that this sentence is written in, where we need to be able to distinguish propositional variables and their instantiations as being distinct syntactic entities.)

Deductive systems for propositional logic

An axiomatization of propositional calculus is a set of tautologies called axioms and one or more inference rules for producing new tautologies from old. A proof in an axiom system A is a finite nonempty sequence of propositions each of which is either an instance of an axiom of A or follows by some rule of A from propositions appearing earlier in the proof (thereby disallowing circular reasoning). The last proposition is the theorem proved by the proof. Every nonempty initial segment of a proof is itself a proof, whence every proposition in a proof is itself a theorem. An axiomatization is sound when every theorem is a tautology, and complete when every tautology is a theorem.^[19]

Sequent calculus

Propositional calculus is commonly organized as a Hilbert system, whose operations are just those of Boolean algebra and whose theorems are Boolean tautologies, those Boolean terms equal to the Boolean constant 1. Another form is sequent calculus, which has two sorts, propositions as in ordinary propositional calculus, and pairs of lists of propositions called sequents, such as A∨B, A∧C,… ${\displaystyle \vdash }$ A, B→C,…. The two halves of a sequent are called the antecedent and the succedent respectively. The customary metavariable denoting an antecedent or part thereof is Γ, and for a succedent Δ; thus Γ,A ${\displaystyle \vdash }$ Δ would denote a sequent whose succedent is a list Δ and whose antecedent is a list Γ with an additional proposition A appended after it. The antecedent is interpreted as the conjunction of its propositions, the succedent as the disjunction of its propositions, and the sequent itself as the entailment of the succedent by the antecedent.
Entailment differs from implication in that whereas the latter is a binary operation that returns a value in a Boolean algebra, the former is a binary relation which either holds or does not hold. In this sense entailment is an external form of implication, meaning external to the Boolean algebra, thinking of the reader of the sequent as also being external and interpreting and comparing antecedents and succedents in some Boolean algebra. The natural interpretation of ${\displaystyle \vdash }$ is as ≤ in the partial order of the Boolean algebra defined by x ≤ y just when x∨y = y. This ability to mix external implication ${\displaystyle \vdash }$ and internal implication → in the one logic is among the essential differences between sequent calculus and propositional calculus.^[20]

Applications

Boolean algebra as the calculus of two values is fundamental to computer circuits, computer programming, and mathematical logic, and is also used in other areas of mathematics such as set theory and statistics.^[4]

Computers

In the early 20th century, several electrical engineers intuitively recognized that Boolean algebra was analogous to the behavior of certain types of electrical circuits. Claude Shannon formally proved such behavior was logically equivalent to Boolean algebra in his 1937 master's thesis, A Symbolic Analysis of Relay and Switching Circuits.

Today, all modern general purpose computers perform their functions using two-value Boolean logic; that is, their electrical circuits are a physical manifestation of two-value Boolean logic. They achieve this in various ways: as voltages on wires in high-speed circuits and capacitive storage devices, as orientations of a magnetic domain in ferromagnetic storage devices, as holes in punched cards or paper tape, and so on. (Some early computers used decimal circuits or mechanisms instead of two-valued logic circuits.)

Of course, it is possible to code more than two symbols in any given medium. For example, one might use respectively 0, 1, 2, and 3 volts to code a four-symbol alphabet on a wire, or holes of different sizes in a punched card. In practice, the tight constraints of high speed, small size, and low power combine to make noise a major factor. This makes it hard to distinguish between symbols when there are several possible symbols that could occur at a single site. Rather than attempting to distinguish between four voltages on one wire, digital designers have settled on two voltages per wire, high and low.

Computers use two-value Boolean circuits for the above reasons. The most common computer architectures use ordered sequences of Boolean values, called bits, of 32 or 64 values, e.g. 01101000110101100101010101001011. When programming in machine code, assembly language, and certain other programming languages, programmers work with the low-level digital structure of the data registers. These registers operate on voltages, where zero volts represents Boolean 0, and a reference voltage (often +5V, +3.3V, +1.8V) represents Boolean 1. Such languages support both numeric operations and logical operations. In this context, "numeric" means that the computer treats sequences of bits as binary numbers (base two numbers) and executes arithmetic operations like add, subtract, multiply, or divide. "Logical" refers to the Boolean logical operations of disjunction, conjunction, and negation between two sequences of bits, in which each bit in one sequence is simply compared to its counterpart in the other sequence. Programmers therefore have the option of working in and applying the rules of either numeric algebra or Boolean algebra as needed. A core differentiating feature between these families of operations is the existence of the carry operation in the first but not the second.

Two-valued logic

Other areas where two values is a good choice are the law and mathematics. In everyday relaxed conversation, nuanced or complex answers such as "maybe" or "only on the weekend" are acceptable. In more focused situations such as a court of law or theorem-based mathematics however it is deemed advantageous to frame questions so as to admit a simple yes-or-no answer—is the defendant guilty or not guilty, is the proposition true or false—and to disallow any other answer. However much of a straitjacket this might prove in practice for the respondent, the principle of the simple yes-no question has become a central feature of both judicial and mathematical logic, making two-valued logic deserving of organization and study in its own right.

A central concept of set theory is membership. Now an organization may permit multiple degrees of membership, such as novice, associate, and full. With sets however an element is either in or out. The candidates for membership in a set work just like the wires in a digital computer: each candidate is either a member or a nonmember, just as each wire is either high or low.

Algebra being a fundamental tool in any area amenable to mathematical treatment, these considerations combine to make the algebra of two values of fundamental importance to computer hardware, mathematical logic, and set theory.

Two-valued logic can be extended to multi-valued logic, notably by replacing the Boolean domain {0, 1} with the unit interval [0,1], in which case rather than only taking values 0 or 1, any value between and including 0 and 1 can be assumed. Algebraically, negation (NOT) is replaced with 1 − x, conjunction (AND) is replaced with multiplication (${\displaystyle xy}$), and disjunction (OR) is defined via De Morgan's law. Interpreting these values as logical truth values yields a multi-valued logic, which forms the basis for fuzzy logic and probabilistic logic. In these interpretations, a value is interpreted as the "degree" of truth – to what extent a proposition is true, or the probability that the proposition is true.

Boolean operations

The original application for Boolean operations was mathematical logic, where it combines the truth values, true or false, of individual formulas.

Natural languages such as English have words for several Boolean operations, in particular conjunction (and), disjunction (or), negation (not), and implication (implies). But not is synonymous with and not. When used to combine situational assertions such as "the block is on the table" and "cats drink milk," which naively are either true or false, the meanings of these logical connectives often have the meaning of their logical counterparts. However, with descriptions of behavior such as "Jim walked through the door", one starts to notice differences such as failure of commutativity, for example the conjunction of "Jim opened the door" with "Jim walked through the door" in that order is not equivalent to their conjunction in the other order, since and usually means and then in such cases. Questions can be similar: the order "Is the sky blue, and why is the sky blue?" makes more sense than the reverse order. Conjunctive commands about behavior are like behavioral assertions, as in get dressed and go to school. Disjunctive commands such love me or leave me or fish or cut bait tend to be asymmetric via the implication that one alternative is less preferable. Conjoined nouns such as tea and milk generally describe aggregation as with set union while tea or milk is a choice. However context can reverse these senses, as in your choices are coffee and tea which usually means the same as your choices are coffee or tea (alternatives). Double negation as in "I don't not like milk" rarely means literally "I do like milk" but rather conveys some sort of hedging, as though to imply that there is a third possibility. "Not not P" can be loosely interpreted as "surely P", and although P necessarily implies "not not P" the converse is suspect in English, much as with intuitionistic logic. In view of the highly idiosyncratic usage of conjunctions in natural languages, Boolean algebra cannot be considered a reliable framework for interpreting them.

Boolean operations are used in digital logic to combine the bits carried on individual wires, thereby interpreting them over {0,1}. When a vector of n identical binary gates are used to combine two bit vectors each of n bits, the individual bit operations can be understood collectively as a single operation on values from a Boolean algebra with 2ⁿ elements.

Naive set theory interprets Boolean operations as acting on subsets of a given set X. As we saw earlier this behavior exactly parallels the coordinate-wise combinations of bit vectors, with the union of two sets corresponding to the disjunction of two bit vectors and so on.

The 256-element free Boolean algebra on three generators is deployed in computer displays based on raster graphics, which use bit blit to manipulate whole regions consisting of pixels, relying on Boolean operations to specify how the source region should be combined with the destination, typically with the help of a third region called the mask. Modern video cards offer all 2²³ = 256 ternary operations for this purpose, with the choice of operation being a one-byte (8-bit) parameter. The constants SRC = 0xaa or 10101010, DST = 0xcc or 11001100, and MSK = 0xf0 or 11110000 allow Boolean operations such as (SRC^DST)&MSK (meaning XOR the source and destination and then AND the result with the mask) to be written directly as a constant denoting a byte calculated at compile time, 0x60 in the (SRC^DST)&MSK example, 0x66 if just SRC^DST, etc. At run time the video card interprets the byte as the raster operation indicated by the original expression in a uniform way that requires remarkably little hardware and which takes time completely independent of the complexity of the expression.

Solid modeling systems for computer aided design offer a variety of methods for building objects from other objects, combination by Boolean operations being one of them. In this method the space in which objects exist is understood as a set S of voxels (the three-dimensional analogue of pixels in two-dimensional graphics) and shapes are defined as subsets of S, allowing objects to be combined as sets via union, intersection, etc. One obvious use is in building a complex shape from simple shapes simply as the union of the latter. Another use is in sculpting understood as removal of material: any grinding, milling, routing, or drilling operation that can be performed with physical machinery on physical materials can be simulated on the computer with the Boolean operation x ∧ ¬y or x − y, which in set theory is set difference, remove the elements of y from those of x. Thus given two shapes one to be machined and the other the material to be removed, the result of machining the former to remove the latter is described simply as their set difference.

Boolean searches

Search engine queries also employ Boolean logic. For this application, each web page on the Internet may be considered to be an "element" of a "set". The following examples use a syntax supported by Google.^[21]

• Doublequotes are used to combine whitespace-separated words into a single search term.^[22]
• Whitespace is used to specify logical AND, as it is the default operator for joining search terms:

"Search term 1" "Search term 2"

• The OR keyword is used for logical OR:

"Search term 1" OR "Search term 2"

• A prefixed minus sign is used for logical NOT:

"Search term 1" −"Search term 2"

Principia Mathematica (Russell)

✸54.43: "From this proposition it will follow, when arithmetical addition has been defined, that 1 + 1 = 2." —Volume I, 1st edition, page 379 (page 362 in 2nd edition; page 360 in abridged version). (The proof is actually completed in Volume II, 1st edition, page 86, accompanied by the comment, "The above proposition is occasionally useful." Τhey go on to say "It is used at least three times, in ✸113.66 and ✸120.123.472.")

The title page of the shortened Principia Mathematica to ✸56

I can remember Bertrand Russell telling me of a horrible dream. He was in the top floor of the University Library, about A.D. 2100. A library assistant was going round the shelves carrying an enormous bucket, taking down books, glancing at them, restoring them to the shelves or dumping them into the bucket. At last he came to three large volumes which Russell could recognize as the last surviving copy of Principia Mathematica. He took down one of the volumes, turned over a few pages, seemed puzzled for a moment by the curious symbolism, closed the volume, balanced it in his hand and hesitated....

Hardy, G. H. (2004) [1940]. A Mathematician's Apology. Cambridge: University Press. p. 83. ISBN 978-0-521-42706-7.

He [Russell] said once, after some contact with the Chinese language, that he was horrified to find that the language of Principia Mathematica was an Indo-European one

Littlewood, J. E. (1985). A Mathematician's Miscellany. Cambridge: University Press. p. 130.

The Principia Mathematica (often abbreviated PM) is a three-volume work on the foundations of mathematics written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913. In 1925–27, it appeared in a second edition with an important Introduction to the Second Edition, an Appendix A that replaced ✸9 and all-new Appendix B and Appendix C.

PM was an attempt to describe a set of axioms and inference rules in symbolic logic from which all mathematical truths could in principle be proven. As such, this ambitious project is of great importance in the history of mathematics and philosophy,^[1] being one of the foremost products of the belief that such an undertaking may be achievable. However, in 1931, Gödel's incompleteness theorem proved definitively that PM, and in fact any other attempt, could never achieve this lofty goal; that is, for any set of axioms and inference rules proposed to encapsulate mathematics, either the system must be inconsistent, or there must in fact be some truths of mathematics which could not be deduced from them.

One of the main inspirations and motivations for PM was the earlier work of Gottlob Frege on logic, which Russell discovered allowed for the construction of paradoxical sets. PM sought to avoid this problem by ruling out the unrestricted creation of arbitrary sets. This was achieved by replacing the notion of a general set with the notion of a hierarchy of sets of different 'types', a set of a certain type only allowed to contain sets of strictly lower types. Contemporary mathematics, however, avoids paradoxes such as Russell's in less unwieldy ways, such as the system of Zermelo–Fraenkel set theory.

PM is not to be confused with Russell's 1903 The Principles of Mathematics. PM states: "The present work was originally intended by us to be comprised in a second volume of Principles of Mathematics... But as we advanced, it became increasingly evident that the subject is a very much larger one than we had supposed; moreover on many fundamental questions which had been left obscure and doubtful in the former work, we have now arrived at what we believe to be satisfactory solutions."

PM has long been known for its typographical complexity. Famously, several hundred pages of PM precede the proof of the validity of the proposition 1+1=2. The Modern Library placed it 23rd in a list of the top 100 English-language nonfiction books of the twentieth century.^[2]

Scope of foundations laid

The Principia covered only set theory, cardinal numbers, ordinal numbers, and real numbers. Deeper theorems from real analysis were not included, but by the end of the third volume it was clear to experts that a large amount of known mathematics could in principle be developed in the adopted formalism. It was also clear how lengthy such a development would be.

A fourth volume on the foundations of geometry had been planned, but the authors admitted to intellectual exhaustion upon completion of the third.

Theoretical basis

As noted in the criticism of the theory by Kurt Gödel (below), unlike a formalist theory, the "logicistic" theory of PM has no "precise statement of the syntax of the formalism". Another observation is that almost immediately in the theory, interpretations (in the sense of model theory) are presented in terms of truth-values for the behaviour of the symbols "⊢" (assertion of truth), "~" (logical not), and "V" (logical inclusive OR).

Truth-values: PM embeds the notions of "truth" and "falsity" in the notion "primitive proposition". A raw (pure) formalist theory would not provide the meaning of the symbols that form a "primitive proposition"—the symbols themselves could be absolutely arbitrary and unfamiliar. The theory would specify only how the symbols behave based on the grammar of the theory. Then later, by assignment of "values", a model would specify an interpretation of what the formulas are saying. Thus in the formal Kleene symbol set below, the "interpretation" of what the symbols commonly mean, and by implication how they end up being used, is given in parentheses, e.g., "¬ (not)". But this is not a pure Formalist theory.

Contemporary construction of a formal theory

The following formalist theory is offered as contrast to the logicistic theory of PM. A contemporary formal system would be constructed as follows:

1. Symbols used: This set is the starting set, and other symbols can appear but only by definition from these beginning symbols. A starting set might be the following set derived from Kleene 1952: logical symbols: "→" (implies, IF-THEN, and "⊃"), "&" (and), "V" (or), "¬" (not), "∀" (for all), "∃" (there exists); predicate symbol "=" (equals); function symbols "+" (arithmetic addition), "∙" (arithmetic multiplication), "'" (successor); individual symbol "0" (zero); variables "a", "b", "c", etc.; and parentheses "(" and ")".^[3]
2. Symbol strings: The theory will build "strings" of these symbols by concatenation (juxtaposition).^[4]
3. Formation rules: The theory specifies the rules of syntax (rules of grammar) usually as a recursive definition that starts with "0" and specifies how to build acceptable strings or "well-formed formulas" (wffs).^[5] This includes a rule for "substitution"^[6] of strings for the symbols called "variables" (as opposed to the other symbol-types).
4. Transformation rule(s): The axioms that specify the behaviours of the symbols and symbol sequences.
5. Rule of inference, detachment, modus ponens : The rule that allows the theory to "detach" a "conclusion" from the "premises" that led up to it, and thereafter to discard the "premises" (symbols to the left of the line │, or symbols above the line if horizontal). If this were not the case, then substitution would result in longer and longer strings that have to be carried forward. Indeed, after the application of modus ponens, nothing is left but the conclusion, the rest disappears forever.

Contemporary theories often specify as their first axiom the classical or modus ponens or "the rule of detachment":

A, A ⊃ B │ B

The symbol "│" is usually written as a horizontal line, here "⊃" means "implies". The symbols A and B are "stand-ins" for strings; this form of notation is called an "axiom schema" (i.e., there is a countable number of specific forms the notation could take). This can be read in a manner similar to IF-THEN but with a difference: given symbol string IF A and A implies B THEN B (and retain only B for further use). But the symbols have no "interpretation" (e.g., no "truth table" or "truth values" or "truth functions") and modus ponens proceeds mechanistically, by grammar alone.

Construction

The theory of PM has both significant similarities, and similar differences, to a contemporary formal theory. Kleene states that "this deduction of mathematics from logic was offered as intuitive axiomatics. The axioms were intended to be believed, or at least to be accepted as plausible hypotheses concerning the world".^[7] Indeed, unlike a Formalist theory that manipulates symbols according to rules of grammar, PM introduces the notion of "truth-values", i.e., truth and falsity in the real-world sense, and the "assertion of truth" almost immediately as the fifth and sixth elements in the structure of the theory (PM 1962:4–36):

1. Variables
2. Uses of various letters
3. The fundamental functions of propositions: "the Contradictory Function" symbolised by "~" and the "Logical Sum or Disjunctive Function" symbolised by "∨" being taken as primitive and logical implication defined (the following example also used to illustrate 9. Definition below) as

p ⊃ q .=. ~ p ∨ q Df. (PM 1962:11)

and logical product defined as

p . q .=. ~(~p ∨ ~q) Df. (PM 1962:12)

1. Equivalence: Logical equivalence, not arithmetic equivalence: "≡" given as a demonstration of how the symbols are used, i.e., "Thus ' p ≡ q ' stands for '( p ⊃ q ) . ( q ⊃ p )'." (PM 1962:7). Notice that to discuss a notation PM identifies a "meta"-notation with "[space] ... [space]":^[8]

Logical equivalence appears again as a definition:

p ≡ q .=. ( p ⊃ q ) . ( q ⊃ p ) (PM 1962:12),

Notice the appearance of parentheses. This grammatical usage is not specified and appears sporadically; parentheses do play an important role in symbol strings, however, e.g., the notation "(x)" for the contemporary "∀x".

1. Truth-values: "The 'Truth-value' of a proposition is truth if it is true, and falsehood if it is false" (this phrase is due to Frege) (PM 1962:7).
2. Assertion-sign: "'⊦'. p may be read 'it is true that' ... thus '⊦: p .⊃. q ' means 'it is true that p implies q ', whereas '⊦. p .⊃⊦. q ' means ' p is true; therefore q is true'. The first of these does not necessarily involve the truth either of p or of q, while the second involves the truth of both" (PM 1962:92).
3. Inference: PM 's version of modus ponens. "[If] '⊦. p ' and '⊦ (p ⊃ q)' have occurred, then '⊦ . q ' will occur if it is desired to put it on record. The process of the inference cannot be reduced to symbols. Its sole record is the occurrence of '⊦. q ' [in other words, the symbols on the left disappear or can be erased]" (PM 1962:9).
4. The use of dots
5. Definitions: These use the "=" sign with "Df" at the right end.
6. Summary of preceding statements: brief discussion of the primitive ideas "~ p" and "p ∨ q" and "⊦" prefixed to a proposition.
7. Primitive propositions: the axioms or postulates. This was significantly modified in the 2nd edition.
8. Propositional functions: The notion of "proposition" was significantly modified in the 2nd edition, including the introduction of "atomic" propositions linked by logical signs to form "molecular" propositions, and the use of substitution of molecular propositions into atomic or molecular propositions to create new expressions.
9. The range of values and total variation
10. Ambiguous assertion and the real variable: This and the next two sections were modified or abandoned in the 2nd edition. In particular, the distinction between the concepts defined in sections 15. Definition and the real variable and 16 Propositions connecting real and apparent variables was abandoned in the second edition.
11. Formal implication and formal equivalence
12. Identity
13. Classes and relations
14. Various descriptive functions of relations
15. Plural descriptive functions
16. Unit classes

Primitive ideas

Cf. PM 1962:90–94, for the first edition:

• (1) Elementary propositions.
• (2) Elementary propositions of functions.
• (3) Assertion: introduces the notions of "truth" and "falsity".
• (4) Assertion of a propositional function.
• (5) Negation: "If p is any proposition, the proposition "not-p", or "p is false," will be represented by "~p" ".
• (6) Disjunction: "If p and q are any propositions, the proposition "p or q, i.e., "either p is true or q is true," where the alternatives are to be not mutually exclusive, will be represented by "p ∨ q" ".
• (cf. section B)

Primitive propositions

The first edition (see discussion relative to the second edition, below) begins with a definition of the sign "⊃"

✸1.01. p ⊃ q .=. ~ p ∨ q. Df.
✸1.1. Anything implied by a true elementary proposition is true. Pp modus ponens
(✸1.11 was abandoned in the second edition.)
✸1.2. ⊦: p ∨ p .⊃. p. Pp principle of tautology
✸1.3. ⊦: q .⊃. p ∨ q. Pp principle of addition
✸1.4. ⊦: p ∨ q .⊃. q ∨ p. Pp principle of permutation
✸1.5. ⊦: p ∨ ( q ∨ r ) .⊃. q ∨ ( p ∨ r ). Pp associative principle
✸1.6. ⊦:. q ⊃ r .⊃: p ∨ q .⊃. p ∨ r. Pp principle of summation
✸1.7. If p is an elementary proposition, ~p is an elementary proposition. Pp
✸1.71. If p and q are elementary propositions, p ∨ q is an elementary proposition. Pp
✸1.72. If φp and ψp are elementary propositional functions which take elementary propositions as arguments, φp ∨ ψp is an elementary proposition. Pp

Together with the "Introduction to the Second Edition", the second edition's Appendix A abandons the entire section ✸9. This includes six primitive propositions ✸9 through ✸9.15 together with the Axioms of reducibility.

The revised theory is made difficult by the introduction of the Sheffer stroke ("|") to symbolise "incompatibility" (i.e., if both elementary propositions p and q are true, their "stroke" p | q is false), the contemporary logical NAND (not-AND). In the revised theory, the Introduction presents the notion of "atomic proposition", a "datum" that "belongs to the philosophical part of logic". These have no parts that are propositions and do not contain the notions "all" or "some". For example: "this is red", or "this is earlier than that". Such things can exist ad finitum, i.e., even an "infinite enumeration" of them to replace "generality" (i.e., the notion of "for all").^[9] PM then "advance[s] to molecular propositions" that are all linked by "the stroke". Definitions give equivalences for "~", "∨", "⊃", and ".".

The new introduction defines "elementary propositions" as atomic and molecular positions together. It then replaces all the primitive propositions ✸1.2 to ✸1.72 with a single primitive proposition framed in terms of the stroke:

"If p, q, r are elementary propositions, given p and p|(q|r), we can infer r. This is a primitive proposition."

The new introduction keeps the notation for "there exists" (now recast as "sometimes true") and "for all" (recast as "always true"). Appendix A strengthens the notion of "matrix" or "predicative function" (a "primitive idea", PM 1962:164) and presents four new Primitive propositions as ✸8.1–✸8.13.

✸88. Multiplicative axiom

✸120. Axiom of infinity

Ramified types and the axiom of reducibility

In simple type theory objects are elements of various disjoint "types". Types are implicitly built up as follows. If τ₁,...,τ_m are types then there is a type (τ₁,...,τ_m) that can be thought of as the class of propositional functions of τ₁,...,τ_m (which in set theory is essentially the set of subsets of τ₁×...×τ_m). In particular there is a type () of propositions, and there may be a type ι (iota) of "individuals" from which other types are built. Russell and Whitehead's notation for building up types from other types is rather cumbersome, and the notation here is due to Church.

In the ramified type theory of PM all objects are elements of various disjoint ramified types. Ramified types are implicitly built up as follows. If τ₁,...,τ_m,σ₁,...,σ_n are ramified types then as in simple type theory there is a type (τ₁,...,τ_m,σ₁,...,σ_n) of "predicative" propositional functions of τ₁,...,τ_m,σ₁,...,σ_n. However, there are also ramified types (τ₁,...,τ_m|σ₁,...,σ_n) that can be thought of as the classes of propositional functions of τ₁,...τ_m obtained from propositional functions of type (τ₁,...,τ_m,σ₁,...,σ_n) by quantifying over σ₁,...,σ_n. When n=0 (so there are no σs) these propositional functions are called predicative functions or matrices. This can be confusing because current mathematical practice does not distinguish between predicative and non-predicative functions, and in any case PM never defines exactly what a "predicative function" actually is: this is taken as a primitive notion.

Russell and Whitehead found it impossible to develop mathematics while maintaining the difference between predicative and non-predicative functions, so they introduced the axiom of reducibility, saying that for every non-predicative function there is a predicative function taking the same values. In practice this axiom essentially means that the elements of type (τ₁,...,τ_m|σ₁,...,σ_n) can be identified with the elements of type (τ₁,...,τ_m), which causes the hierarchy of ramified types to collapse down to simple type theory. (Strictly speaking this is not quite correct, because PM allows two propositional functions to be different even it they take the same values on all arguments; this differs from current mathematical practice where one normally identifies two such functions.)

In Zermelo set theory one can model the ramified type theory of PM as follows. One picks a set ι to be the type of individuals. For example, ι might be the set of natural numbers, or the set of atoms (in a set theory with atoms) or any other set one is interested in. Then if τ₁,...,τ_m are types, the type (τ₁,...,τ_m) is the power set of the product τ₁×...×τ_m, which can also be thought of informally as the set of (propositional predicative) functions from this product to a 2-element set {true,false}. The ramified type (τ₁,...,τ_m|σ₁,...,σ_n) can be modeled as the product of the type (τ₁,...,τ_m,σ₁,...,σ_n) with the set of sequences of n quantifiers (∀ or ∃) indicating which quantifier should be applied to each variable σ_i. (One can vary this slightly by allowing the σs to be quantified in any order, or allowing them to occur before some of the τs, but this makes little difference except to the bookkeeping.)

Notation

One author^[1] observes that "The notation in that work has been superseded by the subsequent development of logic during the 20th century, to the extent that the beginner has trouble reading PM at all"; while much of the symbolic content can be converted to modern notation, the original notation itself is "a subject of scholarly dispute", and some notation "embod[y] substantive logical doctrines so that it cannot simply be replaced by contemporary symbolism".^[10]
Kurt Gödel was harshly critical of the notation:

"It is to be regretted that this first comprehensive and thorough-going presentation of a mathematical logic and the derivation of mathematics from it [is] so greatly lacking in formal precision in the foundations (contained in ✸1–✸21 of Principia [i.e., sections ✸1–✸5 (propositional logic), ✸8–14 (predicate logic with identity/equality), ✸20 (introduction to set theory), and ✸21 (introduction to relations theory)]) that it represents in this respect a considerable step backwards as compared with Frege. What is missing, above all, is a precise statement of the syntax of the formalism. Syntactical considerations are omitted even in cases where they are necessary for the cogency of the proofs".^[11]

This is reflected in the example below of the symbols "p", "q", "r" and "⊃" that can be formed into the string "p ⊃ q ⊃ r". PM requires a definition of what this symbol-string means in terms of other symbols; in contemporary treatments the "formation rules" (syntactical rules leading to "well formed formulas") would have prevented the formation of this string.

Source of the notation: Chapter I "Preliminary Explanations of Ideas and Notations" begins with the source of the elementary parts of the notation (the symbols =⊃≡−ΛVε and the system of dots):

"The notation adopted in the present work is based upon that of Peano, and the following explanations are to some extent modeled on those which he prefixes to his Formulario Mathematico [i.e., Peano 1889]. His use of dots as brackets is adopted, and so are many of his symbols" (PM 1927:4).^[12]

PM changed Peano's Ɔ to ⊃, and also adopted a few of Peano's later symbols, such as ℩ and ι, and Peano's practice of turning letters upside down.

PM adopts the assertion sign "⊦" from Frege's 1879 Begriffsschrift:^[13]

"(I)t may be read 'it is true that'"^[14]

Thus to assert a proposition p PM writes:

"⊦. p." (PM 1927:92)

(Observe that, as in the original, the left dot is square and of greater size than the period on the right.)
Most of the rest of the notation in PM was invented by Whitehead.^{[citation needed]}

An introduction to the notation of "Section A Mathematical Logic" (formulas ✸1–✸5.71)

PM 's dots^[15] are used in a manner similar to parentheses. Each dot (or multiple dot) represents either a left or right parenthesis or the logical symbol ∧. More than one dot indicates the "depth" of the parentheses, for example, ".", ":" or ":.", "::". However the position of the matching right or left parenthesis is not indicated explicitly in the notation but has to be deduced from some rules that are complicated, confusing and sometimes ambiguous. Moreover, when the dots stand for a logical symbol ∧ its left and right operands have to be deduced using similar rules. First one has to decide based on context whether the dots stand for a left or right parenthesis or a logical symbol. Then one has to decide how far the other corresponding parenthesis is: here one carries on until one meets either a larger number of dots, or the same number of dots next that have equal or greater "force", or the end of the line. Dots next to the signs ⊃, ≡,∨, =Df have greater force than dots next to (x), (∃x) and so on, which have greater force than dots indicating a logical product ∧.

Example 1. The line

✸3.12. ⊢ : ~p . v . ~q . v . p . q

corresponds to

(((~p) v (~q)) v (p ∧ q))

where the colon represents the outer (), the next two dots represent the parentheses around ~p and ~q, the third dot represents the parentheses around p ∧ q, and the fourth dot (rather confusingly) represents the logical symbol ∧ rather than a pair of parentheses. This uses the definition (followed by the explanatory comment):

✸2.33 p v q v r .=. (p v q) v r Df

This definition serves only for the avoidance of brackets.

Example 2, with double, triple, and quadruple dots:

✸9.521. ⊢ : : (∃x). φx . ⊃ . q : ⊃ : . (∃x). φx . v . r : ⊃ . q v r

stands for

((((∃x)(φx)) ⊃ (q)) ⊃ ((((∃x) (φx)) v (r)) ⊃ (q v r)))

Example 3, with a double dot indicating a logical symbol (from volume 1, page 10):

p⊃q:q⊃r.⊃.p⊃r

stands for

(p⊃q) ∧ ((q⊃r)⊃(p⊃r))

where the double dot represents the logical symbol ∧, and its right operand consists of everything after it because it has priority over the single dots.

Later in section ✸14, brackets "[ ]" appear, and in sections ✸20 and following, braces "{ }" appear. Whether these symbols have specific meanings or are just for visual clarification is unclear. Unfortunately the single dot (but also ":", ":.", "::", etc.) is also used to symbolise "logical product" (contemporary logical AND often symbolised by "&" or "∧").

Logical implication is represented by Peano's "Ɔ" simplified to "⊃", logical negation is symbolised by an elongated tilde, i.e., "~" (contemporary "~" or "¬"), the logical OR by "v". The symbol "=" together with "Df" is used to indicate "is defined as", whereas in sections ✸13 and following, "=" is defined as (mathematically) "identical with", i.e., contemporary mathematical "equality" (cf. discussion in section ✸13). Logical equivalence is represented by "≡" (contemporary "if and only if"); "elementary" propositional functions are written in the customary way, e.g., "f(p)", but later the function sign appears directly before the variable without parenthesis e.g., "φx", "χx", etc.

Example, PM introduces the definition of "logical product" as follows:

✸3.01. p . q .=. ~(~p v ~q) Df.

where "p . q" is the logical product of p and q.

✸3.02. p ⊃ q ⊃ r .=. p ⊃ q . q ⊃ r Df.

This definition serves merely to abbreviate proofs.

Translation of the formulas into contemporary symbols: Various authors use alternate symbols, so no definitive translation can be given. However, because of criticisms such as that of Kurt Gödel below, the best contemporary treatments will be very precise with respect to the "formation rules" (the syntax) of the formulas.

The first formula might be converted into modern symbolism as follows:^[16]

(p & q) =_df (~(~p v ~q))

alternately

(p & q) =_df (¬(¬p v ¬q))

alternately

(p ∧ q) =_df (¬(¬p v ¬q))

etc.

The second formula might be converted as follows:

(p → q → r) =_df (p → q) & (q → r)

But note that this is not (logically) equivalent to (p → (q → r)) nor to ((p → q) → r), and these two are not logically equivalent either.

An introduction to the notation of "Section B Theory of Apparent Variables" (formulas ✸8–✸14.34)

These sections concern what is now known as predicate logic, and predicate logic with identity (equality).

• NB: As a result of criticism and advances, the second edition of PM (1927) replaces ✸9 with a new ✸8 (Appendix A). This new section eliminates the first edition's distinction between real and apparent variables, and it eliminates "the primitive idea 'assertion of a propositional function'.^[17] To add to the complexity of the treatment, ✸8 introduces the notion of substituting a "matrix", and the Sheffer stroke:

• Matrix: In contemporary usage, PM 's matrix is (at least for propositional functions), a truth table, i.e., all truth-values of a propositional or predicate function.
• Sheffer stroke: Is the contemporary logical NAND (NOT-AND), i.e., "incompatibility", meaning:

"Given two propositions p and q, then ' p | q ' means "proposition p is incompatible with proposition q", i.e., if both propositions p and q evaluate as true, then and only then p | q evaluates as false." After section ✸8 the Sheffer stroke sees no usage.

Section ✸10: The existential and universal "operators": PM adds "(x)" to represent the contemporary symbolism "for all x " i.e., " ∀x", and it uses a backwards serifed E to represent "there exists an x", i.e., "(Ǝx)", i.e., the contemporary "∃x". The typical notation would be similar to the following:

"(x) . φx" means "for all values of variable x, function φ evaluates to true"

"(Ǝx) . φx" means "for some value of variable x, function φ evaluates to true"

Sections ✸10, ✸11, ✸12: Properties of a variable extended to all individuals: section ✸10 introduces the notion of "a property" of a "variable". PM gives the example: φ is a function that indicates "is a Greek", and ψ indicates "is a man", and χ indicates "is a mortal" these functions then apply to a variable x. PM can now write, and evaluate:

(x) . ψx

The notation above means "for all x, x is a man". Given a collection of individuals, one can evaluate the above formula for truth or falsity. For example, given the restricted collection of individuals { Socrates, Plato, Russell, Zeus } the above evaluates to "true" if we allow for Zeus to be a man. But it fails for:

(x) . φx

because Russell is not Greek. And it fails for

(x) . χx

because Zeus is not a mortal.

Equipped with this notation PM can create formulas to express the following: "If all Greeks are men and if all men are mortals then all Greeks are mortals". (PM 1962:138)

(x) . φx ⊃ ψx :(x). ψx ⊃ χx :⊃: (x) . φx ⊃ χx

Another example: the formula:

✸10.01. (Ǝx). φx . = . ~(x) . ~φx Df.

means "The symbols representing the assertion 'There exists at least one x that satisfies function φ' is defined by the symbols representing the assertion 'It's not true that, given all values of x, there are no values of x satisfying φ'".

The symbolisms ⊃_x and "≡_x" appear at ✸10.02 and ✸10.03. Both are abbreviations for universality (i.e., for all) that bind the variable x to the logical operator. Contemporary notation would have simply used parentheses outside of the equality ("=") sign:

✸10.02 φx ⊃_x ψx .=. (x). φx ⊃ ψx Df

Contemporary notation: ∀x(φ(x) → ψ(x)) (or a variant)

✸10.03 φx ≡_x ψx .=. (x). φx ≡ ψx Df

Contemporary notation: ∀x(φ(x) ↔ ψ(x)) (or a variant)

PM attributes the first symbolism to Peano.

Section ✸11 applies this symbolism to two variables. Thus the following notations: ⊃_x, ⊃_y, ⊃_{x, y} could all appear in a single formula.

Section ✸12 reintroduces the notion of "matrix" (contemporary truth table), the notion of logical types, and in particular the notions of first-order and second-order functions and propositions.

New symbolism "φ ! x" represents any value of a first-order function. If a circumflex "＾" is placed over a variable, then this is an "individual" value of y, meaning that "ŷ" indicates "individuals" (e.g., a row in a truth table); this distinction is necessary because of the matrix/extensional nature of propositional functions.

Now equipped with the matrix notion, PM can assert its controversial axiom of reducibility: a function of one or two variables (two being sufficient for PM 's use) where all its values are given (i.e., in its matrix) is (logically) equivalent ("≡") to some "predicative" function of the same variables. The one-variable definition is given below as an illustration of the notation (PM 1962:166–167):

✸12.1 ⊢: (Ǝ f): φx .≡_x. f ! x Pp;

Pp is a "Primitive proposition" ("Propositions assumed without proof") (PM 1962:12, i.e., contemporary "axioms"), adding to the 7 defined in section ✸1 (starting with ✸1.1 modus ponens). These are to be distinguished from the "primitive ideas" that include the assertion sign "⊢", negation "~", logical OR "V", the notions of "elementary proposition" and "elementary propositional function"; these are as close as PM comes to rules of notational formation, i.e., syntax.

This means: "We assert the truth of the following: There exists a function f with the property that: given all values of x, their evaluations in function φ (i.e., resulting their matrix) is logically equivalent to some f evaluated at those same values of x. (and vice versa, hence logical equivalence)". In other words: given a matrix determined by property φ applied to variable x, there exists a function f that, when applied to the x is logically equivalent to the matrix. Or: every matrix φx can be represented by a function f applied to x, and vice versa.

✸13: The identity operator "=" : This is a definition that uses the sign in two different ways, as noted by the quote from PM:

✸13.01. x = y .=: (φ): φ ! x . ⊃ . φ ! y Df

means:

"This definition states that x and y are to be called identical when every predicative function satisfied by x is also satisfied by y ... Note that the second sign of equality in the above definition is combined with "Df", and thus is not really the same symbol as the sign of equality which is defined."

The not-equals sign "≠" makes its appearance as a definition at ✸13.02.

✸14: Descriptions:

"A description is a phrase of the form "the term y which satisfies φŷ, where φŷ is some function satisfied by one and only one argument."^[18]

From this PM employs two new symbols, a forward "E" and an inverted iota "℩". Here is an example:

✸14.02. E ! ( ℩y) (φy) .=: ( Ǝb):φy . ≡_y . y = b Df.

This has the meaning:

"The y satisfying φŷ exists," which holds when, and only when φŷ is satisfied by one value of y and by no other value." (PM 1967:173–174)

Introduction to the notation of the theory of classes and relations

The text leaps from section ✸14 directly to the foundational sections ✸20 GENERAL THEORY OF CLASSES and ✸21 GENERAL THEORY OF RELATIONS. "Relations" are what is known in contemporary set theory as sets of ordered pairs. Sections ✸20 and ✸22 introduce many of the symbols still in contemporary usage. These include the symbols "ε", "⊂", "∩", "∪", "–", "Λ", and "V": "ε" signifies "is an element of" (PM 1962:188); "⊂" (✸22.01) signifies "is contained in", "is a subset of"; "∩" (✸22.02) signifies the intersection (logical product) of classes (sets); "∪" (✸22.03) signifies the union (logical sum) of classes (sets); "–" (✸22.03) signifies negation of a class (set); "Λ" signifies the null class; and "V" signifies the universal class or universe of discourse.

Small Greek letters (other than "ε", "ι", "π", "φ", "ψ", "χ", and "θ") represent classes (e.g., "α", "β", "γ", "δ", etc.) (PM 1962:188):

x ε α

"The use of single letter in place of symbols such as ẑ(φz) or ẑ(φ ! z) is practically almost indispensable, since otherwise the notation rapidly becomes intolerably cumbrous. Thus ' x ε α' will mean ' x is a member of the class α'". (PM 1962:188)

α ∪ –α = V

The union of a set and its inverse is the universal (completed) set.^[19]

α ∩ –α = Λ

The intersection of a set and its inverse is the null (empty) set.

When applied to relations in section ✸23 CALCULUS OF RELATIONS, the symbols "⊂", "∩", "∪", and "–" acquire a dot: for example: "⊍", "∸".^[20]

The notion, and notation, of "a class" (set): In the first edition PM asserts that no new primitive ideas are necessary to define what is meant by "a class", and only two new "primitive propositions" called the axioms of reducibility for classes and relations respectively (PM 1962:25).^[21] But before this notion can be defined, PM feels it necessary to create a peculiar notation "ẑ(φz)" that it calls a "fictitious object". (PM 1962:188)

⊢: x ε ẑ(φz) .≡. (φx)

"i.e., ' x is a member of the class determined by (φẑ)' is [logically] equivalent to ' x satisfies (φẑ),' or to '(φx) is true.'". (PM 1962:25)

At least PM can tell the reader how these fictitious objects behave, because "A class is wholly determinate when its membership is known, that is, there cannot be two different classes having the same membership" (PM 1962:26). This is symbolised by the following equality (similar to ✸13.01 above:

ẑ(φz) = ẑ(ψz) . ≡ : (x): φx .≡. ψx

"This last is the distinguishing characteristic of classes, and justifies us in treating ẑ(ψz) as the class determined by [the function] ψẑ." (PM 1962:188)

Perhaps the above can be made clearer by the discussion of classes in Introduction to the 2nd Edition, which disposes of the Axiom of Reducibility and replaces it with the notion: "All functions of functions are extensional" (PM 1962:xxxix), i.e.,

φx ≡_x ψx .⊃. (x): ƒ(φẑ) ≡ ƒ(ψẑ) (PM 1962:xxxix)

This has the reasonable meaning that "IF for all values of x the truth-values of the functions φ and ψ of x are [logically] equivalent, THEN the function ƒ of a given φẑ and ƒ of ψẑ are [logically] equivalent." PM asserts this is "obvious":

"This is obvious, since φ can only occur in ƒ(φẑ) by the substitution of values of φ for p, q, r, ... in a [logical-] function, and, if φx ≡ ψx, the substitution of φx for p in a [logical-] function gives the same truth-value to the truth-function as the substitution of ψx. Consequently there is no longer any reason to distinguish between functions classes, for we have, in virtue of the above,

φx ≡_x ψx .⊃. (x). φẑ = . ψẑ".

Observe the change to the equality "=" sign on the right. PM goes on to state that will continue to hang onto the notation "ẑ(φz)", but this is merely equivalent to φẑ, and this is a class. (all quotes: PM 1962:xxxix).

Consistency and criticisms

According to Carnap's "Logicist Foundations of Mathematics", Russell wanted a theory that could plausibly be said to derive all of mathematics from purely logical axioms. However, Principia Mathematica required, in addition to the basic axioms of type theory, three further axioms that seemed to not be true as mere matters of logic, namely the axiom of infinity, the axiom of choice, and the axiom of reducibility. Since the first two were existential axioms, Russell phrased mathematical statements depending on them as conditionals. But reducibility was required to be sure that the formal statements even properly express statements of real analysis, so that statements depending on it could not be reformulated as conditionals. Frank P. Ramsey tried to argue that Russell's ramification of the theory of types was unnecessary, so that reducibility could be removed, but these arguments seemed inconclusive.

Beyond the status of the axioms as logical truths, one can ask the following questions about any system such as PM:

• whether a contradiction could be derived from the axioms (the question of inconsistency), and
• whether there exists a mathematical statement which could neither be proven nor disproven in the system (the question of completeness).

Propositional logic itself was known to be consistent, but the same had not been established for Principia's axioms of set theory. Russell and Whitehead suspected that the system in PM is incomplete: for example, they pointed out that it does not seem powerful enough to show that the cardinal ℵ_ω exists. However, one can ask if some recursively axiomatizable extension of it is complete and consistent.

Gödel 1930, 1931

In 1930, Gödel's completeness theorem showed that first-order predicate logic itself was complete in a much weaker sense—that is, any sentence that is unprovable from a given set of axioms must actually be false in some model of the axioms. However, this is not the stronger sense of completeness desired for Principia Mathematica, since a given system of axioms (such as those of Principia Mathematica) may have many models, in some of which a given statement is true and in others of which that statement is false, so that the statement is left undecided by the axioms.
Gödel's incompleteness theorems cast unexpected light on these two related questions.

Gödel's first incompleteness theorem showed that no recursive extension of Principia could be both consistent and complete for arithmetic statements. (As mentioned above, Principia itself was already known to be incomplete for some non-arithmetic statements.) According to the theorem, within every sufficiently powerful recursive logical system (such as Principia), there exists a statement G that essentially reads, "The statement G cannot be proved." Such a statement is a sort of Catch-22: if G is provable, then it is false, and the system is therefore inconsistent; and if G is not provable, then it is true, and the system is therefore incomplete.

Gödel's second incompleteness theorem (1931) shows that no formal system extending basic arithmetic can be used to prove its own consistency. Thus, the statement "there are no contradictions in the Principia system" cannot be proven in the Principia system unless there are contradictions in the system (in which case it can be proven both true and false).

Wittgenstein 1919, 1939

By the second edition of PM, Russell had removed his axiom of reducibility to a new axiom (although he does not state it as such). Gödel 1944:126 describes it this way:

"This change is connected with the new axiom that functions can occur in propositions only "through their values", i.e., extensionally . . . [this is] quite unobjectionable even from the constructive standpoint . . . provided that quantifiers are always restricted to definite orders". This change from a quasi-intensional stance to a fully extensional stance also restricts predicate logic to the second order, i.e. functions of functions: "We can decide that mathematics is to confine itself to functions of functions which obey the above assumption" (PM 2nd Edition p. 401, Appendix C).

This new proposal resulted in a dire outcome. An "extensional stance" and restriction to a second-order predicate logic means that a propositional function extended to all individuals such as "All 'x' are blue" now has to list all of the 'x' that satisfy (are true in) the proposition, listing them in a possibly infinite conjunction: e.g. x₁ ∧ x₂ ∧ . . . ∧ x_n ∧ . . .. Ironically, this change came about as the result of criticism from Wittgenstein in his 1919 Tractatus Logico-Philosophicus. As described by Russell in the Preface to the 2nd edition of PM:

"There is another course, recommended by Wittgenstein† (†Tractatus Logico-Philosophicus, *5.54ff) for philosophical reasons. This is to assume that functions of propositions are always truth-functions, and that a function can only occur in a proposition through its values. . . . [Working through the consequences] it appears that everything in Vol. I remains true . . . the theory of inductive cardinals and ordinals survives; but it seems that the theory of infinite Dedekindian and well-ordered series largely collapses, so that irrationals, and real numbers generally, can no longer be adequately dealt with. Also Cantor's proof that 2ⁿ > n breaks down unless n is finite." (PM 2nd edition reprinted 1962:xiv, also cf new Appendix C).

In other words, the fact that an infinite list cannot realistically be specified means that the concept of "number" in the infinite sense (i.e. the continuum) cannot be described by the new theory proposed in PM Second Edition.

Wittgenstein in his Lectures on the Foundations of Mathematics, Cambridge 1939 criticised Principia on various grounds, such as:

• It purports to reveal the fundamental basis for arithmetic. However, it is our everyday arithmetical practices such as counting which are fundamental; for if a persistent discrepancy arose between counting and Principia, this would be treated as evidence of an error in Principia (e.g., that Principia did not characterise numbers or addition correctly), not as evidence of an error in everyday counting.
• The calculating methods in Principia can only be used in practice with very small numbers. To calculate using large numbers (e.g., billions), the formulae would become too long, and some short-cut method would have to be used, which would no doubt rely on everyday techniques such as counting (or else on non-fundamental and hence questionable methods such as induction). So again Principia depends on everyday techniques, not vice versa.

Wittgenstein did, however, concede that Principia may nonetheless make some aspects of everyday arithmetic clearer.

Gödel 1944

In his 1944 Russell's mathematical logic, Gödel offers a "critical but sympathetic discussion of the logicistic order of ideas":^[22]

"It is to be regretted that this first comprehensive and thorough-going presentation of a mathematical logic and the derivation of mathematics from it [is] so greatly lacking in formal precision in the foundations (contained in *1-*21 of Principia) that it represents in this respect a considerable step backwards as compared with Frege. What is missing, above all, is a precise statement of the syntax of the formalism. Syntactical considerations are omitted even in cases where they are necessary for the cogency of the proofs . . . The matter is especially doubtful for the rule of substitution and of replacing defined symbols by their definiens . . . it is chiefly the rule of substitution which would have to be proved" (Gödel 1944:124)^[23]

Contents

Part I Mathematical logic. Volume I ✸1 to ✸43

This section describes the propositional and predicate calculus, and gives the basic properties of classes, relations, and types.

Part II Prolegomena to cardinal arithmetic. Volume I ✸50 to ✸97

This part covers various properties of relations, especially those needed for cardinal arithmetic.

Part III Cardinal arithmetic. Volume II ✸100 to ✸126

This covers the definition and basic properties of cardinals. A cardinal is defined to be an equivalence class of similar classes (as opposed to ZFC, where a cardinal is a special sort of von Neumann ordinal). Each type has its own collection of cardinals associated with it, and there is a considerable amount of bookkeeping necessary for comparing cardinals of different types. PM define addition, multiplication and exponentiation of cardinals, and compare different definitions of finite and infinite cardinals. ✸120.03 is the Axiom of infinity.

Part IV Relation-arithmetic. Volume II ✸150 to ✸186

A "relation-number" is an equivalence class of isomorphic relations. PM defines analogues of addition, multiplication, and exponentiation for arbitrary relations. The addition and multiplication is similar to the usual definition of addition and multiplication of ordinals in ZFC, though the definition of exponentiation of relations in PM is not equivalent to the usual one used in ZFC.

Part V Series. Volume II ✸200 to ✸234 and volume III ✸250 to ✸276

This covers series, which is PM's term for what is now called a totally ordered set. In particular it covers complete series, continuous functions between series with the order topology (though of course they do not use this terminology), well-ordered series, and series without "gaps" (those with a member strictly between any two given members).

Part VI Quantity. Volume III ✸300 to ✸375

This section constructs the ring of integers, the fields of rational and real numbers, and "vector-families", which are related to what are now called torsors over abelian groups.

Comparison with set theory

This section compares the system in PM with the usual mathematical foundations of ZFC. The system of PM is roughly comparable in strength with Zermelo set theory (or more precisely a version of it where the axiom of separation has all quantifiers bounded).

• The system of propositional logic and predicate calculus in PM is essentially the same as that used now, except that the notation and terminology has changed.
• The most obvious difference between PM and set theory is that in PM all objects belong to one of a number of disjoint types. This means that everything gets duplicated for each (infinite) type: for example, each type has its own ordinals, cardinals, real numbers, and so on. This results in a lot of bookkeeping to relate the various types with each other.
• In ZFC functions are normally coded as sets of ordered pairs. In PM functions are treated rather differently. First of all, "function" means "propositional function", something taking values true or false. Second, functions are not determined by their values: it is possible to have several different functions all taking the same values (for example, one might regard 2x+2 and 2(x+1) as different functions on grounds that the computer programs for evaluating them are different). The functions in ZFC given by sets of ordered pairs correspond to what PM call "matrices", and the more general functions in PM are coded by quantifying over some variables. In particular PM distinguishes between functions defined using quantification and functions not defined using quantification, whereas ZFC does not make this distinction.
• PM has no analogue of the axiom of replacement, though this is of little practical importance as this axiom is used very little in mathematics outside set theory.
• PM emphasizes relations as a fundamental concept, whereas in current mathematical practice it is functions rather than relations that are treated as more fundamental; for example, category theory emphasizes morphisms or functions rather than relations. (However, there is an analogue of categories called allegories that models relations rather than functions, and is quite similar to the type system of PM.)
• In PM, cardinals are defined as classes of similar classes, whereas in ZFC cardinals are special ordinals. In PM there is a different collection of cardinals for each type with some complicated machinery for moving cardinals between types, whereas in ZFC there is only 1 sort of cardinal. Since PM does not have any equivalent of the axiom of replacement, it is unable to prove the existence of cardinals greater than ℵ_ω.
• In PM ordinals are treated as equivalence classes of well-ordered sets, and as with cardinals there is a different collection of ordinals for each type. In ZFC there is only one collection of ordinals, usually defined as von Neumann ordinals. One strange quirk of PM is that they do not have an ordinal corresponding to 1, which causes numerous unnecessary complications in their theorems. The definition of ordinal exponentiation α^β in PM is not equivalent to the usual definition in ZFC and has some rather undesirable properties: for example, it is not continuous in β and is not well ordered (so is not even an ordinal).
• The constructions of the integers, rationals and real numbers in ZFC have been streamlined considerably over time since the constructions in PM.

Differences between editions

Apart from corrections of misprints, the main text of PM is unchanged between the first and second editions. In the second edition volumes 2 and 3 are essentially unchanged apart from a change of page numbering, but volume 1 has five new additions:

• A 54-page introduction by Russell describing the changes they would have made had they had more time and energy. The main change he suggests is the removal of the controversial axiom of reducibility, though he admits that he knows no satisfactory substitute for it. He also seems more favorable to the idea that a function should be determined by its values (as is usual in current mathematical practice).
• Appendix A, numbered as *8, 15 pages about the Sheffer stroke.
• Appendix B, numbered as *89, discussing induction without the axiom of reducibility
• Appendix C, 8 pages discussing propositional functions
• An 8-page list of definitions at the end, giving a much-needed index to the 500 or so notations used.

In 1962 Cambridge University Press published a shortened paperback edition containing parts of the second edition of volume 1: the new introduction, the main text up to *56, and appendices A and C.