Mechanical advantage

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Mechanical_advantage 

 

Mechanical advantage is a measure of the force amplification achieved by using a tool, mechanical device or machine system. The device preserves the input power and simply trades off forces against movement to obtain a desired amplification in the output force. The model for this is the law of the lever. Machine components designed to manage forces and movement in this way are called mechanisms. An ideal mechanism transmits power without adding to or subtracting from it. This means the ideal mechanism does not include a power source, is frictionless, and is constructed from rigid bodies that do not deflect or wear. The performance of a real system relative to this ideal is expressed in terms of efficiency factors that take into account departures from the ideal.

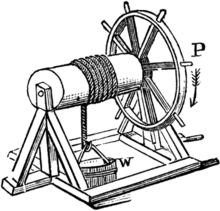
Lever

The lever is a movable bar that pivots on a fulcrum attached to or positioned on or across a fixed point. The lever operates by applying forces at different distances from the fulcrum, or pivot. The location of the fulcrum determines a lever's class. Where a lever rotates, continuously, it functions as a rotary 2nd-class lever. The motion of the lever's end-point describes a fixed orbit, where mechanical energy can be exchanged. (see a hand-crank as an example.)

In modern times, this kind of rotary leverage is widely used; see a (rotary) 2nd-class lever; see gears, pulleys or friction drive, used in a mechanical power transmission scheme. It is common for mechanical advantage to be manipulated in a 'collapsed' form, via the use of more than one gear (a gearset). In such a gearset, gears having smaller radii and less inherent mechanical advantage are used. In order to make use of non-collapsed mechanical advantage, it is necessary to use a 'true length' rotary lever. See, also, the incorporation of mechanical advantage into the design of certain types of electric motors; one design is an 'outrunner'. 

As the lever pivots on the fulcrum, points farther from this pivot move faster than points closer to the pivot. The power into and out of the lever is the same, so must come out the same when calculations are being done. Power is the product of force and velocity, so forces applied to points farther from the pivot must be less than when applied to points closer in.

If a and b are distances from the fulcrum to points A and B and if force F_A applied to A is the input force and F_B exerted at B is the output, the ratio of the velocities of points A and B is given by a/b so the ratio of the output force to the input force, or mechanical advantage, is given by

$${\displaystyle MA={\frac {F_{b}}{F_{a}}}={\frac {a}{b}}.}$$

This is the law of the lever, which was proven by Archimedes using geometric reasoning. It shows that if the distance a from the fulcrum to where the input force is applied (point A) is greater than the distance b from fulcrum to where the output force is applied (point B), then the lever amplifies the input force. If the distance from the fulcrum to the input force is less than from the fulcrum to the output force, then the lever reduces the input force. Recognizing the profound implications and practicalities of the law of the lever, Archimedes has been famously attributed the quotation "Give me a place to stand and with a lever I will move the whole world."

The use of velocity in the static analysis of a lever is an application of the principle of virtual work.

Speed ratio

The requirement for power input to an ideal mechanism to equal power output provides a simple way to compute mechanical advantage from the input-output speed ratio of the system.

The power input to a gear train with a torque T_A applied to the drive pulley which rotates at an angular velocity of ω_A is P=T_Aω_A.

Because the power flow is constant, the torque T_B and angular velocity ω_B of the output gear must satisfy the relation

${\displaystyle P=T_{A}\omega _{A}=T_{B}\omega _{B},\!}$

which yields

${\displaystyle MA={\frac {T_{B}}{T_{A}}}={\frac {\omega _{A}}{\omega _{B}}}.}$

This shows that for an ideal mechanism the input-output speed ratio equals the mechanical advantage of the system. This applies to all mechanical systems ranging from robots to linkages.

Gear trains

Gear teeth are designed so that the number of teeth on a gear is proportional to the radius of its pitch circle, and so that the pitch circles of meshing gears roll on each other without slipping. The speed ratio for a pair of meshing gears can be computed from ratio of the radii of the pitch circles and the ratio of the number of teeth on each gear, its gear ratio. 

Two meshing gears transmit rotational motion.

 

The velocity v of the point of contact on the pitch circles is the same on both gears, and is given by

${\displaystyle v=r_{A}\omega _{A}=r_{B}\omega _{B},\!}$

where input gear A has radius r_A and meshes with output gear B of radius r_B, therefore,

${\displaystyle {\frac {\omega _{A}}{\omega _{B}}}={\frac {r_{B}}{r_{A}}}={\frac {N_{B}}{N_{A}}}.}$

where N_A is the number of teeth on the input gear and N_B is the number of teeth on the output gear.

The mechanical advantage of a pair of meshing gears for which the input gear has N_A teeth and the output gear has N_B teeth is given by

${\displaystyle MA={\frac {r_{B}}{r_{A}}}={\frac {N_{B}}{N_{A}}}.}$

This shows that if the output gear G_B has more teeth than the input gear G_A, then the gear train amplifies the input torque. And, if the output gear has fewer teeth than the input gear, then the gear train reduces the input torque. 

If the output gear of a gear train rotates more slowly than the input gear, then the gear train is called a speed reducer (Force multiplier). In this case, because the output gear must have more teeth than the input gear, the speed reducer will amplify the input torque.

Chain and belt drives

Mechanisms consisting of two sprockets connected by a chain, or two pulleys connected by a belt are designed to provide a specific mechanical advantage in power transmission systems.

The velocity v of the chain or belt is the same when in contact with the two sprockets or pulleys:

${\displaystyle v=r_{A}\omega _{A}=r_{B}\omega _{B},\!}$

where the input sprocket or pulley A meshes with the chain or belt along the pitch radius r_A and the output sprocket or pulley B meshes with this chain or belt along the pitch radius r_B,

therefore

${\displaystyle {\frac {\omega _{A}}{\omega _{B}}}={\frac {r_{B}}{r_{A}}}={\frac {N_{B}}{N_{A}}}.}$

where N_A is the number of teeth on the input sprocket and N_B is the number of teeth on the output sprocket. For a toothed belt drive, the number of teeth on the sprocket can be used. For friction belt drives the pitch radius of the input and output pulleys must be used.

The mechanical advantage of a pair of a chain drive or toothed belt drive with an input sprocket with N_A teeth and the output sprocket has N_B teeth is given by

${\displaystyle MA={\frac {T_{B}}{T_{A}}}={\frac {N_{B}}{N_{A}}}.}$

The mechanical advantage for friction belt drives is given by

${\displaystyle MA={\frac {T_{B}}{T_{A}}}={\frac {r_{B}}{r_{A}}}.}$

Chains and belts dissipate power through friction, stretch and wear, which means the power output is actually less than the power input, which means the mechanical advantage of the real system will be less than that calculated for an ideal mechanism. A chain or belt drive can lose as much as 5% of the power through the system in friction heat, deformation and wear, in which case the efficiency of the drive is 95%.

Example: bicycle chain drive

Mechanical advantage in different gears of a bicycle. Typical forces applied to the bicycle pedal and to the ground are shown, as are corresponding distances moved by the pedal and rotated by the wheel. Note that even in low gear the MA of a bicycle is less than 1.

 

Consider the 18-speed bicycle with 7 in (radius) cranks and 26 in (diameter) wheels. If the sprockets at the crank and at the rear drive wheel are the same size, then the ratio of the output force on the tire to the input force on the pedal can be calculated from the law of the lever to be

${\displaystyle MA={\frac {F_{B}}{F_{A}}}={\frac {7}{13}}=0.54.}$

Now, assume that the front sprockets have a choice of 28 and 52 teeth, and that the rear sprockets have a choice of 16 and 32 teeth. Using different combinations, we can compute the following speed ratios between the front and rear sprockets 

Speed ratios and total MA

	input (small)	input (large)	output (small)	output (large)	speed ratio	crank-wheel ratio	total MA
low speed	28	-	-	32	1.14	0.54	0.62
mid 1	-	52	-	32	0.62	0.54	0.33
mid 2	28	-	16	-	0.57	0.54	0.31
high speed	-	52	16	-	0.30	0.54	0.16

The ratio of the force driving the bicycle to the force on the pedal, which is the total mechanical advantage of the bicycle, is the product of the speed ratio (or teeth ratio of output sproket/input sproket) and the crank-wheel lever ratio.

Notice that in every case the force on the pedals is greater than the force driving the bicycle forward (in the illustration above, the corresponding backward-directed reaction force on the ground is indicated). This low mechanical advantage keeps the pedal crank speed low relative to the speed of the drive wheel, even in low gears.

Block and tackle

A block and tackle is an assembly of a rope and pulleys that is used to lift loads. A number of pulleys are assembled together to form the blocks, one that is fixed and one that moves with the load. The rope is threaded through the pulleys to provide mechanical advantage that amplifies that force applied to the rope.

In order to determine the mechanical advantage of a block and tackle system consider the simple case of a gun tackle, which has a single mounted, or fixed, pulley and a single movable pulley. The rope is threaded around the fixed block and falls down to the moving block where it is threaded around the pulley and brought back up to be knotted to the fixed block.

The mechanical advantage of a block and tackle equals the number of sections of rope that support the moving block; shown here it is 2, 3, 4, 5, and 6, respectively.

 

Let S be the distance from the axle of the fixed block to the end of the rope, which is A where the input force is applied. Let R be the distance from the axle of the fixed block to the axle of the moving block, which is B where the load is applied.

The total length of the rope L can be written as

${\displaystyle L=2R+S+K,\!}$

where K is the constant length of rope that passes over the pulleys and does not change as the block and tackle moves.

The velocities V_A and V_B of the points A and B are related by the constant length of the rope, that is

${\displaystyle {\dot {L}}=2{\dot {R}}+{\dot {S}}=0,}$

or

${\displaystyle {\dot {S}}=-2{\dot {R}}.}$

The negative sign shows that the velocity of the load is opposite to the velocity of the applied force, which means as we pull down on the rope the load moves up.

Let V_A be positive downwards and V_B be positive upwards, so this relationship can be written as the speed ratio

${\displaystyle {\frac {V_{A}}{V_{B}}}={\frac {\dot {S}}{-{\dot {R}}}}=2,}$

where 2 is the number of rope sections supporting the moving block.

Let F_A be the input force applied at A the end of the rope, and let F_B be the force at B on the moving block. Like the velocities F_A is directed downwards and F_B is directed upwards.

For an ideal block and tackle system there is no friction in the pulleys and no deflection or wear in the rope, which means the power input by the applied force F_AV_A must equal the power out acting on the load F_BV_B, that is

${\displaystyle F_{A}V_{A}=F_{B}V_{B}.\!}$

The ratio of the output force to the input force is the mechanical advantage of an ideal gun tackle system,

${\displaystyle MA={\frac {F_{B}}{F_{A}}}={\frac {V_{A}}{V_{B}}}=2.\!}$

This analysis generalizes to an ideal block and tackle with a moving block supported by n rope sections,

${\displaystyle MA={\frac {F_{B}}{F_{A}}}={\frac {V_{A}}{V_{B}}}=n.\!}$

This shows that the force exerted by an ideal block and tackle is n times the input force, where n is the number of sections of rope that support the moving block.

Efficiency

Mechanical advantage that is computed using the assumption that no power is lost through deflection, friction and wear of a machine is the maximum performance that can be achieved. For this reason, it is often called the ideal mechanical advantage (IMA). In operation, deflection, friction and wear will reduce the mechanical advantage. The amount of this reduction from the ideal to the actual mechanical advantage (AMA) is defined by a factor called efficiency, a quantity which is determined by experimentation.

As an example, using a block and tackle with six rope sections and a 600 lb load, the operator of an ideal system would be required to pull the rope six feet and exert 100 lb_F of force to lift the load one foot. Both the ratios F_out / F_in and V_in / V_out show that the IMA is six. For the first ratio, 100 lb_F of force input results in 600 lb_F of force out. In an actual system, the force out would be less than 600 pounds due to friction in the pulleys. The second ratio also yields a MA of 6 in the ideal case but a smaller value in the practical scenario; it does not properly account for energy losses such as rope stretch. Subtracting those losses from the IMA or using the first ratio yields the AMA.

Ideal mechanical advantage

The ideal mechanical advantage (IMA), or theoretical mechanical advantage, is the mechanical advantage of a device with the assumption that its components do not flex, there is no friction, and there is no wear. It is calculated using the physical dimensions of the device and defines the maximum performance the device can achieve.

The assumptions of an ideal machine are equivalent to the requirement that the machine does not store or dissipate energy; the power into the machine thus equals the power out. Therefore, the power P is constant through the machine and force times velocity into the machine equals the force times velocity out—that is,

${\displaystyle P=F_{in}v_{in}=F_{out}v_{out}.}$

The ideal mechanical advantage is the ratio of the force out of the machine (load) to the force into the machine (effort), or

${\displaystyle IMA={\frac {F_{out}}{F_{in}}}.}$

Applying the constant power relationship yields a formula for this ideal mechanical advantage in terms of the speed ratio:

${\displaystyle IMA={\frac {F_{out}}{F_{in}}}={\frac {v_{in}}{v_{out}}}.}$

The speed ratio of a machine can be calculated from its physical dimensions. The assumption of constant power thus allows use of the speed ratio to determine the maximum value for the mechanical advantage.

Actual mechanical advantage

The actual mechanical advantage (AMA) is the mechanical advantage determined by physical measurement of the input and output forces. Actual mechanical advantage takes into account energy loss due to deflection, friction, and wear.

The AMA of a machine is calculated as the ratio of the measured force output to the measured force input,

${\displaystyle AMA={\frac {F_{out}}{F_{in}}},}$

where the input and output forces are determined experimentally.

The ratio of the experimentally determined mechanical advantage to the ideal mechanical advantage is the mechanical efficiency η of the machine,

${\displaystyle \eta ={\frac {AMA}{IMA}}.}$

Wheel and axle

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Wheel_and_axle 

 

The windlass is a well-known application of the wheel and axle.

The wheel and axle is a machine consisting of a wheel attached to a smaller axle so that these two parts rotate together in which a force is transferred from one to the other. A hinge or bearing supports the axle, allowing rotation. It can amplify force; a small force applied to the periphery of the large wheel can move a larger load attached to the axle.

The wheel and axle can be viewed as a version of the lever, with a drive force applied tangentially to the perimeter of the wheel and a load force applied to the axle, respectively, that are balanced around the hinge which is the fulcrum. The mechanical advantage of the wheel and axle is the ratio of the distances from the fulcrum to the applied loads, or what is the same thing the ratio of the diameter of the wheel and axle. A major application is in wheeled vehicles, in which the wheel and axle are used to reduce friction of the moving vehicle with the ground. Other examples of devices which use the wheel and axle are capstans, belt drives and gears.

Capstan bars inserted into the capstan provide the mechanical advantage of a wheel and axle to lift an anchor

 

Turning a doorknob rotates the spindle which moves the latch.

 

Waterwheel driving a rope winch to lift loads in medieval mining

 

Ljubljana Marshes Wheel with axle is oldest wooden wheel yet discovered dating to Copper Age (approx. 5,150 BP)

History

The Halaf culture of 6500–5100 BCE has been credited with the earliest depiction of a wheeled vehicle, but this is doubtful as there is no evidence of Halafians using either wheeled vehicles or even pottery wheels.

One of the first applications of the wheel to appear was the potter's wheel, used by prehistoric cultures to fabricate clay pots. The earliest type, known as "tournettes" or "slow wheels", were known in the Middle East by the 5th millennium BCE. One of the earliest examples was discovered at Tepe Pardis, Iran, and dated to 5200–4700 BCE. These were made of stone or clay and secured to the ground with a peg in the center, but required significant effort to turn. True potter's wheels, which are freely-spinning and have a wheel and axle mechanism, were developed in Mesopotamia (Iraq) by 4200–4000 BCE. The oldest surviving example, which was found in Ur (modern day Iraq), dates to approximately 3100 BCE.

Evidence of wheeled vehicles appeared by the late 4th millennium BCE. Depictions of wheeled wagons found on clay tablet pictographs at the Eanna district of Uruk, in the Sumerian civilization of Mesopotamia, are dated between 3700–3500 BCE. In the second half of the 4th millennium BCE, evidence of wheeled vehicles appeared near-simultaneously in the Northern Caucasus (Maykop culture) and Eastern Europe (Cucuteni–Trypillian culture). Depictions of a wheeled vehicle appeared between 3500 and 3350 BCE in the Bronocice clay pot excavated in a Funnelbeaker culture settlement in southern Poland. In nearby Olszanica, a 2.2 m wide door was constructed (2.2 wide doors were constructed) for wagon entry; this barn was 40 m long and had 3 doors. Surviving evidence of a wheel–axle combination, from Stare Gmajne near Ljubljana in Slovenia (Ljubljana Marshes Wooden Wheel), is dated within two standard deviations to 3340–3030 BCE, the axle to 3360–3045 BCE. Two types of early Neolithic European wheel and axle are known; a circumalpine type of wagon construction (the wheel and axle rotate together, as in Ljubljana Marshes Wheel), and that of the Baden culture in Hungary (axle does not rotate). They both are dated to c. 3200–3000 BCE. Historians believe that there was a diffusion of the wheeled vehicle from the Near East to Europe around the mid-4th millennium BCE.

An early example of a wooden wheel and its axle was found in 2002 at the Ljubljana Marshes some 20 km south of Ljubljana, the capital of Slovenia. According to radiocarbon dating, it is between 5,100 and 5,350 years old. The wheel was made of ash and oak and had a radius of 70 cm and the axle was 120 cm long and made of oak.

In Roman Egypt, Hero of Alexandria identified the wheel and axle as one of the simple machines used to lift weights. This is thought to have been in the form of the windlass which consists of a crank or pulley connected to a cylindrical barrel that provides mechanical advantage to wind up a rope and lift a load such as a bucket from the well.

The wheel and axle was identified as one of six simple machines by Renaissance scientists, drawing from Greek texts on technology.

Mechanical advantage

The simple machine called a wheel and axle refers to the assembly formed by two disks, or cylinders, of different diameters mounted so they rotate together around the same axis.The thin rod which needs to be turned is called the axle and the wider object fixed to the axle, on which we apply force is called the wheel. A tangential force applied to the periphery of the large disk can exert a larger force on a load attached to the axle, achieving mechanical advantage. When used as the wheel of a wheeled vehicle the smaller cylinder is the axle of the wheel, but when used in a windlass, winch, and other similar applications (see medieval mining lift to right) the smaller cylinder may be separate from the axle mounted in the bearings. It cannot be used separately.

Assuming the wheel and axle does not dissipate or store energy, that is it has no friction or elasticity, the power input by the force applied to the wheel must equal the power output at the axle. As the wheel and axle system rotates around its bearings, points on the circumference, or edge, of the wheel move faster than points on the circumference, or edge, of the axle. Therefore, a force applied to the edge of the wheel must be less than the force applied to the edge of the axle, because power is the product of force and velocity.

Let a and b be the distances from the center of the bearing to the edges of the wheel A and the axle B. If the input force F_A is applied to the edge of the wheel A and the force F_B at the edge of the axle B is the output, then the ratio of the velocities of points A and B is given by a/b, so the ratio of the output force to the input force, or mechanical advantage, is given by

${\displaystyle MA={\frac {F_{B}}{F_{A}}}={\frac {a}{b}}.}$

The mechanical advantage of a simple machine like the wheel and axle is computed as the ratio of the resistance to the effort. The larger the ratio the greater the multiplication of force (torque) created or distance achieved. By varying the radii of the axle and/or wheel, any amount of mechanical advantage may be gained. In this manner, the size of the wheel may be increased to an inconvenient extent. In this case a system or combination of wheels (often toothed, that is, gears) are used. As a wheel and axle is a type of lever, a system of wheels and axles is like a compound lever.

Ideal mechanical advantage

The mechanical advantage of a wheel and axle with no friction is called the ideal mechanical advantage (IMA). It is calculated with the following formula:

${\displaystyle \mathrm {IMA} ={F_{\text{out}} \over F_{\text{in}}}={\mathrm {Radius} _{\text{wheel}} \over \mathrm {Radius} _{\text{axle}}}}$

Actual mechanical advantage

All actual wheels have friction, which dissipates some of the power as heat. The actual mechanical advantage (AMA) of a wheel and axle is calculated with the following formula:

${\displaystyle \mathrm {AMA} ={F_{\text{out}} \over F_{\text{in}}}=\eta \cdot {\mathrm {Radius} _{\text{wheel}} \over \mathrm {Radius} _{\text{axle}}}}$

where

${\displaystyle \eta ={P_{\text{out}} \over P_{\text{in}}}}$ is the efficiency of the wheel, the ratio of power output to power input

Tool

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Tool 

Display of agricultural tools

 

A modern toolbox

A tool is an object used to extend the ability of an individual to modify features of the surrounding environment. Although many animals use simple tools, only human beings, whose use of stone tools dates back hundreds of millennia, have been observed using tools to make other tools. The set of tools required to perform different tasks that are part of the same activity is called gear or equipment.

While one may apply the term tool loosely to many things that are means to an end (e.g., a fork), strictly speaking an object is a tool only if, besides being constructed to be held, it is also made of a material that allows its user to apply to it various degrees of force. If repeated use wears part of the tool down (like a knife blade), it may be possible to restore it; if it wears the tool out or breaks it, the tool must be replaced. Thus tool falls under the taxonomic category implement, and is on the same taxonomic rank as instrument, utensil, device, or ware.

History

Prehistoric stone tools over 10,000 years old, found in Les Combarelles cave, France

 

Carpentry tools recovered from the wreck of a 16th-century sailing ship, the Mary Rose. From the top, a mallet, brace, plane, handle of a T-auger, handle of a gimlet, possible handle of a hammer, and rule.

 

Stone and metal knives

 

An upholstery regulator

Anthropologists believe that the use of tools was an important step in the evolution of mankind. Because tools are used extensively by both humans and wild chimpanzees, it is widely assumed that the first routine use of tools took place prior to the divergence between the two species. These early tools, however, were likely made of perishable materials such as sticks, or consisted of unmodified stones that cannot be distinguished from other stones as tools.

Stone artifacts only date back to about 2.5 million years ago. However, a 2010 study suggests the hominin species Australopithecus afarensis ate meat by carving animal carcasses with stone implements. This finding pushes back the earliest known use of stone tools among hominins to about 3.4 million years ago.

Finds of actual tools date back at least 2.6 million years in Ethiopia. One of the earliest distinguishable stone tool forms is the hand axe.

Up until recently, weapons found in digs were the only tools of “early man” that were studied and given importance. Now, more tools are recognized as culturally and historically relevant. As well as hunting, other activities required tools such as preparing food, “...nutting, leatherworking, grain harvesting and woodworking...” Included in this group are “flake stone tools".

Tools are the most important items that the ancient humans used to climb to the top of the food chain; by inventing tools, they were able to accomplish tasks that human bodies could not, such as using a spear or bow and arrow to kill prey, since their teeth were not sharp enough to pierce many animals' skins. “Man the hunter” as the catalyst for Hominin change has been questioned. Based on marks on the bones at archaeological sites, it is now more evident that pre-humans were scavenging off of other predators' carcasses rather than killing their own food.

Mechanical devices experienced a major expansion in their use in Ancient Greece and Ancient Rome with the systematic employment of new energy sources, especially waterwheels. Their use expanded through the Dark Ages with the addition of windmills.

Machine tools occasioned a surge in producing new tools in the industrial revolution. Advocates of nanotechnology expect a similar surge as tools become microscopic in size.

Functions

One can classify tools according to their basic functions:

• Cutting and edge tools, such as the knife, sickle, scythe, hatchet, and axe are wedge-shaped implements that produce a shearing force along a narrow face. Ideally, the edge of the tool needs to be harder than the material being cut or else the blade will become dulled with repeated use. But even resilient tools will require periodic sharpening, which is the process of removing deformation wear from the edge. Other examples of cutting tools include gouges and drill bits.
• Moving tools move large and tiny items. Many are levers which give the user a mechanical advantage. Examples of force-concentrating tools include the hammer which moves a nail or the maul which moves a stake. These operate by applying physical compression to a surface. In the case of the screwdriver, the force is rotational and called torque. By contrast, an anvil concentrates force on an object being hammered by preventing it from moving away when struck. Writing implements deliver a fluid to a surface via compression to activate the ink cartridge. Grabbing and twisting nuts and bolts with pliers, a glove, a wrench, etc. likewise move items by applying torque (rotational force).
• Tools that enact chemical changes, including temperature and ignition, such as lighters and blowtorches.
• Guiding, measuring and perception tools include the ruler, glasses, set square, sensors, straightedge, theodolite, microscope, monitor, clock, phone, printer
• Shaping tools, such as molds, jigs, trowels.
• Fastening tools, such as welders, rivet guns, nail guns, or glue guns.
• Information and data manipulation tools, such as computers, IDE, spreadsheets

Some tools may be combinations of other tools. An alarm-clock is for example a combination of a measuring tool (the clock) and a perception tool (the alarm). This enables the alarm-clock to be a tool that falls outside of all the categories mentioned above.

There is some debate on whether to consider protective gear items as tools, because they do not directly help perform work, just protect the worker like ordinary clothing. They do meet the general definition of tools and in many cases are necessary for the completion of the work. Personal protective equipment includes such items as gloves, safety glasses, ear defenders and biohazard suits.

Simple machines

A simple machine is a mechanical device that changes the direction or magnitude of a force. In general, they are the simplest mechanisms that use mechanical advantage (also called leverage) to multiply force. The six classical simple machines which were defined by Renaissance scientists are:

• Lever
• Wheel and axle
• Pulley
• Inclined plane
• Wedge
• Screw

Tool substitution

Often, by design or coincidence, a tool may share key functional attributes with one or more other tools. In this case, some tools can substitute for other tools, either as a makeshift solution or as a matter of practical efficiency. "One tool does it all" is a motto of some importance for workers who cannot practically carry every specialized tool to the location of every work task; such as a carpenter who does not necessarily work in a shop all day and needs to do jobs in a customer's house. Tool substitution may be divided broadly into two classes: substitution "by-design", or "multi-purpose", and substitution as makeshift. Substitution "by-design" would be tools that are designed specifically to accomplish multiple tasks using only that one tool.

Substitution as makeshift is when human ingenuity comes into play and a tool is used for its unintended purpose such as a mechanic using a long screw driver to separate a cars control arm from a ball joint instead of using a tuning fork. In many cases, the designed secondary functions of tools are not widely known. As an example of the former, many wood-cutting hand saws integrate a carpenter's square by incorporating a specially shaped handle that allows 90° and 45° angles to be marked by aligning the appropriate part of the handle with an edge and scribing along the back edge of the saw. The latter is illustrated by the saying "All tools can be used as hammers." Nearly all tools can be used to function as a hammer, even though very few tools are intentionally designed for it and even fewer work as well as the original.

Tools are also often used to substitute for many mechanical apparatuses, especially in older mechanical devices. In many cases a cheap tool could be used to occupy the place of a missing mechanical part. A window roller in a car could easily be replaced with a pair of vise-grips or regular pliers. A transmission shifter or ignition switch would be able to be replaced with a screw-driver. Again, these would be considered tools that are being used for their unintended purposes, substitution as makeshift. Tools such as a rotary tool would be considered the substitution "by-design", or "multi-purpose". This class of tools allows the use of one tool that has at least two different capabilities. "Multi-purpose" tools are basically multiple tools in one device/tool. Tools such as this are often power tools that come with many different attachments like a rotary tool does, so you could say that a power drill is a "multi-purpose" tool because you can do more than just one thing with a power drill.

Multi-use tools

Bicycle multi-tool

 

A multi-tool is a hand tool that incorporates several tools into a single, portable device; the Swiss army knife represents one of the earliest examples. Other tools have a primary purpose but also incorporate other functionality – for example, lineman's pliers incorporate a gripper and cutter, and are often used as a hammer; and some hand saws incorporate a carpenter's square in the right-angle between the blade's dull edge and the saw's handle. This would also be the category of "multi-purpose" tools, since they are also multiple tools in one (multi-use and multi-purpose can be used interchangeably – compare hand axe). These types of tools were specifically made to catch the eye of many different craftsman who traveled to do their work. To these workers these types of tools were revolutionary because they were one tool or one device that could do several different things. With this new revolution of tools the traveling craftsman would not have to carry so many tools with them to job sites, in that their space would be limited to the vehicle or to the beast of burden they were driving. Multi-use tools solve the problem of having to deal with many different tools.

Use by other animals

A Bonobo at the San Diego Zoo "fishing" for termites

Observation has confirmed that a number of species can use tools including monkeys, apes, elephants, several birds, and sea otters. Philosophers originally thought that only humans had the ability to make tools, until zoologists observed birds and apes making tools. Now the unique relationship of humans with tools is considered to be that we are the only species that uses tools to make other tools.

Recently, a Visayan warty pig was observed using a stick in digging a hole on the ground at a French zoo.

Tool metaphors

A telephone is a communication tool that interfaces between two people engaged in conversation at one level. It also interfaces between each user and the communication network at another level. It is in the domain of media and communications technology that a counter-intuitive aspect of our relationships with our tools first began to gain popular recognition. Marshall McLuhan famously said "We shape our tools. And then our tools shape us." McLuhan was referring to the fact that our social practices co-evolve with our use of new tools and the refinements we make to existing tools.

Fedspeak

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Fedspeak 

 

In monetary policy of the United States, the term Fedspeak (also known as Greenspeak) is what Alan Blinder called "a turgid dialect of English" used by Federal Reserve Board chairmen in making wordy, vague, and ambiguous statements. The strategy, which was used most prominently by Alan Greenspan, was used to prevent financial markets from overreacting to the chairman's remarks. The coinage is an intentional parallel to Newspeak of Nineteen Eighty-Four, a novel by George Orwell.
Fedspeak when used by Alan Greenspan is often called Greenspeak. An alternative definition of Greenspeak is "the coded and careful language employed by U.S. Federal Reserve Board Chairman Alan Greenspan."

Edwin le Heron and Emmanuel Carre state that "Nowadays, 'Fedspeak' (Bernanke, 2004) means clear and extensive communication of the Fed's action." Chairman Ben Bernanke and Chairwoman Yellen have effected a major change in Fed communication policy departing from the obfuscation that characterized the previous three decades. In 2014 a new detailed level of Fed communication was dubbed Fedspeak 3.0. In 2018, Chairman Jerome Powell would begin press conferences with a summary statement in plain English, in contrast to his predecessors who would read lengthy prepared statements loaded with monetary policy jargon.

Origin

The notion of fed speak originated from the fact that financial markets placed a heavy value on the statements made by Federal Reserve governors, which could in turn lead to a self-fulfilling prophecy. To prevent this, the governors developed a language, termed Fedspeak, in which ambiguous and cautious statements were made to purposefully obscure and detract meaning from the statement.

Though previous "Fed" chairmen Arthur Burns and Paul Volcker were known for blowing smoke, both literally and figuratively, when appearing before Congress, Alan Greenspan is credited with making Fedspeak a "high-art". It is unclear whether the term Fedspeak was used widely prior to Greenspan, but with historical hindsight the modern term could be used to describe Burns's and Volcker's method.

Usage by Alan Greenspan

He used to take pride in the resulting obfuscation—even characterizing his own way of communicating as 'mumbling with great incoherence'. In a famous incident, he once told a US senator who claimed to have understood what the famously obscurantist chairman had just said, "in that case, I must have misspoken".

— How do central banks talk?

Although it was originally believed by some that Alan Greenspan, who is generally credited for popularizing Fedspeak, may have used such language unintentionally, he revealed in his 2007 book The Age of Turbulence, that the method of avoiding the issues directly when a clear message was not desired was indeed intentional. Greenspan states that the confusion, which often resulted in conflicting interpretations, was used to prevent unintended jolts to the markets as confusing statements were typically ignored.

He noted that he came upon the dialect while at the Fed: "What I've learned at the Federal Reserve is a new language which is called 'Fed-speak'. You soon learn to mumble with great incoherence."

In an interview with 60 Minutes's Lesley Stahl on September 16, 2007, Stahl stated how "In public, Greenspan was inscrutable whenever congress asked about interest rates. He resorted to an indecipherable delphic dialect known as fedspeak" to which Greenspan responded that "I would engage in some form of syntax destruction which sounded as though I were answering the question, but in fact, had not." When Stahl noted that Greenspan's responses were "impenetrably profound" and that this resulted in "two newspapers getting opposing headlines coming out of the same hearing", Greenspan responded that "I succeeded".

In an interview with CNBC's Maria Bartiromo on September 17, 2007, when asked to describe Fedspeak, Greenspan described it as:

It's a—a language of purposeful obfuscation to avoid certain questions coming up, which you know you can't answer, and saying—'I will not answer or basically no comment is, in fact, an answer.' So, you end up with when, say, a Congressman asks you a question, and don't wanna say, 'No comment', or 'I won't answer', or something like that. So, I proceed with four or five sentences which get increasingly obscure. The Congressman thinks I answered the question and goes onto the next one.

In an interview with BusinessWeek in August 2012, when asked "about practicing the art of constructive ambiguity", Greenspan replied:

As Fed chairman, every time I expressed a view, I added or subtracted 10 basis points from the credit market. That was not helpful. But I nonetheless had to testify before Congress. On questions that were too market-sensitive to answer, 'no comment' was indeed an answer. And so you construct what we used to call Fed-speak. I would hypothetically think of a little plate in front of my eyes, which was the Washington Post, the following morning's headline, and I would catch myself in the middle of a sentence. Then, instead of just stopping, I would continue on resolving the sentence in some obscure way which made it incomprehensible. But nobody was quite sure I wasn't saying something profound when I wasn't. And that became the so-called Fed-speak which I became an expert on over the years. It's a self-protection mechanism ... when you're in an environment where people are shooting questions at you, and you've got to be very careful about the nuances of what you're going to say and what you don't say.

Examples of Greenspeak

The Fed has a language all its own, and unfortunately, the folks over at Rosetta Stone have yet to create a program to help laypeople understand what the hell the fed is talking about.

— Ron Insana

As of 2011, the Federal Reserve Bank of Dallas website still maintains a "Greenspeak" page with dozens of excerpts from Greenspan's past statements as head of the Federal Reserve Bank. Each quotation has a pointer to its full context in his speech, and is posted without commentary or interpretation.

The members of the Board of Governors and the Reserve Bank presidents foresee an implicit strengthening of activity after the current rebalancing is over, although the central tendency of their individual forecasts for real GDP still shows a substantial slowdown, on balance, for the year as a whole.

— Alan Greenspan, Testimony from the Federal Reserve Board's semiannual monetary policy report to the Congress before the Committee on Banking, Housing, and Urban Affairs, U.S. Senate on February 13, 2001

Risk takers have been encouraged by a perceived increase in economic stability to reach out to more distant time horizons. But long periods of relative stability often engender unrealistic expectations of it[s] permanence and, at times, may lead to financial excess and economic stress.

— Alan Greenspan, testimony on his 35th appearance before the Financial Services Committee of the US House of Representatives on July 20, 2005

Clearly, sustained low inflation implies less uncertainty about the future, and lower risk premiums imply higher prices of stocks and other earning assets. We can see that in the inverse relationship exhibited by price/earnings ratios and the rate of inflation in the past. But how do we know when irrational exuberance has unduly escalated asset values, which then become subject to unexpected and prolonged contractions as they have in Japan over the past decade?

— Alan Greenspan, "The Challenge of Central Banking in a Democratic Society", 1996-12-05 

I would generally expect that today in Washington DC the probability of changes in the weather is highly uncertain, but we are monitoring the data in such a way that we will be able to update people on changes that are important.

— Alan Greenspan, Greenspan describing the weather in response to a question by Owen Bennett-Jones on BBC's The Interview (October 2007)

Other usage

In the 2010s, the Federal Reserve Open Market rate-setting committee (FOMC) began publishing dot plots to tabulate all individual committee member projections of target interest rates in a single graphic. In 2016, the president of the St. Louis Fed James Bullard began a movement away from the dot plot exercise, citing a gap of opinion between market economists and FOMC members. As of 2018, the FOMC has continued to publish dot plots in its economic projections, detailing the variety of opinions of the committee members for the "appropriate target range for the federal funds rate" in future years.

Commentary

The University of Virginia Writing Program Instructor Site offers some selected quotations from Greenspan, with a suggestion that students be given writing exercise assignments of clarifying their expression of ideas.

A public relations firm cites an example of "Greenspeak" as the statement of one of the "master practitioners of creative ambiguity over the years". The brief essay mentions two other master practitioners of obfuscation, Hubert H. Humphrey and Casey Stengel. The overall tone of the essay is one of awed admiration for a sometimes-necessary skill in obscurantism. In closing, the writer notes that, "As professional performers say, to deliberately sing off-key requires a highly skilled singer."