Stern–Gerlach experiment

From Wikipedia, the free encyclopedia

Stern–Gerlach experiment: Silver atoms travelling through an inhomogeneous magnetic field, and being deflected up or down depending on their spin; (1) furnace, (2) beam of silver atoms, (3) inhomogeneous magnetic field, (4) classically expected result, (5) observed result

 

The Stern–Gerlach experiment demonstrated that the spatial orientation of angular momentum is quantized. Thus an atomic-scale system was shown to have intrinsically quantum properties. In the original experiment, silver atoms were sent through a spatially varying magnetic field, which deflected them before they struck a detector screen, such as a glass slide. Particles with non-zero magnetic moment are deflected, due to the magnetic field gradient, from a straight path. The screen reveals discrete points of accumulation, rather than a continuous distribution, owing to their quantized spin. Historically, this experiment was decisive in convincing physicists of the reality of angular-momentum quantization in all atomic-scale systems.

After its conception by Otto Stern in 1921, the experiment was first successfully conducted by Walther Gerlach in early 1922.

Description

Play media

Video explaining quantum spin versus classical magnet in the Stern–Gerlach experiment

The Stern–Gerlach experiment involves sending a beam of silver atoms through an inhomogeneous magnetic field and observing their deflection.

The results show that particles possess an intrinsic angular momentum that is closely analogous to the angular momentum of a classically spinning object, but that takes only certain quantized values. Another important result is that only one component of a particle's spin can be measured at one time, meaning that the measurement of the spin along the z-axis destroys information about a particle's spin along the x and y axis.

The experiment is normally conducted using electrically neutral particles such as silver atoms. This avoids the large deflection in the path of a charged particle moving through a magnetic field and allows spin-dependent effects to dominate.

If the particle is treated as a classical spinning magnetic dipole, it will precess in a magnetic field because of the torque that the magnetic field exerts on the dipole (see torque-induced precession). If it moves through a homogeneous magnetic field, the forces exerted on opposite ends of the dipole cancel each other out and the trajectory of the particle is unaffected. However, if the magnetic field is inhomogeneous then the force on one end of the dipole will be slightly greater than the opposing force on the other end, so that there is a net force which deflects the particle's trajectory. If the particles were classical spinning objects, one would expect the distribution of their spin angular momentum vectors to be random and continuous. Each particle would be deflected by an amount proportional to its magnetic moment, producing some density distribution on the detector screen. Instead, the particles passing through the Stern–Gerlach apparatus are deflected either up or down by a specific amount. This was a measurement of the quantum observable now known as spin angular momentum, which demonstrated possible outcomes of a measurement where the observable has a discrete set of values or point spectrum.

Although some discrete quantum phenomena, such as atomic spectra, were observed much earlier, the Stern–Gerlach experiment allowed scientists to directly observe separation between discrete quantum states for the first time in the history of science.

Theoretically, quantum angular momentum of any kind has a discrete spectrum, which is sometimes briefly expressed as "angular momentum is quantized".

Experiment using particles with +​¹⁄₂ or −​¹⁄₂ spin

If the experiment is conducted using charged particles like electrons, there will be a Lorentz force that tends to bend the trajectory in a circle. This force can be cancelled by an electric field of appropriate magnitude oriented transverse to the charged particle's path.

Spin values for fermions

Electrons are spin-​¹⁄₂ particles. These have only two possible spin angular momentum values measured along any axis, ${\displaystyle +{\frac {\hbar }{2}}}$ or ${\displaystyle -{\frac {\hbar }{2}}}$, a purely quantum mechanical phenomenon. Because its value is always the same, it is regarded as an intrinsic property of electrons, and is sometimes known as "intrinsic angular momentum" (to distinguish it from orbital angular momentum, which can vary and depends on the presence of other particles). If one measures the spin along a vertical axis, electrons are described as "spin up" or "spin down", based on the magnetic moment pointing up or down, respectively.

To mathematically describe the experiment with spin ${\displaystyle +{\frac {1}{2}}}$ particles, it is easiest to use Dirac's bra–ket notation. As the particles pass through the Stern–Gerlach device, they are deflected either up or down, and observed by the detector which resolves to either spin up or spin down. These are described by the angular momentum quantum number ${\displaystyle j}$, which can take on one of the two possible allowed values, either ${\displaystyle +{\frac {\hbar }{2}}}$ or ${\displaystyle -{\frac {\hbar }{2}}}$. The act of observing (measuring) the momentum along the ${\displaystyle z}$ axis corresponds to the operator ${\displaystyle J_{z}}$. In mathematical terms, the initial state of the particles is

${\displaystyle |\psi \rangle =c_{1}\left|\psi _{j=+{\frac {\hbar }{2}}}\right\rangle +c_{2}\left|\psi _{j=-{\frac {\hbar }{2}}}\right\rangle }$

where constants ${\displaystyle c_{1}}$ and ${\displaystyle c_{2}}$ are complex numbers. This initial state spin can point in any direction. The squares of the absolute values ${\displaystyle |c_{1}|^{2}}$ and ${\displaystyle |c_{2}|^{2}}$ determine the probabilities that for a system in the initial state ${\displaystyle |\psi \rangle }$ one of the two possible values of ${\displaystyle j}$ is found after the measurement is made. The constants ${\displaystyle c_{1}}$ and ${\displaystyle c_{2}}$ must also be normalized in order that the probability of finding either one of the values be unity, that is we must ensure that ${\displaystyle |c_{1}|^{2}+|c_{2}|^{2}=1}$. However, this information is not sufficient to determine the values of ${\displaystyle c_{1}}$ and ${\displaystyle c_{2}}$, because they are complex numbers. Therefore, the measurement yields only the squared magnitudes of the constants, which are interpreted as probabilities.

Sequential experiments

If we link multiple Stern–Gerlach apparatuses (the rectangles containing S-G), we can clearly see that they do not act as simple selectors, i.e. filtering out particles with one of the states (pre-existing to the measurement) and blocking the others. Instead they alter the state by observing it (as in light polarization). In the figure below, x and z name the directions of the (inhomogenous) magnetic field, with the x-z-plane being orthogonal to the particle beam. In the three S-G systems shown below, the cross-hatched squares denote the blocking of a given output, i.e. each of the S-G systems with a blocker allows only particles with one of two states to enter the next S-G apparatus in the sequence.

Exp. 1 - Notice that no z- neutrons are detected at the second S-G analyzer

Experiment 1

The top illustration shows that when a second, identical, S-G apparatus is placed at the exit of the z+ beam resulting of the first apparatus, only z+ is seen in the output of the second apparatus. This result is expected since all neutrons at this point are expected to have z+ spin, as only the z+ beam from the first apparatus entered the second apparatus.

Exp. 2 - The z-spin is known, now measuring the x-spin.

Experiment 2

The middle system shows what happens when a different S-G apparatus is placed at the exit of the z+ beam resulting of the first apparatus, the second apparatus measuring the deflection of the beams on the x axis instead of the z axis. The second apparatus produces x+ and x- outputs. Now classically we would expect to have one beam with the x characteristic oriented + and the z characteristic oriented +, and another with the x characteristic oriented - and the z characteristic oriented +.

Exp. 3 - Neutrons thought to have only z+ spin are measured again, finding that the z-spin has been 'reset'.

Experiment 3

The bottom system contradicts that expectation. The output of the third apparatus which measures the deflection on the z axis again shows an output of z- as well as z+. Given that the input to the second S-G apparatus consisted only of z+, it can be inferred that a S-G apparatus must be altering the states of the particles that pass through it. This experiment can be interpreted to exhibit the uncertainty principle: since the angular momentum cannot be measured on two perpendicular directions at the same time, the measurement of the angular momentum on the x direction destroys the previous determination of the angular momentum in the z direction. That's why the third apparatus measures renewed z+ and z- beams like the x measurement really made a clean slate of the z+ output.

History

A plaque at the Frankfurt institute commemorating the experiment

The Stern–Gerlach experiment was conceived by Otto Stern in 1921 and performed by him and Walther Gerlach in Frankfurt in 1922. At the time, Stern was an assistant to Max Born at the University of Frankfurt's Institute for Theoretical Physics, and Gerlach was an assistant at the same university's Institute for Experimental Physics.

At the time of the experiment, the most prevalent model for describing the atom was the Bohr model, which described electrons as going around the positively charged nucleus only in certain discrete atomic orbitals or energy levels. Since the electron was quantized to be only in certain positions in space, the separation into distinct orbits was referred to as space quantization. The Stern–Gerlach experiment was meant to test the Bohr–Sommerfeld hypothesis that the direction of the angular momentum of a silver atom is quantized.

Note that the experiment was performed several years before Uhlenbeck and Goudsmit formulated their hypothesis of the existence of the electron spin. Even though the result of the Stern−Gerlach experiment has later turned out to be in agreement with the predictions of quantum mechanics for a spin-​¹⁄₂ particle, the experiment should be seen as a corroboration of the Bohr–Sommerfeld theory.

In 1927, T.E. Phipps and J.B. Taylor reproduced the effect using hydrogen atoms in their ground state, thereby eliminating any doubts that may have been caused by the use of silver atoms. However, in 1926 the non-relativistic Schrödinger equation had incorrectly predicted the magnetic moment of hydrogen to be zero in its ground state. To correct this problem Wolfgang Pauli introduced "by hand", so to speak, the 3 Pauli matrices which now bear his name, but which were later shown by Paul Dirac in 1928 to be intrinsic in his relativistic equation.

The experiment was first performed with an electromagnet that allowed the non-uniform magnetic field to be turned on gradually from a null value. When the field was null, the silver atoms were deposited as a single band on the detecting glass slide. When the field was made stronger, the middle of the band began to widen and eventually to split into two, so that the glass-slide image looked like a lip-print, with an opening in the middle, and closure at either end. In the middle, where the magnetic field was strong enough to split the beam into two, statistically half of the silver atoms had been deflected by the non-uniformity of the field.

Importance

The Stern–Gerlach experiment strongly influenced later developments in modern physics:

• In the decade that followed, scientists showed using similar techniques, that the nuclei of some atoms also have quantized angular momentum. It is the interaction of this nuclear angular momentum with the spin of the electron that is responsible for the hyperfine structure of the spectroscopic lines.
• In the 1930s, using an extended version of the Stern–Gerlach apparatus, Isidor Rabi and colleagues showed that by using a varying magnetic field, one can force the magnetic moment to go from one state to the other. The series of experiments culminated in 1937 when they discovered that state transitions could be induced using time varying fields or RF fields. The so-called Rabi oscillation is the working mechanism for the Magnetic Resonance Imaging equipment found in hospitals.
• Norman F. Ramsey later modified the Rabi apparatus to increase the interaction time with the field. The extreme sensitivity due to the frequency of the radiation makes this very useful for keeping accurate time, and it is still used today in atomic clocks.
• In the early sixties, Ramsey and Daniel Kleppner used a Stern–Gerlach system to produce a beam of polarized hydrogen as the source of energy for the hydrogen maser, which is still one of the most popular frequency standards.
• The direct observation of the spin is the most direct evidence of quantization in quantum mechanics.
• The Stern–Gerlach experiment has become a prototype for quantum measurement, demonstrating the observation of a single, real value (eigenvalue) of an initially unknown physical property. Entering the Stern-Gerlach magnet, the direction of the silver atom’s magnetic moment is indefinite, but it is observed to be either parallel, or anti-parallel to the direction of the magnetic field, B, at the exit of the magnet. Atoms with a magnetic moment parallel to B have been accelerated in that direction by the magnetic field gradient; those with anti-parallel moments were accelerated the opposite way. So, each atom traversing the magnet will strike the detector ((5) in the diagram) at just one of the two spots. According to quantum measurement theory, the wavefunction representing the atom’s magnetic moment is in a superposition of those two directions entering the magnet. A single, spin-direction eigenvalue is recorded when a momentum quantum is transferred, from the magnetic field, to the atom, initiating acceleration, and displacement, in that momentum direction.

Double-slit experiment

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Double-slit_experiment 

Photons or particles of matter (like an electron) produce a wave pattern when two slits are used

 

Light from a green laser passing through two slits 0.4mm wide and 0.1mm apart

In modern physics, the double-slit experiment is a demonstration that light and matter can display characteristics of both classically defined waves and particles; moreover, it displays the fundamentally probabilistic nature of quantum mechanical phenomena. This type of experiment was first performed, using light, by Thomas Young in 1801, as a demonstration of the wave behavior of light. At that time it was thought that light consisted of either waves or particles. With the beginning of modern physics, about a hundred years later, it was realized that light could in fact show behavior characteristic of both waves and particles. In 1927, Davisson and Germer demonstrated that electrons show the same behavior, which was later extended to atoms and molecules. Thomas Young's experiment with light was part of classical physics well before quantum mechanics, and the concept of wave-particle duality. He believed it demonstrated that the wave theory of light was correct, and his experiment is sometimes referred to as Young's experiment or Young's slits.

The experiment belongs to a general class of "double path" experiments, in which a wave is split into two separate waves that later combine into a single wave. Changes in the path-lengths of both waves result in a phase shift, creating an interference pattern. Another version is the Mach–Zehnder interferometer, which splits the beam with a beam splitter.

In the basic version of this experiment, a coherent light source, such as a laser beam, illuminates a plate pierced by two parallel slits, and the light passing through the slits is observed on a screen behind the plate. The wave nature of light causes the light waves passing through the two slits to interfere, producing bright and dark bands on the screen – a result that would not be expected if light consisted of classical particles. However, the light is always found to be absorbed at the screen at discrete points, as individual particles (not waves); the interference pattern appears via the varying density of these particle hits on the screen. Furthermore, versions of the experiment that include detectors at the slits find that each detected photon passes through one slit (as would a classical particle), and not through both slits (as would a wave). However, such experiments demonstrate that particles do not form the interference pattern if one detects which slit they pass through. These results demonstrate the principle of wave–particle duality.

Other atomic-scale entities, such as electrons, are found to exhibit the same behavior when fired towards a double slit. Additionally, the detection of individual discrete impacts is observed to be inherently probabilistic, which is inexplicable using classical mechanics.

The experiment can be done with entities much larger than electrons and photons, although it becomes more difficult as size increases. The largest entities for which the double-slit experiment has been performed were molecules that each comprised 810 atoms (whose total mass was over 10,000 atomic mass units).

The double-slit experiment (and its variations) has become a classic for its clarity in expressing the central puzzles of quantum mechanics. Because it demonstrates the fundamental limitation of the ability of the observer to predict experimental results, Richard Feynman called it "a phenomenon which is impossible […] to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery [of quantum mechanics]."

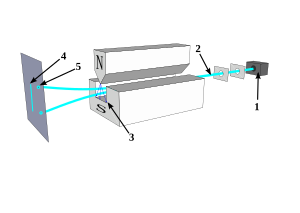
Numerical simulation of the double-slit experiment with electrons. Figure on the left: evolution (from left to right) of the intensity of the electron beam at the exit of the slits (left) up to the detection screen located 10cm after the slits (right). The higher the intensity, the more the color is light blue - Figure in the center: impacts of the electrons observed on the screen - Figure on the right: intensity of the electrons in the far field approximation (on the screen). Numerical data from Claus Jönsson's experiment (1961). Photons, atoms and molecules follow a similar evolution.

Overview

Same double-slit assembly (0.7 mm between slits); in top image, one slit is closed. In the single-slit image, a diffraction pattern (the faint spots on either side of the main band) forms due to the nonzero width of the slit. This diffraction pattern is also seen in the double-slit image, but with many smaller interference fringes.

If light consisted strictly of ordinary or classical particles, and these particles were fired in a straight line through a slit and allowed to strike a screen on the other side, we would expect to see a pattern corresponding to the size and shape of the slit. However, when this "single-slit experiment" is actually performed, the pattern on the screen is a diffraction pattern in which the light is spread out. The smaller the slit, the greater the angle of spread. The top portion of the image shows the central portion of the pattern formed when a red laser illuminates a slit and, if one looks carefully, two faint side bands. More bands can be seen with a more highly refined apparatus. Diffraction explains the pattern as being the result of the interference of light waves from the slit.

Simulation of a particle wave function: double slit experiment. The white blur represents the wave. The whiter the pixel, the greater the probability of finding a particle in that place if measured.

If one illuminates two parallel slits, the light from the two slits again interferes. Here the interference is a more pronounced pattern with a series of alternating light and dark bands. The width of the bands is a property of the frequency of the illuminating light. (See the bottom photograph to the right.) When Thomas Young (1773–1829) first demonstrated this phenomenon, it indicated that light consists of waves, as the distribution of brightness can be explained by the alternately additive and subtractive interference of wavefronts. Young's experiment, performed in the early 1800s, played a crucial role in the understanding of the wave theory of light, vanquishing the corpuscular theory of light proposed by Isaac Newton, which had been the accepted model of light propagation in the 17th and 18th centuries. However, the later discovery of the photoelectric effect demonstrated that under different circumstances, light can behave as if it is composed of discrete particles. These seemingly contradictory discoveries made it necessary to go beyond classical physics and take the quantum nature of light into account.

Feynman was fond of saying that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment. He also proposed (as a thought experiment) that if detectors were placed before each slit, the interference pattern would disappear.

The Englert–Greenberger duality relation provides a detailed treatment of the mathematics of double-slit interference in the context of quantum mechanics.

A low-intensity double-slit experiment was first performed by G. I. Taylor in 1909, by reducing the level of incident light until photon emission/absorption events were mostly non-overlapping. A double-slit experiment was not performed with anything other than light until 1961, when Claus Jönsson of the University of Tübingen performed it with electron beams. In 1974, the Italian physicists Pier Giorgio Merli, Gian Franco Missiroli, and Giulio Pozzi repeated the experiment using single electrons and biprism (instead of slits), showing that each electron interferes with itself as predicted by quantum theory. In 2002, the single-electron version of the experiment was voted "the most beautiful experiment" by readers of Physics World.

In 2012, Stefano Frabboni and co-workers eventually performed the double-slit experiment with electrons and real slits, following the original scheme proposed by Feynman. They sent single electrons onto nanofabricated slits (about 100 nm wide) and, by collecting the transmitted electrons with a single-electron detector, they could show the build-up of a double-slit interference pattern.

In 2019, single particle interference was demonstrated for antimatter by Marco Giammarchi and coworkers.

Variations of the experiment

Interference of individual particles

Buildup of interference pattern from individual particle detections

An important version of this experiment involves single particles. Sending particles through a double-slit apparatus one at a time results in single particles appearing on the screen, as expected. Remarkably, however, an interference pattern emerges when these particles are allowed to build up one by one (see the adjacent image). This demonstrates the wave–particle duality, which states that all matter exhibits both wave and particle properties: the particle is measured as a single pulse at a single position, while the wave describes the probability of absorbing the particle at a specific place on the screen. This phenomenon has been shown to occur with photons, electrons, atoms and even some molecules, including buckyballs.

The probability of detection is the square of the amplitude of the wave and can be calculated with classical waves (see below). Ever since the origination of quantum mechanics, some theorists have searched for ways to incorporate additional determinants or "hidden variables" that, were they to become known, would account for the location of each individual impact with the target.

Mach-Zehnder interferometer

Photons in a Mach–Zehnder interferometer exhibit wave-like interference and particle-like detection at single-photon detectors.

The Mach–Zehnder interferometer can be seen as a simplified version of the double-slit experiment. Instead of propagating through free space after the two slits, and hitting any position in an extended screen, in the interferometer the photons can only propagate via two paths, and hit two discrete photodetectors. This makes it possible to describe it via simple linear algebra in dimension 2, rather than differential equations.

A photon emitted by the laser hits the first beam splitter and is then in a superposition between the two possible paths. In the second beam splitter these paths interfere, causing the photon to hit the photodetector on the right with probability one, and the photodetector on the bottom with probability zero. It is interesting to consider what would happen if the photon were definitely in either of paths between the beam splitters. This can be accomplished by blocking one of the paths, or equivalently by detecting the presence of a photon there. In both cases there will be no interference between the paths anymore, and both photodectors will be hit with probability 1/2. From this we can conclude that the photon does not take one path or another after the first beam splitter, but rather that it is in a genuine quantum superposition of the two paths.

"Which-way" experiments and the principle of complementarity

A well-known thought experiment predicts that if particle detectors are positioned at the slits, showing through which slit a photon goes, the interference pattern will disappear. This which-way experiment illustrates the complementarity principle that photons can behave as either particles or waves, but cannot be observed as both at the same time. Despite the importance of this thought experiment in the history of quantum mechanics (for example, see the discussion on Einstein's version of this experiment), technically feasible realizations of this experiment were not proposed until the 1970s. (Naive implementations of the textbook gedanken experiment are not possible because photons cannot be detected without absorbing the photon.) Currently, multiple experiments have been performed illustrating various aspects of complementarity.

An experiment performed in 1987 produced results that demonstrated that information could be obtained regarding which path a particle had taken without destroying the interference altogether. This showed the effect of measurements that disturbed the particles in transit to a lesser degree and thereby influenced the interference pattern only to a comparable extent. In other words, if one does not insist that the method used to determine which slit each photon passes through be completely reliable, one can still detect a (degraded) interference pattern.

Delayed choice and quantum eraser variations

A diagram of Wheeler's delayed choice experiment, showing the principle of determining the path of the photon after it passes through the slit

Wheeler's delayed choice experiments demonstrate that extracting "which path" information after a particle passes through the slits can seem to retroactively alter its previous behavior at the slits.

Quantum eraser experiments demonstrate that wave behavior can be restored by erasing or otherwise making permanently unavailable the "which path" information.

A simple do-it-at-home illustration of the quantum eraser phenomenon was given in an article in Scientific American. If one sets polarizers before each slit with their axes orthogonal to each other, the interference pattern will be eliminated. The polarizers can be considered as introducing which-path information to each beam. Introducing a third polarizer in front of the detector with an axis of 45° relative to the other polarizers "erases" this information, allowing the interference pattern to reappear. This can also be accounted for by considering the light to be a classical wave, and also when using circular polarizers and single photons. Implementations of the polarizers using entangled photon pairs have no classical explanation.

Weak measurement

In a highly publicized experiment in 2012, researchers claimed to have identified the path each particle had taken without any adverse effects at all on the interference pattern generated by the particles. In order to do this, they used a setup such that particles coming to the screen were not from a point-like source, but from a source with two intensity maxima. However, commentators such as Svensson have pointed out that there is in fact no conflict between the weak measurements performed in this variant of the double-slit experiment and the Heisenberg uncertainty principle. Weak measurement followed by post-selection did not allow simultaneous position and momentum measurements for each individual particle, but rather allowed measurement of the average trajectory of the particles that arrived at different positions. In other words, the experimenters were creating a statistical map of the full trajectory landscape.

Other variations

A laboratory double-slit assembly; distance between top posts approximately 2.5 cm (one inch).

 

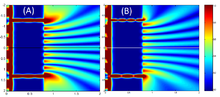
Near-field intensity distribution patterns for plasmonic slits with equal widths (A) and non-equal widths (B).

In 1967, Pfleegor and Mandel demonstrated two-source interference using two separate lasers as light sources.

It was shown experimentally in 1972 that in a double-slit system where only one slit was open at any time, interference was nonetheless observed provided the path difference was such that the detected photon could have come from either slit. The experimental conditions were such that the photon density in the system was much less than unity.

In 1999, the double-slit experiment was successfully performed with buckyball molecules (each of which comprises 60 carbon atoms). A buckyball is large enough (diameter about 0.7 nm, nearly half a million times larger than a proton) to be seen under an electron microscope.

In 2005, E. R. Eliel presented an experimental and theoretical study of the optical transmission of a thin metal screen perforated by two subwavelength slits, separated by many optical wavelengths. The total intensity of the far-field double-slit pattern is shown to be reduced or enhanced as a function of the wavelength of the incident light beam.

In 2012, researchers at the University of Nebraska–Lincoln performed the double-slit experiment with electrons as described by Richard Feynman, using new instruments that allowed control of the transmission of the two slits and the monitoring of single-electron detection events. Electrons were fired by an electron gun and passed through one or two slits of 62 nm wide × 4 μm tall.

In 2013, the double-slit experiment was successfully performed with molecules that each comprised 810 atoms (whose total mass was over 10,000 atomic mass units). The record was raised to 2000 atoms (25,000 amu) in 2019.

Hydrodynamic pilot wave analogs

Hydrodynamic analogs have been developed that can recreate various aspects of quantum mechanical systems, including single-particle interference through a double-slit. A silicone oil droplet, bouncing along the surface of a liquid, self-propels via resonant interactions with its own wave field. The droplet gently sloshes the liquid with every bounce. At the same time, ripples from past bounces affect its course. The droplet's interaction with its own ripples, which form what is known as a pilot wave, causes it to exhibit behaviors previously thought to be peculiar to elementary particles – including behaviors customarily taken as evidence that elementary particles are spread through space like waves, without any specific location, until they are measured.

Behaviors mimicked via this hydrodynamic pilot-wave system include quantum single particle diffraction, tunneling, quantized orbits, orbital level splitting, spin, and multimodal statistics. It is also possible to infer uncertainty relations and exclusion principles. Videos are available illustrating various features of this system.

However, more complicated systems that involve two or more particles in superposition are not amenable to such a simple, classically intuitive explanation. Accordingly, no hydrodynamic analog of entanglement has been developed. Nevertheless, optical analogs are possible.

Classical wave-optics formulation

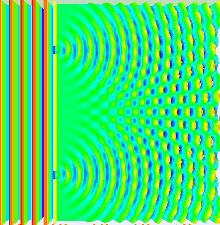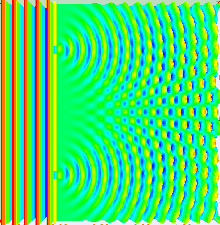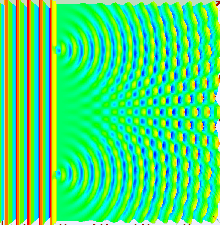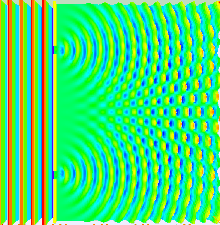
Two-slit diffraction pattern by a plane wave

 

Photo of the double-slit interference of sunlight.

 

Two slits are illuminated by a plane wave.

Much of the behaviour of light can be modelled using classical wave theory. The Huygens–Fresnel principle is one such model; it states that each point on a wavefront generates a secondary wavelet, and that the disturbance at any subsequent point can be found by summing the contributions of the individual wavelets at that point. This summation needs to take into account the phase as well as the amplitude of the individual wavelets. Only the intensity of a light field can be measured—this is proportional to the square of the amplitude.

In the double-slit experiment, the two slits are illuminated by a single laser beam. If the width of the slits is small enough (less than the wavelength of the laser light), the slits diffract the light into cylindrical waves. These two cylindrical wavefronts are superimposed, and the amplitude, and therefore the intensity, at any point in the combined wavefronts depends on both the magnitude and the phase of the two wavefronts. The difference in phase between the two waves is determined by the difference in the distance travelled by the two waves.

If the viewing distance is large compared with the separation of the slits (the far field), the phase difference can be found using the geometry shown in the figure below right. The path difference between two waves travelling at an angle θ is given by:

${\displaystyle d\sin \theta \approx d\theta }$

Where d is the distance between the two slits. When the two waves are in phase, i.e. the path difference is equal to an integral number of wavelengths, the summed amplitude, and therefore the summed intensity is maximum, and when they are in anti-phase, i.e. the path difference is equal to half a wavelength, one and a half wavelengths, etc., then the two waves cancel and the summed intensity is zero. This effect is known as interference. The interference fringe maxima occur at angles

${\displaystyle ~d\theta _{n}=n\lambda ,~n=0,1,2,\ldots }$

where λ is the wavelength of the light. The angular spacing of the fringes, θ_f, is given by

${\displaystyle \theta _{f}\approx \lambda /d}$

The spacing of the fringes at a distance z from the slits is given by

${\displaystyle ~w=z\theta _{f}=z\lambda /d}$

For example, if two slits are separated by 0.5 mm (d), and are illuminated with a 0.6μm wavelength laser (λ), then at a distance of 1m (z), the spacing of the fringes will be 1.2 mm.

If the width of the slits b is greater than the wavelength, the Fraunhofer diffraction equation gives the intensity of the diffracted light as:

${\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi d\sin \theta }{\lambda }}\right]~\mathrm {sinc} ^{2}\left[{\frac {\pi b\sin \theta }{\lambda }}\right]\end{aligned}}}$

Where the sinc function is defined as sinc(x) = sin(x)/x for x ≠ 0, and sinc(0) = 1.

This is illustrated in the figure above, where the first pattern is the diffraction pattern of a single slit, given by the sinc function in this equation, and the second figure shows the combined intensity of the light diffracted from the two slits, where the cos function represent the fine structure, and the coarser structure represents diffraction by the individual slits as described by the sinc function.

Similar calculations for the near field can be done using the Fresnel diffraction equation. As the plane of observation gets closer to the plane in which the slits are located, the diffraction patterns associated with each slit decrease in size, so that the area in which interference occurs is reduced, and may vanish altogether when there is no overlap in the two diffracted patterns.

Interpretations of the experiment

Like the Schrödinger's cat thought experiment, the double-slit experiment is often used to highlight the differences and similarities between the various interpretations of quantum mechanics.

Copenhagen interpretation

The Copenhagen interpretation, put forth by some of the pioneers in the field of quantum mechanics, asserts that it is undesirable to posit anything that goes beyond the mathematical formulae and the kinds of physical apparatus and reactions that enable us to gain some knowledge of what goes on at the atomic scale. One of the mathematical constructs that enables experimenters to predict very accurately certain experimental results is sometimes called a probability wave. In its mathematical form it is analogous to the description of a physical wave, but its "crests" and "troughs" indicate levels of probability for the occurrence of certain phenomena (e.g., a spark of light at a certain point on a detector screen) that can be observed in the macro world of ordinary human experience.

The probability "wave" can be said to "pass through space" because the probability values that one can compute from its mathematical representation are dependent on time. One cannot speak of the location of any particle such as a photon between the time it is emitted and the time it is detected simply because in order to say that something is located somewhere at a certain time one has to detect it. The requirement for the eventual appearance of an interference pattern is that particles be emitted, and that there be a screen with at least two distinct paths for the particle to take from the emitter to the detection screen. Experiments observe nothing whatsoever between the time of emission of the particle and its arrival at the detection screen. If a ray tracing is next made as if a light wave (as understood in classical physics) is wide enough to take both paths, then that ray tracing will accurately predict the appearance of maxima and minima on the detector screen when many particles pass through the apparatus and gradually "paint" the expected interference pattern.

Path-integral formulation

One of an infinite number of equally likely paths used in the Feynman path integral

The Copenhagen interpretation is similar to the path integral formulation of quantum mechanics provided by Feynman. The path integral formulation replaces the classical notion of a single, unique trajectory for a system, with a sum over all possible trajectories. The trajectories are added together by using functional integration.

Each path is considered equally likely, and thus contributes the same amount. However, the phase of this contribution at any given point along the path is determined by the action along the path:

${\displaystyle A_{\text{path}}(x,y,z,t)=e^{iS(x,y,z,t)}}$

All these contributions are then added together, and the magnitude of the final result is squared, to get the probability distribution for the position of a particle:

${\displaystyle p(x,y,z,t)\propto \left\vert \int _{\text{all paths}}e^{iS(x,y,z,t)}\right\vert ^{2}}$

As is always the case when calculating probability, the results must then be normalized by imposing:

${\displaystyle \iiint _{\text{all space}}p(x,y,z,t)\,\mathrm {d} V=1}$

To summarize, the probability distribution of the outcome is the normalized square of the norm of the superposition, over all paths from the point of origin to the final point, of waves propagating proportionally to the action along each path. The differences in the cumulative action along the different paths (and thus the relative phases of the contributions) produces the interference pattern observed by the double-slit experiment. Feynman stressed that his formulation is merely a mathematical description, not an attempt to describe a real process that we can measure.

Relational interpretation

An example of the uncertainty principle related to the relational interpretation. The more that is known about the position of a particle, the less is known about the velocity, and vice versa

According to the relational interpretation of quantum mechanics, first proposed by Carlo Rovelli, observations such as those in the double-slit experiment result specifically from the interaction between the observer (measuring device) and the object being observed (physically interacted with), not any absolute property possessed by the object. In the case of an electron, if it is initially "observed" at a particular slit, then the observer–particle (photon–electron) interaction includes information about the electron's position. This partially constrains the particle's eventual location at the screen. If it is "observed" (measured with a photon) not at a particular slit but rather at the screen, then there is no "which path" information as part of the interaction, so the electron's "observed" position on the screen is determined strictly by its probability function. This makes the resulting pattern on the screen the same as if each individual electron had passed through both slits.

Many-worlds interpretation

Physicist David Deutsch argues in his book The Fabric of Reality that the double-slit experiment is evidence for the many-worlds interpretation. However, since every interpretation of quantum mechanics is empirically indistinguishable, some scientists are skeptical of this claim.

De Broglie–Bohm theory

Trajectories of particles under De Broglie–Bohm theory in the double-slit experiment.

An alternative to the standard understanding of quantum mechanics, the De Broglie–Bohm theory states that particles also have precise locations at all times, and that their velocities are defined by the wave-function. So while a single particle will travel through one particular slit in the double-slit experiment, the so-called "pilot wave" that influences it will travel through both. The two slit de Broglie-Bohm trajectories were first calculated by Chris Dewdney while working with Chris Philippidis and Basil Hiley at Birkbeck College (London). The de Broglie-Bohm theory produces the same statistical results as standard quantum mechanics, but dispenses with many of its conceptual difficulties.

100 trajectories guided by the wave function. In De Broglie-Bohm's theory, a particle is represented, at any time, by a wave function and a position (center of mass). This is a kind of augmented reality compared to the standard interpretation.