In mathematics, a Möbius strip, band, or loop (US: /ˈmoʊbiəs, ˈmeɪ-/ MOH-bee-əs, MAY-, UK: /ˈmɜːbiəs/; German: [ˈmøːbi̯ʊs]), also spelled Mobius or Moebius, is a surface with only one side (when embedded in three-dimensional Euclidean space) and only one boundary curve. The Möbius strip is the simplest non-orientable surface. It can be realized as a ruled surface. Its discovery is attributed independently to the German mathematicians Johann Benedict Listing and August Ferdinand Möbius in 1858, though similar structures can be seen in Roman mosaics c. 200–250 AD. Möbius published his results in his articles "Theorie der elementaren Verwandtschaft" (1863) and "Ueber die Bestimmung des Inhaltes eines Polyëders" (1865).
An example of a Möbius strip can be created by taking a strip of paper and giving one end a half-twist, then joining the ends to form a loop; its boundary is a simple closed curve which can be traced by a single unknotted string. Any topological space homeomorphic to this example is also called a Möbius strip, allowing for a very wide variety of geometric realizations as surfaces with a definite size and shape. For example, any rectangle can be glued left-edge to right-edge with a reversal of orientation. Some, but not all, of these can be smoothly modeled as surfaces in Euclidean space. A closely related, but not homeomorphic, surface is the complete open Möbius band, a surface with no boundaries in which the width of the strip is extended infinitely to become a Euclidean line.
A half-twist clockwise gives an embedding of the Möbius strip which cannot be moved or stretched to give the half-twist counterclockwise; thus, a Möbius strip embedded in Euclidean space is a chiral object with right- or left-handedness. The Möbius strip can also be embedded by twisting the strip any odd number of times, or by knotting and twisting the strip before joining its ends.
Finding algebraic equations cutting out a Möbius strip is straightforward, but these equations do not describe the same geometric shape as the twisted paper model above. Such paper models are developable surfaces having zero Gaussian curvature, and can be described by differential-algebraic equations.
The Euler characteristic of the Möbius strip is zero.
Properties
The Möbius strip has several curious properties. A line drawn along the edge travels in a full circle to a point opposite the starting point. If continued, the line returns to the starting point, and is double the length of the original strip: this single continuous curve traverses the entire boundary.
Cutting a Möbius strip along the center line with a pair of scissors yields one long strip with two full twists in it, rather than two separate strips; the result is not a Möbius strip, but homeomorphic to a cylinder. This happens because the original strip only has one edge, twice as long as the original strip. Cutting creates a second independent edge of the same length, half on each side of the scissors. Cutting this new, longer, strip down the middle creates two strips wound around each other, each with two full twists.
If the strip is cut along about a third in from the edge, it creates two linked strips. The center third is a thinner Möbius strip, the same length as the original strip. The other is a thin strip with two full twists, a neighborhood of the edge of the original strip, with twice the length of the original strip.
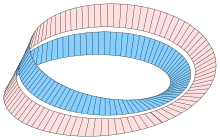
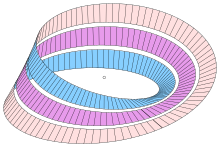
Other analogous strips can be obtained by similarly joining strips with two or more half-twists in them instead of one. For example, a strip with three half-twists, when divided lengthwise, becomes a twisted strip tied in a trefoil knot; if this knot is unraveled, it is found to contain eight half-twists. A strip with N half-twists, when bisected, becomes a strip with N + 1 full twists. Giving it extra twists and reconnecting the ends produces figures called Paradromic Rings.
Geometry and topology
One way to represent the Möbius strip embedded in three-dimensional Euclidean space is by the parameterization:
for and . This creates a Möbius strip of width 1, whose center circle has radius 1, lies in the -plane and is centered at . The parameter u runs around the strip while v moves from one edge to the other.
In cylindrical polar coordinates , an unbounded version of the Möbius strip can be represented by the equation:
Widest isometric embedding in 3-space
If a smooth Möbius strip in three-space is a rectangular one – that is, created from identifying two opposite sides of a geometrical rectangle with bending but not stretching the surface – then such an embedding is known to be possible if the aspect ratio of the rectangle is greater than , with the shorter sides identified. (For a smaller aspect ratio, it is not known whether a smooth embedding is possible.) As the aspect ratio decreases toward , any such embedding seems to approach a shape that can be thought of as a strip of three equilateral triangles, folded on top of one another to occupy an equilateral triangle.
If the Möbius strip in three-space is only once continuously differentiable (class ), however, then the theorem of Nash-Kuiper shows that no lower bound exists.
A method of making a Möbius strip from a rectangular strip too wide to simply twist and join (e.g., a rectangle only one unit long and one unit wide) is to first fold the wide direction back and forth using an even number of folds—an "accordion fold"—so that the folded strip becomes narrow enough that it can be twisted and joined, much as a single long-enough strip can be joined. With two folds, for example, a strip would become a folded strip whose cross section is in the shape of an 'N' and would remain an 'N' after a half-twist. This folded strip, three times as long as it is wide, would be long enough to then join at the ends. This method works in principle, but becomes impractical after sufficiently many folds, if paper is used. Using normal paper, this construction can be folded flat, with all the layers of the paper in a single plane, but mathematically, whether this is possible without stretching the surface of the rectangle is not clear.
Topology
Topologically, the Möbius strip can be defined as the square with its top and bottom sides identified by the relation for , as in the diagram.
A less used presentation of the Möbius strip is as the topological quotient of a torus. A torus can be constructed as the square with the edges identified as (glue left to right) and (glue bottom to top). If one then also identified , then one obtains the Möbius strip. The diagonal of the square (the points where both coordinates agree) becomes the boundary of the Möbius strip, and carries an orbifold structure, which geometrically corresponds to "reflection" – geodesics (straight lines) in the Möbius strip reflect off the edge back into the strip. Notationally, this is written as – the 2-torus quotiented by the group action of the symmetric group on two letters (switching coordinates), and it can be thought of as the configuration space of two unordered points on the circle, possibly the same (the edge corresponds to the points being the same), with the torus corresponding to two ordered points on the circle.
The Möbius strip is a two-dimensional compact manifold (i.e. a surface) with boundary. It is a standard example of a surface that is not orientable. In fact, the Möbius strip is the epitome of the topological phenomenon of nonorientability. This is because two-dimensional shapes (surfaces) are the lowest-dimensional shapes for which nonorientability is possible and the Möbius strip is the only surface that is topologically a subspace of every nonorientable surface. As a result, any surface is nonorientable if and only if it contains a Möbius band as a subspace.
The Möbius strip is also a standard example used to illustrate the mathematical concept of a fiber bundle. Specifically, it is a nontrivial bundle over the circle with its fiber equal to the unit interval, . Looking only at the edge of the Möbius strip gives a nontrivial two point (or ) bundle over .
Computer graphics
A simple construction of the Möbius strip that can be used to portray it in computer graphics or modeling packages is:
- Take a rectangular strip. Rotate it around a fixed point not in its plane. At every step, also rotate the strip along a line in its plane (the line that divides the strip in two) and perpendicular to the main orbital radius. The surface generated on one complete revolution is the Möbius strip.
- Take a Möbius strip and cut it along the middle of the strip. This forms a new strip, which is a rectangle joined by rotating one end a whole turn. By cutting it down the middle again, this forms two interlocking whole-turn strips.
Geometry of the open Möbius band
The open Möbius band is formed by deleting the boundary of the standard Möbius band. It is constructed from the set by identifying (glueing) the points and for all .
It may be constructed as a surface of constant positive, negative, or zero (Gaussian) curvature. In the cases of negative and zero curvature, the Möbius band can be constructed as a (geodesically) complete surface, which means that all geodesics ("straight lines" on the surface) may be extended indefinitely in either direction.
Constant negative curvature:
Like the plane and the open cylinder, the open Möbius band admits not only a complete metric of constant curvature 0, but also a complete metric of constant negative curvature. One way to see this is to begin with the upper half plane (Poincaré) model of the hyperbolic plane, a geometry of constant curvature whose lines are represented in the model by semicircles that meet the -axis at right angles. Take the subset of the upper half-plane between two nested semicircles, and identify the outer semicircle with the left-right reversal of the inner semicircle. The result is topologically a complete and non-compact Möbius band with constant negative curvature.
(Constant) zero curvature:
This may also be constructed as a complete surface, by starting with portion of the plane defined by and identifying with for all . The resulting metric makes the open Möbius band into a (geodesically) complete flat surface (i.e., having Gaussian curvature equal to 0 everywhere). This is the only metric on the Möbius band, up to uniform scaling, that is both flat and complete.
Constant positive curvature:
A Möbius band of constant positive curvature cannot be complete, since it is known that the only complete surfaces of constant positive curvature are the sphere and the projective plane. The projective plane of constant curvature +1 may be constructed as the quotient of the unit sphere in by the antipodal map defined by . The open Möbius band is homeomorphic to the once-punctured projective plane, that is, with any one point removed. This may be thought of as the closest that a Möbius band of constant positive curvature can get to being a complete surface: just one point away.
The space of unoriented lines in the plane is diffeomorphic to the open Möbius band. To see why, let denote the line through the origin at an angle to the positive -axis. For each there is the family of all lines in the plane that are perpendicular to . Topologically, the family is just a line (because each line in intersects the line in just one point). In this way, as increases in the range , the line represents a line's worth of distinct lines in the plane. But when reaches , is identical to , and so the families and of perpendicular lines are also identical families. The line , however, has returned to itself as pointed in the opposite direction. Every line in the plane corresponds to exactly one line in some family , for exactly one , for , and is identical to but returns pointed in the opposite direction. This ensures that the space of all lines in the plane – the union of all the for – is an open Möbius band.
The group of bijective linear transformations of the plane to itself (real matrices with non-zero determinant) naturally induces bijections of the space of lines in the plane to itself, which form a group of self-homeomorphisms of the space of lines. Hence the same group forms a group of self-homeomorphisms of the Möbius band described in the previous paragraph. But there is no metric on the space of lines in the plane that is invariant under the action of this group of homeomorphisms. In this sense, the space of lines in the plane has no natural metric on it. This means that the Möbius band possesses a natural 4-dimensional Lie group of self-homeomorphisms, given by , but this high degree of symmetry cannot be exhibited as the group of isometries of any metric.
Möbius band with round boundary
The edge, or boundary, of a Möbius strip is homeomorphic (topologically equivalent) to a circle. Under the usual embeddings of the strip in Euclidean space, as above, the boundary is not a true circle. However, it is possible to embed a Möbius strip in three dimensions so that the boundary is a perfect circle lying in some plane. For example, see Figures 307, 308, and 309 of "Geometry and the imagination".
A much more geometric embedding begins with a minimal Klein bottle immersed in the 3-sphere, as discovered by Blaine Lawson. We then take half of this Klein bottle to get a Möbius band embedded in the 3-sphere (the unit sphere in 4-space). The result is sometimes called the "Sudanese Möbius Band", where "sudanese" refers not to the country Sudan but to the names of two topologists, Sue Goodman and Daniel Asimov. Applying stereographic projection to the Sudanese band places it in three-dimensional space, as can be seen below – a version due to George Francis can be found here.
From Lawson's minimal Klein bottle we derive an embedding of the band into the 3-sphere S3, regarded as a subset of C2, which is geometrically the same as R4. We map angles η, φ to complex numbers z1, z2 via
Here the parameter η runs from 0 to π and φ runs from 0 to 2π. Since |z1|2 + |z2|2 = 1, the embedded surface lies entirely in S3. The boundary of the strip is given by |z2| = 1 (corresponding to η = 0, π), which is clearly a circle on the 3-sphere.
To obtain an embedding of the Möbius strip in R3 one maps S3 to R3 via a stereographic projection. The projection point can be any point on S3 that does not lie on the embedded Möbius strip (this rules out all the usual projection points). One possible choice is . Stereographic projections map circles to circles and preserves the circular boundary of the strip. The result is a smooth embedding of the Möbius strip into R3 with a circular edge and no self-intersections.
The Sudanese Möbius band in the three-sphere S3 is geometrically a fibre bundle over a great circle, whose fibres are great semicircles. The most symmetrical image of a stereographic projection of this band into R3 is obtained by using a projection point that lies on that great circle that runs through the midpoint of each of the semicircles. Each choice of such a projection point results in an image that is congruent to any other. But because such a projection point lies on the Möbius band itself, two aspects of the image are significantly different from the case (illustrated above) where the point is not on the band: 1) the image in R3 is not the full Möbius band, but rather the band with one point removed (from its centerline); and 2) the image is unbounded – and as it gets increasingly far from the origin of R3, it increasingly approximates a plane. Yet this version of the stereographic image has a group of 4 symmetries in R3 (it is isomorphic to the Klein 4-group), as compared with the bounded version illustrated above having its group of symmetries the unique group of order 2. (If all symmetries and not just orientation-preserving isometries of R3 are allowed, the numbers of symmetries in each case doubles.)
But the most geometrically symmetrical version of all is the original Sudanese Möbius band in the three-sphere S3, where its full group of symmetries is isomorphic to the Lie group O(2). Having an infinite cardinality (that of the continuum), this is far larger than the symmetry group of any possible embedding of the Möbius band in R3.
Projective geometry
Using projective geometry, an open Möbius band can be described as the set of solutions to a polynomial equation. Adding a polynomial inequality results in a closed Möbius band. These relate Möbius bands to the geometry of line bundles and the operation of blowing up in algebraic geometry.
The real projective line is the set modulo scaling. That is, a point in is an equivalence class of the form
Every equivalence class with has a unique representative whose second coordinate is 1, namely . These points form a copy of the Euclidean line . However, the equivalence class of has no such representative. This extra point behaves like an unsigned infinity, making topologically the same as the circle . The advantage of over the circle is that some geometric objects have simpler equations in terms of A and B. This is the case for the Möbius band.
A realization of an open Möbius band is given by the set
If we delete the line from M (or in fact any line), then the resulting subset can be embedded in Euclidean space . Deleting this line gives the set
where m corresponds to .
There is a realization of the closed Möbius band as a similar set, but with an additional inequality to create a boundary:
The boundary of N is the set of all points with . The geometry of N is very similar to that of M, so we will focus on M in what follows.
The geometry of M can be described in terms of lines through the origin. Every line through the origin in is the solution set of an equation . The solution set does not change when is rescaled, so the line only depends on the equivalence class . That is, the lines through the origin are parametrized by . Furthermore, every point in , except for , lies on a unique line through the origin, specifically, the line defined by . The point , however, lies on every line through the origin. For this point, the equation degenerates to . This is always true, so every is a solution. Consequently, the set M may be described as the disjoint union of the set of lines through the origin. This is the same as the union of the lines through the origin, except that it contains one copy of the origin for each line. These additional copies of the origin are a copy of and constitute the center circle of the Möbius band. The lines themselves describe the ruling of the Möbius band. This point of view on M exhibits it both as the total space of the tautological line bundle on as well as the blow-up of the origin in .
To see the half-twist in M, begin with the point in . This corresponds to a unique point of M, namely . Draw the counterclockwise half circle to produce a path on M given by . The path stops at , where it gives the point . Except for P and Q, every point in the path lies on a different line through the origin. Therefore travels once around the center circle of M. However, while P and Q lie in the same line of the ruling, they are on opposite sides of the origin. This change in sign is the algebraic manifestation of the half-twist.
Related objects
A closely related 'strange' geometrical object is the Klein bottle. A Klein bottle could in theory be produced by gluing two Möbius strips together along their edges; however this cannot be done in ordinary three-dimensional Euclidean space without creating self-intersections.
Another closely related manifold is the real projective plane. If a circular disk is cut out of the real projective plane, what is left is a Möbius strip. Going in the other direction, if one glues a disk to a Möbius strip by identifying their boundaries, the result is the projective plane. To visualize this, it is helpful to deform the Möbius strip so that its boundary is an ordinary circle (see above). The real projective plane, like the Klein bottle, cannot be embedded in three-dimensions without self-intersections.
In graph theory, the Möbius ladder is a cubic graph closely related to the Möbius strip.
In 1968, Gonzalo Vélez Jahn (UCV, Caracas, Venezuela) discovered three dimensional bodies with Möbian characteristics; these were later described by Martin Gardner as prismatic rings that became toroidal polyhedrons in his August 1978 Mathematical Games column in Scientific American.
Applications
There have been several technical applications for the Möbius strip. Giant Möbius strips have been used as conveyor belts that last longer because the entire surface area of the belt gets the same amount of wear, and as continuous-loop recording tapes (to double the playing time). Möbius strips are common in the manufacture of fabric computer printer and typewriter ribbons, as they let the ribbon be twice as wide as the print head while using both halves evenly.
A Möbius resistor is an electronic circuit element that cancels its own inductive reactance. Nikola Tesla patented similar technology in 1894: "Coil for Electro Magnets" was intended for use with his system of global transmission of electricity without wires.
The Möbius strip is the configuration space of two unordered points on a circle. Consequently, in music theory, the space of all two-note chords, known as dyads, takes the shape of a Möbius strip; this and generalizations to more points is a significant application of orbifolds to music theory.
In physics/electro-technology as:
- A compact resonator with a resonance frequency that is half that of identically constructed linear coils
- An inductionless resistor
- Superconductors with high transition temperature
- Möbius resonator
In chemistry/nano-technology as:
- Molecular knots with special characteristics (Knotane, Chirality)
- Molecular engines
- Graphene volume (nano-graphite) with new electronic characteristics, like helical magnetism
- A special type of aromaticity: Möbius aromaticity
- Charged particles caught in the magnetic field of the Earth that can move on a Möbius band
- The cyclotide (cyclic protein) kalata B1, active substance of the plant Oldenlandia affinis, contains Möbius topology for the peptide backbone.
Arts and entertainment
The Möbius strip principle has been used as a method of creating the illusion of magic. The trick, known as the Afghan bands, was very popular in the first half of the twentieth century. Many versions of this trick exist and have been performed by famous illusionists such as Harry Blackstone Sr. and Thomas Nelson Downs.
In creative works
The universal recycling symbol (♲) design has its three arrows forming a Möbius loop. According to its designer Gary Anderson, "the figure was designed as a Mobius strip to symbolize continuity within a finite entity".















![{\displaystyle [0,1]\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f35a051af39d8299688d7c4a63e39ee5f95c8b)








![I=[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/87ec65159c44769434523e46928bc1b82681f842)

































![{\displaystyle [A:B]=\{(\lambda A,\lambda B):\lambda \in \mathbf {R} \setminus \{0\}\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1703ee596b1a95aff033e95cb094f748509b4960)
![{\displaystyle [A:B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33dede24122dab634ef6f1bd8655cfed1922ce0a)



![{\displaystyle [1:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c9d83f60abcf946cc50d3cb984fecd2df57977b)
![{\displaystyle M=\{((x,y),[A:B])\in \mathbf {R} ^{2}\times \mathbf {RP} ^{1}:Ax=By\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b404d0e84ae1eda5eab105bc8e3922a87937efc)


![{\displaystyle {\begin{aligned}M'&=\{((x,y),[A:B])\in \mathbf {R} ^{2}\times \mathbf {RP} ^{1}:Ax=By,\ B\neq 0\}\\&=\{(x,y,m)\in \mathbf {R} ^{3}:mx=y\},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcf3b7938d9e36db364fc7a559a516d0e9a9cb9c)

![{\displaystyle N=\{((x,y),[A:B])\in \mathbf {R} ^{2}\times \mathbf {RP} ^{1}:Ax=By,\ x^{2}+y^{2}\leq 1\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b2f6cc02685f04099ed246d0abef0d90983481)






![{\displaystyle [-y:x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86fd60d8c2287388ac6c39f3768881a5b1791661)





![{\displaystyle P=((1,0),[0:1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82494e67b7475f512a85350bff1a409dbfff6e3e)
![{\displaystyle \gamma (t)=((\cos(2\pi t),\sin(2\pi t)),[-\sin(2\pi t),\cos(2\pi t)])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e4fca428e81158af73db9be51c049bcaae2550c)

![{\displaystyle Q=((-1,0),[0:1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70844f757d63a3ab25862cb0d874d64120901951)








