Mound Builders

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Mound_Builders 

Monks Mound, built c. 950–1100 CE and located at the Cahokia Mounds UNESCO World Heritage Site near Collinsville, Illinois, is the largest pre-Columbian earthwork in America north of Mesoamerica.

A number of pre-Columbian cultures are collectively termed "Mound Builders". The term does not refer to a specific people or archaeological culture, but refers to the characteristic mound earthworks erected for an extended period of more than 5,000 years. The "Mound Builder" cultures span the period of roughly 3500 BCE (the construction of Watson Brake) to the 16th century CE, including the Archaic period, Woodland period (Calusa culture, Adena and Hopewell cultures), and Mississippian period. Geographically, the cultures were present in the region of the Great Lakes, the Ohio River Valley, and the Mississippi River valley and its tributary waters.

The first mound building was an early marker of political and social complexity among the cultures in the Eastern United States. Watson Brake in Louisiana, constructed about 3500 BCE during the Middle Archaic period, is currently the oldest known and dated mound complex in North America. It is one of 11 mound complexes from this period found in the Lower Mississippi Valley. These cultures generally had developed hierarchical societies that had an elite. These commanded hundreds or even thousands of workers to dig up tons of earth with the hand tools available, move the soil long distances, and finally, workers to create the shape with layers of soils as directed by the builders.

From about 800 CE, the mound building cultures were dominated by the Mississippian culture, a large archaeological horizon, whose youngest descendants, the Plaquemine culture and the Fort Ancient culture, were still active at the time of European contact in the 16th century. One tribe of the Fort Ancient culture has been identified as the Mosopelea, presumably of southeast Ohio, who were speakers of an Ohio Valley Siouan language. The bearers of the Plaquemine culture were presumably speakers of the Natchez language isolate. The first description of these cultures is due to Spanish explorer Hernando de Soto, written between 1540 and 1542.

Mounds

A mound diagram of the platform mound showing the multiple layers of mound construction, mound structures such as temples or mortuaries, ramps with log stairs, and prior structures under later layers, multiple terraces, and intrusive burials

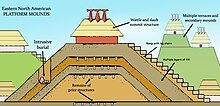
The namesake cultural trait of the Mound Builders was the building of mounds and other earthworks. These burial and ceremonial structures were typically flat-topped pyramids or platform mounds, flat-topped or rounded cones, elongated ridges, and sometimes a variety of other forms. They were generally built as part of complex villages. The early earthworks built in Louisiana around 3500 BCE are the only ones known to have been built by a hunter-gatherer culture, rather than a more settled culture based on agricultural surpluses.

The best-known flat-topped pyramidal structure is Monks Mound at Cahokia, near present-day Collinsville, Illinois. This mound appears to have been the main ceremonial and residential mound for the religious and political leaders; it is more than 100 feet (30 m) tall and is the largest pre-Columbian earthwork north of Mexico. This site had numerous mounds, some with conical or ridge tops, as well as a Woodhenge, and palisaded stockades protecting the large settlement and elite quarter. At its maximum about 1150 CE, Cahokia was an urban settlement with 20,000–30,000 people; this population was not exceeded by North American European settlements until after 1800.

A depiction of the Serpent Mound in southern Ohio, as published in the magazine The Century, April 1890

Some effigy mounds were constructed in the shapes or outlines of culturally significant animals. The most famous effigy mound, Serpent Mound in southern Ohio, ranges from 1 foot (0.30 m) to just over 3 feet (0.91 m) tall, 20 feet (6.1 m) wide, more than 1,330 feet (410 m) long, and shaped as an undulating serpent.

Early descriptions

Illustration of the Parkin site, thought to be the capital of the Province of Casqui visited by de Soto

Between 1540 and 1542, Hernando de Soto, the Spanish conquistador, traversed what became the southeastern United States. There he encountered many different mound-builder peoples who were perhaps descendants of the great Mississippian culture. De Soto observed people living in fortified towns with lofty mounds and plazas, and surmised that many of the mounds served as foundations for priestly temples. Near present-day Augusta, Georgia, de Soto encountered a group ruled by a queen, Cofitachequi. She told him that the mounds within her territory served as the burial places for nobles.

Engraving after Jacques le Moyne, showing the burial of a Timucua chief

The artist Jacques le Moyne, who had accompanied French settlers to northeastern Florida during the 1560s, likewise noted Native American groups using existing mounds and constructing others. He produced a series of watercolor paintings depicting scenes of native life. Although most of his paintings have been lost, some engravings were copied from the originals and published in 1591 by a Flemish company. Among these is a depiction of the burial of an aboriginal Floridian tribal chief, an occasion of great mourning and ceremony. The original caption reads:

Sometimes the deceased king of this province is buried with great solemnity, and his great cup from which he was accustomed to drink is placed on a tumulus with many arrows set about it.

— Jacques le Moyne, 1560s

Maturin Le Petit, a Jesuit priest, met the Natchez people, as did Le Page du Pratz (1758), a French explorer. Both observed them in the area that today is known as Mississippi. The Natchez were devout worshippers of the sun. Having a population of some 4,000, they occupied at least nine villages and were presided over by a paramount chief, known as the Great Sun, who wielded absolute power. Both observers noted the high temple mounds which the Natchez had built so that the Great Sun could commune with God, the sun. His large residence was built atop the highest mound, from "which, every morning, he greeted the rising sun, invoking thanks and blowing tobacco smoke to the four cardinal directions".

Archaeological surveys

A depiction of the Portsmouth Earthworks in Ancient Monuments of the Mississippi Valley

The most complete reference for these earthworks is Ancient Monuments of the Mississippi Valley, written by Ephraim G. Squier and Edwin H. Davis. It was published in 1848 by the Smithsonian Institution. Since many of the features which the authors documented have since been destroyed or diminished by farming and development, their surveys, sketches, and descriptions are still used by modern archaeologists. All of the sites which they identified as located in Kentucky came from the manuscripts of C. S. Rafinesque.

Chronology

Archaic era

Main article: Archaic period in the Americas

 

Illustration of Watson Brake, the oldest known mound complex in North America

 

Illustration of Poverty Point in West Carroll Parish, Louisiana

Radiocarbon dating has established the age of the earliest Archaic mound complex in southeastern Louisiana. One of the two Monte Sano Site mounds, excavated in 1967 before being destroyed for new construction at Baton Rouge, was dated at 6220 BP (plus or minus 140 years). Researchers at the time thought that such societies were not organizationally capable of this type of construction. It has since been dated as about 6500 BP, or 4500 BCE, although not all agree.

Watson Brake is located in the floodplain of the Ouachita River near Monroe in northern Louisiana. Securely dated to about 5,400 years ago (around 3500 BCE), in the Middle Archaic period, it consists of a formation of 11 mounds from 3 feet (0.91 m) to 25 feet (7.6 m) tall, connected by ridges to form an oval nearly 900 feet (270 m) across. In the Americas, building of complex earthwork mounds started at an early date, well before the pyramids of Egypt were constructed. Watson Brake was being constructed nearly 2,000 years before the better-known Poverty Point, and building continued for 500 years. Middle Archaic mound construction seems to have ceased about 2800 BCE, and scholars have not ascertained the reason, but it may have been because of changes in river patterns or other environmental factors.

With the 1990s dating of Watson Brake and similar complexes, scholars established that pre-agricultural, pre-ceramic American societies could organize to accomplish complex construction during extended periods of time, invalidating scholars' traditional ideas of Archaic society. Watson Brake was built by a hunter-gatherer society, the people of which occupied the area on only a seasonal basis, but where successive generations organized to build the complex mounds over a 500-year period. Their food consisted mostly of fish and deer, as well as available plants.

Poverty Point, built about 1500 BCE in what is now Louisiana, is a prominent example of Late Archaic mound-builder construction (around 2500 BCE – 1000 BCE). It is a striking complex of more than 1 square mile (2.6 km²), where six earthwork crescent ridges were built in concentric arrangement, interrupted by radial aisles. Three mounds are also part of the main complex, and evidence of residences extends for about 3 miles (4.8 km) along the bank of Bayou Macon. It is the major site among 100 associated with the Poverty Point culture and is one of the best-known early examples of earthwork monumental architecture. Unlike the localized societies during the Middle Archaic, this culture showed evidence of a wide trading network outside its area, which is one of its distinguishing characteristics.

Horr's Island, Florida, now a gated community next to Marco Island, when excavated by Michael Russo in 1980 found an Archaic Indian village site. Mound A was a burial mound that dated to 3400 BCE, making it the oldest known burial mound in North America.

Woodland period

Main article: Woodland period

 

Grave Creek Mound, Moundsville, West Virginia, Adena culture

The oldest mound associated with the Woodland period was the mortuary mound and pond complex at the Fort Center site in Glade County, Florida. 2012 excavations and dating by Thompson and Pluckhahn show that work began around 2600 BCE, seven centuries before the mound-builders in Ohio.

The Archaic period was followed by the Woodland period (circa 1000 BCE). Some well-understood examples are the Adena culture of Ohio, West Virginia, and parts of nearby states. The subsequent Hopewell culture built monuments from present-day Illinois to Ohio; it is renowned for its geometric earthworks. The Adena and Hopewell were not the only mound-building peoples during this time period. Contemporaneous mound-building cultures existed throughout what is now the Eastern United States, stretching as far south as Crystal River in western Florida. During this time, in parts of present-day Mississippi, Arkansas, and Louisiana, the Hopewellian Marksville culture degenerated and was succeeded by the Baytown culture. Reasons for degeneration include attacks from other tribes or the impact of severe climatic changes undermining agriculture.

Coles Creek culture

Illustration of Kings Crossing site in Warren County, Mississippi

 

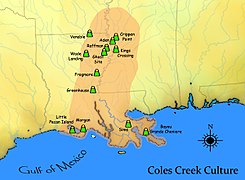
Main article: Coles Creek culture

The Coles Creek culture is a Late Woodland culture (700–1200 CE) in the Lower Mississippi Valley in the Southern United States that marks a significant change of the cultural history of the area. Population and cultural and political complexity increased, especially by the end of the Coles Creek period. Although many of the classic traits of chiefdom societies were not yet made, by 1000 CE, the formation of simple elite polities had begun. Coles Creek sites are found in Arkansas, Louisiana, Oklahoma, Mississippi, and Texas. The Coles Creek culture is considered ancestral to the Plaquemine culture.

Mississippian cultures

Illustration of Cahokia with the large Monks Mound in the central precinct, encircled by a palisade, surrounded by four plazas, notably the Grand Plaza to the south

 

Main article: Mississippian culture

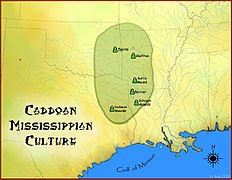
Around 900–1450 CE, the Mississippian culture developed and spread through the Eastern United States, primarily along the river valleys. The largest regional center where the Mississippian culture is first definitely developed is located in Illinois near the Mississippi, and is referred to presently as Cahokia. It had several regional variants including the Middle Mississippian culture of Cahokia, the South Appalachian Mississippian variant at Moundville and Etowah, the Plaquemine Mississippian variant in south Louisiana and Mississippi, and the Caddoan Mississippian culture of northwestern Louisiana, eastern Texas, and southwestern Arkansas. Like the mound builders of the Ohio, these people built gigantic mounds as burial and ceremonial places.

Fort Ancient culture

Artist's conception of the Fort Ancient culture SunWatch Indian Village

 

Main article: Fort Ancient culture

Fort Ancient is the name for a Native American culture that flourished from 1000 to 1650 CE among a people who predominantly inhabited land along the Ohio River in areas of modern-day southern Ohio, northern Kentucky, and western West Virginia.

Plaquemine culture

Illustration of the Holly Bluff site in Yazoo County, Mississippi

 

Main article: Plaquemine culture

A continuation of the Coles Creek culture in the lower Mississippi River Valley in western Mississippi and eastern Louisiana. Examples include the Medora site in West Baton Rouge Parish, Louisiana; and the Anna and Emerald Mound sites in Mississippi. Sites inhabited by Plaquemine peoples continued to be used as vacant ceremonial centers without large village areas much as their Coles Creek ancestors had done, although their layout began to show influences from Middle Mississippian peoples to the north. The Winterville and Holly Bluff (Lake George) sites in western Mississippi are good examples that exemplify this change of layout, but continuation of site usage. During the Terminal Coles Creek period (1150 to 1250 CE), contact increased with Mississippian cultures centered upriver near St. Louis, Missouri. This resulted in the adaption of new pottery techniques, as well as new ceremonial objects and possibly new social patterns during the Plaquemine period. As more Mississippian culture influences were absorbed, the Plaquemine area as a distinct culture began to shrink after CE 1350. Eventually, the last enclave of purely Plaquemine culture was the Natchez Bluffs area, while the Yazoo Basin and adjacent areas of Louisiana became a hybrid Plaquemine-Mississippian culture. This division was recorded by Europeans when they first arrived in the area. In the Natchez Bluffs area, the Taensa and Natchez people had held out against Mississippian influence and continued to use the same sites as their ancestors, and the Plaquemine culture is considered directly ancestral to these historic period groups encountered by Europeans. Groups who appear to have absorbed more Mississippian influence were identified as those tribes speaking the Tunican, Chitimachan, and Muskogean languages.

Disappearance

Following the description by Jacques le Moyne in 1560, the mound building cultures seem to have disappeared within the next century. However, there were also other European accounts, earlier than 1560, that gives a first-hand description of the enormous earth-built mounds being constructed by the Native Americans. One of them was Garcilaso de la Vega (c.1539–1616), a Spanish chronicler also known as "El Inca" because of his Incan mother, who was also the record-keeper of the infamous De Soto expedition that landed in present-day Florida on May 31, 1538. Garcilaso gave a first-hand description through his Historia de la Florida (published in 1605, Lisbon, as La Florida del Inca) describing how the Indians had built mounds and how the Native American Mound Cultures practiced their traditional way of life. De la Vega's accounts also include vital details about the Native American tribes' systems of government present in the South-East, tribal territories, and construction of mounds and temples. A few French expeditions in 1560s reported staying with Indian societies who had built mounds also.

Diseases

Later explorers to the same regions, only a few decades after mound-building settlements had been reported, found the regions largely depopulated with its residents vanished and the mounds untended. Conflicts with Europeans were dismissed by historians as the major cause of populations reduction, since only few clashes had occurred between the natives and the Europeans in the area during the same period. The most-widely accepted explanation behind the disappearances were the infectious diseases from the Old World, such as smallpox and influenza, which had decimated most of the Native Americans from the last mound-builder civilization. The Fort Ancient culture of the Ohio River valley is considered a "sister culture" of the Mississippian horizon, or one of the "Mississippianised" cultures adjacent to the main areal of the mound building cultures. This culture was also mostly extinct in the 17th century, but remnants may have survived into the first half of the 18th century. While this culture shows strong Mississippian influences, its bearers were most likely ethno-linguistically distinct from the Mississippians, possibly belonging to the Siouan phylum. The only tribal name associated with the Fort Ancient culture in the historical record are the Mosopelea, recorded by Jean-Baptiste-Louis Franquelin in 1684 as inhabiting eight villages north of the Ohio River. The Mosopelea are most likely identical to the Ofo (Oufé, Offogoula) recorded in the same area in the 18th century. The Ofo language was formerly classified as Muskogean but is now recognized as an eccentric member of the Western Siouan phylum. The late survival of the Fort Ancient culture is suggested by the remarkable amount of European made goods in the archaeological record which would have been acquired by trade even before direct European contact. These artefacts include brass and steel items, glassware, and melted down or broken goods reforged into new items. The Fort Ancient peoples are known to have been severely affected by disease in the 17th century (Beaver Wars period), and Carbon dating seems to indicate that they were wiped out by successive waves of disease.

Massacre and revolt

Because of the disappearance of the cultures by the end of the 17th century, the identification of the bearers of these cultures was an open question in 19th-century ethnography. Modern stratigraphic dating has established that the "Mound builders" have spanned the extended period of more than five millennia, so that any ethno-linguistic continuity is unlikely. The spread of the Mississippian culture from the late 1st millennium CE most likely involved cultural assimilation, in archaeological terminology called "Mississippianised" cultures.

19th-century ethnography assumed that the Mound-builders were an ancient prehistoric race with no direct connection to the Southeastern Woodland peoples of the historical period. A reference to this idea appears in the poem "The Prairies" (1832) by William Cullen Bryant.

The cultural stage of the Southeastern Woodland natives encountered in the 18th and 19th centuries by British colonists was deemed incompatible with the comparatively advanced stone, metal, and clay artifacts of the archaeological record. The age of the earthworks was also partly over-estimated. Caleb Atwater's misunderstanding of stratigraphy caused him to significantly overestimate the age of the earthworks. In his book, Antiquities Discovered in the Western States (1820), Atwater claimed that "Indian remains" were always found right beneath the surface of the earth, while artifacts associated with the Mound Builders were found fairly deep in the ground. Atwater argued that they must be from a different group of people. The discovery of metal artifacts further convinced people that the Mound Builders were not identical to the Southeast Woodland Native Americans of the 18th century.

It is now thought that the most likely bearers of the Plaquemine culture, a late variant of the Mississippian culture, were ancestral to the related Natchez and Taensa peoples. The Natchez language is a language isolate, supporting the scenario that after the collapse of the Mound builder cultures in the 17th century, there was an influx of unrelated peoples into the area. The Natchez are known to have historically occupied the Lower Mississippi Valley. They are first mentioned in French sources of around 1700, when they were centuered around the Grand Village close to present day Natchez, Mississippi. In 1729 the Natchez revolted, and massacred the French colony of Fort Rosalie, and the French retaliated by destroying all the Natchez villages. The remaining Natchez fled in scattered bands to live among the Chickasaw, Creek and Cherokee, whom they followed on the trail of tears when Indian removal policies of the mid 19th century forced them to relocate to Oklahoma. The Natchez language was extinct in the 20th century, with the death of the last known native speaker, Nancy Raven, in 1957.

Maps

• 

  Hopewell traditions

• 

  Adena culture

• 

  Troyville culture and Baytown culture

• 

  Coles Creek culture

• 

  Mississippian culture

• 

  Caddoan Mississippian culture

• 

  Fort Ancient culture

• 

  Plaquemine culture

Popular mythology

Alternative scenarios and hoaxes

See also: Archaeology and the Book of Mormon and Zelph

Based on the idea that the origins of the mound builders lay with a mysterious ancient people, there were various other suggestions belonging to the more general genre of Pre-Columbian trans-oceanic contact theories, specifically involving Vikings, Atlantis, and the Ten Lost Tribes of Israel, summarised by Feder (2006) under the heading of "The Myth of a Vanished Race".

Benjamin Smith Barton in his Observations on Some Parts of Natural History (1787) proposed the theory that the Mound Builders were associated with "Danes", i.e. with the Norse colonization of North America. In 1797, Barton reconsidered his position and correctly identified the mounds as part of indigenous prehistory.

Notable for the association with the Ten Lost Tribes is the Book of Mormon (1830). In this narrative, the Jaredites (3000–2000 BCE) and an Israelite group in 590 BCE (termed Nephites, Lamanites, and Mulekites). While the Nephites, Lamanites, and Mulekites were all of Jewish origin coming from Israel around 590 BCE, the Jaradites were a non-Abrahamic people separate in all aspects, except in a belief in Jehovah, from the Nephites. The Book of Mormon depicts these settlers building magnificent cities, which were destroyed by warfare about CE 385. The Book of Mormon can be placed in the tradition of the "Mound-Builder literature" of the period. Dahl (1961) states that it is "the most famous and certainly the most influential of all Mound-Builder literature". Later authors placing the Book of Mormon in this context include Silverberg (1969), Brodie (1971), Kennedy (1994) and Garlinghouse (2001).

Some nineteenth-century archaeological finds (e.g., earth and timber fortifications and towns, the use of a plaster-like cement, ancient roads, metal points and implements, copper breastplates, head-plates, textiles, pearls, native North American inscriptions, North American elephant remains etc.) were well-publicized at the time of the publication of the Book of Mormon and there is incorporation of some of these ideas into the narrative. References are made in the Book of Mormon to then-current understanding of pre-Columbian civilizations, including the formative Mesoamerican civilizations such as the (Pre-Classic) Olmec, Maya, and Zapotec.

Lafcadio Hearn in 1876 suggested that the mounds were built by people from the lost continent of Atlantis. The Reverend Landon West in 1901 claimed that Serpent Mound in Ohio was built by God, or by man inspired by him. He believed that God built the mound and placed it as a symbol of the story of the Garden of Eden.

More recently, Black nationalist websites claiming association with the Moorish Science Temple of America, have taken up the Atlantean ("Mu") association of the Mound Builders. Similarly, the "Washitaw Nation", a group associated with the Moorish Science Temple of America established in the 1990s, has been associated with mound-building in Black nationalist online articles of the early 2000s.

Kinderhook plates

On April 23, 1843, nine men unearthed human bones and six small, bell-shaped plates in Kinderhook, Illinois. Both sides of the plates apparently contained some sort of ancient writings. The plates, later known as the Kinderhook plates, were presented to Joseph Smith, who was an American religious leader and founder of Mormonism. He was reported to have said, "I have translated a portion of them, and find they contain the history of the person with whom they were found. He was a descendant of Ham, through the loins of Pharaoh, king of Egypt, and that he received his kingdom from the Ruler of heaven and earth."

In later letters, two eyewitnesses among the nine people who were present at the excavation of the plates, W. P. Harris and Wilbur Fugate, confessed that the whole thing was a hoax. With a group of other conspirators, they had manufactured the plates to give them the appearance of antiquity, buried them in a mound, and later pretended to excavate them, all for the purpose of trapping Joseph Smith into pretending to translate. However, it was not until 1980, when the only remaining plate was forensically examined, that the plates were conclusively determined to be, in fact, a nineteenth-century production.Up to 1980 most Latter-day Saints rejected the confessions and believed the plates were authentic. Not only did skeptics accept the confessors’ statements, but some continue to this day to argue that Joseph Smith pretended to translate a portion of the faked plates, claiming that he could not have been a true prophet.

The purpose for faking the Kinderhook plates is mainly to prove that the book of Mormon is true according to the witness Fulgate, "We learn there was a Mormon present when the plates were found, who it is said, leaped for joy at the discovery, and remarked that it would go to prove the authenticity of the Book of Mormon. The Mormons wanted to take the plates to Joe Smith, but we refused to let them go. Some time afterward a man assuming the name of Savage, of Quincy, borrowed the plates of Wiley to show to his literary friends there, and took them to Joe Smith."

Newark Holy Stone

Keystone

On June 29, 1860, David Wyrick, the surveyor of Licking County near Newark, discovered the so called Keystone in a shallow excavation at the monumental Newark Earthworks, which is an extraordinary set of ancient geometric enclosures created by Indigenous people. There he dug up a four-sided, plumb-bob-shaped stone with Hebrew letters engraved on each of its faces. The local Episcopal minister John W. McCarty translated the four inscriptions as "Law of the Lord," “Word of the Lord," “Holy of Holies," and "King of the Earth." Charles Whittlesey, who was one of the foremost archaeologists at that time, pronounced the stone to be authentic. The Newark Holy Stones, if genuine, would provide support for monogenesis, since they would establish that American Indians could be encompassed within Biblical history.

Decalogue Stone

After his first expedition, Wyrick uncovered a small stone box that was found to contain an intricately carved slab of black limestone covered with archaic-looking Hebrew letters along with a representation of a man in flowing robes. When translated, once again by McCarty, the inscription was found to include the entire Ten Commandments, and the robed figure was identified as Moses. Naturally enough, it became known as the Decalogue Stone.

Rather than being found beneath only a foot or two of soil, the Decalogue Stone was claimed to have been buried beneath a forty-foot-tall stone mound. Instead of modern Hebrew typography, the characters on the stone were blocky and appeared to be an ancient form of the Hebrew alphabet. Finally, the stone bore no resemblance to any modern Masonic artifact. In 1870, Whittlesey declared finally that the Holy Stones and other similar artifacts were "Archaeological Frauds."

Giants

In 19th-century America, a number of popular mythologies surrounding the origin of the mounds were in circulation, typically involving the mounds being built by a race of giants. A New York Times article from 1897 described a mound in Wisconsin in which a giant human skeleton measuring over 9 feet (2.7 m) in length was found. From 1886, another New York Times article described water receding from a mound in Cartersville, Georgia, which uncovered acres of skulls and bones, some of which were said to be gigantic. Two thigh bones were measured with the height of their owners estimated at 14 feet (4.3 m). President Lincoln made reference to the giants whose bones fill the mounds of America.

But still there is more. It calls up the indefinite past. When Columbus first sought this continent – when Christ suffered on the cross – when Moses led Israel through the Red-Sea – nay, even, when Adam first came from the hand of his Maker – then as now, Niagara was roaring here. The eyes of that species of extinct giants, whose bones fill the mounds of America, have gazed on Niagara, as ours do now. Co[n]temporary with the whole race of men, and older than the first man, Niagara is strong, and fresh to-day as ten thousand years ago. The Mammoth and Mastodon – now so long dead, that fragments of their monstrous bones, alone testify, that they ever lived, have gazed on Niagara. In that long – long time, never still for a single moment. Never dried, never froze, never slept, never rested.

The antiquarian author William Pidgeon in 1858 created fraudulent surveys of mound groups that did not exist.

Beginning in the 1880s, the supposed origin of the earthworks with a race of giants was increasingly recognized as spurious. Pidgeon's fraudulent claims about the archaeological record was shown to be a hoax by Theodore Lewis in 1886. A major factor contributing to public acceptance of the earthworks as a regular part of North American prehistory was the 1894 report by Cyrus Thomas of the Bureau of American Ethnology. Earlier authors making a similar case include Thomas Jefferson, who excavated a mound and from the artifacts and burial practices, noted similarities between mound-builder funeral practices and those of Native Americans in his time.

Walam Olum

The Walam Olum hoax had considerable influence on perceptions of the Mound Builders. In 1836, Constantine Samuel Rafinesque published his translation of a text he claimed had been written in pictographs on wooden tablets. This text explained that the Lenape Indians originated in Asia, told of their passage over the Bering Strait, and narrated their subsequent migration across the North American continent. This "Walam Olum" tells of battles with native peoples already in America before the Lenape arrived. People hearing of the account believed that the "original people" were the Mound Builders, and that the Lenape overthrew them and destroyed their culture. David Oestreicher later asserted that Rafinesque's account was a hoax. He argued that the Walam Olum glyphs derived from Chinese, Egyptian, and Mayan alphabets. Meanwhile, the belief that the Native Americans destroyed the mound-builder culture had gained widespread acceptance.

Symmetry in mathematics

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Symmetry_in_mathematics 

The root system of the exceptional Lie group E₈. Lie groups have many symmetries.

Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that a mathematical object remains unchanged under a set of operations or transformations.

Given a structured object X of any sort, a symmetry is a mapping of the object onto itself which preserves the structure. This can occur in many ways; for example, if X is a set with no additional structure, a symmetry is a bijective map from the set to itself, giving rise to permutation groups. If the object X is a set of points in the plane with its metric structure or any other metric space, a symmetry is a bijection of the set to itself which preserves the distance between each pair of points (i.e., an isometry).

In general, every kind of structure in mathematics will have its own kind of symmetry, many of which are listed in the given points mentioned above.

Symmetry in geometry

Main article: Symmetry (geometry)

The types of symmetry considered in basic geometry include reflectional symmetry, rotation symmetry, translational symmetry and glide reflection symmetry, which are described more fully in the main article Symmetry (geometry).

Symmetry in calculus

Even and odd functions

Main article: Even and odd functions

Even functions

ƒ(x) = x² is an example of an even function.

Let f(x) be a real-valued function of a real variable, then f is even if the following equation holds for all x and -x in the domain of f:

${\displaystyle f(x)=f(-x)}$

Geometrically speaking, the graph face of an even function is symmetric with respect to the y-axis, meaning that its graph remains unchanged after reflection about the y-axis. Examples of even functions include |x|, x², x⁴, cos(x), and cosh(x).

Odd functions

ƒ(x) = x³ is an example of an odd function.

Again, let f(x) be a real-valued function of a real variable, then f is odd if the following equation holds for all x and -x in the domain of f:

${\displaystyle -f(x)=f(-x)}$

That is,

${\displaystyle f(x)+f(-x)=0\,.}$

Geometrically, the graph of an odd function has rotational symmetry with respect to the origin, meaning that its graph remains unchanged after rotation of 180 degrees about the origin. Examples of odd functions are x, x³, sin(x), sinh(x), and erf(x).

Integrating

The integral of an odd function from −A to +A is zero, provided that A is finite and that the function is integrable (e.g., has no vertical asymptotes between −A and A).

The integral of an even function from −A to +A is twice the integral from 0 to +A, provided that A is finite and the function is integrable (e.g., has no vertical asymptotes between −A and A). This also holds true when A is infinite, but only if the integral converges.

Series

• The Maclaurin series of an even function includes only even powers.
• The Maclaurin series of an odd function includes only odd powers.
• The Fourier series of a periodic even function includes only cosine terms.
• The Fourier series of a periodic odd function includes only sine terms.

Symmetry in linear algebra

Symmetry in matrices

In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose (i.e., it is invariant under matrix transposition). Formally, matrix A is symmetric if

${\displaystyle A=A^{T}.}$

By the definition of matrix equality, which requires that the entries in all corresponding positions be equal, equal matrices must have the same dimensions (as matrices of different sizes or shapes cannot be equal). Consequently, only square matrices can be symmetric.

The entries of a symmetric matrix are symmetric with respect to the main diagonal. So if the entries are written as A = (a_ij), then a_ij = a_ji, for all indices i and j.

For example, the following 3×3 matrix is symmetric:

${\displaystyle {\begin{bmatrix}1&7&3\\7&4&-5\\3&-5&6\end{bmatrix}}}$

Every square diagonal matrix is symmetric, since all off-diagonal entries are zero. Similarly, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative.

In linear algebra, a real symmetric matrix represents a self-adjoint operator over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refers to one which has real-valued entries. Symmetric matrices appear naturally in a variety of applications, and typical numerical linear algebra software makes special accommodations for them.

Symmetry in abstract algebra

Symmetric groups

Main article: Symmetric group

The symmetric group S_n (on a finite set of n symbols) is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself. Since there are n! (n factorial) possible permutations of a set of n symbols, it follows that the order (i.e., the number of elements) of the symmetric group S_n is n!.

Symmetric polynomials

Main article: Symmetric polynomial

A symmetric polynomial is a polynomial P(X₁, X₂, ..., X_n) in n variables, such that if any of the variables are interchanged, one obtains the same polynomial. Formally, P is a symmetric polynomial if for any permutation σ of the subscripts 1, 2, ..., n, one has P(X_σ(1), X_σ(2), ..., X_σ(n)) = P(X₁, X₂, ..., X_n).

Symmetric polynomials arise naturally in the study of the relation between the roots of a polynomial in one variable and its coefficients, since the coefficients can be given by polynomial expressions in the roots, and all roots play a similar role in this setting. From this point of view, the elementary symmetric polynomials are the most fundamental symmetric polynomials. A theorem states that any symmetric polynomial can be expressed in terms of elementary symmetric polynomials, which implies that every symmetric polynomial expression in the roots of a monic polynomial can alternatively be given as a polynomial expression in the coefficients of the polynomial.

Examples

In two variables X₁ and X₂, one has symmetric polynomials such as:

• ${\displaystyle X_{1}^{3}+X_{2}^{3}-7}$
• ${\displaystyle 4X_{1}^{2}X_{2}^{2}+X_{1}^{3}X_{2}+X_{1}X_{2}^{3}+(X_{1}+X_{2})^{4}}$

and in three variables X₁, X₂ and X₃, one has as a symmetric polynomial:

• ${\displaystyle X_{1}X_{2}X_{3}-2X_{1}X_{2}-2X_{1}X_{3}-2X_{2}X_{3}\,}$

Symmetric tensors

Main article: Symmetric tensor

In mathematics, a symmetric tensor is tensor that is invariant under a permutation of its vector arguments:

${\displaystyle T(v_{1},v_{2},\dots ,v_{r})=T(v_{\sigma 1},v_{\sigma 2},\dots ,v_{\sigma r})}$

for every permutation σ of the symbols {1,2,...,r}. Alternatively, an r^th order symmetric tensor represented in coordinates as a quantity with r indices satisfies

${\displaystyle T_{i_{1}i_{2}\dots i_{r}}=T_{i_{\sigma 1}i_{\sigma 2}\dots i_{\sigma r}}.}$

The space of symmetric tensors of rank r on a finite-dimensional vector space is naturally isomorphic to the dual of the space of homogeneous polynomials of degree r on V. Over fields of characteristic zero, the graded vector space of all symmetric tensors can be naturally identified with the symmetric algebra on V. A related concept is that of the antisymmetric tensor or alternating form. Symmetric tensors occur widely in engineering, physics and mathematics.

Galois theory

Main article: Galois theory

Given a polynomial, it may be that some of the roots are connected by various algebraic equations. For example, it may be that for two of the roots, say A and B, that A² + 5B³ = 7. The central idea of Galois theory is to consider those permutations (or rearrangements) of the roots having the property that any algebraic equation satisfied by the roots is still satisfied after the roots have been permuted. An important proviso is that we restrict ourselves to algebraic equations whose coefficients are rational numbers. Thus, Galois theory studies the symmetries inherent in algebraic equations.

Automorphisms of algebraic objects

Main article: Automorphism

In abstract algebra, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.

Examples

• In set theory, an arbitrary permutation of the elements of a set X is an automorphism. The automorphism group of X is also called the symmetric group on X.
• In elementary arithmetic, the set of integers, Z, considered as a group under addition, has a unique nontrivial automorphism: negation. Considered as a ring, however, it has only the trivial automorphism. Generally speaking, negation is an automorphism of any abelian group, but not of a ring or field.
• A group automorphism is a group isomorphism from a group to itself. Informally, it is a permutation of the group elements such that the structure remains unchanged. For every group G there is a natural group homomorphism G → Aut(G) whose image is the group Inn(G) of inner automorphisms and whose kernel is the center of G. Thus, if G has trivial center it can be embedded into its own automorphism group.
• In linear algebra, an endomorphism of a vector space V is a linear operator V → V. An automorphism is an invertible linear operator on V. When the vector space is finite-dimensional, the automorphism group of V is the same as the general linear group, GL(V).
• A field automorphism is a bijective ring homomorphism from a field to itself. In the cases of the rational numbers (Q) and the real numbers (R) there are no nontrivial field automorphisms. Some subfields of R have nontrivial field automorphisms, which however do not extend to all of R (because they cannot preserve the property of a number having a square root in R). In the case of the complex numbers, C, there is a unique nontrivial automorphism that sends R into R: complex conjugation, but there are infinitely (uncountably) many "wild" automorphisms (assuming the axiom of choice).^[6] Field automorphisms are important to the theory of field extensions, in particular Galois extensions. In the case of a Galois extension L/K the subgroup of all automorphisms of L fixing K pointwise is called the Galois group of the extension.

Symmetry in representation theory

Symmetry in quantum mechanics: bosons and fermions

In quantum mechanics, bosons have representatives that are symmetric under permutation operators, and fermions have antisymmetric representatives.

This implies the Pauli exclusion principle for fermions. In fact, the Pauli exclusion principle with a single-valued many-particle wavefunction is equivalent to requiring the wavefunction to be antisymmetric. An antisymmetric two-particle state is represented as a sum of states in which one particle is in state ${\displaystyle \scriptstyle |x\rangle }$ and the other in state ${\displaystyle \scriptstyle |y\rangle }$:

${\displaystyle |\psi \rangle =\sum _{x,y}A(x,y)|x,y\rangle }$

and antisymmetry under exchange means that A(x,y) = −A(y,x). This implies that A(x,x) = 0, which is Pauli exclusion. It is true in any basis, since unitary changes of basis keep antisymmetric matrices antisymmetric, although strictly speaking, the quantity A(x,y) is not a matrix but an antisymmetric rank-two tensor.

Conversely, if the diagonal quantities A(x,x) are zero in every basis, then the wavefunction component:

${\displaystyle A(x,y)=\langle \psi |x,y\rangle =\langle \psi |(|x\rangle \otimes |y\rangle )}$

is necessarily antisymmetric. To prove it, consider the matrix element:

${\displaystyle \langle \psi |((|x\rangle +|y\rangle )\otimes (|x\rangle +|y\rangle ))\,}$

This is zero, because the two particles have zero probability to both be in the superposition state ${\displaystyle \scriptstyle |x\rangle +|y\rangle }$. But this is equal to

${\displaystyle \langle \psi |x,x\rangle +\langle \psi |x,y\rangle +\langle \psi |y,x\rangle +\langle \psi |y,y\rangle \,}$

The first and last terms on the right hand side are diagonal elements and are zero, and the whole sum is equal to zero. So the wavefunction matrix elements obey:

${\displaystyle \langle \psi |x,y\rangle +\langle \psi |y,x\rangle =0\,}$.

or

${\displaystyle A(x,y)=-A(y,x)\,}$

Symmetry in set theory

Symmetric relation

Main article: Symmetric relation

We call a relation symmetric if every time the relation stands from A to B, it stands too from B to A. Note that symmetry is not the exact opposite of antisymmetry.

Symmetry in metric spaces

Isometries of a space

Main article: Isometry

An isometry is a distance-preserving map between metric spaces. Given a metric space, or a set and scheme for assigning distances between elements of the set, an isometry is a transformation which maps elements to another metric space such that the distance between the elements in the new metric space is equal to the distance between the elements in the original metric space. In a two-dimensional or three-dimensional space, two geometric figures are congruent if they are related by an isometry: related by either a rigid motion, or a composition of a rigid motion and a reflection. Up to a relation by a rigid motion, they are equal if related by a direct isometry.

Isometries have been used to unify the working definition of symmetry in geometry and for functions, probability distributions, matrices, strings, graphs, etc.

Symmetries of differential equations

A symmetry of a differential equation is a transformation that leaves the differential equation invariant. Knowledge of such symmetries may help solve the differential equation.

A Line symmetry of a system of differential equations is a continuous symmetry of the system of differential equations. Knowledge of a Line symmetry can be used to simplify an ordinary differential equation through reduction of order.

For ordinary differential equations, knowledge of an appropriate set of Lie symmetries allows one to explicitly calculate a set of first integrals, yielding a complete solution without integration.

Symmetries may be found by solving a related set of ordinary differential equations. Solving these equations is often much simpler than solving the original differential equations.

Symmetry in probability

In the case of a finite number of possible outcomes, symmetry with respect to permutations (relabelings) implies a discrete uniform distribution.

In the case of a real interval of possible outcomes, symmetry with respect to interchanging sub-intervals of equal length corresponds to a continuous uniform distribution.

In other cases, such as "taking a random integer" or "taking a random real number", there are no probability distributions at all symmetric with respect to relabellings or to exchange of equally long subintervals. Other reasonable symmetries do not single out one particular distribution, or in other words, there is not a unique probability distribution providing maximum symmetry.

There is one type of isometry in one dimension that may leave the probability distribution unchanged, that is reflection in a point, for example zero.

A possible symmetry for randomness with positive outcomes is that the former applies for the logarithm, i.e., the outcome and its reciprocal have the same distribution. However this symmetry does not single out any particular distribution uniquely.

For a "random point" in a plane or in space, one can choose an origin, and consider a probability distribution with circular or spherical symmetry, respectively.