Empirical evidence

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Empirical_evidence

Empirical evidence for a proposition is evidence, i.e. what supports or counters this proposition, that is constituted by or accessible to sense experience or experimental procedure. Empirical evidence is of central importance to the sciences and plays a role in various other fields, like epistemology and law.

There is no general agreement on how the terms evidence and empirical are to be defined. Often different fields work with quite different conceptions. In epistemology, evidence is what justifies beliefs or what determines whether holding a certain belief is rational. This is only possible if the evidence is possessed by the person, which has prompted various epistemologists to conceive evidence as private mental states like experiences or other beliefs. In philosophy of science, on the other hand, evidence is understood as that which confirms or disconfirms scientific hypotheses and arbitrates between competing theories. For this role, it is important that evidence is public and uncontroversial, like observable physical objects or events and unlike private mental states, so that evidence may foster scientific consensus. The term empirical comes from Greek ἐμπειρία empeiría, i.e. 'experience'. In this context, it is usually understood as what is observable, in contrast to unobservable or theoretical objects. It is generally accepted that unaided perception constitutes observation, but it is disputed to what extent objects accessible only to aided perception, like bacteria seen through a microscope or positrons detected in a cloud chamber, should be regarded as observable.

Empirical evidence is essential to a posteriori knowledge or empirical knowledge, knowledge whose justification or falsification depends on experience or experiment. A priori knowledge, on the other hand, is seen either as innate or as justified by rational intuition and therefore as not dependent on empirical evidence. Rationalism fully accepts that there is knowledge a priori, which is either outright rejected by empiricism or accepted only in a restricted way as knowledge of relations between our concepts but not as pertaining to the external world.

Scientific evidence is closely related to empirical evidence but not all forms of empirical evidence meet the standards dictated by scientific methods. Sources of empirical evidence are sometimes divided into observation and experimentation, the difference being that only experimentation involves manipulation or intervention: phenomena are actively created instead of being passively observed.

Background

Main article: Evidence

The concept of evidence is of central importance in epistemology and in philosophy of science but plays different roles in these two fields. In epistemology, evidence is what justifies beliefs or what determines whether holding a certain doxastic attitude is rational. For example, the olfactory experience of smelling smoke justifies or makes it rational to hold the belief that something is burning. It is usually held that for justification to work, the evidence has to be possessed by the believer. The most straightforward way to account for this type of evidence possession is to hold that evidence consists of the private mental states possessed by the believer.

Some philosophers restrict evidence even further, for example, to only conscious, propositional or factive mental states. Restricting evidence to conscious mental states has the implausible consequence that many simple everyday beliefs would be unjustified. This is why it is more common to hold that all kinds of mental states, including stored but currently unconscious beliefs, can act as evidence. Various of the roles played by evidence in reasoning, for example, in explanatory, probabilistic and deductive reasoning, suggest that evidence has to be propositional in nature, i.e. that it is correctly expressed by propositional attitude verbs like "believe" together with a that-clause, like "that something is burning". But it runs counter to the common practice of treating non-propositional sense-experiences, like bodily pains, as evidence. Its defenders sometimes combine it with the view that evidence has to be factive, i.e. that only attitudes towards true propositions constitute evidence. In this view, there is no misleading evidence. The olfactory experience of smoke would count as evidence if it was produced by a fire but not if it was produced by a smoke generator. This position has problems in explaining why it is still rational for the subject to believe that there is a fire even though the olfactory experience cannot be considered evidence.

In philosophy of science, evidence is understood as that which confirms or disconfirms scientific hypotheses and arbitrates between competing theories. Measurements of Mercury's "anomalous" orbit, for example, constitute evidence that plays the role of neutral arbiter between Newton's and Einstein's theory of gravitation by confirming Einstein's theory. For scientific consensus, it is central that evidence is public and uncontroversial, like observable physical objects or events and unlike private mental states. This way it can act as a shared ground for proponents of competing theories. Two issues threatening this role are the problem of underdetermination and theory-ladenness. The problem of underdetermination concerns the fact that the available evidence often provides equal support to either theory and therefore cannot arbitrate between them. Theory-ladenness refers to the idea that evidence already includes theoretical assumptions. These assumptions can hinder it from acting as neutral arbiter. It can also lead to a lack of shared evidence if different scientists do not share these assumptions. Thomas Kuhn is an important advocate of the position that theory-ladenness in relation to scientific paradigms plays a central role in science.

Definition

A thing is evidence for a proposition if it epistemically supports this proposition or indicates that the supported proposition is true. Evidence is empirical if it is constituted by or accessible to sensory experience. There are various competing theories about the exact definition of the terms evidence and empirical. Different fields, like epistemology, the sciences or legal systems, often associate different concepts with these terms. An important distinction among theories of evidence is whether they identify evidence with private mental states or with public physical objects. Concerning the term empirical, there is a dispute about where to draw the line between observable or empirical objects in contrast to unobservable or merely theoretical objects.

The traditional view proposes that evidence is empirical if it is constituted by or accessible to sensory experience. This involves experiences arising from the stimulation of the sense organs, like visual or auditory experiences, but the term is often used in a wider sense including memories and introspection. It is usually seen as excluding purely intellectual experiences, like rational insights or intuitions used to justify basic logical or mathematical principles. The terms empirical and observable are closely related and sometimes used as synonyms.

There is an active debate in contemporary philosophy of science as to what should be regarded as observable or empirical in contrast to unobservable or merely theoretical objects. There is general consensus that everyday objects like books or houses are observable since they are accessible via unaided perception, but disagreement starts for objects that are only accessible through aided perception. This includes using telescopes to study distant galaxies, microscopes to study bacteria or using cloud chambers to study positrons. So the question is whether distant galaxies, bacteria or positrons should be regarded as observable or merely theoretical objects. Some even hold that any measurement process of an entity should be considered an observation of this entity. So in this sense, the interior of the sun is observable since neutrinos originating there can be detected. The difficulty with this debate is that there is a continuity of cases going from looking at something with the naked eye, through a window, through a pair of glasses, through a microscope, etc. Because of this continuity, drawing the line between any two adjacent cases seems to be arbitrary. One way to avoid these difficulties is to hold that it is a mistake to identify the empirical with what is observable or sensible. Instead, it has been suggested that empirical evidence can include unobservable entities as long as they are detectable through suitable measurements. A problem with this approach is that it is rather far from the original meaning of "empirical", which contains the reference to experience.

Related concepts

Knowledge a posteriori and a priori

Main article: A priori and a posteriori

Knowledge or the justification of a belief is said to be a posteriori if it is based on empirical evidence. A posteriori refers to what depends on experience (what comes after experience), in contrast to a priori, which stands for what is independent of experience (what comes before experience). For example, the proposition that "all bachelors are unmarried" is knowable a priori since its truth only depends on the meanings of the words used in the expression. The proposition "some bachelors are happy", on the other hand, is only knowable a posteriori since it depends on experience of the world as its justifier. Immanuel Kant held that the difference between a posteriori and a priori is tantamount to the distinction between empirical and non-empirical knowledge.

Two central questions for this distinction concern the relevant sense of "experience" and of "dependence". The paradigmatic justification of knowledge a posteriori consists in sensory experience, but other mental phenomena, like memory or introspection, are also usually included in it. But purely intellectual experiences, like rational insights or intuitions used to justify basic logical or mathematical principles, are normally excluded from it. There are different senses in which knowledge may be said to depend on experience. In order to know a proposition, the subject has to be able to entertain this proposition, i.e. possess the relevant concepts. For example, experience is necessary to entertain the proposition "if something is red all over then it is not green all over" because the terms "red" and "green" have to be acquired this way. But the sense of dependence most relevant to empirical evidence concerns the status of justification of a belief. So experience may be needed to acquire the relevant concepts in the example above, but once these concepts are possessed, no further experience providing empirical evidence is needed to know that the proposition is true, which is why it is considered to be justified a priori.

Empiricism and rationalism

In its strictest sense, empiricism is the view that all knowledge is based on experience or that all epistemic justification arises from empirical evidence. This stands in contrast to the rationalist view, which holds that some knowledge is independent of experience, either because it is innate or because it is justified by reason or rational reflection alone. Expressed through the distinction between knowledge a priori and a posteriori from the previous section, rationalism affirms that there is knowledge a priori, which is denied by empiricism in this strict form. One difficulty for empiricists is to account for the justification of knowledge pertaining to fields like mathematics and logic, for example, that 3 is a prime number or that modus ponens is a valid form of deduction. The difficulty is due to the fact that there seems to be no good candidate of empirical evidence that could justify these beliefs. Such cases have prompted empiricists to allow for certain forms of knowledge a priori, for example, concerning tautologies or relations between our concepts. These concessions preserve the spirit of empiricism insofar as the restriction to experience still applies to knowledge about the external world. In some fields, like metaphysics or ethics, the choice between empiricism and rationalism makes a difference not just for how a given claim is justified but for whether it is justified at all. This is best exemplified in metaphysics, where empiricists tend to take a skeptical position, thereby denying the existence of metaphysical knowledge, while rationalists seek justification for metaphysical claims in metaphysical intuitions.

Scientific evidence

Main article: Scientific evidence

Scientific evidence is closely related to empirical evidence. Some theorists, like Carlos Santana, have argued that there is a sense in which not all empirical evidence constitutes scientific evidence. One reason for this is that the standards or criteria that scientists apply to evidence exclude certain evidence that is legitimate in other contexts. For example, anecdotal evidence from a friend about how to treat a certain disease constitutes empirical evidence that this treatment works but would not be considered scientific evidence. Others have argued that the traditional empiricist definition of empirical evidence as perceptual evidence is too narrow for much of scientific practice, which uses evidence from various kinds of non-perceptual equipment.

Central to scientific evidence is that it was arrived at by following scientific method in the context of some scientific theory. But people rely on various forms of empirical evidence in their everyday lives that have not been obtained this way and therefore do not qualify as scientific evidence. One problem with non-scientific evidence is that it is less reliable, for example, due to cognitive biases like the anchoring effect, in which information obtained earlier is given more weight, although science done poorly is also subject to such biases, as in the example of p-hacking.

Observation, experimentation and scientific method

In the philosophy of science, it is sometimes held that there are two sources of empirical evidence: observation and experimentation. The idea behind this distinction is that only experimentation involves manipulation or intervention: phenomena are actively created instead of being passively observed. For example, inserting viral DNA into a bacterium is a form of experimentation while studying planetary orbits through a telescope belongs to mere observation. In these cases, the mutated DNA was actively produced by the biologist while the planetary orbits are independent of the astronomer observing them. Applied to the history of science, it is sometimes held that ancient science is mainly observational while the emphasis on experimentation is only present in modern science and responsible for the scientific revolution. This is sometimes phrased through the expression that modern science actively "puts questions to nature". This distinction also underlies the categorization of sciences into experimental sciences, like physics, and observational sciences, like astronomy. While the distinction is relatively intuitive in paradigmatic cases, it has proven difficult to give a general definition of "intervention" applying to all cases, which is why it is sometimes outright rejected.

Empirical evidence is required for a hypothesis to gain acceptance in the scientific community. Normally, this validation is achieved by the scientific method of forming a hypothesis, experimental design, peer review, reproduction of results, conference presentation, and journal publication. This requires rigorous communication of hypothesis (usually expressed in mathematics), experimental constraints and controls (expressed in terms of standard experimental apparatus), and a common understanding of measurement. In the scientific context, the term semi-empirical is used for qualifying theoretical methods that use, in part, basic axioms or postulated scientific laws and experimental results. Such methods are opposed to theoretical ab initio methods, which are purely deductive and based on first principles. Typical examples of both ab initio and semi-empirical methods can be found in computational chemistry.

Electrical resistance and conductance

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Electrical_resistance_and_conductance

The electrical resistance of an object is a measure of its opposition to the flow of electric current. Its reciprocal quantity is electrical conductance, measuring the ease with which an electric current passes. Electrical resistance shares some conceptual parallels with mechanical friction. The SI unit of electrical resistance is the ohm (Ω), while electrical conductance is measured in siemens (S) (formerly called the 'mho' and then represented by ℧).

The resistance of an object depends in large part on the material it is made of. Objects made of electrical insulators like rubber tend to have very high resistance and low conductance, while objects made of electrical conductors like metals tend to have very low resistance and high conductance. This relationship is quantified by resistivity or conductivity. The nature of a material is not the only factor in resistance and conductance, however; it also depends on the size and shape of an object because these properties are extensive rather than intensive. For example, a wire's resistance is higher if it is long and thin, and lower if it is short and thick. All objects resist electrical current, except for superconductors, which have a resistance of zero.

The resistance R of an object is defined as the ratio of voltage V across it to current I through it, while the conductance G is the reciprocal:

$${\displaystyle R=\frac{V}{I},G=\frac{I}{V}=\frac{1}{R}}$$

For a wide variety of materials and conditions, V and I are directly proportional to each other, and therefore R and G are constants (although they will depend on the size and shape of the object, the material it is made of, and other factors like temperature or strain). This proportionality is called Ohm's law, and materials that satisfy it are called ohmic materials.

In other cases, such as a transformer, diode or battery, V and I are not directly proportional. The ratio V/I is sometimes still useful, and is referred to as a chordal resistance or static resistance, since it corresponds to the inverse slope of a chord between the origin and an I–V curve. In other situations, the derivative $\frac{\mathrm{d}V}{\mathrm{d}I}$ may be most useful; this is called the differential resistance.

Introduction

The hydraulic analogy compares electric current flowing through circuits to water flowing through pipes. When a pipe (left) is filled with hair (right), it takes a larger pressure to achieve the same flow of water. Pushing electric current through a large resistance is like pushing water through a pipe clogged with hair: It requires a larger push (electromotive force) to drive the same flow (electric current).

In the hydraulic analogy, current flowing through a wire (or resistor) is like water flowing through a pipe, and the voltage drop across the wire is like the pressure drop that pushes water through the pipe. Conductance is proportional to how much flow occurs for a given pressure, and resistance is proportional to how much pressure is required to achieve a given flow.

The voltage drop (i.e., difference between voltages on one side of the resistor and the other), not the voltage itself, provides the driving force pushing current through a resistor. In hydraulics, it is similar: the pressure difference between two sides of a pipe, not the pressure itself, determines the flow through it. For example, there may be a large water pressure above the pipe, which tries to push water down through the pipe. But there may be an equally large water pressure below the pipe, which tries to push water back up through the pipe. If these pressures are equal, no water flows. (In the image at right, the water pressure below the pipe is zero.)

The resistance and conductance of a wire, resistor, or other element is mostly determined by two properties:

• geometry (shape), and
• material

Geometry is important because it is more difficult to push water through a long, narrow pipe than a wide, short pipe. In the same way, a long, thin copper wire has higher resistance (lower conductance) than a short, thick copper wire.

Materials are important as well. A pipe filled with hair restricts the flow of water more than a clean pipe of the same shape and size. Similarly, electrons can flow freely and easily through a copper wire, but cannot flow as easily through a steel wire of the same shape and size, and they essentially cannot flow at all through an insulator like rubber, regardless of its shape. The difference between copper, steel, and rubber is related to their microscopic structure and electron configuration, and is quantified by a property called resistivity.

In addition to geometry and material, there are various other factors that influence resistance and conductance, such as temperature; see below.

Conductors and resistors

A 75 Ω resistor, as identified by its electronic color code (violet–green–black–gold–red). An ohmmeter could be used to verify this value.

Substances in which electricity can flow are called conductors. A piece of conducting material of a particular resistance meant for use in a circuit is called a resistor. Conductors are made of high-conductivity materials such as metals, in particular copper and aluminium. Resistors, on the other hand, are made of a wide variety of materials depending on factors such as the desired resistance, amount of energy that it needs to dissipate, precision, and costs.

Ohm's law

Main article: Ohm's law

 

The current–voltage characteristics of four devices: Two resistors, a diode, and a battery. The horizontal axis is voltage drop, the vertical axis is current. Ohm's law is satisfied when the graph is a straight line through the origin. Therefore, the two resistors are ohmic, but the diode and battery are not.

For many materials, the current I through the material is proportional to the voltage V applied across it:

$${\displaystyle I\propto V}$$

over a wide range of voltages and currents. Therefore, the resistance and conductance of objects or electronic components made of these materials is constant. This relationship is called Ohm's law, and materials which obey it are called ohmic materials. Examples of ohmic components are wires and resistors. The current–voltage graph of an ohmic device consists of a straight line through the origin with positive slope.

Other components and materials used in electronics do not obey Ohm's law; the current is not proportional to the voltage, so the resistance varies with the voltage and current through them. These are called nonlinear or non-ohmic. Examples include diodes and fluorescent lamps. The current-voltage curve of a nonohmic device is a curved line.

Relation to resistivity and conductivity

Main article: Electrical resistivity and conductivity

 

A piece of resistive material with electrical contacts on both ends.

The resistance of a given object depends primarily on two factors: what material it is made of, and its shape. For a given material, the resistance is inversely proportional to the cross-sectional area; for example, a thick copper wire has lower resistance than an otherwise-identical thin copper wire. Also, for a given material, the resistance is proportional to the length; for example, a long copper wire has higher resistance than an otherwise-identical short copper wire. The resistance R and conductance G of a conductor of uniform cross section, therefore, can be computed as

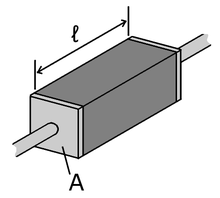
$${\displaystyle \begin{array}{rl}R& =\rho \frac{\ell }{A},\\ G& =\sigma \frac{A}{\ell }.\end{array}}$$

where ${\displaystyle \ell }$ is the length of the conductor, measured in metres (m), A is the cross-sectional area of the conductor measured in square metres (m²), σ (sigma) is the electrical conductivity measured in siemens per meter (S·m⁻¹), and ρ (rho) is the electrical resistivity (also called specific electrical resistance) of the material, measured in ohm-metres (Ω·m). The resistivity and conductivity are proportionality constants, and therefore depend only on the material the wire is made of, not the geometry of the wire. Resistivity and conductivity are reciprocals: ${\displaystyle \rho =1/\sigma }$. Resistivity is a measure of the material's ability to oppose electric current.

This formula is not exact, as it assumes the current density is totally uniform in the conductor, which is not always true in practical situations. However, this formula still provides a good approximation for long thin conductors such as wires.

Another situation for which this formula is not exact is with alternating current (AC), because the skin effect inhibits current flow near the center of the conductor. For this reason, the geometrical cross-section is different from the effective cross-section in which current actually flows, so resistance is higher than expected. Similarly, if two conductors near each other carry AC current, their resistances increase due to the proximity effect. At commercial power frequency, these effects are significant for large conductors carrying large currents, such as busbars in an electrical substation, or large power cables carrying more than a few hundred amperes.

The resistivity of different materials varies by an enormous amount: For example, the conductivity of teflon is about 10³⁰ times lower than the conductivity of copper. Loosely speaking, this is because metals have large numbers of "delocalized" electrons that are not stuck in any one place, so they are free to move across large distances. In an insulator, such as Teflon, each electron is tightly bound to a single molecule so a great force is required to pull it away. Semiconductors lie between these two extremes. More details can be found in the article: Electrical resistivity and conductivity. For the case of electrolyte solutions, see the article: Conductivity (electrolytic).

Resistivity varies with temperature. In semiconductors, resistivity also changes when exposed to light. See below.

Measurement

Main article: Ohmmeter

 

An ohmmeter

An instrument for measuring resistance is called an ohmmeter. Simple ohmmeters cannot measure low resistances accurately because the resistance of their measuring leads causes a voltage drop that interferes with the measurement, so more accurate devices use four-terminal sensing.

Typical values

See also: Electrical resistivities of the elements (data page) and Electrical resistivity and conductivity

Typical resistance values for selected objects

Component	Resistance (Ω)
1 meter of copper wire with 1 mm diameter	0.02
1 km overhead power line (typical)	0.03
AA battery (typical internal resistance)	0.1
Incandescent light bulb filament (typical)	200–1000
Human body	1000–100,000

Static and differential resistance

See also: Small-signal model

 

The current–voltage curve of a non-ohmic device (purple). The static resistance at point A is the inverse slope of line B through the origin. The differential resistance at A is the inverse slope of tangent line C.

 

The current–voltage curve of a component with negative differential resistance, an unusual phenomenon where the current–voltage curve is non-monotonic.

Many electrical elements, such as diodes and batteries do not satisfy Ohm's law. These are called non-ohmic or non-linear, and their current–voltage curves are not straight lines through the origin.

Resistance and conductance can still be defined for non-ohmic elements. However, unlike ohmic resistance, non-linear resistance is not constant but varies with the voltage or current through the device; i.e., its operating point. There are two types of resistance:

Static resistance

Also called chordal or DC resistance

This corresponds to the usual definition of resistance; the voltage divided by the current

$${\displaystyle R_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}}=\frac{U}{I}.}$$

It is the slope of the line (chord) from the origin through the point on the curve. Static resistance determines the power dissipation in an electrical component. Points on the current–voltage curve located in the 2nd or 4th quadrants, for which the slope of the chordal line is negative, have negative static resistance. Passive devices, which have no source of energy, cannot have negative static resistance. However active devices such as transistors or op-amps can synthesize negative static resistance with feedback, and it is used in some circuits such as gyrators.

Differential resistance

Also called dynamic, incremental, or small-signal resistance

Differential resistance is the derivative of the voltage with respect to the current; the slope of the current–voltage curve at a point

$${\displaystyle R_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}}=\frac{\mathrm{d}U}{\mathrm{d}I}.}$$

If the current–voltage curve is nonmonotonic (with peaks and troughs), the curve has a negative slope in some regions—so in these regions the device has negative differential resistance. Devices with negative differential resistance can amplify a signal applied to them, and are used to make amplifiers and oscillators. These include tunnel diodes, Gunn diodes, IMPATT diodes, magnetron tubes, and unijunction transistors.

AC circuits

Impedance and admittance

Main articles: Electrical impedance and Admittance

 

The voltage (red) and current (blue) versus time (horizontal axis) for a capacitor (top) and inductor (bottom). Since the amplitude of the current and voltage sinusoids are the same, the absolute value of impedance is 1 for both the capacitor and the inductor (in whatever units the graph is using). On the other hand, the phase difference between current and voltage is −90° for the capacitor; therefore, the complex phase of the impedance of the capacitor is −90°. Similarly, the phase difference between current and voltage is +90° for the inductor; therefore, the complex phase of the impedance of the inductor is +90°.

When an alternating current flows through a circuit, the relation between current and voltage across a circuit element is characterized not only by the ratio of their magnitudes, but also the difference in their phases. For example, in an ideal resistor, the moment when the voltage reaches its maximum, the current also reaches its maximum (current and voltage are oscillating in phase). But for a capacitor or inductor, the maximum current flow occurs as the voltage passes through zero and vice versa (current and voltage are oscillating 90° out of phase, see image below). Complex numbers are used to keep track of both the phase and magnitude of current and voltage:

$${\displaystyle \begin{array}{cl}u(t)& ={\mathcal{R}}_{\mathcal{e}}\left(U_0\cdot e^{j\omega t}\right)\\ i(t)& ={\mathcal{R}}_{\mathcal{e}}\left(I_0\cdot e^{j(\omega t+\phi )}\right)\\ Z& =\frac{U}{I}\\ Y& =\frac{1}{Z}=\frac{I}{U}\end{array}}$$

where:

• t is time;
• u(t) and i(t) are the voltage and current as a function of time, respectively;
• U₀ and I₀ indicate the amplitude of the voltage and current, respectively;
• ${\displaystyle \omega }$ is the angular frequency of the AC current;
• ${\displaystyle \phi }$ is the displacement angle;
• U and I are the complex-valued voltage and current, respectively;
• Z and Y are the complex impedance and admittance, respectively;
• ${\displaystyle {\mathcal{R}}_{\mathcal{e}}}$ indicates the real part of a complex number; and
• ${\displaystyle j\equiv \sqrt{-1}}$ is the imaginary unit.

The impedance and admittance may be expressed as complex numbers that can be broken into real and imaginary parts:

$${\displaystyle \begin{array}{rl}Z& =R+jX\\ Y& =G+jB.\end{array}}$$

where R is resistance, G is conductance, X is reactance, and B is susceptance. These lead to the complex number identities

$${\displaystyle \begin{array}{rlr}R& =\frac{G}{G^2+B^2},& X=\frac{-B}{G^2+B^2},\\ G& =\frac{R}{R^2+X^2},& B=\frac{-X}{R^2+X^2},\end{array}}$$

which are true in all cases, whereas ${\displaystyle R=1/G}$ is only true in the special cases of either DC or reactance-free current.

The complex angle ${\displaystyle \theta =\arg (Z)=-\arg (Y)}$ is the phase difference between the voltage and current passing through a component with impedance Z. For capacitors and inductors, this angle is exactly -90° or +90°, respectively, and X and B are nonzero. Ideal resistors have an angle of 0°, since X is zero (and hence B also), and Z and Y reduce to R and G respectively. In general, AC systems are designed to keep the phase angle close to 0° as much as possible, since it reduces the reactive power, which does no useful work at a load. In a simple case with an inductive load (causing the phase to increase), a capacitor may be added for compensation at one frequency, since the capacitor's phase shift is negative, bringing the total impedance phase closer to 0° again.

Y is the reciprocal of Z (${\displaystyle Z=1/Y}$) for all circuits, just as ${\displaystyle R=1/G}$ for DC circuits containing only resistors, or AC circuits for which either the reactance or susceptance happens to be zero (X or B = 0, respectively) (if one is zero, then for realistic systems both must be zero).

Frequency dependence

A key feature of AC circuits is that the resistance and conductance can be frequency-dependent, a phenomenon known as the universal dielectric response. One reason, mentioned above is the skin effect (and the related proximity effect). Another reason is that the resistivity itself may depend on frequency (see Drude model, deep-level traps, resonant frequency, Kramers–Kronig relations, etc.)

Energy dissipation and Joule heating

Main article: Joule heating

 

Running current through a material with resistance creates heat, in a phenomenon called Joule heating. In this picture, a cartridge heater, warmed by Joule heating, is glowing red hot.

Resistors (and other elements with resistance) oppose the flow of electric current; therefore, electrical energy is required to push current through the resistance. This electrical energy is dissipated, heating the resistor in the process. This is called Joule heating (after James Prescott Joule), also called ohmic heating or resistive heating.

The dissipation of electrical energy is often undesired, particularly in the case of transmission losses in power lines. High voltage transmission helps reduce the losses by reducing the current for a given power.

On the other hand, Joule heating is sometimes useful, for example in electric stoves and other electric heaters (also called resistive heaters). As another example, incandescent lamps rely on Joule heating: the filament is heated to such a high temperature that it glows "white hot" with thermal radiation (also called incandescence).

The formula for Joule heating is:

$${\displaystyle P=I^{2}R}$$

where P is the power (energy per unit time) converted from electrical energy to thermal energy, R is the resistance, and I is the current through the resistor.

Dependence on other conditions

Temperature dependence

Main article: Electrical resistivity and conductivity § Temperature dependence

Near room temperature, the resistivity of metals typically increases as temperature is increased, while the resistivity of semiconductors typically decreases as temperature is increased. The resistivity of insulators and electrolytes may increase or decrease depending on the system. For the detailed behavior and explanation, see Electrical resistivity and conductivity.

As a consequence, the resistance of wires, resistors, and other components often change with temperature. This effect may be undesired, causing an electronic circuit to malfunction at extreme temperatures. In some cases, however, the effect is put to good use. When temperature-dependent resistance of a component is used purposefully, the component is called a resistance thermometer or thermistor. (A resistance thermometer is made of metal, usually platinum, while a thermistor is made of ceramic or polymer.)

Resistance thermometers and thermistors are generally used in two ways. First, they can be used as thermometers: by measuring the resistance, the temperature of the environment can be inferred. Second, they can be used in conjunction with Joule heating (also called self-heating): if a large current is running through the resistor, the resistor's temperature rises and therefore its resistance changes. Therefore, these components can be used in a circuit-protection role similar to fuses, or for feedback in circuits, or for many other purposes. In general, self-heating can turn a resistor into a nonlinear and hysteretic circuit element. For more details see Thermistor#Self-heating effects.

If the temperature T does not vary too much, a linear approximation is typically used:

$${\displaystyle R(T)=R_0[1+\alpha (T-T_0)]}$$

where ${\displaystyle \alpha }$ is called the temperature coefficient of resistance, ${\displaystyle T_0}$ is a fixed reference temperature (usually room temperature), and ${\displaystyle R_0}$ is the resistance at temperature ${\displaystyle T_0}$. The parameter ${\displaystyle \alpha }$ is an empirical parameter fitted from measurement data. Because the linear approximation is only an approximation, ${\displaystyle \alpha }$ is different for different reference temperatures. For this reason it is usual to specify the temperature that ${\displaystyle \alpha }$ was measured at with a suffix, such as ${\displaystyle {\alpha }_{15}}$, and the relationship only holds in a range of temperatures around the reference.

The temperature coefficient ${\displaystyle \alpha }$ is typically +3×10⁻³ K−1 to +6×10⁻³ K−1 for metals near room temperature. It is usually negative for semiconductors and insulators, with highly variable magnitude.

Strain dependence

Main article: Strain gauge

Just as the resistance of a conductor depends upon temperature, the resistance of a conductor depends upon strain. By placing a conductor under tension (a form of stress that leads to strain in the form of stretching of the conductor), the length of the section of conductor under tension increases and its cross-sectional area decreases. Both these effects contribute to increasing the resistance of the strained section of conductor. Under compression (strain in the opposite direction), the resistance of the strained section of conductor decreases. See the discussion on strain gauges for details about devices constructed to take advantage of this effect.

Light illumination dependence

Main articles: Photoresistor and Photoconductivity

Some resistors, particularly those made from semiconductors, exhibit photoconductivity, meaning that their resistance changes when light is shining on them. Therefore, they are called photoresistors (or light dependent resistors). These are a common type of light detector.

Superconductivity

Main article: Superconductivity

Superconductors are materials that have exactly zero resistance and infinite conductance, because they can have V = 0 and I ≠ 0. This also means there is no joule heating, or in other words no dissipation of electrical energy. Therefore, if superconductive wire is made into a closed loop, current flows around the loop forever. Superconductors require cooling to temperatures near 4 K with liquid helium for most metallic superconductors like niobium–tin alloys, or cooling to temperatures near 77 K with liquid nitrogen for the expensive, brittle and delicate ceramic high temperature superconductors. Nevertheless, there are many technological applications of superconductivity, including superconducting magnets.