Woodward–Hoffmann rules

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Woodward%E2%80%93Hoffmann_rules

Thermolysis converts 1 to (E,E) geometric isomer 2, but 3 to (E,Z) isomer 4.

The Woodward–Hoffmann rules (or the pericyclic selection rules) are a set of rules devised by Robert Burns Woodward and Roald Hoffmann to rationalize or predict certain aspects of the stereochemistry and activation energy of pericyclic reactions, an important class of reactions in organic chemistry. The rules originate in certain symmetries of the molecule's orbital structure that any molecular Hamiltonian conserves. Consequently, any symmetry-violating reaction must couple extensively to the environment; this imposes an energy barrier on its occurrence, and such reactions are called symmetry-forbidden. Their opposites are symmetry-allowed.

Although the symmetry-imposed barrier is often formidable (up to ca. 5 eV or 480 kJ/mol in the case of a forbidden [2+2] cycloaddition), the prohibition is not absolute, and symmetry-forbidden reactions can still take place if other factors (e.g. strain release) favor the reaction. Likewise, a symmetry-allowed reaction may be preempted by an insurmountable energetic barrier resulting from factors unrelated to orbital symmetry. All known cases only violate the rules superficially; instead, different parts of the mechanism become asynchronous, and each step conforms to the rules.

Background and terminology

A pericyclic reaction is an organic reaction that proceeds via a single concerted and cyclic transition state, the geometry of which allows for the continuous overlap of a cycle of (π and/or σ) orbitals.

The terms conrotatory and disrotatory describe the relative sense of bond rotation involved in electrocyclic ring-opening and -closing reactions. In a disrotatory process, the breaking or forming bond's two ends rotate in opposing directions (one clockwise, one counterclockwise); in a conrotatory process, they rotate in the same direction (both clockwise or both counterclockwise), the process is conrotatory.

Eventually, it was recognized that thermally-promoted pericyclic reactions in general obey a single set of generalized selection rules, depending on the electron count and topology of the orbital interactions. The key concept of orbital topology or faciality was introduced to unify several classes of pericyclic reactions under a single conceptual framework. In short, a set of contiguous atoms and their associated orbitals that react as one unit in a pericyclic reaction is known as a component, and each component is said to be antarafacial or suprafacial depending on whether the orbital lobes that interact during the reaction are on the opposite or same side of the nodal plane, respectively. (The older terms conrotatory and disrotatory, which are applicable to electrocyclic ring opening and closing only, are subsumed by the terms antarafacial and suprafacial, respectively, under this more general classification system.)

History

Woodward and Hoffmann developed the pericyclic selection rules after performing extensive orbital-overlap calculations. At the time, Woodward wanted to know whether certain electrocyclic reactions might help synthesize vitamin B₁₂. Chemists knew that such reactions exhibited striking stereospecificity, but could not predict which stereoisomer a reaction might select. In 1965, Woodward–Hoffmann realized that a simple set of rules explained the observed stereospecificity at the ends of open-chain conjugated polyenes when heated or irradiated. In their original publication, they summarized the experimental evidence and molecular orbital analysis as follows:

• In an open-chain system containing 4n π electrons, the orbital symmetry of the highest occupied molecule orbital is such that a bonding interaction between the ends must involve overlap between orbital envelopes on opposite faces of the system and this can only be achieved in a conrotatory process.
• In open systems containing (4n + 2) π electrons, terminal bonding interaction within ground-state molecules requires overlap of orbital envelopes on the same face of the system, attainable only by disrotatory displacements.
• In a photochemical reaction an electron in the HOMO of the reactant is promoted to an excited state leading to a reversal of terminal symmetry relationships and stereospecificity.

In 1969, they would use correlation diagrams to state a generalized pericyclic selection rule equivalent to that now attached to their name: a pericyclic reaction is allowed if the sum of the number of suprafacial 4q + 2 components and number of antarafacial 4r components is odd. .

In the intervening four years, Howard Zimmerman and Michael J. S. Dewar proposed an equally general conceptual framework: the Möbius-Hückel concept, or aromatic transition state theory. In the Dewar-Zimmerman approach the orbital overlap topology (Hückel or Möbius) and electron count (4n + 2 or 4n) results in either an aromatic or antiaromatic transition state.

Meanwhile, Kenichi Fukui analyzed the frontier orbitals of such systems. A process in which the HOMO-LUMO interaction is constructive (results in a net bonding interaction) is favorable and considered symmetry-allowed, while a process in which the HOMO-LUMO interaction is non-constructive (results in bonding and antibonding interactions that cancel) is disfavorable and considered symmetry-forbidden.

Though conceptually distinct, aromatic transition state theory (Zimmerman and Dewar), frontier molecular orbital theory (Fukui), and orbital symmetry conservation (Woodward and Hoffmann) all make identical predictions. The Woodward–Hoffmann rules exemplify molecular orbital theory's power, and indeed helped demonstate that useful chemical results could arise from orbital analysis. The discovery would earn Hoffmann and Fukui the 1981 Nobel Prize in Chemistry. By that time, Woodward had died, and so was ineligible for the prize.

Illustrative examples

The interconversion of model cyclobutene and butadiene derivatives under thermal (heating) and photochemical (Ultraviolet irradiation) conditions is illustrative.

The Woodward–Hoffmann rules apply to either direction of a pericyclic process. Due to the inherent ring strain of cyclobutene derivatives, the equilibrium between the cyclobutene and the 1,3-butadiene lies far to the right. Hence, under thermal conditions, the ring opening of the cyclobutene to the 1,3-butadiene is strongly favored by thermodynamics. On the other hand, under irradiation by ultraviolet light, a photostationary state is reached, a composition which depends on both absorbance and quantum yield of the forward and reverse reactions at a particular wavelength. Due to the different degrees of conjugation of 1,3-butadienes and cyclobutenes, only the 1,3-butadiene will have a significant absorbance at higher wavelengths, assuming the absence of other chromophores. Hence, irradiation of the 1,3-butadiene at such a wavelength can result in high conversion to the cyclobutene. Thermolysis of trans-1,2,3,4-tetramethyl-1-cyclobutene (1) afforded only one geometric isomer, (E,E)-3,4-dimethyl-2,4-hexadiene (2); the (Z,Z) and the (E,Z) geometric isomers were not detected in the product mixture. Similarly, thermolysis of cis-1,2,3,4-tetramethyl-1-cyclobutene (3) afforded only (E,Z) isomer 4. In both ring opening reactions, the carbons on the ends of the breaking σ-bond rotate in the same direction. On the other hand, the opposite stereochemical course was followed under photochemical activation: When the related compound (E,E)-2,4-hexadiene (5) was exposed to light, cis-3,4-dimethyl-1-cyclobutene (6) was formed exclusively as a result of electrocyclic ring closure. This requires the ends of the π-system to rotate in opposite directions to form the new σ-bond. Thermolysis of 6 follows the same stereochemical course as 3: electrocyclic ring opening leads to the formation of (E,Z)-2,4-hexadiene (7) and not 5.

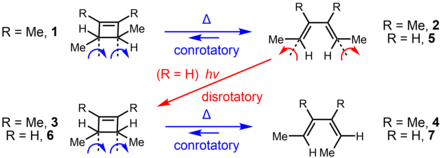
The Woodward-Hoffmann rules explain these results through orbital overlap:

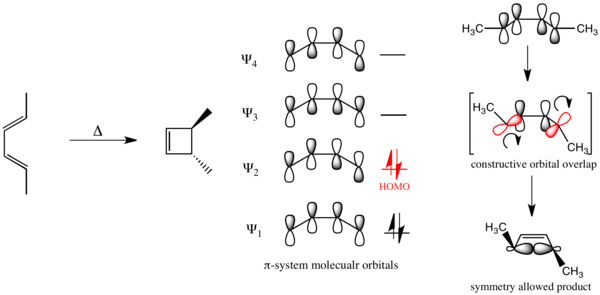
In the case of a photochemically driven electrocyclic ring-closure of buta-1,3-diene, electronic promotion causes ${\displaystyle {\mathrm{\Psi }}_3}$ to become the HOMO and the reaction mechanism must be disrotatory.

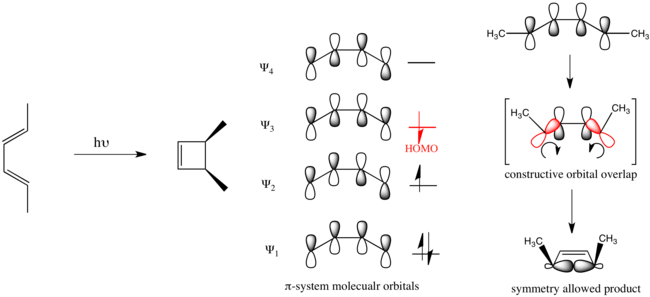
Conversely in the electrocyclic ring-closure of the substituted hexa-1,3,5-triene pictured below, the reaction proceeds through a disrotatory mechanism.

Rule

The Woodward–Hoffmann rules can be stated succinctly as a single sentence:

Generalized pericyclic selection rule. A ground-state pericyclic process involving N electron pairs and A antarafacial components is symmetry-allowed if and only if N + A is odd.

A ground-state pericyclic process is brought about by addition of thermal energy (i.e., heating the system, symbolized by Δ). In contrast, an excited-state pericyclic process takes place if a reactant is promoted to an electronically excited state by activation with ultraviolet light (i.e., irradiating the system, symbolized by hν). It is important to recognize, however, that the operative mechanism of a formally pericyclic reaction taking place under photochemical irradiation is generally not as simple or clearcut as this dichotomy suggests. Several modes of electronic excitation are usually possible, and electronically excited molecules may undergo intersystem crossing, radiationless decay, or relax to an unfavorable equilibrium geometry before the excited-state pericyclic process can take place. Thus, many apparent pericyclic reactions that take place under irradiation are actually thought to be stepwise processes involving diradical intermediates. Nevertheless, it is frequently observed that the pericyclic selection rules become reversed when switching from thermal to photochemical activation. This can be rationalized by considering the correlation of the first electronic excited states of the reactants and products. Although more of a useful heuristic than a rule, a corresponding generalized selection principle for photochemical pericyclic reactions can be stated:

A pericyclic process involving N electron pairs and A antarafacial components is often favored under photochemical conditions if N + A is even.

Pericyclic reactions involving an odd number of electrons are also known. With respect to application of the generalized pericyclic selection rule, these systems can generally be treated as though one more electron were involved.

In the language of aromatic transition state theory, the Woodward–Hoffmann rules can be restated as follows: A pericyclic transition state involving (4n + 2) electrons with Hückel topology or 4n electrons with Möbius topology is aromatic and allowed, while a pericyclic transition state involving 4n-electrons with Hückel topology or (4n + 2)-electrons with Möbius topology is antiaromatic and forbidden.

Correlation diagrams

Longuet-Higgins and E. W. Abrahamson showed that the Woodward–Hoffmann rules can best be derived by examining the correlation diagram of a given reaction. A symmetry element is a point of reference (usually a plane or a line) about which an object is symmetric with respect to a symmetry operation. If a symmetry element is present throughout the reaction mechanism (reactant, transition state, and product), it is called a conserved symmetry element. Then, throughout the reaction, the symmetry of molecular orbitals with respect to this element must be conserved. That is, molecular orbitals that are symmetric with respect to the symmetry element in the starting material must be correlated to (transform into) orbitals symmetric with respect to that element in the product. Conversely, the same statement holds for antisymmetry with respect to a conserved symmetry element. A molecular orbital correlation diagram correlates molecular orbitals of the starting materials and the product based upon conservation of symmetry. From a molecular orbital correlation diagram one can construct an electronic state correlation diagram that correlates electronic states (i.e. ground state, and excited states) of the reactants with electronic states of the products. Correlation diagrams can then be used to predict the height of transition state barriers.

Although orbital "symmetry" is used as a tool for sketching orbital and state correlation diagrams, the absolute presence or absence of a symmetry element is not critical for the determination of whether a reaction is allowed or forbidden. That is, the introduction of a simple substituent that formally disrupts a symmetry plane or axis (e.g., a methyl group) does not generally affect the assessment of whether a reaction is allowed or forbidden. Instead, the symmetry present in an unsubstituted analog is used to simplify the construction of orbital correlation diagrams and avoid the need to perform calculations. Only the phase relationships between orbitals are important when judging whether a reaction is "symmetry"-allowed or forbidden. Moreover, orbital correlations can still be made, even if there are no conserved symmetry elements (e.g., 1,5-sigmatropic shifts and ene reactions). For this reason, the Woodward–Hoffmann, Fukui, and Dewar–Zimmerman analyses are equally broad in their applicability, though a certain approach may be easier or more intuitive to apply than another, depending on the reaction one wishes to analyze.

Electrocyclic reactions

The transition state of a conrotatory closure has C₂ symmetry, whereas the transition state of a disrotatory opening has mirror symmetry.

MOs of butadiene are shown with the element with which they are symmetric. They are antisymmetric with respect to the other.

Considering the electrocyclic ring closure of the substituted 1,3-butadiene, the reaction can proceed through either a conrotatory or a disrotatory reaction mechanism. As shown to the left, in the conrotatory transition state there is a C₂ axis of symmetry and in the disrotatory transition state there is a σ mirror plane of symmetry. In order to correlate orbitals of the starting material and product, one must determine whether the molecular orbitals are symmetric or antisymmetric with respect to these symmetry elements. The π-system molecular orbitals of butadiene are shown to the right along with the symmetry element with which they are symmetric. They are antisymmetric with respect to the other. For example, Ψ₂ of 1,3-butadiene is symmetric with respect to 180^o rotation about the C₂ axis, and antisymmetric with respect to reflection in the mirror plane.

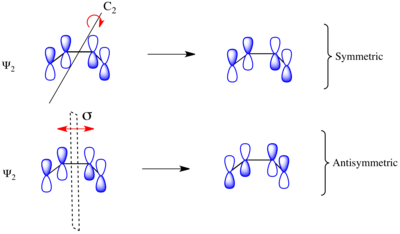
Ψ₁ and Ψ₃ are symmetric with respect to the mirror plane as the sign of the p-orbital lobes is preserved under the symmetry transformation. Similarly, Ψ₁ and Ψ₃ are antisymmetric with respect to the C₂ axis as the rotation inverts the sign of the p-orbital lobes uniformly. Conversely Ψ₂ and Ψ₄ are symmetric with respect to the C₂ axis and antisymmetric with respect to the σ mirror plane.

The same analysis can be carried out for the molecular orbitals of cyclobutene. The result of both symmetry operations on each of the MOs is shown to the left. As the σ and σ^* orbitals lie entirely in the plane containing C₂ perpendicular to σ, they are uniformly symmetric and antisymmetric (respectively) to both symmetry elements. On the other hand, π is symmetric with respect to reflection and antisymmetric with respect to rotation, while π^* is antisymmetric with respect to reflection and symmetric with respect to rotation.

Correlation lines are drawn to connect molecular orbitals in the starting material and the product that have the same symmetry with respect to the conserved symmetry element. In the case of the conrotatory 4 electron electrocyclic ring closure of 1,3-butadiene, the lowest molecular orbital Ψ₁ is asymmetric (A) with respect to the C₂ axis. So this molecular orbital is correlated with the π orbital of cyclobutene, the lowest energy orbital that is also (A) with respect to the C₂ axis. Similarly, Ψ₂, which is symmetric (S) with respect to the C₂ axis, is correlated with σ of cyclobutene. The final two correlations are between the antisymmetric (A) molecular orbitals Ψ₃ and σ^*, and the symmetric (S) molecular orbitals Ψ₄ and π^*.

Similarly, there exists a correlation diagram for a disrotatory mechanism. In this mechanism, the symmetry element that persists throughout the entire mechanism is the σ mirror plane of reflection. Here the lowest energy MO Ψ₁ of 1,3-butadiene is symmetric with respect to the reflection plane, and as such correlates with the symmetric σ MO of cyclobutene. Similarly the higher energy pair of symmetric molecular orbitals Ψ₃ and π correlate. As for the asymmetric molecular orbitals, the lower energy pair Ψ₂ and π^* form a correlation pair, as do Ψ₄ and σ^*.

Evaluating the two mechanisms, the conrotatory mechanism is predicted to have a lower barrier because it transforms the electrons from ground-state orbitals of the reactants (Ψ₁ and Ψ₂) into ground-state orbitals of the product (σ and π). Conversely, the disrotatory mechanism forces the conversion of the Ψ₁ orbital into the σ orbital, and the Ψ₂ orbital into the π^* orbital. Thus the two electrons in the ground-state Ψ₂ orbital are transferred to an excited antibonding orbital, creating a doubly excited electronic state of the cyclobutene. This would lead to a significantly higher transition state barrier to reaction.

First excited state (ES-1) of butadiene.

However, as reactions do not take place between disjointed molecular orbitals, but electronic states, the final analysis involves state correlation diagrams. A state correlation diagram correlates the overall symmetry of electronic states in the starting material and product. The ground state of 1,3-butadiene, as shown above, has 2 electrons in Ψ₁ and 2 electrons in Ψ₂, so it is represented as Ψ₁²Ψ₂². The overall symmetry of the state is the product of the symmetries of each filled orbital with multiplicity for doubly populated orbitals. Thus, as Ψ₁ is asymmetric with respect to the C₂ axis, and Ψ₂ is symmetric, the total state is represented by A²S². To see why this particular product is mathematically overall S, that S can be represented as (+1) and A as (−1). This derives from the fact that signs of the lobes of the p-orbitals are multiplied by (+1) if they are symmetric with respect to a symmetry transformation (i.e. unaltered) and multiplied by (−1) if they are antisymmetric with respect to a symmetry transformation (i.e. inverted). Thus A²S²=(−1)²(+1)²=+1=S. The first excited state (ES-1) is formed from promoting an electron from the HOMO to the LUMO, and thus is represented as Ψ₁²Ψ₂Ψ₃. As Ψ₁is A, Ψ₂ is S, and Ψ₃ is A, the symmetry of this state is given by A²SA=A.Now considering the electronic states of the product, cyclobutene, the ground-state is given by σ²π², which has symmetry S²A²=S. The first excited state (ES-1') is again formed from a promotion of an electron from the HOMO to the LUMO, so in this case it is represented as σ²ππ^*. The symmetry of this state is S²AS=A.

The ground state Ψ₁²Ψ₂² of 1,3-butadiene correlates with the ground state σ²π² of cyclobutene as demonstrated in the MO correlation diagram above. Ψ₁ correlates with π and Ψ₂ correlates with σ. Thus the orbitals making up Ψ₁²Ψ₂² must transform into the orbitals making up σ²π² under a conrotatory mechanism. However, the state ES-1 does not correlate with the state ES-1' as the molecular orbitals do not transform into each other under the symmetry-requirement seen in the molecular orbital correlation diagram. Instead as Ψ₁ correlates with π, Ψ₂ correlates with σ, and Ψ₃ correlates with σ^*, the state Ψ₁²Ψ₂Ψ₃ attempts to transform into π²σσ^*, which is a different excited state. So ES-1 attempts to correlate with ES-2'=σπ²σ^*, which is higher in energy than Es-1'. Similarly ES-1'=σ²ππ^* attempts to correlate with ES-2=Ψ₁Ψ₂²Ψ₄. These correlations can not actually take place due to the quantum-mechanical rule known as the avoided crossing rule. This says that energetic configurations of the same symmetry can not cross on an energy level correlation diagram. In short, this is caused by mixing of states of the same symmetry when brought close enough in energy. So instead a high energetic barrier is formed between a forced transformation of ES-1 into ES-1'. In the diagram below the symmetry-preferred correlations are shown in dashed lines and the bold curved lines indicate the actual correlation with the high energetic barrier.

The same analysis can be applied to the disrotatory mechanism to create the following state correlation diagram.

Thus if the molecule is in the ground state it will proceed through the conrotatory mechanism (i.e. under thermal control) to avoid an electronic barrier. However, if the molecule is in the first excited state (i.e. under photochemical control), the electronic barrier is present in the conrotatory mechanism and the reaction will proceed through the disrotatory mechanism. These are not completely distinct as both the conrotatory and disrotatory mechanisms lie on the same potential surface. Thus a more correct statement is that as a ground state molecule explores the potential energy surface, it is more likely to achieve the activation barrier to undergo a conrotatory mechanism.

Cycloaddition reactions

The Woodward–Hoffmann rules can also explain bimolecular cycloaddition reactions through correlation diagrams. A [_πp + _πq] cycloaddition brings together two components, one with p π-electrons, and the other with q π-electrons. Cycloaddition reactions are further characterized as suprafacial (s) or antarafacial (a) with respect to each of the π components. (See below "General formulation" for a detailed description of the generalization of WH notation to all pericyclic processes.)

[2+2] Cycloadditions

For ordinary alkenes, [2+2] cycloadditions only observed under photochemical activation.

The rationale for the non-observation of thermal [2+2] cycloadditions begins with the analysis of the four possible stereochemical consequences for the [2+2] cycloaddition: [_π2_s + _π2_s], [_π2_a + _π2_s], [_π2_s + _π2_a], [_π2_a + _π2_a]. The geometrically most plausible [_π2_s + _π2_s] mode is forbidden under thermal conditions, while the [_π2_a + _π2_s], [_π2_s + _π2_a] approaches are allowed from the point of view of symmetry but are rare due to an unfavorable strain and steric profile.

The [2_s + 2_s] cycloaddition retains stereochemistry.

Symmetry elements of the [2+2] cycloaddition.

Considering the [_π2_s + _π2_s] cycloaddition. This mechanism leads to a retention of stereochemistry in the product, as illustrated to the right. Two symmetry elements are present in the starting materials, transition state, and product: σ₁ and σ₂. σ₁ is the mirror plane between the components perpendicular to the p-orbitals; σ₂ splits the molecules in half perpendicular to the σ-bonds. These are both local-symmetry elements in the case that the components are not identical.

To determine symmetry and asymmetry with respect to σ₁ and σ₂, the starting material molecular orbitals must be considered in tandem. The figure to the right shows the molecular orbital correlation diagram for the [_π2_s + _π2_s] cycloaddition. The two π and π^* molecular orbitals of the starting materials are characterized by their symmetry with respect to first σ₁ and then σ₂. Similarly, the σ and σ^* molecular orbitals of the product are characterized by their symmetry. In the correlation diagram, molecular orbitals transformations over the course of the reaction must conserve the symmetry of the molecular orbitals. Thus π_SS correlates with σ_SS, π_AS correlates with σ^*_AS, π^*_SA correlates with σ_SA, and finally π^*_AA correlates with σ^*_AA. Due to conservation of orbital symmetry, the bonding orbital π_AS is forced to correlate with the antibonding orbital σ^*_AS. Thus a high barrier is predicted.

This is made precise in the state correlation diagram below. The ground state in the starting materials is the electronic state where π_SS and π_AS are both doubly populated – i.e. the state (SS)²(AS)². As such, this state attempts to correlate with the electronic state in the product where both σ_SS and σ^*_AS are doubly populated – i.e. the state (SS)²(AS)². However, this state is neither the ground state (SS)²(SA)² of cyclobutane, nor the first excited state ES-1'=(SS)²(SA)(AS), where an electron is promoted from the HOMO to the LUMO.

[4+2] cycloadditions

The mirror plane is the only conserved symmetry element of the Diels-Alder [4+2]-cycloaddition.

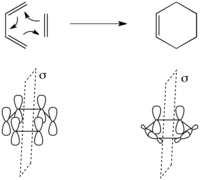
A [4+2] cycloaddition is exemplified by the Diels-Alder reaction. The simplest case is the reaction of 1,3-butadiene with ethylene to form cyclohexene.

One symmetry element is conserved in this transformation – the mirror plane through the center of the reactants as shown to the left. The molecular orbitals of the reactants are the set {Ψ₁, Ψ₂, Ψ₃, Ψ₄} of molecular orbitals of 1,3-butadiene shown above, along with π and π^* of ethylene. Ψ₁ is symmetric, Ψ₂ is antisymmetric, Ψ₃ is symmetric, and Ψ₄ is antisymmetric with respect to the mirror plane. Similarly π is symmetric and π^* is antisymmetric with respect to the mirror plane.

The molecular orbitals of the product are the symmetric and antisymmetric combinations of the two newly formed σ and σ^* bonds and the π and π^* bonds as shown below.

Correlating the pairs of orbitals in the starting materials and product of the same symmetry and increasing energy gives the correlation diagram to the right. As this transforms the ground state bonding molecular orbitals of the starting materials into the ground state bonding orbitals of the product in a symmetry conservative manner this is predicted to not have the great energetic barrier present in the ground state [2+2] reaction above.

To make the analysis precise, one can construct the state correlation diagram for the general [4+2]-cycloaddition. As before, the ground state is the electronic state depicted in the molecular orbital correlation diagram to the right. This can be described as Ψ₁²π²Ψ₂², of total symmetry S²S² A²=S. This correlates with the ground state of the cyclohexene σ_Sσ_Aπ² which is also S²S²A²=S. As such this ground state reaction is not predicted to have a high symmetry-imposed barrier.

One can also construct the excited-state correlations as is done above. Here, there is a high energetic barrier to a photo-induced Diels-Alder reaction under a suprafacial-suprafacial bond topology due to the avoided crossing shown below.

Group transfer reactions

Transfer of a pair of hydrogen atoms from ethane to perdeuterioethylene.

The symmetry-imposed barrier heights of group transfer reactions can also be analyzed using correlation diagrams. A model reaction is the transfer of a pair of hydrogen atoms from ethane to perdeuterioethylene shown to the right.

The only conserved symmetry element in this reaction is the mirror plane through the center of the molecules as shown to the left.

Conserved mirror plane in transfer reaction.

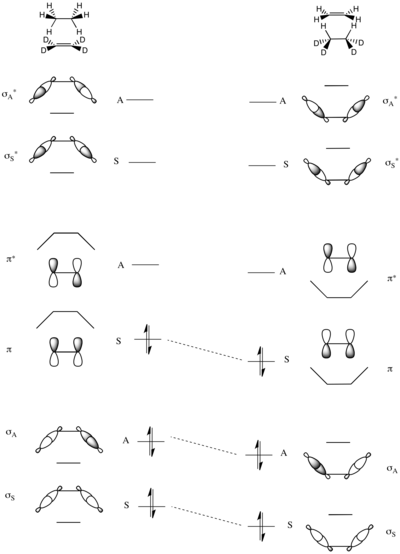
The molecular orbitals of the system are constructed as symmetric and antisymmetric combinations of σ and σ^* C–H bonds in ethane and π and π^* bonds in the deutero-substituted ethene. Thus the lowest energy MO is the symmetric sum of the two C–H σ-bond (σ_S), followed by the antisymmetric sum (σ_A). The two highest energy MOs are formed from linear combinations of the σ_CH antibonds – highest is the antisymmetric σ^*_A, preceded by the symmetric σ^*_A at a slightly lower energy. In the middle of the energetic scale are the two remaining MOs that are the π_CC and π^*_CC of ethene.

The full molecular orbital correlation diagram is constructed in by matching pairs of symmetric and asymmetric MOs of increasing total energy, as explained above. As can be seen in the adjacent diagram, as the bonding orbitals of the reactants exactly correlate with the bonding orbitals of the products, this reaction is not predicted to have a high electronic symmetry-imposed barrier.

Selection rules

Using correlation diagrams one can derive selection rules for the following generalized classes of pericyclic reactions. Each of these particular classes is further generalized in the generalized Woodward–Hoffmann rules. The more inclusive bond topology descriptors antarafacial and suprafacial subsume the terms conrotatory and disrotatory, respectively. Antarafacial refers to bond making or breaking through the opposite face of a π system, p orbital, or σ bond, while suprafacial refers to the process occurring through the same face. A suprafacial transformation at a chiral center preserves stereochemistry, whereas an antarafacial transformation reverses stereochemistry.

Electrocyclic reactions

The selection rule of electrocyclization reactions is given in the original statement of the Woodward–Hoffmann rules. If a generalized electrocyclic ring closure occurs in a polyene of 4n π-electrons, then it is conrotatory under thermal conditions and disrotatory under photochemical conditions. Conversely in a polyene of 4n + 2 π-electrons, an electrocyclic ring closure is disrotatory under thermal conditions and conrotatory under photochemical conditions.

This result can either be derived via an FMO analysis based upon the sign of p orbital lobes of the HOMO of the polyene or with correlation diagrams. Taking first the first possibility, in the ground state, if a polyene has 4n electrons, the outer p-orbitals of the HOMO that form the σ bond in the electrocyclized product are of opposite signs. Thus a constructive overlap is only produced under a conrotatory or antarafacial process. Conversely for a polyene with 4n + 2 electrons, the outer p-orbitals of the ground state HOMO are of the same sign. Thus constructive orbital overlap occurs with a disrotatory or suprafacical process.

A 4n electron electrocyclic reaction achieves constructive HOMO orbital overlap if it is conrotatory, while a 4n+2 electrocyclic reaction achieves constructive overlap if it is disrotatory.

Additionally, the correlation diagram for any 4n electrocyclic reaction will resemble the diagram for the 4 electron cyclization of 1,3-butadiene, while the correlation diagram any 4n + 2 electron electrocyclic reaction will resemble the correlation diagram for the 6 electron cyclization of 1,3,5-hexatriene.

This is summarized in the following table:

	Thermally allowed	Photochemically allowed
4n	conrotatory	disrotatory
4n + 2	disrotatory	conrotatory

Sigmatropic rearrangement reactions

A general sigmatropic rearrangement can be classified as order [i,j], meaning that a σ bond originally between atoms denoted 1 and 1', adjacent to one or more π systems, is shifted to between atoms i and j. Thus it migrates (i − 1), (j − 1) atoms away from its original position.

A formal symmetry analysis via correlation diagrams is of no use in the study of sigmatropic rearrangements as there are, in general, only symmetry elements present in the transition state. Except in special cases (e.g. [3,3]-rearrangements), there are no symmetry elements that are conserved as the reaction coordinate is traversed. Nevertheless, orbital correlations between starting materials and products can still be analyzed, and correlations of starting material orbitals with high energy product orbitals will, as usual, result in "symmetry-forbidden" processes. However, an FMO based approach (or the Dewar-Zimmerman analysis) is more straightforward to apply.

In [1,j]-sigmatropic rearrangements if 1+j = 4n, then supra/antara is thermally allowed, and if 1+j = 4n+2, then supra/supra or antara/antara is thermally allowed.

One of the most prevalent classes of sigmatropic shifts is classified as [1,j], where j is odd. That means one terminus of the σ-bond migrates (j − 1) bonds away across a π-system while the other terminus does not migrate. It is a reaction involving j + 1 electrons: j − 1 from the π-system and 2 from σ-bond. Using FMO analysis, [1,j]-sigmatropic rearrangements are allowed if the transition state has constructive overlap between the migrating group and the accepting p orbital of the HOMO. In [1,j]-sigmatropic rearrangements if j + 1 = 4n, then supra/antara is thermally allowed, and if j + 1 = 4n + 2, then supra/supra or antara/antara is thermally allowed.

The other prevalent class of sigmatropic rearrangements are [3,3], notably the Cope and Claisen rearrangements. Here, the constructive interactions must be between the HOMOs of the two allyl radical fragments in the transition state. The ground state HOMO Ψ₂ of the allyl fragment is shown below. As the terminal p-orbitals are of opposite sign, this reaction can either take place in a supra/supra topology, or an antara/antara topology.

The [3,3]-sigmatropic ground state reaction is allowed via either a supra/supra or antara/antara topology.

The selection rules for an [i,j]-sigmatropic rearrangement are as follows:

• For supra/supra or antara/antara [i,j]-sigmatropic shifts, if i + j = 4n + 2 they are thermally allowed and if i + j = 4n they are photochemically allowed
• For supra/antara [i,j]-sigmatropic shifts, if i + j = 4n they are thermally allowed, and if i + j = 4n + 2 they are photochemically allowed

This is summarized in the following table:

i + j	Thermally allowed	Photochemically allowed
4n	is + ja or ia + js	is + js or ia + ja
4n + 2	is + js or ia + ja	is + ja or ia + js

Cycloaddition reactions

A general [p+q]-cycloaddition is a concerted addition reaction between two components, one with p π-electrons, and one with q π-electrons. This reaction is symmetry allowed under the following conditions:

• For a supra/supra or antara/antara cycloaddition, it is thermally allowed if p + q = 4n + 2 and photochemically allowed if p + q = 4n
• For a supra/antara cycloaddition, it is thermally allowed if p + q = 4n and photochemically allowed if p + q = 4n + 2

This is summarized in the following table:

p + q	Thermally allowed	Photochemically allowed
4n	ps + qa or pa + qs	ps + qs or pa + qa
4n + 2	ps + qs or pa + qa	ps + qa or pa + qs

Group transfer reactions

A general double group transfer reaction which is synchronous can be represented as an interaction between a component with p π electrons and a component with q π electrons as shown.

Generalized synchronous double group transfer reaction between a component with p π electrons and a component with q π electrons.

Then the selection rules are the same as for the generalized cycloaddition reactions. That is

• For supra/supra or antara/antara double group transfers, if p + q = 4n + 2 it is thermally allowed, and if p + q = 4n it is photochemically allowed
• For supra/antara double group transfers, if p + q = 4n it is thermally allowed, and if p + q = 4n + 2 it is photochemically allowed

This is summarized in the following table:

p + q	Thermally allowed	Photochemically allowed
4n	ps + qa or pa + qs	ps + qs or pa + qa
4n + 2	ps + qs or pa + qa	ps + qa or pa + qs

The case of q = 0 corresponds to the thermal elimination of the "transferred" R groups. There is evidence that the pyrolytic eliminations of dihydrogen and ethane from 1,4-cyclohexadiene and 3,3,6,6-tetramethyl-1,4-cyclohexadiene, respectively, represent examples of this type of pericyclic process.

The ene reaction is often classified as a type of group transfer process, even though it does not involve the transfer of two σ-bonded groups. Rather, only one σ-bond is transferred while a second σ-bond is formed from a broken π-bond. As an all suprafacial process involving 6 electrons, it is symmetry-allowed under thermal conditions. The Woodward-Hoffmann symbol for the ene reaction is [_π2_s + _π2_s + _σ2_s] (see below).

General formulation

Though the Woodward–Hoffmann rules were first stated in terms of electrocyclic processes, they were eventually generalized to all pericyclic reactions, as the similarity and patterns in the above selection rules should indicate.

Conrotatory motion is antarafacial, while disrotatory motion is suprafacial.

In the generalized Woodward–Hoffmann rules, everything is characterized in terms of antarafacial and suprafacial bond topologies. The terms conrotatory and disrotatory are sufficient for describing the relative sense of bond rotation in electrocyclic ring closing or opening reactions, as illustrated on the right. However, they are unsuitable for describing the topologies of bond forming and breaking taking place in a general pericyclic reaction. As described in detail below, in the general formulation of the Woodward–Hoffmann rules, the bond rotation terms conrotatory and disrotatory are subsumed by the bond topology (or faciality) terms antarafacial and suprafacial, respectively. These descriptors can be used to characterize the topology of the bond forming and breaking that takes place in any pericyclic process.

Woodward-Hoffmann notation

A component is any part of a molecule or molecules that function as a unit in a pericyclic reaction. A component consists of one or more atoms and any of the following types of associated orbitals:

• An isolated p- or sp^x-orbital (unfilled or filled, symbol ω)
• A conjugated π system (symbol π)
• A σ bond (symbol σ)

The electron count of a component is the number of electrons in the orbital(s) of the component:

• The electron count of an unfilled ω orbital (i.e., an empty p orbital) is 0, while that of a filled ω orbital (i.e., a lone pair) is 2.
• The electron count of a conjugated π system with n double bonds is 2n (or 2n + 2, if a (formal) lone pair from a heteroatom or carbanion is conjugated thereto).
• The electron count of a σ bond is 2.

The bond topology of a component can be suprafacial and antarafacial:

• The relationship is suprafacial (symbol: s) when the interactions with the π system or p orbital occur on the same side of the nodal plane (think syn). For a σ bond, it corresponds to interactions occurring on the two "interior" lobes or two "exterior" lobes of the bond.
• The relationship is antarafacial (symbol: a) when the interactions with the π system or p orbital occur on opposite sides of the nodal plane (think anti). For a σ bond, it corresponds to interactions occurring on one "interior" lobe and one "exterior" lobe of the bond.

Illustration of the assignment of orbital overlap as suprafacial or antarafacial for common pericyclic components.

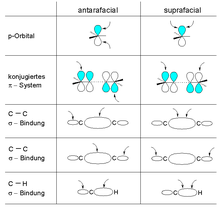
Using this notation, all pericyclic reactions can be assigned a descriptor, consisting of a series of symbols _σ/π/ωN_s/a, connected by + signs and enclosed in brackets, describing, in order, the type of orbital(s), number of electrons, and bond topology involved for each component. Some illustrative examples follow:

• The Diels-Alder reaction (a (4+2)-cycloaddition) is [_π4_s + _π2_s].
• The 1,3-dipolar cycloaddition of ozone and an olefin in the first step of ozonolysis (a (3+2)-cycloaddition) is [_π4_s + _π2_s].
• The cheletropic addition of sulfur dioxide to 1,3-butadiene (a (4+1)-cheletropic addition) is [_ω0_a + _π4_s] + [_ω2_s + _π4_s].
• The Cope rearrangement (a [3,3]-sigmatropic shift) is [_π2_s + _σ2_s + _π2_s] or [_π2_a + _σ2_s + _π2_a].
• The [1,3]-alkyl migration with inversion at carbon discovered by Berson (a [1,3]-sigmatropic shift) is [_σ2_a + _π2_s].
• The conrotatory electrocyclic ring closing of 1,3-butadiene (a 4π-electrocyclization) is [_π4_a].
• The conrotatory electrocyclic ring opening of cyclobutene (a reverse 4π-electrocyclization) is [_σ2_a + _π2_s] or [_σ2_s + _π2_a].
• The disrotatory electrocyclic ring closing of 1,3-cyclooctadien-5-ide anion (a 6π-electrocyclization) is [_π6_s].
• A Wagner-Meerwein shift of a carbocation (a [1,2]-sigmatropic shift) is [_ω0_s + _σ2_s].

Antarafacial and suprafacial are associated with (conrotation or inversion) and (disrotation or retention), respectively. A single descriptor may correspond to two pericyclic processes that are chemically distinct, that a reaction and its microscopic reverse are often described with two different descriptors, and that a single process may have more than a one correct descriptor. One can verify, using the pericyclic selection rule given below, that all of these reactions are allowed processes.

Original statement

Using this notation, Woodward and Hoffmann state in their 1969 review the general formulation for all pericyclic reactions as follows:

A ground-state pericyclic change is symmetry-allowed when the total number of (4q+2)_s and (4r)_a components is odd.

Here, (4q + 2)_s and (4r)_a refer to suprafacial (4q + 2)-electron and antarafacial (4r)-electron components, respectively. Moreover, this criterion should be interpreted as both sufficient (stated above) as well as necessary (not explicitly stated above, see: if and only if)

Derivation of an alternative statement

Alternatively, the general statement can be formulated in terms of the total number of electrons using simple rules of divisibility by a straightforward analysis of two cases.

First, consider the case where the total number of electrons is 4n + 2:

4n + 2 = a(4q + 2)_s + b(4p + 2)_a + c(4t)_s + d(4r)_a,

where a, b, c, and d are coefficients indicating the number of each type of component. This equation implies that one of, but not both, a or b is odd, for if a and b are both even or both odd, then the sum of the four terms is 0 (mod 4).

The generalized statement of the Woodward–Hoffmann rules states that a + d is odd if the reaction is allowed. Now, if a is even, then this implies that d is odd. Since b is odd in this case, the number of antarafacial components, b + d, is even. Likewise, if a is odd, then d is even. Since b even in this case, the number of antarafacial components, b + d, is again even. Thus, regardless of the initial assumption of parity for a and b, the number of antarafacial components is even when the electron count is 4n + 2. Contrariwise,, b + d is odd.

In the case where the total number of electrons is 4n, similar arguments (omitted here) lead to the conclusion that the number of antarafacial components b + d must be odd in the allowed case and even in the forbidden case.

Finally, to complete the argument, and show that this new criterion is truly equivalent to the original criterion, one needs to argue the converse statements as well, namely, that the number of antarafacial components b + d and the electron count (4n + 2 or 4n) implies the parity of a + d that is given by the Woodward–Hoffmann rules (odd for allowed, even for forbidden). Another round of (somewhat tedious) case analyses will easily show this to be the case. The pericyclic selection rule states:

A pericyclic process involving 4n+2 or 4n electrons is thermally allowed if and only if the number of antarafacial components involved is even or odd, respectively.

Summary of the results of the equivalent Dewar–Zimmerman aromatic transition state theory

	Hückel	Möbius
4n+2 e–	Allowed aromatic	Forbidden anti-aromatic
4n e–	Forbidden anti-aromatic	Allowed aromatic

In this formulation, the electron count refers to the entire reacting system, rather than to individual components, as enumerated in Woodward and Hoffmann's original statement. In practice, an even or odd number of antarafacial components usually means zero or one antarafacial components, respectively, as transition states involving two or more antarafacial components are typically disfavored by strain. As exceptions, certain intramolecular reactions may be geometrically constrained in such a way that enforces an antarafacial trajectory for multiple components. In addition, in some cases, e.g., the Cope rearrangement, the same (not necessarily strained) transition state geometry can be considered to contain two supra or two antara π components, depending on how one draws the connections between orbital lobes. (This ambiguity is a consequence of the convention that overlap of either both interior or both exterior lobes of a σ component can be considered to be suprafacial.)

This alternative formulation makes the equivalence of the Woodward–Hoffmann rules to the Dewar–Zimmerman analysis (see below) clear. An even total number of phase inversions is equivalent to an even number of antarafacial components and corresponds to Hückel topology, requiring 4n + 2 electrons for aromaticity, while an odd total number of phase inversions is equivalent to an odd number of antarafacial components and corresponds to Möbius topology, requiring 4n electrons for aromaticity. To summarize aromatic transition state theory: Thermal pericyclic reactions proceed via (4n + 2)-electron Hückel or (4n)-electron Möbius transition states.

As a mnemonic, the above formulation can be further restated as the following:

A ground-state pericyclic process involving N electron pairs and A antarafacial components is symmetry-allowed if and only if N + A is odd.

Alternative proof of equivalence

The equivalence of the two formulations can also be seen by a simple parity argument without appeal to case analysis.

Proposition. The following formulations of the Woodward–Hoffmann rules are equivalent:

(A) For a pericyclic reaction, if the sum of the number of suprafacial 4q + 2 components and antarafacial 4r components is odd then it is thermally allowed; otherwise the reaction is thermally forbidden.

(B) For a pericyclic reaction, if the total number of antarafacial components of a (4n + 2)-electron reaction is even or the total number of antarafacial components of a 4n-electron reaction is odd then it is thermally allowed; otherwise the reaction is thermally forbidden.

Proof of equivalence: Index the components of a k-component pericyclic reaction ${\displaystyle i=1,2,\dots ,k}$ and assign component i with Woodward-Hoffmann symbol _σ/π/ωN_s/a the electron count and topology parity symbol ${\displaystyle (n_i,p_i,i)}$ according to the following rules:

${\displaystyle n_i=\{\begin{array}{ll}0,& N\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}4)\\ 1,& N\equiv 2(\mathrm{m}\mathrm{o}\mathrm{d}4)\end{array}\mathrm{a}\mathrm{n}\mathrm{d}{p}_i=\{\begin{array}{ll}0,& i\text{ is supra}\\ 1,& i\text{ is antara}\end{array}.}$

We have a mathematically equivalent restatement of (A):

(A') A collection of symbols ${\displaystyle \{(n_i,p_i,i)\}}$ is thermally allowed if and only if the number of symbols with the property ${\displaystyle n_i\ne p_i}$ is odd.

Since the total electron count is 4n + 2 or 4n precisely when $\sum _i{n}_i$ (the number of (4q + 2)-electron components) is odd or even, respectively, while $\sum _i{p}_i$ gives the number of antarafacial components, we can also restate (B):

(B') A collection of symbols ${\displaystyle \{(n_i,p_i,i)\}}$ is thermally allowed if and only if exactly one of $\sum _i{n}_i$ or $\sum _i{p}_i$ is odd.

It suffices to show that (A') and (B') are equivalent. Exactly one of $\sum _i{n}_i$ or $\sum _i{p}_i$ is odd if and only if $\sum _i{n}_i+\sum _i{p}_i=\sum _i{n}_i+p_i$ is odd. If ${\displaystyle n_i=p_i}$, ${\displaystyle n_i+p_i\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}2)}$ holds; hence, omission of symbols with the property ${\displaystyle n_i=p_i}$ from a collection will not change the parity of $\sum _i{n}_i+p_i$. On the other hand, when ${\displaystyle n_i\ne p_i}$, we have ${\displaystyle n_i+p_i=1}$, but $\sum _{n_i\ne p_i}1$ simply enumerates the number of components with the property ${\displaystyle n_i\ne p_i}$. Therefore,

${\displaystyle \sum _i{n}_i+p_i\equiv \sum _{n_i\ne p_i}{n}_i+p_i=\sum _{n_i\ne p_i}1=\mathrm{\#}\{(n_i,p_i,i)|n_i\ne p_i\}(\mathrm{m}\mathrm{o}\mathrm{d}2)}$.

Thus, $\sum _i{n}_i+p_i$ and the number of symbols in a collection with the property ${\displaystyle n_i\ne p_i}$ have the same parity. Since formulations (A') and (B') are equivalent, so are (A) and (B), as claimed. 

To give a concrete example, a hypothetical reaction with the descriptor [_π6_s + _π4_a + _π2_a] would be assigned the collection {(1, 0, 1), (0, 1, 2), (1, 1, 3)} in the scheme above. There are two components, (1, 0, 1) and (0, 1, 2), with the property ${\displaystyle n_i\ne p_i}$, so the reaction is not allowed by (A'). Likewise, $\sum _i{n}_i=2$ and $\sum _i{p}_i=2$ are both even, so (B') yields the same conclusion (as it must): the reaction is not allowed.

Examples

This formulation for a 2 component reaction is equivalent to the selection rules for a [p + q]-cycloaddition reactions shown in the following table:

p + q	Thermally allowed	Photochemically allowed
4n	ps + qa or pa + qs	ps + qs or pa + qa
4n + 2	ps + qs or pa + qa	ps + qa or pa + qs

If the total number of electrons is 4n + 2, then one is in the bottom row of the table. The reaction is thermally allowed if it is suprafacial with respect to both components or antarafacial with respect to both components. That is to say the number of antarafacial components is even (it is 0 or 2). Similarly if the total number of electrons is 4n, then one is in the top row of the table. This is thermally allowed if it is suprafacial with respect to one component and antarafacial with respect to the other. Thus the total number of antarafacial components is always odd as it is always 1.

The following are some common ground state (i.e. thermal) reaction classes analyzed in light of the generalized Woodward–Hoffmann rules.

[2+2] Cycloaddition

A thermally-allowed supra-antara [2+2]-dimerization of a strained trans-olefin

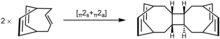
A [2+2]-cycloaddition is a 4 electron process that brings together two components. Thus, by the above general WH rules, it is only allowed if the reaction is antarafacial with respect to exactly one component. This is the same conclusion reached with correlation diagrams in the section above.

A rare but stereochemically unambiguous example of a [_π2_s + _π2_a]-cycloaddition is shown on the right. The strain and steric properties of the trans double bond enables this generally kinetically unfavorable process. cis, trans-1,5-Cyclooctadiene is also believed to undergo dimerization via this mode. Ketenes are a large class of reactants favoring [2 + 2] cycloaddition with olefins. The MO analysis of ketene cycloaddition is rendered complicated and ambiguous by the simultaneous but independent interaction of the orthogonal orbitals of the ketene but may involve a [_π2_s + _π2_a] interaction as well.

[4+2] Cycloaddition

The synchronous 6π-electron Diels-Alder reaction is a [_π4_s + _π2_s]-cycloaddition (i.e. suprafacial with respect to both components), as exemplified by the reaction to the right.

The Diels-Alder reaction is suprafacial with respect to both components.

Thus as the total number of antarafacial components is 0, which is even, the reaction is symmetry-allowed. This prediction agrees with experiment as the Diels-Alder reaction is a rather facile pericyclic reaction.

4n Electrocyclic Reaction

A 4n electron electrocyclic ring opening reaction can be considered to have 2 components – the π-system and the breaking σ-bond. With respect to the π-system, the reaction is suprafacial. However, with a conrotatory mechanism, as shown in the figure above, the reaction is antarafacial with respect to the σ-bond. Conversely with a disrotatory mechanism it is suprafacial with respect to the breaking σ-bond.

By the above rules, for a 4n electron pericyclic reaction of 2 components, there must be one antarafacial component. Thus the reaction must proceed through a conrotatory mechanism. This agrees with the result derived in the correlation diagrams above.

4n + 2 electrocyclic reaction

A 4n + 2 electrocyclic ring opening reaction is also a 2-component pericyclic reaction which is suprafacial with respect to the π-system. Thus, in order for the reaction to be allowed, the number of antarafacial components must be 0, i.e. it must be suprafacial with respect to the breaking σ-bond as well. Thus a disrotatory mechanism is symmetry-allowed.

[1,j]-sigmatropic rearrangement

Berson's classic (1967) example of a [1,3]-sigmatropic alkyl shift proceeding with stereochemical inversion (WH symbol [_σ2_a + _π2_s])

A [1,j]-sigmatropic rearrangement is also a two component pericyclic reaction: one component is the π-system, the other component is the migrating group. The simplest case is a [1,j]-hydride shift across a π-system where j is odd. In this case, as the hydrogen has only a spherically symmetric s orbital, the reaction must be suprafacial with respect to the hydrogen. The total number of electrons involved is (j + 1) as there are (j − 1)/2 π-bond plus the σ bond involved in the reaction. If j = 4n − 1 then it must be antarafacial, and if j = 4n + 1, then it must be suprafacial. This agrees with experiment that [1,3]-hydride shifts are generally not observed as the symmetry-allowed antarafacial process is not feasible, but [1,5]-hydride shifts are quite facile.

For a [1,j]-alkyl shift, where the reaction can be antarafacial (i.e. invert stereochemistry) with respect to the carbon center, the same rules apply. If j = 4n − 1 then the reaction is symmetry-allowed if it is either antarafacial with respect to the π-system, or inverts stereochemistry at the carbon. If j = 4n + 1 then the reaction is symmetry-allowed if it is suprafacial with respect to the π-system and retains stereochemistry at the carbon center.

On the right is one of the first examples of a [1,3]-sigmatropic shift to be discovered, reported by Berson in 1967. In order to allow for inversion of configuration, as the σ bond breaks, the C(H)(D) moiety twists around at the transition state, with the hybridization of the carbon approximating sp², so that the remaining unhybridized p orbital maintains overlap with both carbons 1 and 3.

Equivalence of other theoretical models

Dewar–Zimmerman analysis

Main article: Möbius–Hückel concept

Hypothetical Huckel versus Mobius aromaticity.

The generalized Woodward–Hoffmann rules, first given in 1969, are equivalent to an earlier general approach, the Möbius-Hückel concept of Zimmerman, which was first stated in 1966 and is also known as aromatic transition state theory. As its central tenet, aromatic transition state theory holds that 'allowed' pericyclic reactions proceed via transition states with aromatic character, while 'forbidden' pericyclic reactions would encounter transition states that are antiaromatic in nature. In the Dewar-Zimmerman analysis, one is concerned with the topology of the transition state of the pericyclic reaction. If the transition state involves 4n electrons, the Möbius topology is aromatic and the Hückel topology is antiaromatic, while if the transition state involves 4n + 2 electrons, the Hückel topology is aromatic and the Möbius topology is antiaromatic. The parity of the number of phase inversions (described in detail below) in the transition state determines its topology. A Möbius topology involves an odd number of phase inversions whereas a Hückel topology involves an even number of phase inversions.

Examples of Dewar-Zimmerman analysis applied to common pericyclic reactions. (The red curves represent phase inversions.)

In connection with Woodward–Hoffmann terminology, the number of antarafacial components and the number of phase inversions always have the same parity. Consequently, an odd number of antarafacial components gives Möbius topology, while an even number gives Hückel topology. Thus, to restate the results of aromatic transition state theory in the language of Woodward and Hoffmann, a 4n-electron reaction is thermally allowed if and only if it has an odd number of antarafacial components (i.e., Möbius topology); a (4n + 2)-electron reaction is thermally allowed if and only if it has an even number of antarafacial components (i.e., Hückel topology).

Procedure for Dewar-Zimmerman analysis (examples shown on the right): Step 1. Shade in all basis orbitals that are part of the pericyclic system. The shading can be arbitrary. In particular the shading does not need to reflect the phasing of the polyene MOs; each basis orbital simply need to have two oppositely phased lobes in the case of p or sp^x hybrid orbitals, or a single phase in the case of an s orbital. Step 2. Draw connections between the lobes of basis orbitals that are geometrically well-disposed to interact at the transition state. The connections to be made depend on the transition state topology. (For example, in the figure, different connections are shown in the cases of con- and disrotatory electrocyclization.) Step 3. Count the number of connections that occur between lobes of opposite shading: each of these connections constitutes a phase inversion. If the number of phase inversions is even, the transition state is Hückel, while if the number of phase inversions is odd, the transition state is Möbius. Step 4. Conclude that the pericyclic reaction is allowed if the electron count is 4n + 2 and the transition state is Hückel, or if the electron count is 4n and the transition state is Möbius; otherwise, conclude that the pericyclic reaction is forbidden.

Importantly, any scheme of assigning relative phases to the basis orbitals is acceptable, as inverting the phase of any single orbital adds 0 or ±2 phase inversions to the total, an even number, so that the parity of the number of inversions (number of inversions modulo 2) is unchanged.

Reinterpretation with conceptual density functional theory

Recently, the Woodward–Hoffmann rules have been reinterpreted using conceptual density functional theory (DFT). The key to the analysis is the dual descriptor function, proposed by Christophe Morell, André Grand and Alejandro Toro-Labbé ${\displaystyle f^{(2)}(r)=\frac{{\mathrm{\partial }}^2\rho (r)}{\mathrm{\partial }{N}^2}}$, the second derivative of the electron density ${\displaystyle \rho (r)}$ with respect to the number of electrons ${\displaystyle N}$. This response function is important as the reaction of two components A and B involving a transfer of electrons will depend on the responsiveness of the electron density to electron donation or acceptance, i.e. the derivative of the Fukui function ${\displaystyle f(r)=\frac{\mathrm{\partial }\rho (r)}{\mathrm{\partial }N}}$. In fact, from a simplistic viewpoint, the dual descriptor function gives a readout on the electrophilicity or nucleophilicity of the various regions of the molecule. For ${\displaystyle f^{(2)}>0}$, the region is electrophilic, and for ${\displaystyle f^{(2)}<0}$, the region is nucleophilic. Using the frontier molecular orbital assumption and a finite difference approximation of the Fukui function, one may write the dual descriptor as

${\displaystyle f^{(2)}(r)=\frac{\mathrm{\partial }f(r)}{\mathrm{\partial }N}\cong |{\varphi }_{\text{LUMO}}(r){|}^2-|{\varphi }_{\text{HOMO}}(r){|}^2}$

This makes intuitive sense as if a region is better at accepting electrons than donating, then the LUMO must dominate and dual descriptor function will be positive. Conversely, if a region is better at donating electrons then the HOMO term will dominate and the descriptor will be negative. Notice that although the concept of phase and orbitals are replaced simply by the notion of electron density, this function still takes both positive and negative values.

Dual-descriptor coloring (red>0, blue<0) of electron density in the Diels-Alder supra/supra transition state.

The Woodward–Hoffmann rules are reinterpreted using this formulation by matching favorable interactions between regions of electron density for which the dual descriptor has opposite signs. This is equivalent to maximizing predicted favorable interactions and minimizing repulsive interactions. For the case of a [4+2] cycloaddition, a simplified schematic of the reactants with the dual descriptor function colored (red=positive, blue=negative) is shown in the optimal supra/supra configuration to the left. This method correctly predicts the WH rules for the major classes of pericyclic reactions.

Exceptions

In Chapter 12 of The Conservation of Orbital Symmetry, entitled "Violations," Woodward and Hoffmann famously stated:

There are none! Nor can violations be expected of so fundamental a principle of maximum bonding.

This pronouncement notwithstanding, it is important to recognize that the Woodward–Hoffmann rules are used to predict relative barrier heights, and thus likely reaction mechanisms, and that they only take into account barriers due to conservation of orbital symmetry. Thus it is not guaranteed that a WH symmetry-allowed reaction actually takes place in a facile manner. Conversely, it is possible, upon enough energetic input, to achieve an anti-Woodward-Hoffmann product. This is especially prevalent in sterically constrained systems, where the WH-product has an added steric barrier to overcome. For example, in the electrocyclic ring-opening of the dimethylbicyclo[0.2.3]heptene derivative (1), a conrotatory mechanism is not possible due to resulting angle strain and the reaction proceeds slowly through a disrotatory mechanism at 400^o C to give a cycloheptadiene product. Violations may also be observed in cases with very strong thermodynamic driving forces. The decomposition of dioxetane-1,2-dione to two molecules of carbon dioxide, famous for its role in the luminescence of glowsticks, has been scrutinized computationally. In the absence of fluorescers, the reaction is now believed to proceed in a concerted (though asynchronous) fashion, via a retro-[2+2]-cycloaddition that formally violates the Woodward–Hoffmann rules.

Anti-WH product via disrotatory mechanism induced by ring strain.

Computationally predicted products of 4e electrocyclic ring opening under thermal, photo, and mechanical control.

Similarly, a recent paper describes how mechanical stress can be used to reshape chemical reaction pathways to lead to products that apparently violate Woodward–Hoffman rules. In this paper, they use ultrasound irradiation to induce a mechanical stress on link-functionalized polymers attached syn or anti on the cyclobutene ring. Computational studies predict that the mechanical force, resulting from friction of the polymers, induces bond lengthening along the reaction coordinate of the conrotatory mechanism in the anti-bisubstituted-cyclobutene, and along the reaction coordinate of the disrotatory mechanism in the syn-bisubstituted-cyclobutene. Thus in the syn-bisubstituted-cyclobutene, the anti-WH product is predicted to be formed.

This computational prediction was backed up by experiment on the system below. Link-functionalized polymers were conjugated to cis benzocyclobutene in both syn- and anti- conformations. As predicted, both products gave the same (Z,Z) product as determined by quenching by a stereospecific Diels-Alder reaction with the substituted maleimide. In particular, the syn-substituted product gave the anti-WH product, presumably as the mechanical stretching along the coordinate of the disrotatory pathway lowered the barrier of the reaction under the disrotatory pathway enough to bias that mechanism.

Controversy

It has been stated that Elias James Corey, also a Nobel Prize winner, feels he is responsible for the ideas that laid the foundation for this research, and that Woodward unfairly neglected to credit him in the discovery. In a 2004 memoir published in the Journal of Organic Chemistry, Corey makes his claim to priority of the idea: "On May 4, 1964, I suggested to my colleague R. B. Woodward a simple explanation involving the symmetry of the perturbed (HOMO) molecular orbitals for the stereoselective cyclobutene to 1,3-butadiene and 1,3,5-hexatriene to cyclohexadiene conversions that provided the basis for the further development of these ideas into what became known as the Woodward–Hoffmann rules".

Corey, then 35, was working into the evening on Monday, May 4, as he and the other driven chemists often did. At about 8:30 p.m., he dropped by Woodward's office, and Woodward posed a question about how to predict the type of ring a chain of atoms would form. After some discussion, Corey proposed that the configuration of electrons governed the course of the reaction. Woodward insisted the solution would not work, but Corey left drawings in the office, sure that he was on to something.

"I felt that this was going to be a really interesting development and was looking forward to some sort of joint undertaking," he wrote. But the next day, Woodward flew into Corey's office as he and a colleague were leaving for lunch and presented Corey's idea as his own – and then left. Corey was stunned.

In a 2004 rebuttal published in the Angewandte Chemie, Roald Hoffmann denied the claim: he quotes Woodward from a lecture given in 1966 saying: "I REMEMBER very clearly—and it still surprises me somewhat—that the crucial flash of enlightenment came to me in algebraic, rather than in pictorial or geometric form. Out of the blue, it occurred to me that the coefficients of the terminal terms in the mathematical expression representing the highest occupied molecular orbital of butadiene were of opposite sign, while those of the corresponding expression for hexatriene possessed the same sign. From here it was but a short step to the geometric, and more obviously chemically relevant, view that in the internal cyclisation of a diene, the top face of one terminal atom should attack the bottom face of the other, while in the triene case, the formation of a new bond should involve the top (or pari passu, the bottom) faces of both terminal atoms."

In addition, Hoffmann points out that in two publications from 1963 and 1965, Corey described a total synthesis of the compound dihydrocostunolide. Although they describe an electrocyclic reaction, Corey has nothing to offer with respect to explaining the stereospecificity of the synthesis.

This photochemical reaction involving 6 = 4×1 + 2 electrons is now recognized as conrotatory.

Organic photochemistry

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Organic_photochemistry

Organic photochemistry encompasses organic reactions that are induced by the action of light. The absorption of ultraviolet light by organic molecules often leads to reactions. In the earliest days, sunlight was employed, while in more modern times ultraviolet lamps are employed. Organic photochemistry has proven to be a very useful synthetic tool. Complex organic products can be obtained simply.

History

Early examples were often uncovered by the observation of precipitates or color changes from samples that were exposed to sunlights. The first reported case was by Ciamician that sunlight converted santonin to a yellow photoproduct:

Exposure of α-santonin to light results in a complex photochemical cascade.

An early example of a precipitate was the photodimerization of anthracene, characterized by Yulii Fedorovich Fritzsche and confirmed by Elbs. Similar observations focused on the dimerization of cinnamic acid to truxillic acid. Many photodimers are now recognized, e.g. pyrimidine dimer, thiophosgene, diamantane.

Another example was uncovered by Egbert Havinga in 1956. The curious result was activation on photolysis by a meta nitro group in contrast to the usual activation by ortho and para groups.

Organic photochemistry advanced with the development of the Woodward-Hoffmann rules. Illustrative, these rules help rationalize the photochemically driven electrocyclic ring-closure of hexa-2,4-diene, which proceeds in a disrotatory fashion.

Organic reactions that obey these rules are said to be symmetry allowed. Reactions that take the opposite course are symmetry forbidden and require substantially more energy to take place if they take place at all.

Key reactions

Organic photochemical reactions are explained in the context of the relevant excited states.

Parallel to the structural studies described above, the role of spin multiplicity – singlet vs triplet – on reactivity was evaluated. The importance of triplet excited species was emphasized. Triplets tend to be longer-lived than singlets and of lower energy than the singlet of the same configuration. Triplets may arise from (A) conversion of the initially formed singlets or by (B) interaction with a higher energy triplet (sensitization).

It is possible to quench triplet reactions.

Common organic photochemical reactions include: Norrish Type I, the Norrish Type II, the racemization of optically active biphenyls, the type A cyclohexadienone rearrangement, the type B cyclohexenone rearrangement, the di-π-methane rearrangement, the type B bicyclo[3.1.0]hexanone rearrangement to phenols, photochemical electrocyclic processes, the rearrangement of epoxyketones to beta-diketones, ring opening of cyclopropyl ketones, heterolysis of 3,5-dimethoxylbenzylic derivatives, and photochemical cyclizations of dienes.

Practical considerations

Photochemical lab reactor with a mercury vapor lamp.

Reactants of the photoreactions can be both gaseous and liquids. In general, it is necessary to bring the reactants close to the light source in order to obtain the highest possible luminous efficacy. For this purpose, the reaction mixture can be irradiated either directly or in a flow-through side arm of a reactor with a suitable light source.

A disadvantage of photochemical processes is the low efficiency of the conversion of electrical energy in the radiation energy of the required wavelength. In addition to the radiation, light sources generate plenty of heat, which in turn requires cooling energy. In addition, most light sources emit polychromatic light, even though only monochromatic light is needed. A high quantum yield, however, compensates for these disadvantages.

Working at low temperatures is advantageous since side reactions are avoided (as the selectivity is increased) and the yield is increased (since gaseous reactants are driven out less from the solvent).

The starting materials can sometimes be cooled before the reaction to such an extent that the reaction heat is absorbed without further cooling of the mixture. In the case of gaseous or low-boiling starting materials, work under overpressure is necessary. Due to the large number of possible raw materials, a large number of processes have been described. Large scale reactions are usually carried out in a stirred tank reactor, a bubble column reactor or a tube reactor, followed by further processing depending on the target product. In case of a stirred tank reactor, the lamp (generally shaped as an elongated cylinder) is provided with a cooling jacket and placed in the reaction solution. Tube reactors are made from quartz or glass tubes, which are irradiated from the outside. Using a stirred tank reactor has the advantage that no light is lost to the environment. However, the intensity of light drops rapidly with the distance to the light source due to adsorption by the reactants.

The influence of the radiation on the reaction rate can often be represented by a power law based on the quantum flow density, i.e. the mole light quantum (previously measured in the unit einstein) per area and time. One objective in the design of reactors is therefore to determine the economically most favorable dimensioning with regard to an optimization of the quantum current density.

Case studies

[2+2] Cycloadditions

Olefins dimerize upon UV-irradiation.

4,4-Diphenylcyclohexadienone rearrangement

Quite parallel to the santonin to lumisantonin example is the rearrangement of 4,4-diphenylcyclohexadienone Here the n-pi* triplet excited state undergoes the same beta-beta bonding. This is followed by intersystem crossing (i.e. ISC) to form the singlet ground state which is seen to be a zwitterion. The final step is the rearrangement to the bicyclic photoproduct. The reaction is termed the type A cyclohexadienone rearrangement.

4,4-diphenylcyclohexenone

To provide further evidence on the mechanism of the dienone in which there is bonding between the two double bonds, the case of 4,4-diphenylcyclohexenone is presented here. It is seen that the rearrangement is quite different; thus two double bonds are required for a type A rearrangement. With one double bond one of the phenyl groups, originally at C-4, has migrated to C-3 (i.e. the beta carbon).

When one of the aryl groups has a para-cyano or para-methoxy group, that substituted aryl group migrates in preference. Inspection of the alternative phenonium-type species, in which an aryl group has begun to migrate to the beta-carbon, reveals the greater electron delocalization with a substituent para on the migrating aryl group and thus a more stabilized pathway.

π-π* reactivity

Still another type of photochemical reaction is the di-π-methane rearrangement. Two further early examples were the rearrangement of 1,1,5,5-tetraphenyl-3,3-dimethyl-1,4-pentadiene (the "Mariano" molecule) and the rearrangement of barrelene to semibullvalene. We note that, in contrast to the cyclohexadienone reactions which used n-π* excited states, the di-π-methane rearrangements utilize π-π* excited states.

Related topics

Photoredox catalysis

In photoredox catalysis, the photon is absorbed by a sensitizer (antenna molecule or ion) which then effects redox reactions on the organic substrate. A common sensitizer is ruthenium(II) tris(bipyridine). Illustrative of photoredox catalysis are some aminotrifluoromethylation reactions.

Photochlorination

Photochlorination is one of the largest implementations of photochemistry to organic synthesis. The photon is however not absorbed by the organic compound, but by chlorine. Photolysis of Cl₂ gives chlorine atoms, which abstract H atoms from hydrocarbons, leading to chlorination.

${\displaystyle \mathrm{C}{\mathrm{l}}_2\stackrel{\mathrm{h}\nu }{\to }\mathrm{C}\mathrm{l}\cdot +\cdot \mathrm{C}\mathrm{l}(\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n})}$

${\displaystyle \mathrm{C}\mathrm{l}\cdot +\mathrm{R}\mathrm{H}⟶\cdot \mathrm{R}+\mathrm{H}\mathrm{C}\mathrm{l}(\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{a}\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n})}$

${\displaystyle \mathrm{R}\cdot +\mathrm{C}{\mathrm{l}}_2⟶\cdot \mathrm{C}\mathrm{l}+\mathrm{R}\mathrm{C}\mathrm{l}(\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{a}\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n})}$

Energy level

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Energy_level

Energy levels for an electron in an atom: ground state and excited states. After absorbing energy, an electron may "jump" from the ground state to a higher energy excited state.

A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized.

In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom's nucleus. The closest shell to the nucleus is called the "1 shell" (also called "K shell"), followed by the "2 shell" (or "L shell"), then the "3 shell" (or "M shell"), and so on farther and farther from the nucleus. The shells correspond with the principal quantum numbers (n = 1, 2, 3, 4, ...) or are labeled alphabetically with letters used in the X-ray notation (K, L, M, N, ...).

Each shell can contain only a fixed number of electrons: The first shell can hold up to two electrons, the second shell can hold up to eight (2 + 6) electrons, the third shell can hold up to 18 (2 + 6 + 10) and so on. The general formula is that the nth shell can in principle hold up to 2n² electrons. Since electrons are electrically attracted to the nucleus, an atom's electrons will generally occupy outer shells only if the more inner shells have already been completely filled by other electrons. However, this is not a strict requirement: atoms may have two or even three incomplete outer shells. (See Madelung rule for more details.) For an explanation of why electrons exist in these shells see electron configuration.

If the potential energy is set to zero at infinite distance from the atomic nucleus or molecule, the usual convention, then bound electron states have negative potential energy.

If an atom, ion, or molecule is at the lowest possible energy level, it and its electrons are said to be in the ground state. If it is at a higher energy level, it is said to be excited, or any electrons that have higher energy than the ground state are excited. An energy level is regarded as degenerate if there is more than one measurable quantum mechanical state associated with it.

Explanation

Wavefunctions of a hydrogen atom, showing the probability of finding the electron in the space around the nucleus. Each stationary state defines a specific energy level of the atom.

Quantized energy levels result from the wave behavior of particles, which gives a relationship between a particle's energy and its wavelength. For a confined particle such as an electron in an atom, the wave functions that have well defined energies have the form of a standing wave. States having well-defined energies are called stationary states because they are the states that do not change in time. Informally, these states correspond to a whole number of wavelengths of the wavefunction along a closed path (a path that ends where it started), such as a circular orbit around an atom, where the number of wavelengths gives the type of atomic orbital (0 for s-orbitals, 1 for p-orbitals and so on). Elementary examples that show mathematically how energy levels come about are the particle in a box and the quantum harmonic oscillator.

Any superposition (linear combination) of energy states is also a quantum state, but such states change with time and do not have well-defined energies. A measurement of the energy results in the collapse of the wavefunction, which results in a new state that consists of just a single energy state. Measurement of the possible energy levels of an object is called spectroscopy.

History

The first evidence of quantization in atoms was the observation of spectral lines in light from the sun in the early 1800s by Joseph von Fraunhofer and William Hyde Wollaston. The notion of energy levels was proposed in 1913 by Danish physicist Niels Bohr in the Bohr theory of the atom. The modern quantum mechanical theory giving an explanation of these energy levels in terms of the Schrödinger equation was advanced by Erwin Schrödinger and Werner Heisenberg in 1926.

Atoms

Intrinsic energy levels

In the formulas for energy of electrons at various levels given below in an atom, the zero point for energy is set when the electron in question has completely left the atom; i.e. when the electron's principal quantum number n = ∞. When the electron is bound to the atom in any closer value of n, the electron's energy is lower and is considered negative.

Orbital state energy level: atom/ion with nucleus + one electron

Assume there is one electron in a given atomic orbital in a hydrogen-like atom (ion). The energy of its state is mainly determined by the electrostatic interaction of the (negative) electron with the (positive) nucleus. The energy levels of an electron around a nucleus are given by:

${\displaystyle E_n=-hc{R}_{\mathrm{\infty }}\frac{Z^2}{n^2}}$

(typically between 1 eV and 10³ eV), where R_∞ is the Rydberg constant, Z is the atomic number, n is the principal quantum number, h is the Planck constant, and c is the speed of light. For hydrogen-like atoms (ions) only, the Rydberg levels depend only on the principal quantum number n.

This equation is obtained from combining the Rydberg formula for any hydrogen-like element (shown below) with E = hν = hc / λ assuming that the principal quantum number n above = n₁ in the Rydberg formula and n₂ = ∞ (principal quantum number of the energy level the electron descends from, when emitting a photon). The Rydberg formula was derived from empirical spectroscopic emission data.

${\displaystyle \frac{1}{\lambda }=R{Z}^2\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)}$

An equivalent formula can be derived quantum mechanically from the time-independent Schrödinger equation with a kinetic energy Hamiltonian operator using a wave function as an eigenfunction to obtain the energy levels as eigenvalues, but the Rydberg constant would be replaced by other fundamental physics constants.

Electron–electron interactions in atoms

If there is more than one electron around the atom, electron–electron interactions raise the energy level. These interactions are often neglected if the spatial overlap of the electron wavefunctions is low.

For multi-electron atoms, interactions between electrons cause the preceding equation to be no longer accurate as stated simply with Z as the atomic number. A simple (though not complete) way to understand this is as a shielding effect, where the outer electrons see an effective nucleus of reduced charge, since the inner electrons are bound tightly to the nucleus and partially cancel its charge. This leads to an approximate correction where Z is substituted with an effective nuclear charge symbolized as Z_eff that depends strongly on the principal quantum number. $${\displaystyle E_{n,\ell }=-hc{R}_{\mathrm{\infty }}\frac{{Z_{\mathrm{e}\mathrm{f}\mathrm{f}}}^2}{n^2}}$$

In such cases, the orbital types (determined by the azimuthal quantum number ℓ) as well as their levels within the molecule affect Z_eff and therefore also affect the various atomic electron energy levels. The Aufbau principle of filling an atom with electrons for an electron configuration takes these differing energy levels into account. For filling an atom with electrons in the ground state, the lowest energy levels are filled first and consistent with the Pauli exclusion principle, the Aufbau principle, and Hund's rule.

Fine structure splitting

Fine structure arises from relativistic kinetic energy corrections, spin–orbit coupling (an electrodynamic interaction between the electron's spin and motion and the nucleus's electric field) and the Darwin term (contact term interaction of s shell electrons inside the nucleus). These affect the levels by a typical order of magnitude of 10⁻³ eV.

Hyperfine structure

Main article: Hyperfine structure

This even finer structure is due to electron–nucleus spin–spin interaction, resulting in a typical change in the energy levels by a typical order of magnitude of 10⁻⁴ eV.

Energy levels due to external fields

Zeeman effect

Main article: Zeeman effect

There is an interaction energy associated with the magnetic dipole moment, μ_L, arising from the electronic orbital angular momentum, L, given by

${\displaystyle U=-{\mathit{\mu }}_L\cdot \mathbf{B}}$

with

${\displaystyle -{\mathit{\mu }}_L={\displaystyle \frac{e\hslash }{2m}}\mathbf{L}={\mu }_B\mathbf{L}}$.

Additionally taking into account the magnetic momentum arising from the electron spin.

Due to relativistic effects (Dirac equation), there is a magnetic momentum, μ_S, arising from the electron spin

${\displaystyle -{\mathit{\mu }}_S=-{\mu }_{\text{B}}{g}_S\mathbf{S}}$,

with g_S the electron-spin g-factor (about 2), resulting in a total magnetic moment, μ,

${\displaystyle \mathit{\mu }={\mathit{\mu }}_L+{\mathit{\mu }}_S}$.

The interaction energy therefore becomes

${\displaystyle U_B=-\mathit{\mu }\cdot \mathbf{B}={\mu }_{\text{B}}B(M_L+g_S{M}_S)}$.

Stark effect

Main article: Stark effect

Molecules

Chemical bonds between atoms in a molecule form because they make the situation more stable for the involved atoms, which generally means the sum energy level for the involved atoms in the molecule is lower than if the atoms were not so bonded. As separate atoms approach each other to covalently bond, their orbitals affect each other's energy levels to form bonding and antibonding molecular orbitals. The energy level of the bonding orbitals is lower, and the energy level of the antibonding orbitals is higher. For the bond in the molecule to be stable, the covalent bonding electrons occupy the lower energy bonding orbital, which may be signified by such symbols as σ or π depending on the situation. Corresponding anti-bonding orbitals can be signified by adding an asterisk to get σ* or π* orbitals. A non-bonding orbital in a molecule is an orbital with electrons in outer shells which do not participate in bonding and its energy level is the same as that of the constituent atom. Such orbitals can be designated as n orbitals. The electrons in an n orbital are typically lone pairs.  In polyatomic molecules, different vibrational and rotational energy levels are also involved.

Roughly speaking, a molecular energy state (i.e., an eigenstate of the molecular Hamiltonian) is the sum of the electronic, vibrational, rotational, nuclear, and translational components, such that: $${\displaystyle E=E_{\text{electronic}}+E_{\text{vibrational}}+E_{\text{rotational}}+E_{\text{nuclear}}+E_{\text{translational}}}$$ where E_electronic is an eigenvalue of the electronic molecular Hamiltonian (the value of the potential energy surface) at the equilibrium geometry of the molecule.

The molecular energy levels are labelled by the molecular term symbols. The specific energies of these components vary with the specific energy state and the substance.

Energy level diagrams

There are various types of energy level diagrams for bonds between atoms in a molecule.

Examples

Molecular orbital diagrams, Jablonski diagrams, and Franck–Condon diagrams.

Energy level transitions

Further information: atomic electron transition and molecular electron transition

An increase in energy level from E₁ to E₂ resulting from absorption of a photon represented by the red squiggly arrow, and whose energy is h ν.

A decrease in energy level from E₂ to E₁ resulting in emission of a photon represented by the red squiggly arrow, and whose energy is h ν.

Electrons in atoms and molecules can change (make transitions in) energy levels by emitting or absorbing a photon (of electromagnetic radiation), whose energy must be exactly equal to the energy difference between the two levels.

Electrons can also be completely removed from a chemical species such as an atom, molecule, or ion. Complete removal of an electron from an atom can be a form of ionization, which is effectively moving the electron out to an orbital with an infinite principal quantum number, in effect so far away so as to have practically no more effect on the remaining atom (ion). For various types of atoms, there are 1st, 2nd, 3rd, etc. ionization energies for removing the 1st, then the 2nd, then the 3rd, etc. of the highest energy electrons, respectively, from the atom originally in the ground state. Energy in corresponding opposite quantities can also be released, sometimes in the form of photon energy, when electrons are added to positively charged ions or sometimes atoms. Molecules can also undergo transitions in their vibrational or rotational energy levels. Energy level transitions can also be nonradiative, meaning emission or absorption of a photon is not involved.

If an atom, ion, or molecule is at the lowest possible energy level, it and its electrons are said to be in the ground state. If it is at a higher energy level, it is said to be excited, or any electrons that have higher energy than the ground state are excited. Such a species can be excited to a higher energy level by absorbing a photon whose energy is equal to the energy difference between the levels. Conversely, an excited species can go to a lower energy level by spontaneously emitting a photon equal to the energy difference. A photon's energy is equal to the Planck constant (h) times its frequency (f) and thus is proportional to its frequency, or inversely to its wavelength (λ).

ΔE = hf = hc / λ,

since c, the speed of light, equals to fλ

Correspondingly, many kinds of spectroscopy are based on detecting the frequency or wavelength of the emitted or absorbed photons to provide information on the material analyzed, including information on the energy levels and electronic structure of materials obtained by analyzing the spectrum.

An asterisk is commonly used to designate an excited state. An electron transition in a molecule's bond from a ground state to an excited state may have a designation such as σ → σ*, π → π*, or n → π* meaning excitation of an electron from a σ bonding to a σ antibonding orbital, from a π bonding to a π antibonding orbital, or from an n non-bonding to a π antibonding orbital. Reverse electron transitions for all these types of excited molecules are also possible to return to their ground states, which can be designated as σ* → σ, π* → π, or π* → n.

A transition in an energy level of an electron in a molecule may be combined with a vibrational transition and called a vibronic transition. A vibrational and rotational transition may be combined by rovibrational coupling. In rovibronic coupling, electron transitions are simultaneously combined with both vibrational and rotational transitions. Photons involved in transitions may have energy of various ranges in the electromagnetic spectrum, such as X-ray, ultraviolet, visible light, infrared, or microwave radiation, depending on the type of transition. In a very general way, energy level differences between electronic states are larger, differences between vibrational levels are intermediate, and differences between rotational levels are smaller, although there can be overlap. Translational energy levels are practically continuous and can be calculated as kinetic energy using classical mechanics.

Higher temperature causes fluid atoms and molecules to move faster increasing their translational energy, and thermally excites molecules to higher average amplitudes of vibrational and rotational modes (excites the molecules to higher internal energy levels). This means that as temperature rises, translational, vibrational, and rotational contributions to molecular heat capacity let molecules absorb heat and hold more internal energy. Conduction of heat typically occurs as molecules or atoms collide transferring the heat between each other. At even higher temperatures, electrons can be thermally excited to higher energy orbitals in atoms or molecules. A subsequent drop of an electron to a lower energy level can release a photon, causing a possibly coloured glow.

An electron farther from the nucleus has higher potential energy than an electron closer to the nucleus, thus it becomes less bound to the nucleus, since its potential energy is negative and inversely dependent on its distance from the nucleus.

Crystalline materials

Crystalline solids are found to have energy bands, instead of or in addition to energy levels. Electrons can take on any energy within an unfilled band. At first this appears to be an exception to the requirement for energy levels. However, as shown in band theory, energy bands are actually made up of many discrete energy levels which are too close together to resolve. Within a band the number of levels is of the order of the number of atoms in the crystal, so although electrons are actually restricted to these energies, they appear to be able to take on a continuum of values. The important energy levels in a crystal are the top of the valence band, the bottom of the conduction band, the Fermi level, the vacuum level, and the energy levels of any defect states in the crystal.

Excited state

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Excited_state

After absorbing energy, an electron may jump from the ground state to a higher energy excited state.

Excitations of copper 3d orbitals on the CuO₂ plane of a high-T_c superconductor. The ground state (blue) is x²–y² orbitals; the excited orbitals are in green; the arrows illustrate inelastic x-ray spectroscopy.

In quantum mechanics, an excited state of a system (such as an atom, molecule or nucleus) is any quantum state of the system that has a higher energy than the ground state (that is, more energy than the absolute minimum). Excitation refers to an increase in energy level above a chosen starting point, usually the ground state, but sometimes an already excited state. The temperature of a group of particles is indicative of the level of excitation (with the notable exception of systems that exhibit negative temperature).

The lifetime of a system in an excited state is usually short: spontaneous or induced emission of a quantum of energy (such as a photon or a phonon) usually occurs shortly after the system is promoted to the excited state, returning the system to a state with lower energy (a less excited state or the ground state). This return to a lower energy level is often loosely described as decay and is the inverse of excitation.

Long-lived excited states are often called metastable. Long-lived nuclear isomers and singlet oxygen are two examples of this.

Atomic excitation

Atoms can be excited by heat, electricity, or light. The hydrogen atom provides a simple example of this concept.

The ground state of the hydrogen atom has the atom's single electron in the lowest possible orbital (that is, the spherically symmetric "1s" wave function, which, so far, has been demonstrated to have the lowest possible quantum numbers). By giving the atom additional energy (for example, by absorption of a photon of an appropriate energy), the electron moves into an excited state (one with one or more quantum numbers greater than the minimum possible). When the electron finds itself between two states, a shift which happens very fast, it's in a superposition of both states. If the photon has too much energy, the electron will cease to be bound to the atom, and the atom will become ionized.

After excitation the atom may return to the ground state or a lower excited state, by emitting a photon with a characteristic energy. Emission of photons from atoms in various excited states leads to an electromagnetic spectrum showing a series of characteristic emission lines (including, in the case of the hydrogen atom, the Lyman, Balmer, Paschen and Brackett series).

An atom in a high excited state is termed a Rydberg atom. A system of highly excited atoms can form a long-lived condensed excited state, Rydberg matter.

Perturbed gas excitation

A collection of molecules forming a gas can be considered in an excited state if one or more molecules are elevated to kinetic energy levels such that the resulting velocity distribution departs from the equilibrium Boltzmann distribution. This phenomenon has been studied in the case of a two-dimensional gas in some detail, analyzing the time taken to relax to equilibrium.

Calculation of excited states

Excited states are often calculated using coupled cluster, Møller–Plesset perturbation theory, multi-configurational self-consistent field, configuration interaction, and time-dependent density functional theory.

Excited-state absorption

The excitation of a system (an atom or molecule) from one excited state to a higher-energy excited state with the absorption of a photon is called excited-state absorption (ESA). Excited-state absorption is possible only when an electron has been already excited from the ground state to a lower excited state. The excited-state absorption is usually an undesired effect, but it can be useful in upconversion pumping. Excited-state absorption measurements are done using pump–probe techniques such as flash photolysis. However, it is not easy to measure them compared to ground-state absorption, and in some cases complete bleaching of the ground state is required to measure excited-state absorption.

Reaction

Main article: Photochemistry

A further consequence of excited-state formation may be reaction of the atom or molecule in its excited state, as in photochemistry.