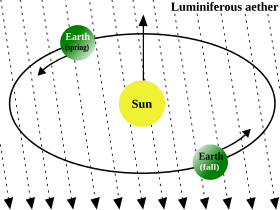
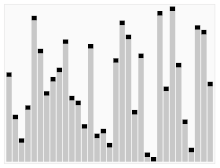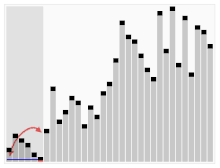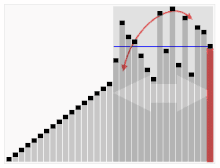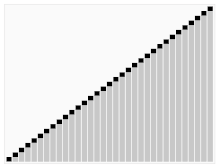
 Animated visualization of the quicksort algorithm. The horizontal lines are pivot values. |
Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.
Quicksort is a divide-and-conquer algorithm. It works by selecting a 'pivot' element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot. For this reason, it is sometimes called partition-exchange sort. The sub-arrays are then sorted recursively. This can be done in-place, requiring small additional amounts of memory to perform the sorting.
Quicksort is a comparison sort, meaning that it can sort items of any type for which a "less-than" relation (formally, a total order) is defined. It is a comparison-based sort since elements a and b are only swapped in case their relative order has been obtained in the transitive closure of prior comparison-outcomes. Most implementations of quicksort are not stable, meaning that the relative order of equal sort items is not preserved.
Mathematical analysis of quicksort shows that, on average, the algorithm takes comparisons to sort n items. In the worst case, it makes comparisons.
History
The quicksort algorithm was developed in 1959 by Tony Hoare while he was a visiting student at Moscow State University. At that time, Hoare was working on a machine translation project for the National Physical Laboratory. As a part of the translation process, he needed to sort the words in Russian sentences before looking them up in a Russian-English dictionary, which was in alphabetical order on magnetic tape. After recognizing that his first idea, insertion sort, would be slow, he came up with a new idea. He wrote the partition part in Mercury Autocode but had trouble dealing with the list of unsorted segments. On return to England, he was asked to write code for Shellsort. Hoare mentioned to his boss that he knew of a faster algorithm and his boss bet a sixpence that he did not. His boss ultimately accepted that he had lost the bet. Hoare published a paper about his algorithm in The Computer Journal Volume 5, Issue 1, 1962, Pages 10–16. Later, Hoare learned about ALGOL and its ability to do recursion that enabled him to publish an improved version of the algorithm in ALGOL in Communications of the Association for Computing Machinery, the premier computer science journal of the time. The ALGOL code is published in Communications of the ACM (CACM), Volume 4, Issue 7 July 1961, pp 321 Algorithm 63: partition and Algorithm 64: Quicksort.
Quicksort gained widespread adoption, appearing, for example, in Unix as the default library sort subroutine. Hence, it lent its name to the C standard library subroutine qsort and in the reference implementation of Java.
Robert Sedgewick's PhD thesis in 1975 is considered a milestone in the study of Quicksort where he resolved many open problems related to the analysis of various pivot selection schemes including Samplesort, adaptive partitioning by Van Emden as well as derivation of expected number of comparisons and swaps. Jon Bentley and Doug McIlroy in 1993 incorporated various improvements for use in programming libraries, including a technique to deal with equal elements and a pivot scheme known as pseudomedian of nine, where a sample of nine elements is divided into groups of three and then the median of the three medians from three groups is chosen. Bentley described another simpler and compact partitioning scheme in his book Programming Pearls that he attributed to Nico Lomuto. Later Bentley wrote that he used Hoare's version for years but never really understood it but Lomuto's version was simple enough to prove correct. Bentley described Quicksort as the "most beautiful code I had ever written" in the same essay. Lomuto's partition scheme was also popularized by the textbook Introduction to Algorithms although it is inferior to Hoare's scheme because it does three times more swaps on average and degrades to O(n2) runtime when all elements are equal. McIlroy would further produce an AntiQuicksort (aqsort) function in 1998, which consistently drives even his 1993 variant of Quicksort into quadratic behavior by producing adversarial data on-the-fly.
Algorithm

Quicksort is a type of divide-and-conquer algorithm for sorting an array, based on a partitioning routine; the details of this partitioning can vary somewhat, so that quicksort is really a family of closely related algorithms. Applied to a range of at least two elements, partitioning produces a division into two consecutive non empty sub-ranges, in such a way that no element of the first sub-range is greater than any element of the second sub-range. After applying this partition, quicksort then recursively sorts the sub-ranges, possibly after excluding from them an element at the point of division that is at this point known to be already in its final location. Due to its recursive nature, quicksort (like the partition routine) has to be formulated so as to be callable for a range within a larger array, even if the ultimate goal is to sort a complete array. The steps for in-place quicksort are:
- If the range has fewer than two elements, return immediately as there is nothing to do. Possibly for other very short lengths a special-purpose sorting method is applied and the remainder of these steps skipped.
- Otherwise pick a value, called a pivot, that occurs in the range (the precise manner of choosing depends on the partition routine, and can involve randomness).
- Partition the range: reorder its elements, while determining a point of division, so that all elements with values less than the pivot come before the division, while all elements with values greater than the pivot come after it; elements that are equal to the pivot can go either way. Since at least one instance of the pivot is present, most partition routines ensure that the value that ends up at the point of division is equal to the pivot, and is now in its final position (but termination of quicksort does not depend on this, as long as sub-ranges strictly smaller than the original are produced).
- Recursively apply quicksort to the sub-range up to the point of division and to the sub-range after it, possibly excluding from both ranges the element equal to the pivot at the point of division. (If the partition produces a possibly larger sub-range near the boundary where all elements are known to be equal to the pivot, these can be excluded as well.)
The choice of partition routine (including the pivot selection) and other details not entirely specified above can affect the algorithm's performance, possibly to a great extent for specific input arrays. In discussing the efficiency of quicksort, it is therefore necessary to specify these choices first. Here we mention two specific partition methods.
Lomuto partition scheme
This scheme is attributed to Nico Lomuto and popularized by Bentley in his book Programming Pearls and Cormen et al. in their book Introduction to Algorithms. In most formulations this scheme chooses as the pivot the last element in the array. The algorithm maintains index i as it scans the array using another index j such that the elements at lo through i-1 (inclusive) are less than the pivot, and the elements at i through j (inclusive) are equal to or greater than the pivot. As this scheme is more compact and easy to understand, it is frequently used in introductory material, although it is less efficient than Hoare's original scheme e.g., when all elements are equal. The complexity of Quicksort with this scheme degrades to O(n2) when the array is already in order, due to the partition being the worst possible one. There have been various variants proposed to boost performance including various ways to select the pivot, deal with equal elements, use other sorting algorithms such as insertion sort for small arrays, and so on. In pseudocode, a quicksort that sorts elements at lo through hi (inclusive) of an array A can be expressed as:
// Sorts (a portion of) an array, divides it into partitions, then sorts those
algorithm quicksort(A, lo, hi) is
// Ensure indices are in correct order
if lo >= hi || lo < 0 then
return
// Partition array and get the pivot index
p := partition(A, lo, hi)
// Sort the two partitions
quicksort(A, lo, p - 1) // Left side of pivot
quicksort(A, p + 1, hi) // Right side of pivot
// Divides array into two partitions
algorithm partition(A, lo, hi) is
pivot := A[hi] // Choose the last element as the pivot
// Temporary pivot index
i := lo
for j := lo to hi - 1 do
// If the current element is less than or equal to the pivot
if A[j] <= pivot then
// Swap the current element with the element at the temporary pivot index
swap A[i] with A[j]
// Move the temporary pivot index forward
i := i + 1
// Swap the pivot with the last element
swap A[i] with A[hi]
return i // the pivot index
Sorting the entire array is accomplished by quicksort(A, 0, length(A) - 1).
Hoare partition scheme

i and j
respectively), the black outlines show the positions of the sorted
elements, and the filled black square shows the value that is being
compared to (pivot).The original partition scheme described by Tony Hoare uses two pointers (indices into the range) that start at both ends of the array being partitioned, then move toward each other, until they detect an inversion: a pair of elements, one greater than the pivot at the first pointer, and one less than the pivot at the second pointer; if at this point the first pointer is still before the second, these elements are in the wrong order relative to each other, and they are then exchanged. After this the pointers are moved inwards, and the search for an inversion is repeated; when eventually the pointers cross (the first points after the second), no exchange is performed; a valid partition is found, with the point of division between the crossed pointers (any entries that might be strictly between the crossed pointers are equal to the pivot and can be excluded from both sub-ranges formed). With this formulation it is possible that one sub-range turns out to be the whole original range, which would prevent the algorithm from advancing. Hoare therefore stipulates that at the end, the sub-range containing the pivot element (which still is at its original position) can be decreased in size by excluding that pivot, after (if necessary) exchanging it with the sub-range element closest to the separation; thus, termination of quicksort is ensured.
With respect to this original description, implementations often make minor but important variations. Notably, the scheme as presented below includes elements equal to the pivot among the candidates for an inversion (so "greater than or equal" and "less than or equal" tests are used instead of "greater than" and "less than" respectively; since the formulation uses do...while rather than repeat...until which is actually reflected by the use of strict comparison operators). While there is no reason to exchange elements equal to the pivot, this change allows tests on the pointers themselves to be omitted, which are otherwise needed to ensure they do not run out of range. Indeed, since at least one instance of the pivot value is present in the range, the first advancement of either pointer cannot pass across this instance if an inclusive test is used; once an exchange is performed, these exchanged elements are now both strictly ahead of the pointer that found them, preventing that pointer from running off. (The latter is true independently of the test used, so it would be possible to use the inclusive test only when looking for the first inversion. However, using an inclusive test throughout also ensures that a division near the middle is found when all elements in the range are equal, which gives an important efficiency gain for sorting arrays with many equal elements.) The risk of producing a non-advancing separation is avoided in a different manner than described by Hoare. Such a separation can only result when no inversions are found, with both pointers advancing to the pivot element at the first iteration (they are then considered to have crossed, and no exchange takes place).
In pseudocode,
// Sorts (a portion of) an array, divides it into partitions, then sorts those
algorithm quicksort(A, lo, hi) is
if lo >= 0 && hi >= 0 && lo < hi then
p := partition(A, lo, hi)
quicksort(A, lo, p) // Note: the pivot is now included
quicksort(A, p + 1, hi)
// Divides array into two partitions
algorithm partition(A, lo, hi) is
// Pivot value
pivot := A[lo] // Choose the first element as the pivot
// Left index
i := lo - 1
// Right index
j := hi + 1
loop forever
// Move the left index to the right at least once and while the element at
// the left index is less than the pivot
do i := i + 1 while A[i] < pivot
// Move the right index to the left at least once and while the element at
// the right index is greater than the pivot
do j := j - 1 while A[j] > pivot
// If the indices crossed, return
if i >= j then return j
// Swap the elements at the left and right indices
swap A[i] with A[j]
The entire array is sorted by quicksort(A, 0, length(A) - 1).
Hoare's scheme is more efficient than Lomuto's partition scheme because it does three times fewer swaps on average. Also, as mentioned, the implementation given creates a balanced partition even when all values are equal, which Lomuto's scheme does not. Like Lomuto's partition scheme, Hoare's partitioning also would cause Quicksort to degrade to O(n2) for already sorted input, if the pivot was chosen as the first or the last element. With the middle element as the pivot, however, sorted data results with (almost) no swaps in equally sized partitions leading to best case behavior of Quicksort, i.e. O(n log(n)). Like others, Hoare's partitioning doesn't produce a stable sort. In this scheme, the pivot's final location is not necessarily at the index that is returned, as the pivot and elements equal to the pivot can end up anywhere within the partition after a partition step, and may not be sorted until the base case of a partition with a single element is reached via recursion. Therefore, the next two segments that the main algorithm recurs on are (lo..p) (elements ≤ pivot) and (p+1..hi) (elements ≥ pivot) as opposed to (lo..p-1) and (p+1..hi) as in Lomuto's scheme.
Subsequent recursions (expansion on previous paragraph)
Let's expand a little bit on the next two segments that the main algorithm recurs on. Because we are using strict comparators (>, <) in the "do...while" loops to prevent ourselves from running out of range, there's a chance that the pivot itself gets swapped with other elements in the partition function. Therefore, the index returned in the partition function isn't necessarily where the actual pivot is. Consider the example of [5, 2, 3, 1, 0], following the scheme, after the first partition the array becomes [0, 2, 1, 3, 5], the "index" returned is 2, which is the number 1, when the real pivot, the one we chose to start the partition with was the number 3. With this example, we see how it is necessary to include the returned index of the partition function in our subsequent recursions. As a result, we are presented with the choices of either recursing on (lo..p) and (p+1..hi), or (lo..p-1) and (p..hi). Which of the two options we choose depends on which index (i or j) we return in the partition function when the indices cross, and how we choose our pivot in the partition function (floor v.s. ceiling).
Let's first examine the choice of recursing on (lo..p) and (p+1..hi), with the example of sorting an array where multiple identical elements exist [0, 0]. If index i (the "latter" index) is returned after indices cross in the partition function, the index 1 would be returned after the first partition. The subsequent recursion on (lo..p)would be on (0, 1), which corresponds to the exact same array [0, 0]. A non-advancing separation that causes infinite recursion is produced. It is therefore obvious that when recursing on (lo..p) and (p+1..hi), because the left half of the recursion includes the returned index, it is the partition function's job to exclude the "tail" in non-advancing scenarios. Which is to say, index j (the "former" index when indices cross) should be returned instead of i. Going with a similar logic, when considering the example of an already sorted array [0, 1], the choice of pivot needs to be "floor" to ensure that the pointers stop on the "former" instead of the "latter" (with "ceiling" as the pivot, the index 1 would be returned and included in (lo..p) causing infinite recursion). It is for the exact same reason why choice of the last element as pivot must be avoided.
The choice of recursing on (lo..p-1) and (p..hi) follows the exact same logic as above. Because the right half of the recursion includes the returned index, it is the partition function's job to exclude the "head" in non-advancing scenarios. The index i (the "latter" index after the indices cross) in the partition function needs to be returned, and "ceiling" needs to be chosen as the pivot. The two nuances are clear, again, when considering the examples of sorting an array where multiple identical elements exist ([0, 0]), and an already sorted array [0, 1] respectively. It is noteworthy that with version of recursion, for the same reason, choice of the first element as pivot must be avoided.
Implementation issues
Choice of pivot
In the very early versions of quicksort, the leftmost element of the partition would often be chosen as the pivot element. Unfortunately, this causes worst-case behavior on already sorted arrays, which is a rather common use-case. The problem was easily solved by choosing either a random index for the pivot, choosing the middle index of the partition or (especially for longer partitions) choosing the median of the first, middle and last element of the partition for the pivot (as recommended by Sedgewick). This "median-of-three" rule counters the case of sorted (or reverse-sorted) input, and gives a better estimate of the optimal pivot (the true median) than selecting any single element, when no information about the ordering of the input is known.
Median-of-three code snippet for Lomuto partition:
mid := ⌊(lo + hi) / 2⌋
if A[mid] < A[lo]
swap A[lo] with A[mid]
if A[hi] < A[lo]
swap A[lo] with A[hi]
if A[mid] < A[hi]
swap A[mid] with A[hi]
pivot := A[hi]
It puts a median into A[hi] first, then that new value of A[hi] is used for a pivot, as in a basic algorithm presented above.
Specifically, the expected number of comparisons needed to sort n elements (see § Analysis of randomized quicksort) with random pivot selection is 1.386 n log n. Median-of-three pivoting brings this down to Cn, 2 ≈ 1.188 n log n, at the expense of a three-percent increase in the expected number of swaps. An even stronger pivoting rule, for larger arrays, is to pick the ninther, a recursive median-of-three (Mo3), defined as
- ninther(a) = median(Mo3(first 1/3 of a), Mo3(middle 1/3 of a), Mo3(final 1/3 of a))
Selecting a pivot element is also complicated by the existence of integer overflow. If the boundary indices of the subarray being sorted are sufficiently large, the naïve expression for the middle index, (lo + hi)/2, will cause overflow and provide an invalid pivot index. This can be overcome by using, for example, lo + (hi−lo)/2 to index the middle element, at the cost of more complex arithmetic. Similar issues arise in some other methods of selecting the pivot element.
Repeated elements
With a partitioning algorithm such as the Lomuto partition scheme described above (even one that chooses good pivot values), quicksort exhibits poor performance for inputs that contain many repeated elements. The problem is clearly apparent when all the input elements are equal: at each recursion, the left partition is empty (no input values are less than the pivot), and the right partition has only decreased by one element (the pivot is removed). Consequently, the Lomuto partition scheme takes quadratic time to sort an array of equal values. However, with a partitioning algorithm such as the Hoare partition scheme, repeated elements generally results in better partitioning, and although needless swaps of elements equal to the pivot may occur, the running time generally decreases as the number of repeated elements increases (with memory cache reducing the swap overhead). In the case where all elements are equal, Hoare partition scheme needlessly swaps elements, but the partitioning itself is best case, as noted in the Hoare partition section above.
To solve the Lomuto partition scheme problem (sometimes called the Dutch national flag problem), an alternative linear-time partition routine can be used that separates the values into three groups: values less than the pivot, values equal to the pivot, and values greater than the pivot. (Bentley and McIlroy call this a "fat partition" and it was already implemented in the qsort of Version 7 Unix.) The values equal to the pivot are already sorted, so only the less-than and greater-than partitions need to be recursively sorted. In pseudocode, the quicksort algorithm becomes:
// Sorts (a portion of) an array, divides it into partitions, then sorts those
algorithm quicksort(A, lo, hi) is
if lo >= 0 && lo < hi then
lt, gt := partition(A, lo, hi) // Multiple return values
quicksort(A, lo, lt - 1)
quicksort(A, gt + 1, hi)
// Divides array into three partitions
algorithm partition(A, lo, hi) is
// Pivot value
pivot := A[(lo + hi) / 2] // Choose the middle element as the pivot (integer division)
// Lesser, equal and greater index
lt := lo
eq := lo
gt := hi
// Iterate and compare all elements with the pivot
while eq <= gt do
if A[eq] < pivot then
// Swap the elements at the equal and lesser indices
swap A[eq] with A[lt]
// Increase lesser index
lt := lt + 1
// Increase equal index
eq := eq + 1
else if A[eq] > pivot then
// Swap the elements at the equal and greater indices
swap A[eq] with A[gt]
// Decrease greater index
gt := gt - 1
else // if A[eq] = pivot then
// Increase equal index
eq := eq + 1
// Return lesser and greater indices
return lt, gt
The partition algorithm returns indices to the first
('leftmost') and to the last ('rightmost') item of the middle partition.
Every other item of the partition is equal to the pivot and is
therefore sorted. Consequently, the items of the partition need not be
included in the recursive calls to quicksort.
The best case for the algorithm now occurs when all elements are equal (or are chosen from a small set of k ≪ n
elements). In the case of all equal elements, the modified quicksort
will perform only two recursive calls on empty subarrays and thus finish
in linear time (assuming the partition subroutine takes no longer than linear time).
Optimizations
Other important optimizations, also suggested by Sedgewick and widely used in practice, are:
- To make sure at most O(log n) space is used, recur first into the smaller side of the partition, then use a tail call to recur into the other, or update the parameters to no longer include the now sorted smaller side, and iterate to sort the larger side.
- When the number of elements is below some threshold (perhaps ten elements), switch to a non-recursive sorting algorithm such as insertion sort that performs fewer swaps, comparisons or other operations on such small arrays. The ideal 'threshold' will vary based on the details of the specific implementation.
- An older variant of the previous optimization: when the number of elements is less than the threshold k, simply stop; then after the whole array has been processed, perform insertion sort on it. Stopping the recursion early leaves the array k-sorted, meaning that each element is at most k positions away from its final sorted position. In this case, insertion sort takes O(kn) time to finish the sort, which is linear if k is a constant. Compared to the "many small sorts" optimization, this version may execute fewer instructions, but it makes suboptimal use of the cache memories in modern computers.
Parallelization
Quicksort's divide-and-conquer formulation makes it amenable to parallelization using task parallelism. The partitioning step is accomplished through the use of a parallel prefix sum algorithm to compute an index for each array element in its section of the partitioned array. Given an array of size n, the partitioning step performs O(n) work in O(log n) time and requires O(n) additional scratch space. After the array has been partitioned, the two partitions can be sorted recursively in parallel. Assuming an ideal choice of pivots, parallel quicksort sorts an array of size n in O(n log n) work in O(log2 n) time using O(n) additional space.
Quicksort has some disadvantages when compared to alternative sorting algorithms, like merge sort, which complicate its efficient parallelization. The depth of quicksort's divide-and-conquer tree directly impacts the algorithm's scalability, and this depth is highly dependent on the algorithm's choice of pivot. Additionally, it is difficult to parallelize the partitioning step efficiently in-place. The use of scratch space simplifies the partitioning step, but increases the algorithm's memory footprint and constant overheads.
Other more sophisticated parallel sorting algorithms can achieve even better time bounds. For example, in 1991 David M W Powers described a parallelized quicksort (and a related radix sort) that can operate in O(log n) time on a CRCW (concurrent read and concurrent write) PRAM (parallel random-access machine) with n processors by performing partitioning implicitly.
Formal analysis
Worst-case analysis
The most unbalanced partition occurs when one of the sublists returned by the partitioning routine is of size n − 1. This may occur if the pivot happens to be the smallest or largest element in the list, or in some implementations (e.g., the Lomuto partition scheme as described above) when all the elements are equal.
If this happens repeatedly in every partition, then each recursive call processes a list of size one less than the previous list. Consequently, we can make n − 1 nested calls before we reach a list of size 1. This means that the call tree is a linear chain of n − 1 nested calls. The ith call does O(n − i) work to do the partition, and , so in that case quicksort takes O(n2) time.
Best-case analysis
In the most balanced case, each time we perform a partition we divide the list into two nearly equal pieces. This means each recursive call processes a list of half the size. Consequently, we can make only log2 n nested calls before we reach a list of size 1. This means that the depth of the call tree is log2 n. But no two calls at the same level of the call tree process the same part of the original list; thus, each level of calls needs only O(n) time all together (each call has some constant overhead, but since there are only O(n) calls at each level, this is subsumed in the O(n) factor). The result is that the algorithm uses only O(n log n) time.
Average-case analysis
To sort an array of n distinct elements, quicksort takes O(n log n) time in expectation, averaged over all n! permutations of n elements with equal probability. Alternatively, if the algorithm selects the pivot uniformly at random from the input array, the same analysis can be used to bound the expected running time for any input sequence; the expectation is then taken over the random choices made by the algorithm (Cormen et al., Introduction to Algorithms, Section 7.3).
We list here three common proofs to this claim providing different insights into quicksort's workings.
Using percentiles
If each pivot has rank somewhere in the middle 50 percent, that is, between the 25th percentile and the 75th percentile, then it splits the elements with at least 25% and at most 75% on each side. If we could consistently choose such pivots, we would only have to split the list at most times before reaching lists of size 1, yielding an O(n log n) algorithm.
When the input is a random permutation, the pivot has a random rank, and so it is not guaranteed to be in the middle 50 percent. However, when we start from a random permutation, in each recursive call the pivot has a random rank in its list, and so it is in the middle 50 percent about half the time. That is good enough. Imagine that a coin is flipped: heads means that the rank of the pivot is in the middle 50 percent, tail means that it isn't. Now imagine that the coin is flipped over and over until it gets k heads. Although this could take a long time, on average only 2k flips are required, and the chance that the coin won't get k heads after 100k flips is highly improbable (this can be made rigorous using Chernoff bounds). By the same argument, Quicksort's recursion will terminate on average at a call depth of only . But if its average call depth is O(log n), and each level of the call tree processes at most n elements, the total amount of work done on average is the product, O(n log n). The algorithm does not have to verify that the pivot is in the middle half—if we hit it any constant fraction of the times, that is enough for the desired complexity.
Using recurrences
An alternative approach is to set up a recurrence relation for the T(n) factor, the time needed to sort a list of size n. In the most unbalanced case, a single quicksort call involves O(n) work plus two recursive calls on lists of size 0 and n−1, so the recurrence relation is
This is the same relation as for insertion sort and selection sort, and it solves to worst case T(n) = O(n2).
In the most balanced case, a single quicksort call involves O(n) work plus two recursive calls on lists of size n/2, so the recurrence relation is
The master theorem for divide-and-conquer recurrences tells us that T(n) = O(n log n).
The outline of a formal proof of the O(n log n) expected time complexity follows. Assume that there are no duplicates as duplicates could be handled with linear time pre- and post-processing, or considered cases easier than the analyzed. When the input is a random permutation, the rank of the pivot is uniform random from 0 to n − 1. Then the resulting parts of the partition have sizes i and n − i − 1, and i is uniform random from 0 to n − 1. So, averaging over all possible splits and noting that the number of comparisons for the partition is n − 1, the average number of comparisons over all permutations of the input sequence can be estimated accurately by solving the recurrence relation:
Solving the recurrence gives C(n) = 2 n ln n ≈ 1.39 n log2 n.
This means that, on average, quicksort performs only about 39% worse than in its best case. In this sense, it is closer to the best case than the worst case. A comparison sort cannot use less than log2(n!) comparisons on average to sort n items (as explained in the article Comparison sort) and in case of large n, Stirling's approximation yields log2(n!) ≈ n(log2 n − log2 e), so quicksort is not much worse than an ideal comparison sort. This fast average runtime is another reason for quicksort's practical dominance over other sorting algorithms.
Using a binary search tree
The following binary search tree (BST) corresponds to each execution of quicksort: the initial pivot is the root node; the pivot of the left half is the root of the left subtree, the pivot of the right half is the root of the right subtree, and so on. The number of comparisons of the execution of quicksort equals the number of comparisons during the construction of the BST by a sequence of insertions. So, the average number of comparisons for randomized quicksort equals the average cost of constructing a BST when the values inserted form a random permutation.
Consider a BST created by insertion of a sequence of values forming a random permutation. Let C denote the cost of creation of the BST. We have , where is a binary random variable expressing whether during the insertion of there was a comparison to .
By linearity of expectation, the expected value of C is .
Fix i and j<i. The values , once sorted, define j+1 intervals. The core structural observation is that is compared to in the algorithm if and only if falls inside one of the two intervals adjacent to .
Observe that since is a random permutation, is also a random permutation, so the probability that is adjacent to is exactly .
We end with a short calculation:
Space complexity
The space used by quicksort depends on the version used.
The in-place version of quicksort has a space complexity of O(log n), even in the worst case, when it is carefully implemented using the following strategies.
- In-place partitioning is used. This unstable partition requires O(1) space.
- After partitioning, the partition with the fewest elements is (recursively) sorted first, requiring at most O(log n) space. Then the other partition is sorted using tail recursion or iteration, which doesn't add to the call stack. This idea, as discussed above, was described by R. Sedgewick, and keeps the stack depth bounded by O(log n).
Quicksort with in-place and unstable partitioning uses only constant additional space before making any recursive call. Quicksort must store a constant amount of information for each nested recursive call. Since the best case makes at most O(log n) nested recursive calls, it uses O(log n) space. However, without Sedgewick's trick to limit the recursive calls, in the worst case quicksort could make O(n) nested recursive calls and need O(n) auxiliary space.
From a bit complexity viewpoint, variables such as lo and hi do not use constant space; it takes O(log n) bits to index into a list of n items. Because there are such variables in every stack frame, quicksort using Sedgewick's trick requires O((log n)2) bits of space. This space requirement isn't too terrible, though, since if the list contained distinct elements, it would need at least O(n log n) bits of space.
Another, less common, not-in-place, version of quicksort uses O(n) space for working storage and can implement a stable sort. The working storage allows the input array to be easily partitioned in a stable manner and then copied back to the input array for successive recursive calls. Sedgewick's optimization is still appropriate.
Relation to other algorithms
Quicksort is a space-optimized version of the binary tree sort. Instead of inserting items sequentially into an explicit tree, quicksort organizes them concurrently into a tree that is implied by the recursive calls. The algorithms make exactly the same comparisons, but in a different order. An often desirable property of a sorting algorithm is stability – that is the order of elements that compare equal is not changed, allowing controlling order of multikey tables (e.g. directory or folder listings) in a natural way. This property is hard to maintain for in-place quicksort (that uses only constant additional space for pointers and buffers, and O(log n) additional space for the management of explicit or implicit recursion). For variant quicksorts involving extra memory due to representations using pointers (e.g. lists or trees) or files (effectively lists), it is trivial to maintain stability. The more complex, or disk-bound, data structures tend to increase time cost, in general making increasing use of virtual memory or disk.
The most direct competitor of quicksort is heapsort. Heapsort has the advantages of simplicity, and a worst case run time of O(n log n), but heapsort's average running time is usually considered slower than in-place quicksort, primarily due to its worse locality of reference.[27] This result is debatable; some publications indicate the opposite. The main disadvantage of quicksort is the implementation complexity required to avoid bad pivot choices and the resultant O(n2) performance. Introsort is a variant of quicksort which solves this problem by switching to heapsort when a bad case is detected. Major programming languages, such as C++ (in the GNU and LLVM implementations), use introsort.
Quicksort also competes with merge sort, another O(n log n) sorting algorithm. Merge sort's main advantages are that it is a stable sort and has excellent worst-case performance. The main disadvantage of merge sort is that it is an out-of-place algorithm, so when operating on arrays, efficient implementations require O(n) auxiliary space (vs. O(log n) for quicksort with in-place partitioning and tail recursion, or O(1) for heapsort).
Merge sort works very well on linked lists, requiring only a small, constant amount of auxiliary storage. Although quicksort can be implemented as a stable sort using linked lists, there is no reason to; it will often suffer from poor pivot choices without random access, and is essentially always inferior to merge sort. Merge sort is also the algorithm of choice for external sorting of very large data sets stored on slow-to-access media such as disk storage or network-attached storage.
Bucket sort with two buckets is very similar to quicksort; the pivot in this case is effectively the value in the middle of the value range, which does well on average for uniformly distributed inputs.
Selection-based pivoting
A selection algorithm chooses the kth smallest of a list of numbers; this is an easier problem in general than sorting. One simple but effective selection algorithm works nearly in the same manner as quicksort, and is accordingly known as quickselect. The difference is that instead of making recursive calls on both sublists, it only makes a single tail-recursive call on the sublist that contains the desired element. This change lowers the average complexity to linear or O(n) time, which is optimal for selection, but the selection algorithm is still O(n2) in the worst case.
A variant of quickselect, the median of medians algorithm, chooses pivots more carefully, ensuring that the pivots are near the middle of the data (between the 30th and 70th percentiles), and thus has guaranteed linear time – O(n). This same pivot strategy can be used to construct a variant of quicksort (median of medians quicksort) with O(n log n) time. However, the overhead of choosing the pivot is significant, so this is generally not used in practice.
More abstractly, given an O(n) selection algorithm, one can use it to find the ideal pivot (the median) at every step of quicksort and thus produce a sorting algorithm with O(n log n) running time. Practical implementations of this variant are considerably slower on average, but they are of theoretical interest because they show an optimal selection algorithm can yield an optimal sorting algorithm.
Variants
Multi-pivot quicksort
Instead of partitioning into two subarrays using a single pivot, multi-pivot quicksort (also multiquicksort) partitions its input into some s number of subarrays using s − 1 pivots. While the dual-pivot case (s = 3) was considered by Sedgewick and others already in the mid-1970s, the resulting algorithms were not faster in practice than the "classical" quicksort. A 1999 assessment of a multiquicksort with a variable number of pivots, tuned to make efficient use of processor caches, found it to increase the instruction count by some 20%, but simulation results suggested that it would be more efficient on very large inputs. A version of dual-pivot quicksort developed by Yaroslavskiy in 2009 turned out to be fast enough to warrant implementation in Java 7, as the standard algorithm to sort arrays of primitives (sorting arrays of objects is done using Timsort). The performance benefit of this algorithm was subsequently found to be mostly related to cache performance, and experimental results indicate that the three-pivot variant may perform even better on modern machines.
External quicksort
For disk files, an external sort based on partitioning similar to quicksort is possible. It is slower than external merge sort, but doesn't require extra disk space. 4 buffers are used, 2 for input, 2 for output. Let number of records in the file, the number of records per buffer, and the number of buffer segments in the file. Data is read (and written) from both ends of the file inwards. Let represent the segments that start at the beginning of the file and represent segments that start at the end of the file. Data is read into the and read buffers. A pivot record is chosen and the records in the and buffers other than the pivot record are copied to the write buffer in ascending order and write buffer in descending order based comparison with the pivot record. Once either or buffer is filled, it is written to the file and the next or buffer is read from the file. The process continues until all segments are read and one write buffer remains. If that buffer is an write buffer, the pivot record is appended to it and the buffer written. If that buffer is a write buffer, the pivot record is prepended to the buffer and the buffer written. This constitutes one partition step of the file, and the file is now composed of two subfiles. The start and end positions of each subfile are pushed/popped to a stand-alone stack or the main stack via recursion. To limit stack space to , the smaller subfile is processed first. For a stand-alone stack, push the larger subfile parameters onto the stack, iterate on the smaller subfile. For recursion, recurse on the smaller subfile first, then iterate to handle the larger subfile. Once a sub-file is less than or equal to 4 B records, the subfile is sorted in-place via quicksort and written. That subfile is now sorted and in place in the file. The process is continued until all sub-files are sorted and in place. The average number of passes on the file is approximately , but worst case pattern is passes (equivalent to for worst case internal sort).
Three-way radix quicksort
This algorithm is a combination of radix sort and quicksort. Pick an element from the array (the pivot) and consider the first character (key) of the string (multikey). Partition the remaining elements into three sets: those whose corresponding character is less than, equal to, and greater than the pivot's character. Recursively sort the "less than" and "greater than" partitions on the same character. Recursively sort the "equal to" partition by the next character (key). Given we sort using bytes or words of length W bits, the best case is O(KN) and the worst case O(2KN) or at least O(N2) as for standard quicksort, given for unique keys N<2K, and K is a hidden constant in all standard comparison sort algorithms including quicksort. This is a kind of three-way quicksort in which the middle partition represents a (trivially) sorted subarray of elements that are exactly equal to the pivot.
Quick radix sort
Also developed by Powers as an O(K) parallel PRAM algorithm. This is again a combination of radix sort and quicksort but the quicksort left/right partition decision is made on successive bits of the key, and is thus O(KN) for N K-bit keys. All comparison sort algorithms implicitly assume the transdichotomous model with K in Θ(log N), as if K is smaller we can sort in O(N) time using a hash table or integer sorting. If K ≫ log N but elements are unique within O(log N) bits, the remaining bits will not be looked at by either quicksort or quick radix sort. Failing that, all comparison sorting algorithms will also have the same overhead of looking through O(K) relatively useless bits but quick radix sort will avoid the worst case O(N2) behaviours of standard quicksort and radix quicksort, and will be faster even in the best case of those comparison algorithms under these conditions of uniqueprefix(K) ≫ log N. See Powers for further discussion of the hidden overheads in comparison, radix and parallel sorting.
BlockQuicksort
In any comparison-based sorting algorithm, minimizing the number of comparisons requires maximizing the amount of information gained from each comparison, meaning that the comparison results are unpredictable. This causes frequent branch mispredictions, limiting performance. BlockQuicksort rearranges the computations of quicksort to convert unpredictable branches to data dependencies. When partitioning, the input is divided into moderate-sized blocks (which fit easily into the data cache), and two arrays are filled with the positions of elements to swap. (To avoid conditional branches, the position is unconditionally stored at the end of the array, and the index of the end is incremented if a swap is needed.) A second pass exchanges the elements at the positions indicated in the arrays. Both loops have only one conditional branch, a test for termination, which is usually taken.
The BlockQuicksort technique is incorporated into LLVM's C++ STL implementation, libcxx, providing a 50% improvement on random integer sequences. Pattern-defeating quicksort (pdqsort), a version of introsort, also incorporates this technique.
Partial and incremental quicksort
Several variants of quicksort exist that separate the k smallest or largest elements from the rest of the input.

















![{\displaystyle \operatorname {E} [C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d00e09c61139656019942c3cd118d16b1cd3878)
![{\displaystyle \operatorname {E} [C]=\sum _{i}\sum _{j<i}\Pr(c_{i,j})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9949df370597c61d1573cace1261c7595d0f1ee7)



![{\displaystyle \operatorname {E} [C]=\sum _{i}\sum _{j<i}{\frac {2}{j+1}}=O\left(\sum _{i}\log i\right)=O(n\log n).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2dadca7408799f6c84e2f2e80c4099e56cbe970)













![Visualization of the orbit of the Sun (yellow dot and white curve) around the Galactic Center (GC) in the last galactic year. The red dots correspond to the positions of the stars studied by the European Southern Observatory in a monitoring program.[15]](https://upload.wikimedia.org/wikipedia/commons/f/f8/Sun_in_orbit_around_Galactic_Centre.gif)