Convection

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Convection

Simulation of thermal convection in the Earth's mantle. Hot areas are shown in red, cold areas are shown in blue. A hot, less-dense material at the bottom moves upwards, and likewise, cold material from the top moves downwards.

Convection is single or multiphase fluid flow that occurs spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow.

Thermal image of a newly lit Ghillie kettle. The plume of hot air resulting from the convection current is visible.

Convective flow may be transient (such as when a multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to gravitational, electromagnetic or fictitious body forces. Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its mantle. Discrete convective cells in the atmosphere can be identified by clouds, with stronger convection resulting in thunderstorms. Natural convection also plays a role in stellar physics. Convection is often categorised or described by the main effect causing the convective flow; for example, thermal convection.

Convection cannot take place in most solids because neither bulk current flows nor significant diffusion of matter can take place. Granular convection is a similar phenomenon in granular material instead of fluids. Advection is the transport of any substance or quantity (such as heat) through fluid motion. Convection is a process involving bulk movement of a fluid that usually leads to a net transfer of heat through advection. Convective heat transfer is the intentional use of convection as a method for heat transfer.

History

Painting of William Prout

 

Fireplace, with grate and chimney

In the 1830s, in The Bridgewater Treatises, the term convection is attested in a scientific sense. In treatise VIII by William Prout, in the book on chemistry, it says:

[...] This motion of heat takes place in three ways, which a common fire-place very well illustrates. If, for instance, we place a thermometer directly before a fire, it soon begins to rise, indicating an increase of temperature. In this case the heat has made its way through the space between the fire and the thermometer, by the process termed radiation. If we place a second thermometer in contact with any part of the grate, and away from the direct influence of the fire, we shall find that this thermometer also denotes an increase of temperature; but here the heat must have travelled through the metal of the grate, by what is termed conduction. Lastly, a third thermometer placed in the chimney, away from the direct influence of the fire, will also indicate a considerable increase of temperature; in this case a portion of the air, passing through and near the fire, has become heated, and has carried up the chimney the temperature acquired from the fire. There is at present no single term in our language employed to denote this third mode of the propagation of heat; but we venture to propose for that purpose, the term convection, [in footnote: [Latin] Convectio, a carrying or conveying] which not only expresses the leading fact, but also accords very well with the two other terms.

Later, in the same treatise VIII, in the book on meteorology, the concept of convection is also applied to "the process by which heat is communicated through water".

Terminology

Today, the word convection has different but related usages in different scientific or engineering contexts or applications.

In fluid mechanics, convection has a broader sense: it refers to the motion of fluid driven by density (or other property) difference.

In thermodynamics, convection often refers to heat transfer by convection, where the prefixed variant Natural Convection is used to distinguish the fluid mechanics concept of Convection (covered in this article) from convective heat transfer.

Some phenomena which result in an effect superficially similar to that of a convective cell may also be (inaccurately) referred to as a form of convection; for example, thermo-capillary convection and granular convection.

Mechanisms

Convection may happen in fluids at all scales larger than a few atoms. There are a variety of circumstances in which the forces required for convection arise, leading to different types of convection, described below. In broad terms, convection arises because of body forces acting within the fluid, such as gravity.

Natural convection

This color schlieren image reveals thermal convection originating from heat conduction from a human hand (in silhouette) to the surrounding still atmosphere, initially by diffusion from the hand to the surrounding air, and subsequently also as advection as the heat causes the air to start to move upwards.

Natural convection is a flow whose motion is caused by some parts of a fluid being heavier than other parts. In most cases this leads to natural circulation: the ability of a fluid in a system to circulate continuously under gravity, with transfer of heat energy.

The driving force for natural convection is gravity. In a column of fluid, pressure increases with depth from the weight of the overlying fluid. The pressure at the bottom of a submerged object then exceeds that at the top, resulting in a net upward buoyancy force equal to the weight of the displaced fluid. Objects of higher density than that of the displaced fluid then sink. For example, regions of warmer low-density air rise, while those of colder high-density air sink. This creates a circulating flow: convection.

Gravity drives natural convection. Without gravity, convection does not occur, so there is no convection in free-fall (inertial) environments, such as that of the orbiting International Space Station. Natural convection can occur when there are hot and cold regions of either air or water, because both water and air become less dense as they are heated. But, for example, in the world's oceans it also occurs due to salt water being heavier than fresh water, so a layer of salt water on top of a layer of fresher water will also cause convection.

Natural convection has attracted a great deal of attention from researchers because of its presence both in nature and engineering applications. In nature, convection cells formed from air raising above sunlight-warmed land or water are a major feature of all weather systems. Convection is also seen in the rising plume of hot air from fire, plate tectonics, oceanic currents (thermohaline circulation) and sea-wind formation (where upward convection is also modified by Coriolis forces). In engineering applications, convection is commonly visualized in the formation of microstructures during the cooling of molten metals, and fluid flows around shrouded heat-dissipation fins, and solar ponds. A very common industrial application of natural convection is free air cooling without the aid of fans: this can happen on small scales (computer chips) to large scale process equipment.

Natural convection will be more likely and more rapid with a greater variation in density between the two fluids, a larger acceleration due to gravity that drives the convection or a larger distance through the convecting medium. Natural convection will be less likely and less rapid with more rapid diffusion (thereby diffusing away the thermal gradient that is causing the convection) or a more viscous (sticky) fluid.

The onset of natural convection can be determined by the Rayleigh number (Ra).

Differences in buoyancy within a fluid can arise for reasons other than temperature variations, in which case the fluid motion is called gravitational convection (see below). However, all types of buoyant convection, including natural convection, do not occur in microgravity environments. All require the presence of an environment which experiences g-force (proper acceleration).

The difference of density in the fluid is the key driving mechanism. If the differences of density are caused by heat, this force is called as "thermal head" or "thermal driving head." A fluid system designed for natural circulation will have a heat source and a heat sink. Each of these is in contact with some of the fluid in the system, but not all of it. The heat source is positioned lower than the heat sink.

Most fluids expand when heated, becoming less dense, and contract when cooled, becoming denser. At the heat source of a system of natural circulation, the heated fluid becomes lighter than the fluid surrounding it, and thus rises. At the heat sink, the nearby fluid becomes denser as it cools, and is drawn downward by gravity. Together, these effects create a flow of fluid from the heat source to the heat sink and back again.

Gravitational or buoyant convection

Gravitational convection is a type of natural convection induced by buoyancy variations resulting from material properties other than temperature. Typically this is caused by a variable composition of the fluid. If the varying property is a concentration gradient, it is known as solutal convection. For example, gravitational convection can be seen in the diffusion of a source of dry salt downward into wet soil due to the buoyancy of fresh water in saline.

Variable salinity in water and variable water content in air masses are frequent causes of convection in the oceans and atmosphere which do not involve heat, or else involve additional compositional density factors other than the density changes from thermal expansion (see thermohaline circulation). Similarly, variable composition within the Earth's interior which has not yet achieved maximal stability and minimal energy (in other words, with densest parts deepest) continues to cause a fraction of the convection of fluid rock and molten metal within the Earth's interior (see below).

Gravitational convection, like natural thermal convection, also requires a g-force environment in order to occur.

Solid-state convection in ice

Ice convection on Pluto is believed to occur in a soft mixture of nitrogen ice and carbon monoxide ice. It has also been proposed for Europa, and other bodies in the outer Solar System.

Thermomagnetic convection

Main article: Thermomagnetic convection

Thermomagnetic convection can occur when an external magnetic field is imposed on a ferrofluid with varying magnetic susceptibility. In the presence of a temperature gradient this results in a nonuniform magnetic body force, which leads to fluid movement. A ferrofluid is a liquid which becomes strongly magnetized in the presence of a magnetic field.

Combustion

In a zero-gravity environment, there can be no buoyancy forces, and thus no convection possible, so flames in many circumstances without gravity smother in their own waste gases. Thermal expansion and chemical reactions resulting in expansion and contraction gases allows for ventilation of the flame, as waste gases are displaced by cool, fresh, oxygen-rich gas. moves in to take up the low pressure zones created when flame-exhaust water condenses.

Examples and applications

Systems of natural circulation include tornadoes and other weather systems, ocean currents, and household ventilation. Some solar water heaters use natural circulation. The Gulf Stream circulates as a result of the evaporation of water. In this process, the water increases in salinity and density. In the North Atlantic Ocean, the water becomes so dense that it begins to sink down.

Convection occurs on a large scale in atmospheres, oceans, planetary mantles, and it provides the mechanism of heat transfer for a large fraction of the outermost interiors of the Sun and all stars. Fluid movement during convection may be invisibly slow, or it may be obvious and rapid, as in a hurricane. On astronomical scales, convection of gas and dust is thought to occur in the accretion disks of black holes, at speeds which may closely approach that of light.

Demonstration experiments

Thermal circulation of air masses

Thermal convection in liquids can be demonstrated by placing a heat source (for example, a Bunsen burner) at the side of a container with a liquid. Adding a dye to the water (such as food colouring) will enable visualisation of the flow.

Another common experiment to demonstrate thermal convection in liquids involves submerging open containers of hot and cold liquid coloured with dye into a large container of the same liquid without dye at an intermediate temperature (for example, a jar of hot tap water coloured red, a jar of water chilled in a fridge coloured blue, lowered into a clear tank of water at room temperature).

A third approach is to use two identical jars, one filled with hot water dyed one colour, and cold water of another colour. One jar is then temporarily sealed (for example, with a piece of card), inverted and placed on top of the other. When the card is removed, if the jar containing the warmer liquid is placed on top no convection will occur. If the jar containing colder liquid is placed on top, a convection current will form spontaneously.

Convection in gases can be demonstrated using a candle in a sealed space with an inlet and exhaust port. The heat from the candle will cause a strong convection current which can be demonstrated with a flow indicator, such as smoke from another candle, being released near the inlet and exhaust areas respectively.

Double diffusive convection

Main article: Double diffusive convection

Convection cells

Main article: Convection cell

Convection cells in a gravity field

A convection cell, also known as a Bénard cell, is a characteristic fluid flow pattern in many convection systems. A rising body of fluid typically loses heat because it encounters a colder surface. In liquid, this occurs because it exchanges heat with colder liquid through direct exchange. In the example of the Earth's atmosphere, this occurs because it radiates heat. Because of this heat loss the fluid becomes denser than the fluid underneath it, which is still rising. Since it cannot descend through the rising fluid, it moves to one side. At some distance, its downward force overcomes the rising force beneath it, and the fluid begins to descend. As it descends, it warms again and the cycle repeats itself. Additionally, convection cells can arise due to density variations resulting from differences in the composition of electrolytes.

Atmospheric convection

Main article: Atmospheric convection

Atmospheric circulation

Main article: Atmospheric circulation

Idealised depiction of the global circulation on Earth

Atmospheric circulation is the large-scale movement of air, and is a means by which thermal energy is distributed on the surface of the Earth, together with the much slower (lagged) ocean circulation system. The large-scale structure of the atmospheric circulation varies from year to year, but the basic climatological structure remains fairly constant.

Latitudinal circulation occurs because incident solar radiation per unit area is highest at the heat equator, and decreases as the latitude increases, reaching minima at the poles. It consists of two primary convection cells, the Hadley cell and the polar vortex, with the Hadley cell experiencing stronger convection due to the release of latent heat energy by condensation of water vapor at higher altitudes during cloud formation.

Longitudinal circulation, on the other hand, comes about because the ocean has a higher specific heat capacity than land (and also thermal conductivity, allowing the heat to penetrate further beneath the surface ) and thereby absorbs and releases more heat, but the temperature changes less than land. This brings the sea breeze, air cooled by the water, ashore in the day, and carries the land breeze, air cooled by contact with the ground, out to sea during the night. Longitudinal circulation consists of two cells, the Walker circulation and El Niño / Southern Oscillation.

Weather

See also: Cloud, Thunderstorm, and Wind

How Foehn is produced

Some more localized phenomena than global atmospheric movement are also due to convection, including wind and some of the hydrologic cycle. For example, a foehn wind is a down-slope wind which occurs on the downwind side of a mountain range. It results from the adiabatic warming of air which has dropped most of its moisture on windward slopes. Because of the different adiabatic lapse rates of moist and dry air, the air on the leeward slopes becomes warmer than at the same height on the windward slopes.

A thermal column (or thermal) is a vertical section of rising air in the lower altitudes of the Earth's atmosphere. Thermals are created by the uneven heating of the Earth's surface from solar radiation. The Sun warms the ground, which in turn warms the air directly above it. The warmer air expands, becoming less dense than the surrounding air mass, and creating a thermal low. The mass of lighter air rises, and as it does, it cools by expansion at lower air pressures. It stops rising when it has cooled to the same temperature as the surrounding air. Associated with a thermal is a downward flow surrounding the thermal column. The downward moving exterior is caused by colder air being displaced at the top of the thermal. Another convection-driven weather effect is the sea breeze.

Stages of a thunderstorm's life.

Warm air has a lower density than cool air, so warm air rises within cooler air, similar to hot air balloons. Clouds form as relatively warmer air carrying moisture rises within cooler air. As the moist air rises, it cools, causing some of the water vapor in the rising packet of air to condense. When the moisture condenses, it releases energy known as latent heat of condensation which allows the rising packet of air to cool less than its surrounding air, continuing the cloud's ascension. If enough instability is present in the atmosphere, this process will continue long enough for cumulonimbus clouds to form, which support lightning and thunder. Generally, thunderstorms require three conditions to form: moisture, an unstable airmass, and a lifting force (heat).

All thunderstorms, regardless of type, go through three stages: the developing stage, the mature stage, and the dissipation stage. The average thunderstorm has a 24 km (15 mi) diameter. Depending on the conditions present in the atmosphere, these three stages take an average of 30 minutes to go through.

Oceanic circulation

Main articles: Gulf Stream and Thermohaline circulation

Ocean currents

Solar radiation affects the oceans: warm water from the Equator tends to circulate toward the poles, while cold polar water heads towards the Equator. The surface currents are initially dictated by surface wind conditions. The trade winds blow westward in the tropics, and the westerlies blow eastward at mid-latitudes. This wind pattern applies a stress to the subtropical ocean surface with negative curl across the Northern Hemisphere, and the reverse across the Southern Hemisphere. The resulting Sverdrup transport is equatorward. Because of conservation of potential vorticity caused by the poleward-moving winds on the subtropical ridge's western periphery and the increased relative vorticity of poleward moving water, transport is balanced by a narrow, accelerating poleward current, which flows along the western boundary of the ocean basin, outweighing the effects of friction with the cold western boundary current which originates from high latitudes. The overall process, known as western intensification, causes currents on the western boundary of an ocean basin to be stronger than those on the eastern boundary.

As it travels poleward, warm water transported by strong warm water current undergoes evaporative cooling. The cooling is wind driven: wind moving over water cools the water and also causes evaporation, leaving a saltier brine. In this process, the water becomes saltier and denser and decreases in temperature. Once sea ice forms, salts are left out of the ice, a process known as brine exclusion. These two processes produce water that is denser and colder. The water across the northern Atlantic Ocean becomes so dense that it begins to sink down through less salty and less dense water. (This open ocean convection is not unlike that of a lava lamp.) This downdraft of heavy, cold and dense water becomes a part of the North Atlantic Deep Water, a south-going stream.

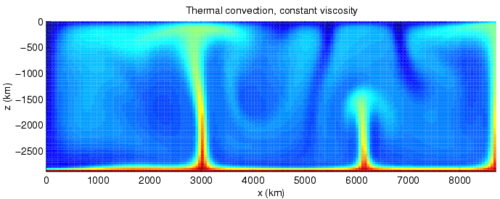
Mantle convection

Main article: Mantle convection

An oceanic plate is added to by upwelling (left) and consumed at a subduction zone (right).

Mantle convection is the slow creeping motion of Earth's rocky mantle caused by convection currents carrying heat from the interior of the Earth to the surface. It is one of 3 driving forces that causes tectonic plates to move around the Earth's surface.

The Earth's surface is divided into a number of tectonic plates that are continuously being created and consumed at their opposite plate boundaries. Creation (accretion) occurs as mantle is added to the growing edges of a plate. This hot added material cools down by conduction and convection of heat. At the consumption edges of the plate, the material has thermally contracted to become dense, and it sinks under its own weight in the process of subduction at an ocean trench. This subducted material sinks to some depth in the Earth's interior where it is prohibited from sinking further. The subducted oceanic crust triggers volcanism.

Convection within Earth's mantle is the driving force for plate tectonics. Mantle convection is the result of a thermal gradient: the lower mantle is hotter than the upper mantle, and is therefore less dense. This sets up two primary types of instabilities. In the first type, plumes rise from the lower mantle, and corresponding unstable regions of lithosphere drip back into the mantle. In the second type, subducting oceanic plates (which largely constitute the upper thermal boundary layer of the mantle) plunge back into the mantle and move downwards towards the core-mantle boundary. Mantle convection occurs at rates of centimeters per year, and it takes on the order of hundreds of millions of years to complete a cycle of convection.

Neutrino flux measurements from the Earth's core (see kamLAND) show the source of about two-thirds of the heat in the inner core is the radioactive decay of ⁴⁰K, uranium and thorium. This has allowed plate tectonics on Earth to continue far longer than it would have if it were simply driven by heat left over from Earth's formation; or with heat produced from gravitational potential energy, as a result of physical rearrangement of denser portions of the Earth's interior toward the center of the planet (that is, a type of prolonged falling and settling).

Stack effect

Main article: Stack effect

The Stack effect or chimney effect is the movement of air into and out of buildings, chimneys, flue gas stacks, or other containers due to buoyancy. Buoyancy occurs due to a difference in indoor-to-outdoor air density resulting from temperature and moisture differences. The greater the thermal difference and the height of the structure, the greater the buoyancy force, and thus the stack effect. The stack effect helps drive natural ventilation and infiltration. Some cooling towers operate on this principle; similarly the solar updraft tower is a proposed device to generate electricity based on the stack effect.

Stellar physics

Main articles: Convection zone and granule (solar physics)

An illustration of the structure of the Sun and a red giant star, showing their convective zones. These are the granular zones in the outer layers of these stars.

The convection zone of a star is the range of radii in which energy is transported outward from the core region primarily by convection rather than radiation. This occurs at radii which are sufficiently opaque that convection is more efficient than radiation at transporting energy.

Granules on the photosphere of the Sun are the visible tops of convection cells in the photosphere, caused by convection of plasma in the photosphere. The rising part of the granules is located in the center where the plasma is hotter. The outer edge of the granules is darker due to the cooler descending plasma. A typical granule has a diameter on the order of 1,000 kilometers and each lasts 8 to 20 minutes before dissipating. Below the photosphere is a layer of much larger "supergranules" up to 30,000 kilometers in diameter, with lifespans of up to 24 hours.

Water convection at freezing temperatures

Water is a fluid that does not obey the Boussinesq approximation. This is because its density varies nonlinearly with temperature, which causes its thermal expansion coefficient to be inconsistent near freezing temperatures. The density of water reaches a maximum at 4 °C and decreases as the temperature deviates. This phenomenon is investigated by experiment and numerical methods. Water is initially stagnant at 10 °C within a square cavity. It is differentially heated between the two vertical walls, where the left and right walls are held at 10 °C and 0 °C, respectively. The density anomaly manifests in its flow pattern. As the water is cooled at the right wall, the density increases, which accelerates the flow downward. As the flow develops and the water cools further, the decrease in density causes a recirculation current at the bottom right corner of the cavity.

Another case of this phenomenon is the event of super-cooling, where the water is cooled to below freezing temperatures but does not immediately begin to freeze.  Under the same conditions as before, the flow is developed. Afterward, the temperature of the right wall is decreased to −10 °C. This causes the water at that wall to become supercooled, create a counter-clockwise flow, and initially overpower the warm current. This plume is caused by a delay in the nucleation of the ice. Once ice begins to form, the flow returns to a similar pattern as before and the solidification propagates gradually until the flow is redeveloped.

Nuclear reactors

In a nuclear reactor, natural circulation can be a design criterion. It is achieved by reducing turbulence and friction in the fluid flow (that is, minimizing head loss), and by providing a way to remove any inoperative pumps from the fluid path. Also, the reactor (as the heat source) must be physically lower than the steam generators or turbines (the heat sink). In this way, natural circulation will ensure that the fluid will continue to flow as long as the reactor is hotter than the heat sink, even when power cannot be supplied to the pumps. Notable examples are the S5G and S8G United States Naval reactors, which were designed to operate at a significant fraction of full power under natural circulation, quieting those propulsion plants. The S6G reactor cannot operate at power under natural circulation, but can use it to maintain emergency cooling while shut down.

By the nature of natural circulation, fluids do not typically move very fast, but this is not necessarily bad, as high flow rates are not essential to safe and effective reactor operation. In modern design nuclear reactors, flow reversal is almost impossible. All nuclear reactors, even ones designed to primarily use natural circulation as the main method of fluid circulation, have pumps that can circulate the fluid in the case that natural circulation is not sufficient.

Mathematical models of convection

A number of dimensionless terms have been derived to describe and predict convection, including the Archimedes number, Grashof number, Richardson number, and the Rayleigh number.

In cases of mixed convection (natural and forced occurring together) one would often like to know how much of the convection is due to external constraints, such as the fluid velocity in the pump, and how much is due to natural convection occurring in the system.

The relative magnitudes of the Grashof number and the square of the Reynolds number determine which form of convection dominates. If ${\displaystyle \mathrm{G}\mathrm{r}/\mathrm{R}{\mathrm{e}}^2\gg 1}$, forced convection may be neglected, whereas if ${\displaystyle \mathrm{G}\mathrm{r}/\mathrm{R}{\mathrm{e}}^2\ll 1}$, natural convection may be neglected. If the ratio, known as the Richardson number, is approximately one, then both forced and natural convection need to be taken into account.

Onset

See also: Heat transfer

The onset of natural convection is determined by the Rayleigh number (Ra). This dimensionless number is given by

${\displaystyle \mathbf{\text{Ra}}=\frac{\mathrm{\Delta }\rho g{L}^3}{D\mu }}$

where

• ${\displaystyle \mathrm{\Delta }\rho }$ is the difference in density between the two parcels of material that are mixing
• ${\displaystyle g}$ is the local gravitational acceleration
• ${\displaystyle L}$ is the characteristic length-scale of convection: the depth of the boiling pot, for example
• ${\displaystyle D}$ is the diffusivity of the characteristic that is causing the convection, and
• ${\displaystyle \mu }$ is the dynamic viscosity.

Natural convection will be more likely and/or more rapid with a greater variation in density between the two fluids, a larger acceleration due to gravity that drives the convection, and/or a larger distance through the convecting medium. Convection will be less likely and/or less rapid with more rapid diffusion (thereby diffusing away the gradient that is causing the convection) and/or a more viscous (sticky) fluid.

For thermal convection due to heating from below, as described in the boiling pot above, the equation is modified for thermal expansion and thermal diffusivity. Density variations due to thermal expansion are given by:

${\displaystyle \mathrm{\Delta }\rho ={\rho }_0\beta \mathrm{\Delta }T}$

where

• ${\displaystyle {\rho }_0}$ is the reference density, typically picked to be the average density of the medium,
• ${\displaystyle \beta }$ is the coefficient of thermal expansion, and
• ${\displaystyle \mathrm{\Delta }T}$ is the temperature difference across the medium.

The general diffusivity, ${\displaystyle D}$, is redefined as a thermal diffusivity, ${\displaystyle \alpha }$.

${\displaystyle D=\alpha }$

Inserting these substitutions produces a Rayleigh number that can be used to predict thermal convection.

${\displaystyle \mathbf{\text{Ra}}=\frac{{\rho }_{0}g\beta \mathrm{\Delta }T{L}^3}{\alpha \mu }}$

Turbulence

The tendency of a particular naturally convective system towards turbulence relies on the Grashof number (Gr).

${\displaystyle Gr=\frac{g\beta \mathrm{\Delta }T{L}^3}{{\nu }^2}}$

In very sticky, viscous fluids (large ν), fluid motion is restricted, and natural convection will be non-turbulent.

Following the treatment of the previous subsection, the typical fluid velocity is of the order of ${\displaystyle g\mathrm{\Delta }\rho L^2/\mu }$, up to a numerical factor depending on the geometry of the system. Therefore, Grashof number can be thought of as Reynolds number with the velocity of natural convection replacing the velocity in Reynolds number's formula. However In practice, when referring to the Reynolds number, it is understood that one is considering forced convection, and the velocity is taken as the velocity dictated by external constraints (see below).

Behavior

The Grashof number can be formulated for natural convection occurring due to a concentration gradient, sometimes termed thermo-solutal convection. In this case, a concentration of hot fluid diffuses into a cold fluid, in much the same way that ink poured into a container of water diffuses to dye the entire space. Then:

${\displaystyle Gr=\frac{g\beta \mathrm{\Delta }C{L}^3}{{\nu }^2}}$

Natural convection is highly dependent on the geometry of the hot surface, various correlations exist in order to determine the heat transfer coefficient. A general correlation that applies for a variety of geometries is

${\displaystyle Nu={\left[N{u}_0^{\frac{1}{2}}+R{a}^{\frac{1}{6}}{\left(\frac{f_4\left(Pr\right)}{300}\right)}^{\frac{1}{6}}\right]}^2}$

The value of f₄(Pr) is calculated using the following formula

${\displaystyle f_4(Pr)={\left[1+{\left(\frac{0.5}{Pr}\right)}^{\frac{9}{16}}\right]}^{\frac{-16}{9}}}$

Nu is the Nusselt number and the values of Nu₀ and the characteristic length used to calculate Re are listed below (see also Discussion):

Geometry	Characteristic length	Nu0
Inclined plane	x (Distance along plane)	0.68
Inclined disk	9D/11 (D = diameter)	0.56
Vertical cylinder	x (height of cylinder)	0.68
Cone	4x/5 (x = distance along sloping surface)	0.54
Horizontal cylinder	${\displaystyle \pi D/2}$ (D = diameter of cylinder)	0.36${\displaystyle \pi }$

Warning: The values indicated for the Horizontal cylinder are wrong; see discussion.

Natural convection from a vertical plate

One example of natural convection is heat transfer from an isothermal vertical plate immersed in a fluid, causing the fluid to move parallel to the plate. This will occur in any system wherein the density of the moving fluid varies with position. These phenomena will only be of significance when the moving fluid is minimally affected by forced convection.

When considering the flow of fluid is a result of heating, the following correlations can be used, assuming the fluid is an ideal diatomic, has adjacent to a vertical plate at constant temperature and the flow of the fluid is completely laminar.

Nu_m = 0.478(Gr^0.25)

Mean Nusselt number = Nu_m = h_mL/k

where

• h_m = mean coefficient applicable between the lower edge of the plate and any point in a distance L (W/m². K)
• L = height of the vertical surface (m)
• k = thermal conductivity (W/m. K)

Grashof number = Gr = ${\displaystyle [g{L}^3(t_s-t_{\mathrm{\infty }})]/v^{2}T}$

where

• g = gravitational acceleration (m/s²)
• L = distance above the lower edge (m)
• t_s = temperature of the wall (K)
• t∞ = fluid temperature outside the thermal boundary layer (K)
• v = kinematic viscosity of the fluid (m²/s)
• T = absolute temperature (K)

When the flow is turbulent different correlations involving the Rayleigh Number (a function of both the Grashof number and the Prandtl number) must be used.

Note that the above equation differs from the usual expression for Grashof number because the value ${\displaystyle \beta }$ has been replaced by its approximation ${\displaystyle 1/T}$, which applies for ideal gases only (a reasonable approximation for air at ambient pressure).

Pattern formation

A fluid under Rayleigh–Bénard convection: the left picture represents the thermal field and the right picture its two-dimensional Fourier transform.

Convection, especially Rayleigh–Bénard convection, where the convecting fluid is contained by two rigid horizontal plates, is a convenient example of a pattern-forming system.

When heat is fed into the system from one direction (usually below), at small values it merely diffuses (conducts) from below upward, without causing fluid flow. As the heat flow is increased, above a critical value of the Rayleigh number, the system undergoes a bifurcation from the stable conducting state to the convecting state, where bulk motion of the fluid due to heat begins. If fluid parameters other than density do not depend significantly on temperature, the flow profile is symmetric, with the same volume of fluid rising as falling. This is known as Boussinesq convection.

As the temperature difference between the top and bottom of the fluid becomes higher, significant differences in fluid parameters other than density may develop in the fluid due to temperature. An example of such a parameter is viscosity, which may begin to significantly vary horizontally across layers of fluid. This breaks the symmetry of the system, and generally changes the pattern of up- and down-moving fluid from stripes to hexagons, as seen at right. Such hexagons are one example of a convection cell.

As the Rayleigh number is increased even further above the value where convection cells first appear, the system may undergo other bifurcations, and other more complex patterns, such as spirals, may begin to appear.

Rayleigh sky model

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Rayleigh_sky_model 

The Rayleigh sky model describes the observed polarization pattern of the daytime sky. Within the atmosphere, Rayleigh scattering of light by air molecules, water, dust, and aerosols causes the sky's light to have a defined polarization pattern. The same elastic scattering processes cause the sky to be blue. The polarization is characterized at each wavelength by its degree of polarization, and orientation (the e-vector angle, or scattering angle).

The polarization pattern of the sky is dependent on the celestial position of the Sun. While all scattered light is polarized to some extent, light is highly polarized at a scattering angle of 90° from the light source. In most cases the light source is the Sun, but the Moon creates the same pattern as well. The degree of polarization first increases with increasing distance from the Sun, and then decreases away from the Sun. Thus, the maximum degree of polarization occurs in a circular band 90° from the Sun. In this band, degrees of polarization near 80% are typically reached.

Degree of polarization in the Rayleigh sky at sunset or sunrise. The zenith is at the center of the graph.

When the Sun is located at the zenith, the band of maximal polarization wraps around the horizon. Light from the sky is polarized horizontally along the horizon. During twilight at either the vernal or autumnal equinox, the band of maximal polarization is defined by the north-zenith-south plane, or meridian. In particular, the polarization is vertical at the horizon in the north and south, where the meridian meets the horizon. The polarization at twilight at an equinox is represented by the figure to the right. The red band represents the circle in the north-zenith-south plane where the sky is highly polarized. The cardinal directions (N, E, S, W) are shown at 12-o'clock, 9 o'clock, 6 o'clock, and 3 o'clock (counter-clockwise around the celestial sphere, since the observer is looking up at the sky).

Note that because the polarization pattern is dependent on the Sun, it changes not only throughout the day but throughout the year. When the sun sets toward the South, in the northern hemisphere's winter, the North-Zenith-South plane is offset, with "effective" North actually located somewhat toward the West. Thus if the sun sets at an azimuth of 255° (15° South of West) the polarization pattern will be at its maximum along the horizon at an azimuth of 345° (15° West of North) and 165° (15° East of South).

During a single day, the pattern rotates with the changing position of the sun. At twilight, it typically appears about 45 minutes before local sunrise and disappears 45 minutes after local sunset. Once established it is very stable, showing change only in its rotation. It can easily be seen on any given day using polarized sunglasses.

Many animals use the polarization patterns of the sky at twilight and throughout the day as a navigation tool. Because it is determined purely by the position of the Sun, it is easily used as a compass for animal orientation. By orienting themselves with respect to the polarization patterns, animals can locate the Sun and thus determine the cardinal directions.

Theory

Geometry

The geometry representing the Rayleigh sky

The geometry for the sky polarization can be represented by a celestial triangle based on the Sun, zenith, and observed pointing (or the point of scattering). In the model, γ is the angular distance between the observed pointing and the Sun, Θ_s is the solar zenith distance (90° – solar altitude), Θ is the angular distance between the observed pointing and the zenith (90° – observed altitude), Φ is the angle between the zenith direction and the solar direction at the observed pointing, and ψ is the angle between the solar direction and the observed pointing at the zenith.

Thus, the spherical triangle is defined not only by the three points located at the Sun, zenith, and observed point but by both the three interior angles as well as the three angular distances. In an altitude-azimuth grid the angular distance between the observed pointing and the Sun and the angular distance between the observed pointing and the zenith change while the angular distance between the Sun and the zenith remains constant at one point in time.

The angular distances between the observed pointing and the Sun when the sun is setting to the west (top plot) and between the observed pointing and the zenith (bottom plot)

The figure to the left shows the two changing angular distances as mapped onto an altitude-azimuth grid (with altitude located on the x-axis and azimuth located on the y-axis). The top plot represents the changing angular distance between the observed pointing and the Sun, which is opposite to the interior angle located at the zenith (or the scattering angle). When the Sun is located at the zenith this distance is greatest along the horizon at every cardinal direction. It then decreases with rising altitude moving closer toward the zenith. At twilight the sun is setting in the west. Hence the distance is greatest when looking directly away from the Sun along the horizon in the east, and lowest along the horizon in the west.

The bottom plot in the figure to the left represents the angular distance from the observed pointing to the zenith, which is opposite to the interior angle located at the Sun. Unlike the distance between the observed pointing and the Sun, this is independent of azimuth, i.e. cardinal direction. It is simply greatest along the horizon at low altitudes and decreases linearly with rising altitude.

The three interior angles of the celestial triangle.

The figure to the right represents the three angular distances. The left one represents the angle at the observed pointing between the zenith direction and the solar direction. This is thus heavily dependent on the changing solar direction as the Sun is perceived as moving across the sky. The middle one represents the angle at the Sun between the zenith direction and the pointing. Again this is heavily dependent on the changing pointing. This is symmetrical between the North and South hemispheres. The right one represents the angle at the zenith between the solar direction and the pointing. It thus rotates around the celestial sphere.

Degree of polarization

The Rayleigh sky model predicts the degree of sky polarization as:

${\displaystyle \delta =\frac{{\delta }_{max}{\sin }^2\gamma }{1+{\cos }^2\gamma }}$

The polarization along the horizon.

As a simple example one can map the degree of polarization on the horizon. As seen in the figure to the right it is high in the North (0° and 360°) and the South (180°). It then resembles a cosine function and decreases toward the East and West reaching zero at these cardinal directions.

The degree of polarization is easily understood when mapped onto an altitude-azimuth grid as shown below. As the sun sets due West, the maximum degree of polarization can be seen in the North-Zenith-South plane. Along the horizon, at an altitude of 0° it is highest in the North and South, and lowest in the East and West. Then as altitude increases approaching the zenith (or the plane of maximum polarization) the polarization remains high in the North and South and increases until it is again maximum at 90° in the East and West, where it is then at the zenith and within the plane of polarization.

The degree of sky polarization as mapped onto the celestial sphere.

The degree of polarization. Red is high (approximately 80%) and black is low (0%).

Click on the adjacent image to view an animation that represents the degree of polarization as shown on the celestial sphere. Black represents areas where the degree of polarization is zero, whereas red represents areas where the degree of polarization is much larger. It is approximately 80%, which is a realistic maximum for the clear Rayleigh sky during day time. The video thus begins when the sun is slightly above the horizon and at an azimuth of 120°. The sky is highly polarized in the effective North-Zenith-South plane. This is slightly offset because the sun's azimuth is not due East. The sun moves across the sky with clear circular polarization patterns surrounding it. When the Sun is located at the zenith the polarization is independent of azimuth and decreases with rising altitude (as it approaches the sun). The pattern then continues as the sun approaches the horizon once again for sunset. The video ends with the sun below the horizon.

Polarization angle

The polarization angle. Red is high (approximately 90°) and black is low (-90°).

The scattering plane is the plane through the Sun, the observer, and the point observed (or the scattering point). The scattering angle, γ, is the angular distance between the Sun and the observed point. The equation for the scattering angle is derived from the law of cosines to the spherical triangle (refer to the figure above in the geometry section). It is given by:

${\displaystyle \cos \gamma =\sin {\theta }_s\sin \theta \cos ({\psi }_s-\psi )+\cos {\theta }_s\cos \theta }$

In the above equation, ψ_s and θ_s are respectively the azimuth and zenith angle of the Sun, and ψ and θ are respectively the azimuth and zenith angle of the observed point.

This equation breaks down at the zenith where the angular distance between the observed pointing and the zenith, θ_s is 0. Here the orientation of polarization is defined as the difference in azimuth between the observed pointing and the solar azimuth.

The angle of polarization (or polarization angle) is defined as the relative angle between a vector tangent to the meridian of the observed point, and an angle perpendicular to the scattering plane.

The polarization angles show a regular shift in polarization angle with azimuth. For example, when the sun is setting in the West the polarization angles proceed around the horizon. At this time the degree of polarization is constant in circular bands centered around the Sun. Thus the degree of polarization as well as its corresponding angle clearly shifts around the horizon. When the Sun is located at the zenith the horizon represents a constant degree of polarization. The corresponding polarization angle still shifts with different directions toward the zenith from different points.

The video to the right represents the polarization angle mapped onto the celestial sphere. It begins with the Sun located in a similar fashion. The angle is zero along the line from the Sun to the zenith and increases clockwise toward the East as the observed point moves clockwise toward the East. Once the sun rises in the East the angle acts in a similar fashion until the sun begins to move across the sky. As the sun moves across the sky the angle is both zero and high along the line defined by the sun, the zenith, and the anti-sun. It is lower South of this line and higher North of this line. When the Sun is at the zenith, the angle is either fully positive or 0. These two values rotate toward the west. The video then repeats a similar fashion when the sun sets in the West.

Q and U Stokes parameters

The q and u input.

The angle of polarization can be unwrapped into the Q and U Stokes parameters. Q and U are defined as the linearly polarized intensities along the position angles 0° and 45° respectively; -Q and -U are along the position angles 90° and −45°.

If the sun is located on the horizon due west, the degree of polarization is then along the North-Zenith-South plane. If the observer faces West and looks at the zenith, the polarization is horizontal with the observer. At this direction Q is 1 and U is 0. If the observer is still facing West but looking North instead then the polarization is vertical with him. Thus Q is −1 and U remains 0. Along the horizon U is always 0. Q is always −1 except in the East and West.

The scattering angle (the angle at the zenith between the solar direction and the observer direction) along the horizon is a circle. From the East through the West it is 180° and from the West through the East it is 90° at twilight. When the sun is setting in the West, the angle is then 180° East through West, and only 90° West through East. The scattering angle at an altitude of 45° is consistent.

The input stokes parameters q and u are then with respect to North but in the altitude-azimuth frame. We can easily unwrap q assuming it is in the +altitude direction. From the basic definition we know that +Q is an angle of 0° and -Q is an angle of 90°. Therefore, Q is calculated from a sine function. Similarly U is calculated from a cosine function. The angle of polarization is always perpendicular to the scattering plane. Therefore, 90° is added to both scattering angles in order to find the polarization angles. From this the Q and U Stokes parameters are determined:

${\displaystyle Q_{in}=\sin (2\theta +90)}$

and

${\displaystyle U_{in}=\cos (2\theta +90)}$

The scattering angle, derived from the law of cosines is with respect to the Sun. The polarization angle is the angle with respect to the zenith, or positive altitude. There is a line of symmetry defined by the Sun and the zenith. It is drawn from the Sun through the zenith to the other side of the celestial sphere where the "anti-sun" would be. This is also the effective East-Zenith-West plane.

The q input. Red is high (approximately 80%) and black is low (0%). (Click for animation)

The u input. Red is high (approximately 80%) and black is low (0%).

The first image to the right represents the q input mapped onto the celestial sphere. It is symmetric about the line defined by the sun-zenith-anti-sun. At twilight, in the North-Zenith-South plane it is negative because it is vertical with the degree of polarization. It is horizontal, or positive in the East-Zenith-West plane. In other words, it is positive in the ±altitude direction and negative in the ±azimuth direction. As the sun moves across the sky the q input remains high along the sun-zenith-anti-sun line. It remains zero around a circle based on the sun and the zenith. As it passes the zenith it rotates toward the south and repeats the same pattern until sunset.

The second image to the right represents the u input mapped onto the celestial sphere. The u stokes parameter changes signs depending on which quadrant it is in. The four quadrants are defined by the line of symmetry, the effective East-Zenith-West plane and the North-Zenith-South plane. It is not symmetric because it is defined by the angles ±45°. In a sense it makes two circles around the line of symmetry as opposed to only one.

It is easily understood when compared with the q input. Where the q input is halfway between 0° and 90°, the u input is either positive at +45° or negative at −45°. Similarly if the q input is positive at 90° or negative at 0° the u input is halfway between +45° and −45°. This can be seen at the non symmetric circles about the line of symmetry. It then follows the same pattern across the sky as the q input.

Neutral points and lines

Areas where the degree of polarization is zero (the skylight is unpolarized), are known as neutral points. Here the Stokes parameters Q and U also equal zero by definition. The degree of polarization therefore increases with increasing distance from the neutral points.

These conditions are met at a few defined locations on the sky. The Arago point is located above the antisolar point, while the Babinet and Brewster points are located above and below the sun respectively. The zenith distance of the Babinet or Arago point increases with increasing solar zenith distance. These neutral points can depart from their regular positions due to interference from dust and other aerosols.

The skylight polarization switches from negative to positive while passing a neutral point parallel to the solar or antisolar meridian. The lines that separate the regions of positive Q and negative Q are called neutral lines.

Depolarization

The Rayleigh sky causes a clearly defined polarization pattern under many different circumstances. The degree of polarization however, does not always remain consistent and may in fact decrease in different situations. The Rayleigh sky may undergo depolarization due to nearby objects such as clouds and large reflecting surfaces such as the ocean. It may also change depending on the time of the day (for instance at twilight or night).

In the night, the polarization of the moonlit sky is very strongly reduced in the presence of urban light pollution, because scattered urban light is not strongly polarized.

Light pollution is mostly unpolarized, and its addition to moonlight results in a decreased polarization signal.

Extensive research shows that the angle of polarization in a clear sky continues underneath clouds if the air beneath the cloud is directly lit by the Sun. The scattering of direct sunlight on those clouds results in the same polarization pattern. In other words, the proportion of the sky that follows the Rayleigh Sky Model is high for both clear skies and cloudy skies. The pattern is also clearly visible in small visible patches of sky. The celestial angle of polarization is unaffected by clouds.

Polarization patterns remain consistent even when the Sun is not present in the sky. Twilight patterns are produced during the time period between the beginning of astronomical twilight (when the Sun is 18° below the horizon) and sunrise, or sunset and the end of astronomical twilight. The duration of astronomical twilight depends on the length of the path taken by the Sun below the horizon. Thus it depends on the time of year as well as the location, but it can last for as long as 1.5 hours.

The polarization pattern caused by twilight remains fairly consistent throughout this time period. This is because the sun is moving below the horizon nearly perpendicular to it, and its azimuth therefore changes very slowly throughout this time period.

At twilight, scattered polarized light originates in the upper atmosphere and then traverses the entire lower atmosphere before reaching the observer. This provides multiple scattering opportunities and causes depolarization. It has been seen that polarization increases by about 10% from the onset of twilight to dawn. Therefore, the pattern remains consistent while the degree changes slightly.

Not only do polarization patterns remain consistent as the sun moves across the sky, but also as the moon moves across the sky at night. The Moon creates the same polarization pattern. Thus it is possible to use the polarization patterns as a tool for navigation at night. The only difference is that the degree of polarization is not quite as strong.

Underlying surface properties can affect the degree of polarization of the daytime sky. The degree of polarization has a strong dependence on surface properties. As the surface reflectance or optical thickness increase, the degree of polarization decreases. The Rayleigh sky near the ocean can therefore be highly depolarized.

Lastly, there is a clear wavelength dependence in Rayleigh scattering. It is greatest at short wavelengths, whereas skylight polarization is greatest at middle to long wavelengths. Initially it is greatest in the ultraviolet, but as light moves to the Earth's surface and interacts via multiple-path scattering it becomes high at middle to long wavelengths. The angle of polarization shows no variation with wavelength.

Uses

Navigation

Many animals, typically insects, are sensitive to the polarization of light and can therefore use the polarization patterns of the daytime sky as a tool for navigation. This theory was first proposed by Karl von Frisch when looking at the celestial orientation of honeybees. The natural sky polarization pattern serves as an easily detected compass. From the polarization patterns, these species can orient themselves by determining the exact position of the Sun without the use of direct sunlight. Thus under cloudy skies, or even at night, animals can find their way.

Using polarized light as a compass however is no easy task. The animal must be capable of detecting and analyzing polarized light. These species have specialized photoreceptors in their eyes that respond to the orientation and the degree of polarization near the zenith. They can extract information on the intensity and orientation of the degree of polarization. They can then incorporate this visually to orient themselves and recognize different properties of surfaces.

There is clear evidence that animals can even orient themselves when the Sun is below the horizon at twilight. How well insects might orient themselves using nocturnal polarization patterns is still a topic of study. So far, it is known that nocturnal crickets have wide-field polarization sensors and should be able to use the night-time polarization patterns to orient themselves. It has also been seen that nocturnally migrating birds become disoriented when the polarization pattern at twilight is unclear.

The best example is the halicitid bee Megalopta genalis, which inhabits the rainforests in Central America and scavenges before sunrise and after sunset. This bee leaves its nest approximately 1 hour before sunrise, forages for up to 30 minutes, and accurately returns to its nest before sunrise. It acts similarly just after sunset.

Thus, this bee is an example of an insect that can perceive polarization patterns throughout astronomical twilight. Not only does this case exemplify the fact that polarization patterns are present during twilight, but it remains as a perfect example that when light conditions are challenging the bee orients itself based on the polarization patterns of the twilight sky.

It has been suggested that Vikings were able to navigate on the open sea in a similar fashion, using the birefringent crystal Iceland spar, which they called "sunstone", to determine the orientation of the sky's polarization. This would allow the navigator to locate the Sun, even when it was obscured by cloud cover. An actual example of such a "sunstone" was found on a sunken (Tudor) ship dated 1592, in proximity to the ship's navigational equipment.

Non-polarized objects

Both artificial and natural objects in the sky can be very difficult to detect using only the intensity of light. These objects include clouds, satellites, and aircraft. However, the polarization of these objects due to resonant scattering, emission, reflection, or other phenomena can differ from that of the background illumination. Thus they can be more easily detected by using polarization imaging. There is a wide range of remote sensing applications in which polarization is useful for detecting objects that are otherwise difficult to see.

Charge carrier

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Charge_carrier

In solid state physics, a charge carrier is a particle or quasiparticle that is free to move, carrying an electric charge, especially the particles that carry electric charges in electrical conductors. Examples are electrons, ions and holes. In a conducting medium, an electric field can exert force on these free particles, causing a net motion of the particles through the medium; this is what constitutes an electric current. The electron and the proton are the elementary charge carriers, each carrying one elementary charge (e), of the same magnitude and opposite sign.

In conductors

In conducting mediums, particles serve to carry charge. In many metals, the charge carriers are electrons. One or two of the valence electrons from each atom are able to move about freely within the crystal structure of the metal. The free electrons are referred to as conduction electrons, and the cloud of free electrons is called a Fermi gas. Many metals have electron and hole bands. In some, the majority carriers are holes.

In electrolytes, such as salt water, the charge carriers are ions, which are atoms or molecules that have gained or lost electrons so they are electrically charged. Atoms that have gained electrons so they are negatively charged are called anions, atoms that have lost electrons so they are positively charged are called cations. Cations and anions of the dissociated liquid also serve as charge carriers in melted ionic solids (see e.g. the Hall–Héroult process for an example of electrolysis of a melted ionic solid). Proton conductors are electrolytic conductors employing positive hydrogen ions as carriers.

In a plasma, an electrically charged gas which is found in electric arcs through air, neon signs, and the sun and stars, the electrons and cations of ionized gas act as charge carriers.

In a vacuum, free electrons can act as charge carriers. In the electronic component known as the vacuum tube (also called valve), the mobile electron cloud is generated by a heated metal cathode, by a process called thermionic emission. When an electric field is applied strongly enough to draw the electrons into a beam, this may be referred to as a cathode ray, and is the basis of the cathode-ray tube display widely used in televisions and computer monitors until the 2000s.

In semiconductors, which are the materials used to make electronic components like transistors and integrated circuits, two types of charge carrier are possible. In p-type semiconductors, "effective particles" known as electron holes with positive charge move through the crystal lattice, producing an electric current. The "holes" are, in effect, electron vacancies in the valence-band electron population of the semiconductor and are treated as charge carriers because they are mobile, moving from atom site to atom site. In n-type semiconductors, electrons in the conduction band move through the crystal, resulting in an electric current.

In some conductors, such as ionic solutions and plasmas, positive and negative charge carriers coexist, so in these cases an electric current consists of the two types of carrier moving in opposite directions. In other conductors, such as metals, there are only charge carriers of one polarity, so an electric current in them simply consists of charge carriers moving in one direction.

In semiconductors

There are two recognized types of charge carriers in semiconductors. One is electrons, which carry a negative electric charge. In addition, it is convenient to treat the traveling vacancies in the valence band electron population (holes) as a second type of charge carrier, which carry a positive charge equal in magnitude to that of an electron.

Carrier generation and recombination

Main article: Carrier generation and recombination

When an electron meets with a hole, they recombine and these free carriers effectively vanish. The energy released can be either thermal, heating up the semiconductor (thermal recombination, one of the sources of waste heat in semiconductors), or released as photons (optical recombination, used in LEDs and semiconductor lasers). The recombination means an electron which has been excited from the valence band to the conduction band falls back to the empty state in the valence band, known as the holes. The holes are the empty states created in the valence band when an electron gets excited after getting some energy to pass the energy gap.

Majority and minority carriers

The more abundant charge carriers are called majority carriers, which are primarily responsible for current transport in a piece of semiconductor. In n-type semiconductors they are electrons, while in p-type semiconductors they are holes. The less abundant charge carriers are called minority carriers; in n-type semiconductors they are holes, while in p-type semiconductors they are electrons. The concentration of holes and electrons in a doped semiconductor is governed by the mass action law.

In an intrinsic semiconductor, which does not contain any impurity, the concentrations of both types of carriers are ideally equal. If an intrinsic semiconductor is doped with a donor impurity then the majority carriers are electrons. If the semiconductor is doped with an acceptor impurity then the majority carriers are holes.

Minority carriers play an important role in bipolar transistors and solar cells. Their role in field-effect transistors (FETs) is a bit more complex: for example, a MOSFET has p-type and n-type regions. The transistor action involves the majority carriers of the source and drain regions, but these carriers traverse the body of the opposite type, where they are minority carriers. However, the traversing carriers hugely outnumber their opposite type in the transfer region (in fact, the opposite type carriers are removed by an applied electric field that creates an inversion layer), so conventionally the source and drain designation for the carriers is adopted, and FETs are called "majority carrier" devices.

Free carrier concentration

Main article: Charge carrier density

Free carrier concentration is the concentration of free carriers in a doped semiconductor. It is similar to the carrier concentration in a metal and for the purposes of calculating currents or drift velocities can be used in the same way. Free carriers are electrons (holes) that have been introduced into the conduction band (valence band) by doping. Therefore, they will not act as double carriers by leaving behind holes (electrons) in the other band. In other words, charge carriers are particles that are free to move, carrying the charge. The free carrier concentration of doped semiconductors shows a characteristic temperature dependence.

In superconductors

Superconductors have zero electrical resistance and are therefore able to carry current indefinitely. This type of conduction is possible by the formation of Cooper pairs. At present, superconductors can only be achieved at very low temperatures, for instance by using cryogenic chilling. As yet, achieving superconductivity at room temperature remains challenging; it is still a field of ongoing research and experimentation. Creating a superconductor that functions at ambient temperature would constitute an important technological break-through, which could potentially contribute to much higher energy efficiency in grid distribution of electricity.

In quantum situations

Under exceptional circumstances, positrons, muons, anti-muons, taus and anti-taus may potentially also carry electric charge. This is theoretically possible, yet the very short life-time of these charged particles would render such a current very challenging to maintain at the current state of technology. It might be possible to artificially create this type of current, or it might occur in nature during very short lapses of time.

In plasmas

Plasmas consist of ionized gas. Electric charge can cause the formation of electromagnetic fields in plasmas, which can lead to the formation of currents or even multiple currents. This phenomenon is used in nuclear fusion reactors. It also occurs naturally in the cosmos, in the form of jets, nebula winds or cosmic filaments that carry charged particles. This cosmic phenomenon is called Birkeland current. Considered in general, the electric conductivity of plasmas is a subject of plasma physics.

Biopsychiatry controversy

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Biopsychiatry_controversy 

The biopsychiatry controversy is a dispute over which viewpoint should predominate and form a basis of psychiatric theory and practice. The debate is a criticism of a claimed strict biological view of psychiatric thinking. Its critics include disparate groups such as the antipsychiatry movement and some academics.

Overview of opposition to biopsychiatry

Biological psychiatry or biopsychiatry aims to investigate determinants of mental disorders devising remedial measures of a primarily somatic nature.

This has been criticized by Alvin Pam for being a "stilted, unidimensional, and mechanistic world-view", so that subsequent "research in psychiatry has been geared toward discovering which aberrant genetic or neurophysiological factors underlie and cause social deviance". According to Pam, the "blame the body" approach, which typically offers medication for mental distress, shifts the focus from disturbed behavior in the family to putative biochemical imbalances.

Research issues

2003 status in biopsychiatric research

Biopsychiatric research has produced reproducible abnormalities of brain structure and function, as well as a strong genetic component for a number of psychiatric disorders (although the latter has been shown to be correlative rather than causative). It has also elucidated some of the mechanisms of action of medications that effectively treat some of these disorders. Still, by their own admission, this research has not progressed to the stage that they can identify clear biomarkers of these disorders.

Research has shown that serious neurobiological disorders such as schizophrenia reveal reproducible abnormalities of brain structure (such as ventricular enlargement) and function. Compelling evidence exists that disorders including schizophrenia, bipolar disorder, and autism to name a few have a strong genetic component. Still, brain science has not advanced to the point where scientists or clinicians can point to readily discernible pathologic lesions or genetic abnormalities that in and of themselves serve as reliable or predictive biomarkers of a given mental disorder or mental disorders as a group. Ultimately, no gross anatomical lesion such as a tumor may ever be found; rather, mental disorders will likely be proven to represent disorders of intercellular communication; or of disrupted neural circuitry. Research already has elucidated some of the mechanisms of action of medications that are effective for depression, schizophrenia, anxiety, attention deficit, and cognitive disorders such as Alzheimer's disease. These medications clearly exert influence on specific neurotransmitters, naturally occurring brain chemicals that effect, or regulate, communication between neurons in regions of the brain that control mood, complex reasoning, anxiety, and cognition. In 1970, The Nobel Prize was awarded to Julius Axelrod, Ph.D., of the National Institute of Mental Health, for his discovery of how anti-depressant medications regulate the availability of neurotransmitters such as norepinephrine in the synapses, or gaps, between nerve cells.

— American Psychiatric Association, Statement on Diagnosis and Treatment of Mental Disorders

Focus on genetic factors

Researchers have proposed that most common psychiatric and drug abuse disorders can be traced to a small number of dimensions of genetic risk and reports show significant associations between specific genomic regions and psychiatric disorders. However, to date, only a few genetic lesions have been demonstrated to be mechanistically responsible for psychiatric conditions. For example, one reported finding suggests that in persons diagnosed with schizophrenia as well as in their relatives with chronic psychiatric illnesses, the gene that encodes phosphodiesterase 4B (PDE4B) is disrupted by a balanced translocation.

The reasons for the relative lack of genetic understanding is that the links between genes and mental states defined as abnormal appear highly complex, involve extensive environmental influences, and can be mediated in numerous different ways, for example, by personality, temperament, or life events. Therefore, while twin studies and other research suggest that personality is heritable to some extent, finding the genetic basis for particular personality or temperament traits, and their links to mental health problems, is "at least as hard as the search for genes involved in other complex disorders." Theodore Lidz and The Gene Illusion. argue that biopsychiatrists use genetic terminology in an unscientific way to reinforce their approach. Joseph maintains that biopsychiatrists disproportionately focus on understanding the genetics of those individuals with mental health problems at the expense of addressing the problems of living in the environments of some extremely abusive families or societies.

Focus on biochemical factors

See also: Monoamine Hypothesis

The chemical imbalance hypothesis states that a chemical imbalance within the brain is the main cause of psychiatric conditions and that these conditions can be improved with medication that corrects this imbalance. In that, emotions within a "normal" spectrum reflect a proper balance of neurotransmitter function. Still, abnormally extreme emotions that are severe enough to impact the daily functioning of patients (as seen in schizophrenia) reflect a profound imbalance. It is the goal of psychiatric intervention, therefore, to regain the homeostasis (via psychopharmacological approaches) that existed before the onset of the disease.

The scientific community has debated this conceptual framework, although no other demonstrably superior hypothesis has emerged. Recently, the biopsychosocial approach to mental illness has been shown to be the most comprehensive and applicable theory in understanding psychiatric disorders. However, there is still much to be discovered in this area of inquiry. As a prime example, while great strides have been made in the field of understanding certain psychiatric disorders (such as schizophrenia), others (such as major depressive disorder) operate via multiple different neurotransmitters and interact in a complex array of systems that are (as yet) not completely understood.

Reductionism

Niall McLaren emphasizes in his books Humanizing Madness and Humanizing Psychiatry that the major problem with psychiatry is that it lacks a unified model of the mind and has become entrapped in a biological reductionist paradigm. The reasons for this biological shift are intuitive, as reductionism has been very effective in other fields of science and medicine. However, despite reductionism's efficacy in explaining the smallest parts of the brain, this does not explain the mind, which is where he contends the majority of psychopathology stems from. An example would be that every aspect of a computer can be understood scientifically down to the last atom; however, this does not reveal the program that drives this hardware. He also argues that the widespread acceptance of the reductionist paradigm leads to a lack of openness to Self-criticism, "a smugness that stops the very engine of scientific progress." He has proposed his own natural dualist model of the mind, the biocognitive model, which is rooted in the theories of David Chalmers and Alan Turing and does not fall into the "dualist's trap" of spiritualism.

Economic influences on psychiatric practice

American Psychiatric Association president Steven S. Sharfstein, M.D. has stated that when the profit motive of pharmaceutical companies and human good are aligned, the results are mutually beneficial for all: "Pharmaceutical companies have developed and brought to market medications that have transformed the lives of millions of psychiatric patients. The proven effectiveness of antidepressant, mood-stabilizing, and antipsychotic medications has helped sensitize the public to the reality of mental illness and taught them that treatment works. In this way, Big Pharma has helped reduce stigma associated with psychiatric treatment and with psychiatrists." However, Sharfstein acknowledged that the goals of individual physicians who deliver direct patient care can be different from the pharmaceutical and medical device industry. Conflicts arising from this disparity raise natural concerns in this regard including:

• a "broken health care system" that allows "many patients [to be] prescribed the wrong drugs or drugs they don't need";
• "medical education opportunities sponsored by pharmaceutical companies [that] are often biased toward one product or another";
• "[d]irect marketing to consumers [that] also leads to increased demand for medications and inflates expectations about the benefits of medications";
• "drug companies [paying] physicians to allow company reps to sit in on patient sessions to learn more about care for patients."

Nevertheless, Sharfstein acknowledged that without pharmaceutical companies developing and producing modern medicines - virtually every medical specialty would have few (if any) treatments for the patients that they care for.

Pharmaceutical industry influences in psychiatry

Studies have shown that promotional marketing by pharmaceutical and other companies has the potential to influence physicians' decision making. Pharmaceutical manufacturers (and other advocates) would argue that in today's modern world, physicians simply do not have the time to continually update their knowledge base on the status of the latest research; that by providing educational materials for both physicians and patients, they are providing an educational perspective; and that it is up to the individual physician to decide what treatment is best for their patients, has been replaced by educationally-based activities that became the basis for the legal and industry reforms involving physician gifts, influence in graduate medical education, physician disclosure of conflicts of interest, and other promotional activities.

In an essay on the effect of advertisements on sales for marketed anti-depressants, evidence showed that both patients and physicians can be influenced by media advertisements, and that this influence has the possibility of increasing the frequency of certain medicines being prescribed over others.