Lagrangian mechanics

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Lagrangian_mechanics

Joseph-Louis Lagrange (1736–1813)

In physics, Lagrangian mechanics is an alternate formulation of classical mechanics founded on the d'Alembert principle of virtual work. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the Turin Academy of Science in 1760 culminating in his 1788 grand opus, Mécanique analytique. Lagrange’s approach greatly simplifies the analysis of many problems in mechanics, and it had crucial influence on other branches of physics, including relativity and quantum field theory.

Lagrangian mechanics describes a mechanical system as a pair (M, L) consisting of a configuration space M and a smooth function $L$ within that space called a Lagrangian. For many systems, L = T − V, where T and V are the kinetic and potential energy of the system, respectively.

The stationary action principle requires that the action functional of the system derived from L must remain at a stationary point (specifically, a maximum, minimum, or saddle point) throughout the time evolution of the system. This constraint allows the calculation of the equations of motion of the system using Lagrange's equations.

Introduction

Bead constrained to move on a frictionless wire. The wire exerts a reaction force C on the bead to keep it on the wire. The non-constraint force N in this case is gravity. Notice the initial position of the bead on the wire can lead to different motions.

Simple pendulum. Since the rod is rigid, the position of the bob is constrained according to the equation f(x, y) = 0, the constraint force C is the tension in the rod. Again the non-constraint force N in this case is gravity.

Newton's laws and the concept of forces are the usual starting point for teaching about mechanical systems. This method works well for many problems, but for others the approach is nightmarishly complicated. For example, in calculation of the motion of a torus rolling on a horizontal surface with a pearl sliding inside, the time-varying constraint forces like the angular velocity of the torus, motion of the pearl in relation to the torus made it difficult to determine the motion of the torus with Newton's equations. Lagrangian mechanics adopts energy rather than force as its basic ingredient, leading to more abstract equations capable of tackling more complex problems.

Particularly, Lagrange's approach was to set up independent generalized coordinates for the position and speed of every object, which allows the writing down of a general form of Lagrangian (total kinetic energy minus potential energy of the system) and summing this over all possible paths of motion of the particles yielded a formula for the 'action', which he minimized to give a generalized set of equations. This summed quantity is minimized along the path that the particle actually takes. This choice eliminates the need for the constraint force to enter into the resultant generalized system of equations. There are fewer equations since one is not directly calculating the influence of the constraint on the particle at a given moment.

For a wide variety of physical systems, if the size and shape of a massive object are negligible, it is a useful simplification to treat it as a point particle. For a system of N point particles with masses m₁, m₂, ..., m_N, each particle has a position vector, denoted r₁, r₂, ..., r_N. Cartesian coordinates are often sufficient, so r₁ = (x₁, y₁, z₁), r₂ = (x₂, y₂, z₂) and so on. In three-dimensional space, each position vector requires three coordinates to uniquely define the location of a point, so there are 3N coordinates to uniquely define the configuration of the system. These are all specific points in space to locate the particles; a general point in space is written r = (x, y, z). The velocity of each particle is how fast the particle moves along its path of motion, and is the time derivative of its position, thus $${\displaystyle {\mathbf{v}}_1=\frac{d{\mathbf{r}}_1}{dt},{\mathbf{v}}_2=\frac{d{\mathbf{r}}_2}{dt},\dots ,{\mathbf{v}}_N=\frac{d{\mathbf{r}}_N}{dt}.}$$ In Newtonian mechanics, the equations of motion are given by Newton's laws. The second law "net force equals mass times acceleration", $${\displaystyle \sum \mathbf{F}=m\frac{d^2\mathbf{r}}{d{t}^2},}$$ applies to each particle. For an N-particle system in 3 dimensions, there are 3N second-order ordinary differential equations in the positions of the particles to solve for.

Lagrangian

Instead of forces, Lagrangian mechanics uses the energies in the system. The central quantity of Lagrangian mechanics is the Lagrangian, a function which summarizes the dynamics of the entire system. Overall, the Lagrangian has units of energy, but no single expression for all physical systems. Any function which generates the correct equations of motion, in agreement with physical laws, can be taken as a Lagrangian. It is nevertheless possible to construct general expressions for large classes of applications. The non-relativistic Lagrangian for a system of particles in the absence of an electromagnetic field is given by $${\displaystyle L=T-V,}$$ where $${\displaystyle T=\frac{1}{2}\sum _{k=1}^N{m}_k{v}_k^2}$$ is the total kinetic energy of the system, equaling the sum Σ of the kinetic energies of the ${\displaystyle N}$ particles. Each particle labeled ${\displaystyle k}$ has mass ${\displaystyle m_k,}$ and v_k² = v_k · v_k is the magnitude squared of its velocity, equivalent to the dot product of the velocity with itself.

Kinetic energy T is the energy of the system's motion and is a function only of the velocities v_k, not the positions r_k, nor time t, so T = T(v₁, v₂, ...).

V, the potential energy of the system, reflects the energy of interaction between the particles, i.e. how much energy any one particle has due to all the others, together with any external influences. For conservative forces (e.g. Newtonian gravity), it is a function of the position vectors of the particles only, so V = V(r₁, r₂, ...). For those non-conservative forces which can be derived from an appropriate potential (e.g. electromagnetic potential), the velocities will appear also, V = V(r₁, r₂, ..., v₁, v₂, ...). If there is some external field or external driving force changing with time, the potential changes with time, so most generally V = V(r₁, r₂, ..., v₁, v₂, ..., t).

Mathematical formulation (for finite particle systems)

An equivalent but more mathematically formal definition of the Lagrangian is as follows. For a system of N particles in three-dimensional space, the configuration space of the system is a smooth manifold ${\displaystyle Q\subseteq {\mathbb{R}}^{3N}}$, where each configuration ${\displaystyle q\in Q}$ specifies the spacial positions of each of the particles at a given instant of time, and the manifold is composed of all the configurations that are allowed by the constraints on the system.

The Lagrangian is a smooth function: ${\displaystyle L:TQ\times \mathbb{R}\to \mathbb{R},}$ where ${\displaystyle TQ\subseteq {\mathbb{R}}^{6N}}$ is the tangent bundle of the configuration space. That is, each element in ${\displaystyle TQ}$ represents both the positions as well as the velocities of the particles, and can be written as a tuple ${\displaystyle (q_1,\dots ,q_N,{\dot{q}}_1,\dots {\dot{q}}_N)}$ with ${\displaystyle q_i}$ and ${\displaystyle {\dot{q}}_i}$ specifying a position and a velocity of the i'th particle respectively. The time dependence ${\displaystyle t\in \mathbb{R}}$ allows for the Lagrangian to describe time-dependent forces or potentials.

A trajectory of the system is a smooth function ${\displaystyle q:[t_0,t_1]\to Q,}$ describing the evolution of the configuration over time. Its velocity is the time derivative ${\displaystyle \dot{q}(t)\in T_{q(t)}Q}$ of ${\displaystyle q(t)}$, and the pair ${\displaystyle (q(t),\dot{q}(t))\in TQ}$ is thus an element of the bundle for any ${\displaystyle t}$. The action functional of the trajectory can therefore be defined as the integral of the Lagrangian along the path: ${\displaystyle S[q]={\int }_{t_0}^{t_1}L(q(t),\dot{q}(t),t)dt.}$

The laws of motion in Lagrangian mechanics are derived from the postulate that among all trajectories between two given configurations, the actual one that will be taken by the system must be a critical point (often but not necessarily a local minimum) of the action functional. This leads to the Euler-Lagrange equations (see also below).

Equations of motion

For a system of particles with masses ${\displaystyle m_1,\dots ,m_N}$, the kinetic energy is: ${\displaystyle T(q,\dot{q})=\frac{1}{2}\sum _{i=1}^N{m}_i\Vert {\dot{q}}_i{\Vert }^2,}$ where ${\displaystyle {\dot{q}}_i\in {\mathbb{R}}^3}$ is the velocity of particle i.

The potential energy ${\displaystyle V(q,t)}$ depends only on the configuration (and possibly on time), and typically arises from conservative forces.

The standard Lagrangian is given by the difference: ${\displaystyle L(q,\dot{q},t)=T(q,\dot{q})-V(q,t).}$

This formulation covers both conservative and time-dependent systems and forms the basis for generalizations to continuous systems (fields), constrained systems, and systems with curved configuration spaces.

If T or V or both depend explicitly on time due to time-varying constraints or external influences, the Lagrangian L(r₁, r₂, ... v₁, v₂, ... t) is explicitly time-dependent. If neither the potential nor the kinetic energy depend on time, then the Lagrangian L(r₁, r₂, ... v₁, v₂, ...) is explicitly independent of time. In either case, the Lagrangian always has implicit time dependence through the generalized coordinates.

With these definitions, Lagrange's equations are

Lagrange's equations

${\displaystyle \frac{\mathrm{\partial }L}{\mathrm{\partial }{\mathbf{r}}_k}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{\mathbf{r}}}_k}+\sum _{i=1}^C{\lambda }_i\frac{\mathrm{\partial }{f}_i}{\mathrm{\partial }{\mathbf{r}}_k}=0,}$

where k = 1, 2, ..., N labels the particles, there is a Lagrange multiplier λ_i for each constraint equation f_i, and $${\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }{\mathbf{r}}_k}\equiv \left(\frac{\mathrm{\partial }}{\mathrm{\partial }{x}_k},\frac{\mathrm{\partial }}{\mathrm{\partial }{y}_k},\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_k}\right),\frac{\mathrm{\partial }}{\mathrm{\partial }{\dot{\mathbf{r}}}_k}\equiv \left(\frac{\mathrm{\partial }}{\mathrm{\partial }{\dot{x}}_k},\frac{\mathrm{\partial }}{\mathrm{\partial }{\dot{y}}_k},\frac{\mathrm{\partial }}{\mathrm{\partial }{\dot{z}}_k}\right)}$$ are each shorthands for a vector of partial derivatives ∂/∂ with respect to the indicated variables (not a derivative with respect to the entire vector).^{[nb 1]} Each overdot is a shorthand for a time derivative. This procedure does increase the number of equations to solve compared to Newton's laws, from 3N to 3N + C, because there are 3N coupled second-order differential equations in the position coordinates and multipliers, plus C constraint equations. However, when solved alongside the position coordinates of the particles, the multipliers can yield information about the constraint forces. The coordinates do not need to be eliminated by solving the constraint equations.

In the Lagrangian, the position coordinates and velocity components are all independent variables, and derivatives of the Lagrangian are taken with respect to these separately according to the usual differentiation rules (e.g. the partial derivative of L with respect to the z velocity component of particle 2, defined by v_z,2 = dz₂/dt, is just ∂L/∂v_z,2; no awkward chain rules or total derivatives need to be used to relate the velocity component to the corresponding coordinate z₂).

In each constraint equation, one coordinate is redundant because it is determined from the other coordinates. The number of independent coordinates is therefore n = 3N − C. We can transform each position vector to a common set of n generalized coordinates, conveniently written as an n-tuple q = (q₁, q₂, ... q_n), by expressing each position vector, and hence the position coordinates, as functions of the generalized coordinates and time: $${\displaystyle {\mathbf{r}}_k={\mathbf{r}}_k(\mathbf{q},t)=(x_k(\mathbf{q},t),y_k(\mathbf{q},t),z_k(\mathbf{q},t),t).}$$

The vector q is a point in the configuration space of the system. The time derivatives of the generalized coordinates are called the generalized velocities, and for each particle the transformation of its velocity vector, the total derivative of its position with respect to time, is $${\displaystyle {\dot{q}}_j=\frac{\mathrm{d}{q}_j}{\mathrm{d}t},{\mathbf{v}}_k=\sum _{j=1}^n\frac{\mathrm{\partial }{\mathbf{r}}_k}{\mathrm{\partial }{q}_j}{\dot{q}}_j+\frac{\mathrm{\partial }{\mathbf{r}}_k}{\mathrm{\partial }t}.}$$

Given this v_k, the kinetic energy in generalized coordinates depends on the generalized velocities, generalized coordinates, and time if the position vectors depend explicitly on time due to time-varying constraints, so ${\displaystyle T=T(\mathbf{q},\dot{\mathbf{q}},t).}$

With these definitions, the Euler–Lagrange equations,

Lagrange's equations

${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_j}\right)=\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_j}}$

are mathematical results from the calculus of variations, which can also be used in mechanics. Substituting in the Lagrangian L(q, dq/dt, t) gives the equations of motion of the system. The number of equations has decreased compared to Newtonian mechanics, from 3N to n = 3N − C coupled second-order differential equations in the generalized coordinates. These equations do not include constraint forces at all, only non-constraint forces need to be accounted for.

Although the equations of motion include partial derivatives, the results of the partial derivatives are still ordinary differential equations in the position coordinates of the particles. The total time derivative denoted d/dt often involves implicit differentiation. Both equations are linear in the Lagrangian, but generally are nonlinear coupled equations in the coordinates.

Extensions

As already noted, this form of L is applicable to many important classes of system, but not everywhere. For relativistic Lagrangian mechanics it must be replaced as a whole by a function consistent with special relativity (scalar under Lorentz transformations) or general relativity (4-scalar). Where a magnetic field is present, the expression for the potential energy needs restating. And for dissipative forces (e.g., friction), another function must be introduced alongside Lagrangian often referred to as a "Rayleigh dissipation function" to account for the loss of energy.

One or more of the particles may each be subject to one or more holonomic constraints; such a constraint is described by an equation of the form f(r, t) = 0. If the number of constraints in the system is C, then each constraint has an equation f₁(r, t) = 0, f₂(r, t) = 0, ..., f_C(r, t) = 0, each of which could apply to any of the particles. If particle k is subject to constraint i, then f_i(r_k, t) = 0. At any instant of time, the coordinates of a constrained particle are linked together and not independent. The constraint equations determine the allowed paths the particles can move along, but not where they are or how fast they go at every instant of time. Nonholonomic constraints depend on the particle velocities, accelerations, or higher derivatives of position. Lagrangian mechanics can only be applied to systems whose constraints, if any, are all holonomic. Three examples of nonholonomic constraints are: when the constraint equations are non-integrable, when the constraints have inequalities, or when the constraints involve complicated non-conservative forces like friction. Nonholonomic constraints require special treatment, and one may have to revert to Newtonian mechanics or use other methods.

From Newtonian to Lagrangian mechanics

Newton's laws

Isaac Newton (1642–1727)

For simplicity, Newton's laws can be illustrated for one particle without much loss of generality (for a system of N particles, all of these equations apply to each particle in the system). The equation of motion for a particle of constant mass m is Newton's second law of 1687, in modern vector notation $${\displaystyle \mathbf{F}=m\mathbf{a},}$$ where a is its acceleration and F the resultant force acting on it. Where the mass is varying, the equation needs to be generalised to take the time derivative of the momentum. In three spatial dimensions, this is a system of three coupled second-order ordinary differential equations to solve, since there are three components in this vector equation. The solution is the position vector r of the particle at time t, subject to the initial conditions of r and v when t = 0.

Newton's laws are easy to use in Cartesian coordinates, but Cartesian coordinates are not always convenient, and for other coordinate systems the equations of motion can become complicated. In a set of curvilinear coordinates ξ = (ξ¹, ξ², ξ³), the law in tensor index notation is the "Lagrangian form" $${\displaystyle F^a=m\left(\frac{{\mathrm{d}}^2{\xi }^a}{\mathrm{d}{t}^2}+{\mathrm{\Gamma }}^a{}_{bc}\frac{\mathrm{d}{\xi }^b}{\mathrm{d}t}\frac{\mathrm{d}{\xi }^c}{\mathrm{d}t}\right)=g^{ak}\left(\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }T}{\mathrm{\partial }{\dot{\xi }}^k}-\frac{\mathrm{\partial }T}{\mathrm{\partial }{\xi }^k}\right),{\dot{\xi }}^a\equiv \frac{\mathrm{d}{\xi }^a}{\mathrm{d}t},}$$ where F^a is the a-th contravariant component of the resultant force acting on the particle, Γ^a_bc are the Christoffel symbols of the second kind, $${\displaystyle T=\frac{1}{2}m{g}_{bc}\frac{\mathrm{d}{\xi }^b}{\mathrm{d}t}\frac{\mathrm{d}{\xi }^c}{\mathrm{d}t}}$$ is the kinetic energy of the particle, and g_bc the covariant components of the metric tensor of the curvilinear coordinate system. All the indices a, b, c, each take the values 1, 2, 3. Curvilinear coordinates are not the same as generalized coordinates.

It may seem like an overcomplication to cast Newton's law in this form, but there are advantages. The acceleration components in terms of the Christoffel symbols can be avoided by evaluating derivatives of the kinetic energy instead. If there is no resultant force acting on the particle, F = 0, it does not accelerate, but moves with constant velocity in a straight line. Mathematically, the solutions of the differential equation are geodesics, the curves of extremal length between two points in space (these may end up being minimal, that is the shortest paths, but not necessarily). In flat 3D real space the geodesics are simply straight lines. So for a free particle, Newton's second law coincides with the geodesic equation and states that free particles follow geodesics, the extremal trajectories it can move along. If the particle is subject to forces F ≠ 0, the particle accelerates due to forces acting on it and deviates away from the geodesics it would follow if free. With appropriate extensions of the quantities given here in flat 3D space to 4D curved spacetime, the above form of Newton's law also carries over to Einstein's general relativity, in which case free particles follow geodesics in curved spacetime that are no longer "straight lines" in the ordinary sense.

However, we still need to know the total resultant force F acting on the particle, which in turn requires the resultant non-constraint force N plus the resultant constraint force C, $${\displaystyle \mathbf{F}=\mathbf{C}+\mathbf{N}.}$$

The constraint forces can be complicated, since they generally depend on time. Also, if there are constraints, the curvilinear coordinates are not independent but related by one or more constraint equations.

The constraint forces can either be eliminated from the equations of motion, so only the non-constraint forces remain, or included by including the constraint equations in the equations of motion.

D'Alembert's principle

Jean d'Alembert (1717–1783)

One degree of freedom.

 

Two degrees of freedom.

 

Constraint force C and virtual displacement δr for a particle of mass m confined to a curve. The resultant non-constraint force is N.

A fundamental result in analytical mechanics is D'Alembert's principle, introduced in 1708 by Jacques Bernoulli to understand static equilibrium, and developed by D'Alembert in 1743 to solve dynamical problems. The principle asserts for N particles the virtual work, i.e. the work along a virtual displacement, δr_k, is zero: $${\displaystyle \sum _{k=1}^N({\mathbf{N}}_k+{\mathbf{C}}_k-m_k{\mathbf{a}}_k)\cdot \delta {\mathbf{r}}_k=0.}$$

The virtual displacements, δr_k, are by definition infinitesimal changes in the configuration of the system consistent with the constraint forces acting on the system at an instant of time, i.e. in such a way that the constraint forces maintain the constrained motion. They are not the same as the actual displacements in the system, which are caused by the resultant constraint and non-constraint forces acting on the particle to accelerate and move it. Virtual work is the work done along a virtual displacement for any force (constraint or non-constraint).

Since the constraint forces act perpendicular to the motion of each particle in the system to maintain the constraints, the total virtual work by the constraint forces acting on the system is zero:$${\displaystyle \sum _{k=1}^N{\mathbf{C}}_k\cdot \delta {\mathbf{r}}_k=0,}$$ so that $${\displaystyle \sum _{k=1}^N({\mathbf{N}}_k-m_k{\mathbf{a}}_k)\cdot \delta {\mathbf{r}}_k=0.}$$

Thus D'Alembert's principle allows us to concentrate on only the applied non-constraint forces, and exclude the constraint forces in the equations of motion. The form shown is also independent of the choice of coordinates. However, it cannot be readily used to set up the equations of motion in an arbitrary coordinate system since the displacements δr_k might be connected by a constraint equation, which prevents us from setting the N individual summands to 0. We will therefore seek a system of mutually independent coordinates for which the total sum will be 0 if and only if the individual summands are 0. Setting each of the summands to 0 will eventually give us our separated equations of motion.

Equations of motion from D'Alembert's principle

If there are constraints on particle k, then since the coordinates of the position r_k = (x_k, y_k, z_k) are linked together by a constraint equation, so are those of the virtual displacements δr_k = (δx_k, δy_k, δz_k). Since the generalized coordinates are independent, we can avoid the complications with the δr_k by converting to virtual displacements in the generalized coordinates. These are related in the same form as a total differential, $${\displaystyle \delta {\mathbf{r}}_k=\sum _{j=1}^n\frac{\mathrm{\partial }{\mathbf{r}}_k}{\mathrm{\partial }{q}_j}\delta q_j.}$$

There is no partial time derivative with respect to time multiplied by a time increment, since this is a virtual displacement, one along the constraints in an instant of time.

The first term in D'Alembert's principle above is the virtual work done by the non-constraint forces N_k along the virtual displacements δr_k, and can without loss of generality be converted into the generalized analogues by the definition of generalized forces $${\displaystyle Q_j=\sum _{k=1}^N{\mathbf{N}}_k\cdot \frac{\mathrm{\partial }{\mathbf{r}}_k}{\mathrm{\partial }{q}_j},}$$ so that $${\displaystyle \sum _{k=1}^N{\mathbf{N}}_k\cdot \delta {\mathbf{r}}_k=\sum _{k=1}^N{\mathbf{N}}_k\cdot \sum _{j=1}^n\frac{\mathrm{\partial }{\mathbf{r}}_k}{\mathrm{\partial }{q}_j}\delta q_j=\sum _{j=1}^n{Q}_j\delta q_j.}$$

This is half of the conversion to generalized coordinates. It remains to convert the acceleration term into generalized coordinates, which is not immediately obvious. Recalling the Lagrange form of Newton's second law, the partial derivatives of the kinetic energy with respect to the generalized coordinates and velocities can be found to give the desired result: $${\displaystyle \sum _{k=1}^N{m}_k{\mathbf{a}}_k\cdot \frac{\mathrm{\partial }{\mathbf{r}}_k}{\mathrm{\partial }{q}_j}=\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }T}{\mathrm{\partial }{\dot{q}}_j}-\frac{\mathrm{\partial }T}{\mathrm{\partial }{q}_j}.}$$

Now D'Alembert's principle is in the generalized coordinates as required, $${\displaystyle \sum _{j=1}^n\left[Q_j-\left(\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }T}{\mathrm{\partial }{\dot{q}}_j}-\frac{\mathrm{\partial }T}{\mathrm{\partial }{q}_j}\right)\right]\delta q_j=0,}$$ and since these virtual displacements δq_j are independent and nonzero, the coefficients can be equated to zero, resulting in Lagrange's equations or the generalized equations of motion, $${\displaystyle Q_j=\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }T}{\mathrm{\partial }{\dot{q}}_j}-\frac{\mathrm{\partial }T}{\mathrm{\partial }{q}_j}}$$

These equations are equivalent to Newton's laws for the non-constraint forces. The generalized forces in this equation are derived from the non-constraint forces only – the constraint forces have been excluded from D'Alembert's principle and do not need to be found. The generalized forces may be non-conservative, provided they satisfy D'Alembert's principle.

Euler–Lagrange equations and Hamilton's principle

As the system evolves, q traces a path through configuration space (only some are shown). The path taken by the system (red) has a stationary action (δS = 0) under small changes in the configuration of the system (δq).

For a non-conservative force which depends on velocity, it may be possible to find a potential energy function V that depends on positions and velocities. If the generalized forces Q_i can be derived from a potential V such that $${\displaystyle Q_j=\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }V}{\mathrm{\partial }{\dot{q}}_j}-\frac{\mathrm{\partial }V}{\mathrm{\partial }{q}_j},}$$ equating to Lagrange's equations and defining the Lagrangian as L = T − V obtains Lagrange's equations of the second kind or the Euler–Lagrange equations of motion $${\displaystyle \frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_j}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_j}=0.}$$

However, the Euler–Lagrange equations can only account for non-conservative forces if a potential can be found as shown. This may not always be possible for non-conservative forces, and Lagrange's equations do not involve any potential, only generalized forces; therefore they are more general than the Euler–Lagrange equations.

The Euler–Lagrange equations also follow from the calculus of variations. The variation of the Lagrangian is $${\displaystyle \delta L=\sum _{j=1}^n\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_j}\delta q_j+\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_j}\delta {\dot{q}}_j\right),\delta {\dot{q}}_j\equiv \delta \frac{\mathrm{d}{q}_j}{\mathrm{d}t}\equiv \frac{\mathrm{d}(\delta q_j)}{\mathrm{d}t},}$$ which has a form similar to the total differential of L, but the virtual displacements and their time derivatives replace differentials, and there is no time increment in accordance with the definition of the virtual displacements. An integration by parts with respect to time can transfer the time derivative of δq_j to the ∂L/∂(dq_j/dt), in the process exchanging d(δq_j)/dt for δq_j, allowing the independent virtual displacements to be factorized from the derivatives of the Lagrangian, $${\displaystyle \begin{array}{rl}{\int }_{t_1}^{t_2}\delta L\mathrm{d}t& ={\int }_{t_1}^{t_2}\sum _{j=1}^n\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_j}\delta q_j+\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_j}\delta q_j\right)-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_j}\delta q_j\right)\mathrm{d}t\\ & =\sum _{j=1}^n{\left[\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_j}\delta q_j\right]}_{t_1}^{t_2}+{\int }_{t_1}^{t_2}\sum _{j=1}^n\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_j}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_j}\right)\delta q_j\mathrm{d}t.\end{array}}$$

Now, if the condition δq_j(t₁) = δq_j(t₂) = 0 holds for all j, the terms not integrated are zero. If in addition the entire time integral of δL is zero, then because the δq_j are independent, and the only way for a definite integral to be zero is if the integrand equals zero, each of the coefficients of δq_j must also be zero. Then we obtain the equations of motion. This can be summarized by Hamilton's principle: $${\displaystyle {\int }_{t_1}^{t_2}\delta L\mathrm{d}t=0.}$$

The time integral of the Lagrangian is another quantity called the action, defined as $${\displaystyle S={\int }_{t_1}^{t_2}L\mathrm{d}t,}$$ which is a functional; it takes in the Lagrangian function for all times between t₁ and t₂ and returns a scalar value. Its dimensions are the same as [angular momentum], [energy]·[time], or [length]·[momentum]. With this definition Hamilton's principle is $${\displaystyle \delta S=0.}$$

Instead of thinking about particles accelerating in response to applied forces, one might think of them picking out the path with a stationary action, with the end points of the path in configuration space held fixed at the initial and final times. Hamilton's principle is one of several action principles.

Historically, the idea of finding the shortest path a particle can follow subject to a force motivated the first applications of the calculus of variations to mechanical problems, such as the Brachistochrone problem solved by Jean Bernoulli in 1696, as well as Leibniz, Daniel Bernoulli, L'Hôpital around the same time, and Newton the following year. Newton himself was thinking along the lines of the variational calculus, but did not publish. These ideas in turn lead to the variational principles of mechanics, of Fermat, Maupertuis, Euler, Hamilton, and others.

Hamilton's principle can be applied to nonholonomic constraints if the constraint equations can be put into a certain form, a linear combination of first order differentials in the coordinates. The resulting constraint equation can be rearranged into first order differential equation. This will not be given here.

Lagrange multipliers and constraints

The Lagrangian L can be varied in the Cartesian r_k coordinates, for N particles, $${\displaystyle {\int }_{t_1}^{t_2}\sum _{k=1}^N\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{\mathbf{r}}_k}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{\mathbf{r}}}_k}\right)\cdot \delta {\mathbf{r}}_k\mathrm{d}t=0.}$$

Hamilton's principle is still valid even if the coordinates L is expressed in are not independent, here r_k, but the constraints are still assumed to be holonomic. As always the end points are fixed δr_k(t₁) = δr_k(t₂) = 0 for all k. What cannot be done is to simply equate the coefficients of δr_k to zero because the δr_k are not independent. Instead, the method of Lagrange multipliers can be used to include the constraints. Multiplying each constraint equation f_i(r_k, t) = 0 by a Lagrange multiplier λ_i for i = 1, 2, ..., C, and adding the results to the original Lagrangian, gives the new Lagrangian $${\displaystyle L^{\prime }=L({\mathbf{r}}_1,{\mathbf{r}}_2,\dots ,{\dot{\mathbf{r}}}_1,{\dot{\mathbf{r}}}_2,\dots ,t)+\sum _{i=1}^C{\lambda }_i(t)f_i({\mathbf{r}}_k,t).}$$

The Lagrange multipliers are arbitrary functions of time t, but not functions of the coordinates r_k, so the multipliers are on equal footing with the position coordinates. Varying this new Lagrangian and integrating with respect to time gives $${\displaystyle {\int }_{t_1}^{t_2}\delta L^{\prime }\mathrm{d}t={\int }_{t_1}^{t_2}\sum _{k=1}^N\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{\mathbf{r}}_k}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{\mathbf{r}}}_k}+\sum _{i=1}^C{\lambda }_i\frac{\mathrm{\partial }{f}_i}{\mathrm{\partial }{\mathbf{r}}_k}\right)\cdot \delta {\mathbf{r}}_k\mathrm{d}t=0.}$$

The introduced multipliers can be found so that the coefficients of δr_k are zero, even though the r_k are not independent. The equations of motion follow. From the preceding analysis, obtaining the solution to this integral is equivalent to the statement $${\displaystyle \frac{\mathrm{\partial }{L}^{\prime }}{\mathrm{\partial }{\mathbf{r}}_k}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }{L}^{\prime }}{\mathrm{\partial }{\dot{\mathbf{r}}}_k}=0\Rightarrow \frac{\mathrm{\partial }L}{\mathrm{\partial }{\mathbf{r}}_k}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{\mathbf{r}}}_k}+\sum _{i=1}^C{\lambda }_i\frac{\mathrm{\partial }{f}_i}{\mathrm{\partial }{\mathbf{r}}_k}=0,}$$ which are Lagrange's equations of the first kind. Also, the λ_i Euler-Lagrange equations for the new Lagrangian return the constraint equations $${\displaystyle \frac{\mathrm{\partial }{L}^{\prime }}{\mathrm{\partial }{\lambda }_i}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }{L}^{\prime }}{\mathrm{\partial }{\dot{\lambda }}_i}=0\Rightarrow f_i({\mathbf{r}}_k,t)=0.}$$

For the case of a conservative force given by the gradient of some potential energy V, a function of the r_k coordinates only, substituting the Lagrangian L = T − V gives $${\displaystyle \underset{-{\mathbf{F}}_k}{\underbrace{\frac{\mathrm{\partial }T}{\mathrm{\partial }{\mathbf{r}}_k}-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }T}{\mathrm{\partial }{\dot{\mathbf{r}}}_k}}}+\underset{{\mathbf{N}}_k}{\underbrace{-\frac{\mathrm{\partial }V}{\mathrm{\partial }{\mathbf{r}}_k}}}+\sum _{i=1}^C{\lambda }_i\frac{\mathrm{\partial }{f}_i}{\mathrm{\partial }{\mathbf{r}}_k}=0,}$$ and identifying the derivatives of kinetic energy as the (negative of the) resultant force, and the derivatives of the potential equaling the non-constraint force, it follows the constraint forces are $${\displaystyle {\mathbf{C}}_k=\sum _{i=1}^C{\lambda }_i\frac{\mathrm{\partial }{f}_i}{\mathrm{\partial }{\mathbf{r}}_k},}$$ thus giving the constraint forces explicitly in terms of the constraint equations and the Lagrange multipliers.

Properties of the Lagrangian

Non-uniqueness

The Lagrangian of a given system is not unique. A Lagrangian L can be multiplied by a nonzero constant a and shifted by an arbitrary constant b, and the new Lagrangian L′ = aL + b will describe the same motion as L. If one restricts as above to trajectories q over a given time interval [t_st, t_fin]} and fixed end points P_st = q(t_st) and P_fin = q(t_fin), then two Lagrangians describing the same system can differ by the "total time derivative" of a function f(q, t): $${\displaystyle L^{\prime }(\mathbf{q},\dot{\mathbf{q}},t)=L(\mathbf{q},\dot{\mathbf{q}},t)+\frac{\mathrm{d}f(\mathbf{q},t)}{\mathrm{d}t},}$$ where $\frac{\mathrm{d}f(\mathbf{q},t)}{\mathrm{d}t}$ means $\frac{\mathrm{\partial }f(\mathbf{q},t)}{\mathrm{\partial }t}+\sum _i\frac{\mathrm{\partial }f(\mathbf{q},t)}{\mathrm{\partial }{q}_i}{\dot{q}}_i.$

Both Lagrangians L and L′ produce the same equations of motion since the corresponding actions S and S′ are related via $${\displaystyle \begin{array}{rl}{S}^{\prime }[\mathbf{q}]& ={\int }_{t_{\text{st}}}^{t_{\text{fin}}}{L}^{\prime }(\mathbf{q}(t),\dot{\mathbf{q}}(t),t)dt\\ & ={\int }_{t_{\text{st}}}^{t_{\text{fin}}}L(\mathbf{q}(t),\dot{\mathbf{q}}(t),t)dt+{\int }_{t_{\text{st}}}^{t_{\text{fin}}}\frac{\mathrm{d}f(\mathbf{q}(t),t)}{\mathrm{d}t}dt\\ & =S[\mathbf{q}]+f(P_{\text{fin}},t_{\text{fin}})-f(P_{\text{st}},t_{\text{st}}),\end{array}}$$ with the last two components f(P_fin, t_fin) and f(P_st, t_st) independent of q.

Invariance under point transformations

Given a set of generalized coordinates q, if we change these variables to a new set of generalized coordinates Q according to a point transformation Q = Q(q, t) which is invertible as q = q(Q, t), the new Lagrangian L′ is a function of the new coordinates and similarly for the constraints $${\displaystyle \begin{array}{rl}{L}^{\prime }(\mathbf{Q},\dot{\mathbf{Q}},t)& =L(\mathbf{q}(\mathbf{Q},t),\dot{\mathbf{q}}(\mathbf{Q},\dot{\mathbf{Q}},t),t),\\ {\varphi }_j^{\prime }(\mathbf{Q},t)& ={\varphi }_j(\mathbf{q}(\mathbf{Q},t),t)\end{array}}$$ and by the chain rule for partial differentiation, Lagrange's equations are invariant under this transformation;

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }{L}^{\prime }}{\mathrm{\partial }{\dot{Q}}_i}=\frac{\mathrm{\partial }{L}^{\prime }}{\mathrm{\partial }{Q}_i}+\sum _j{\lambda }_j\frac{\mathrm{\partial }{\varphi }_j^{\prime }}{\mathrm{\partial }{Q}_i}.}$$

Proof

For a coordinate transformation ${\displaystyle Q_i=Q_i(\mathbf{q},t)}$, we have $${\displaystyle d{Q}_i=\sum _k\frac{\mathrm{\partial }{Q}_i}{\mathrm{\partial }{q}_k}d{q}_k+\frac{\mathrm{\partial }{Q}_k}{\mathrm{\partial }t}dt,}$$ which implies that ${\displaystyle \dot{Q_i}=\sum _k\frac{\mathrm{\partial }{Q}_i}{\mathrm{\partial }{q}_k}(\mathbf{q},t){\dot{q}}_k+\frac{\mathrm{\partial }{Q}_k}{\mathrm{\partial }t}(\mathbf{q},t)}$ which implies that ${\displaystyle \frac{\mathrm{\partial }\dot{Q_i}}{\mathrm{\partial }{\dot{q}}_k}=\frac{\mathrm{\partial }{Q}_i}{\mathrm{\partial }{q}_k}}$.

It also follows that: $${\displaystyle \frac{\mathrm{\partial }\dot{Q_i}}{\mathrm{\partial }{q}_j}=\sum _k\frac{{\mathrm{\partial }}^2{Q}_i}{\mathrm{\partial }{q}_j\mathrm{\partial }{q}_k}(\mathbf{q},t){\dot{q}}_k+\frac{{\mathrm{\partial }}^2{Q}_k}{\mathrm{\partial }{q}_j\mathrm{\partial }t}(\mathbf{q},t)}$$ and similarly: $${\displaystyle \frac{d}{dt}\left(\frac{\mathrm{\partial }{Q}_i}{\mathrm{\partial }{q}_j}\right)=\sum _k\frac{{\mathrm{\partial }}^2{Q}_i}{\mathrm{\partial }{q}_k\mathrm{\partial }{q}_j}(\mathbf{q},t){\dot{q}}_k+\frac{{\mathrm{\partial }}^2{Q}_k}{\mathrm{\partial }t\mathrm{\partial }{q}_j}(\mathbf{q},t)}$$ which imply that ${\displaystyle \frac{d}{dt}\left(\frac{\mathrm{\partial }{Q}_i}{\mathrm{\partial }{q}_k}\right)=\frac{\mathrm{\partial }{\dot{Q}}_i}{\mathrm{\partial }{q}_k}}$. The two derived relations can be employed in the proof.

Starting from Euler Lagrange equations in initial set of generalized coordinates, we have: $${\displaystyle \begin{array}{r}\frac{d}{dt}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i}-\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_i}-\sum _j{\lambda }_j\frac{\mathrm{\partial }{\varphi }_j}{\mathrm{\partial }{q}_i}=0\\ \sum _k\left(\frac{d}{dt}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{Q}}_k}\frac{\mathrm{\partial }{\dot{Q}}_k}{\mathrm{\partial }{\dot{q}}_i}\right)-\frac{\mathrm{\partial }L}{\mathrm{\partial }{Q}_k}\frac{\mathrm{\partial }{Q}_k}{\mathrm{\partial }{q}_i}-\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{Q}}_k}\frac{\mathrm{\partial }{\dot{Q}}_k}{\mathrm{\partial }{q}_i}-\sum _j{\lambda }_j\frac{\mathrm{\partial }{\varphi }_j}{\mathrm{\partial }{Q}_k}\frac{\mathrm{\partial }{Q}_k}{\mathrm{\partial }{q}_i}\right)=0\\ \sum _k\left(\frac{d}{dt}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{Q}}_k}\right)\frac{\mathrm{\partial }{\dot{Q}}_k}{\mathrm{\partial }{\dot{q}}_i}+\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{Q}}_k}\frac{d}{dt}\left(\frac{\mathrm{\partial }{\dot{Q}}_k}{\mathrm{\partial }{\dot{q}}_i}\right)-\frac{\mathrm{\partial }L}{\mathrm{\partial }{Q}_k}\frac{\mathrm{\partial }{\dot{Q}}_k}{\mathrm{\partial }{\dot{q}}_i}-\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{Q}}_k}\frac{d}{dt}\left(\frac{\mathrm{\partial }{Q}_k}{\mathrm{\partial }{q}_i}\right)-\sum _j{\lambda }_j\frac{\mathrm{\partial }{\varphi }_j}{\mathrm{\partial }{Q}_k}\frac{\mathrm{\partial }{Q}_k}{\mathrm{\partial }{q}_i}\right)=0\\ \sum _k\left(\frac{d}{dt}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{Q}}_k}\right)-\frac{\mathrm{\partial }L}{\mathrm{\partial }{Q}_k}-\sum _j{\lambda }_j\frac{\mathrm{\partial }{\varphi }_j}{\mathrm{\partial }{Q}_k}\right)\frac{\mathrm{\partial }{Q}_k}{\mathrm{\partial }{q}_i}=0\end{array}}$$

Since the transformation from ${\displaystyle q\to Q}$ is invertible, it follows that the form of the Euler-Lagrange equation is invariant i.e., $${\displaystyle \frac{d}{dt}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{Q}}_i}-\frac{\mathrm{\partial }L}{\mathrm{\partial }{Q}_i}-\sum _j{\lambda }_j\frac{\mathrm{\partial }{\varphi }_j}{\mathrm{\partial }{Q}_i}=0.}$$

Cyclic coordinates and conserved momenta

An important property of the Lagrangian is that conserved quantities can easily be read off from it. The generalized momentum "canonically conjugate to" the coordinate q_i is defined by $${\displaystyle p_i=\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i}.}$$

If the Lagrangian L does not depend on some coordinate q_i, it follows immediately from the Euler–Lagrange equations that $${\displaystyle {\dot{p}}_i=\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i}=\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_i}=0}$$ and integrating shows the corresponding generalized momentum equals a constant, a conserved quantity. This is a special case of Noether's theorem. Such coordinates are called "cyclic" or "ignorable".

For example, a system may have a Lagrangian $${\displaystyle L(r,\theta ,\dot{s},\dot{z},\dot{r},\dot{\theta },\dot{\varphi },t),}$$ where r and z are lengths along straight lines, s is an arc length along some curve, and θ and φ are angles. Notice z, s, and φ are all absent in the Lagrangian even though their velocities are not. Then the momenta $${\displaystyle p_z=\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{z}},p_s=\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{s}},p_{\varphi }=\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\varphi }},}$$ are all conserved quantities. The units and nature of each generalized momentum will depend on the corresponding coordinate; in this case p_z is a translational momentum in the z direction, p_s is also a translational momentum along the curve s is measured, and p_φ is an angular momentum in the plane the angle φ is measured in. However complicated the motion of the system is, all the coordinates and velocities will vary in such a way that these momenta are conserved.

Energy

Given a Lagrangian ${\displaystyle L,}$ the Hamiltonian of the corresponding mechanical system is, by definition, $${\displaystyle H=(\sum _{i=1}^n{\dot{q}}_i\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i})-L.}$$ This quantity will be equivalent to energy if the generalized coordinates are natural coordinates, i.e., they have no explicit time dependence when expressing position vector: ${\displaystyle \mathbf{r}=\mathbf{r}(q_1,\cdots ,q_n)}$. From: $${\displaystyle T=\frac{m}{2}{v}^2=\frac{m}{2}\sum _{i,j}\left(\frac{\mathrm{\partial }\overrightarrow{r}}{\mathrm{\partial }{q}_i}{\dot{q}}_i\right)\cdot \left(\frac{\mathrm{\partial }\overrightarrow{r}}{\mathrm{\partial }{q}_j}{\dot{q}}_j\right)=\frac{m}{2}\sum _{i,j}{a}_{ij}{\dot{q}}_i{\dot{q}}_j}$$ $${\displaystyle \sum _{k=1}^n{\dot{q}}_k\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_k}=\sum _{k=1}^n{\dot{q}}_k\frac{\mathrm{\partial }T}{\mathrm{\partial }{\dot{q}}_k}=\frac{m}{2}\left(2\sum _{i,j}{a}_{ij}{\dot{q}}_i{\dot{q}}_j\right)=2T}$$ $${\displaystyle H=\left(\sum _{i=1}^n{\dot{q}}_i\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i}\right)-L=2T-(T-V)=T+V=E}$$ where ${\displaystyle a_{ij}=\frac{\mathrm{\partial }\mathbf{r}}{\mathrm{\partial }{q}_i}\cdot \frac{\mathrm{\partial }\mathbf{r}}{\mathrm{\partial }{q}_j}}$ is a symmetric matrix that is defined for the derivation.

Invariance under coordinate transformations

At every time instant t, the energy is invariant under configuration space coordinate changes q → Q, i.e. (using natural coordinates) $${\displaystyle E(\mathbf{q},\dot{\mathbf{q}},t)=E(\mathbf{Q},\dot{\mathbf{Q}},t).}$$ Besides this result, the proof below shows that, under such change of coordinates, the derivatives ${\displaystyle \mathrm{\partial }L/\mathrm{\partial }{\dot{q}}_i}$ change as coefficients of a linear form.

Proof

For a coordinate transformation Q = F(q), we have $${\displaystyle d\mathbf{Q}=F_{\ast }(\mathbf{q})d\mathbf{q},}$$ where ${\displaystyle F_{\ast }(\mathbf{q})}$ is the tangent map of the vector space $${\displaystyle \left\{\sum _{i=1}^n{\dot{q}}_i\cdot \left({\frac{\mathrm{\partial }}{\mathrm{\partial }{q}_i}|}_{\mathbf{q}}\right)|{\dot{q}}_i\in \mathbb{R}\right\}}$$ to the vector space $${\displaystyle \left\{\sum _{i=1}^n{\dot{Q}}_i\cdot \left({\frac{\mathrm{\partial }}{\mathrm{\partial }{Q}_i}|}_{F(\mathbf{q})}\right)|{\dot{Q}}_i\in \mathbb{R}\right\},}$$ and $${\displaystyle F_{\ast }(\mathbf{q})={\left({\frac{\mathrm{\partial }{F}_i}{\mathrm{\partial }{q}_j}|}_{\mathbf{q}}\right)}_{i,j=1}^n}$$ is the Jacobian. In the coordinates ${\displaystyle {\dot{q}}_i}$ and ${\displaystyle {\dot{Q}}_i,}$ the previous formula for ${\displaystyle d\mathbf{Q}}$ has the form ${\displaystyle \dot{\mathbf{Q}}=F_{\ast }(\mathbf{q})\dot{\mathbf{q}}.}$ After differentiation involving the product rule, $${\displaystyle d\dot{\mathbf{Q}}=G(\mathbf{q},\dot{\mathbf{q}})d\mathbf{q}+F_{\ast }(\mathbf{q})d\dot{\mathbf{q}},}$$ where $${\displaystyle \begin{array}{rl}G(\mathbf{q},\dot{\mathbf{q}})d\mathbf{q}& \stackrel{\text{def}}{=}d(F_{\ast }(\mathbf{q}))\dot{\mathbf{q}}={\left(\sum _{k=1}^n\frac{{\mathrm{\partial }}^2{F}_i}{\mathrm{\partial }{q}_j\mathrm{\partial }{q}_k}{|}_{\mathbf{q}}d{q}_k\right)}_{i,j=1}^n\dot{\mathbf{q}}={\left(\sum _{j=1}^n{\dot{q}}_j\sum _{k=1}^n\frac{{\mathrm{\partial }}^2{F}_i}{\mathrm{\partial }{q}_j\mathrm{\partial }{q}_k}{|}_{\mathbf{q}}d{q}_k\right)}_{i=1,\dots ,n}^T\\ & ={\left(\sum _{k=1}^{n}d{q}_k\sum _{j=1}^n\frac{{\mathrm{\partial }}^2{F}_i}{\mathrm{\partial }{q}_j\mathrm{\partial }{q}_k}{|}_{\mathbf{q}}{\dot{q}}_j\right)}_{i=1,\dots ,n}^T={\left(\sum _{j=1}^n\frac{{\mathrm{\partial }}^2{F}_i}{\mathrm{\partial }{q}_j\mathrm{\partial }{q}_k}{|}_{\mathbf{q}}{\dot{q}}_j\right)}_{i,k=1}^{n}d\mathbf{q}.\end{array}}$$

In vector notation, $${\displaystyle \begin{array}{rl}dL(\mathbf{Q},\dot{\mathbf{Q}},t)& =\frac{\mathrm{\partial }L}{\mathrm{\partial }\mathbf{Q}}d\mathbf{Q}+\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{Q}}}d\dot{\mathbf{Q}}+\frac{\mathrm{\partial }L}{\mathrm{\partial }t}dt\\ & =\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }\mathbf{Q}}{F}_{\ast }(\mathbf{q})+\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{Q}}}G(\mathbf{q},\dot{\mathbf{q}})\right)d\mathbf{q}+\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{Q}}}{F}_{\ast }(\mathbf{q})d\dot{\mathbf{q}}+\frac{\mathrm{\partial }L}{\mathrm{\partial }t}.\end{array}}$$

On the other hand, $${\displaystyle dL(\mathbf{q},\dot{\mathbf{q}},t)=\frac{\mathrm{\partial }L}{\mathrm{\partial }\mathbf{q}}d\mathbf{q}+\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{q}}}d\dot{\mathbf{q}}+\frac{\mathrm{\partial }L}{\mathrm{\partial }t}dt.}$$

It was mentioned earlier that Lagrangians do not depend on the choice of configuration space coordinates, i.e. ${\displaystyle L(\mathbf{Q},\dot{\mathbf{Q}},t)=L(\mathbf{q},\dot{\mathbf{q}},t).}$ One implication of this is that ${\displaystyle dL(\mathbf{Q},\dot{\mathbf{Q}},t)=dL(\mathbf{q},\dot{\mathbf{q}},t),}$ and $${\displaystyle \frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{Q}}}{F}_{\ast }(\mathbf{q})=\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{q}}}.}$$ This demonstrates that, for each ${\displaystyle \mathbf{q},}$ ${\displaystyle \dot{\mathbf{q}},}$ and ${\displaystyle t,}$ ${\displaystyle \sum _{i=1}^n\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i}d{\dot{q}}_i}$ is a well-defined linear form whose coefficients ${\displaystyle \frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i}}$ are contravariant 1-tensors. Applying both sides of the equation to ${\displaystyle \dot{\mathbf{q}}}$ and using the above formula for ${\displaystyle \dot{\mathbf{Q}}}$ yields $${\displaystyle \dot{\mathbf{Q}}\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{Q}}}=\dot{\mathbf{q}}\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{q}}}.}$$ The invariance of the energy ${\displaystyle E}$ follows.

Conservation

In Lagrangian mechanics, the system is closed if and only if its Lagrangian ${\displaystyle L}$ does not explicitly depend on time. The energy conservation law states that the energy ${\displaystyle E}$ of a closed system is an integral of motion.

More precisely, let q = q(t) be an extremal. (In other words, q satisfies the Euler–Lagrange equations). Taking the total time-derivative of L along this extremal and using the EL equations leads to $${\displaystyle \begin{array}{rl}\frac{dL}{dt}& =\dot{\mathbf{q}}\frac{\mathrm{\partial }L}{\mathrm{\partial }\mathbf{q}}+\ddot{\mathbf{q}}\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{q}}}+\frac{\mathrm{\partial }L}{\mathrm{\partial }t}\\ -\frac{\mathrm{\partial }L}{\mathrm{\partial }t}& =\frac{d}{dt}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{q}}}\right)\dot{\mathbf{q}}+\ddot{\mathbf{q}}\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{q}}}-\dot{L}\\ -\frac{\mathrm{\partial }L}{\mathrm{\partial }t}& =\frac{d}{dt}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{q}}}\dot{\mathbf{q}}-L\right)=\frac{dH}{dt}\end{array}}$$

If the Lagrangian L does not explicitly depend on time, then ∂L/∂t = 0, then H does not vary with time evolution of particle, indeed, an integral of motion, meaning that $${\displaystyle H(\mathbf{q}(t),\dot{\mathbf{q}}(t),t)=\text{constant of time}.}$$ Hence, if the chosen coordinates were natural coordinates, the energy is conserved.

Kinetic and potential energies

Under all these circumstances, the constant $${\displaystyle E=T+V}$$ is the total energy of the system. The kinetic and potential energies still change as the system evolves, but the motion of the system will be such that their sum, the total energy, is constant. This is a valuable simplification, since the energy E is a constant of integration that counts as an arbitrary constant for the problem, and it may be possible to integrate the velocities from this energy relation to solve for the coordinates.

Mechanical similarity

Main article: Mechanical similarity

If the potential energy is a homogeneous function of the coordinates and independent of time, and all position vectors are scaled by the same nonzero constant α, r_k′ = αr_k, so that $${\displaystyle V(\alpha {\mathbf{r}}_1,\alpha {\mathbf{r}}_2,\dots ,\alpha {\mathbf{r}}_N)={\alpha }^{N}V({\mathbf{r}}_1,{\mathbf{r}}_2,\dots ,{\mathbf{r}}_N)}$$ and time is scaled by a factor β, t′ = βt, then the velocities v_k are scaled by a factor of α/β and the kinetic energy T by (α/β)². The entire Lagrangian has been scaled by the same factor if $${\displaystyle \frac{{\alpha }^2}{{\beta }^2}={\alpha }^N\Rightarrow \beta ={\alpha }^{1-\frac{N}{2}}.}$$

Since the lengths and times have been scaled, the trajectories of the particles in the system follow geometrically similar paths differing in size. The length l traversed in time t in the original trajectory corresponds to a new length l′ traversed in time t′ in the new trajectory, given by the ratios $${\displaystyle \frac{t^{\prime }}{t}={\left(\frac{l^{\prime }}{l}\right)}^{1-\frac{N}{2}}.}$$

Interacting particles

For a given system, if two subsystems A and B are non-interacting, the Lagrangian L of the overall system is the sum of the Lagrangians L_A and L_B for the subsystems: $${\displaystyle L=L_A+L_B.}$$

If they do interact this is not possible. In some situations, it may be possible to separate the Lagrangian of the system L into the sum of non-interacting Lagrangians, plus another Lagrangian L_AB containing information about the interaction, $${\displaystyle L=L_A+L_B+L_{AB}.}$$

This may be physically motivated by taking the non-interacting Lagrangians to be kinetic energies only, while the interaction Lagrangian is the system's total potential energy. Also, in the limiting case of negligible interaction, L_AB tends to zero reducing to the non-interacting case above.

The extension to more than two non-interacting subsystems is straightforward – the overall Lagrangian is the sum of the separate Lagrangians for each subsystem. If there are interactions, then interaction Lagrangians may be added.

Consequences of singular Lagrangians

From the Euler-Lagrange equations, it follows that: $${\displaystyle \begin{array}{rl}& \frac{d}{dt}\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i}-\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_i}=0\\ & \frac{{\mathrm{\partial }}^{2}L}{\mathrm{\partial }{q}_j\mathrm{\partial }{\dot{q}}_i}\frac{d{q}_j}{dt}+\frac{{\mathrm{\partial }}^{2}L}{\mathrm{\partial }{\dot{q}}_j\mathrm{\partial }{\dot{q}}_i}\frac{d{\dot{q}}_j}{dt}+\frac{\mathrm{\partial }L}{\mathrm{\partial }t}-\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_i}=0\\ & \sum _j{W}_{ij}(q,\dot{q},t){\ddot{q}}_j=\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_i}-\frac{\mathrm{\partial }L}{\mathrm{\partial }t}-\sum _j\frac{{\mathrm{\partial }}^{2}L}{\mathrm{\partial }{\dot{q}}_i\mathrm{\partial }{q}_j}{\dot{q}}_j,\end{array}}$$

where the matrix is defined as ${\displaystyle W_{ij}=\frac{{\mathrm{\partial }}^{2}L}{\mathrm{\partial }{\dot{q}}_i\mathrm{\partial }{\dot{q}}_j}}$. If the matrix ${\displaystyle W}$ is non-singular, the above equations can be solved to represent ${\displaystyle \ddot{q}}$ as a function of ${\displaystyle (\dot{q},q,t)}$. If the matrix is non-invertible, it would not be possible to represent all ${\displaystyle \ddot{q}}$'s as a function of ${\displaystyle (\dot{q},q,t)}$ but also, the Hamiltonian equations of motions will not take the standard form.

Examples

The following examples apply Lagrange's equations of the second kind to mechanical problems.

Conservative force

A particle of mass m moves under the influence of a conservative force derived from the gradient ∇ of a scalar potential, $${\displaystyle \mathbf{F}=-\mathbf{\nabla }V(\mathbf{r}).}$$

If there are more particles, in accordance with the above results, the total kinetic energy is a sum over all the particle kinetic energies, and the potential is a function of all the coordinates.

Cartesian coordinates

The Lagrangian of the particle can be written $${\displaystyle L(x,y,z,\dot{x},\dot{y},\dot{z})=\frac{1}{2}m({\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2)-V(x,y,z).}$$

The equations of motion for the particle are found by applying the Euler–Lagrange equation, for the x coordinate $${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{x}}\right)=\frac{\mathrm{\partial }L}{\mathrm{\partial }x},}$$ with derivatives $${\displaystyle \frac{\mathrm{\partial }L}{\mathrm{\partial }x}=-\frac{\mathrm{\partial }V}{\mathrm{\partial }x},\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{x}}=m\dot{x},\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{x}}\right)=m\ddot{x},}$$ hence $${\displaystyle m\ddot{x}=-\frac{\mathrm{\partial }V}{\mathrm{\partial }x},}$$ and similarly for the y and z coordinates. Collecting the equations in vector form we find $${\displaystyle m\ddot{\mathbf{r}}=-\mathbf{\nabla }V}$$ which is Newton's second law of motion for a particle subject to a conservative force.

Polar coordinates in 2D and 3D

Using the spherical coordinates (r, θ, φ) as commonly used in physics (ISO 80000-2:2019 convention), where r is the radial distance to origin, θ is polar angle (also known as colatitude, zenith angle, normal angle, or inclination angle), and φ is the azimuthal angle, the Lagrangian for a central potential is $${\displaystyle L=\frac{m}{2}({\dot{r}}^2+r^2{\dot{\theta }}^2+r^2{\sin }^2\theta {\dot{\phi }}^2)-V(r).}$$ So, in spherical coordinates, the Euler–Lagrange equations are $${\displaystyle m\ddot{r}-mr({\dot{\theta }}^2+{\sin }^2\theta {\dot{\phi }}^2)+\frac{\mathrm{\partial }V}{\mathrm{\partial }r}=0,}$$ $${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}(m{r}^2\dot{\theta })-m{r}^2\sin \theta \cos \theta {\dot{\phi }}^2=0,}$$ $${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}(m{r}^2{\sin }^2\theta \dot{\phi })=0.}$$ The φ coordinate is cyclic since it does not appear in the Lagrangian, so the conserved momentum in the system is the angular momentum $${\displaystyle p_{\phi }=\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\phi }}=m{r}^2{\sin }^2\theta \dot{\phi },}$$ in which r, θ and dφ/dt can all vary with time, but only in such a way that p_φ is constant.

The Lagrangian in two-dimensional polar coordinates is recovered by fixing θ to the constant value π/2.

Pendulum on a movable support

Sketch of the situation with definition of the coordinates (click to enlarge)

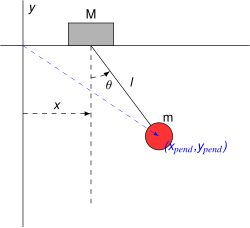
Consider a pendulum of mass m and length ℓ, which is attached to a support with mass M, which can move along a line in the ${\displaystyle x}$-direction. Let ${\displaystyle x}$ be the coordinate along the line of the support, and let us denote the position of the pendulum by the angle ${\displaystyle \theta }$ from the vertical. The coordinates and velocity components of the pendulum bob are $${\displaystyle \begin{array}{rll}& x_{\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}}=x+\ell \sin \theta & \Rightarrow {\dot{x}}_{\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}}=\dot{x}+\ell \dot{\theta }\cos \theta \\ & y_{\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}}=-\ell \cos \theta & \Rightarrow {\dot{y}}_{\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}}=\ell \dot{\theta }\sin \theta .\end{array}}$$

The generalized coordinates can be taken to be ${\displaystyle x}$ and ${\displaystyle \theta }$. The kinetic energy of the system is then $${\displaystyle T=\frac{1}{2}M{\dot{x}}^2+\frac{1}{2}m\left({\dot{x}}_{\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}}^2+{\dot{y}}_{\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}}^2\right)}$$ and the potential energy is $${\displaystyle V=mg{y}_{\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}}}$$ giving the Lagrangian $${\displaystyle \begin{array}{rcl}L& =& T-V\\ & =& \frac{1}{2}M{\dot{x}}^2+\frac{1}{2}m\left[{\left(\dot{x}+\ell \dot{\theta }\cos \theta \right)}^2+{\left(\ell \dot{\theta }\sin \theta \right)}^2\right]+mg\ell \cos \theta \\ & =& \frac{1}{2}\left(M+m\right){\dot{x}}^2+m\dot{x}\ell \dot{\theta }\cos \theta +\frac{1}{2}m{\ell }^2{\dot{\theta }}^2+mg\ell \cos \theta .\end{array}}$$

Since x is absent from the Lagrangian, it is a cyclic coordinate. The conserved momentum is $${\displaystyle p_x=\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{x}}=(M+m)\dot{x}+m\ell \dot{\theta }\cos \theta ,}$$ and the Lagrange equation for the support coordinate ${\displaystyle x}$ is $${\displaystyle (M+m)\ddot{x}+m\ell \ddot{\theta }\cos \theta -m\ell {\dot{\theta }}^2\sin \theta =0.}$$

The Lagrange equation for the angle θ is $${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\left[m(\dot{x}\ell \cos \theta +{\ell }^2\dot{\theta })\right]+m\ell (\dot{x}\dot{\theta }+g)\sin \theta =0;}$$ and simplifying $${\displaystyle \ddot{\theta }+\frac{\ddot{x}}{\ell }\cos \theta +\frac{g}{\ell }\sin \theta =0.}$$

These equations may look quite complicated, but finding them with Newton's laws would have required carefully identifying all forces, which would have been much more laborious and prone to errors. By considering limit cases, the correctness of this system can be verified: For example, ${\displaystyle \ddot{x}\to 0}$ should give the equations of motion for a simple pendulum that is at rest in some inertial frame, while ${\displaystyle \ddot{\theta }\to 0}$ should give the equations for a pendulum in a constantly accelerating system, etc. Furthermore, it is trivial to obtain the results numerically, given suitable starting conditions and a chosen time step, by stepping through the results iteratively.

Two-body central force problem

Main articles: Two-body problem and Central force

Two bodies of masses m₁ and m₂ with position vectors r₁ and r₂ are in orbit about each other due to an attractive central potential V. We may write down the Lagrangian in terms of the position coordinates as they are, but it is an established procedure to convert the two-body problem into a one-body problem as follows. Introduce the Jacobi coordinates; the separation of the bodies r = r₂ − r₁ and the location of the center of mass R = (m₁r₁ + m₂r₂)/(m₁ + m₂). The Lagrangian is then$${\displaystyle L=\underset{L_{\text{cm}}}{\underbrace{\frac{1}{2}M{\dot{\mathbf{R}}}^2}}+\underset{L_{\text{rel}}}{\underbrace{\frac{1}{2}\mu {\dot{\mathbf{r}}}^2-V(|\mathbf{r}|)}}}$$ where M = m₁ + m₂ is the total mass, μ = m₁m₂/(m₁ + m₂) is the reduced mass, and V the potential of the radial force, which depends only on the magnitude of the separation |r| = |r₂ − r₁|. The Lagrangian splits into a center-of-mass term L_cm and a relative motion term L_rel.

The Euler–Lagrange equation for R is simply $${\displaystyle M\ddot{\mathbf{R}}=0,}$$ which states the center of mass moves in a straight line at constant velocity.

Since the relative motion only depends on the magnitude of the separation, it is ideal to use polar coordinates (r, θ) and take r = |r|, $${\displaystyle L_{\text{rel}}=\frac{1}{2}\mu \left({\dot{r}}^2+r^2{\dot{\theta }}^2\right)-V(r),}$$ so θ is a cyclic coordinate with the corresponding conserved (angular) momentum $${\displaystyle p_{\theta }=\frac{\mathrm{\partial }{L}_{\text{rel}}}{\mathrm{\partial }\dot{\theta }}=\mu r^2\dot{\theta }=\ell .}$$

The radial coordinate r and angular velocity dθ/dt can vary with time, but only in such a way that ℓ is constant. The Lagrange equation for r is $${\displaystyle \mu r{\dot{\theta }}^2-\frac{dV}{dr}=\mu \ddot{r}.}$$

This equation is identical to the radial equation obtained using Newton's laws in a co-rotating reference frame, that is, a frame rotating with the reduced mass so it appears stationary. Eliminating the angular velocity dθ/dt from this radial equation, $${\displaystyle \mu \ddot{r}=-\frac{\mathrm{d}V}{\mathrm{d}r}+\frac{{\ell }^2}{\mu r^3}.}$$ which is the equation of motion for a one-dimensional problem in which a particle of mass μ is subjected to the inward central force −dV/dr and a second outward force, called in this context the (Lagrangian) centrifugal force (see centrifugal force#Other uses of the term): $${\displaystyle F_{\mathrm{c}\mathrm{f}}=\mu r{\dot{\theta }}^2=\frac{{\ell }^2}{\mu r^3}.}$$

Of course, if one remains entirely within the one-dimensional formulation, ℓ enters only as some imposed parameter of the external outward force, and its interpretation as angular momentum depends upon the more general two-dimensional problem from which the one-dimensional problem originated.

If one arrives at this equation using Newtonian mechanics in a co-rotating frame, the interpretation is evident as the centrifugal force in that frame due to the rotation of the frame itself. If one arrives at this equation directly by using the generalized coordinates (r, θ) and simply following the Lagrangian formulation without thinking about frames at all, the interpretation is that the centrifugal force is an outgrowth of using polar coordinates. As Hildebrand says:

"Since such quantities are not true physical forces, they are often called inertia forces. Their presence or absence depends, not upon the particular problem at hand, but upon the coordinate system chosen." In particular, if Cartesian coordinates are chosen, the centrifugal force disappears, and the formulation involves only the central force itself, which provides the centripetal force for a curved motion.

This viewpoint, that fictitious forces originate in the choice of coordinates, often is expressed by users of the Lagrangian method. This view arises naturally in the Lagrangian approach, because the frame of reference is (possibly unconsciously) selected by the choice of coordinates. For example, see for a comparison of Lagrangians in an inertial and in a noninertial frame of reference. See also the discussion of "total" and "updated" Lagrangian formulations in. Unfortunately, this usage of "inertial force" conflicts with the Newtonian idea of an inertial force. In the Newtonian view, an inertial force originates in the acceleration of the frame of observation (the fact that it is not an inertial frame of reference), not in the choice of coordinate system. To keep matters clear, it is safest to refer to the Lagrangian inertial forces as generalized inertial forces, to distinguish them from the Newtonian vector inertial forces. That is, one should avoid following Hildebrand when he says (p. 155) "we deal always with generalized forces, velocities accelerations, and momenta. For brevity, the adjective "generalized" will be omitted frequently."

It is known that the Lagrangian of a system is not unique. Within the Lagrangian formalism the Newtonian fictitious forces can be identified by the existence of alternative Lagrangians in which the fictitious forces disappear, sometimes found by exploiting the symmetry of the system.

Extensions to include non-conservative forces

Dissipative forces

Dissipation (i.e. non-conservative systems) can also be treated with an effective Lagrangian formulated by a certain doubling of the degrees of freedom.

In a more general formulation, the forces could be both conservative and viscous. If an appropriate transformation can be found from the F_i, Rayleigh suggests using a dissipation function, D, of the following form: $${\displaystyle D=\frac{1}{2}\sum _{j=1}^m\sum _{k=1}^m{C}_{jk}{\dot{q}}_j{\dot{q}}_k,}$$ where C_jk are constants that are related to the damping coefficients in the physical system, though not necessarily equal to them. If D is defined this way, then $${\displaystyle Q_j=-\frac{\mathrm{\partial }V}{\mathrm{\partial }{q}_j}-\frac{\mathrm{\partial }D}{\mathrm{\partial }{\dot{q}}_j}}$$ and $${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_j}\right)-\frac{\mathrm{\partial }L}{\mathrm{\partial }{q}_j}+\frac{\mathrm{\partial }D}{\mathrm{\partial }{\dot{q}}_j}=0.}$$

Electromagnetism

A test particle is a particle whose mass and charge are assumed to be so small that its effect on external system is insignificant. It is often a hypothetical simplified point particle with no properties other than mass and charge. Real particles like electrons and up quarks are more complex and have additional terms in their Lagrangians. Not only can the fields form non conservative potentials, these potentials can also be velocity dependent.

The Lagrangian for a charged particle with electrical charge q, interacting with an electromagnetic field, is the prototypical example of a velocity-dependent potential. The electric scalar potential ϕ = ϕ(r, t) and magnetic vector potential A = A(r, t) are defined from the electric field E = E(r, t) and magnetic field B = B(r, t) as follows: $${\displaystyle \mathbf{E}=-\mathbf{\nabla }\varphi -\frac{\mathrm{\partial }\mathbf{A}}{\mathrm{\partial }t},\mathbf{B}=\mathbf{\nabla }\times \mathbf{A}.}$$

The Lagrangian of a massive charged test particle in an electromagnetic field $${\displaystyle L=\frac{1}{2}m{\dot{\mathbf{r}}}^2+q\dot{\mathbf{r}}\cdot \mathbf{A}-q\varphi ,}$$ is called minimal coupling. This is a good example of when the common rule of thumb that the Lagrangian is the kinetic energy minus the potential energy is incorrect. Combined with Euler–Lagrange equation, it produces the Lorentz force law $${\displaystyle m\ddot{\mathbf{r}}=q\mathbf{E}+q\dot{\mathbf{r}}\times \mathbf{B}}$$

Under gauge transformation: $${\displaystyle \mathbf{A}\to \mathbf{A}+\mathbf{\nabla }f,\varphi \to \varphi -\dot{f},}$$ where f(r,t) is any scalar function of space and time, the aforementioned Lagrangian transforms like: $${\displaystyle L\to L+q\left(\dot{\mathbf{r}}\cdot \mathbf{\nabla }+\frac{\mathrm{\partial }}{\mathrm{\partial }t}\right)f=L+q\frac{df}{dt},}$$ which still produces the same Lorentz force law.

Note that the canonical momentum (conjugate to position r) is the kinetic momentum plus a contribution from the A field (known as the potential momentum): $${\displaystyle \mathbf{p}=\frac{\mathrm{\partial }L}{\mathrm{\partial }\dot{\mathbf{r}}}=m\dot{\mathbf{r}}+q\mathbf{A}.}$$

This relation is also used in the minimal coupling prescription in quantum mechanics and quantum field theory. From this expression, we can see that the canonical momentum p is not gauge invariant, and therefore not a measurable physical quantity; However, if r is cyclic (i.e. Lagrangian is independent of position r), which happens if the ϕ and A fields are uniform, then this canonical momentum p given here is the conserved momentum, while the measurable physical kinetic momentum mv is not.

Other contexts and formulations

The ideas in Lagrangian mechanics have numerous applications in other areas of physics, and can adopt generalized results from the calculus of variations.

Alternative formulations of classical mechanics

A closely related formulation of classical mechanics is Hamiltonian mechanics. The Hamiltonian is defined by $${\displaystyle H=\sum _{i=1}^n{\dot{q}}_i\frac{\mathrm{\partial }L}{\mathrm{\partial }{\dot{q}}_i}-L}$$ and can be obtained by performing a Legendre transformation on the Lagrangian, which introduces new variables canonically conjugate to the original variables. For example, given a set of generalized coordinates, the variables canonically conjugate are the generalized momenta. This doubles the number of variables, but makes differential equations first order. The Hamiltonian is a particularly ubiquitous quantity in quantum mechanics (see Hamiltonian (quantum mechanics)).

Routhian mechanics is a hybrid formulation of Lagrangian and Hamiltonian mechanics, which is not often used in practice but an efficient formulation for cyclic coordinates.

Momentum space formulation

Main article: Position and momentum space § Lagrangian mechanics

The Euler–Lagrange equations can also be formulated in terms of the generalized momenta rather than generalized coordinates. Performing a Legendre transformation on the generalized coordinate Lagrangian L(q, dq/dt, t) obtains the generalized momenta Lagrangian L′(p, dp/dt, t) in terms of the original Lagrangian, as well the EL equations in terms of the generalized momenta. Both Lagrangians contain the same information, and either can be used to solve for the motion of the system. In practice generalized coordinates are more convenient to use and interpret than generalized momenta.

Higher derivatives of generalized coordinates

There is no mathematical reason to restrict the derivatives of generalized coordinates to first order only. It is possible to derive modified EL equations for a Lagrangian containing higher order derivatives, see Euler–Lagrange equation for details. However, from the physical point-of-view there is an obstacle to include time derivatives higher than the first order, which is implied by Ostrogradsky's construction of a canonical formalism for nondegenerate higher derivative Lagrangians, see Ostrogradsky instability

Optics

Main article: Hamiltonian optics

Lagrangian mechanics can be applied to geometrical optics, by applying variational principles to rays of light in a medium, and solving the EL equations gives the equations of the paths the light rays follow.

Relativistic formulation

Main article: Relativistic Lagrangian mechanics

Lagrangian mechanics can be formulated in special relativity and general relativity. Some features of Lagrangian mechanics are retained in the relativistic theories but difficulties quickly appear in other respects. In particular, the EL equations take the same form, and the connection between cyclic coordinates and conserved momenta still applies, however the Lagrangian must be modified and is not simply the kinetic minus the potential energy of a particle. Also, it is not straightforward to handle multiparticle systems in a manifestly covariant way, it may be possible if a particular frame of reference is singled out.

Quantum mechanics

In quantum mechanics, action and quantum-mechanical phase are related via the Planck constant, and the principle of stationary action can be understood in terms of constructive interference of wave functions.

In 1948, Feynman discovered the path integral formulation extending the principle of least action to quantum mechanics for electrons and photons. In this formulation, particles travel every possible path between the initial and final states; the probability of a specific final state is obtained by summing over all possible trajectories leading to it. In the classical regime, the path integral formulation cleanly reproduces Hamilton's principle, and Fermat's principle in optics.

Classical field theory

In Lagrangian mechanics, the generalized coordinates form a discrete set of variables that define the configuration of a system. In classical field theory, the physical system is not a set of discrete particles, but rather a continuous field ϕ(r, t) defined over a region of 3D space. Associated with the field is a Lagrangian density $${\displaystyle \mathcal{L}(\varphi ,\mathrm{\nabla }\varphi ,\dot{\varphi },\mathbf{r},t)}$$ defined in terms of the field and its space and time derivatives at a location r and time t. Analogous to the particle case, for non-relativistic applications the Lagrangian density is also the kinetic energy density of the field, minus its potential energy density (this is not true in general, and the Lagrangian density has to be "reverse engineered"). The Lagrangian is then the volume integral of the Lagrangian density over 3D space $${\displaystyle L(t)=\int \mathcal{L}{\mathrm{d}}^3\mathbf{r}}$$ where d³r is a 3D differential volume element. The Lagrangian is a function of time since the Lagrangian density has implicit space dependence via the fields, and may have explicit spatial dependence, but these are removed in the integral, leaving only time in as the variable for the Lagrangian.

Noether's theorem

The action principle, and the Lagrangian formalism, are tied closely to Noether's theorem, which connects physical conserved quantities to continuous symmetries of a physical system.

If the Lagrangian is invariant under a symmetry, then the resulting equations of motion are also invariant under that symmetry. This characteristic is very helpful in showing that theories are consistent with either special relativity or general relativity.

Philosophy of space and time

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Philosophy_of_space_and_time

Philosophy of space and time is a branch of philosophy concerned with ideas about knowledge and understanding within space and time. Such ideas have been central to philosophy from its inception.

The philosophy of space and time was both an inspiration for and a central aspect of early analytic philosophy. The subject focuses on a number of basic issues, including whether time and space exist independently of the mind, whether they exist independently of one another, what accounts for time's apparently unidirectional flow, whether times other than the present moment exist, and questions about the nature of identity (particularly the nature of identity over time).

Ancient and medieval views

The earliest recorded philosophy of time was expounded by the ancient Egyptian thinker Ptahhotep (c. 2650–2600 BC), who said:

Follow your desire as long as you live, and do not perform more than is ordered, do not lessen the time of the following desire, for the wasting of time is an abomination to the spirit...

— 11th maxim of Ptahhotep

The Vedas, the earliest texts on Indian philosophy and Hindu philosophy, dating back to the late 2nd millennium BC, describe ancient Hindu cosmology, in which the universe goes through repeated cycles of creation, destruction, and rebirth, with each cycle lasting 4,320,000,000 years. Ancient Greek philosophers, including Parmenides and Heraclitus, wrote essays on the nature of time.

Incas regarded space and time as a single concept, named pacha (Quechua: pacha, Aymara: pacha).

Plato, in the Timaeus, identified time with the period of motion of the heavenly bodies, and space as that in which things come to be. Aristotle, in Book IV of his Physics, defined time as the number of changes with respect to before and after, and the place of an object as the innermost motionless boundary of that which surrounds it.

In Book 11 of St. Augustine's Confessions, he reflects on the nature of time, asking, "What then is time? If no one asks me, I know: if I wish to explain it to one who asks, I know not." He goes on to comment on the difficulty of thinking about time, pointing out the inaccuracy of common speech: "For but few things are there of which we speak properly; of most things we speak improperly, still, the things intended are understood." But Augustine presented the first philosophical argument for the reality of Creation (against Aristotle) in the context of his discussion of time, saying that knowledge of time depends on the knowledge of the movement of things, and therefore time cannot be where there are no creatures to measure its passing (Confessions Book XI ¶30; City of God Book XI ch.6).

In contrast to ancient Greek philosophers who believed that the universe had an infinite past with no beginning, medieval philosophers and theologians developed the concept of the universe having a finite past with a beginning, now known as temporal finitism. John Philoponus presented early arguments, adopted by later Christian philosophers and theologians of the form "argument from the impossibility of the existence of an actual infinite", which states:

"An actual infinite cannot exist."

"An infinite temporal regress of events is an actual infinite."

"∴ An infinite temporal regress of events cannot exist."

In the early 11th century, the Muslim physicist Ibn al-Haytham (Alhacen or Alhazen) discussed space perception and its epistemological implications in his Book of Optics (1021). He also rejected Aristotle's definition of topos (Physics IV) by way of geometric demonstrations and defined place as a mathematical spatial extension. His experimental disproof of the extramission hypothesis of vision led to changes in the understanding of the visual perception of space, contrary to the previous emission theory of vision supported by Euclid and Ptolemy. In "tying the visual perception of space to prior bodily experience, Alhacen unequivocally rejected the intuitiveness of spatial perception and, therefore, the autonomy of vision. Without tangible notions of distance and size for correlation, sight can tell us next to nothing about such things."

Realism and anti-realism

A traditional realist position in ontology is that time and space have existence apart from the human mind. Idealists, by contrast, deny or doubt the existence of objects independent of the mind. Some anti-realists, whose ontological position is that objects outside the mind do exist, nevertheless doubt the independent existence of time and space.

In 1781, Immanuel Kant published the Critique of Pure Reason, one of the most influential works in the history of the philosophy of space and time. He describes time as an a priori notion that, together with other a priori notions such as space, allows us to comprehend sense experience. Kant holds that neither space nor time are substance, entities in themselves, or learned by experience; he holds, rather, that both are elements of a systematic framework we use to structure our experience. Spatial measurements are used to quantify how far apart objects are, and temporal measurements are used to quantitatively compare the interval between (or duration of) events. Although space and time are held to be transcendentally ideal in this sense—that is, mind-dependent—they are also empirically real—that is, according to Kant's definitions, a priori features of experience, and therefore not simply "subjective," variable, or accidental perceptions in a given consciousness.

Some idealist writers, such as J. M. E. McTaggart in The Unreality of Time, have argued that time is an illusion (see also: § Flow of time, below).

The writers discussed here are for the most part realists in this regard; for instance, Gottfried Leibniz held that his monads existed, at least independently of the mind of the observer.

Absolutism and relationalism

Leibniz and Newton

The great debate between defining notions of space and time as real objects themselves (absolute), or mere orderings upon actual objects (relational), began between physicists Isaac Newton (via his spokesman, Samuel Clarke) and Gottfried Leibniz in the papers of the Leibniz–Clarke correspondence.

Arguing against the absolutist position, Leibniz offers a number of thought experiments with the purpose of showing that there is contradiction in assuming the existence of facts such as absolute location and velocity. These arguments trade heavily on two principles central to his philosophy: the principle of sufficient reason and the identity of indiscernibles. The principle of sufficient reason holds that for every fact, there is a reason that is sufficient to explain what and why it is the way it is and not otherwise. The identity of indiscernibles states that if there is no way of telling two entities apart, then they are one and the same thing.

The example Leibniz uses involves two proposed universes situated in absolute space. The only discernible difference between them is that the latter is positioned five feet to the left of the first. The example is only possible if such a thing as absolute space exists. Such a situation, however, is not possible, according to Leibniz, for if it were, a universe's position in absolute space would have no sufficient reason, as it might very well have been anywhere else. Therefore, it contradicts the principle of sufficient reason, and there could exist two distinct universes that were in all ways indiscernible, thus contradicting the identity of indiscernibles.

Standing out in Clarke's (and Newton's) response to Leibniz's arguments is the bucket argument: Water in a bucket, hung from a rope and set to spin, will start with a flat surface. As the water begins to spin in the bucket, the surface of the water will become concave. If the bucket is stopped, the water will continue to spin, and while the spin continues, the surface will remain concave. The concave surface is apparently not the result of the interaction of the bucket and the water, since the surface is flat when the bucket first starts to spin; the surface of the water becomes concave as the water itself, influenced by the spinning motion of the bucket, also begins to spin, and the surface remains concave as the bucket stops.

In this response, Clarke argues for the necessity of the existence of absolute space to account for phenomena like rotation and acceleration that cannot be accounted for on a purely relationalist account. Clarke argues that since the curvature of the water occurs in the rotating bucket as well as in the stationary bucket containing spinning water, it can only be explained by stating that the water is rotating in relation to the presence of some third thing—absolute space.

Leibniz describes a space that exists only as a relation between objects, and which has no existence apart from the existence of those objects. Motion exists only as a relation between those objects. Newtonian space provided the absolute frame of reference within which objects can have motion. In Newton's system, the frame of reference exists independently of the objects contained within it. These objects can be described as moving in relation to space itself. For almost two centuries, the evidence of a concave water surface held authority.

Mach

Another important figure in this debate is 19th-century physicist Ernst Mach. While he did not deny the existence of phenomena like that seen in the bucket argument, he still denied the absolutist conclusion by offering a different answer as to what the bucket was rotating in relation to: the fixed stars.

Mach suggested that thought experiments like the bucket argument are problematic. If we were to imagine a universe that only contains a bucket, on Newton's account, this bucket could be set to spin relative to absolute space, and the water it contained would form the characteristic concave surface. But in the absence of anything else in the universe, it would be difficult to confirm that the bucket was indeed spinning. It seems equally possible that the surface of the water in the bucket would remain flat.

Mach argued that, in effect, the water experiment in an otherwise empty universe would remain flat. But if another object were introduced into this universe, perhaps a distant star, there would now be something relative to which the bucket could be seen as rotating. The water inside the bucket could possibly have a slight curve. To account for the curve that we observe, an increase in the number of objects in the universe also increases the curvature in the water. Mach argued that the momentum of an object, whether angular or linear, exists as a result of the sum of the effects of other objects in the universe (Mach's Principle).

Einstein

Albert Einstein proposed that the laws of physics should be based on the principle of relativity. This principle holds that the rules of physics must be the same for all observers, regardless of the frame of reference that is used, and that light propagates at the same speed in all reference frames. This theory was motivated by Maxwell's equations, which show that electromagnetic waves propagate in a vacuum at the speed of light. However, Maxwell's equations give no indication of what this speed is relative to. Prior to Einstein, it was thought that this speed was relative to a fixed medium, called the luminiferous ether. In contrast, the theory of special relativity postulates that light propagates at the speed of light in all inertial frames, and examines the implications of this postulate.

All attempts to measure any speed relative to this ether failed, which can be seen as a confirmation of Einstein's postulate that light propagates at the same speed in all reference frames. Special relativity is a formalization of the principle of relativity that does not contain a privileged inertial frame of reference, such as the luminiferous ether or absolute space, from which Einstein inferred that no such frame exists.

Einstein generalized relativity to frames of reference that were non-inertial. He achieved this by positing the Equivalence Principle, which states that the force felt by an observer in a given gravitational field and that felt by an observer in an accelerating frame of reference are indistinguishable. This led to the conclusion that the mass of an object warps the geometry of the space-time surrounding it, as described in Einstein's field equations.

In classical physics, an inertial reference frame is one in which an object that experiences no forces does not accelerate. In general relativity, an inertial frame of reference is one that is following a geodesic of space-time. An object that moves against a geodesic experiences a force. An object in free fall does not experience a force, because it is following a geodesic. An object standing on the earth, however, will experience a force, as it is being held against the geodesic by the surface of the planet.

Einstein partially advocates Mach's principle in that distant stars explain inertia because they provide the gravitational field against which acceleration and inertia occur. But contrary to Leibniz's account, this warped space-time is as integral a part of an object as are its other defining characteristics, such as volume and mass. If one holds, contrary to idealist beliefs, that objects exist independently of the mind, it seems that relativistics commits one to also hold the idea that space and temporality have exactly the same type of independent existence.

Conventionalism

The position of conventionalism states that there is no fact of the matter as to the geometry of space and time, but that it is decided by convention. The first proponent of such a view, Henri Poincaré, reacting to the creation of the new non-Euclidean geometry, argued that which geometry applied to a space was decided by convention, since different geometries will describe a set of objects equally well, based on considerations from his sphere-world.

This view was developed and updated to include considerations from relativistic physics by Hans Reichenbach. Reichenbach's conventionalism, applying to space and time, focuses around the idea of coordinative definition.

Coordinative definition has two major features. The first has to do with coordinating units of length with certain physical objects. This is motivated by the fact that we can never directly apprehend length. Instead we must choose some physical object, say the Standard Metre at the Bureau International des Poids et Mesures (International Bureau of Weights and Measures), or the wavelength of cadmium to stand in as our unit of length. The second feature deals with separated objects. Although we can, presumably, directly test the equality of length of two measuring rods when they are next to one another, we can not find out as much for two rods distant from one another. Even supposing that two rods, whenever brought near to one another are seen to be equal in length, we are not justified in stating that they are always equal in length. This impossibility undermines our ability to decide the equality of length of two distant objects. Sameness of length, to the contrary, must be set by definition.

Such a use of coordinative definition is in effect, on Reichenbach's conventionalism, in the General Theory of Relativity where light is assumed, i.e. not discovered, to mark out equal distances in equal times. After this setting of coordinative definition, however, the geometry of spacetime is set.

As in the absolutism/relationalism debate, contemporary philosophy is still in disagreement as to the correctness of the conventionalist doctrine.

Structure of space-time

Building from a mix of insights from the historical debates of absolutism and conventionalism as well as reflecting on the import of the technical apparatus of the General Theory of Relativity, details as to the structure of space-time have made up a large proportion of discussion within the philosophy of space and time, as well as the philosophy of physics. The following is a short list of topics.

Relativity of simultaneity

According to special relativity each point in the universe can have a different set of events that compose its present instant. This has been used in the Rietdijk–Putnam argument to demonstrate that relativity predicts a block universe in which events are fixed in four dimensions.

Historical frameworks

A further application of the modern mathematical methods, in league with the idea of invariance and covariance groups, is to try to interpret historical views of space and time in modern, mathematical language.

In these translations, a theory of space and time is seen as a manifold paired with vector spaces, the more vector spaces the more facts there are about objects in that theory. The historical development of spacetime theories is generally seen to start from a position where many facts about objects are incorporated in that theory, and as history progresses, more and more structure is removed.

For example, Aristotelian space and time has both absolute position and special places, such as the center of the cosmos and the circumference. Newtonian space and time has absolute position and is Galilean invariant, but does not have special positions.

Direction of time

The problem of the direction of time arises directly from two contradictory facts. Firstly, the fundamental physical laws are time-reversal invariant; if a cinematographic film were taken of any process describable by means of the aforementioned laws and then played backwards, it would still portray a physically possible process. Secondly, our experience of time, at the macroscopic level, is not time-reversal invariant. Glasses can fall and break, but shards of glass cannot reassemble and fly up onto tables. We have memories of the past, and none of the future. We feel we cannot change the past but can influence the future. There is no future without our past.

Causation solution

One solution to this problem takes a metaphysical view, in which the direction of time follows from an asymmetry of causation. We know more about the past because the elements of the past are causes for the effects that compose our perception. We cannot affect the past, but we can affect the outcomes of the future.

There are two main objections to this view. First is the problem of distinguishing the cause from the effect in a non-arbitrary way. The use of causation in constructing a temporal ordering could easily become circular. The second problem with this view is its explanatory power. While the causation account, if successful, may account for some time-asymmetric phenomena like perception and action, it does not account for many others.

However, asymmetry of causation can be observed in a non-arbitrary way which is not metaphysical in the case of a human hand dropping a cup of water which smashes into fragments on a hard floor, spilling the liquid. In this order, the causes of the resultant pattern of cup fragments and water spill is easily attributable in terms of the trajectory of the cup, irregularities in its structure, angle of its impact on the floor, etc. However, applying the same event in reverse, it is difficult to explain why the various pieces of the cup should fly up into the human hand and reassemble precisely into the shape of a cup, or why the water should position itself entirely within the cup. The causes of the resultant structure and shape of the cup and the encapsulation of the water by the hand within the cup are not easily attributable, as neither hand nor floor can achieve such formations of the cup or water. This asymmetry is perceivable on account of two features: i) the relationship between the agent capacities of the human hand (i.e., what it is and is not capable of and what it is for) and non-animal agency (i.e., what floors are and are not capable of and what they are for) and ii) that the pieces of cup came to possess exactly the nature and number of those of a cup before assembling. In short, such asymmetry is attributable to the relationship between i) temporal direction and ii) the implications of form and functional capacity.

The application of these ideas of form and functional capacity only dictates temporal direction in relation to complex scenarios involving specific, non-metaphysical agency which is not merely dependent on human perception of time. However, this last observation in itself is not sufficient to invalidate the implications of the example for the progressive nature of time in general.

Thermodynamics solution

The second major family of solutions to this problem, and by far the one that has generated the most literature, finds the existence of the direction of time as relating to the nature of thermodynamics.

The answer from classical thermodynamics states that while our basic physical theory is, in fact, time-reversal symmetric, thermodynamics is not. In particular, the second law of thermodynamics states that the net entropy of a closed system never decreases, and this explains why we often see glass breaking, but not coming back together.

But in statistical mechanics things become more complicated. On one hand, statistical mechanics is far superior to classical thermodynamics, in that thermodynamic behavior, such as glass breaking, can be explained by the fundamental laws of physics paired with a statistical postulate. But statistical mechanics, unlike classical thermodynamics, is time-reversal symmetric. The second law of thermodynamics, as it arises in statistical mechanics, merely states that it is overwhelmingly likely that net entropy will increase, but it is not an absolute law.

Current thermodynamic solutions to the problem of the direction of time aim to find some further fact, or feature of the laws of nature to account for this discrepancy.

Laws solution

A third type of solution to the problem of the direction of time, although much less represented, argues that the laws are not time-reversal symmetric. For example, certain processes in quantum mechanics, relating to the weak nuclear force, are not time-reversible, keeping in mind that when dealing with quantum mechanics time-reversibility comprises a more complex definition. But this type of solution is insufficient because 1) the time-asymmetric phenomena in quantum mechanics are too few to account for the uniformity of macroscopic time-asymmetry and 2) it relies on the assumption that quantum mechanics is the final or correct description of physical processes.

One recent proponent of the laws solution is Tim Maudlin who argues that the fundamental laws of physics are laws of temporal evolution (see Maudlin [2007]). However, elsewhere Maudlin argues: "[the] passage of time is an intrinsic asymmetry in the temporal structure of the world... It is the asymmetry that grounds the distinction between sequences that runs from past to future and sequences which run from future to past" [ibid, 2010 edition, p. 108]. Thus it is arguably difficult to assess whether Maudlin is suggesting that the direction of time is a consequence of the laws or is itself primitive.

Flow of time

The problem of the flow of time, as it has been treated in analytic philosophy, owes its beginning to a paper written by J. M. E. McTaggart, in which he proposes two "temporal series". The first series, which means to account for our intuitions about temporal becoming, or the moving Now, is called the A-series. The A-series orders events according to their being in the past, present or future, simpliciter and in comparison to each other. The B-series eliminates all reference to the present, and the associated temporal modalities of past and future, and orders all events by the temporal relations earlier than and later than. In many ways, the debate between proponents of these two views can be seen as a continuation of the early modern debate between the view that there is absolute time (defended by Isaac Newton) and the view that there is only merely relative time (defended by Gottfried Leibniz).

McTaggart, in his paper "The Unreality of Time", argues that time is unreal since a) the A-series is inconsistent and b) the B-series alone cannot account for the nature of time as the A-series describes an essential feature of it.

Building from this framework, two camps of solution have been offered. The first, the A-theorist solution, takes becoming as the central feature of time, and tries to construct the B-series from the A-series by offering an account of how B-facts come to be out of A-facts. The second camp, the B-theorist solution, takes as decisive McTaggart's arguments against the A-series and tries to construct the A-series out of the B-series, for example, by temporal indexicals.

Presentism and eternalism

Main articles: Presentism (philosophy of time) and Eternalism (philosophy of time)

According to Presentism, time is an ordering of various realities. At a certain time, some things exist and others do not. This is the only reality we can deal with. We cannot, for example, say that Homer exists because at the present time he does not. An Eternalist, on the other hand, holds that time is a dimension of reality on a par with the three spatial dimensions, and hence that all things—past, present and future—can be said to be just as real as things in the present. According to this theory, then, Homer really does exist, though we must still use special language when talking about somebody who exists at a distant time—just as we would use special language when talking about something far away (the very words near, far, above, below, and such are directly comparable to phrases such as in the past, a minute ago, and so on).

Philosophers such as Vincent Conitzer and Caspar Hare have argued that the philosophy of time is connected to the philosophy of self. Conitzer argues that the metaphysics of the self are connected to the A-theory of time, and that arguments in favor of A-theory are more effective as arguments for the combined position of both A-theory being true and the "I" being metaphysically privileged from other perspectives. Caspar Hare has made similar arguments with the theories of egocentric presentism and perspectival realism, of which several other philosophers have written reviews.

Endurantism and perdurantism

Main articles: Endurantism and Perdurantism

The positions on the persistence of objects are somewhat similar. An endurantist holds that for an object to persist through time is for it to exist completely at different times (each instance of existence we can regard as somehow separate from previous and future instances, though still numerically identical with them). A perdurantist on the other hand holds that for a thing to exist through time is for it to exist as a continuous reality, and that when we consider the thing as a whole we must consider an aggregate of all its "temporal parts" or instances of existing. Endurantism is seen as the conventional view and flows out of our pre-philosophical ideas (when I talk to somebody I think I am talking to that person as a complete object, and not just a part of a cross-temporal being), but perdurantists such as David Lewis have attacked this position. They argue that perdurantism is the superior view for its ability to take account of change in objects.

On the whole, Presentists are also endurantists and Eternalists are also perdurantists (and vice versa), but this is not a necessary relation and it is possible to claim, for instance, that time's passage indicates a series of ordered realities, but that objects within these realities somehow exist outside of the reality as a whole, even though the realities as wholes are not related. However, such positions are rarely adopted.

Quantum suicide and immortality

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Quantum_suicide_and_immortality

Quantum suicide is a thought experiment in quantum mechanics and the philosophy of physics. Purportedly, it can falsify any interpretation of quantum mechanics other than the Everett many-worlds interpretation by means of a variation of the Schrödinger's cat thought experiment, from the cat's point of view. Quantum immortality refers to the subjective experience of surviving quantum suicide. This concept is sometimes conjectured to be applicable to real-world causes of death as well.

As a thought experiment, quantum suicide is an intellectual exercise in which an abstract setup is followed through to its logical consequences merely to prove a theoretical point. Virtually all physicists and philosophers of science who have described it, especially in popularized treatments, underscore that it relies on contrived, idealized circumstances that may be impossible or exceedingly difficult to realize in real life, and that its theoretical premises are controversial even among supporters of the many-worlds interpretation. Thus, as cosmologist Anthony Aguirre warns, "[...] it would be foolish (and selfish) in the extreme to let this possibility guide one's actions in any life-and-death question."

History

Hugh Everett did not mention quantum suicide or quantum immortality in writing; his work was intended as a solution to the paradoxes of quantum mechanics. Eugene Shikhovtsev's biography of Everett states that "Everett firmly believed that his many-worlds theory guaranteed him immortality: his consciousness, he argued, is bound at each branching to follow whatever path does not lead to death". Peter Byrne, author of a biography of Everett, reports that Everett also privately discussed quantum suicide (such as to play high-stakes Russian roulette and survive in the winning branch), but adds that "[i]t is unlikely, however, that Everett subscribed to this [quantum immortality] view, as the only sure thing it guarantees is that the majority of your copies will die, hardly a rational goal."

Among scientists, the thought experiment was introduced by Euan Squires in 1986. Afterwards, it was published independently by Hans Moravec in 1987 and Bruno Marchal in 1988; it was also described by Huw Price in 1997, who credited it to Dieter Zeh, and independently presented formally by Max Tegmark in 1998. It was later discussed by philosophers Peter J. Lewis in 2000 and David Lewis in 2001.

Thought experiment

The quantum suicide thought experiment involves a similar apparatus to Schrödinger's cat – a box which kills the occupant in a given time frame with probability one-half due to quantum uncertainty. The only difference is to have the experimenter recording observations be the one inside the box. The significance of this thought experiment is that someone whose life or death depends on a qubit could possibly distinguish between interpretations of quantum mechanics. By definition, fixed observers cannot.

At the start of the first iteration, under both interpretations, the probability of surviving the experiment is 50%, as given by the squared norm of the wave function. At the start of the second iteration, assuming a single-world interpretation of quantum mechanics (like the widely-held Copenhagen interpretation) is true, the wave function has already collapsed; thus, if the experimenter is already dead, there is a 0% chance of survival for any further iterations. However, if the many-worlds interpretation is true, a superposition of the live experimenter necessarily exists (as also does the one who dies). Now, barring the possibility of life after death, after every iteration only one of the two experimenter superpositions – the live one – is capable of having any sort of conscious experience. Putting aside the philosophical problems associated with individual identity and its persistence, under the many-worlds interpretation, the experimenter, or at least a version of them, continues to exist through all of their superpositions where the outcome of the experiment is that they live. In other words, a version of the experimenter survives all iterations of the experiment. Since the superpositions where a version of the experimenter lives occur by quantum necessity (under the many-worlds interpretation), it follows that their survival, after any realizable number of iterations, is physically necessary; hence, the notion of quantum immortality.

A version of the experimenter surviving stands in stark contrast to the implications of the Copenhagen interpretation, according to which, although the survival outcome is possible in every iteration, its probability tends towards zero as the number of iterations increases. According to the many-worlds interpretation, the above scenario has the opposite property: the probability of a version of the experimenter living is necessarily one for any number of iterations.

In the book Our Mathematical Universe, Max Tegmark lays out three criteria that, in abstract, a quantum suicide experiment must fulfill:

• The random number generator must be quantum, not deterministic, so that the experimenter enters a state of superposition of being dead and alive.
• The experimenter must be rendered dead (or at least unconscious) on a time scale shorter than that on which they can become aware of the outcome of the quantum measurement.
• The experiment must be virtually certain to kill the experimenter, and not merely injure them.

Analysis of real-world feasibility

In response to questions about "subjective immortality" from normal causes of death, Tegmark suggested that the flaw in that reasoning is that dying is not a binary event as in the thought experiment; it is a progressive process, with a continuum of states of decreasing consciousness. He states that in most real causes of death, one experiences such a gradual loss of self-awareness. It is only within the confines of an abstract scenario that an observer finds they defy all odds. Referring to the above criteria, he elaborates as follows: "[m]ost accidents and common causes of death clearly don't satisfy all three criteria, suggesting you won't feel immortal after all. In particular, regarding criterion 2, under normal circumstances dying isn't a binary thing where you're either alive or dead [...] What makes the quantum suicide work is that it forces an abrupt transition."

David Lewis' commentary and subsequent criticism

The philosopher David Lewis explored the possibility of quantum immortality in a 2001 lecture titled "How Many Lives Has Schrödinger's Cat?", his first academic foray into the field of the interpretation of quantum mechanics – and his last, due to his death less than four months afterwards. In the lecture, published posthumously in 2004, Lewis rejected the many-worlds interpretation, allowing that it offers initial theoretical attractions, but also arguing that it suffers from irremediable flaws, mainly regarding probabilities, and came to tentatively endorse the Ghirardi–Rimini–Weber theory instead. Lewis concluded the lecture by stating that the quantum suicide thought experiment, if applied to real-world causes of death, would entail what he deemed a "terrifying corollary": as all causes of death are ultimately quantum-mechanical in nature, if the many-worlds interpretation were true, in Lewis' view an observer should subjectively "expect with certainty to go on forever surviving whatever dangers [he or she] may encounter", as there will always be possibilities of survival, no matter how unlikely; faced with branching events of survival and death, an observer should not "equally expect to experience life and death", as there is no such thing as experiencing death, and should thus divide his or her expectations only among branches where he or she survives. If survival is guaranteed, however, this is not the case for good health or integrity. This would lead to a Tithonus-like deterioration of one's body that continues indefinitively, leaving the subject forever just short of death.

Interviewed for the 2004 book Schrödinger's Rabbits, Tegmark rejected this scenario for the reason that "the fading of consciousness is a continuous process. Although I cannot experience a world line in which I am altogether absent, I can enter one in which my speed of thought is diminishing, my memories and other faculties fading [...] [Tegmark] is confident that even if he cannot die all at once, he can gently fade away." In the same book, philosopher of science and many-worlds proponent David Wallace undermines the case for real-world quantum immortality on the basis that death can be understood as a continuum of decreasing states of consciousness not only in time, as argued by Tegmark, but also in space: "our consciousness is not located at one unique point in the brain, but is presumably a kind of emergent or holistic property of a sufficiently large group of neurons [...] our consciousness might not be able to go out like a light, but it can dwindle exponentially until it is, for all practical purposes, gone."

Directly responding to Lewis' lecture, British philosopher and many-worlds proponent David Papineau, while finding Lewis' other objections to the many-worlds interpretation lacking, strongly denies that any modification to the usual probability rules is warranted in death situations. Assured subjective survival can follow from the quantum suicide idea only if an agent reasons in terms of "what will be experienced next" instead of the more obvious "what will happen next, whether will be experienced or not". He writes: "[I]t is by no means obvious why Everettians should modify their intensity rule in this way. For it seems perfectly open for them to apply the unmodified intensity rule in life-or-death situations, just as elsewhere. If they do this, then they can expect all futures in proportion to their intensities, whether or not those futures contain any of their live successors. For example, even when you know you are about to be the subject in a fifty-fifty Schrödinger’s experiment, you should expect a future branch where you perish, to just the same degree as you expect a future branch where you survive."

On a similar note, quoting Lewis' position that death should not be expected as an experience, philosopher of science Charles Sebens concedes that, in a quantum suicide experiment, "[i]t is tempting to think you should expect survival with certainty." However, he remarks that expectation of survival could follow only if the quantum branching and death were absolutely simultaneous, otherwise normal chances of death apply: "[i]f death is indeed immediate on all branches but one, the thought has some plausibility. But if there is any delay it should be rejected. In such a case, there is a short period of time when there are multiple copies of you, each (effectively) causally isolated from the others and able to assign a credence to being the one who will live. Only one will survive. Surely rationality does not compel you to be maximally optimistic in such a scenario." Sebens also explores the possibility that death might not be simultaneous to branching, but still faster than a human can mentally realize the outcome of the experiment. Again, an agent should expect to die with normal probabilities: "[d]o the copies need to last long enough to have thoughts to cause trouble? I think not. If you survive, you can consider what credences you should have assigned during the short period after splitting when you coexisted with the other copies."

Writing in the journal Ratio, philosopher István Aranyosi, while noting that "[the] tension between the idea of states being both actual and probable is taken as the chief weakness of the many-worlds interpretation of quantum mechanics," summarizes that most of the critical commentary of Lewis' immortality argument has revolved around its premises. But even if, for the sake of argument, one were willing to entirely accept Lewis' assumptions, Aranyosi strongly denies that the "terrifying corollary" would be the correct implication of said premises. Instead, the two scenarios that would most likely follow would be what Aranyosi describes as the "comforting corollary", in which an observer should never expect to get very sick in the first place, or the "momentary life" picture, in which an observer should expect "eternal life, spent almost entirely in an unconscious state", punctuated by extremely brief, amnesiac moments of consciousness. Thus, Aranyosi concludes that while "[w]e can't assess whether one or the other [of the two alternative scenarios] gets the lion's share of the total intensity associated with branches compatible with self-awareness, [...] we can be sure that they together (i.e. their disjunction) do indeed get the lion's share, which is much reassuring."

Analysis by other proponents of the many-worlds interpretation

Physicist David Deutsch, though a proponent of the many-worlds interpretation, states regarding quantum suicide that "that way of applying probabilities does not follow directly from quantum theory, as the usual one does. It requires an additional assumption, namely that when making decisions one should ignore the histories in which the decision-maker is absent....[M]y guess is that the assumption is false."

Tegmark now believes experimenters should only expect a normal probability of survival, not immortality. The experimenter's probability amplitude in the wavefunction decreases significantly, meaning they exist with a much lower measure than they had before. Per the anthropic principle, a person is less likely to find themselves in a world where they are less likely to exist, that is, a world with a lower measure has a lower probability of being observed by them. Therefore, the experimenter will have a lower probability of observing the world in which they survive than the earlier world in which they set up the experiment. This same problem of reduced measure was pointed out by Lev Vaidman in the Stanford Encyclopedia of Philosophy. In the 2001 paper, "Probability and the many-worlds interpretation of quantum theory", Vaidman writes that an agent should not agree to undergo a quantum suicide experiment: "The large 'measures' of the worlds with dead successors is a good reason not to play." Vaidman argues that it is the instantaneity of death that may seem to imply subjective survival of the experimenter, but that normal probabilities nevertheless must apply even in this special case: "[i]ndeed, the instantaneity makes it difficult to establish the probability postulate, but after it has been justified in the wide range of other situations it is natural to apply the postulate for all cases."

In his 2013 book The Emergent Multiverse, Wallace opines that the reasons for expecting subjective survival in the thought experiment "do not really withstand close inspection", although he concedes that it would be "probably fair to say [...] that precisely because death is philosophically complicated, my objections fall short of being a knock-down refutation". Besides re-stating that there appears to be no motive to reason in terms of expectations of experience instead of expectations of what will happen, he suggests that a decision-theoretic analysis shows that "an agent who prefers certain life to certain death is rationally compelled to prefer life in high-weight branches and death in low-weight branches to the opposite."

Physicist Sean M. Carroll, another proponent of the many-worlds interpretation, states regarding quantum suicide that neither experiences nor rewards should be thought of as being shared between future versions of oneself, as they become distinct persons when the world splits. He further states that one cannot pick out some future versions of oneself as "really you" over others, and that quantum suicide still cuts off the existence of some of these future selves, which would be worth objecting to just as if there were a single world.

Analysis by skeptics of the many-worlds interpretation

Cosmologist Anthony Aguirre, while personally skeptical of most accounts of the many-worlds interpretation, in his book Cosmological Koans writes that "[p]erhaps reality actually is this bizarre, and we really do subjectively 'survive' any form of death that is both instantaneous and binary." Aguirre notes, however, that most causes of death do not fulfill these two requirements: "If there are degrees of survival, things are quite different." If loss of consciousness was binary like in the thought experiment, the quantum suicide effect would prevent an observer from subjectively falling asleep or undergoing anesthesia, conditions in which mental activities are greatly diminished but not altogether abolished. Consequently, upon most causes of death, even outwardly sudden, if the quantum suicide effect holds true an observer is more likely to progressively slip into an attenuated state of consciousness, rather than remain fully awake by some very improbable means. Aguirre further states that quantum suicide as a whole might be characterized as a sort of reductio ad absurdum against the current understanding of both the many-worlds interpretation and theory of mind. He finally hypothesizes that a different understanding of the relationship between the mind and time should remove the bizarre implications of necessary subjective survival.

Physicist and writer Philip Ball, a critic of the many-worlds interpretation, in his book Beyond Weird, describes the quantum suicide experiment as "cognitively unstable" and exemplificatory of the difficulties of the many-worlds theory with probabilities. While he acknowledges Lev Vaidman's argument that an experimenter should subjectively expect outcomes in proportion of the "measure of existence" of the worlds in which they happen, Ball ultimately rejects this explanation. "What this boils down to is the interpretation of probabilities in the MWI. If all outcomes occur with 100% probability, where does that leave the probabilistic character of quantum mechanics?" Furthermore, Ball explains that such arguments highlight what he recognizes as another major problem of the many-worlds interpretation, connected but independent from the issue of probability: the incompatibility with the notion of selfhood. Ball ascribes most attempts of justifying probabilities in the many-worlds interpretation to "saying that quantum probabilities are just what quantum mechanics look like when consciousness is restricted to only one world" but that "there is in fact no meaningful way to explain or justify such a restriction." Before performing a quantum measurement, an "Alice before" experimenter "can't use quantum mechanics to predict what will happen to her in a way that can be articulated – because there is no logical way to talk about 'her' at any moment except the conscious present (which, in a frantically splitting universe, doesn't exist). Because it is logically impossible to connect the perceptions of Alice Before to Alice After [the experiment], "Alice" has disappeared. [...] [The MWI] eliminates any coherent notion of what we can experience, or have experienced, or are experiencing right now."

Philosopher of science Peter J. Lewis, a critic of the many-worlds interpretation, considers the whole thought experiment an example of the difficulty of accommodating probability within the many-worlds framework: "Standard quantum mechanics yields probabilities for various future occurrences, and these probabilities can be fed into an appropriate decision theory. But if every physically possible consequence of the current state of affairs is certain to occur, on what basis should I decide what to do? For example, if I point a gun at my head and pull the trigger, it looks like Everett's theory entails that I am certain to survive—and that I am certain to die. This is at least worrying, and perhaps rationally disabling." In his book Quantum Ontology, Lewis explains that for the subjective immortality argument to be drawn out of the many-worlds theory, one has to adopt an understanding of probability – the so-called "branch-counting" approach, in which an observer can meaningfully ask "which post-measurement branch will I end up on?" – that is ruled out by experimental, empirical evidence as it would yield probabilities that do not match with the well-confirmed Born rule. Lewis identifies instead in the Deutsch-Wallace decision-theoretic analysis the most promising (although still, to his judgement, incomplete) way of addressing probabilities in the many-worlds interpretation, in which it is not possible to count branches (and, similarly, the persons that "end up" on each branch). Lewis concludes that "[t]he immortality argument is perhaps best viewed as a dramatic demonstration of the fundamental conflict between branch-counting (or person-counting) intuitions about probability and the decision theoretic approach. The many-worlds theory, to the extent that it is viable, does not entail that you should expect to live forever."

Space travel in science fiction

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Space_travel_in_science_fiction

Rocket on cover of Other Worlds sci-fi magazine, September 1951

Space travel, or space flight (less often, starfaring or star voyaging) is a science fiction theme that has captivated the public and is almost archetypal for science fiction.^[4] Space travel, interplanetary or interstellar, is usually performed in space ships, and spacecraft propulsion in various works ranges from the scientifically plausible to the totally fictitious.

While some writers focus on realistic, scientific, and educational aspects of space travel, other writers see this concept as a metaphor for freedom, including "free[ing] mankind from the prison of the solar system". Though the science fiction rocket has been described as a 20th-century icon, according to The Encyclopedia of Science Fiction "The means by which space flight has been achieved in sf – its many and various spaceships – have always been of secondary importance to the mythical impact of the theme". Works related to space travel have popularized such concepts as time dilation, space stations, and space colonization.

While generally associated with science fiction, space travel has also occasionally featured in fantasy, sometimes involving magic or supernatural entities such as angels.

History

Science and Mechanics, November 1931, showing a proposed sub-orbital spaceship that would reach a 700-mile altitude on a one-hour flight from Berlin to New York

Still from Lost in Space TV series premiere (1965), depicting space travelers in suspended animation

A classic, defining trope of the science fiction genre is that the action takes place in space, either aboard a spaceship or on another planet. Early works of science fiction, termed "proto SF" – such as novels by 17th-century writers Francis Godwin and Cyrano de Bergerac, and by astronomer Johannes Kepler – include "lunar romances", much of whose action takes place on the Moon. Science fiction critic George Slusser also pointed to Christopher Marlowe's Doctor Faustus (1604) – in which the main character is able to see the entire Earth from high above – and noted the connections of space travel to earlier dreams of flight and air travel, as far back as the writings of Plato and Socrates. In such a grand view, space travel, and inventions such as various forms of "star drive", can be seen as metaphors for freedom, including "free[ing] mankind from the prison of the solar system".

In the following centuries, while science fiction addressed many aspects of futuristic science as well as space travel, space travel proved the more influential with the genre's writers and readers, evoking their sense of wonder. Most works were mainly intended to amuse readers, but a small number, often by authors with a scholarly background, sought to educate readers about related aspects of science, including astronomy; this was the motive of the influential American editor Hugo Gernsback, who dubbed it "sugar-coated science" and "scientifiction". Science fiction magazines, including Gernsback's Science Wonder Stories, alongside works of pure fiction, discussed the feasibility of space travel; many science fiction writers also published nonfiction works on space travel, such as Willy Ley's articles and David Lasser's book, The Conquest of Space (1931). 

Roadside replica of Star Trek starship Enterprise

From the late 19th and early 20th centuries on, there was a visible distinction between the more "realistic", scientific fiction (which would later evolve into hard sf)), whose authors, often scientists like Konstantin Tsiolkovsky and Max Valier, focused on the more plausible concept of interplanetary travel (to the Moon or Mars); and the more grandiose, less realistic stories of "escape from Earth into a Universe filled with worlds", which gave rise to the genre of space opera, pioneered by E. E. Smith and popularized by the television series Star Trek, which debuted in 1966. This trend continues to the present, with some works focusing on "the myth of space flight", and others on "realistic examination of space flight"; the difference can be described as that between the authors' concern with the "imaginative horizons rather than hardware".

The successes of 20th-century space programs, such as the Apollo 11 Moon landing, have often been described as "science fiction come true" and have served to further "demystify" the concept of space travel within the Solar System. Henceforth writers who wanted to focus on the "myth of space travel" were increasingly likely to do so through the concept of interstellar travel. Edward James wrote that many science fiction stories have "explored the idea that without the constant expansion of humanity, and the continual extension of scientific knowledge, comes stagnation and decline." While the theme of space travel has generally been seen as optimistic, some stories by revisionist authors, often more pessimistic and disillusioned, juxtapose the two types, contrasting the romantic myth of space travel with a more down-to-Earth reality. George Slusser suggests that "science fiction travel since World War II has mirrored the United States space program: anticipation in the 1950s and early 1960s, euphoria into the 1970s, modulating into skepticism and gradual withdrawal since the 1980s."

On the screen, the 1902 French film A Trip to the Moon, by Georges Méliès, described as the first science fiction film, linked special effects to depictions of spaceflight. With other early films, such as Woman in the Moon (1929) and Things to Come (1936), it contributed to an early recognition of the rocket as the iconic, primary means of space travel, decades before space programs began. Later milestones in film and television include the Star Trek series and films, and the film 2001: A Space Odyssey by Stanley Kubrick (1968), which visually advanced the concept of space travel, allowing it to evolve from the simple rocket toward a more complex space ship. Stanley Kubrick's 1968 epic film featured a lengthy sequence of interstellar travel through a mysterious "star gate". This sequence, noted for its psychedelic special effects conceived by Douglas Trumbull, influenced a number of later cinematic depictions of superluminal and hyperspatial travel, such as Star Trek: The Motion Picture (1979).

Means of travel

Artist rendition of a spaceship entering warp drive

Generic terms for engines enabling science fiction spacecraft propulsion include "space drive" and "star drive". In 1977 The Visual Encyclopedia of Science Fiction listed the following means of space travel: anti-gravity, atomic (nuclear), bloater, cannon one-shot, Dean drive, faster-than-light (FTL), hyperspace, inertialess drive, ion thruster, photon rocket, plasma propulsion engine, Bussard ramjet, R. force, solar sail, spindizzy, and torchship.

The 2007 Brave New Words: The Oxford Dictionary of Science Fiction lists the following terms related to the concept of space drive: gravity drive, hyperdrive, ion drive, jump drive, overdrive, ramscoop (a synonym for ram-jet), reaction drive, stargate, ultradrive, warp drive and torchdrive. Several of these terms are entirely fictitious or are based on "rubber science", while others are based on real scientific theories. Many fictitious means of travelling through space, in particular, faster than light travel, tend to go against the current understanding of physics, in particular, the theory of relativity. Some works sport numerous alternative star drives; for example the Star Trek universe, in addition to its iconic "warp drive", has introduced concepts such as "transwarp", "slipstream" and "spore drive", among others.

Many, particularly early, writers of science fiction did not address means of travel in much detail, and many writings of the "proto-SF" era were disadvantaged by their authors' living in a time when knowledge of space was very limited — in fact, many early works did not even consider the concept of vacuum and instead assumed that an atmosphere of sorts, composed of air or "aether", continued indefinitely. Highly influential in popularizing the science of science fiction was the 19th-century French writer Jules Verne, whose means of space travel in his 1865 novel, From the Earth to the Moon (and its sequel, Around the Moon), was explained mathematically, and whose vehicle — a gun-launched space capsule — has been described as the first such vehicle to be "scientifically conceived" in fiction. Percy Greg's Across the Zodiac (1880) featured a spaceship with a small garden, an early precursor of hydroponics. Another writer who attempted to merge concrete scientific ideas with science fiction was the turn-of-the-century Russian writer and scientist, Konstantin Tsiolkovsky, who popularized the concept of rocketry. George Mann mentions Robert A. Heinlein's Rocket Ship Galileo (1947) and Arthur C. Clarke's Prelude to Space (1951) as early, influential modern works that emphasized the scientific and engineering aspects of space travel. From the 1960s on, growing popular interest in modern technology also led to increasing depictions of interplanetary spaceships based on advanced plausible extensions of real modern technology. The Alien franchise features ships with ion propulsion, a developing technology at the time that would be used years later in the Deep Space 1, Hayabusa 1 and SMART-1 spacecraft.

Interstellar travel

Slower than light

With regard to interstellar travel, in which faster-than-light speeds are generally considered unrealistic, more realistic depictions of interstellar travel have often focused on the idea of "generation ships" that travel at sub-light speed for many generations before arriving at their destinations. Other scientifically plausible concepts of interstellar travel include suspended animation and, less often, ion drive, solar sail, Bussard ramjet, and time dilation.

Faster than light

Artist rendition of a ship traveling through a wormhole

Some works discuss Einstein's general theory of relativity and challenges that it faces from quantum mechanics, and include concepts of space travel through wormholes or black holes. Many writers, however, gloss over such problems, introducing entirely fictional concepts such as hyperspace (also, subspace, nulspace, overspace, jumpspace, or slipstream) travel using inventions such as hyperdrive, jump drive, warp drive, or space folding. Invention of completely made-up devices enabling space travel has a long tradition — already in the early 20th century, Verne criticized H. G. Wells' The First Men in the Moon (1901) for abandoning realistic science (his spaceship relied on anti-gravitic material called "cavorite"). Of fictitious drives, by the mid-1970s the concept of hyperspace travel was described as having achieved the most popularity, and would subsequently be further popularized — as hyperdrive — through its use in the Star Wars franchise. While the fictitious drives "solved" problems related to physics (the difficulty of faster-than-light travel), some writers introduce new wrinkles — for example, a common trope involves the difficulty of using such drives in close proximity to other objects, in some cases allowing their use only beginning from the outskirts of the planetary systems.

While usually the means of space travel is just a means to an end, in some works, particularly short stories, it is a central plot device. These works focus on themes such as the mysteries of hyperspace, or the consequences of getting lost after an error or malfunction.