Quaternary glaciation

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Quaternary_glaciation

Extent of maximum glaciation (in black) in the Northern Hemisphere during the Pleistocene. The formation of 3 to 4 km (1.9 to 2.5 mi) thick ice sheets equate to a global sea level drop of about 120 m (390 ft)

The Quaternary glaciation, also known as the Pleistocene glaciation, is an alternating series of glacial and interglacial periods during the Quaternary period that began 2.58 Ma (million years ago) and is ongoing. Although geologists describe this entire period up to the present as an "ice age", in popular culture this term usually refers to the most recent glacial period, or to the Pleistocene epoch in general. Since Earth still has polar ice sheets, geologists consider the Quaternary glaciation to be ongoing, though currently in an interglacial period.

During the Quaternary glaciation, ice sheets appeared, expanding during glacial periods and contracting during interglacial periods. Since the end of the last glacial period, only the Antarctic and Greenland ice sheets have survived, while other sheets formed during glacial periods, such as the Laurentide Ice Sheet, have completely melted.

Diagram of key climate-carbon cycle feedbacks linking Quaternary climate temperatures (GMT) to atmospheric CO₂ and ice sheets. Positive feedbacks amplify and negative feedbacks dampen environmental change, with slow-acting responses shown as dashed arrows.

The major effects of the Quaternary glaciation have been the continental erosion of land and the deposition of material; the modification of river systems; the formation of millions of lakes, including the development of pluvial lakes far from the ice margins; changes in sea level; the isostatic adjustment of the Earth's crust; flooding; and abnormal winds. The ice sheets, by raising the albedo (the ratio of solar radiant energy reflected from Earth back into space), generated significant feedback to further cool the climate. These effects have shaped land and ocean environments and biological communities.

Long before the Quaternary glaciation, land-based ice appeared and then disappeared during at least four other ice ages. The Quaternary glaciation can be considered a part of a Late Cenozoic Ice Age that began 33.9 Ma and is ongoing.

Discovery

Main article: Ice age § Origin of ice age theory

Evidence for the Quaternary glaciation was first understood in the 18th and 19th centuries as part of the Scientific Revolution. Over the last century, extensive field observations have provided evidence that continental glaciers covered large parts of Europe, North America, and Siberia. Maps of glacial features were compiled after many years of fieldwork by hundreds of geologists who mapped the location and orientation of drumlins, eskers, moraines, striations, and glacial stream channels to reveal the extent of the ice sheets, the direction of their flow, and the systems of meltwater channels. They also allowed scientists to decipher a history of multiple advances and retreats of the ice. Even before the theory of worldwide glaciation was generally accepted, many observers recognized that more than a single advance and retreat of the ice had occurred.

Description

Further information: Marine isotope stages

Graph of reconstructed temperature (blue), CO₂ (green), and dust (red) from the Vostok Station ice core for the past 420,000 years

To geologists, an ice age is defined by the presence of large amounts of land-based ice. Prior to the Quaternary glaciation, land-based ice formed during at least four earlier geologic periods: the late Paleozoic (360–260 Ma), Andean-Saharan (450–420 Ma), Cryogenian (720–635 Ma) and Huronian (2,400–2,100 Ma).

Within the Quaternary ice age, there were also periodic fluctuations of the total volume of land ice, the sea level, and global temperatures. During the colder episodes (referred to as glacial periods or glacials) large ice sheets at least 4 km (2.5 mi) thick at their maximum covered parts of Europe, North America, and Siberia. The shorter warm intervals between glacials, when continental glaciers retreated, are referred to as interglacials. These are evidenced by buried soil profiles, peat beds, and lake and stream deposits separating the unsorted, unstratified deposits of glacial debris.

Initially the glacial/interglacial cycle length was about 41,000 years, but following the Mid-Pleistocene Transition about 1 Ma, it slowed to about 100,000 years, as evidenced most clearly by ice cores for the past 800,000 years and marine sediment cores for the earlier period. Over the past 740,000 years there have been eight glacial cycles.

The entire Quaternary period, starting 2.58 Ma, is referred to as an ice age because at least one permanent large ice sheet—the Antarctic ice sheet—has existed continuously. There is uncertainty over how much of Greenland was covered by ice during each interglacial. Currently, Earth is in an interglacial period, the Holocene epoch beginning 11,700 years ago; this has caused the ice sheets from the Last Glacial Period to slowly melt. The remaining glaciers, now occupying about 10% of the world's land surface, cover Greenland, Antarctica and some mountainous regions. During the glacial periods, the present (i.e., interglacial) hydrologic system was completely interrupted throughout large areas of the world and was considerably modified in others. The volume of ice on land resulted in a sea level about 120 metres (394 ft) lower than present.

Causes

Further information: Ice age

Earth's history of glaciation is a product of the internal variability of Earth's climate system (e.g., ocean currents, carbon cycle), interacting with external forcing by phenomena outside the climate system (e.g., changes in Earth's orbit, volcanism, and changes in solar output).

Astronomical cycles

Main articles: Milankovitch cycles and orbital forcing

See also: 100,000-year problem

The role of Earth's orbital changes in controlling climate was first advanced by James Croll in the late 19th century. Later, the Serbian geophysicist Milutin Milanković elaborated on the theory and calculated that these irregularities in Earth's orbit could cause the climatic cycles now known as Milankovitch cycles. They are the result of the additive behavior of several types of cyclical changes in Earth's orbital properties.

Relationship of Earth's orbit to periods of glaciation

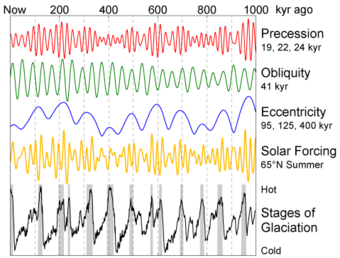
Firstly, changes in the orbital eccentricity of Earth occur on a cycle of about 100,000 years. Secondly, the inclination or tilt of Earth's axis varies between 22° and 24.5° in a cycle 41,000 years long. The tilt of Earth's axis is responsible for the seasons; the greater the tilt, the greater the contrast between summer and winter temperatures. Thirdly, precession of the equinoxes, or wobbles in the Earth's rotation axis, have a periodicity of 26,000 years. According to the Milankovitch theory, these factors cause a periodic cooling of Earth, with the coldest part in the cycle occurring about every 40,000 years. The main effect of the Milankovitch cycles is to change the contrast between the seasons, not the annual amount of solar heat Earth receives. The result is less ice melting than accumulating, and glaciers build up.

Milankovitch worked out the ideas of climatic cycles in the 1920s and 1930s, but it was not until the 1970s that a sufficiently long and detailed chronology of the Quaternary temperature changes was worked out to test the theory adequately. Studies of deep-sea cores and their fossils indicate that the fluctuation of climate during the last few hundred thousand years is remarkably close to that predicted by Milankovitch.

Atmospheric composition

One theory holds that decreases in atmospheric CO
₂, an important greenhouse gas, started the long-term cooling trend that eventually led to the formation of continental ice sheets in the Arctic. Geological evidence indicates a decrease of more than 90% in atmospheric CO₂ since the middle of the Mesozoic Era. An analysis of CO₂ reconstructions from alkenone records shows that CO₂ in the atmosphere declined before and during Antarctic glaciation, and supports a substantial CO₂ decrease as the primary cause of Antarctic glaciation. Decreasing carbon dioxide levels during the late Pliocene may have contributed substantially to global cooling and the onset of Northern Hemisphere glaciation. This decrease in atmospheric carbon dioxide concentrations may have come about by way of the decreasing ventilation of deep water in the Southern Ocean.

CO₂ levels also play an important role in the transitions between interglacials and glacials. High CO₂ contents correspond to warm interglacial periods, and low CO₂ to glacial periods. However, studies indicate that CO
₂ may not be the primary cause of the interglacial-glacial transitions, but instead acts as a feedback. The explanation for this observed CO
₂ variation "remains a difficult attribution problem".

Plate tectonics and ocean currents

Further information: Plate tectonics and ocean current

An important component in the development of long-term ice ages is the positions of the continents. These can control the circulation of the oceans and the atmosphere, affecting how ocean currents carry heat to high latitudes. Throughout most of geologic time, the North Pole appears to have been in a broad, open ocean that allowed major ocean currents to move unabated. Equatorial waters flowed into the polar regions, warming them. This produced mild, uniform climates that persisted throughout most of geologic time.

But during the Cenozoic Era, the large North American and South American continental plates drifted westward from the Eurasian Plate. This interlocked with the development of the Atlantic Ocean, running north–south, with the North Pole in the small, nearly landlocked basin of the Arctic Ocean. The Drake Passage opened 33.9 million years ago (the Eocene-Oligocene transition), severing Antarctica from South America. The Antarctic Circumpolar Current could then flow through it, isolating Antarctica from warm waters and triggering the formation of its huge ice sheets. The weakening of the North Atlantic Current (NAC) around 3.65 to 3.5 million years ago resulted in cooling and freshening of the Arctic Ocean, nurturing the development of Arctic sea ice and preconditioning the formation of continental glaciers later in the Pliocene. A dinoflagellate cyst turnover in the eastern North Atlantic approximately ~2.60 Ma, during MIS 104, has been cited as evidence that the NAC shifted significantly to the south at this time, causing an abrupt cooling of the North Sea and northwestern Europe by reducing heat transport to high latitude waters of the North Atlantic. The Isthmus of Panama developed at a convergent plate margin about 2.6 million years ago and further separated oceanic circulation, closing the last strait, outside the polar regions, that had connected the Pacific and Atlantic Oceans. This increased poleward salt and heat transport, strengthening the North Atlantic thermohaline circulation, which supplied enough moisture to Arctic latitudes to initiate the Northern Hemisphere glaciation. The change in the biogeography of the nannofossil Coccolithus pelagicus around 2.74 Ma is believed to reflect this onset of glaciation. However, model simulations suggest reduced ice volume due to increased ablation at the edge of the ice sheet under warmer conditions.

Collapse of permanent El Niño

A permanent El Niño state existed in the early-mid-Pliocene. Warmer temperature in the eastern equatorial Pacific caused an increased water vapor greenhouse effect and reduced the area covered by highly reflective stratus clouds, thus decreasing the albedo of the planet. Propagation of the El Niño effect through planetary waves may have warmed the polar region and delayed the onset of glaciation in the Northern Hemisphere. Therefore, the appearance of cold surface water in the east equatorial Pacific around 3 million years ago may have contributed to global cooling and modified the global climate’s response to Milankovitch cycles.

Rise of mountains

The elevation of continental surface, often as mountain formation, is thought to have contributed to cause the Quaternary glaciation. The gradual movement of the bulk of Earth's landmasses away from the tropics in addition to increased mountain formation in the Late Cenozoic meant more land at high altitude and high latitude, favouring the formation of glaciers. For example, the Greenland ice sheet formed in connection to the uplift of the west Greenland and east Greenland uplands in two phases, 10 and 5 Ma, respectively. These mountains constitute passive continental margins. Uplift of the Rocky Mountains and Greenland’s west coast has been speculated to have cooled the climate due to jet stream deflection and increased snowfall due to higher surface elevation. Computer models show that such uplift would have enabled glaciation through increased orographic precipitation and cooling of surface temperatures. For the Andes it is known that the Principal Cordillera had risen to heights that allowed for the development of valley glaciers about 1 Ma.

Effects

The presence of so much ice upon the continents had a profound effect upon almost every aspect of Earth's hydrologic system. Most obvious are the spectacular mountain scenery and other continental landscapes fashioned both by glacial erosion and deposition instead of running water. Entirely new landscapes covering millions of square kilometers were formed in a relatively short period of geologic time. In addition, the vast bodies of glacial ice affected Earth well beyond the glacier margins. Directly or indirectly, the effects of glaciation were felt in every part of the world.

Lakes

Further information: Glacial lake

The Quaternary glaciation produced more lakes than all other geologic processes combined. The reason is that a continental glacier completely disrupts the preglacial drainage system. The surface over which the glacier moved was scoured and eroded by the ice, leaving many closed, undrained depressions in the bedrock. These depressions filled with water and became lakes.

A diagram of the formation of the Great Lakes

Very large lakes were formed along the glacial margins. The ice on both North America and Europe was about 3,000 m (10,000 ft) thick near the centers of maximum accumulation, but it tapered toward the glacier margins. Ice weight caused crustal subsidence, which was greatest beneath the thickest accumulation of ice. As the ice melted, rebound of the crust lagged behind, producing a regional slope toward the ice. This slope formed basins that have lasted for thousands of years. These basins became lakes or were invaded by the ocean. The Baltic Sea and the Great Lakes of North America were formed primarily in this way.

The numerous lakes of the Canadian Shield, Sweden, and Finland are thought to have originated at least partly from glaciers' selective erosion of weathered bedrock.

Pluvial lakes

Main article: Pluvial lake

The climatic conditions that cause glaciation had an indirect effect on arid and semiarid regions far removed from the large ice sheets. The increased precipitation that fed the glaciers also increased the runoff of major rivers and intermittent streams, resulting in the growth and development of large pluvial lakes. Most pluvial lakes developed in relatively arid regions where there typically was insufficient rain to establish a drainage system leading to the sea. Instead, stream runoff flowed into closed basins and formed playa lakes. With increased rainfall, the playa lakes enlarged and overflowed. Pluvial lakes were most extensive during glacial periods. During interglacial stages, with less rain, the pluvial lakes shrank to form small salt flats.

Isostatic adjustment

Main article: Post-glacial rebound

Major isostatic adjustments of the lithosphere during the Quaternary glaciation were caused by the weight of the ice, which depressed the continents. In Canada, a large area around Hudson Bay was depressed below (modern) sea level, as was the area in Europe around the Baltic Sea. The land has been rebounding from these depressions since the ice melted. Some of these isostatic movements triggered large earthquakes in Scandinavia about 9,000 years ago. These earthquakes are unique in that they are not associated with plate tectonics.

Studies have shown that the uplift has taken place in two distinct stages. The initial uplift following deglaciation was rapid (called "elastic"), and took place as the ice was being unloaded. After this "elastic" phase, uplift proceed by "slow viscous flow" so the rate decreased exponentially after that. Today, typical uplift rates are of the order of 1 cm per year or less, except in areas of North America, especially Alaska, where the rate of uplift is 2.54 cm per year (1 inch or more). In northern Europe, this is clearly shown by the GPS data obtained by the BIFROST GPS network. Studies suggest that rebound will continue for at least another 10,000 years. The total uplift from the end of deglaciation depends on the local ice load and could be several hundred meters near the center of rebound.

Winds

The presence of ice over so much of the continents greatly modified patterns of atmospheric circulation. Winds near the glacial margins were strong and persistent because of the abundance of dense, cold air coming off the glacier fields. These winds picked up and transported large quantities of loose, fine-grained sediment brought down by the glaciers. This dust accumulated as loess (wind-blown silt), forming irregular blankets over much of the Missouri River valley, central Europe, and northern China. The trade winds over northern Africa intensified with the onset of Quaternary glaciation, evidenced by the increase in dust accumulation on the northwest African margin.

Sand dunes were much more widespread and active in many areas during the early Quaternary period. A good example is the Sand Hills region in Nebraska which covers an area of about 60,000 km² (23,166 sq mi). This region was a large, active dune field during the Pleistocene epoch but today is largely stabilized by grass cover.

Ocean currents

Thick glaciers were heavy enough to reach the sea bottom in several important areas, which blocked the passage of ocean water and affected ocean currents. In addition to these direct effects, it also caused feedback effects, as ocean currents contribute to global heat transfer.

Gold deposits

Moraines and till deposited by Quaternary glaciers have contributed to the formation of valuable placer deposits of gold. This is the case of southernmost Chile where reworking of Quaternary moraines have concentrated gold offshore.

Records of prior glaciation

Main article: Timeline of glaciation

See also: Ice age and paleoclimatology

500 million years of climate change.

Glaciation has been a rare event in Earth's history, but there is evidence of widespread glaciation during the late Paleozoic Era (300 to 200 Ma) and the late Precambrian (i.e., the Neoproterozoic Era, 800 to 600 Ma). Before the current ice age, which began 2 to 3 Ma, Earth's climate was typically mild and uniform for long periods of time. This climatic history is implied by the types of fossil plants and animals and by the characteristics of sediments preserved in the stratigraphic record. There are, however, widespread glacial deposits, recording several major periods of ancient glaciation in various parts of the geologic record. Such evidence suggests major periods of glaciation prior to the current Quaternary glaciation.

One of the best documented records of pre-Quaternary glaciation, called the Karoo Ice Age, is found in the late Paleozoic rocks in South Africa, India, South America, Antarctica, and Australia. Exposures of ancient glacial deposits are numerous in these areas. Deposits of even older glacial sediment exist on every continent except South America. These indicate that two other periods of widespread glaciation occurred during the late Precambrian, producing the Snowball Earth during the Cryogenian period.

Next glacial period

Further information: Milankovitch cycles, Past sea level, Climate change, and Human impact on the environment

Increase in atmospheric CO
₂ since the Industrial Revolution

The warming trend following the Last Glacial Maximum, since about 20,000 years ago, has resulted in a sea level rise by about 121 metres (397 ft). This warming trend subsided about 6,000 years ago, and sea level has been comparatively stable since the Neolithic. The present interglacial period (the Holocene climatic optimum) has been stable and warm compared to the preceding ones, which were interrupted by numerous cold spells lasting hundreds of years. This stability might have allowed the Neolithic Revolution and by extension human civilization.

Based on orbital models, the cooling trend initiated about 6,000 years ago will continue for another 23,000 years. Slight changes in the Earth's orbital parameters may, however, indicate that, even without any human contribution, there will not be another glacial period for the next 50,000 years. It is possible that the current cooling trend might be interrupted by an interstadial phase (a warmer period) in about 60,000 years, with the next glacial maximum reached only in about 100,000 years.

Based on past estimates for interglacial durations of about 10,000 years, in the 1970s there was some concern that the next glacial period would be imminent. However, slight changes in the eccentricity of Earth's orbit around the Sun suggest a lengthy interglacial period lasting about another 50,000 years. Other models, based on periodic variations in solar output, give a different projection of the start of the next glacial period at around 10,000 years from now. Additionally, human impact is now seen as possibly extending what would already be an unusually long warm period. Projection of the timeline for the next glacial maximum depend crucially on the amount of CO
₂ in the atmosphere. Models assuming increased CO
₂ levels at 750 parts per million (ppm; current levels are at 417 ppm) have estimated the persistence of the current interglacial period for another 50,000 years. However, more recent studies concluded that the amount of heat trapping gases emitted into Earth's oceans and atmosphere will prevent the next glacial (ice age), which otherwise would begin in around 50,000 years, and likely more glacial cycles.

Climate change may weaken the Atlantic meridional overturning circulation through increases in ocean heat content and elevated flows of freshwater from melting ice sheets. The collapse of the AMOC would be a severe climate catastrophe, resulting in a cooling of the Northern Hemisphere. It would have devastating and irreversible impacts especially for Nordic countries, but also for other parts of the world.

Quantification of margins and uncertainties

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Quantification_of_margins_and_uncertainties

Quantification of Margins and Uncertainty (QMU) is a decision support methodology for complex technical decisions. QMU focuses on the identification, characterization, and analysis of performance thresholds and their associated margins for engineering systems that are evaluated under conditions of uncertainty, particularly when portions of those results are generated using computational modeling and simulation. QMU has traditionally been applied to complex systems where comprehensive experimental test data is not readily available and cannot be easily generated for either end-to-end system execution or for specific subsystems of interest. Examples of systems where QMU has been applied include nuclear weapons performance, qualification, and stockpile assessment. QMU focuses on characterizing in detail the various sources of uncertainty that exist in a model, thus allowing the uncertainty in the system response output variables to be well quantified. These sources are frequently described in terms of probability distributions to account for the stochastic nature of complex engineering systems. The characterization of uncertainty supports comparisons of design margins for key system performance metrics to the uncertainty associated with their calculation by the model. QMU supports risk-informed decision-making processes where computational simulation results provide one of several inputs to the decision-making authority. There is currently no standardized methodology across the simulation community for conducting QMU; the term is applied to a variety of different modeling and simulation techniques that focus on rigorously quantifying model uncertainty in order to support comparison to design margins.

History

The fundamental concepts of QMU were originally developed concurrently at several national laboratories supporting nuclear weapons programs in the late 1990s, including Lawrence Livermore National Laboratory, Sandia National Laboratory, and Los Alamos National Laboratory. The original focus of the methodology was to support nuclear stockpile decision-making, an area where full experimental test data could no longer be generated for validation due to bans on nuclear weapons testing. The methodology has since been applied in other applications where safety or mission critical decisions for complex projects must be made using results based on modeling and simulation. Examples outside of the nuclear weapons field include applications at NASA for interplanetary spacecraft and rover development, missile six-degree-of-freedom (6DOF) simulation results, and characterization of material properties in terminal ballistic encounters.

Overview

QMU focuses on quantification of the ratio of design margin to model output uncertainty. The process begins with the identification of the key performance thresholds for the system, which can frequently be found in the systems requirements documents. These thresholds (also referred to as performance gates) can specify an upper bound of performance, a lower bound of performance, or both in the case where the metric must remain within the specified range. For each of these performance thresholds, the associated performance margin must be identified. The margin represents the targeted range the system is being designed to operate in to safely avoid the upper and lower performance bounds. These margins account for aspects such as the design safety factor the system is being developed to as well as the confidence level in that safety factor. QMU focuses on determining the quantified uncertainty of the simulation results as they relate to the performance threshold margins. This total uncertainty includes all forms of uncertainty related to the computational model as well as the uncertainty in the threshold and margin values. The identification and characterization of these values allows the ratios of margin-to-uncertainty (M/U) to be calculated for the system. These M/U values can serve as quantified inputs that can help authorities make risk-informed decisions regarding how to interpret and act upon results based on simulations.

Overview of General QMU Process.

QMU recognizes that there are multiple types of uncertainty that propagate through a model of a complex system. The simulation in the QMU process produces output results for the key performance thresholds of interest, known as the Best Estimate Plus Uncertainty (BE+U). The best estimate component of BE+U represents the core information that is known and understood about the model response variables. The basis that allows high confidence in these estimates is usually ample experimental test data regarding the process of interest which allows the simulation model to be thoroughly validated.

The types of uncertainty that contribute to the value of the BE+U can be broken down into several categories:

• Aleatory uncertainty: This type of uncertainty is naturally present in the system being modeled and is sometimes known as “irreducible uncertainty” and “stochastic variability.” Examples include processes that are naturally stochastic such as wind gust parameters and manufacturing tolerances.
• Epistemic uncertainty: This type of uncertainty is due to a lack of knowledge about the system being modeled and is also known as “reducible uncertainty.” Epistemic uncertainty can result from uncertainty about the correct underlying equations of the model, incomplete knowledge of the full set of scenarios to be encountered, and lack of experimental test data defining the key model input parameters.

The system may also suffer from requirements uncertainty related to the specified thresholds and margins associated with the system requirements. QMU acknowledges that in some situations, the system designer may have high confidence in what the correct value for a specific metric may be, while at other times, the selected value may itself suffer from uncertainty due to lack of experience operating in this particular regime. QMU attempts to separate these uncertainty values and quantify each of them as part of the overall inputs to the process.

QMU can also factor in human error in the ability to identify the unknown unknowns that can affect a system. These errors can be quantified to some degree by looking at the limited experimental data that may be available for previous system tests and identifying what percentage of tests resulted in system thresholds being exceeded in an unexpected manner. This approach attempts to predict future events based on the past occurrences of unexpected outcomes.

The underlying parameters that serve as inputs to the models are frequently modeled as samples from a probability distribution. The input parameter model distributions as well as the model propagation equations determine the distribution of the output parameter values. The distribution of a specific output value must be considered when determining what is an acceptable M/U ratio for that performance variable. If the uncertainty limit for U includes a finite upper bound due to the particular distribution of that variable, a lower M/U ratio may be acceptable. However, if U is modeled as a normal or exponential distribution which can potentially include outliers from the far tails of the distribution, a larger value may be required in order to reduce system risk to an acceptable level.

Ratios of acceptable M/U for safety critical systems can vary from application to application. Studies have cited acceptable M/U ratios as being in the 2:1 to 10:1 range for nuclear weapons stockpile decision-making. Intuitively, the larger the value of M/U, the less of the available performance margin is being consumed by uncertainty in the simulation outputs. A ratio of 1:1 could result in a simulation run where the simulated performance threshold is not exceeded when in actuality the entire design margin may have been consumed. It is important to note that rigorous QMU does not ensure that the system itself is capable of meeting its performance margin; rather, it serves to ensure that the decision-making authority can make judgments based on accurately characterized results.

The underlying objective of QMU is to present information to decision-makers that fully characterizes the results in light of the uncertainty as understood by the model developers. This presentation of results allows decision makers an opportunity to make informed decisions while understanding what sensitivities exist in the results due to the current understanding of uncertainty. Advocates of QMU recognize that decisions for complex systems cannot be made strictly based on the quantified M/U metrics. Subject matter expert (SME) judgment and other external factors such as stakeholder opinions and regulatory issues must also be considered by the decision-making authority before a final outcome is decided.

Verification and validation

Verification and validation (V & V) of a model is closely interrelated with QMU. Verification is broadly acknowledged as the process of determining if a model was built correctly; validation activities focus on determining if the correct model was built. V&V against available experimental test data is an important aspect of accurately characterizing the overall uncertainty of the system response variables. V&V seeks to make maximum use of component and subsystem-level experimental test data to accurately characterize model input parameters and the physics-based models associated with particular sub-elements of the system. The use of QMU in the simulation process helps to ensure that the stochastic nature of the input variables (due to both aleatory and epistemic uncertainties) as well as the underlying uncertainty in the model are properly accounted for when determining the simulation runs required to establish model credibility prior to accreditation.

Advantages and disadvantages

QMU has the potential to support improved decision-making for programs that must rely heavily on modeling and simulation. Modeling and simulation results are being used more often during the acquisition, development, design, and testing of complex engineering systems. One of the major challenges of developing simulations is to know how much fidelity should be built into each element of the model. The pursuit of higher fidelity can significantly increase development time and total cost of the simulation development effort. QMU provides a formal method for describing the required fidelity relative to the design threshold margins for key performance variables. This information can also be used to prioritize areas of future investment for the simulation. Analysis of the various M/U ratios for the key performance variables can help identify model components that are in need of fidelity upgrades to order to increase simulation effectiveness.

A variety of potential issues related to the use of QMU have also been identified. QMU can lead to longer development schedules and increased development costs relative to traditional simulation projects due to the additional rigor being applied. Proponents of QMU state that the level of uncertainty quantification required is driven by certification requirements for the intended application of the simulation. Simulations used for capability planning or system trade analyses must generally model the overall performance trends of the systems and components being analyzed. However, for safety-critical systems where experimental test data is lacking, simulation results provide a critical input to the decision-making process. Another potential risk related to the use of QMU is a false sense of confidence regarding protection from unknown risks. The use of quantified results for key simulation parameters can lead decision makers to believe all possible risks have been fully accounted for, which is particularly challenging for complex systems. Proponents of QMU advocate for a risk-informed decision-making process to counter this risk; in this paradigm, M/U results as well as SME judgment and other external factors are always factored into the final decision.

Poincaré group

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Poincar%C3%A9_group

Henri Poincaré

The Poincaré group, named after Henri Poincaré (1905), was first defined by Hermann Minkowski (1908) as the isometry group of Minkowski spacetime. It is a ten-dimensional non-abelian Lie group that is of importance as a model in our understanding of the most basic fundamentals of physics.

Overview

The Poincaré group consists of all coordinate transformations of Minkowski space that do not change the spacetime interval between events. For example, if everything were postponed by two hours, including the two events and the path you took to go from one to the other, then the time interval between the events recorded by a stopwatch that you carried with you would be the same. Or if everything were shifted five kilometres to the west, or turned 60 degrees to the right, you would also see no change in the interval. It turns out that the proper length of an object is also unaffected by such a shift.

In total, there are ten degrees of freedom for such transformations. They may be thought of as translation through time or space (four degrees, one per dimension); reflection through a plane (three degrees, the freedom in orientation of this plane); or a "boost" in any of the three spatial directions (three degrees). Composition of transformations is the operation of the Poincaré group, with rotations being produced as the composition of an even number of reflections.

In classical physics, the Galilean group is a comparable ten-parameter group that acts on absolute time and space. Instead of boosts, it features shear mappings to relate co-moving frames of reference.

In general relativity, i.e. under the effects of gravity, Poincaré symmetry applies only locally. A treatment of symmetries in general relativity is not in the scope of this article.

Poincaré symmetry

Poincaré symmetry is the full symmetry of special relativity. It includes:

• translations (displacements) in time and space, forming the abelian Lie group of spacetime translations (P);
• rotations in space, forming the non-abelian Lie group of three-dimensional rotations (J);
• boosts, transformations connecting two uniformly moving bodies (K).

The last two symmetries, J and K, together make the Lorentz group (see also Lorentz invariance); the semi-direct product of the spacetime translations group and the Lorentz group then produce the Poincaré group. Objects that are invariant under this group are then said to possess Poincaré invariance or relativistic invariance.

10 generators (in four spacetime dimensions) associated with the Poincaré symmetry, by Noether's theorem, imply 10 conservation laws:

• 1 for the energy – associated with translations through time
• 3 for the momentum – associated with translations through spatial dimensions
• 3 for the angular momentum – associated with rotations between spatial dimensions
• 3 for a quantity involving the velocity of the center of mass – associated with hyperbolic rotations between each spatial dimension and time

Poincaré group

The Poincaré group is the group of Minkowski spacetime isometries. It is a ten-dimensional noncompact Lie group. The four-dimensional abelian group of spacetime translations is a normal subgroup, while the six-dimensional Lorentz group is also a subgroup, the stabilizer of the origin. The Poincaré group itself is the minimal subgroup of the affine group which includes all translations and Lorentz transformations. More precisely, it is a semidirect product of the spacetime translations group and the Lorentz group,

${\displaystyle {\mathbf{R}}^{1,3}⋊\mathrm{O}(1,3),}$

with group multiplication

${\displaystyle (\alpha ,f)\cdot (\beta ,g)=(\alpha +f\cdot \beta ,f\cdot g)}$.

Another way of putting this is that the Poincaré group is a group extension of the Lorentz group by a vector representation of it; it is sometimes dubbed, informally, as the inhomogeneous Lorentz group. In turn, it can also be obtained as a group contraction of the de Sitter group SO(4, 1) ~ Sp(2, 2), as the de Sitter radius goes to infinity.

Its positive energy unitary irreducible representations are indexed by mass (nonnegative number) and spin (integer or half integer) and are associated with particles in quantum mechanics (see Wigner's classification).

In accordance with the Erlangen program, the geometry of Minkowski space is defined by the Poincaré group: Minkowski space is considered as a homogeneous space for the group.

In quantum field theory, the universal cover of the Poincaré group

${\displaystyle {\mathbf{R}}^{1,3}⋊\mathrm{SL}(2,\mathbf{C}),}$

which may be identified with the double cover

${\displaystyle {\mathbf{R}}^{1,3}⋊\mathrm{Spin}(1,3),}$

is more important, because representations of ${\displaystyle \mathrm{SO}(1,3)}$ are not able to describe fields with spin 1/2; i.e. fermions. Here ${\displaystyle \mathrm{SL}(2,\mathbf{C})}$ is the group of complex ${\displaystyle 2\times 2}$ matrices with unit determinant, isomorphic to the Lorentz-signature spin group ${\displaystyle \mathrm{Spin}(1,3)}$.

Poincaré algebra

Lie groups and Lie algebras

The Poincaré algebra is the Lie algebra of the Poincaré group. It is a Lie algebra extension of the Lie algebra of the Lorentz group. More specifically, the proper ($det\mathrm{\Lambda }=1$), orthochronous (${{\mathrm{\Lambda }}^0}_0\ge 1$) part of the Lorentz subgroup (its identity component), $\mathrm{S}\mathrm{O}(1,3{)}_{+}^{\uparrow }$, is connected to the identity and is thus provided by the exponentiation $\exp \left(i{a}_{\mu }{P}^{\mu }\right)\exp \left(\frac{i}{2}{\omega }_{\mu \nu }{M}^{\mu \nu }\right)$ of this Lie algebra. In component form, the Poincaré algebra is given by the commutation relations:

${\displaystyle \begin{array}{rl}[P_{\mu },P_{\nu }]& =0\\ \frac{1}{i}[M_{\mu \nu },P_{\rho }]& ={\eta }_{\mu \rho }{P}_{\nu }-{\eta }_{\nu \rho }{P}_{\mu }\\ \frac{1}{i}[M_{\mu \nu },M_{\rho \sigma }]& ={\eta }_{\mu \rho }{M}_{\nu \sigma }-{\eta }_{\mu \sigma }{M}_{\nu \rho }-{\eta }_{\nu \rho }{M}_{\mu \sigma }+{\eta }_{\nu \sigma }{M}_{\mu \rho },\end{array}}$

where ${\displaystyle P}$ is the generator of translations, ${\displaystyle M}$ is the generator of Lorentz transformations, and ${\displaystyle \eta }$ is the ${\displaystyle (+,-,-,-)}$ Minkowski metric (see Sign convention).

A diagram of the commutation structure of the Poincaré algebra. The edges of the diagram connect generators with nonzero commutators.

The bottom commutation relation is the ("homogeneous") Lorentz group, consisting of rotations, $J_i=\frac{1}{2}{ϵ}_{imn}{M}^{mn}$, and boosts, $K_i=M_{i0}$. In this notation, the entire Poincaré algebra is expressible in noncovariant (but more practical) language as

${\displaystyle \begin{array}{rl}[J_m,P_n]& =i{ϵ}_{mnk}{P}_k,\\ [J_i,P_0]& =0,\\ [K_i,P_k]& =i{\eta }_{ik}{P}_0,\\ [K_i,P_0]& =-i{P}_i,\\ [J_m,J_n]& =i{ϵ}_{mnk}{J}_k,\\ [J_m,K_n]& =i{ϵ}_{mnk}{K}_k,\\ [K_m,K_n]& =-i{ϵ}_{mnk}{J}_k,\end{array}}$

where the bottom line commutator of two boosts is often referred to as a "Wigner rotation". The simplification $[J_m+i{K}_m,J_n-i{K}_n]=0$ permits reduction of the Lorentz subalgebra to $\mathfrak{s}\mathfrak{u}(2)\oplus \mathfrak{s}\mathfrak{u}(2)$ and efficient treatment of its associated representations. In terms of the physical parameters, we have

${\displaystyle \begin{array}{rl}\left[\mathcal{H},p_i\right]& =0\\ \left[\mathcal{H},L_i\right]& =0\\ \left[\mathcal{H},K_i\right]& =i\hslash c{p}_i\\ \left[p_i,p_j\right]& =0\\ \left[p_i,L_j\right]& =i\hslash {ϵ}_{ijk}{p}_k\\ \left[p_i,K_j\right]& =\frac{i\hslash }{c}\mathcal{H}{\delta }_{ij}\\ \left[L_i,L_j\right]& =i\hslash {ϵ}_{ijk}{L}_k\\ \left[L_i,K_j\right]& =i\hslash {ϵ}_{ijk}{K}_k\\ \left[K_i,K_j\right]& =-i\hslash {ϵ}_{ijk}{L}_k\end{array}}$

The Casimir invariants of this algebra are $P_{\mu }{P}^{\mu }$ and $W_{\mu }{W}^{\mu }$ where $W_{\mu }$ is the Pauli–Lubanski pseudovector; they serve as labels for the representations of the group.

The Poincaré group is the full symmetry group of any relativistic field theory. As a result, all elementary particles fall in representations of this group. These are usually specified by the four-momentum squared of each particle (i.e. its mass squared) and the intrinsic quantum numbers $J^{PC}$, where ${\displaystyle J}$ is the spin quantum number, ${\displaystyle P}$ is the parity and ${\displaystyle C}$ is the charge-conjugation quantum number. In practice, charge conjugation and parity are violated by many quantum field theories; where this occurs, ${\displaystyle P}$ and ${\displaystyle C}$ are forfeited. Since CPT symmetry is invariant in quantum field theory, a time-reversal quantum number may be constructed from those given.

As a topological space, the group has four connected components: the component of the identity; the time reversed component; the spatial inversion component; and the component which is both time-reversed and spatially inverted.

Other dimensions

The definitions above can be generalized to arbitrary dimensions in a straightforward manner. The d-dimensional Poincaré group is analogously defined by the semi-direct product

${\displaystyle \mathrm{IO}(1,d-1):={\mathbf{R}}^{1,d-1}⋊\mathrm{O}(1,d-1)}$

with the analogous multiplication

${\displaystyle (\alpha ,f)\cdot (\beta ,g)=(\alpha +f\cdot \beta ,f\cdot g)}$.

The Lie algebra retains its form, with indices µ and ν now taking values between 0 and d − 1. The alternative representation in terms of J_i and K_i has no analogue in higher dimensions.