Number theory

From Wikipedia, the free encyclopedia

A Lehmer sieve, which is a primitive digital computer once used for finding primes and solving simple Diophantine equations.

Number theory, or in older usage arithmetic, is a branch of pure mathematics devoted primarily to the study of the integers. It is sometimes called "The Queen of Mathematics" because of its foundational place in the discipline.^[1] Number theorists study prime numbers as well as the properties of objects made out of integers (e.g., rational numbers) or defined as generalizations of the integers (e.g., algebraic integers).

Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of analytical objects (e.g., the Riemann zeta function) that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, e.g., as approximated by the latter (Diophantine approximation).

The older term for number theory is arithmetic. By the early twentieth century, it had been superseded by "number theory".^{[note 1]} (The word "arithmetic" is used by the general public to mean "elementary calculations"; it has also acquired other meanings in mathematical logic, as in Peano arithmetic, and computer science, as in floating point arithmetic.) The use of the term arithmetic for number theory regained some ground in the second half of the 20th century, arguably in part due to French influence.^{[note 2]} In particular, arithmetical is preferred as an adjective to number-theoretic.

History

Origins

Dawn of arithmetic

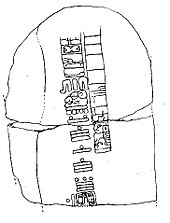
The first historical find of an arithmetical nature is a fragment of a table: the broken clay tablet Plimpton 322 (Larsa, Mesopotamia, ca. 1800 BC) contains a list of "Pythagorean triples", i.e., integers ${\displaystyle (a,b,c)}$ such that ${\displaystyle a^{2}+b^{2}=c^{2}}$. The triples are too many and too large to have been obtained by brute force. The heading over the first column reads: "The takiltum of the diagonal which has been subtracted such that the width..."^[2]

The Plimpton 322 tablet

The table's layout suggests^[3] that it was constructed by means of what amounts, in modern language, to the identity

${\displaystyle \left({\frac {1}{2}}\left(x-{\frac {1}{x}}\right)\right)^{2}+1=\left({\frac {1}{2}}\left(x+{\frac {1}{x}}\right)\right)^{2},}$

which is implicit in routine Old Babylonian exercises.^[4] If some other method was used,^[5] the triples were first constructed and then reordered by ${\displaystyle c/a}$, presumably for actual use as a "table", i.e., with a view to applications.

It is not known what these applications may have been, or whether there could have been any; Babylonian astronomy, for example, truly came into its own only later. It has been suggested instead that the table was a source of numerical examples for school problems.^{[6][note 3]}

While Babylonian number theory—or what survives of Babylonian mathematics that can be called thus—consists of this single, striking fragment, Babylonian algebra (in the secondary-school sense of "algebra") was exceptionally well developed.^[7] Late Neoplatonic sources^[8] state that Pythagoras learned mathematics from the Babylonians. Much earlier sources^[9] state that Thales and Pythagoras traveled and studied in Egypt.

Euclid IX 21—34 is very probably Pythagorean;^[10] it is very simple material ("odd times even is even", "if an odd number measures [= divides] an even number, then it also measures [= divides] half of it"), but it is all that is needed to prove that ${\displaystyle {\sqrt {2}}}$ is irrational.^[11] Pythagorean mystics gave great importance to the odd and the even.^[12] The discovery that ${\displaystyle {\sqrt {2}}}$ is irrational is credited to the early Pythagoreans (pre-Theodorus).^[13] By revealing (in modern terms) that numbers could be irrational, this discovery seems to have provoked the first foundational crisis in mathematical history; its proof or its divulgation are sometimes credited to Hippasus, who was expelled or split from the Pythagorean sect.^[14] This forced a distinction between numbers (integers and the rationals—the subjects of arithmetic), on the one hand, and lengths and proportions (which we would identify with real numbers, whether rational or not), on the other hand.

The Pythagorean tradition spoke also of so-called polygonal or figurate numbers.^[15] While square numbers, cubic numbers, etc., are seen now as more natural than triangular numbers, pentagonal numbers, etc., the study of the sums of triangular and pentagonal numbers would prove fruitful in the early modern period (17th to early 19th century).

We know of no clearly arithmetical material in ancient Egyptian or Vedic sources, though there is some algebra in both. The Chinese remainder theorem appears as an exercise ^[16] in Sunzi Suanjing (3rd, 4th or 5th century CE.)^[17] (There is one important step glossed over in Sunzi's solution:^{[note 4]} it is the problem that was later solved by Āryabhaṭa's Kuṭṭaka – see below.)

There is also some numerical mysticism in Chinese mathematics,^{[note 5]} but, unlike that of the Pythagoreans, it seems to have led nowhere. Like the Pythagoreans' perfect numbers, magic squares have passed from superstition into recreation.

Classical Greece and the early Hellenistic period

Aside from a few fragments, the mathematics of Classical Greece is known to us either through the reports of contemporary non-mathematicians or through mathematical works from the early Hellenistic period.^[18] In the case of number theory, this means, by and large, Plato and Euclid, respectively.
While Asian mathematics influenced Greek and Hellenistic learning, it seems to be the case that Greek mathematics is also an indigenous tradition.

Eusebius, PE X, chapter 4 mentions of Pythagoras:

"In fact the said Pythagoras, while busily studying the wisdom of each nation, visited Babylon, and Egypt, and all Persia, being instructed by the Magi and the priests: and in addition to these he is related to have studied under the Brahmans (these are Indian philosophers); and from some he gathered astrology, from others geometry, and arithmetic and music from others, and different things from different nations, and only from the wise men of Greece did he get nothing, wedded as they were to a poverty and dearth of wisdom: so on the contrary he himself became the author of instruction to the Greeks in the learning which he had procured from abroad."^[19]

Aristotle claimed that the philosophy of Plato closely followed the teachings of the Pythagoreans,^[20] and Cicero repeats this claim: Platonem ferunt didicisse Pythagorea omnia ("They say Plato learned all things Pythagorean").^[21]

Plato had a keen interest in mathematics, and distinguished clearly between arithmetic and calculation. (By arithmetic he meant, in part, theorising on number, rather than what arithmetic or number theory have come to mean.) It is through one of Plato's dialogues—namely, Theaetetus—that we know that Theodorus had proven that ${\displaystyle {\sqrt {3}},{\sqrt {5}},\dots ,{\sqrt {17}}}$ are irrational. Theaetetus was, like Plato, a disciple of Theodorus's; he worked on distinguishing different kinds of incommensurables, and was thus arguably a pioneer in the study of number systems. (Book X of Euclid's Elements is described by Pappus as being largely based on Theaetetus's work.)

Euclid devoted part of his Elements to prime numbers and divisibility, topics that belong unambiguously to number theory and are basic to it (Books VII to IX of Euclid's Elements). In particular, he gave an algorithm for computing the greatest common divisor of two numbers (the Euclidean algorithm; Elements, Prop. VII.2) and the first known proof of the infinitude of primes (Elements, Prop. IX.20).

In 1773, Lessing published an epigram he had found in a manuscript during his work as a librarian; it claimed to be a letter sent by Archimedes to Eratosthenes.^[22][23] The epigram proposed what has become known as Archimedes's cattle problem; its solution (absent from the manuscript) requires solving an indeterminate quadratic equation (which reduces to what would later be misnamed Pell's equation). As far as we know, such equations were first successfully treated by the Indian school. It is not known whether Archimedes himself had a method of solution.

Diophantus

Title page of the 1621 edition of Diophantus's Arithmetica, translated into Latin by Claude Gaspard Bachet de Méziriac.

Very little is known about Diophantus of Alexandria; he probably lived in the third century CE, that is, about five hundred years after Euclid. Six out of the thirteen books of Diophantus's Arithmetica survive in the original Greek; four more books survive in an Arabic translation. The Arithmetica is a collection of worked-out problems where the task is invariably to find rational solutions to a system of polynomial equations, usually of the form ${\displaystyle f(x,y)=z^{2}}$ or ${\displaystyle f(x,y,z)=w^{2}}$. Thus, nowadays, we speak of Diophantine equations when we speak of polynomial equations to which rational or integer solutions must be found.

One may say that Diophantus was studying rational points — i.e., points whose coordinates are rational — on curves and algebraic varieties; however, unlike the Greeks of the Classical period, who did what we would now call basic algebra in geometrical terms, Diophantus did what we would now call basic algebraic geometry in purely algebraic terms. In modern language, what Diophantus did was to find rational parametrizations of varieties; that is, given an equation of the form (say) ${\displaystyle f(x_{1},x_{2},x_{3})=0}$, his aim was to find (in essence) three rational functions ${\displaystyle g_{1},g_{2},g_{3}}$ such that, for all values of ${\displaystyle r}$ and ${\displaystyle s}$, setting ${\displaystyle x_{i}=g_{i}(r,s)}$ for ${\displaystyle i=1,2,3}$ gives a solution to ${\displaystyle f(x_{1},x_{2},x_{3})=0.}$

Diophantus also studied the equations of some non-rational curves, for which no rational parametrisation is possible. He managed to find some rational points on these curves (elliptic curves, as it happens, in what seems to be their first known occurrence) by means of what amounts to a tangent construction: translated into coordinate geometry (which did not exist in Diophantus's time), his method would be visualised as drawing a tangent to a curve at a known rational point, and then finding the other point of intersection of the tangent with the curve; that other point is a new rational point. (Diophantus also resorted to what could be called a special case of a secant construction.)

While Diophantus was concerned largely with rational solutions, he assumed some results on integer numbers, in particular that every integer is the sum of four squares (though he never stated as much explicitly).

Āryabhaṭa, Brahmagupta, Bhāskara

While Greek astronomy probably influenced Indian learning, to the point of introducing trigonometry,^[24] it seems to be the case that Indian mathematics is otherwise an indigenous tradition;^[25] in particular, there is no evidence that Euclid's Elements reached India before the 18th century.^[26]

Āryabhaṭa (476–550 CE) showed that pairs of simultaneous congruences ${\displaystyle n\equiv a_{1}{\bmod {m}}_{1}}$, ${\displaystyle n\equiv a_{2}{\bmod {m}}_{2}}$ could be solved by a method he called kuṭṭaka, or pulveriser;^[27] this is a procedure close to (a generalisation of) the Euclidean algorithm, which was probably discovered independently in India.^[28] Āryabhaṭa seems to have had in mind applications to astronomical calculations.^[24]

Brahmagupta (628 CE) started the systematic study of indefinite quadratic equations—in particular, the misnamed Pell equation, in which Archimedes may have first been interested, and which did not start to be solved in the West until the time of Fermat and Euler. Later Sanskrit authors would follow, using Brahmagupta's technical terminology. A general procedure (the chakravala, or "cyclic method") for solving Pell's equation was finally found by Jayadeva (cited in the eleventh century; his work is otherwise lost); the earliest surviving exposition appears in Bhāskara II's Bīja-gaṇita (twelfth century).^[29]

Indian mathematics remained largely unknown in Europe until the late eighteenth century;^[30] Brahmagupta and Bhāskara's work was translated into English in 1817 by Henry Colebrooke.^[31]

Arithmetic in the Islamic golden age

Al-Haytham seen by the West: frontispice of Selenographia, showing Alhasen [sic] representing knowledge through reason, and Galileo representing knowledge through the senses.

In the early ninth century, the caliph Al-Ma'mun ordered translations of many Greek mathematical works and at least one Sanskrit work (the Sindhind, which may ^[32] or may not^[33] be Brahmagupta's Brāhmasphuṭasiddhānta). Diophantus's main work, the Arithmetica, was translated into Arabic by Qusta ibn Luqa (820–912). Part of the treatise al-Fakhri (by al-Karajī, 953 – ca. 1029) builds on it to some extent. According to Rashed Roshdi, Al-Karajī's contemporary Ibn al-Haytham knew^[34] what would later be called Wilson's theorem.

Western Europe in the Middle Ages

Other than a treatise on squares in arithmetic progression by Fibonacci — who lived and studied in north Africa and Constantinople during his formative years, ca. 1175–1200 — no number theory to speak of was done in western Europe during the Middle Ages. Matters started to change in Europe in the late Renaissance, thanks to a renewed study of the works of Greek antiquity. A catalyst was the textual emendation and translation into Latin of Diophantus's Arithmetica (Bachet, 1621, following a first attempt by Xylander, 1575).

Early modern number theory

Fermat

Pierre de Fermat

Pierre de Fermat (1601–1665) never published his writings; in particular, his work on number theory is contained almost entirely in letters to mathematicians and in private marginal notes.^[35] He wrote down nearly no proofs in number theory; he had no models in the area.^[36] He did make repeated use of mathematical induction, introducing the method of infinite descent.

One of Fermat's first interests was perfect numbers (which appear in Euclid, Elements IX) and amicable numbers;^{[note 6]} this led him to work on integer divisors, which were from the beginning among the subjects of the correspondence (1636 onwards) that put him in touch with the mathematical community of the day.^[37] He had already studied Bachet's edition of Diophantus carefully;^[38] by 1643, his interests had shifted largely to Diophantine problems and sums of squares^[39] (also treated by Diophantus).

Fermat's achievements in arithmetic include:

• Fermat's little theorem (1640),^[40] stating that, if a is not divisible by a prime p, then ${\displaystyle a^{p-1}\equiv 1{\bmod {p}}.}$^{[note 7]}
• If a and b are coprime, then ${\displaystyle a^{2}+b^{2}}$ is not divisible by any prime congruent to −1 modulo 4;^[41] and every prime congruent to 1 modulo 4 can be written in the form ${\displaystyle a^{2}+b^{2}}$.^[42] These two statements also date from 1640; in 1659, Fermat stated to Huygens that he had proven the latter statement by the method of infinite descent.^[43] Fermat and Frenicle also did some work (some of it erroneous)^[44] on other quadratic forms.
• Fermat posed the problem of solving ${\displaystyle x^{2}-Ny^{2}=1}$ as a challenge to English mathematicians (1657). The problem was solved in a few months by Wallis and Brouncker.^[45] Fermat considered their solution valid, but pointed out they had provided an algorithm without a proof (as had Jayadeva and Bhaskara, though Fermat would never know this). He states that a proof can be found by descent.
• Fermat developed methods for (doing what in our terms amounts to) finding points on curves of genus 0 and 1. As in Diophantus, there are many special procedures and what amounts to a tangent construction, but no use of a secant construction.^[46]
• Fermat states and proves (by descent) in the appendix to Observations on Diophantus (Obs. XLV)^[47] that ${\displaystyle x^{4}+y^{4}=z^{4}}$ has no non-trivial solutions in the integers. Fermat also mentioned to his correspondents that ${\displaystyle x^{3}+y^{3}=z^{3}}$ has no non-trivial solutions, and that this could be proven by descent.^[48] The first known proof is due to Euler (1753; indeed by descent).^[49]

Fermat's claim ("Fermat's last theorem") to have shown there are no solutions to ${\displaystyle x^{n}+y^{n}=z^{n}}$ for all ${\displaystyle n\geq 3}$ appears only in his annotations on the margin of his copy of Diophantus.

Euler

Leonhard Euler

The interest of Leonhard Euler (1707–1783) in number theory was first spurred in 1729, when a friend of his, the amateur^{[note 8]} Goldbach, pointed him towards some of Fermat's work on the subject.^[50][51] This has been called the "rebirth" of modern number theory,^[38] after Fermat's relative lack of success in getting his contemporaries' attention for the subject.^[52] Euler's work on number theory includes the following:^[53]

• Proofs for Fermat's statements. This includes Fermat's little theorem (generalised by Euler to non-prime moduli); the fact that ${\displaystyle p=x^{2}+y^{2}}$ if and only if ${\displaystyle p\equiv 1{\bmod {4}}}$; initial work towards a proof that every integer is the sum of four squares (the first complete proof is by Joseph-Louis Lagrange (1770), soon improved by Euler himself^[54]); the lack of non-zero integer solutions to ${\displaystyle x^{4}+y^{4}=z^{2}}$ (implying the case n=4 of Fermat's last theorem, the case n=3 of which Euler also proved by a related method).
• Pell's equation, first misnamed by Euler.^[55] He wrote on the link between continued fractions and Pell's equation.^[56]
• First steps towards analytic number theory. In his work of sums of four squares, partitions, pentagonal numbers, and the distribution of prime numbers, Euler pioneered the use of what can be seen as analysis (in particular, infinite series) in number theory. Since he lived before the development of complex analysis, most of his work is restricted to the formal manipulation of power series. He did, however, do some very notable (though not fully rigorous) early work on what would later be called the Riemann zeta function.^[57]
• Quadratic forms. Following Fermat's lead, Euler did further research on the question of which primes can be expressed in the form ${\displaystyle x^{2}+Ny^{2}}$, some of it prefiguring quadratic reciprocity.^{[58] [59][60]}
• Diophantine equations. Euler worked on some Diophantine equations of genus 0 and 1.^[61][62] In particular, he studied Diophantus's work; he tried to systematise it, but the time was not yet ripe for such an endeavour – algebraic geometry was still in its infancy.^[63] He did notice there was a connection between Diophantine problems and elliptic integrals,^[63] whose study he had himself initiated.

Lagrange, Legendre, and Gauss

Carl Friedrich Gauss's Disquisitiones Arithmeticae, first edition

Joseph-Louis Lagrange (1736–1813) was the first to give full proofs of some of Fermat's and Euler's work and observations – for instance, the four-square theorem and the basic theory of the misnamed "Pell's equation" (for which an algorithmic solution was found by Fermat and his contemporaries, and also by Jayadeva and Bhaskara II before them.) He also studied quadratic forms in full generality (as opposed to ${\displaystyle mX^{2}+nY^{2}}$) — defining their equivalence relation, showing how to put them in reduced form, etc.

Adrien-Marie Legendre (1752–1833) was the first to state the law of quadratic reciprocity. He also conjectured what amounts to the prime number theorem and Dirichlet's theorem on arithmetic progressions. He gave a full treatment of the equation ${\displaystyle ax^{2}+by^{2}+cz^{2}=0}$^[64] and worked on quadratic forms along the lines later developed fully by Gauss.^[65] In his old age, he was the first to prove "Fermat's last theorem" for ${\displaystyle n=5}$ (completing work by Peter Gustav Lejeune Dirichlet, and crediting both him and Sophie Germain).^[66]

Carl Friedrich Gauss

In his Disquisitiones Arithmeticae (1798), Carl Friedrich Gauss (1777–1855) proved the law of quadratic reciprocity and developed the theory of quadratic forms (in particular, defining their composition). He also introduced some basic notation (congruences) and devoted a section to computational matters, including primality tests.^[67] The last section of the Disquisitiones established a link between roots of unity and number theory:

The theory of the division of the circle...which is treated in sec. 7 does not belong by itself to arithmetic, but its principles can only be drawn from higher arithmetic.^[68]

In this way, Gauss arguably made a first foray towards both Évariste Galois's work and algebraic number theory.

Maturity and division into subfields

Ernst Kummer

Peter Gustav Lejeune 

Dirichlet

Starting early in the nineteenth century, the following developments gradually took place:

• The rise to self-consciousness of number theory (or higher arithmetic) as a field of study.^[69]
• The development of much of modern mathematics necessary for basic modern number theory: complex analysis, group theory, Galois theory—accompanied by greater rigor in analysis and abstraction in algebra.
• The rough subdivision of number theory into its modern subfields—in particular, analytic and algebraic number theory.

Algebraic number theory may be said to start with the study of reciprocity and cyclotomy, but truly came into its own with the development of abstract algebra and early ideal theory and valuation theory; see below. A conventional starting point for analytic number theory is Dirichlet's theorem on arithmetic progressions (1837),^{[70] [71]} whose proof introduced L-functions and involved some asymptotic analysis and a limiting process on a real variable.^[72] The first use of analytic ideas in number theory actually goes back to Euler (1730s),^{[73] [74]} who used formal power series and non-rigorous (or implicit) limiting arguments. The use of complex analysis in number theory comes later: the work of Bernhard Riemann (1859) on the zeta function is the canonical starting point;^[75] Jacobi's four-square theorem (1839), which predates it, belongs to an initially different strand that has by now taken a leading role in analytic number theory (modular forms).^[76]

The history of each subfield is briefly addressed in its own section below; see the main article of each subfield for fuller treatments. Many of the most interesting questions in each area remain open and are being actively worked on.

Main subdivisions

Elementary tools

The term elementary generally denotes a method that does not use complex analysis. For example, the prime number theorem was first proven using complex analysis in 1896, but an elementary proof was found only in 1949 by Erdős and Selberg.^[77] The term is somewhat ambiguous: for example, proofs based on complex Tauberian theorems (e.g. Wiener–Ikehara) are often seen as quite enlightening but not elementary, in spite of using Fourier analysis, rather than complex analysis as such. Here as elsewhere, an elementary proof may be longer and more difficult for most readers than a non-elementary one.

Number theory has the reputation of being a field many of whose results can be stated to the layperson. At the same time, the proofs of these results are not particularly accessible, in part because the range of tools they use is, if anything, unusually broad within mathematics.^[78]

Analytic number theory

Riemann zeta function ζ(s) in the complex plane. The color of a point s gives the value of ζ(s): dark colors denote values close to zero and hue gives the value's argument.

The action of the modular group on the upper half plane. The region in grey is the standard fundamental domain.

Analytic number theory may be defined

• in terms of its tools, as the study of the integers by means of tools from real and complex analysis;^[70] or
• in terms of its concerns, as the study within number theory of estimates on size and density, as opposed to identities.^[79]

Some subjects generally considered to be part of analytic number theory, e.g., sieve theory,^{[note 9]} are better covered by the second rather than the first definition: some of sieve theory, for instance, uses little analysis,^{[note 10]} yet it does belong to analytic number theory.

The following are examples of problems in analytic number theory: the prime number theorem, the Goldbach conjecture (or the twin prime conjecture, or the Hardy–Littlewood conjectures), the Waring problem and the Riemann hypothesis. Some of the most important tools of analytic number theory are the circle method, sieve methods and L-functions (or, rather, the study of their properties). The theory of modular forms (and, more generally, automorphic forms) also occupies an increasingly central place in the toolbox of analytic number theory.^[80]

One may ask analytic questions about algebraic numbers, and use analytic means to answer such questions; it is thus that algebraic and analytic number theory intersect. For example, one may define prime ideals (generalizations of prime numbers in the field of algebraic numbers) and ask how many prime ideals there are up to a certain size. This question can be answered by means of an examination of Dedekind zeta functions, which are generalizations of the Riemann zeta function, a key analytic object at the roots of the subject.^[81] This is an example of a general procedure in analytic number theory: deriving information about the distribution of a sequence (here, prime ideals or prime numbers) from the analytic behavior of an appropriately constructed complex-valued function.^[82]

Algebraic number theory

An algebraic number is any complex number that is a solution to some polynomial equation ${\displaystyle f(x)=0}$ with rational coefficients; for example, every solution ${\displaystyle x}$ of ${\displaystyle x^{5}+(11/2)x^{3}-7x^{2}+9=0}$ (say) is an algebraic number. Fields of algebraic numbers are also called algebraic number fields, or shortly number fields. Algebraic number theory studies algebraic number fields.^[83] Thus, analytic and algebraic number theory can and do overlap: the former is defined by its methods, the latter by its objects of study.
It could be argued that the simplest kind of number fields (viz., quadratic fields) were already studied by Gauss, as the discussion of quadratic forms in Disquisitiones arithmeticae can be restated in terms of ideals and norms in quadratic fields. (A quadratic field consists of all numbers of the form ${\displaystyle a+b{\sqrt {d}}}$, where ${\displaystyle a}$ and ${\displaystyle b}$ are rational numbers and ${\displaystyle d}$ is a fixed rational number whose square root is not rational.) For that matter, the 11th-century chakravala method amounts—in modern terms—to an algorithm for finding the units of a real quadratic number field. However, neither Bhāskara nor Gauss knew of number fields as such.

The grounds of the subject as we know it were set in the late nineteenth century, when ideal numbers, the theory of ideals and valuation theory were developed; these are three complementary ways of dealing with the lack of unique factorisation in algebraic number fields. (For example, in the field generated by the rationals and ${\displaystyle {\sqrt {-5}}}$, the number ${\displaystyle 6}$ can be factorised both as ${\displaystyle 6=2\cdot 3}$ and ${\displaystyle 6=(1+{\sqrt {-5}})(1-{\sqrt {-5}})}$; all of ${\displaystyle 2}$, ${\displaystyle 3}$, ${\displaystyle 1+{\sqrt {-5}}}$ and ${\displaystyle 1-{\sqrt {-5}}}$ are irreducible, and thus, in a naïve sense, analogous to primes among the integers.) The initial impetus for the development of ideal numbers (by Kummer) seems to have come from the study of higher reciprocity laws,^[84]i.e., generalisations of quadratic reciprocity.

Number fields are often studied as extensions of smaller number fields: a field L is said to be an extension of a field K if L contains K. (For example, the complex numbers C are an extension of the reals R, and the reals R are an extension of the rationals Q.) Classifying the possible extensions of a given number field is a difficult and partially open problem. Abelian extensions—that is, extensions L of K such that the Galois group^{[note 11]} Gal(L/K) of L over K is an abelian group—are relatively well understood. Their classification was the object of the programme of class field theory, which was initiated in the late 19th century (partly by Kronecker and Eisenstein) and carried out largely in 1900—1950.

An example of an active area of research in algebraic number theory is Iwasawa theory. The Langlands program, one of the main current large-scale research plans in mathematics, is sometimes described as an attempt to generalise class field theory to non-abelian extensions of number fields.

Diophantine geometry

The central problem of Diophantine geometry is to determine when a Diophantine equation has solutions, and if it does, how many. The approach taken is to think of the solutions of an equation as a geometric object.

For example, an equation in two variables defines a curve in the plane. More generally, an equation, or system of equations, in two or more variables defines a curve, a surface or some other such object in n-dimensional space. In Diophantine geometry, one asks whether there are any rational points (points all of whose coordinates are rationals) or integral points (points all of whose coordinates are integers) on the curve or surface. If there are any such points, the next step is to ask how many there are and how they are distributed. A basic question in this direction is: are there finitely or infinitely many rational points on a given curve (or surface)? What about integer points?

An example here may be helpful. Consider the Pythagorean equation ${\displaystyle x^{2}+y^{2}=1}$; we would like to study its rational solutions, i.e., its solutions ${\displaystyle (x,y)}$ such that x and y are both rational. This is the same as asking for all integer solutions to ${\displaystyle a^{2}+b^{2}=c^{2}}$; any solution to the latter equation gives us a solution ${\displaystyle x=a/c}$, ${\displaystyle y=b/c}$ to the former. It is also the same as asking for all points with rational coordinates on the curve described by ${\displaystyle x^{2}+y^{2}=1}$. (This curve happens to be a circle of radius 1 around the origin.)

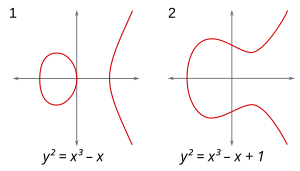
Two examples of an elliptic curve, i.e., a curve of genus 1 having at least one rational point. (Either graph can be seen as a slice of a torus in four-dimensional space.)

The rephrasing of questions on equations in terms of points on curves turns out to be felicitous. The finiteness or not of the number of rational or integer points on an algebraic curve—that is, rational or integer solutions to an equation ${\displaystyle f(x,y)=0}$, where ${\displaystyle f}$ is a polynomial in two variables—turns out to depend crucially on the genus of the curve. The genus can be defined as follows:^{[note 12]} allow the variables in ${\displaystyle f(x,y)=0}$ to be complex numbers; then ${\displaystyle f(x,y)=0}$ defines a 2-dimensional surface in (projective) 4-dimensional space (since two complex variables can be decomposed into four real variables, i.e., four dimensions). Count the number of (doughnut) holes in the surface; call this number the genus of ${\displaystyle f(x,y)=0}$. Other geometrical notions turn out to be just as crucial.

There is also the closely linked area of Diophantine approximations: given a number ${\displaystyle x}$, how well can it be approximated by rationals? (We are looking for approximations that are good relative to the amount of space that it takes to write the rational: call ${\displaystyle a/q}$ (with ${\displaystyle \gcd(a,q)=1}$) a good approximation to ${\displaystyle x}$ if ${\displaystyle |x-a/q|<{\frac {1}{q^{c}}}}$, where ${\displaystyle c}$ is large.) This question is of special interest if ${\displaystyle x}$ is an algebraic number. If ${\displaystyle x}$ cannot be well approximated, then some equations do not have integer or rational solutions. Moreover, several concepts (especially that of height) turn out to be crucial both in Diophantine geometry and in the study of Diophantine approximations. This question is also of special interest in transcendental number theory: if a number can be better approximated than any algebraic number, then it is a transcendental number. It is by this argument that π and e have been shown to be transcendental.

Diophantine geometry should not be confused with the geometry of numbers, which is a collection of graphical methods for answering certain questions in algebraic number theory. Arithmetic geometry, on the other hand, is a contemporary term for much the same domain as that covered by the term Diophantine geometry. The term arithmetic geometry is arguably used most often when one wishes to emphasise the connections to modern algebraic geometry (as in, for instance, Faltings's theorem) rather than to techniques in Diophantine approximations.

Recent approaches and subfields

The areas below date as such from no earlier than the mid-twentieth century, even if they are based on older material. For example, as is explained below, the matter of algorithms in number theory is very old, in some sense older than the concept of proof; at the same time, the modern study of computability dates only from the 1930s and 1940s, and computational complexity theory from the 1970s.

Probabilistic number theory

Take a number at random between one and a million. How likely is it to be prime? This is just another way of asking how many primes there are between one and a million. Further: how many prime divisors will it have, on average? How many divisors will it have altogether, and with what likelihood? What is the probability that it will have many more or many fewer divisors or prime divisors than the average?

Much of probabilistic number theory can be seen as an important special case of the study of variables that are almost, but not quite, mutually independent. For example, the event that a random integer between one and a million be divisible by two and the event that it be divisible by three are almost independent, but not quite.

It is sometimes said that probabilistic combinatorics uses the fact that whatever happens with probability greater than ${\displaystyle 0}$ must happen sometimes; one may say with equal justice that many applications of probabilistic number theory hinge on the fact that whatever is unusual must be rare. If certain algebraic objects (say, rational or integer solutions to certain equations) can be shown to be in the tail of certain sensibly defined distributions, it follows that there must be few of them; this is a very concrete non-probabilistic statement following from a probabilistic one.

At times, a non-rigorous, probabilistic approach leads to a number of heuristic algorithms and open problems, notably Cramér's conjecture.

Arithmetic combinatorics

Let A be a set of N integers. Consider the set A + A = { m + n | m, n ∈ A } consisting of all sums of two elements of A. Is A + A much larger than A? Barely larger? If A + A is barely larger than A, must A have plenty of arithmetic structure, for example, does A resemble an arithmetic progression?
If we begin from a fairly "thick" infinite set ${\displaystyle A}$, does it contain many elements in arithmetic progression: ${\displaystyle a}$, ${\displaystyle a+b,a+2b,a+3b,\ldots ,a+10b}$, say? Should it be possible to write large integers as sums of elements of ${\displaystyle A}$?

These questions are characteristic of arithmetic combinatorics. This is a presently coalescing field; it subsumes additive number theory (which concerns itself with certain very specific sets ${\displaystyle A}$ of arithmetic significance, such as the primes or the squares) and, arguably, some of the geometry of numbers, together with some rapidly developing new material. Its focus on issues of growth and distribution accounts in part for its developing links with ergodic theory, finite group theory, model theory, and other fields. The term additive combinatorics is also used; however, the sets ${\displaystyle A}$ being studied need not be sets of integers, but rather subsets of non-commutative groups, for which the multiplication symbol, not the addition symbol, is traditionally used; they can also be subsets of rings, in which case the growth of ${\displaystyle A+A}$ and ${\displaystyle A}$·${\displaystyle A}$ may be compared.

Computations in number theory

While the word algorithm goes back only to certain readers of al-Khwārizmī, careful descriptions of methods of solution are older than proofs: such methods (that is, algorithms) are as old as any recognisable mathematics—ancient Egyptian, Babylonian, Vedic, Chinese—whereas proofs appeared only with the Greeks of the classical period. An interesting early case is that of what we now call the Euclidean algorithm. In its basic form (namely, as an algorithm for computing the greatest common divisor) it appears as Proposition 2 of Book VII in Elements, together with a proof of correctness. However, in the form that is often used in number theory (namely, as an algorithm for finding integer solutions to an equation ${\displaystyle ax+by=c}$, or, what is the same, for finding the quantities whose existence is assured by the Chinese remainder theorem) it first appears in the works of Āryabhaṭa (5th–6th century CE) as an algorithm called kuṭṭaka ("pulveriser"), without a proof of correctness.

There are two main questions: "can we compute this?" and "can we compute it rapidly?". Anyone can test whether a number is prime or, if it is not, split it into prime factors; doing so rapidly is another matter. We now know fast algorithms for testing primality, but, in spite of much work (both theoretical and practical), no truly fast algorithm for factoring.

The difficulty of a computation can be useful: modern protocols for encrypting messages (e.g., RSA) depend on functions that are known to all, but whose inverses (a) are known only to a chosen few, and (b) would take one too long a time to figure out on one's own. For example, these functions can be such that their inverses can be computed only if certain large integers are factorized. While many difficult computational problems outside number theory are known, most working encryption protocols nowadays are based on the difficulty of a few number-theoretical problems.

On a different note — some things may not be computable at all; in fact, this can be proven in some instances. For instance, in 1970, it was proven, as a solution to Hilbert's 10th problem, that there is no Turing machine which can solve all Diophantine equations.^[85] In particular, this means that, given a computably enumerable set of axioms, there are Diophantine equations for which there is no proof, starting from the axioms, of whether the set of equations has or does not have integer solutions. (We would necessarily be speaking of Diophantine equations for which there are no integer solutions, since, given a Diophantine equation with at least one solution, the solution itself provides a proof of the fact that a solution exists. We cannot prove, of course, that a particular Diophantine equation is of this kind, since this would imply that it has no solutions.)

Applications

The number-theorist Leonard Dickson (1874–1954) said "Thank God that number theory is unsullied by any application". Such a view is no longer applicable to number theory.^[86] In 1974, Donald Knuth said "...virtually every theorem in elementary number theory arises in a natural, motivated way in connection with the problem of making computers do high-speed numerical calculations".^[87] Elementary number theory is taught in discrete mathematics courses for computer scientists; on the other hand, number theory also has applications to the continuous in numerical analysis.^[88] As well as the well-known applications to cryptography, there are also applications to many other areas of mathematics.^{[89][90][specify]}

History of the Hindu–Arabic numeral system

From Wikipedia, the free encyclopedia

The Hindu–Arabic numeral system is a decimal place-value numeral system that uses a zero glyph as in "205".^[1]

Its glyphs are descended from the Indian Brahmi numerals. The full system emerged by the 8th to 9th centuries, and is first described in Al-Khwarizmi's On the Calculation with Hindu Numerals (ca. 825), and Al-Kindi's four-volume work On the Use of the Indian Numerals (ca. 830).^[2] Today the name Hindu–Arabic numerals is usually used.

Decimal system

Historians trace modern numerals in most languages to the Brahmi numerals, which were in use around the middle of the 3rd century BC.^[3] The place value system, however, developed later. The Brahmi numerals have been found in inscriptions in caves and on coins in regions near Pune^[2], and Uttar Pradesh. These numerals (with slight variations) were in use up to the 4th century.^[3]

During the Gupta period (early 4th century to the late 6th century), the Gupta numerals developed from the Brahmi numerals and were spread over large areas by the Gupta empire as they conquered territory.^[3] Beginning around 7th century, the Gupta numerals developed into the Nagari numerals.

Development in India

During the Vedic period (1500–500 BCE), motivated by geometric construction of the fire altars and astronomy, the use of a numerical system and of basic mathematical operations developed in northern India.^[4][5] Hindu cosmology required the mastery of very large numbers such as the kalpa (the lifetime of the universe) said to be 4,320,000,000 years and the "orbit of the heaven" said to be 18,712,069,200,000,000 yojanas.^[6] Numbers were expressed using a "named place-value notation", using names for the powers of 10, like dasa, shatha, sahasra, ayuta, niyuta, prayuta, arbuda, nyarbuda, samudra, madhya, anta, parardha etc., the last of these being the name for a trillion (10¹²).^[7] For example, the number 26,432 was expressed as "2 ayuta, 6 sahasra, 4 shatha, 3 dasa, 2."^[8] In the Buddhist text Lalitavistara, the Buddha is said to have narrated a scheme of numbers up to 10⁵³.^[9][10]

The form of numerals in Ashoka's inscriptions in the Brahmi script (middle of the third century BCE) involved separate signs for the numbers 1 to 9, 10 to 90, 100 and 1000. A multiple of 100 or 1000 was represented by a modification (or "enciphering"^[11]) of the sign for the number using the sign for the multiplier number.^[12] Such enciphered numerals directly represented the named place-value numerals used verbally. They continued to be used in inscriptions until the end of the 9th century.

In his seminal text of 499 CE, Aryabhata devised a novel positional number system, using Sanskrit consonants for small numbers and vowels for powers of 10. Using the system, numbers up to a billion could be expressed using short phrases, e. g., khyu-ghṛ representing the number 4,320,000. The system did not catch on because it produced quite unpronounceable phrases, but it might have driven home the principle of positional number system (called dasa-gunottara, exponents of 10) to later mathematicians.^[13] A more elegant katapayadi scheme was devised in later centuries representing a place-value system including zero.^[14]

Place-value numerals without zero

While the numerals in texts and inscriptions used a named place-value notation, a more efficient notation might have been employed in calculations, possibly from the 1st century CE. Computations were carried out on clay tablets covered with a thin layer of sand, giving rise to the term dhuli-karana ("sand-work") for higher computation. Karl Menninger believes that, in such computations, they must have dispensed with the enciphered numerals and written down just sequences of digits to represent the numbers. A zero would have been represented as a "missing place," such as a dot.^[15] The single manuscript with worked examples available to us, the Bakhshali manuscript (of unclear date), uses a place value system with a dot to denote the zero. The dot was called the shunya-sthāna, "empty-place." The same symbol was also used in algebraic expressions for the unknown (as in the canonical x in modern algebra).^[16]

Textual references to a place-value system are seen from the 1st century CE onward. The Buddhist philosopher Vasubandhu in the 1st century says "when [the same] clay counting-piece is in the place of units, it is denoted as one, when in hundreds, one hundred." A commentary on Patanjali's Yoga Sutras from the 5th century reads, "Just as a line in the hundreds place [means] a hundred, in the tens place ten, and one in the ones place, so one and the same woman is called mother, daughter and sister."^[17]

A system called bhūta-sankhya ("object numbers" or "concrete numbers") was employed for representing numerals in Sanskrit verses, by using a concept representing a digit to stand for the digit itself. The Jain text entitled the Lokavibhaga, dated 458 CE,^[18] mentions the objectified numeral

"panchabhyah khalu shunyebhyah param dve sapta chambaram ekam trini cha rupam cha"

meaning, "five voids, then two and seven, the sky, one and three and the form", i.e., the number 13107200000.^[19][20] Such objectified numbers were used extensively from the 6th century onward, especially after Varahamihira (c. 575 CE). Zero is explicitly represented in such numbers as "the void" (sunya) or the "heaven-space" (ambara akasha).^[21] Correspondingly, the dot used in place of zero in written numerals was referred to as a sunya-bindu.^[22]

Place-value numerals with zero

In 628 CE, astronomer-mathematician Brahmagupta wrote his text Brahma Sphuta Siddhanta which contained the first mathematical treatment of zero. He defined zero as the result of subtracting a number from itself, postulated negative numbers and discussed their properties under arithmetical operations. His word for zero was shunya (void), the same term previously used for the empty spot in 9-digit place-value system.^[23] This provided a new perspective on the shunya-bindu as a numeral and paved the way for the eventual evolution of a zero digit. The dot continued to be used for at least 100 years afterwards, and transmitted to Southeast Asia and Arabia. Kashmir's Sharada script has retained the dot for zero until this day.

By the end of the 7th century, decimal numbers begin to appear in inscriptions in Southeast Asia as well as in India.^[22] Some scholars hold that they appeared even earlier. A 6th century copper-plate grant at Mankani bearing the numeral 346 (corresponding to 594 CE) is often cited.^[24] But its reliability is subject to dispute.^[22][25] The first indisputable occurrence of 0 in an inscription occurs at Gwalior in 876 CE, containing a numeral "270" in a notation surprisingly similar to ours.^[26] Throughout the 8th and 9th centuries, both the old Brahmi numerals and the new decimal numerals were used, sometimes appearing in the same inscriptions. In some documents, a transition is seen to occur around 866 CE.^[22]

Adoption by the Arabs

Before the rise of the Caliphate, the Hindu–Arabic numeral system was already moving West and was mentioned in Syria in 662 AD by the Nestorian scholar Severus Sebokht who wrote the following:

"I will omit all discussion of the science of the Indians, ..., of their subtle discoveries in astronomy, discoveries that are more ingenious than those of the Greeks and the Babylonians, and of their valuable methods of calculation which surpass description. I wish only to say that this computation is done by means of nine signs. If those who believe, because they speak Greek, that they have arrived at the limits of science, would read the Indian texts, they would be convinced, even if a little late in the day, that there are others who know something of value."[1]

According to al-Qifti's chronology of the scholars [2]:

"... a person from India presented himself before the Caliph al-Mansur in the year [776 AD] who was well versed in the siddhanta method of calculation related to the movement of the heavenly bodies, and having ways of calculating equations based on the half-chord [essentially the sine] calculated in half-degrees ... This is all contained in a work ... from which he claimed to have taken the half-chord calculated for one minute. Al-Mansur ordered this book to be translated into Arabic, and a work to be written, based on the translation, to give the Arabs a solid base for calculating the movements of the planets ..."

The work was most likely to have been Brahmagupta's Brahma Sphuta Siddhanta (Ifrah) [3] (The Opening of the Universe) which was written in 628 [4]. Irrespective of whether Ifrah is right, since all Indian texts after Aryabhata's Aryabhatiya used the Indian number system, certainly from this time the Arabs had a translation of a text written in the Indian number system. [5]

In his text The Arithmetic of Al-Uqlîdisî (Dordrecht: D. Reidel, 1978), A.S. Saidan's studies were unable to answer in full how the numerals reached the Arab world:

"It seems plausible that it drifted gradually, probably before the 7th century, through two channels, one starting from Sind, undergoing Persian filtration and spreading in what is now known as the Middle East, and the other starting from the coasts of the Indian Ocean and extending to the southern coasts of the Mediterranean."[6]

Al-Uqlidisi developed a notation to represent decimal fractions.^[27][28] The numerals came to fame due to their use in the pivotal work of the Persian mathematician Al-Khwarizmi, whose book On the Calculation with Hindu Numerals was written about 825, and the Arab mathematician Al-Kindi, who wrote four volumes (see [2]) "On the Use of the Indian Numerals" (Ketab fi Isti'mal al-'Adad al-Hindi) about 830. They, amongst other works, contributed to the diffusion of the Indian system of numeration in the Middle-East and the West.

Adoption in Europe

The first Arabic numerals in Europe appeared in the Codex Vigilanus in the year 976.

Medieval Arabic Numbers at World map from Ptolemy, Cosmographia. Ulm: Lienhart Holle, 1482

Libro Intitulado Arithmetica Practica, 1549

• 976. The first Arabic numerals in Europe appeared in the Codex Vigilanus in the year 976.
• 1202. Fibonacci, an Italian mathematician who had studied in Béjaïa (Bougie), Algeria, promoted the Arabic numeral system in Europe with his book Liber Abaci, which was published in 1202.
• 1482. The system did not come into wide use in Europe, however, until the invention of printing. (See, for example, the 1482 Ptolemaeus map of the world printed by Lienhart Holle in Ulm, and other examples in the Gutenberg Museum in Mainz, Germany.)
• 1549. These are correct format and sequence of the "modern numbers" in titlepage of the Libro Intitulado Arithmetica Practica by Juan de Yciar, the Basque calligrapher and mathematician, Zaragoza 1549.

In the last few centuries, the European variety of Arabic numbers was spread around the world and gradually became the most commonly used numeral system in the world.

Even in many countries in languages which have their own numeral systems, the European Arabic numerals are widely used in commerce and mathematics.

Impact on arithmetic

The significance of the development of the positional number system is described by the French mathematician Pierre Simon Laplace (1749–1827) who wrote:

"It is India that gave us the ingenuous method of expressing all numbers by the means of ten symbols, each symbol receiving a value of position, as well as an absolute value; a profound and important idea which appears so simple to us now that we ignore its true merit, but its very simplicity, the great ease which it has lent to all computations, puts our arithmetic in the first rank of useful inventions, and we shall appreciate the grandeur of this achievement when we remember that it escaped the genius of Archimedes and Apollonius, two of the greatest minds produced by antiquity."

0 (Zero)

From Wikipedia, the free encyclopedia

0 (zero) is both a number^[1] and the numerical digit used to represent that number in numerals. The number 0 fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems.  Names for the number 0 in English include zero, nought (UK), naught (US) (/nɔːt/), nil, or—in contexts where at least one adjacent digit distinguishes it from the letter "O"—oh or o (/oʊ/). Informal or slang terms for zero include zilch and zip.^[2] Ought and aught (/ɔːt/),^[3] as well as cipher,^[4] have also been used historically.^[5]

Etymology

The word zero came into the English language via French zéro from Italian zero, Italian contraction of Venetian zevero form of 'Italian zefiro via ṣafira or ṣifr.^[6] In pre-Islamic time the word ṣifr (Arabic صفر) had the meaning "empty".^[7] Sifr evolved to mean zero when it was used to translate śūnya (Sanskrit: शून्य) from India.^[7] The first known English use of zero was in 1598.^[8]

The Italian mathematician Fibonacci (c. 1170–1250), who grew up in North Africa and is credited with introducing the decimal system to Europe, used the term zephyrum. This became zefiro in Italian, and was then contracted to zero in Venetian. The Italian word zefiro was already in existence (meaning "west wind" from Latin and Greek zephyrus) and may have influenced the spelling when transcribing Arabic ṣifr.^[9]

Modern usage

There are different words used for the number or concept of zero depending on the context. For the simple notion of lacking, the words nothing and none are often used. Sometimes the words nought, naught and aught^[10] are used. Several sports have specific words for zero, such as nil in association football (soccer), love in tennis and a duck in cricket. It is often called oh in the context of telephone numbers. Slang words for zero include zip, zilch, nada, and scratch. Duck egg and goose egg are also slang for zero.^[11]

History

Ancient Near East

Ancient Egyptian numerals were base 10. They used hieroglyphs for the digits and were not positional. By 1770 BC, the Egyptians had a symbol for zero in accounting texts. The symbol nfr, meaning beautiful, was also used to indicate the base level in drawings of tombs and pyramids and distances were measured relative to the base line as being above or below this line.^[12]

By the middle of the 2nd millennium BC, the Babylonian mathematics had a sophisticated sexagesimal positional numeral system. The lack of a positional value (or zero) was indicated by a space between sexagesimal numerals. By 300 BC, a punctuation symbol (two slanted wedges) was co-opted as a placeholder in the same Babylonian system. In a tablet unearthed at Kish (dating from about 700 BC), the scribe Bêl-bân-aplu wrote his zeros with three hooks, rather than two slanted wedges.^[13]

The Babylonian placeholder was not a true zero because it was not used alone. Nor was it used at the end of a number. Thus numbers like 2 and 120 (2×60), 3 and 180 (3×60), 4 and 240 (4×60), looked the same because the larger numbers lacked a final sexagesimal placeholder. Only context could differentiate them.

Pre-Columbian Americas

The back of Epi-Olmec stela C from Tres Zapotes, the second oldest Long Count date discovered. The numerals 7.16.6.16.18 translate to September, 32 BC (Julian). The glyphs surrounding the date are thought to be one of the few surviving examples of Epi-Olmec script.

The Mesoamerican Long Count calendar developed in south-central Mexico and Central America required the use of zero as a place-holder within its vigesimal (base-20) positional numeral system. Many different glyphs, including this partial quatrefoil——were used as a zero symbol for these Long Count dates, the earliest of which (on Stela 2 at Chiapa de Corzo, Chiapas) has a date of 36 BC.^[a]

Since the eight earliest Long Count dates appear outside the Maya homeland,^[14] it is generally believed that the use of zero in the Americas predated the Maya and was possibly the invention of the Olmecs.^[15] Many of the earliest Long Count dates were found within the Olmec heartland, although the Olmec civilization ended by the 4th century BC, several centuries before the earliest known Long Count dates.

Although zero became an integral part of Maya numerals, with a different, empty tortoise-like "shell shape" used for many depictions of the "zero" numeral, it is assumed to have not influenced Old World numeral systems.

Quipu, a knotted cord device, used in the Inca Empire and its predecessor societies in the Andean region to record accounting and other digital data, is encoded in a base ten positional system. Zero is represented by the absence of a knot in the appropriate position.

Classical antiquity

The ancient Greeks had no symbol for zero (μηδέν), and did not use a digit placeholder for it.^[16] They seemed unsure about the status of zero as a number. They asked themselves, "How can nothing be something?", leading to philosophical and, by the medieval period, religious arguments about the nature and existence of zero and the vacuum. The paradoxes of Zeno of Elea depend in large part on the uncertain interpretation of zero.

Example of the early Greek symbol for zero (lower right corner) from a 2nd-century papyrus

By 130 AD, Ptolemy, influenced by Hipparchus and the Babylonians, was using a symbol for zero (a small circle with a long overbar) in his work on mathematical astronomy called the Syntaxis Mathematica, also known as the Almagest. The way in which it is used can be seen in his table of chords in that book. Ptolemy's zero was used within a sexagesimal numeral system otherwise using alphabetic Greek numerals. Because it was used alone, not just as a placeholder, this Hellenistic zero was perhaps the earliest documented use of a numeral representing zero in the Old World.^[17] However, the positions were usually limited to the fractional part of a number (called minutes, seconds, thirds, fourths, etc.)—they were not used for the integral part of a number, indicating a concept perhaps better expressed as "none", rather than "zero" in the modern sense. In later Byzantine manuscripts of Ptolemy's Almagest, the Hellenistic zero had morphed into the Greek letter omicron (otherwise meaning 70).

Another zero was used in tables alongside Roman numerals by 525 (first known use by Dionysius Exiguus), but as a word, nulla meaning "nothing", not as a symbol.^[18] When division produced zero as a remainder, nihil, also meaning "nothing", was used. These medieval zeros were used by all future medieval calculators of Easter. The initial "N" was used as a zero symbol in a table of Roman numerals by Bede or his colleagues around 725.

China

This is a depiction of zero expressed in Chinese counting rods, based on the example provided by A History of Mathematics. An empty space is used to represent zero.^[19]

The Sūnzĭ Suànjīng, of unknown date but estimated to be dated from the 1st to 5th centuries AD, and Japanese records dated from the 18th century, describe how the c. 4th century BC Chinese counting rods system enables one to perform decimal calculations. According to A History of Mathematics, the rods "gave the decimal representation of a number, with an empty space denoting zero."^[19] The counting rod system is considered a positional notation system.^[20]

In AD 690, Empress Wǔ promulgated Zetian characters, one of which was "〇". The word is now used as a synonym for the number zero.

Zero was not treated as a number at that time, but as a "vacant position".^[21] Qín Jiǔsháo's 1247 Mathematical Treatise in Nine Sections is the oldest surviving Chinese mathematical text using a round symbol for zero.^[22] Chinese authors had been familiar with the idea of negative numbers by the Han Dynasty (2nd century AD), as seen in The Nine Chapters on the Mathematical Art,^[23] much earlier than the 15th century when they became well-established in Europe.^[22]

India

Pingala (c. 3rd/2nd century BC^[24]), a Sanskrit prosody scholar,^[25] used binary numbers in the form of short and long syllables (the latter equal in length to two short syllables), a notation similar to Morse code.^[26] Pingala used the Sanskrit word śūnya explicitly to refer to zero.^[27]

It was considered that the earliest text to use a decimal place-value system, including a zero, is the Lokavibhāga, a Jain text on cosmology surviving in a medieval Sanskrit translation of the Prakrit original, which is internally dated to AD 458 (Saka era 380). In this text, śūnya ("void, empty") is also used to refer to zero.^[28]

A symbol for zero, a large dot likely to be the precursor of the still-current hollow symbol, is used throughout the Bakhshali manuscript, a practical manual on arithmetic for merchants,^[29] the date of which was uncertain. In 2017 three samples from the manuscript were shown by radiocarbon dating to come from three different centuries: from 224-383 AD, 680-779 AD, and 885-993 AD, making it the world's oldest recorded use of the zero symbol. It is not known how the birch bark fragments from different centuries that form the manuscript came to be packaged together.^[30][31][32]

The origin of the modern decimal-based place value notation can be traced to the Aryabhatiya (c. 500), which states sthānāt sthānaṁ daśaguṇaṁ syāt "from place to place each is ten times the preceding."^{[33][33][34][35]} The concept of zero as a digit in the decimal place value notation was developed in India, presumably as early as during the Gupta period (c. 5th century), with the oldest unambiguous evidence dating to the 7th century.^[36]

The rules governing the use of zero appeared for the first time in Brahmagupta's Brahmasputha Siddhanta (7th century). This work considers not only zero, but negative numbers, and the algebraic rules for the elementary operations of arithmetic with such numbers. In some instances, his rules differ from the modern standard, specifically the definition of the value of zero divided by zero as zero.^[37]

Epigraphy

The number 605 in Khmer numerals, from the Sambor inscription (Saka era 605 corresponds to AD 683). The earliest known material use of zero as a decimal figure.

There are numerous copper plate inscriptions, with the same small o in them, some of them possibly dated to the 6th century, but their date or authenticity may be open to doubt.^[13]

A stone tablet found in the ruins of a temple near Sambor on the Mekong, Kratié Province, Cambodia, includes the inscription of "605" in Khmer numerals (a set of numeral glyphs of the Hindu numerals family). The number is the year of the inscription in the Saka era, corresponding to a date of AD 683.^[38]

The first known use of special glyphs for the decimal digits that includes the indubitable appearance of a symbol for the digit zero, a small circle, appears on a stone inscription found at the Chaturbhuja Temple at Gwalior in India, dated 876.^[39][40] Zero is also used as a placeholder in the Bakhshali manuscript, portions of which date from AD 224–383.^[41]

Middle Ages

Transmission to Islamic culture

The Arabic-language inheritance of science was largely Greek,^[42] followed by Hindu influences.^[43] In 773, at Al-Mansur's behest, translations were made of many ancient treatises including Greek, Roman, Indian, and others.

In AD 813, astronomical tables were prepared by a Persian mathematician, Muḥammad ibn Mūsā al-Khwārizmī, using Hindu numerals;^[43] and about 825, he published a book synthesizing Greek and Hindu knowledge and also contained his own contribution to mathematics including an explanation of the use of zero.^[44] This book was later translated into Latin in the 12th century under the title Algoritmi de numero Indorum. This title means "al-Khwarizmi on the Numerals of the Indians". The word "Algoritmi" was the translator's Latinization of Al-Khwarizmi's name, and the word "Algorithm" or "Algorism" started meaning any arithmetic based on decimals.^[43]

Muhammad ibn Ahmad al-Khwarizmi, in 976, stated that if no number appears in the place of tens in a calculation, a little circle should be used "to keep the rows". This circle was called ṣifr.^[45]

Transmission to Europe

The Hindu–Arabic numeral system (base 10) reached Europe in the 11th century, via the Iberian Peninsula through Spanish Muslims, the Moors, together with knowledge of astronomy and instruments like the astrolabe, first imported by Gerbert of Aurillac. For this reason, the numerals came to be known in Europe as "Arabic numerals". The Italian mathematician Fibonacci or Leonardo of Pisa was instrumental in bringing the system into European mathematics in 1202, stating:

After my father's appointment by his homeland as state official in the customs house of Bugia for the Pisan merchants who thronged to it, he took charge; and in view of its future usefulness and convenience, had me in my boyhood come to him and there wanted me to devote myself to and be instructed in the study of calculation for some days. There, following my introduction, as a consequence of marvelous instruction in the art, to the nine digits of the Hindus, the knowledge of the art very much appealed to me before all others, and for it I realized that all its aspects were studied in Egypt, Syria, Greece, Sicily, and Provence, with their varying methods; and at these places thereafter, while on business. I pursued my study in depth and learned the give-and-take of disputation. But all this even, and the algorism, as well as the art of Pythagoras, I considered as almost a mistake in respect to the method of the Hindus (Modus Indorum). Therefore, embracing more stringently that method of the Hindus, and taking stricter pains in its study, while adding certain things from my own understanding and inserting also certain things from the niceties of Euclid's geometric art. I have striven to compose this book in its entirety as understandably as I could, dividing it into fifteen chapters. Almost everything which I have introduced I have displayed with exact proof, in order that those further seeking this knowledge, with its pre-eminent method, might be instructed, and further, in order that the Latin people might not be discovered to be without it, as they have been up to now. If I have perchance omitted anything more or less proper or necessary, I beg indulgence, since there is no one who is blameless and utterly provident in all things. The nine Indian figures are: 9 8 7 6 5 4 3 2 1. With these nine figures, and with the sign 0 ... any number may be written.^[46][47]

Here Leonardo of Pisa uses the phrase "sign 0", indicating it is like a sign to do operations like addition or multiplication. From the 13th century, manuals on calculation (adding, multiplying, extracting roots, etc.) became common in Europe where they were called algorismus after the Persian mathematician al-Khwārizmī. The most popular was written by Johannes de Sacrobosco, about 1235 and was one of the earliest scientific books to be printed in 1488. Until the late 15th century, Hindu–Arabic numerals seem to have predominated among mathematicians, while merchants preferred to use the Roman numerals. In the 16th century, they became commonly used in Europe.

Mathematics

0 is the integer immediately preceding 1. Zero is an even number^[48] because it is divisible by 2 with no remainder. 0 is neither positive nor negative.^[49] By most definitions^[50] 0 is a natural number, and then the only natural number not to be positive. Zero is a number which quantifies a count or an amount of null size. In most cultures, 0 was identified before the idea of negative things, or quantities less than zero, was accepted.

The value, or number, zero is not the same as the digit zero, used in numeral systems using positional notation. Successive positions of digits have higher weights, so inside a numeral the digit zero is used to skip a position and give appropriate weights to the preceding and following digits. A zero digit is not always necessary in a positional number system, for example, in the number 02. In some instances, a leading zero may be used to distinguish a number.

Elementary algebra

The number 0 is the smallest non-negative integer. The natural number following 0 is 1 and no natural number precedes 0. The number 0 may or may not be considered a natural number, but it is a whole number and hence a rational number and a real number (as well as an algebraic number and a complex number).

The number 0 is neither positive nor negative and is usually displayed as the central number in a number line. It is neither a prime number nor a composite number. It cannot be prime because it has an infinite number of factors, and cannot be composite because it cannot be expressed as a product of prime numbers (0 must always be one of the factors).^[51] Zero is, however, even (as well as being a multiple of any other integer, rational, or real number).

The following are some basic (elementary) rules for dealing with the number 0. These rules apply for any real or complex number x, unless otherwise stated.

• Addition: x + 0 = 0 + x = x. That is, 0 is an identity element (or neutral element) with respect to addition.
• Subtraction: x − 0 = x and 0 − x = −x.
• Multiplication: x · 0 = 0 · x = 0.
• Division: 0/x = 0, for nonzero x. But x/0 is undefined, because 0 has no multiplicative inverse (no real number multiplied by 0 produces 1), a consequence of the previous rule.
• Exponentiation: x⁰ = x/x = 1, except that the case x = 0 may be left undefined in some contexts. For all positive real x, 0^x = 0.

The expression 0/0, which may be obtained in an attempt to determine the limit of an expression of the form f(x)/g(x) as a result of applying the lim operator independently to both operands of the fraction, is a so-called "indeterminate form". That does not simply mean that the limit sought is necessarily undefined; rather, it means that the limit of f(x)/g(x), if it exists, must be found by another method, such as l'Hôpital's rule.

The sum of 0 numbers (the empty sum) is 0, and the product of 0 numbers (the empty product) is 1. The factorial 0! evaluates to 1, as a special case of the empty product.

Other branches of mathematics

• In set theory, 0 is the cardinality of the empty set: if one does not have any apples, then one has 0 apples. In fact, in certain axiomatic developments of mathematics from set theory, 0 is defined to be the empty set. When this is done, the empty set is the Von Neumann cardinal assignment for a set with no elements, which is the empty set. The cardinality function, applied to the empty set, returns the empty set as a value, thereby assigning it 0 elements.
• Also in set theory, 0 is the lowest ordinal number, corresponding to the empty set viewed as a well-ordered set.
• In propositional logic, 0 may be used to denote the truth value false.
• In abstract algebra, 0 is commonly used to denote a zero element, which is a neutral element for addition (if defined on the structure under consideration) and an absorbing element for multiplication (if defined).
• In lattice theory, 0 may denote the bottom element of a bounded lattice.
• In category theory, 0 is sometimes used to denote an initial object of a category.
• In recursion theory, 0 can be used to denote the Turing degree of the partial computable functions.

Related mathematical terms

• A zero of a function f is a point x in the domain of the function such that f(x) = 0. When there are finitely many zeros these are called the roots of the function. This is related to zeros of a holomorphic function.
• The zero function (or zero map) on a domain D is the constant function with 0 as its only possible output value, i.e., the function f defined by f(x) = 0 for all x in D. The zero function is the only function that is both even and odd. A particular zero function is a zero morphism in category theory; e.g., a zero map is the identity in the additive group of functions. The determinant on non-invertible square matrices is a zero map.
• Several branches of mathematics have zero elements, which generalize either the property 0 + x = x, or the property 0 · x = 0, or both.

Physics

The value zero plays a special role for many physical quantities. For some quantities, the zero level is naturally distinguished from all other levels, whereas for others it is more or less arbitrarily chosen. For example, for an absolute temperature (as measured in kelvins) zero is the lowest possible value (negative temperatures are defined, but negative-temperature systems are not actually colder). This is in contrast to for example temperatures on the Celsius scale, where zero is arbitrarily defined to be at the freezing point of water. Measuring sound intensity in decibels or phons, the zero level is arbitrarily set at a reference value—for example, at a value for the threshold of hearing. In physics, the zero-point energy is the lowest possible energy that a quantum mechanical physical system may possess and is the energy of the ground state of the system.

Chemistry

Zero has been proposed as the atomic number of the theoretical element tetraneutron. It has been shown that a cluster of four neutrons may be stable enough to be considered an atom in its own right. This would create an element with no protons and no charge on its nucleus.

As early as 1926, Andreas von Antropoff coined the term neutronium for a conjectured form of matter made up of neutrons with no protons, which he placed as the chemical element of atomic number zero at the head of his new version of the periodic table. It was subsequently placed as a noble gas in the middle of several spiral representations of the periodic system for classifying the chemical elements.

Computer science

The most common practice throughout human history has been to start counting at one, and this is the practice in early classic computer science programming languages such as Fortran and COBOL. However, in the late 1950s LISP introduced zero-based numbering for arrays while Algol 58 introduced completely flexible basing for array subscripts (allowing any positive, negative, or zero integer as base for array subscripts), and most subsequent programming languages adopted one or other of these positions. For example, the elements of an array are numbered starting from 0 in C, so that for an array of n items the sequence of array indices runs from 0 to n−1. This permits an array element's location to be calculated by adding the index directly to address of the array, whereas 1-based languages precalculate the array's base address to be the position one element before the first.^{[citation needed]}

There can be confusion between 0- and 1-based indexing, for example Java's JDBC indexes parameters from 1 although Java itself uses 0-based indexing.^{[citation needed]}

In databases, it is possible for a field not to have a value. It is then said to have a null value.^[52] For numeric fields it is not the value zero. For text fields this is not blank nor the empty string. The presence of null values leads to three-valued logic. No longer is a condition either true or false, but it can be undetermined. Any computation including a null value delivers a null result.^{[citation needed]}

A null pointer is a pointer in a computer program that does not point to any object or function. In C, the integer constant 0 is converted into the null pointer at compile time when it appears in a pointer context, and so 0 is a standard way to refer to the null pointer in code. However, the internal representation of the null pointer may be any bit pattern (possibly different values for different data types).^{[citation needed]}

In mathematics −0 = +0 = 0; both −0 and +0 represent exactly the same number, i.e., there is no "positive zero" or "negative zero" distinct from zero. However, in some computer hardware signed number representations, zero has two distinct representations, a positive one grouped with the positive numbers and a negative one grouped with the negatives; this kind of dual representation is known as signed zero, with the latter form sometimes called negative zero. These representations include the signed magnitude and one's complement binary integer representations (but not the two's complement binary form used in most modern computers), and most floating point number representations (such as IEEE 754 and IBM S/390 floating point formats).

In binary, 0 represents the value for "off", which means no electricity flow.^[53]

Zero is the value of false in many programming languages.

The Unix epoch (the date and time associated with a zero timestamp) begins the midnight before the first of January 1970.^[54][55][56]

The MacOS epoch and Palm OS epoch (the date and time associated with a zero timestamp) begins the midnight before the first of January 1904.^[57]

Many APIs and operating systems that require applications to return an integer value as an exit status typically use zero to indicate success and non-zero values to indicate specific error or warning conditions.

Other fields

• In telephony, pressing 0 is often used for dialling out of a company network or to a different city or region, and 00 is used for dialling abroad. In some countries, dialling 0 places a call for operator assistance.
• DVDs that can be played in any region are sometimes referred to as being "region 0"
• Roulette wheels usually feature a "0" space (and sometimes also a "00" space), whose presence is ignored when calculating payoffs (thereby allowing the house to win in the long run).
• In Formula One, if the reigning World Champion no longer competes in Formula One in the year following their victory in the title race, 0 is given to one of the drivers of the team that the reigning champion won the title with. This happened in 1993 and 1994, with Damon Hill driving car 0, due to the reigning World Champion (Nigel Mansell and Alain Prost respectively) not competing in the championship.
• On the U.S. Interstate Highway System, in most states exits are numbered based on the nearest milepost from the highway's western or southern terminus within that state. Several that are less than half a mile (800 m) from state boundaries in that direction are numbered as Exit 0.

Symbols and representations

The modern numerical digit 0 is usually written as a circle or ellipse. Traditionally, many print typefaces made the capital letter O more rounded than the narrower, elliptical digit 0.^[58] Typewriters originally made no distinction in shape between O and 0; some models did not even have a separate key for the digit 0. The distinction came into prominence on modern character displays.^[58]

A slashed zero can be used to distinguish the number from the letter. The digit 0 with a dot in the center seems to have originated as an option on IBM 3270 displays and has continued with some modern computer typefaces such as Andalé Mono, and in some airline reservation systems. One variation uses a short vertical bar instead of the dot. Some fonts designed for use with computers made one of the capital-O–digit-0 pair more rounded and the other more angular (closer to a rectangle). A further distinction is made in falsification-hindering typeface as used on German car number plates by slitting open the digit 0 on the upper right side. Sometimes the digit 0 is used either exclusively, or not at all, to avoid confusion altogether.

Year label

In the BC calendar era, the year 1 BC is the first year before AD 1; there is not a year zero. By contrast, in astronomical year numbering, the year 1 BC is numbered 0, the year 2 BC is numbered −1, and so on.^[59]