Isotope

From Wikipedia, the free encyclopedia

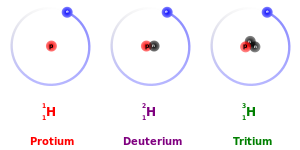
The three naturally-occurring isotopes of hydrogen. The fact that each isotope has one proton makes them all variants of hydrogen: the identity of the isotope is given by the number of neutrons. From left to right, the isotopes are protium (¹H) with zero neutrons, deuterium (²H) with one neutron, and tritium (³H) with two neutrons.

Isotopes are variants of a particular chemical element which differ in neutron number. All isotopes of a given element have the same number of protons in each atom. The term isotope is formed from the Greek roots isos (ἴσος "equal") and topos (τόπος "place"), meaning "the same place"; thus, the meaning behind the name is that different isotopes of a single element occupy the same position on the periodic table.

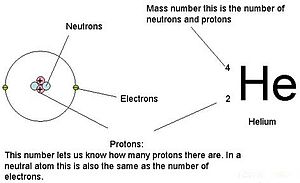
The number of protons within the atom's nucleus is called atomic number and is equal to the number of electrons in the neutral (non-ionized) atom. Each atomic number identifies a specific element, but not the isotope; an atom of a given element may have a wide range in its number of neutrons. The number of nucleons (both protons and neutrons) in the nucleus is the atom's mass number, and each isotope of a given element has a different mass number.

For example, carbon-12, carbon-13 and carbon-14 are three isotopes of the element carbon with mass numbers 12, 13 and 14 respectively. The atomic number of carbon is 6, which means that every carbon atom has 6 protons, so that the neutron numbers of these isotopes are 6, 7 and 8 respectively.

Isotope vs. nuclide

A nuclide is a species of an atom with a specific number of protons and neutrons in the nucleus, for example carbon-13 with 6 protons and 7 neutrons. The nuclide concept (referring to individual nuclear species) emphasizes nuclear properties over chemical properties, whereas the isotope concept (grouping all atoms of each element) emphasizes chemical over nuclear. The neutron number has large effects on nuclear properties, but its effect on chemical properties is negligible for most elements. Even in the case of the lightest elements where the ratio of neutron number to atomic number varies the most between isotopes it usually has only a small effect, although it does matter in some circumstances (for hydrogen, the lightest element, the isotope effect is large enough to strongly affect biology). The term isotopes (originally also isotopic elements^[1], now sometimes isotopic nuclides^[2]) is intended to imply comparison (like synonyms or isomers), for example: the nuclides ¹²
₆C
, ¹³
₆C
, ¹⁴
₆C
are isotopes (nuclides with the same atomic number but different mass numbers^[3]), but ⁴⁰
₁₈Ar
, ⁴⁰
₁₉K
, ⁴⁰
₂₀Ca
are isobars (nuclides with the same mass number^[4]). However, because isotope is the older term, it is better known than nuclide, and is still sometimes used in contexts where nuclide might be more appropriate, such as nuclear technology and nuclear medicine.

Definition of isotopes

Isotopes are atoms of the same element having the same numbers of protons (atomic number), but different numbers of neutrons. They have same chemical properties due to the same electronic configuration but different physical properties.

Notation

An isotope and/or nuclide is specified by the name of the particular element (this indicates the atomic number) followed by a hyphen and the mass number (e.g. helium-3, helium-4, carbon-12, carbon-14, uranium-235 and uranium-239).^[5] When a chemical symbol is used, e.g. "C" for carbon, standard notation (now known as "AZE notation" because A is the mass number, Z the atomic number, and E for element) is to indicate the mass number (number of nucleons) with a superscript at the upper left of the chemical symbol and to indicate the atomic number with a subscript at the lower left (e.g. ³
₂He
, ⁴
₂He
, ¹²
₆C
, ¹⁴
₆C
, ²³⁵
₉₂U
, and ²³⁹
₉₂U
).^[6] Because the atomic number is given by the element symbol, it is common to state only the mass number in the superscript and leave out the atomic number subscript (e.g. ³He
, ⁴He
, ¹²C
, ¹⁴C
, ²³⁵U
, and ²³⁹U
). The letter m is sometimes appended after the mass number to indicate a nuclear isomer, a metastable or energetically-excited nuclear state (as opposed to the lowest-energy ground state), for example ^180m
₇₃Ta
(tantalum-180m).

The common pronunciation of the AZE notation is different from how it is written: ⁴
₂He
is commonly pronounced as helium-four instead of four-two-helium, and ²³⁵
₉₂U
as uranium two-thirty-five (American English) or uranium-two-three-five (British) instead of 235-92-uranium.

Radioactive, primordial, and stable isotopes

Some isotopes/nuclides are radioactive, and are therefore referred to as radioisotopes or radionuclides, whereas others have never been observed to decay radioactively and are referred to as stable isotopes or stable nuclides. For example, ¹⁴C
is a radioactive form of carbon, whereas ¹²C
and ¹³C
are stable isotopes. There are about 339 naturally occurring nuclides on Earth,^[7] of which 286 are primordial nuclides, meaning that they have existed since the Solar System's formation.

Primordial nuclides include 32 nuclides with very long half-lives (over 100 million years) and 253 that are formally considered as "stable nuclides",^[7] because they have not been observed to decay. In most cases, for obvious reasons, if an element has stable isotopes, those isotopes predominate in the elemental abundance found on Earth and in the Solar System. However, in the cases of three elements (tellurium, indium, and rhenium) the most abundant isotope found in nature is actually one (or two) extremely long-lived radioisotope(s) of the element, despite these elements having one or more stable isotopes.

Theory predicts that many apparently "stable" isotopes/nuclides are radioactive, with extremely long half-lives (discounting the possibility of proton decay, which would make all nuclides ultimately unstable). Of the 253 nuclides never observed to decay, only 90 of these (all from the first 40 elements) are theoretically stable to all known forms of decay. Element 41 (niobium) is theoretically unstable via spontaneous fission, but this has never been detected. Many other stable nuclides are in theory energetically susceptible to other known forms of decay, such as alpha decay or double beta decay, but no decay products have yet been observed, and so these isotopes are said to be "observationally stable". The predicted half-lives for these nuclides often greatly exceed the estimated age of the universe, and in fact there are also 27 known radionuclides (see primordial nuclide) with half-lives longer than the age of the universe.

Adding in the radioactive nuclides that have been created artificially, there are 3,339 currently known nuclides.^[8] These include 905 nuclides that are either stable or have half-lives longer than 60 minutes. See list of nuclides for details.

History

Radioactive isotopes

The existence of isotopes was first suggested in 1913 by the radiochemist Frederick Soddy, based on studies of radioactive decay chains that indicated about 40 different species referred to as radioelements (i.e. radioactive elements) between uranium and lead, although the periodic table only allowed for 11 elements from uranium to lead.^[9][10][11]

Several attempts to separate these new radioelements chemically had failed.^[12] For example, Soddy had shown in 1910 that mesothorium (later shown to be ²²⁸Ra), radium (²²⁶Ra, the longest-lived isotope), and thorium X (²²⁴Ra) are impossible to separate.^[13] Attempts to place the radioelements in the periodic table led Soddy and Kazimierz Fajans independently to propose their radioactive displacement law in 1913, to the effect that alpha decay produced an element two places to the left in the periodic table, whereas beta decay emission produced an element one place to the right.^[14] Soddy recognized that emission of an alpha particle followed by two beta particles led to the formation of an element chemically identical to the initial element but with a mass four units lighter and with different radioactive properties.

Soddy proposed that several types of atoms (differing in radioactive properties) could occupy the same place in the table.^[11] For example, the alpha-decay of uranium-235 forms thorium-231, whereas the beta decay of actinium-230 forms thorium-230.^[12] The term "isotope", Greek for "at the same place",^[11] was suggested to Soddy by Margaret Todd, a Scottish physician and family friend, during a conversation in which he explained his ideas to her.^{[13][15][16][17][18][19]} He won the 1921 Nobel Prize in Chemistry in part for his work on isotopes.^[20]

In the bottom right corner of J. J. Thomson's photographic plate are the separate impact marks for the two isotopes of neon: neon-20 and neon-22.

In 1914 T. W. Richards found variations between the atomic weight of lead from different mineral sources, attributable to variations in isotopic composition due to different radioactive origins.^[12][20]

Stable isotopes

The first evidence for multiple isotopes of a stable (non-radioactive) element was found by J. J. Thomson in 1913 as part of his exploration into the composition of canal rays (positive ions).^[21][22] Thomson channeled streams of neon ions through a magnetic and an electric field and measured their deflection by placing a photographic plate in their path. Each stream created a glowing patch on the plate at the point it struck. Thomson observed two separate patches of light on the photographic plate (see image), which suggested two different parabolas of deflection. Thomson eventually concluded that some of the atoms in the neon gas were of higher mass than the rest.

F. W. Aston subsequently discovered multiple stable isotopes for numerous elements using a mass spectrograph. In 1919 Aston studied neon with sufficient resolution to show that the two isotopic masses are very close to the integers 20 and 22, and that neither is equal to the known molar mass (20.2) of neon gas. This is an example of Aston's whole number rule for isotopic masses, which states that large deviations of elemental molar masses from integers are primarily due to the fact that the element is a mixture of isotopes. Aston similarly showed^[when?] that the molar mass of chlorine (35.45) is a weighted average of the almost integral masses for the two isotopes ³⁵Cl and ³⁷Cl.^[23]

Variation in properties between isotopes

Chemical and molecular properties

A neutral atom has the same number of electrons as protons. Thus different isotopes of a given element all have the same number of electrons and share a similar electronic structure. Because the chemical behavior of an atom is largely determined by its electronic structure, different isotopes exhibit nearly identical chemical behavior.

The main exception to this is the kinetic isotope effect: due to their larger masses, heavier isotopes tend to react somewhat more slowly than lighter isotopes of the same element. This is most pronounced by far for protium (¹H
), deuterium (²H
), and tritium (³H
), because deuterium has twice the mass of protium and tritium has three times the mass of protium. These mass differences also affect the behavior of their respective chemical bonds, by changing the center of gravity (reduced mass) of the atomic systems. However, for heavier elements the relative mass difference between isotopes is much less, so that the mass-difference effects on chemistry are usually negligible. (Heavy elements also have relatively more neutrons than lighter elements, so the ratio of the nuclear mass to the collective electronic mass is slightly greater.)

Isotope half-lives. The plot for stable isotopes diverges from the line Z = N as the element number Z becomes larger

Similarly, two molecules that differ only in the isotopes of their atoms (isotopologues) have identical electronic structure, and therefore almost indistinguishable physical and chemical properties (again with deuterium and tritium being the primary exceptions). The vibrational modes of a molecule are determined by its shape and by the masses of its constituent atoms; so different isotopologues have different sets of vibrational modes. Because vibrational modes allow a molecule to absorb photons of corresponding energies, isotopologues have different optical properties in the infrared range.

Nuclear properties and stability

Atomic nuclei consist of protons and neutrons bound together by the residual strong force. Because protons are positively charged, they repel each other. Neutrons, which are electrically neutral, stabilize the nucleus in two ways. Their copresence pushes protons slightly apart, reducing the electrostatic repulsion between the protons, and they exert the attractive nuclear force on each other and on protons. For this reason, one or more neutrons are necessary for two or more protons to bind into a nucleus. As the number of protons increases, so does the ratio of neutrons to protons necessary to ensure a stable nucleus (see graph at right). For example, although the neutron:proton ratio of ³
₂He
is 1:2, the neutron:proton ratio of ²³⁸
₉₂U
is greater than 3:2. A number of lighter elements have stable nuclides with the ratio 1:1 (Z = N). The nuclide ⁴⁰
₂₀Ca
(calcium-40) is observationally the heaviest stable nuclide with the same number of neutrons and protons; (theoretically, the heaviest stable one is sulfur-32). All stable nuclides heavier than calcium-40 contain more neutrons than protons.

Numbers of isotopes per element

Of the 80 elements with a stable isotope, the largest number of stable isotopes observed for any element is ten (for the element tin). No element has nine stable isotopes. Xenon is the only element with eight stable isotopes. Four elements have seven stable isotopes, eight have six stable isotopes, ten have five stable isotopes, nine have four stable isotopes, five have three stable isotopes, 16 have two stable isotopes (counting ^180m
₇₃Ta
as stable), and 26 elements have only a single stable isotope (of these, 19 are so-called mononuclidic elements, having a single primordial stable isotope that dominates and fixes the atomic weight of the natural element to high precision; 3 radioactive mononuclidic elements occur as well).^[24] In total, there are 253 nuclides that have not been observed to decay. For the 80 elements that have one or more stable isotopes, the average number of stable isotopes is 253/80 = 3.1625 isotopes per element.

Even and odd nucleon numbers

The proton:neutron ratio is not the only factor affecting nuclear stability. It depends also on evenness or oddness of its atomic number Z, neutron number N and, consequently, of their sum, the mass number A. Oddness of both Z and N tends to lower the nuclear binding energy, making odd nuclei, generally, less stable. This remarkable difference of nuclear binding energy between neighbouring nuclei, especially of odd-A isobars, has important consequences: unstable isotopes with a nonoptimal number of neutrons or protons decay by beta decay (including positron decay), electron capture or other exotic means, such as spontaneous fission and cluster decay.
The majority of stable nuclides are even-proton-even-neutron, where all numbers Z, N, and A are even. The odd-A stable nuclides are divided (roughly evenly) into odd-proton-even-neutron, and even-proton-odd-neutron nuclides. Odd-proton-odd-neutron nuclei are the least common.

Even atomic number

The 148 even-proton, even-neutron (EE) nuclides comprise ~ 58% of all stable nuclides and all have spin 0 because of pairing. There are also 22 primordial long-lived even-even nuclides. As a result, each of the 41 even-numbered elements from 2 to 82 has at least one stable isotope, and most of these elements have several primordial isotopes. Half of these even-numbered elements have six or more stable isotopes. The extreme stability of helium-4 due to a double pairing of 2 protons and 2 neutrons prevents any nuclides containing five or eight nucleons from existing for long enough to serve as platforms for the buildup of heavier elements via nuclear fusion in stars (see triple alpha process).

These 53 stable nuclides have an even number of protons and an odd number of neutrons. They are a minority in comparison to the even-even isotopes, which are about 3 times as numerous. Among the 41 even-Z elements that have a stable nuclide, only two elements (argon and cerium) have no even-odd stable nuclides. One element (tin) has three. There are 24 elements that have one even-odd nuclide and 13 that have two odd-even nuclides. Of 35 primordial radionuclides there exist four even-odd nuclides (see table at right), including the fissile ²³⁵
₉₂U
. Because of their odd neutron numbers, the even-odd nuclides tend to have large neutron capture cross sections, due to the energy that results from neutron-pairing effects. These stable even-proton odd-neutron nuclides tend to be uncommon by abundance in nature, generally because, to form and enter into primordial abundance, they must have escaped capturing neutrons to form yet other stable even-even isotopes, during both the s-process and r-process of neutron capture, during nucleosynthesis in stars. For this reason, only ¹⁹⁵
₇₈Pt
and ⁹
₄Be
are the most naturally abundant isotopes of their element.

Odd atomic number

Forty-eight stable odd-proton-even-neutron nuclides, stabilized by their even numbers of paired neutrons, form most of the stable isotopes of the odd-numbered elements; the very few odd-proton-odd-neutron nuclides comprise the others. There are 41 odd-numbered elements with Z = 1 through 81, of which 39 have stable isotopes (the elements technetium (
₄₃Tc
) and promethium (
₆₁Pm
) have no stable isotopes). Of these 39 odd Z elements, 30 elements (including hydrogen-1 where 0 neutrons is even) have one stable odd-even isotope, and nine elements: chlorine (
₁₇Cl
), potassium (
₁₉K
), copper (
₂₉Cu
), gallium (
₃₁Ga
), bromine (
₃₅Br
), silver (
₄₇Ag
), antimony (
₅₁Sb
), iridium (
₇₇Ir
), and thallium (
₈₁Tl
), have two odd-even stable isotopes each. This makes a total 30 + 2(9) = 48 stable odd-even isotopes.

There are also five primordial long-lived radioactive odd-even isotopes, ⁸⁷
₃₇Rb
, ¹¹⁵
₄₉In
, ¹⁸⁷
₇₅Re
, ¹⁵¹
₆₃Eu
, and ²⁰⁹
₈₃Bi
. The last two were only recently found to decay, with half-lives greater than 10¹⁸ years.
Only five stable nuclides contain both an odd number of protons and an odd number of neutrons. The first four "odd-odd" nuclides occur in low mass nuclides, for which changing a proton to a neutron or vice versa would lead to a very lopsided proton-neutron ratio (²
₁H
, ⁶
₃Li
, ¹⁰
₅B
, and ¹⁴
₇N
; spins 1, 1, 3, 1). The only other entirely "stable" odd-odd nuclide is ^180m
₇₃Ta
(spin 9) is thought to be the rarest of the 253 stable isotopes, and is the only primordial nuclear isomer, which has not yet been observed to decay despite experimental attempts.^[25]

Many odd-odd radionuclides (like tantalum-180) with comparatively short half lives are known. Usually, they beta-decay to their nearby even-even isobars that have paired protons and paired neutrons. Of the nine primordial odd-odd nuclides (five stable and four radioactive with long half lives), only ¹⁴
₇N
is the most common isotope of a common element. This is the case because it is a part of the CNO cycle. The nuclides ⁶
₃Li
and ¹⁰
₅B
are minority isotopes of elements that are themselves rare compared to other light elements, whereas the other six isotopes make up only a tiny percentage of the natural abundance of their elements.

Odd neutron number

Actinides with odd neutron number are generally fissile (with thermal neutrons), whereas those with even neutron number are generally not, though they are fissionable with fast neutrons. All observationally stable odd-odd nuclides have nonzero integer spin. This is because the single unpaired neutron and unpaired proton have a larger nuclear force attraction to each other if their spins are aligned (producing a total spin of at least 1 unit), instead of anti-aligned. See deuterium for the simplest case of this nuclear behavior.

Only ¹⁹⁵
₇₈Pt
, ⁹
₄Be
and ¹⁴
₇N
have odd neutron number and are the most naturally abundant isotope of their element.

Occurrence in nature

Elements are composed of one nuclide (mononuclidic elements) or of more naturally occurring isotopes. The unstable (radioactive) isotopes are either primordial or postprimordial. Primordial isotopes were a product of stellar nucleosynthesis or another type of nucleosynthesis such as cosmic ray spallation, and have persisted down to the present because their rate of decay is so slow (e.g. uranium-238 and potassium-40). Post-primordial isotopes were created by cosmic ray bombardment as cosmogenic nuclides (e.g., tritium, carbon-14), or by the decay of a radioactive primordial isotope to a radioactive radiogenic nuclide daughter (e.g. uranium to radium). A few isotopes are naturally synthesized as nucleogenic nuclides, by some other natural nuclear reaction, such as when neutrons from natural nuclear fission are absorbed by another atom.

As discussed above, only 80 elements have any stable isotopes, and 26 of these have only one stable isotope. Thus, about two-thirds of stable elements occur naturally on Earth in multiple stable isotopes, with the largest number of stable isotopes for an element being ten, for tin (
₅₀Sn
). There are about 94 elements found naturally on Earth (up to plutonium inclusive), though some are detected only in very tiny amounts, such as plutonium-244. Scientists estimate that the elements that occur naturally on Earth (some only as radioisotopes) occur as 339 isotopes (nuclides) in total.^[26] Only 253 of these naturally occurring nuclides are stable in the sense of never having been observed to decay as of the present time. An additional 35 primordial nuclides (to a total of 289 primordial nuclides), are radioactive with known half-lives, but have half-lives longer than 80 million years, allowing them to exist from the beginning of the Solar System. See list of nuclides for details.

All the known stable nuclides occur naturally on Earth; the other naturally occurring nuclides are radioactive but occur on Earth due to their relatively long half-lives, or else due to other means of ongoing natural production. These include the afore-mentioned cosmogenic nuclides, the nucleogenic nuclides, and any radiogenic nuclides formed by ongoing decay of a primordial radioactive nuclide, such as radon and radium from uranium.

An additional ~3000 radioactive nuclides not found in nature have been created in nuclear reactors and in particle accelerators. Many short-lived nuclides not found naturally on Earth have also been observed by spectroscopic analysis, being naturally created in stars or supernovae. An example is aluminium-26, which is not naturally found on Earth, but is found in abundance on an astronomical scale.

The tabulated atomic masses of elements are averages that account for the presence of multiple isotopes with different masses. Before the discovery of isotopes, empirically determined noninteger values of atomic mass confounded scientists. For example, a sample of chlorine contains 75.8% chlorine-35 and 24.2% chlorine-37, giving an average atomic mass of 35.5 atomic mass units.

According to generally accepted cosmology theory, only isotopes of hydrogen and helium, traces of some isotopes of lithium and beryllium, and perhaps some boron, were created at the Big Bang, while all other nuclides were synthesized later, in stars and supernovae, and in interactions between energetic particles such as cosmic rays, and previously produced nuclides. (See nucleosynthesis for details of the various processes thought responsible for isotope production.) The respective abundances of isotopes on Earth result from the quantities formed by these processes, their spread through the galaxy, and the rates of decay for isotopes that are unstable. After the initial coalescence of the Solar System, isotopes were redistributed according to mass, and the isotopic composition of elements varies slightly from planet to planet. This sometimes makes it possible to trace the origin of meteorites.

Atomic mass of isotopes

The atomic mass (m_r) of an isotope (nuclide) is determined mainly by its mass number (i.e. number of nucleons in its nucleus). Small corrections are due to the binding energy of the nucleus (see mass defect), the slight difference in mass between proton and neutron, and the mass of the electrons associated with the atom, the latter because the electron:nucleon ratio differs among isotopes.

The mass number is a dimensionless quantity. The atomic mass, on the other hand, is measured using the atomic mass unit based on the mass of the carbon-12 atom. It is denoted with symbols "u" (for unified atomic mass unit) or "Da" (for dalton).

The atomic masses of naturally occurring isotopes of an element determine the atomic mass of the element. When the element contains N isotopes, the expression below is applied for the average atomic mass ${\displaystyle {\overline {m}}_{a}}$:

${\displaystyle {\overline {m}}_{a}=m_{1}x_{1}+m_{2}x_{2}+...+m_{N}x_{N}}$


where m₁, m₂, …, m_N are the atomic masses of each individual isotope, and x₁, …, x_N are the relative abundances of these isotopes.

Applications of isotopes

Purification of isotopes

Several applications exist that capitalize on properties of the various isotopes of a given element. Isotope separation is a significant technological challenge, particularly with heavy elements such as uranium or plutonium. Lighter elements such as lithium, carbon, nitrogen, and oxygen are commonly separated by gas diffusion of their compounds such as CO and NO. The separation of hydrogen and deuterium is unusual because it is based on chemical rather than physical properties, for example in the Girdler sulfide process. Uranium isotopes have been separated in bulk by gas diffusion, gas centrifugation, laser ionization separation, and (in the Manhattan Project) by a type of production mass spectrometry.

Use of chemical and biological properties

• Isotope analysis is the determination of isotopic signature, the relative abundances of isotopes of a given element in a particular sample. For biogenic substances in particular, significant variations of isotopes of C, N and O can occur. Analysis of such variations has a wide range of applications, such as the detection of adulteration in food products^[27] or the geographic origins of products using isoscapes. The identification of certain meteorites as having originated on Mars is based in part upon the isotopic signature of trace gases contained in them.^[28]
• Isotopic substitution can be used to determine the mechanism of a chemical reaction via the kinetic isotope effect.
• Another common application is isotopic labeling, the use of unusual isotopes as tracers or markers in chemical reactions. Normally, atoms of a given element are indistinguishable from each other. However, by using isotopes of different masses, even different nonradioactive stable isotopes can be distinguished by mass spectrometry or infrared spectroscopy. For example, in 'stable isotope labeling with amino acids in cell culture (SILAC)' stable isotopes are used to quantify proteins. If radioactive isotopes are used, they can be detected by the radiation they emit (this is called radioisotopic labeling).
• Isotopes are commonly used to determine the concentration of various elements or substances using the isotope dilution method, whereby known amounts of isotopically-substituted compounds are mixed with the samples and the isotopic signatures of the resulting mixtures are determined with mass spectrometry.

Use of nuclear properties

• A technique similar to radioisotopic labeling is radiometric dating: using the known half-life of an unstable element, one can calculate the amount of time that has elapsed since a known concentration of isotope existed. The most widely known example is radiocarbon dating used to determine the age of carbonaceous materials.
• Several forms of spectroscopy rely on the unique nuclear properties of specific isotopes, both radioactive and stable. For example, nuclear magnetic resonance (NMR) spectroscopy can be used only for isotopes with a nonzero nuclear spin. The most common nuclides used with NMR spectroscopy are ¹H, ²D, ¹⁵N, ¹³C, and ³¹P.
• Mössbauer spectroscopy also relies on the nuclear transitions of specific isotopes, such as ⁵⁷Fe.
• Radionuclides also have important uses. Nuclear power and nuclear weapons development require relatively large quantities of specific isotopes. Nuclear medicine and radiation oncology utilize radioisotopes respectively for medical diagnosis and treatment.

Atomic mass

From Wikipedia, the free encyclopedia

Stylized lithium-7 atom: 3 protons, 4 neutrons, & 3 electrons (total electrons are ~​¹⁄₄₃₀₀th of the mass of the nucleus). It has a mass of 7.016 u. Rare lithium-6 (mass of 6.015 u) has only 3 neutrons, reducing the atomic weight (average) of lithium to 6.941.

The atomic mass (m_a) is the mass of an atom. Its unit is the unified atomic mass units (symbol: u, or Da) where 1 unified atomic mass unit is defined as ​¹⁄₁₂ of the mass of a single carbon-12 atom, at rest.^[1] For atoms, the protons and neutrons of the nucleus account for almost all of the mass, and the atomic mass measured in u has nearly the same value as the mass number.

When divided by unified atomic mass units or daltons to form a pure numeric ratio, the atomic mass of an atom becomes a dimensionless value called the relative isotopic mass (see section below). Thus, the atomic mass of a carbon-12 atom is 12 u or 12 daltons (Da), but the relative isotopic mass of a carbon-12 atom is simply 12.

The atomic mass or relative isotopic mass refers to the mass of a single particle, and therefore is tied to a certain specific isotope of an element. The dimensionless standard atomic weight instead refers to the average (mathematical mean) of atomic mass values of a typical naturally-occurring mixture of isotopes for a sample of an element. Atomic mass values are thus commonly reported to many more significant figures than atomic weights. Standard atomic weight is related to atomic mass by the abundance ranking of isotopes for each element. It is usually about the same value as the atomic mass of the most abundant isotope, other than what looks like (but is not actually) a rounding difference.

The atomic mass of atoms, ions, or atomic nuclei is slightly less than the sum of the masses of their constituent protons, neutrons, and electrons, due to binding energy mass loss (as per E=mc²).^[2]

Relative isotopic mass: the same quantity as atomic mass, but with different units

Relative isotopic mass (a property of a single atom) is not to be confused with the averaged quantity atomic weight (see above), that is an average of values for many atoms in a given sample of a chemical element.

Relative isotopic mass is similar to atomic mass and has exactly the same numerical value as atomic mass, whenever atomic mass is expressed in unified atomic mass units. The only difference in that case, is that relative isotopic mass is a pure number with no units. This loss of units results from the use of a scaling ratio with respect to a carbon-12 standard, and the word "relative" in the term "relative isotopic mass" refers to this scaling relative to carbon-12.

The relative isotopic mass, then, is the mass of a given isotope (specifically, any single nuclide), when this value is scaled by the mass of carbon-12, when the latter is set equal to 12. Equivalently, the relative isotopic mass of an isotope or nuclide is the mass of the isotope relative to 1/12 of the mass of a carbon-12 atom.

For example, the relative isotopic mass of a carbon-12 atom is exactly 12. For comparison, the atomic mass of a carbon-12 atom is exactly 12 daltons or 12 unified atomic mass units. Alternately, the atomic mass of a carbon-12 atom may be expressed in any other mass units: for example, the atomic mass of a carbon-12 atom is about 1.998467052 × 10⁻²⁶ kilograms.

As in the case of atomic mass, no nuclides other than carbon-12 have exactly whole-number values of relative isotopic mass. As is the case for the related atomic mass when expressed in unified atomic mass units or daltons, the relative isotopic mass numbers of nuclides other than carbon-12 are not whole numbers, but are always close to whole numbers. This is discussed more fully below.

Similar terms for different quantities

The atomic mass and relative isotopic mass are sometimes confused, or incorrectly used, as synonyms of standard atomic weight (also known as atomic weight) and the standard atomic weight (a particular variety of atomic weight, in the sense that is a standardized atomic weight). However, as noted in the introduction, atomic weight and standard atomic weight represent terms for (abundance-weighted) averages of atomic masses in elemental samples, not for single nuclides. As such, atomic weight and standard atomic weight often differ numerically from relative isotopic mass and atomic mass, and they can also have different units than atomic mass when this quantity is not expressed in unified atomic mass units (see the linked article for atomic weight).

The atomic mass (relative isotopic mass) is defined as the mass of a single atom, which can only be one isotope (nuclide) at a time, and is not an abundance-weighted average, as in the case of relative atomic mass/atomic weight. The atomic mass or relative isotopic mass of each isotope and nuclide of a chemical element is therefore a number that can in principle be measured to a very great precision, since every specimen of such a nuclide is expected to be exactly identical to every other specimen, as all atoms of a given type in the same energy state, and every specimen of a particular nuclide, are expected to be exactly identical in mass to every other specimen of that nuclide. For example, every atom of oxygen-16 is expected to have exactly the same atomic mass (relative isotopic mass) as every other atom of oxygen-16.

In the case of many elements that have one naturally occurring isotope (mononuclidic elements) or one dominant isotope, the actual numerical similarity/difference between the atomic mass of the most common isotope, and the (standard) relative atomic mass or (standard) atomic weight can be small or even nil, and does not affect most bulk calculations. However, such an error can exist and even be important when considering individual atoms for elements that are not mononuclidic.

For non-mononuclidic elements that have more than one common isotope, the numerical difference in relative atomic mass (atomic weight) from even the most common relative isotopic mass, can be half a mass unit or more (e.g. see the case of chlorine where atomic weight and standard atomic weight are about 35.45). The atomic mass (relative isotopic mass) of an uncommon isotope can differ from the relative atomic mass, atomic weight, or standard atomic weight, by several mass units.

Atomic masses expressed in unified atomic mass units (i.e. relative isotopic masses) are always close to whole-number values, but never (except in the case of carbon-12) exactly a whole number, for two reasons:

• protons and neutrons have different masses, and different nuclides have different ratios of protons and neutrons.
• atomic masses are reduced, to different extents, by their binding energies.

The ratio of atomic mass to mass number (number of nucleons) varies from about 0.99884 for ⁵⁶Fe to 1.00782505 for ¹H.

Any mass defect due to nuclear binding energy is experimentally a small fraction (less than 1%) of the mass of equal number of free nucleons. When compared to the average mass per nucleon in carbon-12, which is moderately strongly-bound compared with other atoms, the mass defect of binding for most atoms is an even smaller fraction of a dalton (unified atomic mass unit, based on carbon-12). Since free protons and neutrons differ from each other in mass by a small fraction of a dalton (about 0.0014 u), rounding the relative isotopic mass, or the atomic mass of any given nuclide given in daltons to the nearest whole number always gives the nucleon count, or mass number. Additionally, the neutron count (neutron number) may then be derived by subtracting the number of protons (atomic number) from the mass number (nucleon count).

Mass defects in atomic masses

Binding energy per nucleon of common isotopes. A graph of the ratio of mass number to atomic mass would be similar.

The amount that the ratio of atomic masses to mass number deviates from 1 is as follows: the deviation starts positive at hydrogen-1, then decreases until it reaches a local minimum at helium-4. Isotopes of lithium, beryllium, and boron are less strongly bound than helium, as shown by their increasing mass-to-mass number ratios.

At carbon, the ratio of mass (in daltons) to mass number is defined as 1, and after carbon it becomes less than one until a minimum is reached at iron-56 (with only slightly higher values for iron-58 and nickel-62), then increases to positive values in the heavy isotopes, with increasing atomic number. This corresponds to the fact that nuclear fission in an element heavier than zirconium produces energy, and fission in any element lighter than niobium requires energy. On the other hand, nuclear fusion of two atoms of an element lighter than scandium (except for helium) produces energy, whereas fusion in elements heavier than calcium requires energy. The fusion of two atoms of He-4 to give beryllium-8 would require energy, and the beryllium would quickly fall apart again. He-4 can fuse with tritium (H-3) or with He-3, and these processes occurred during Big Bang nucleosynthesis. The formation of elements with more than seven nucleons requires the fusion of three atoms of He-4 in the so-called triple alpha process, skipping over lithium, beryllium, and boron to produce carbon.

Here are some values of the ratio of atomic mass to mass number:

Nuclide	Ratio of atomic mass to mass number
1H	1.00782505
2H	1.0070508885
3H	1.0053497592
3He	1.0053431064
4He	1.0006508135
6Li	1.0025204658
12C	1
14N	1.0002195718
16O	0.9996821637
56Fe	0.9988381696
210Po	0.9999184462
232Th	1.0001640315
238U	1.0002133958

Measurement of atomic masses

Direct comparison and measurement of the masses of atoms is achieved with mass spectrometry.

Conversion factor between atomic mass units and grams

The standard scientific unit used to quantify the amount of a substance in macroscopic quantities is the mole (symbol: mol), which is defined arbitrarily as the amount of a substance which has as many atoms or molecules as there are atoms in 12 grams of the carbon isotope C-12. The number of atoms in a mole is called Avogadro's number, the value of which is approximately 6.022 × 10²³.

One mole of a substance always contains almost exactly the standard atomic weight or molar mass of that substance; however, this may or may not be true for the atomic mass, depending on whether or not the element exists naturally in more than one isotope. For example, the standard atomic weight of iron is 55.847 g/mol, and therefore one mole of iron as commonly found on earth has a mass of 55.847 grams. The atomic mass of the ⁵⁶Fe isotope is 55.935 u and one mole of ⁵⁶Fe atoms would then in theory have a mass of 55.935 g, but such amounts of pure ⁵⁶Fe have never been found (or separated out) on Earth. However, there are 22 mononuclidic elements of which essentially only a single isotope is found in nature (common examples are fluorine, sodium, aluminum and phosphorus) and for these elements the standard atomic weight and atomic mass are the same. Samples of these elements therefore may serve as reference standards for certain atomic mass values.

The formula for conversion between atomic mass units and SI mass in grams for a single atom is:

${\displaystyle 1\ {\rm {u}}={M_{\rm {u}} \over N_{\rm {A}}}\ ={{1\ {\rm {g/mol}}} \over N_{\rm {A}}}}$

where ${\displaystyle M_{\rm {u}}}$ is the Molar mass constant and ${\displaystyle N_{\rm {A}}}$ is the Avogadro constant.

Relationship between atomic and molecular masses

Similar definitions apply to molecules. One can compute the molecular mass of a compound by adding the atomic masses of its constituent atoms (nuclides). One can compute the molar mass of a compound by adding the relative atomic masses of the elements given in the chemical formula. In both cases the multiplicity of the atoms (the number of times it occurs) must be taken into account, usually by multiplication of each unique mass by its multiplicity.

History

The first scientists to determine relative atomic masses were John Dalton and Thomas Thomson between 1803 and 1805 and Jöns Jakob Berzelius between 1808 and 1826. Relative atomic mass (Atomic weight) was originally defined relative to that of the lightest element, hydrogen, which was taken as 1.00, and in the 1820s Prout's hypothesis stated that atomic masses of all elements would prove to be exact multiples of that of hydrogen. Berzelius, however, soon proved that this was not even approximately true, and for some elements, such as chlorine, relative atomic mass, at about 35.5, falls almost exactly halfway between two integral multiples of that of hydrogen. Still later, this was shown to be largely due to a mix of isotopes, and that the atomic masses of pure isotopes, or nuclides, are multiples of the hydrogen mass, to within about 1%.

In the 1860s Stanislao Cannizzaro refined relative atomic masses by applying Avogadro's law (notably at the Karlsruhe Congress of 1860). He formulated a law to determine relative atomic masses of elements: the different quantities of the same element contained in different molecules are all whole multiples of the atomic weight and determined relative atomic masses and molecular masses by comparing the vapor density of a collection of gases with molecules containing one or more of the chemical element in question.^[3]

In the 20th century, until the 1960s chemists and physicists used two different atomic-mass scales. The chemists used a "atomic mass unit" (amu) scale such that the natural mixture of oxygen isotopes had an atomic mass 16, while the physicists assigned the same number 16 to only the atomic mass of the most common oxygen isotope (¹⁶O, containing eight protons and eight neutrons). However, because oxygen-17 and oxygen-18 are also present in natural oxygen this led to two different tables of atomic mass. The unified scale based on carbon-12, ¹²C, met the physicists' need to base the scale on a pure isotope, while being numerically close to the chemists' scale.

The term atomic weight is being phased out slowly and being replaced by relative atomic mass, in most current usage. This shift in nomenclature reaches back to the 1960s and has been the source of much debate in the scientific community, which was triggered by the adoption of the unified atomic mass unit and the realization that weight was in some ways an inappropriate term. The argument for keeping the term "atomic weight" was primarily that it was a well understood term to those in the field, that the term "atomic mass" was already in use (as it is currently defined) and that the term "relative atomic mass" might be easily confused with relative isotopic mass (the mass of a single atom of a given nuclide, expressed dimensionlessly relative to 1/12 of the mass of carbon-12; see section above).

In 1979, as a compromise, the term "relative atomic mass" was introduced as a secondary synonym for atomic weight. Twenty years later the primacy of these synonyms was reversed, and the term "relative atomic mass" is now the preferred term.

However, the term "standard atomic weights" (referring to the standardized expectation atomic weights of differing samples) have maintained the same name.^[4] In the case of this latter term, simple replacement of the "atomic weight" term with "relative atomic mass" would have resulted in the term "standard relative atomic mass."

Henry Moseley

From Wikipedia, the free encyclopedia

Henry Moseley
Henry G. J. Moseley in the Balliol-Trinity Laboratories, Oxford University (1910).
Born	23 November 1887 Weymouth, Dorset, England
Died	10 August 1915 (aged 27) Gallipoli, Turkey
Nationality	English
Citizenship	British
Education	Trinity College, University of Oxford University of Manchester
Known for	Atomic Number, Moseley's Law
Awards	Matteucci Medal (1919)
Scientific career
Fields	Physics, chemistry
Influences	Ernest Rutherford

Henry Gwyn Jeffreys Moseley (23 November 1887 – 10 August 1915) was an English physicist, whose contribution to the science of physics was the justification from physical laws of the previous empirical and chemical concept of the atomic number. This stemmed from his development of Moseley's law in X-ray spectra.

Moseley's law advanced atomic physics, nuclear physics and quantum physics by providing the first experimental evidence in favour of Niels Bohr's theory, aside from the hydrogen atom spectrum which the Bohr theory was designed to reproduce. That theory refined Ernest Rutherford's and Antonius van den Broek's model, which proposed that the atom contains in its nucleus a number of positive nuclear charges that is equal to its (atomic) number in the periodic table.^[1][2] This remains the accepted model today.

When World War I broke out in Western Europe, Moseley left his research work at the University of Oxford behind to volunteer for the Royal Engineers of the British Army. Moseley was assigned to the force of British Empire soldiers that invaded the region of Gallipoli, Turkey, in April 1915, as a telecommunications officer. Moseley was shot and killed during the Battle of Gallipoli on 10 August 1915, at the age of 27. Experts have speculated that Moseley could have been awarded the Nobel Prize in Physics in 1916, had he not been killed.^[3][4] As a consequence, the British government instituted new policies for eligibility for combat duty.^[5]

Biography

Henry G. J. Moseley, known to his friends as Harry,^[6] was born in Weymouth in Dorset in 1887. His father Henry Nottidge Moseley (1844–91), who died when Henry Moseley was quite young, was a biologist and also a professor of anatomy and physiology at the University of Oxford, who had been a member of the Challenger Expedition.^[7] Moseley's mother was Amabel Gwyn Jeffreys Moseley, the daughter of the Welsh biologist and conchologist John Gwyn Jeffreys.^[a]

Henry Moseley had been a very promising schoolboy at Summer Fields School (where one of the four 'leagues' is named after him), and he was awarded a King's scholarship to attend Eton College.^[8] In 1906 he won the chemistry and physics prizes at Eton.^[9] In 1906, Moseley entered Trinity College of the University of Oxford, where he earned his bachelor's degree. Immediately after graduation from Oxford in 1910, Moseley became a demonstrator in physics at the University of Manchester under the supervision of Sir Ernest Rutherford.^[10] During Moseley's first year at Manchester, he had a teaching load as a graduate teaching assistant, but following that first year, he was reassigned from his teaching duties to work as a graduate research assistant. He declined a fellowship offered by Rutherford, preferring to move back to Oxford, in November 1913, where he was given laboratory facilities but no support.^[11]

Scientific work

Experimenting with the energy of beta particles in 1912, Moseley showed that high potentials were attainable from a radioactive source of radium, thereby inventing the first atomic battery, though he was unable to produce the 1MeV necessary to stop the particles.^[12]

In 1913, Moseley observed and measured the X-ray spectra of various chemical elements (mostly metals) that were found by the method of diffraction through crystals.^[13] This was a pioneering use of the method of X-ray spectroscopy in physics, using Bragg's diffraction law to determine the X-ray wavelengths. Moseley discovered a systematic mathematical relationship between the wavelengths of the X-rays produced and the atomic numbers of the metals that were used as the targets in X-ray tubes. This has become known as Moseley's law.

Before Moseley's discovery, the atomic numbers (or elemental number) of an element had been thought of as a semi-arbitrary sequential number, based on the sequence of atomic masses, but modified somewhat where chemists found this modification to be desirable, such as by the Russian chemist, Dmitri Ivanovich Mendeleev. In his invention of the Periodic Table of the Elements, Mendeleev had interchanged the orders of a few pairs of elements in order to put them in more appropriate places in this table of the elements. For example, the metals cobalt and nickel had been assigned the atomic numbers 27 and 28, respectively, based on their known chemical and physical properties, even though they have nearly the same atomic masses. In fact, the atomic mass of cobalt is slightly larger than that of nickel, which would have placed them in backwards order if they had been placed in the Periodic Table blindly according to atomic mass. Moseley's experiments in X-ray spectroscopy showed directly from their physics that cobalt and nickel have the different atomic numbers, 27 and 28, and that they are placed in the Periodic Table correctly by Moseley's objective measurements of their atomic numbers. Hence, Moseley's discovery demonstrated that the atomic numbers of elements are not just rather arbitrary numbers based on chemistry and the intuition of chemists, but rather, they have a firm experimental basis from the physics of their X-ray spectra.

In addition, Moseley showed that there were gaps in the atomic number sequence at numbers 43, 61, 72, and 75. These spaces are now known, respectively, to be the places of the radioactive synthetic elements technetium and promethium, and also the last two quite rare naturally occurring stable elements hafnium (discovered 1923) and rhenium (discovered 1925). Nothing was known about these four elements in Moseley's lifetime, not even their very existence. Based on the intuition of a very experienced chemist, Dmitri Mendeleev had predicted the existence of a missing element in the Periodic Table, which was later found to be filled by technetium, and Bohuslav Brauner had predicted the existence of another missing element in this Table, which was later found to be filled by promethium. Henry Moseley's experiments confirmed these predictions, by showing exactly what the missing atomic numbers were, 43 and 61. In addition, Moseley predicted the existence of two more undiscovered elements, those with the atomic numbers 72 and 75, and gave very strong evidence that there were no other gaps in the Periodic Table between the elements aluminium (atomic number 13) and gold (atomic number 79).

This latter question about the possibility of more undiscovered ("missing") elements had been a standing problem among the chemists of the world, particularly given the existence of the large family of the lanthanide series of rare earth elements. Moseley was able to demonstrate that these lanthanide elements, i.e. lanthanum through lutetium, must have exactly 15 members – no more and no less. The number of elements in the lanthanides had been a question that was very far from being settled by the chemists of the early 20th Century. They could not yet produce pure samples of all the rare-earth elements, even in the form of their salts, and in some cases they were unable to distinguish between mixtures of two very similar (adjacent) rare-earth elements from the nearby pure metals in the Periodic Table. For example, there was a so-called "element" that was even given the chemical name of "didymium". "Didymium" was found some years later to be simply a mixture of two genuine rare-earth elements, and these were given the names neodymium and praseodymium, meaning "new twin" and "green twin". Also, the method of separating the rare-earth elements by the method of ion exchange had not been invented yet in Moseley's time.

Moseley's method in early X-ray spectroscopy was able to sort out the above chemical problems promptly, some of which had occupied chemists for a number of years. Moseley also predicted the existence of element 61, a lanthanide whose existence was previously unsuspected. Quite a few years later, this element 61 was created artificially in nuclear reactors and was named promethium.^[14]

Contribution to understanding of the atom

Before Moseley and his law, atomic numbers had been thought of as a semi-arbitrary ordering number, vaguely increasing with atomic weight but not strictly defined by it. Moseley's discovery showed that atomic numbers were not arbitrarily assigned, but rather, they have a definite physical basis. Moseley postulated that each successive element has a nuclear charge exactly one unit greater than its predecessor. Moseley redefined the idea of atomic numbers from its previous status as an ad hoc numerical tag to help sorting the elements into an exact sequence of ascending atomic numbers that made the Periodic Table exact. (This was later to be the basis of the Aufbau principle in atomic studies.) As noted by Bohr, Moseley's law provided a reasonably complete experimental set of data that supported the (new from 1911) conception by Ernest Rutherford and Antonius van den Broek of the atom, with a positively charged nucleus surrounded by negatively charged electrons in which the atomic number is understood to be the exact physical number of positive charges (later discovered and called protons) in the central atomic nuclei of the elements. Moseley mentioned the two scientists above in his research paper, but he did not actually mention Bohr, who was rather new on the scene then. Simple modification of Rydberg's and Bohr's formulas were found to give theoretical justification for Moseley's empirically derived law for determining atomic numbers.

Use of X-ray spectrometer

X-ray spectrometers are the foundation-stones of X-ray crystallography. The X-ray spectrometers as Moseley knew them worked as follows. A glass-bulb electron tube was used, similar to that held by Moseley in the photo at the top of this article. Inside the evacuated tube, electrons were fired at a metallic substance (i.e. a sample of pure element in Moseley's work), causing the ionization of electrons from the inner electron shells of the element. The rebound of electrons into these holes in the inner shells next causes the emission of X-ray photons that were led out of the tube in a semi-beam, through an opening in the external X-ray shielding. These are next diffracted by a standardized salt crystal, with angular results read out as photographic lines by the exposure of an X-ray film fixed at the outside the vacuum tube at a known distance. Application of Bragg's law (after some initial guesswork of the mean distances between atoms in the metallic crystal, based on its density) next allowed the wavelength of the emitted -rays to be calculated.

Moseley participated in the design and development of early X-ray spectrometry equipment, learning some techniques from William Henry Bragg and William Lawrence Bragg at the University of Leeds, and developing others himself. Many of the techniques of X-ray spectroscopy were inspired by the methods that are used with visible light spectroscopes and spectrograms, by substituting crystals, ionization chambers, and photographic plates for their analogs in light spectroscopy. In some cases, Moseley found it necessary to modify his equipment to detect particularly soft [lower frequency] X-rays that could not penetrate either air or paper, by working with his instruments in a vacuum chamber.

Death and aftermath

Sometime in the first half of 1914, Moseley resigned from his position at Manchester, with plans to return to Oxford and continue his physics research there. However, World War I broke out in August 1914, and Moseley turned down this job offer to instead enlist with the Royal Engineers of the British Army. His family and friends tried to persuade him not to join, but he thought it was his duty.^[15] Moseley served as a technical officer in communications during the Battle of Gallipoli, in Turkey, beginning in April 1915, where he was killed in action on 10 August 1915. Moseley was shot in the head by a Turkish sniper while in the act of telephoning a military order.

Blue plaque erected by the Royal Society of Chemistry on the Townsend Building of the Clarendon Laboratory at Oxford in 2007, commemorating Moseley's early 20th-century research work on X-rays emitted by elements.

Only twenty-seven years old at the time of his death, Moseley could, in the opinion of some scientists, have contributed much to the knowledge of atomic structure had he survived. Niels Bohr said in 1962 that the Rutherford's work "was not taken seriously at all" and that the "great change came from Moseley."^[16]

Robert Millikan wrote, "In a research which is destined to rank as one of the dozen most brilliant in conception, skillful in execution, and illuminating in results in the history of science, a young man twenty-six years old threw open the windows through which we can glimpse the sub-atomic world with a definiteness and certainty never dreamed of before. Had the European War had no other result than the snuffing out of this young life, that alone would make it one of the most hideous and most irreparable crimes in history."^[17]

Isaac Asimov wrote, "In view of what he [Moseley] might still have accomplished … his death might well have been the most costly single death of the War to mankind generally."^[18] Because of Moseley's death in World War I, and after much lobbying by Ernest Rutherford,^[19] the British government instituted a policy of no longer allowing its prominent and promising scientists to enlist for combat duty in the armed forces of the Crown.^[5]

Isaac Asimov also speculated that, in the event that he had not been killed while in the service of the British Empire, Moseley might very well have been awarded the 1916 Nobel Prize in Physics, which, along with the prize for chemistry, was not awarded to anyone that year. Additional credence is given to this idea by noting the recipients of the Nobel Prize in Physics in the two preceding years, 1914 and 1915, and in the following year, 1917. In 1914, Max von Laue of Germany won the Nobel Prize in Physics for his discovery of the diffraction of X-rays by crystals, which was a crucial step towards the invention of X-ray spectroscopy. Then, in 1915, William Henry Bragg and William Lawrence Bragg, a British father-son pair, shared this Nobel Prize for their discoveries in the reverse problem — determining the structure of crystals using X-rays (Robert Charles Bragg, William Henry Bragg's other son, had also been killed at Gallipoli, on 2 September 1915^[20]). Next, Moseley used the diffraction of X-rays by known crystals in measuring the X-ray spectra of metals. This was the first use of X-ray spectroscopy and also one more step towards the creation of X-ray crystallography. In addition, Moseley's methods and analyses substantially supported the concept of atomic number, placing it on a firm, physics-based foundation. Moreover, Charles Barkla of Great Britain was awarded the Nobel Prize in 1917 for his experimental work in using X-ray spectroscopy in discovering the characteristic X-ray frequencies emitted by the various elements, especially the metals. "Siegbahn, who carried on Moseley's work, received one [the 1924 Nobel Prize in Physics]."^[21] Moseley's discoveries were thus of the same scope as those of his peers, and in addition, Moseley made the larger step of demonstrating the actual foundation of atomic numbers. Ernest Rutherford commented that Moseley's work, "Allowed him to complete during two years at the outset of his career a set of researches that would surely have brought him a Nobel prize".^[22]

Memorial plaques to Moseley were installed at Manchester and Eton, and a Royal Society scholarship, established by his will, had as its second recipient the physicist P. M. S. Blackett, who later became president of the Society.^[23]

Atomic number

From Wikipedia, the free encyclopedia

An explanation of the superscripts and subscripts seen in atomic number notation. Atomic number is the number of protons, and therefore also the total positive charge, in the atomic nucleus.

The Rutherford–Bohr model of the hydrogen atom (Z = 1) or a hydrogen-like ion (Z > 1). In this model it is an essential feature that the photon energy (or frequency) of the electromagnetic radiation emitted (shown) when an electron jumps from one orbital to another, be proportional to the mathematical square of atomic charge (Z²). Experimental measurement by Henry Moseley of this radiation for many elements (from Z = 13 to 92) showed the results as predicted by Bohr. Both the concept of atomic number and the Bohr model were thereby given scientific credence.

The atomic number or proton number (symbol Z) of a chemical element is the number of protons found in the nucleus of an atom. It is identical to the charge number of the nucleus. The atomic number uniquely identifies a chemical element. In an uncharged atom, the atomic number is also equal to the number of electrons.

The sum of the atomic number Z and the number of neutrons, N, gives the mass number A of an atom. Since protons and neutrons have approximately the same mass (and the mass of the electrons is negligible for many purposes) and the mass defect of nucleon binding is always small compared to the nucleon mass, the atomic mass of any atom, when expressed in unified atomic mass units (making a quantity called the "relative isotopic mass"), is within 1% of the whole number A.

Atoms with the same atomic number Z but different neutron numbers N, and hence different atomic masses, are known as isotopes. A little more than three-quarters of naturally occurring elements exist as a mixture of isotopes (see monoisotopic elements), and the average isotopic mass of an isotopic mixture for an element (called the relative atomic mass) in a defined environment on Earth, determines the element's standard atomic weight. Historically, it was these atomic weights of elements (in comparison to hydrogen) that were the quantities measurable by chemists in the 19th century.

The conventional symbol Z comes from the German word Zahl meaning number, which, prior to the modern synthesis of ideas from chemistry and physics, merely denoted an element's numerical place in the periodic table, whose order is approximately, but not completely, consistent with the order of the elements by atomic weights. Only after 1915, with the suggestion and evidence that this Z number was also the nuclear charge and a physical characteristic of atoms, did the word Atomzahl (and its English equivalent atomic number) come into common use in this context.

History

The periodic table and a natural number for each element

Russian chemist Dmitri Mendeleev, creator of the periodic table.

Loosely speaking, the existence or construction of a periodic table of elements creates an ordering of the elements, and so they can be numbered in order.

Dmitri Mendeleev claimed that he arranged his first periodic tables in order of atomic weight ("Atomgewicht").^[1] However, in consideration of the elements' observed chemical properties, he changed the order slightly and placed tellurium (atomic weight 127.6) ahead of iodine (atomic weight 126.9).^[1][2] This placement is consistent with the modern practice of ordering the elements by proton number, Z, but that number was not known or suspected at the time.

A simple numbering based on periodic table position was never entirely satisfactory, however. Besides the case of iodine and tellurium, later several other pairs of elements (such as argon and potassium, cobalt and nickel) were known to have nearly identical or reversed atomic weights, thus requiring their placement in the periodic table to be determined by their chemical properties. However the gradual identification of more and more chemically similar lanthanide elements, whose atomic number was not obvious, led to inconsistency and uncertainty in the periodic numbering of elements at least from lutetium (element 71) onwards (hafnium was not known at this time).

Niels Bohr, creator of the Bohr model.

The Rutherford-Bohr model and van den Broek

In 1911, Ernest Rutherford gave a model of the atom in which a central core held most of the atom's mass and a positive charge which, in units of the electron's charge, was to be approximately equal to half of the atom's atomic weight, expressed in numbers of hydrogen atoms. This central charge would thus be approximately half the atomic weight (though it was almost 25% different from the atomic number of gold (Z = 79, A = 197), the single element from which Rutherford made his guess). Nevertheless, in spite of Rutherford's estimation that gold had a central charge of about 100 (but was element Z = 79 on the periodic table), a month after Rutherford's paper appeared, Antonius van den Broek first formally suggested that the central charge and number of electrons in an atom was exactly equal to its place in the periodic table (also known as element number, atomic number, and symbolized Z). This proved eventually to be the case.

Moseley's 1913 experiment

Henry Moseley in his lab.

The experimental position improved dramatically after research by Henry Moseley in 1913.^[3] Moseley, after discussions with Bohr who was at the same lab (and who had used Van den Broek's hypothesis in his Bohr model of the atom), decided to test Van den Broek's and Bohr's hypothesis directly, by seeing if spectral lines emitted from excited atoms fitted the Bohr theory's postulation that the frequency of the spectral lines be proportional to the square of Z.

To do this, Moseley measured the wavelengths of the innermost photon transitions (K and L lines) produced by the elements from aluminum (Z = 13) to gold (Z = 79) used as a series of movable anodic targets inside an x-ray tube.^[4] The square root of the frequency of these photons (x-rays) increased from one target to the next in an arithmetic progression. This led to the conclusion (Moseley's law) that the atomic number does closely correspond (with an offset of one unit for K-lines, in Moseley's work) to the calculated electric charge of the nucleus, i.e. the element number Z. Among other things, Moseley demonstrated that the lanthanide series (from lanthanum to lutetium inclusive) must have 15 members—no fewer and no more—which was far from obvious from the chemistry at that time.

(DJS:  Mosely tragically and needlessly died in WWI, during the futile British attack on Gallipoli.)

Missing elements

After Moseley's death in 1915, the atomic numbers of all known elements from hydrogen to uranium (Z = 92) were examined by his method. There were seven elements (with Z < 92) which were not found and therefore identified as still undiscovered, corresponding to atomic numbers 43, 61, 72, 75, 85, 87 and 91.^[5] From 1918 to 1947, all seven of these missing elements were discovered.^[6] By this time the first four transuranium elements had also been discovered, so that the periodic table was complete with no gaps as far as curium (Z = 96).

The proton and the idea of nuclear electrons

In 1915 the reason for nuclear charge being quantized in units of Z, which were now recognized to be the same as the element number, was not understood. An old idea called Prout's hypothesis had postulated that the elements were all made of residues (or "protyles") of the lightest element hydrogen, which in the Bohr-Rutherford model had a single electron and a nuclear charge of one. However, as early as 1907 Rutherford and Thomas Royds had shown that alpha particles, which had a charge of +2, were the nuclei of helium atoms, which had a mass four times that of hydrogen, not two times. If Prout's hypothesis were true, something had to be neutralizing some of the charge of the hydrogen nuclei present in the nuclei of heavier atoms.

In 1917 Rutherford succeeded in generating hydrogen nuclei from a nuclear reaction between alpha particles and nitrogen gas,^[7] and believed he had proven Prout's law. He called the new heavy nuclear particles protons in 1920 (alternate names being proutons and protyles). It had been immediately apparent from the work of Moseley that the nuclei of heavy atoms have more than twice as much mass as would be expected from their being made of hydrogen nuclei, and thus there was required a hypothesis for the neutralization of the extra protons presumed present in all heavy nuclei. A helium nucleus was presumed to be composed of four protons plus two "nuclear electrons" (electrons bound inside the nucleus) to cancel two of the charges. At the other end of the periodic table, a nucleus of gold with a mass 197 times that of hydrogen, was thought to contain 118 nuclear electrons in the nucleus to give it a residual charge of + 79, consistent with its atomic number.

The discovery of the neutron makes Z the proton number

All consideration of nuclear electrons ended with James Chadwick's discovery of the neutron in 1932. An atom of gold now was seen as containing 118 neutrons rather than 118 nuclear electrons, and its positive charge now was realized to come entirely from a content of 79 protons. After 1932, therefore, an element's atomic number Z was also realized to be identical to the proton number of its nuclei.

The symbol of Z

The conventional symbol Z possibly comes from the German word Atomzahl (atomic number).^[8] However, prior to 1915, the word Zahl (simply number) was used for an element's assigned number in the periodic table.

Chemical properties

Each element has a specific set of chemical properties as a consequence of the number of electrons present in the neutral atom, which is Z (the atomic number). The configuration of these electrons follows from the principles of quantum mechanics. The number of electrons in each element's electron shells, particularly the outermost valence shell, is the primary factor in determining its chemical bonding behavior. Hence, it is the atomic number alone that determines the chemical properties of an element; and it is for this reason that an element can be defined as consisting of any mixture of atoms with a given atomic number.

New elements

The quest for new elements is usually described using atomic numbers. As of 2010, all elements with atomic numbers 1 to 118 have been observed. Synthesis of new elements is accomplished by bombarding target atoms of heavy elements with ions, such that the sum of the atomic numbers of the target and ion elements equals the atomic number of the element being created. In general, the half-life becomes shorter as atomic number increases, though an "island of stability" may exist for undiscovered isotopes with certain numbers of protons and neutrons.