"An abstraction" is the outcome of this process—a concept that acts as a super-categorical noun for all subordinate concepts, and connects any related concepts as a group, field, or category.
Conceptual abstractions may be formed by filtering the information content of a concept or an observable phenomenon, selecting only the aspects which are relevant for a particular subjectively valued purpose. For example, abstracting a leather soccer ball to the more general idea of a ball selects only the information on general ball attributes and behavior, excluding, but not eliminating, the other phenomenal and cognitive characteristics of that particular ball. In a type–token distinction, a type (e.g., a 'ball') is more abstract than its tokens (e.g., 'that leather soccer ball').
Abstraction in its secondary use is a material process, discussed in the themes below.
Origins
Thinking in abstractions is considered by anthropologists, archaeologists, and sociologists to be one of the key traits in modern human behaviour,
which is believed to have developed between 50,000 and 100,000 years
ago. Its development is likely to have been closely connected with the
development of human language, which (whether spoken or written) appears to both involve and facilitate abstract thinking.
History
Abstraction
involves induction of ideas or the synthesis of particular facts into
one general theory about something. It is the opposite of specification,
which is the analysis or breaking-down of a general idea or abstraction
into concrete facts. Abstraction can be illustrated with Francis Bacon's Novum Organum (1620), a book of modern scientific philosophy written in the late Elizabethan era of England to encourage modern thinkers to collect specific facts before making any generalizations.
Bacon used and promoted induction as an abstraction tool, and it countered the ancient deductive-thinking approach that had dominated the intellectual world since the times of Greek philosophers like Thales, Anaximander, and Aristotle.
Thales (c. 624–546 BCE) believed that everything in the universe comes
from one main substance, water. He deduced or specified from a general
idea, "everything is water", to the specific forms of water such as ice,
snow, fog, and rivers.
Modern scientists can also use the opposite approach of
abstraction, or going from particular facts collected into one general
idea, such as the motion of the planets (Newton (1642–1727)). When determining that the sun is the center of our solar system (Copernicus
(1473–1543)), scientists had to utilize thousands of measurements to
finally conclude that Mars moves in an elliptical orbit about the sun (Kepler (1571–1630)), or to assemble multiple specific facts into the law of falling bodies (Galileo (1564–1642)).
Themes
Compression
An abstraction can be seen as a compression process, mapping multiple different pieces of constituent data to a single piece of abstract data;
based on similarities in the constituent data, for example, many
different physical cats map to the abstraction "CAT". This conceptual
scheme emphasizes the inherent equality of both constituent and abstract
data, thus avoiding problems arising from the distinction between
"abstract" and "concrete".
In this sense the process of abstraction entails the identification of
similarities between objects, and the process of associating these
objects with an abstraction (which is itself an object). For example, picture 1 below illustrates the concrete relationship "Cat sits on Mat".
Chains of abstractions can be construed, moving from neural impulses arising from sensory perception to basic abstractions such as color or shape, to experiential abstractions such as a specific cat, to semantic abstractions such as the "idea" of a CAT, to classes of objects such as "mammals" and even categories such as "object" as opposed to "action".
- For example, graph 1 below expresses the abstraction "agent sits on location". This conceptual scheme entails no specific hierarchical taxonomy (such as the one mentioned involving cats and mammals), only a progressive exclusion of detail.
Instantiation
Non-existent
things in any particular place and time are often seen as abstract. By
contrast, instances, or members, of such an abstract thing might exist
in many different places and times.
Those abstract things are then said to be multiply instantiated, in the sense of picture 1, picture 2, etc., shown below. It is not sufficient, however, to define abstract ideas as those that can be instantiated and to define abstraction
as the movement in the opposite direction to instantiation. Doing so
would make the concepts "cat" and "telephone" abstract ideas since
despite their varying appearances, a particular cat or a particular
telephone is an instance of the concept "cat" or the concept
"telephone". Although the concepts "cat" and "telephone" are abstractions, they are not abstract in the sense of the objects in graph 1 below. We might look at other graphs, in a progression from cat to mammal to animal, and see that animal is more abstract than mammal; but on the other hand mammal is a harder idea to express, certainly in relation to marsupial or monotreme.
Perhaps confusingly, some philosophies refer to tropes (instances of properties) as abstract particulars—e.g., the particular redness of a particular apple is an abstract particular. This is similar to qualia and sumbebekos.
Material process
Still
retaining the primary meaning of 'abstrere' or 'to draw away from', the
abstraction of money, for example, works by drawing away from the
particular value of things allowing completely incommensurate objects to
be compared (see the section on 'Physicality' below). Karl Marx's writing on the commodity abstraction recognizes a parallel process.
The state (polity)
as both concept and material practice exemplifies the two sides of this
process of abstraction. Conceptually, 'the current concept of the state
is an abstraction from the much more concrete early-modern use as the
standing or status of the prince, his visible estates'. At the same
time, materially, the 'practice of statehood is now constitutively and
materially more abstract than at the time when princes ruled as the
embodiment of extended power'.
Ontological status
The way that physical objects, like rocks and trees, have being differs from the way that properties of abstract concepts or relations have being, for example the way the concrete, particular, individuals pictured in picture 1 exist differs from the way the concepts illustrated in graph 1 exist. That difference accounts for the ontological
usefulness of the word "abstract". The word applies to properties and
relations to mark the fact that, if they exist, they do not exist in
space or time, but that instances of them can exist, potentially in many
different places and times.
Physicality
A physical object (a possible referent of a concept or word) is considered concrete (not abstract) if it is a particular individual
that occupies a particular place and time. However, in the secondary
sense of the term 'abstraction', this physical object can carry
materially abstracting processes. For example, record-keeping aids
throughout the Fertile Crescent
included calculi (clay spheres, cones, etc.) which represented counts
of items, probably livestock or grains, sealed in containers. According
to Schmandt-Besserat & (1981),
these clay containers contained tokens, the total of which were the
count of objects being transferred. The containers thus served as
something of a bill of lading
or an accounts book. In order to avoid breaking open the containers for
the count, marks were placed on the outside of the containers. These
physical marks, in other words, acted as material abstractions of a
materially abstract process of accounting, using conceptual abstractions
(numbers) to communicate its meaning.
Abstract things are sometimes defined as those things that do not exist in reality or exist only as sensory experiences, like the color red.
That definition, however, suffers from the difficulty of deciding which
things are real (i.e. which things exist in reality). For example, it
is difficult to agree to whether concepts like God, the number three, and goodness are real, abstract, or both.
An approach to resolving such difficulty is to use predicates as a general term for whether things are variously real, abstract, concrete, or of a particular property (e.g., good). Questions about the properties of things are then propositions about predicates, which propositions remain to be evaluated by the investigator. In the graph 1 below, the graphical relationships like the arrows joining boxes and ellipses might denote predicates.
Referencing and referring
Abstractions sometimes have ambiguous referents; for example, "happiness" (when used as an abstraction) can refer to as many things as there are people and events or states of being which make them happy. Likewise, "architecture" refers not only to the design of safe, functional buildings, but also to elements of creation and innovation which aim at elegant solutions to construction problems, to the use of space, and to the attempt to evoke an emotional response in the builders, owners, viewers and users of the building.
Simplification and ordering
Abstraction uses a strategy of simplification, wherein formerly concrete details are left ambiguous, vague, or undefined; thus effective communication about things in the abstract requires an intuitive
or common experience between the communicator and the communication
recipient. This is true for all verbal/abstract communication.
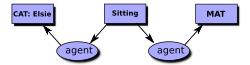
Conceptual graph for A Cat sitting on the Mat (graph 1)
Cat on Mat (picture 1)
For example, many different things can be red. Likewise, many things sit on surfaces (as in picture 1, to the right). The property of redness and the relation sitting-on are therefore abstractions of those objects. Specifically, the conceptual diagram graph 1 identifies only three boxes, two ellipses, and four arrows (and their five labels), whereas the picture 1
shows much more pictorial detail, with the scores of implied
relationships as implicit in the picture rather than with the nine
explicit details in the graph.
Graph 1 details some explicit relationships between the objects of the diagram. For example, the arrow between the agent and CAT:Elsie depicts an example of an is-a relationship, as does the arrow between the location and the MAT. The arrows between the gerund/present participle SITTING and the nouns agent and location express the diagram's basic relationship; "agent is SITTING on location"; Elsie is an instance of CAT.
Although the description sitting-on (graph 1) is more
abstract than the graphic image of a cat sitting on a mat (picture 1),
the delineation of abstract things from concrete things is somewhat
ambiguous; this ambiguity or vagueness is characteristic of abstraction.
Thus something as simple as a newspaper might be specified to six
levels, as in Douglas Hofstadter's illustration of that ambiguity, with a progression from abstract to concrete in Gödel, Escher, Bach (1979):
- (1) a publication
- (2) a newspaper
- (3) The San Francisco Chronicle
- (4) the May 18 edition of The San Francisco Chronicle
- (5) my copy of the May 18 edition of The San Francisco Chronicle
- (6) my copy of the May 18 edition of The San Francisco Chronicle as it was when I first picked it up (as contrasted with my copy as it was a few days later: in my fireplace, burning)
- (5) my copy of the May 18 edition of The San Francisco Chronicle
- (4) the May 18 edition of The San Francisco Chronicle
- (3) The San Francisco Chronicle
- (2) a newspaper
An abstraction can thus encapsulate each of these levels of detail with no loss of generality.
But perhaps a detective or philosopher/scientist/engineer might seek to
learn about something, at progressively deeper levels of detail, to
solve a crime or a puzzle.
Thought processes
In philosophical terminology, abstraction is the thought process wherein ideas are distanced from objects.
As used in different disciplines
In art
Typically, abstraction is used in the arts as a synonym for abstract art
in general. Strictly speaking, it refers to art unconcerned with the
literal depiction of things from the visible world—it can, however,
refer to an object or image which has been distilled from the real
world, or indeed, another work of art.
Artwork that reshapes the natural world for expressive purposes is
called abstract; that which derives from, but does not imitate a
recognizable subject is called nonobjective abstraction. In the 20th
century the trend toward abstraction coincided with advances in science,
technology, and changes in urban life, eventually reflecting an
interest in psychoanalytic theory.
Later still, abstraction was manifest in more purely formal terms, such
as color, freedom from objective context, and a reduction of form to
basic geometric designs.
In computer science
Computer scientists
use abstraction to make models that can be used and re-used without
having to re-write all the program code for each new application on
every different type of computer. They communicate their solutions with the computer by writing source code in some particular computer language which can be translated into machine code
for different types of computers to execute. Abstraction allows program
designers to separate a framework (categorical concepts related to
computing problems) from specific instances which implement details.
This means that the program code can be written so that code doesn't
have to depend on the specific details of supporting applications, operating system
software, or hardware, but on a categorical concept of the solution. A
solution to the problem can then be integrated into the system
framework with minimal additional work. This allows programmers to take
advantage of another programmer's work, while requiring only an abstract
understanding of the implementation of another's work, apart from the
problem that it solves.
In general semantics
Abstractions and levels of abstraction play an important role in the theory of general semantics originated by Alfred Korzybski. Anatol Rapoport wrote: "Abstracting is a mechanism by which an infinite variety of experiences can be mapped on short noises (words)."
In history
Francis Fukuyama defines history as "a deliberate attempt of abstraction in which we separate out important from unimportant events".
In linguistics
Researchers in linguistics
frequently apply abstraction so as to allow analysis of the phenomena
of language at the desired level of detail. A commonly used abstraction,
the phoneme, abstracts speech sounds
in such a way as to neglect details that cannot serve to differentiate
meaning. Other analogous kinds of abstractions (sometimes called "emic units") considered by linguists include morphemes, graphemes, and lexemes.
Abstraction also arises in the relation between syntax, semantics, and pragmatics.
Pragmatics involves considerations that make reference to the user of
the language; semantics considers expressions and what they denote (the designata) abstracted from the language user; and syntax considers only the expressions themselves, abstracted from the designata.
In mathematics
Abstraction in mathematics
is the process of extracting the underlying essence of a mathematical
concept, removing any dependence on real world objects with which it
might originally have been connected, and generalizing it so that it has
wider applications or matching among other abstract descriptions of
equivalent phenomena.
The advantages of abstraction in mathematics are:
- It reveals deep connections between different areas of mathematics
- Known results in one area can suggest conjectures in a related area
- Techniques and methods from one area can be applied to prove results in a related area
The main disadvantage of abstraction is that highly abstract concepts are more difficult to learn, and require a degree of mathematical maturity and experience before they can be assimilated.
In music
In music, the term abstraction can be used to describe improvisatory approaches to interpretation, and may sometimes indicate abandonment of tonality. Atonal music has no key signature, and is characterized by the exploration of internal numeric relationships.
In neurology
A recent meta-analysis suggests that the verbal system has greater
engagement for abstract concepts when the perceptual system is more
engaged for processing of concrete concepts. This is because abstract
concepts elicit greater brain activity in the inferior frontal gyrus and
middle temporal gyrus compared to concrete concepts which elicit
greater activity in the posterior cingulate, precuneus, fusiform gyrus,
and parahippocampal gyrus. Other research into the human brain
suggests that the left and right hemispheres differ in their handling
of abstraction. For example, one meta-analysis reviewing human brain
lesions has shown a left hemisphere bias during tool usage.
In philosophy
Abstraction in philosophy is the process (or, to some, the alleged process) in concept formation of recognizing some set of common features in individuals,
and on that basis forming a concept of that feature. The notion of
abstraction is important to understanding some philosophical
controversies surrounding empiricism and the problem of universals. It has also recently become popular in formal logic under predicate abstraction. Another philosophical tool for discussion of abstraction is thought space.
In psychology
Carl Jung's
definition of abstraction broadened its scope beyond the thinking
process to include exactly four mutually exclusive, different
complementary psychological functions: sensation, intuition, feeling,
and thinking. Together they form a structural totality of the
differentiating abstraction process. Abstraction operates in one of
these functions when it excludes the simultaneous influence of the other
functions and other irrelevancies, such as emotion. Abstraction
requires selective use of this structural split of abilities in the
psyche. The opposite of abstraction is concretism. Abstraction is one of Jung's 57 definitions in Chapter XI of Psychological Types.
There is an abstract thinking, just as there is abstract feeling, sensation and intuition. Abstract thinking singles out the rational, logical qualities ... Abstract feeling does the same with ... its feeling-values. ... I put abstract feelings on the same level as abstract thoughts. ... Abstract sensation would be aesthetic as opposed to sensuous sensation and abstract intuition would be symbolic as opposed to fantastic intuition. (Jung, [1921] (1971): par. 678).
In social theory
In social theory, abstraction is used as both an ideational and material process. Alfred Sohn-Rethel, asked "Can there be abstraction other than by thought?"
He used the example of commodity abstraction to show that abstraction
occurs in practice as people create systems of abstract exchange that
extend beyond the immediate physicality of the object and yet have real
and immediate consequences. This work was extended through the
'Constitutive Abstraction' approach of writers associated with the
Journal Arena. Two books that have taken this theme of the abstraction of social relations as an organizing process in human history are Nation Formation: Towards a Theory of Abstract Community.(1996) and the second volume of Towards a Theory of Abstract Community, published in 2006: Globalism, Nationalism, Tribalism: Bringing Theory Back In – Volume 2 of Towards a Theory of Abstract Community.
These books argue that the nation is an abstract community bringing
together strangers who will never meet as such; thus constituting
materially real and substantial, but abstracted and mediated relations.
The books suggest that contemporary processes of globalization and
mediatization have contributed to materially abstracting relations
between people, with major consequences for how we live our lives.
It can be easily argued that abstraction is an elementary
methodological tool in several disciplines of social science. These
disciplines have definite and different man concepts that highlight
those aspects of man and his behaviour by idealization that are relevant
for the given human science. For example, homo sociologicus is the man
as sociology abstracts and idealizes it, depicting man as a social
being. Moreover, we could talk about homo cyber sapiens (the man who can extend his biologically determined intelligence thanks to new technologies), or homo creativus (who is simply creative).
Abstraction (combined with Weberian idealization) plays a crucial role in economics. Breaking away from directly experienced reality was a common trend in 19th century sciences (especially physics),
and this was the effort which was fundamentally determined the way
economics tried and still tries to approach the economic aspects of
social life. It is abstraction we meet in the case of both Newton’s
physics and the neoclassical theory, since the goal was to grasp the
unchangeable and timeless essence of phenomena. For example, Newton
created the concept of the material point by following the abstraction
method so that he abstracted from the dimension and shape of any
perceptible object, preserving only inertial and translational motion.
Material point is the ultimate and common feature of all bodies. Neoclassical economists created the indefinitely abstract notion of homo economicus
by following the same procedure. Economists abstract from all
individual and personal qualities in order to get to those
characteristics that embody the essence of economic activity.
Eventually, it is the substance of the economic man that they try to
grasp. Any characteristic beyond it only disturbs the functioning of
this essential core.