https://en.wikipedia.org/wiki/Enthalpy
Enthalpy, a property of a thermodynamic system, is equal to the system's internal energy plus the product of its pressure and volume.
In a system enclosed so as to prevent mass transfer, for processes at
constant pressure, the heat absorbed or released equals the change in
enthalpy.
The unit of measurement for enthalpy in the International System of Units (SI) is the joule. Other historical conventional units still in use include the British thermal unit (BTU) and the calorie.
Enthalpy comprises a system's internal energy, which is the energy required to create the system, plus the amount of work required to make room for it by displacing its environment and establishing its volume and pressure.
Enthalpy is a state function that depends only on the prevailing equilibrium state identified by the system's internal energy, pressure, and volume. It is an extensive quantity.
Change in enthalpy (ΔH) is the preferred expression of system energy change in many chemical, biological, and physical measurements at constant pressure, because it simplifies the description of energy transfer. In a system enclosed so as to prevent matter transfer, at constant pressure, the enthalpy change equals the energy transferred from the environment through heat transfer or work other than expansion work.
The total enthalpy, H, of a system cannot be measured directly. The same situation exists in classical mechanics: only a change or difference in energy carries physical meaning. Enthalpy itself is a thermodynamic potential, so in order to measure the enthalpy of a system, we must refer to a defined reference point; therefore what we measure is the change in enthalpy, ΔH. The ΔH is a positive change in endothermic reactions, and negative in heat-releasing exothermic processes.
For processes under constant pressure, ΔH is equal to the change in the internal energy of the system, plus the pressure-volume work p ΔV done by the system on its surroundings (which is positive for an expansion and negative for a contraction). This means that the change in enthalpy under such conditions is the heat absorbed or released by the system through a chemical reaction or by external heat transfer. Enthalpies for chemical substances at constant pressure usually refer to standard state: most commonly 1 bar (100 kPa) pressure. Standard state does not, strictly speaking, specify a temperature, but expressions for enthalpy generally reference the standard heat of formation at 25 °C (298 K).
The enthalpy of an ideal gas is a function of temperature only, so does not depend on pressure. Real materials at common temperatures and pressures usually closely approximate this behavior, which greatly simplifies enthalpy calculation and use in practical designs and analyses.
Enthalpy comprises a system's internal energy, which is the energy required to create the system, plus the amount of work required to make room for it by displacing its environment and establishing its volume and pressure.
Enthalpy is a state function that depends only on the prevailing equilibrium state identified by the system's internal energy, pressure, and volume. It is an extensive quantity.
Change in enthalpy (ΔH) is the preferred expression of system energy change in many chemical, biological, and physical measurements at constant pressure, because it simplifies the description of energy transfer. In a system enclosed so as to prevent matter transfer, at constant pressure, the enthalpy change equals the energy transferred from the environment through heat transfer or work other than expansion work.
The total enthalpy, H, of a system cannot be measured directly. The same situation exists in classical mechanics: only a change or difference in energy carries physical meaning. Enthalpy itself is a thermodynamic potential, so in order to measure the enthalpy of a system, we must refer to a defined reference point; therefore what we measure is the change in enthalpy, ΔH. The ΔH is a positive change in endothermic reactions, and negative in heat-releasing exothermic processes.
For processes under constant pressure, ΔH is equal to the change in the internal energy of the system, plus the pressure-volume work p ΔV done by the system on its surroundings (which is positive for an expansion and negative for a contraction). This means that the change in enthalpy under such conditions is the heat absorbed or released by the system through a chemical reaction or by external heat transfer. Enthalpies for chemical substances at constant pressure usually refer to standard state: most commonly 1 bar (100 kPa) pressure. Standard state does not, strictly speaking, specify a temperature, but expressions for enthalpy generally reference the standard heat of formation at 25 °C (298 K).
The enthalpy of an ideal gas is a function of temperature only, so does not depend on pressure. Real materials at common temperatures and pressures usually closely approximate this behavior, which greatly simplifies enthalpy calculation and use in practical designs and analyses.
History
The word enthalpy was coined relatively late, in the early 20th century, in analogy with the 19th-century terms energy (introduced in its modern sense by Thomas Young in 1802) and entropy (coined in analogy to energy by Rudolf Clausius in 1865). Where energy uses the root of the Greek word ἔργον (ergon) "work" to express the idea of "work-content" and where entropy uses the Greek word τροπή (tropē) "transformation" to express the idea of "transformation-content", so by analogy, enthalpy uses the root of the Greek word θάλπος (thalpos) "warmth, heat" to express the idea of "heat-content".
The term does in fact stand in for the older term "heat content",
a term which is now mostly deprecated as misleading, as dH refers to the amount of heat absorbed in a process at constant pressure only,
but not in the general case (when pressure is variable).
Josiah Willard Gibbs used the term "a heat function for constant pressure" for clarity.
Introduction of the concept of "heat content" H is associated with Benoît Paul Émile Clapeyron and Rudolf Clausius (Clausius–Clapeyron relation, 1850).
The term enthalpy first appeared in print in 1909. It is attributed to Heike Kamerlingh Onnes, who most likely introduced it orally the year before, at the first meeting of the Institute of Refrigeration in Paris.
It gained currency only in the 1920s, notably with the Mollier Steam Tables and Diagrams, published in 1927.
Until the 1920s, the symbol H was used, somewhat inconsistently, for "heat" in general.
The definition of H as strictly limited to enthalpy or "heat content at constant pressure" was formally proposed by Alfred W. Porter in 1922.
Formal definition
The enthalpy of a thermodynamic system is defined as
- H = U + pV,
where
- H is enthalpy,
- U is the internal energy of the system,
- p is pressure,
- V is the volume of the system.
Enthalpy is an extensive property.
This means that, for homogeneous systems, the enthalpy is proportional
to the size of the system. It is convenient to introduce the specific enthalpy h = Hm, where m is the mass of the system, or the molar enthalpy Hm = Hn, where n is the number of moles (h and Hm are intensive properties). For inhomogeneous systems the enthalpy is the sum of the enthalpies of the composing subsystems:
where
- H is the total enthalpy of all the subsystems,
- k refers to the various subsystems,
- Hk refers to the enthalpy of each subsystem.
A closed system may lie in thermodynamic equilibrium in a static gravitational field, so that its pressure p varies continuously with altitude, while, because of the equilibrium requirement, its temperature T is invariant with altitude. (Correspondingly, the system's gravitational potential energy density also varies with altitude.) Then the enthalpy summation becomes an integral:
where
- ρ ("rho") is density (mass per unit volume),
- h is the specific enthalpy (enthalpy per unit mass),
- (ρh) represents the enthalpy density (enthalpy per unit volume),
- dV denotes an infinitesimally small element of volume within the system, for example, the volume of an infinitesimally thin horizontal layer,
- the integral therefore represents the sum of the enthalpies of all the elements of the volume.
The enthalpy of a closed homogeneous system is its cardinal energy function H(S,p), with natural state variables its entropy S[p] and its pressure p. A differential relation for it can be derived as follows. We start from the first law of thermodynamics for closed systems for an infinitesimal process:
where
- ΔQ is a small amount of heat added to the system,
- ΔW a small amount of work performed by the system.
In a homogeneous system in which only reversible, or quasi-static, processes are considered, the second law of thermodynamics gives ΔQ = T dS, with T the absolute temperature and dS the infinitesimal change in entropy S of the system. Furthermore, if only pV work is done, ΔW = p dV. As a result,
Adding d(pV) to both sides of this expression gives
or
So
Other expressions
The above expression of dH
in terms of entropy and pressure may be unfamiliar to some readers.
However, there are expressions in terms of more familiar variables such
as temperature and pressure:
Here Cp is the heat capacity at constant pressure and α is the coefficient of (cubic) thermal expansion:
With this expression one can, in principle, determine the enthalpy if Cp and V are known as functions of p and T.
Note that for an ideal gas, αT = 1, so that
In a more general form, the first law describes the internal energy with additional terms involving the chemical potential and the number of particles of various types. The differential statement for dH then becomes
where μi is the chemical potential per particle for an i-type particle, and Ni is the number of such particles. The last term can also be written as μi dni (with dni the number of moles of component i added to the system and, in this case, μi the molar chemical potential) or as μi dmi (with dmi the mass of component i added to the system and, in this case, μi the specific chemical potential).
Cardinal functions
The enthalpy, H(S[p],p,{Ni}), expresses the thermodynamics of a system in the energy representation. As a function of state, its arguments include both one intensive and several extensive state variables. The state variables S[p], p, and {Ni} are said to be the natural state variables
in this representation. They are suitable for describing processes in
which they are experimentally controlled. For example, in an idealized
process, S[p] and p
can be controlled by preventing heat and matter transfer by enclosing
the system with a wall that is adiathermal and impermeable to matter,
and by making the process infinitely slow, and by varying only the
external pressure on the piston that controls the volume of the system.
This is the basis of the so-called adiabatic approximation that is used in meteorology.
Alongside the enthalpy, with these arguments, the other cardinal
function of state of a thermodynamic system is its entropy, as a
function, S[p](H,p,{Ni}), of the same list of variables of state, except that the entropy, S[p], is replaced in the list by the enthalpy, H. It expresses the entropy representation. The state variables H, p, and {Ni} are said to be the natural state variables in this representation. They are suitable for describing processes in which they are experimentally controlled. For example, H and p
can be controlled by allowing heat transfer, and by varying only the
external pressure on the piston that sets the volume of the system.
Physical interpretation
The U term can be interpreted as the energy required to create the system, and the pV term as the work
that would be required to "make room" for the system if the pressure of
the environment remained constant. When a system, for example, n moles of a gas of volume V at pressure p and temperature T, is created or brought to its present state from absolute zero, energy must be supplied equal to its internal energy U plus pV, where pV is the work done in pushing against the ambient (atmospheric) pressure.
In basic physics and statistical mechanics it may be more interesting to study the internal properties of the system and therefore the internal energy is used. In basic chemistry, experiments are often conducted at constant atmospheric pressure, and the pressure-volume work represents an energy exchange with the atmosphere that cannot be accessed or controlled, so that ΔH is the expression chosen for the heat of reaction.
For a heat engine a change in its internal energy is the difference between the heat input and the pressure-volume work
done by the working substance while a change in its enthalpy is the
difference between the heat input and the work done by the engine:
where the work W done by the engine is:
Relationship to heat
In
order to discuss the relation between the enthalpy increase and heat
supply, we return to the first law for closed systems, with the physics
sign convention: dU = δQ − δW, where the heat δQ is supplied by conduction, radiation, and Joule heating.
We apply it to the special case with a constant pressure at the
surface. In this case the work term can be split into two contributions,
the so-called pV work, given by p dV (where here p is the pressure at the surface, dV is the increase of the volume of the system), and the so-called isochoric mechanical work δW′,
such as stirring by a shaft with paddles or by an externally driven
magnetic field acting on an internal rotor. Cases of long range
electromagnetic interaction require further state variables in their
formulation, and are not considered here. So we write δW = p dV + δW′. In this case the first law reads:
Now,
So
With sign convention of physics, δW' < 0, because isochoric
shaft work done by an external device on the system adds energy to the
system, and may be viewed as virtually adding heat. The only
thermodynamic mechanical work done by the system is expansion work, p dV.
The system is under constant pressure (dp = 0). Consequently, the increase in enthalpy of the system is equal to the added heat and virtual heat:
This is why the now-obsolete term heat content was used in the 19th century.
Applications
In
thermodynamics, one can calculate enthalpy by determining the
requirements for creating a system from "nothingness"; the mechanical
work required, pV, differs based upon the conditions that obtain during the creation of the thermodynamic system.
Energy
must be supplied to remove particles from the surroundings to make
space for the creation of the system, assuming that the pressure p remains constant; this is the pV term. The supplied energy must also provide the change in internal energy, U, which includes activation energies,
ionization energies, mixing energies, vaporization energies, chemical
bond energies, and so forth. Together, these constitute the change in
the enthalpy U + pV. For systems at constant pressure, with no external work done other than the pV work, the change in enthalpy is the heat received by the system.
For a simple system, with a constant number of particles, the
difference in enthalpy is the maximum amount of thermal energy derivable
from a thermodynamic process in which the pressure is held constant.
Heat of reaction
The total enthalpy of a system cannot be measured directly; the enthalpy change of a system is measured instead. Enthalpy change is defined by the following equation:
where
- ΔH is the "enthalpy change",
- Hf is the final enthalpy of the system (in a chemical reaction, the enthalpy of the products),
- Hi is the initial enthalpy of the system (in a chemical reaction, the enthalpy of the reactants).
For an exothermic reaction at constant pressure,
the system's change in enthalpy equals the energy released in the
reaction, including the energy retained in the system and lost through
expansion against its surroundings. In a similar manner, for an endothermic reaction, the system's change in enthalpy is equal to the energy absorbed in the reaction, including the energy lost by the system and gained from compression from its surroundings. If ΔH
is positive, the reaction is endothermic, that is heat is absorbed by
the system due to the products of the reaction having a greater enthalpy
than the reactants. On the other hand, if ΔH is negative, the reaction is exothermic, that is the overall decrease in enthalpy is achieved by the generation of heat.
From the definition of enthalpy as H = U + pV, the enthalpy change at constant pressure ΔH = ΔU + p ΔV. However for most chemical reactions, the work term p ΔV is much smaller than the internal energy change ΔU which is approximately equal to ΔH. As an example, for the combustion of carbon monoxide 2 CO(g) + O2(g) → 2 CO2(g), ΔH = −566.0 kJ and ΔU = −563.5 kJ.
Since the differences are so small, reaction enthalpies are often
loosely described as reaction energies and analyzed in terms of bond energies.
Specific enthalpy
The specific enthalpy of a uniform system is defined as h = Hm where m is the mass of the system. The SI unit for specific enthalpy is joule per kilogram. It can be expressed in other specific quantities by h = u + pv, where u is the specific internal energy, p is the pressure, and v is specific volume, which is equal to 1ρ, where ρ is the density.
Enthalpy changes
An
enthalpy change describes the change in enthalpy observed in the
constituents of a thermodynamic system when undergoing a transformation
or chemical reaction. It is the difference between the enthalpy after
the process has completed, i.e. the enthalpy of the products, and the initial enthalpy of the system, namely the reactants. These processes are reversible and the enthalpy for the reverse process is the negative value of the forward change.
A common standard enthalpy change is the enthalpy of formation,
which has been determined for a large number of substances. Enthalpy
changes are routinely measured and compiled in chemical and physical
reference works, such as the CRC Handbook of Chemistry and Physics. The following is a selection of enthalpy changes commonly recognized in thermodynamics.
When used in these recognized terms the qualifier change is usually dropped and the property is simply termed enthalpy of 'process'.
Since these properties are often used as reference values it is very
common to quote them for a standardized set of environmental parameters,
or standard conditions, including:
- A temperature of 25 °C or 298.15 K,
- A pressure of one atmosphere (1 atm or 101.325 kPa),
- A concentration of 1.0 M when the element or compound is present in solution,
- Elements or compounds in their normal physical states, i.e. standard state.
For such standardized values the name of the enthalpy is commonly prefixed with the term standard, e.g. standard enthalpy of formation.
Chemical properties:
- Enthalpy of reaction, defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of substance reacts completely.
- Enthalpy of formation, defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of a compound is formed from its elementary antecedents.
- Enthalpy of combustion, defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of a substance burns completely with oxygen.
- Enthalpy of hydrogenation, defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of an unsaturated compound reacts completely with an excess of hydrogen to form a saturated compound.
- Enthalpy of atomization, defined as the enthalpy change required to atomize one mole of compound completely.
- Enthalpy of neutralization, defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of water is formed when an acid and a base react.
- Standard Enthalpy of solution, defined as the enthalpy change observed in a constituent of a thermodynamic system when one mole of a solute is dissolved completely in an excess of solvent, so that the solution is at infinite dilution.
- Standard enthalpy of Denaturation (biochemistry), defined as the enthalpy change required to denature one mole of compound.
- Enthalpy of hydration, defined as the enthalpy change observed when one mole of gaseous ions are completely dissolved in water forming one mole of aqueous ions.
Physical properties:
- Enthalpy of fusion, defined as the enthalpy change required to completely change the state of one mole of substance between solid and liquid states.
- Enthalpy of vaporization, defined as the enthalpy change required to completely change the state of one mole of substance between liquid and gaseous states.
- Enthalpy of sublimation, defined as the enthalpy change required to completely change the state of one mole of substance between solid and gaseous states.
- Lattice enthalpy, defined as the energy required to separate one mole of an ionic compound into separated gaseous ions to an infinite distance apart (meaning no force of attraction).
- Enthalpy of mixing, defined as the enthalpy change upon mixing of two (non-reacting) chemical substances.
Open systems
In thermodynamic open systems,
mass (of substances) may flow in and out of the system boundaries. The
first law of thermodynamics for open systems states: The increase in the
internal energy of a system is equal to the amount of energy added to
the system by mass flowing in and by heating, minus the amount lost by
mass flowing out and in the form of work done by the system:
where Uin is the average internal energy entering the system, and Uout is the average internal energy leaving the system.
During steady, continuous
operation, an energy balance applied to an open system equates shaft
work performed by the system to heat added plus net enthalpy added
The region of space enclosed by the boundaries of the open system is usually called a control volume,
and it may or may not correspond to physical walls. If we choose the
shape of the control volume such that all flow in or out occurs
perpendicular to its surface, then the flow of mass into the system
performs work as if it were a piston of fluid pushing mass into the
system, and the system performs work on the flow of mass out as if it
were driving a piston of fluid. There are then two types of work
performed: flow work described above, which is performed on the fluid (this is also often called pV work), and shaft work, which may be performed on some mechanical device.
These two types of work are expressed in the equation
Substitution into the equation above for the control volume (cv) yields:
The definition of enthalpy, H, permits us to use this thermodynamic potential to account for both internal energy and pV work in fluids for open systems:
If we allow also the system boundary to move (e.g. due to moving
pistons), we get a rather general form of the first law for open
systems. In terms of time derivatives it reads:
with sums over the various places k where heat is supplied, mass flows into the system, and boundaries are moving. The Ḣk terms represent enthalpy flows, which can be written as
with ṁk the mass flow and ṅk the molar flow at position k respectively. The term dVkdt represents the rate of change of the system volume at position k that results in pV power done by the system. The parameter P
represents all other forms of power done by the system such as shaft
power, but it can also be, say, electric power produced by an electrical
power plant.
Note that the previous expression holds true only if the kinetic energy flow rate is conserved between system inlet and outlet. Otherwise, it has to be included in the enthalpy balance. During steady-state operation of a device, the average dUdt may be set equal to zero. This yields a useful expression for the average power generation for these devices in the absence of chemical reactions:
where the angle brackets
denote time averages. The technical importance of the enthalpy is
directly related to its presence in the first law for open systems, as
formulated above.
Diagrams
T–s diagram of nitrogen.
The red curve at the left is the melting curve. The red dome represents
the two-phase region with the low-entropy side the saturated liquid and
the high-entropy side the saturated gas. The black curves give the T–s
relation along isobars. The pressures are indicated in bar. The blue
curves are isenthalps (curves of constant enthalpy). The values are
indicated in blue in kJ/kg. The specific points a, b, etc., are treated in the main text.
The enthalpy values of important substances can be obtained using
commercial software. Practically all relevant material properties can be
obtained either in tabular or in graphical form. There are many types
of diagrams, such as h–T diagrams, which give the specific enthalpy as function of temperature for various pressures, and h–p diagrams, which give h as function of p for various T. One of the most common diagrams is the temperature–specific entropy diagram (T–s
diagram). It gives the melting curve and saturated liquid and vapor
values together with isobars and isenthalps. These diagrams are powerful
tools in the hands of the thermal engineer.
Some basic applications
The points a through h in the figure play a role in the discussion in this section.
Point T (K) p (bar) s (kJ/(kg K)) h (kJ/kg) a 300 1 6.85 461 b 380 2 6.85 530 c 300 200 5.16 430 d 270 1 6.79 430 e 108 13 3.55 100 f 77.2 1 3.75 100 g 77.2 1 2.83 28 h 77.2 1 5.41 230
Points e and g are saturated liquids, and point h is a saturated gas.
Throttling
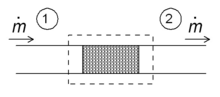
Schematic
diagram of a throttling in the steady state. Fluid enters the system
(dotted rectangle) at point 1 and leaves it at point 2. The mass flow is
ṁ.
One of the simple applications of the concept of enthalpy is the so-called throttling process, also known as Joule-Thomson expansion.
It concerns a steady adiabatic flow of a fluid through a flow
resistance (valve, porous plug, or any other type of flow resistance) as
shown in the figure. This process is very important, since it is at the
heart of domestic refrigerators,
where it is responsible for the temperature drop between ambient
temperature and the interior of the refrigerator. It is also the final
stage in many types of liquefiers.
For a steady state flow regime, the enthalpy of the system (dotted rectangle) has to be constant. Hence
Since the mass flow is constant, the specific enthalpies at the two sides of the flow resistance are the same:
that is, the enthalpy per unit mass does not change during the
throttling. The consequences of this relation can be demonstrated using
the T–s diagram above. Point c
is at 200 bar and room temperature (300 K). A Joule–Thomson expansion
from 200 bar to 1 bar follows a curve of constant enthalpy of roughly
425 kJ/kg (not shown in the diagram) lying between the 400 and 450 kJ/kg
isenthalps and ends in point d, which is at a temperature of
about 270 K. Hence the expansion from 200 bar to 1 bar cools nitrogen
from 300 K to 270 K. In the valve, there is a lot of friction, and a lot
of entropy is produced, but still the final temperature is below the
starting value.
Point e is chosen so that it is on the saturated liquid line with h = 100 kJ/kg. It corresponds roughly with p = 13 bar and T = 108 K. Throttling from this point to a pressure of 1 bar ends in the two-phase region (point f).
This means that a mixture of gas and liquid leaves the throttling
valve. Since the enthalpy is an extensive parameter, the enthalpy in f (hf) is equal to the enthalpy in g (hg) multiplied by the liquid fraction in f (xf) plus the enthalpy in h (hh) multiplied by the gas fraction in f (1 − xf). So
With numbers: 100 = xf × 28 + (1 − xf) × 230, so xf = 0.64. This means that the mass fraction of the liquid in the liquid–gas mixture that leaves the throttling valve is 64%.
Compressors
Schematic
diagram of a compressor in the steady state. Fluid enters the system
(dotted rectangle) at point 1 and leaves it at point 2. The mass flow is
ṁ. A power P is applied and a heat flow Q̇ is released to the surroundings at ambient temperature Ta.
A power P is applied e.g. as electrical power. If the compression is adiabatic,
the gas temperature goes up. In the reversible case it would be at
constant entropy, which corresponds with a vertical line in the T–s diagram. For example, compressing nitrogen from 1 bar (point a) to 2 bar (point b) would result in a temperature increase from 300 K to 380 K. In order to let the compressed gas exit at ambient temperature Ta,
heat exchange, e.g. by cooling water, is necessary. In the ideal case
the compression is isothermal. The average heat flow to the surroundings
is Q̇. Since the system is in the steady state the first law gives
The minimal power needed for the compression is realized if the compression is reversible. In that case the second law of thermodynamics for open systems gives
Eliminating Q̇ gives for the minimal power
For example, compressing 1 kg of nitrogen from 1 bar to 200 bar costs at least (hc − ha) − Ta(sc − sa). With the data, obtained with the T–s diagram, we find a value of (430 − 461) − 300 × (5.16 − 6.85) = 476 kJ/kg.
The relation for the power can be further simplified by writing it as
With dh = T ds + v dp, this results in the final relation