Function (mathematics)

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Function_(mathematics) 

Function
x ↦ f (x)
Examples of domains and codomains
${\displaystyle X}$ → ${\displaystyle \mathbb {B} }$, ${\displaystyle \mathbb {B} }$ → ${\displaystyle X}$, ${\displaystyle \mathbb {B} ^{n}}$ → ${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle \mathbb {Z} }$, ${\displaystyle \mathbb {Z} }$ → ${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle \mathbb {R} }$, ${\displaystyle \mathbb {R} }$ → ${\displaystyle X}$, ${\displaystyle \mathbb {R} ^{n}}$ → ${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle \mathbb {C} }$, ${\displaystyle \mathbb {C} }$ → ${\displaystyle X}$, ${\displaystyle \mathbb {C} ^{n}}$ → ${\displaystyle X}$
Classes/properties
Constant Identity Linear Polynomial Rational Algebraic Analytic Smooth Continuous Measurable Injective Surjective Bijective
Constructions
Restriction Composition λ Inverse
Generalizations
Partial Multivalued Implicit

In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.

Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a function of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly enlarged the domains of application of the concept.

A function is most often denoted by letters such as f, g and h, and the value of a function f at an element x of its domain is denoted by f(x).

A function is uniquely represented by the set of all pairs (x, f (x)), called the graph of the function. When the domain and the codomain are sets of real numbers, each such pair may be thought of as the Cartesian coordinates of a point in the plane. The set of these points is called the graph of the function; it is a popular means of illustrating the function.

Functions are widely used in science, and in most fields of mathematics. It has been said that functions are "the central objects of investigation" in most fields of mathematics.

Schematic depiction of a function described metaphorically as a "machine" or "black box" that for each input yields a corresponding output

 

The red curve is the graph of a function, because any vertical line has exactly one crossing point with the curve.

 

A function that associates any of the four colored shapes to its color.

Definition

Diagram of a function, with domain X = {1, 2, 3} and codomain Y = {A, B, C, D}, which is defined by the set of ordered pairs {(1, D), (2, C), (3, C)} . The image/range is the set {C, D}.

 

This diagram, representing the set of pairs {(1,D), (2,B), (2,C)} , does not define a function. One reason is that 2 is the first element in more than one ordered pair, (2, B) and (2, C), of this set. Two other reasons, also sufficient by themselves, is that neither 3 nor 4 are first elements (input) of any ordered pair therein.

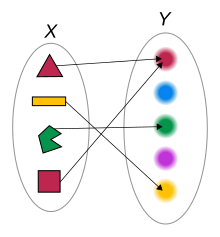
A function from a set X to a set Y is an assignment of an element of Y to each element of X. The set X is called the domain of the function and the set Y is called the codomain of the function.

A function, its domain, and its codomain, are declared by the notation f: X→Y, and the value of a function f at an element x of X, denoted by f(x), is called the image of x under f, or the value of f applied to the argument x.

Functions are also called maps or mappings, though some authors make some distinction between "maps" and "functions" (see § Other terms).

Two functions f and g are equal if their domain and codomain sets are the same and their output values agree on the whole domain. More formally, given f: X → Y and g: X → Y, we have f = g if and only if f(x) = g(x) for all x ∈ X.

The domain and codomain are not always explicitly given when a function is defined, and, without some (possibly difficult) computation, one might only know that the domain is contained in a larger set. Typically, this occurs in mathematical analysis, where "a function from X to Y " often refers to a function that may have a proper subset^{[note 3]} of X as domain. For example, a "function from the reals to the reals" may refer to a real-valued function of a real variable. However, a "function from the reals to the reals" does not mean that the domain of the function is the whole set of the real numbers, but only that the domain is a set of real numbers that contains a non-empty open interval. Such a function is then called a partial function. For example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1/f(x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0.

The range or image of a function is the set of the images of all elements in the domain.

Total, univalent relation

Any subset of the Cartesian product of two sets X and Y defines a binary relation R ⊆ X × Y between these two sets. It is immediate that an arbitrary relation may contain pairs that violate the necessary conditions for a function given above.

A binary relation is univalent (also called right-unique) if

${\displaystyle \forall x\in X,\forall y\in Y,\forall z\in Y,\quad ((x,y)\in R\land (x,z)\in R)\implies y=z.}$

A binary relation is total if

${\displaystyle \forall x\in X,\exists y\in Y,\quad (x,y)\in R.}$

A partial function is a binary relation that is univalent, and a function is a binary relation that is univalent and total.

Various properties of functions and function composition may be reformulated in the language of relations. For example, a function is injective if the converse relation R^T ⊆ Y × X is univalent, where the converse relation is defined as R^T = {(y, x) | (x, y) ∈ R}.

Set exponentiation

See also: Exponentiation § Sets as exponents

The set of all functions from a set ${\displaystyle X}$ to a set ${\displaystyle Y}$ is commonly denoted as

${\displaystyle Y^{X},}$

which is read as ${\displaystyle Y}$ to the power ${\displaystyle X}$.

This notation is the same as the notation for the Cartesian product of a family of copies of ${\displaystyle Y}$ indexed by ${\displaystyle X}$:

${\displaystyle Y^{X}=\prod _{x\in X}Y.}$

The identity of these two notations is motivated by the fact that a function ${\displaystyle f}$ can be identified with the element of the Cartesian product such that the component of index ${\displaystyle x}$ is ${\displaystyle f(x)}$.

When ${\displaystyle Y}$ has two elements, ${\displaystyle Y^{X}}$ is commonly denoted ${\displaystyle 2^{X}}$ and called the powerset of X. It can be identified with the set of all subsets of ${\displaystyle X}$, through the one-to-one correspondence that associates to each subset ${\displaystyle S\subseteq X}$ the function ${\displaystyle f}$ such that ${\displaystyle f(x)=1}$ if ${\displaystyle x\in X}$ and ${\displaystyle f(x)=0}$ otherwise.

Notation

There are various standard ways for denoting functions. The most commonly used notation is functional notation, which is the first notation described below.

Functional notation

In functional notation, the function is immediately given a name, such as f, and its definition is given by what f does to the explicit argument x, using a formula in terms of x. For example, the function which takes a real number as input and outputs that number plus 1 is denoted by

${\displaystyle f(x)=x+1}$.

If a function is defined in this notation, its domain and codomain are implicitly taken to both be ${\displaystyle \mathbb {R} }$, the set of real numbers. If the formula cannot be evaluated at all real numbers, then the domain is implicitly taken to be the maximal subset of ${\displaystyle \mathbb {R} }$ on which the formula can be evaluated; see Domain of a function.

A more complicated example is the function

${\displaystyle f(x)=\sin(x^{2}+1)}$.

In this example, the function f takes a real number as input, squares it, then adds 1 to the result, then takes the sine of the result, and returns the final result as the output.

When the symbol denoting the function consists of several characters and no ambiguity may arise, the parentheses of functional notation might be omitted. For example, it is common to write sin x instead of sin(x).

Functional notation was first used by Leonhard Euler in 1734. Some widely used functions are represented by a symbol consisting of several letters (usually two or three, generally an abbreviation of their name). In this case, a roman type is customarily used instead, such as "sin" for the sine function, in contrast to italic font for single-letter symbols.

When using this notation, one often encounters the abuse of notation whereby the notation f(x) can refer to the value of f at x, or to the function itself. If the variable x was previously declared, then the notation f(x) unambiguously means the value of f at x. Otherwise, it is useful to understand the notation as being both simultaneously; this allows one to denote composition of two functions f and g in a succinct manner by the notation f(g(x)).

However, distinguishing f and f(x) can become important in cases where functions themselves serve as inputs for other functions. (A function taking another function as an input is termed a functional.) Other approaches of notating functions, detailed below, avoid this problem but are less commonly used.

Arrow notation

Arrow notation defines the rule of a function inline, without requiring a name to be given to the function. For example, ${\displaystyle x\mapsto x+1}$ is the function which takes a real number as input and outputs that number plus 1. Again a domain and codomain of ${\displaystyle \mathbb {R} }$ is implied.

The domain and codomain can also be explicitly stated, for example:

${\displaystyle {\begin{aligned}\operatorname {sqr} \colon \mathbb {Z} &\to \mathbb {Z} \\x&\mapsto x^{2}.\end{aligned}}}$

This defines a function sqr from the integers to the integers that returns the square of its input.

As a common application of the arrow notation, suppose ${\displaystyle f\colon X\times X\to Y;\;(x,t)\mapsto f(x,t)}$ is a function in two variables, and we want to refer to a partially applied function ${\displaystyle X\to Y}$ produced by fixing the second argument to the value t₀ without introducing a new function name. The map in question could be denoted ${\displaystyle x\mapsto f(x,t_{0})}$ using the arrow notation. The expression ${\displaystyle x\mapsto f(x,t_{0})}$ (read: "the map taking x to f(x, t₀)") represents this new function with just one argument, whereas the expression f(x₀, t₀) refers to the value of the function f at the point (x₀, t₀).

Index notation

Index notation is often used instead of functional notation. That is, instead of writing f (x), one writes ${\displaystyle f_{x}.}$

This is typically the case for functions whose domain is the set of the natural numbers. Such a function is called a sequence, and, in this case the element ${\displaystyle f_{n}}$ is called the nth element of sequence.

The index notation is also often used for distinguishing some variables called parameters from the "true variables". In fact, parameters are specific variables that are considered as being fixed during the study of a problem. For example, the map ${\displaystyle x\mapsto f(x,t)}$ (see above) would be denoted ${\displaystyle f_{t}}$ using index notation, if we define the collection of maps ${\displaystyle f_{t}}$ by the formula ${\displaystyle f_{t}(x)=f(x,t)}$ for all ${\displaystyle x,t\in X}$.

Dot notation

In the notation ${\displaystyle x\mapsto f(x),}$ the symbol x does not represent any value, it is simply a placeholder meaning that, if x is replaced by any value on the left of the arrow, it should be replaced by the same value on the right of the arrow. Therefore, x may be replaced by any symbol, often an interpunct " ⋅ ". This may be useful for distinguishing the function f (⋅) from its value f (x) at x.

For example, ${\displaystyle a(\cdot )^{2}}$ may stand for the function ${\displaystyle x\mapsto ax^{2}}$, and ${\textstyle \int _{a}^{\,(\cdot )}f(u)\,du}$ may stand for a function defined by an integral with variable upper bound: ${\textstyle x\mapsto \int _{a}^{x}f(u)\,du}$.

Specialized notations

There are other, specialized notations for functions in sub-disciplines of mathematics. For example, in linear algebra and functional analysis, linear forms and the vectors they act upon are denoted using a dual pair to show the underlying duality. This is similar to the use of bra–ket notation in quantum mechanics. In logic and the theory of computation, the function notation of lambda calculus is used to explicitly express the basic notions of function abstraction and application. In category theory and homological algebra, networks of functions are described in terms of how they and their compositions commute with each other using commutative diagrams that extend and generalize the arrow notation for functions described above.

Other terms

For broader coverage of this topic, see Map (mathematics).

 

Term	Distinction from "function"
Map/Mapping	None; the terms are synonymous.
	A map can have any set as its codomain, while, in some contexts, typically in older books, the codomain of a function is specifically the set of real or complex numbers.
	Alternatively, a map is associated with a special structure (e.g. by explicitly specifying a structured codomain in its definition). For example, a linear map.
Homomorphism	A function between two structures of the same type that preserves the operations of the structure (e.g. a group homomorphism).
Morphism	A generalisation of homomorphisms to any category, even when the objects of the category are not sets (for example, a group defines a category with only one object, which has the elements of the group as morphisms; see Category (mathematics) § Examples for this example and other similar ones).

A function is often also called a map or a mapping, but some authors make a distinction between the term "map" and "function". For example, the term "map" is often reserved for a "function" with some sort of special structure (e.g. maps of manifolds). In particular map is often used in place of homomorphism for the sake of succinctness (e.g., linear map or map from G to H instead of group homomorphism from G to H). Some authors reserve the word mapping for the case where the structure of the codomain belongs explicitly to the definition of the function.

Some authors, such as Serge Lang, use "function" only to refer to maps for which the codomain is a subset of the real or complex numbers, and use the term mapping for more general functions.

In the theory of dynamical systems, a map denotes an evolution function used to create discrete dynamical systems. See also Poincaré map.

Whichever definition of map is used, related terms like domain, codomain, injective, continuous have the same meaning as for a function.

Specifying a function

Given a function ${\displaystyle f}$, by definition, to each element ${\displaystyle x}$ of the domain of the function ${\displaystyle f}$, there is a unique element associated to it, the value ${\displaystyle f(x)}$ of ${\displaystyle f}$ at ${\displaystyle x}$. There are several ways to specify or describe how ${\displaystyle x}$ is related to ${\displaystyle f(x)}$, both explicitly and implicitly. Sometimes, a theorem or an axiom asserts the existence of a function having some properties, without describing it more precisely. Often, the specification or description is referred to as the definition of the function ${\displaystyle f}$.

By listing function values

On a finite set, a function may be defined by listing the elements of the codomain that are associated to the elements of the domain. For example, if ${\displaystyle A=\{1,2,3\}}$, then one can define a function ${\displaystyle f\colon A\to \mathbb {R} }$ by ${\displaystyle f(1)=2,f(2)=3,f(3)=4.}$

By a formula

Functions are often defined by a formula that describes a combination of arithmetic operations and previously defined functions; such a formula allows computing the value of the function from the value of any element of the domain. For example, in the above example, ${\displaystyle f}$ can be defined by the formula ${\displaystyle f(n)=n+1}$, for ${\displaystyle n\in \{1,2,3\}}$.

When a function is defined this way, the determination of its domain is sometimes difficult. If the formula that defines the function contains divisions, the values of the variable for which a denominator is zero must be excluded from the domain; thus, for a complicated function, the determination of the domain passes through the computation of the zeros of auxiliary functions. Similarly, if square roots occur in the definition of a function from ${\displaystyle \mathbb {R} }$ to ${\displaystyle \mathbb {R} ,}$ the domain is included in the set of the values of the variable for which the arguments of the square roots are nonnegative.

For example, ${\displaystyle f(x)={\sqrt {1+x^{2}}}}$ defines a function ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ whose domain is ${\displaystyle \mathbb {R} ,}$ because ${\displaystyle 1+x^{2}}$ is always positive if x is a real number. On the other hand, ${\displaystyle f(x)={\sqrt {1-x^{2}}}}$ defines a function from the reals to the reals whose domain is reduced to the interval [−1, 1]. (In old texts, such a domain was called the domain of definition of the function.)

Functions are often classified by the nature of formulas that define them:

• A quadratic function is a function that may be written ${\displaystyle f(x)=ax^{2}+bx+c,}$ where a, b, c are constants.
• More generally, a polynomial function is a function that can be defined by a formula involving only additions, subtractions, multiplications, and exponentiation to nonnegative integers. For example, ${\displaystyle f(x)=x^{3}-3x-1,}$ and ${\displaystyle f(x)=(x-1)(x^{3}+1)+2x^{2}-1.}$
• A rational function is the same, with divisions also allowed, such as ${\displaystyle f(x)={\frac {x-1}{x+1}},}$ and ${\displaystyle f(x)={\frac {1}{x+1}}+{\frac {3}{x}}-{\frac {2}{x-1}}.}$
• An algebraic function is the same, with nth roots and roots of polynomials also allowed.
• An elementary function is the same, with logarithms and exponential functions allowed.

Inverse and implicit functions

A function ${\displaystyle f\colon X\to Y,}$ with domain X and codomain Y, is bijective, if for every y in Y, there is one and only one element x in X such that y = f(x). In this case, the inverse function of f is the function ${\displaystyle f^{-1}\colon Y\to X}$ that maps ${\displaystyle y\in Y}$ to the element ${\displaystyle x\in X}$ such that y = f(x). For example, the natural logarithm is a bijective function from the positive real numbers to the real numbers. It thus has an inverse, called the exponential function, that maps the real numbers onto the positive numbers.

If a function ${\displaystyle f\colon X\to Y}$ is not bijective, it may occur that one can select subsets ${\displaystyle E\subseteq X}$ and ${\displaystyle F\subseteq Y}$ such that the restriction of f to E is a bijection from E to F, and has thus an inverse. The inverse trigonometric functions are defined this way. For example, the cosine function induces, by restriction, a bijection from the interval [0, π] onto the interval [−1, 1], and its inverse function, called arccosine, maps [−1, 1] onto [0, π]. The other inverse trigonometric functions are defined similarly.

More generally, given a binary relation R between two sets X and Y, let E be a subset of X such that, for every ${\displaystyle x\in E,}$ there is some ${\displaystyle y\in Y}$ such that x R y. If one has a criterion allowing selecting such an y for every ${\displaystyle x\in E,}$ this defines a function ${\displaystyle f\colon E\to Y,}$ called an implicit function, because it is implicitly defined by the relation R.

For example, the equation of the unit circle ${\displaystyle x^{2}+y^{2}=1}$ defines a relation on real numbers. If −1 < x < 1 there are two possible values of y, one positive and one negative. For x = ± 1, these two values become both equal to 0. Otherwise, there is no possible value of y. This means that the equation defines two implicit functions with domain [−1, 1] and respective codomains [0, +∞) and (−∞, 0].

In this example, the equation can be solved in y, giving ${\displaystyle y=\pm {\sqrt {1-x^{2}}},}$ but, in more complicated examples, this is impossible. For example, the relation ${\displaystyle y^{5}+y+x=0}$ defines y as an implicit function of x, called the Bring radical, which has ${\displaystyle \mathbb {R} }$ as domain and range. The Bring radical cannot be expressed in terms of the four arithmetic operations and nth roots.

The implicit function theorem provides mild differentiability conditions for existence and uniqueness of an implicit function in the neighborhood of a point.

Using differential calculus

Many functions can be defined as the antiderivative of another function. This is the case of the natural logarithm, which is the antiderivative of 1/x that is 0 for x = 1. Another common example is the error function.

More generally, many functions, including most special functions, can be defined as solutions of differential equations. The simplest example is probably the exponential function, which can be defined as the unique function that is equal to its derivative and takes the value 1 for x = 0.

Power series can be used to define functions on the domain in which they converge. For example, the exponential function is given by ${\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}}$. However, as the coefficients of a series are quite arbitrary, a function that is the sum of a convergent series is generally defined otherwise, and the sequence of the coefficients is the result of some computation based on another definition. Then, the power series can be used to enlarge the domain of the function. Typically, if a function for a real variable is the sum of its Taylor series in some interval, this power series allows immediately enlarging the domain to a subset of the complex numbers, the disc of convergence of the series. Then analytic continuation allows enlarging further the domain for including almost the whole complex plane. This process is the method that is generally used for defining the logarithm, the exponential and the trigonometric functions of a complex number.

By recurrence

Main article: Recurrence relation

Functions whose domain are the nonnegative integers, known as sequences, are often defined by recurrence relations.

The factorial function on the nonnegative integers (${\displaystyle n\mapsto n!}$) is a basic example, as it can be defined by the recurrence relation

${\displaystyle n!=n(n-1)!\quad {\text{for}}\quad n>0,}$

and the initial condition

${\displaystyle 0!=1.}$

Representing a function

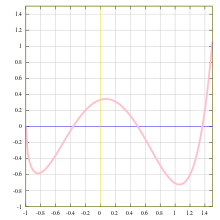
A graph is commonly used to give an intuitive picture of a function. As an example of how a graph helps to understand a function, it is easy to see from its graph whether a function is increasing or decreasing. Some functions may also be represented by bar charts.

Graphs and plots

Main article: Graph of a function

 

The function mapping each year to its US motor vehicle death count, shown as a line chart

 

The same function, shown as a bar chart

Given a function ${\displaystyle f\colon X\to Y,}$ its graph is, formally, the set

${\displaystyle G=\{(x,f(x))\mid x\in X\}.}$

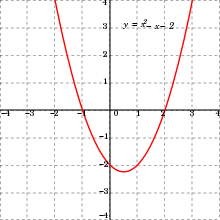
In the frequent case where X and Y are subsets of the real numbers (or may be identified with such subsets, e.g. intervals), an element ${\displaystyle (x,y)\in G}$ may be identified with a point having coordinates x, y in a 2-dimensional coordinate system, e.g. the Cartesian plane. Parts of this may create a plot that represents (parts of) the function. The use of plots is so ubiquitous that they too are called the graph of the function. Graphic representations of functions are also possible in other coordinate systems. For example, the graph of the square function

${\displaystyle x\mapsto x^{2},}$

consisting of all points with coordinates ${\displaystyle (x,x^{2})}$ for ${\displaystyle x\in \mathbb {R} ,}$ yields, when depicted in Cartesian coordinates, the well known parabola. If the same quadratic function ${\displaystyle x\mapsto x^{2},}$ with the same formal graph, consisting of pairs of numbers, is plotted instead in polar coordinates ${\displaystyle (r,\theta )=(x,x^{2}),}$ the plot obtained is Fermat's spiral.

Tables

Main article: Mathematical table

A function can be represented as a table of values. If the domain of a function is finite, then the function can be completely specified in this way. For example, the multiplication function ${\displaystyle f\colon \{1,\ldots ,5\}^{2}\to \mathbb {R} }$ defined as ${\displaystyle f(x,y)=xy}$ can be represented by the familiar multiplication table

y x	1	2	3	4	5
1	1	2	3	4	5
2	2	4	6	8	10
3	3	6	9	12	15
4	4	8	12	16	20
5	5	10	15	20	25

On the other hand, if a function's domain is continuous, a table can give the values of the function at specific values of the domain. If an intermediate value is needed, interpolation can be used to estimate the value of the function. For example, a portion of a table for the sine function might be given as follows, with values rounded to 6 decimal places:

x	sin x
1.289	0.960557
1.290	0.960835
1.291	0.961112
1.292	0.961387
1.293	0.961662

Before the advent of handheld calculators and personal computers, such tables were often compiled and published for functions such as logarithms and trigonometric functions.

Bar chart

Main article: Bar chart

Bar charts are often used for representing functions whose domain is a finite set, the natural numbers, or the integers. In this case, an element x of the domain is represented by an interval of the x-axis, and the corresponding value of the function, f(x), is represented by a rectangle whose base is the interval corresponding to x and whose height is f(x) (possibly negative, in which case the bar extends below the x-axis).

General properties

This section describes general properties of functions, that are independent of specific properties of the domain and the codomain.

Standard functions

There are a number of standard functions that occur frequently:

• For every set X, there is a unique function, called the empty function, or empty map, from the empty set to X. The graph of an empty function is the empty set. The existence of the empty function is a convention that is needed for the coherency of the theory and for avoiding exceptions concerning the empty set in many statements.
• For every set X and every singleton set {s}, there is a unique function from X to {s}, which maps every element of X to s. This is a surjection (see below) unless X is the empty set.
• Given a function ${\displaystyle f\colon X\to Y,}$ the canonical surjection of f onto its image ${\displaystyle f(X)=\{f(x)\mid x\in X\}}$ is the function from X to f(X) that maps x to f(x).
• For every subset A of a set X, the inclusion map of A into X is the injective (see below) function that maps every element of A to itself.
• The identity function on a set X, often denoted by id_X, is the inclusion of X into itself.

Function composition

Main article: Function composition

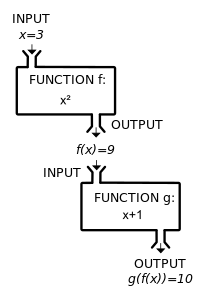
Given two functions ${\displaystyle f\colon X\to Y}$ and ${\displaystyle g\colon Y\to Z}$ such that the domain of g is the codomain of f, their composition is the function ${\displaystyle g\circ f\colon X\rightarrow Z}$ defined by

${\displaystyle (g\circ f)(x)=g(f(x)).}$

That is, the value of ${\displaystyle g\circ f}$ is obtained by first applying f to x to obtain y = f(x) and then applying g to the result y to obtain g(y) = g(f(x)). In the notation the function that is applied first is always written on the right.

The composition ${\displaystyle g\circ f}$ is an operation on functions that is defined only if the codomain of the first function is the domain of the second one. Even when both ${\displaystyle g\circ f}$ and ${\displaystyle f\circ g}$ satisfy these conditions, the composition is not necessarily commutative, that is, the functions ${\displaystyle g\circ f}$ and ${\displaystyle f\circ g}$ need not be equal, but may deliver different values for the same argument. For example, let f(x) = x² and g(x) = x + 1, then ${\displaystyle g(f(x))=x^{2}+1}$ and ${\displaystyle f(g(x))=(x+1)^{2}}$ agree just for ${\displaystyle x=0.}$

The function composition is associative in the sense that, if one of ${\displaystyle (h\circ g)\circ f}$ and ${\displaystyle h\circ (g\circ f)}$ is defined, then the other is also defined, and they are equal. Thus, one writes

${\displaystyle h\circ g\circ f=(h\circ g)\circ f=h\circ (g\circ f).}$

The identity functions ${\displaystyle \operatorname {id} _{X}}$ and ${\displaystyle \operatorname {id} _{Y}}$ are respectively a right identity and a left identity for functions from X to Y. That is, if f is a function with domain X, and codomain Y, one has ${\displaystyle f\circ \operatorname {id} _{X}=\operatorname {id} _{Y}\circ f=f.}$

• 

  A composite function g(f(x)) can be visualized as the combination of two "machines".

• 

  A simple example of a function composition

  

• Another composition. In this example, (g ∘ f )(c) = #.

Image and preimage

Main article: Image (mathematics)

Let ${\displaystyle f\colon X\to Y.}$ The image under f of an element x of the domain X is f(x). If A is any subset of X, then the image of A under f, denoted f(A), is the subset of the codomain Y consisting of all images of elements of A, that is,

${\displaystyle f(A)=\{f(x)\mid x\in A\}.}$

The image of f is the image of the whole domain, that is, f(X). It is also called the range of f, although the term range may also refer to the codomain.

On the other hand, the inverse image or preimage under f of an element y of the codomain Y is the set of all elements of the domain X whose images under f equal y. In symbols, the preimage of y is denoted by ${\displaystyle f^{-1}(y)}$ and is given by the equation

${\displaystyle f^{-1}(y)=\{x\in X\mid f(x)=y\}.}$

Likewise, the preimage of a subset B of the codomain Y is the set of the preimages of the elements of B, that is, it is the subset of the domain X consisting of all elements of X whose images belong to B. It is denoted by ${\displaystyle f^{-1}(B)}$ and is given by the equation

${\displaystyle f^{-1}(B)=\{x\in X\mid f(x)\in B\}.}$

For example, the preimage of ${\displaystyle \{4,9\}}$ under the square function is the set ${\displaystyle \{-3,-2,2,3\}}$.

By definition of a function, the image of an element x of the domain is always a single element of the codomain. However, the preimage ${\displaystyle f^{-1}(y)}$ of an element y of the codomain may be empty or contain any number of elements. For example, if f is the function from the integers to themselves that maps every integer to 0, then ${\displaystyle f^{-1}(0)=\mathbb {Z} }$.

If ${\displaystyle f\colon X\to Y}$ is a function, A and B are subsets of X, and C and D are subsets of Y, then one has the following properties:

• ${\displaystyle A\subseteq B\Longrightarrow f(A)\subseteq f(B)}$
• ${\displaystyle C\subseteq D\Longrightarrow f^{-1}(C)\subseteq f^{-1}(D)}$
• ${\displaystyle A\subseteq f^{-1}(f(A))}$
• ${\displaystyle C\supseteq f(f^{-1}(C))}$
• ${\displaystyle f(f^{-1}(f(A)))=f(A)}$
• ${\displaystyle f^{-1}(f(f^{-1}(C)))=f^{-1}(C)}$

The preimage by f of an element y of the codomain is sometimes called, in some contexts, the fiber of y under f.

If a function f has an inverse (see below), this inverse is denoted ${\displaystyle f^{-1}.}$ In this case ${\displaystyle f^{-1}(C)}$ may denote either the image by ${\displaystyle f^{-1}}$ or the preimage by f of C. This is not a problem, as these sets are equal. The notation ${\displaystyle f(A)}$ and ${\displaystyle f^{-1}(C)}$ may be ambiguous in the case of sets that contain some subsets as elements, such as ${\displaystyle \{x,\{x\}\}.}$ In this case, some care may be needed, for example, by using square brackets ${\displaystyle f[A],f^{-1}[C]}$ for images and preimages of subsets and ordinary parentheses for images and preimages of elements.

Injective, surjective and bijective functions

Let ${\displaystyle f\colon X\to Y}$ be a function.

The function f is injective (or one-to-one, or is an injection) if f(a) ≠ f(b) for any two different elements a and b of X. Equivalently, f is injective if and only if, for any ${\displaystyle y\in Y,}$ the preimage ${\displaystyle f^{-1}(y)}$ contains at most one element. An empty function is always injective. If X is not the empty set, then f is injective if and only if there exists a function ${\displaystyle g\colon Y\to X}$ such that ${\displaystyle g\circ f=\operatorname {id} _{X},}$ that is, if f has a left inverse. Proof: If f is injective, for defining g, one chooses an element ${\displaystyle x_{0}}$ in X (which exists as X is supposed to be nonempty), and one defines g by ${\displaystyle g(y)=x}$ if ${\displaystyle y=f(x)}$ and ${\displaystyle g(y)=x_{0}}$ if ${\displaystyle y\not \in f(X).}$ Conversely, if ${\displaystyle g\circ f=\operatorname {id} _{X},}$ and ${\displaystyle y=f(x),}$ then ${\displaystyle x=g(y),}$ and thus ${\displaystyle f^{-1}(y)=\{x\}.}$

The function f is surjective (or onto, or is a surjection) if its range ${\displaystyle f(X)}$ equals its codomain ${\displaystyle Y}$, that is, if, for each element ${\displaystyle y}$ of the codomain, there exists some element ${\displaystyle x}$ of the domain such that ${\displaystyle f(x)=y}$ (in other words, the preimage ${\displaystyle f^{-1}(y)}$ of every ${\displaystyle y\in Y}$ is nonempty). If, as usual in modern mathematics, the axiom of choice is assumed, then f is surjective if and only if there exists a function ${\displaystyle g\colon Y\to X}$ such that ${\displaystyle f\circ g=\operatorname {id} _{Y},}$ that is, if f has a right inverse. The axiom of choice is needed, because, if f is surjective, one defines g by ${\displaystyle g(y)=x,}$ where ${\displaystyle x}$ is an arbitrarily chosen element of ${\displaystyle f^{-1}(y).}$

The function f is bijective (or is a bijection or a one-to-one correspondence) if it is both injective and surjective. That is, f is bijective if, for any ${\displaystyle y\in Y,}$ the preimage ${\displaystyle f^{-1}(y)}$ contains exactly one element. The function f is bijective if and only if it admits an inverse function, that is, a function ${\displaystyle g\colon Y\to X}$ such that ${\displaystyle g\circ f=\operatorname {id} _{X}}$ and ${\displaystyle f\circ g=\operatorname {id} _{Y}.}$ (Contrarily to the case of surjections, this does not require the axiom of choice; the proof is straightforward).

Every function ${\displaystyle f\colon X\to Y}$ may be factorized as the composition ${\displaystyle i\circ s}$ of a surjection followed by an injection, where s is the canonical surjection of X onto f(X) and i is the canonical injection of f(X) into Y. This is the canonical factorization of f.

"One-to-one" and "onto" are terms that were more common in the older English language literature; "injective", "surjective", and "bijective" were originally coined as French words in the second quarter of the 20th century by the Bourbaki group and imported into English. As a word of caution, "a one-to-one function" is one that is injective, while a "one-to-one correspondence" refers to a bijective function. Also, the statement "f maps X onto Y" differs from "f maps X into B", in that the former implies that f is surjective, while the latter makes no assertion about the nature of f. In a complicated reasoning, the one letter difference can easily be missed. Due to the confusing nature of this older terminology, these terms have declined in popularity relative to the Bourbakian terms, which have also the advantage of being more symmetrical.

Restriction and extension

Main article: Restriction (mathematics)

If ${\displaystyle f\colon X\to Y}$ is a function and S is a subset of X, then the restriction of ${\displaystyle f}$ to S, denoted ${\displaystyle f|_{S}}$, is the function from S to Y defined by

${\displaystyle f|_{S}(x)=f(x)}$

for all x in S. Restrictions can be used to define partial inverse functions: if there is a subset S of the domain of a function ${\displaystyle f}$ such that ${\displaystyle f|_{S}}$ is injective, then the canonical surjection of ${\displaystyle f|_{S}}$ onto its image ${\displaystyle f|_{S}(S)=f(S)}$ is a bijection, and thus has an inverse function from ${\displaystyle f(S)}$ to S. One application is the definition of inverse trigonometric functions. For example, the cosine function is injective when restricted to the interval [0, π]. The image of this restriction is the interval [−1, 1], and thus the restriction has an inverse function from [−1, 1] to [0, π], which is called arccosine and is denoted arccos.

Function restriction may also be used for "gluing" functions together. Let ${\textstyle X=\bigcup _{i\in I}U_{i}}$ be the decomposition of X as a union of subsets, and suppose that a function ${\displaystyle f_{i}\colon U_{i}\to Y}$ is defined on each ${\displaystyle U_{i}}$ such that for each pair ${\displaystyle i,j}$ of indices, the restrictions of ${\displaystyle f_{i}}$ and ${\displaystyle f_{j}}$ to ${\displaystyle U_{i}\cap U_{j}}$ are equal. Then this defines a unique function ${\displaystyle f\colon X\to Y}$ such that ${\displaystyle f|_{U_{i}}=f_{i}}$ for all i. This is the way that functions on manifolds are defined.

An extension of a function f is a function g such that f is a restriction of g. A typical use of this concept is the process of analytic continuation, that allows extending functions whose domain is a small part of the complex plane to functions whose domain is almost the whole complex plane.

Here is another classical example of a function extension that is encountered when studying homographies of the real line. A homography is a function ${\displaystyle h(x)={\frac {ax+b}{cx+d}}}$ such that ad − bc ≠ 0. Its domain is the set of all real numbers different from ${\displaystyle -d/c,}$ and its image is the set of all real numbers different from ${\displaystyle a/c.}$ If one extends the real line to the projectively extended real line by including ∞, one may extend h to a bijection from the extended real line to itself by setting ${\displaystyle h(\infty )=a/c}$ and ${\displaystyle h(-d/c)=\infty }$.

Multivariate function

Further information: Real multivariate function

A binary operation is a typical example of a bivariate function which assigns to each pair ${\displaystyle (x,y)}$ the result ${\displaystyle x\circ y}$.

A multivariate function, or function of several variables is a function that depends on several arguments. Such functions are commonly encountered. For example, the position of a car on a road is a function of the time travelled and its average speed.

More formally, a function of n variables is a function whose domain is a set of n-tuples. For example, multiplication of integers is a function of two variables, or bivariate function, whose domain is the set of all pairs (2-tuples) of integers, and whose codomain is the set of integers. The same is true for every binary operation. More generally, every mathematical operation is defined as a multivariate function.

The Cartesian product ${\displaystyle X_{1}\times \cdots \times X_{n}}$ of n sets ${\displaystyle X_{1},\ldots ,X_{n}}$ is the set of all n-tuples ${\displaystyle (x_{1},\ldots ,x_{n})}$ such that ${\displaystyle x_{i}\in X_{i}}$ for every i with ${\displaystyle 1\leq i\leq n}$. Therefore, a function of n variables is a function

${\displaystyle f\colon U\to Y,}$

where the domain U has the form

${\displaystyle U\subseteq X_{1}\times \cdots \times X_{n}.}$

When using function notation, one usually omits the parentheses surrounding tuples, writing ${\displaystyle f(x_{1},x_{2})}$ instead of ${\displaystyle f((x_{1},x_{2})).}$

In the case where all the ${\displaystyle X_{i}}$ are equal to the set ${\displaystyle \mathbb {R} }$ of real numbers, one has a function of several real variables. If the ${\displaystyle X_{i}}$ are equal to the set ${\displaystyle \mathbb {C} }$ of complex numbers, one has a function of several complex variables.

It is common to also consider functions whose codomain is a product of sets. For example, Euclidean division maps every pair (a, b) of integers with b ≠ 0 to a pair of integers called the quotient and the remainder:

${\displaystyle {\begin{aligned}{\text{Euclidean division}}\colon \quad \mathbb {Z} \times (\mathbb {Z} \setminus \{0\})&\to \mathbb {Z} \times \mathbb {Z} \\(a,b)&\mapsto (\operatorname {quotient} (a,b),\operatorname {remainder} (a,b)).\end{aligned}}}$

The codomain may also be a vector space. In this case, one talks of a vector-valued function. If the domain is contained in a Euclidean space, or more generally a manifold, a vector-valued function is often called a vector field.

In calculus

The idea of function, starting in the 17th century, was fundamental to the new infinitesimal calculus (see History of the function concept). At that time, only real-valued functions of a real variable were considered, and all functions were assumed to be smooth. But the definition was soon extended to functions of several variables and to functions of a complex variable. In the second half of the 19th century, the mathematically rigorous definition of a function was introduced, and functions with arbitrary domains and codomains were defined.

Functions are now used throughout all areas of mathematics. In introductory calculus, when the word function is used without qualification, it means a real-valued function of a single real variable. The more general definition of a function is usually introduced to second or third year college students with STEM majors, and in their senior year they are introduced to calculus in a larger, more rigorous setting in courses such as real analysis and complex analysis.

Real function

See also: Real analysis

 

Graph of a linear function

 

Graph of a polynomial function, here a quadratic function.

 

Graph of two trigonometric functions: sine and cosine.

A real function is a real-valued function of a real variable, that is, a function whose codomain is the field of real numbers and whose domain is a set of real numbers that contains an interval. In this section, these functions are simply called functions.

The functions that are most commonly considered in mathematics and its applications have some regularity, that is they are continuous, differentiable, and even analytic. This regularity insures that these functions can be visualized by their graphs. In this section, all functions are differentiable in some interval.

Functions enjoy pointwise operations, that is, if f and g are functions, their sum, difference and product are functions defined by

${\displaystyle {\begin{aligned}(f+g)(x)&=f(x)+g(x)\\(f-g)(x)&=f(x)-g(x)\\(f\cdot g)(x)&=f(x)\cdot g(x)\\\end{aligned}}.}$

The domains of the resulting functions are the intersection of the domains of f and g. The quotient of two functions is defined similarly by

${\displaystyle {\frac {f}{g}}(x)={\frac {f(x)}{g(x)}},}$

but the domain of the resulting function is obtained by removing the zeros of g from the intersection of the domains of f and g.

The polynomial functions are defined by polynomials, and their domain is the whole set of real numbers. They include constant functions, linear functions and quadratic functions. Rational functions are quotients of two polynomial functions, and their domain is the real numbers with a finite number of them removed to avoid division by zero. The simplest rational function is the function ${\displaystyle x\mapsto {\frac {1}{x}},}$ whose graph is a hyperbola, and whose domain is the whole real line except for 0.

The derivative of a real differentiable function is a real function. An antiderivative of a continuous real function is a real function that has the original function as a derivative. For example, the function ${\displaystyle x\mapsto {\frac {1}{x}}}$ is continuous, and even differentiable, on the positive real numbers. Thus one antiderivative, which takes the value zero for x = 1, is a differentiable function called the natural logarithm.

A real function f is monotonic in an interval if the sign of ${\displaystyle {\frac {f(x)-f(y)}{x-y}}}$ does not depend of the choice of x and y in the interval. If the function is differentiable in the interval, it is monotonic if the sign of the derivative is constant in the interval. If a real function f is monotonic in an interval I, it has an inverse function, which is a real function with domain f(I) and image I. This is how inverse trigonometric functions are defined in terms of trigonometric functions, where the trigonometric functions are monotonic. Another example: the natural logarithm is monotonic on the positive real numbers, and its image is the whole real line; therefore it has an inverse function that is a bijection between the real numbers and the positive real numbers. This inverse is the exponential function.

Many other real functions are defined either by the implicit function theorem (the inverse function is a particular instance) or as solutions of differential equations. For example, the sine and the cosine functions are the solutions of the linear differential equation

${\displaystyle y''+y=0}$

such that

${\displaystyle \sin 0=0,\quad \cos 0=1,\quad {\frac {\partial \sin x}{\partial x}}(0)=1,\quad {\frac {\partial \cos x}{\partial x}}(0)=0.}$

Vector-valued function

Main articles: Vector-valued function and Vector field

When the elements of the codomain of a function are vectors, the function is said to be a vector-valued function. These functions are particularly useful in applications, for example modeling physical properties. For example, the function that associates to each point of a fluid its velocity vector is a vector-valued function.

Some vector-valued functions are defined on a subset of ${\displaystyle \mathbb {R} ^{n}}$ or other spaces that share geometric or topological properties of ${\displaystyle \mathbb {R} ^{n}}$, such as manifolds. These vector-valued functions are given the name vector fields.

Function space

Main articles: Function space and Functional analysis

In mathematical analysis, and more specifically in functional analysis, a function space is a set of scalar-valued or vector-valued functions, which share a specific property and form a topological vector space. For example, the real smooth functions with a compact support (that is, they are zero outside some compact set) form a function space that is at the basis of the theory of distributions.

Function spaces play a fundamental role in advanced mathematical analysis, by allowing the use of their algebraic and topological properties for studying properties of functions. For example, all theorems of existence and uniqueness of solutions of ordinary or partial differential equations result of the study of function spaces.

Multi-valued functions

Main article: Multi-valued function

 

Together, the two square roots of all nonnegative real numbers form a single smooth curve.

 

 

Several methods for specifying functions of real or complex variables start from a local definition of the function at a point or on a neighbourhood of a point, and then extend by continuity the function to a much larger domain. Frequently, for a starting point ${\displaystyle x_{0},}$ there are several possible starting values for the function.

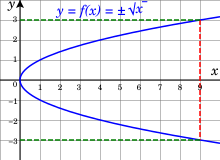
For example, in defining the square root as the inverse function of the square function, for any positive real number ${\displaystyle x_{0},}$ there are two choices for the value of the square root, one of which is positive and denoted ${\displaystyle {\sqrt {x_{0}}},}$ and another which is negative and denoted ${\displaystyle -{\sqrt {x_{0}}}.}$ These choices define two continuous functions, both having the nonnegative real numbers as a domain, and having either the nonnegative or the nonpositive real numbers as images. When looking at the graphs of these functions, one can see that, together, they form a single smooth curve. It is therefore often useful to consider these two square root functions as a single function that has two values for positive x, one value for 0 and no value for negative x.

In the preceding example, one choice, the positive square root, is more natural than the other. This is not the case in general. For example, let consider the implicit function that maps y to a root x of ${\displaystyle x^{3}-3x-y=0}$ (see the figure on the right). For y = 0 one may choose either ${\displaystyle 0,{\sqrt {3}},{\text{ or }}-{\sqrt {3}}}$ for x. By the implicit function theorem, each choice defines a function; for the first one, the (maximal) domain is the interval [−2, 2] and the image is [−1, 1]; for the second one, the domain is [−2, ∞) and the image is [1, ∞); for the last one, the domain is (−∞, 2] and the image is (−∞, −1]. As the three graphs together form a smooth curve, and there is no reason for preferring one choice, these three functions are often considered as a single multi-valued function of y that has three values for −2 < y < 2, and only one value for y ≤ −2 and y ≥ −2.

Usefulness of the concept of multi-valued functions is clearer when considering complex functions, typically analytic functions. The domain to which a complex function may be extended by analytic continuation generally consists of almost the whole complex plane. However, when extending the domain through two different paths, one often gets different values. For example, when extending the domain of the square root function, along a path of complex numbers with positive imaginary parts, one gets i for the square root of −1; while, when extending through complex numbers with negative imaginary parts, one gets −i. There are generally two ways of solving the problem. One may define a function that is not continuous along some curve, called a branch cut. Such a function is called the principal value of the function. The other way is to consider that one has a multi-valued function, which is analytic everywhere except for isolated singularities, but whose value may "jump" if one follows a closed loop around a singularity. This jump is called the monodromy.

In the foundations of mathematics and set theory

The definition of a function that is given in this article requires the concept of set, since the domain and the codomain of a function must be a set. This is not a problem in usual mathematics, as it is generally not difficult to consider only functions whose domain and codomain are sets, which are well defined, even if the domain is not explicitly defined. However, it is sometimes useful to consider more general functions.

For example, the singleton set may be considered as a function ${\displaystyle x\mapsto \{x\}.}$ Its domain would include all sets, and therefore would not be a set. In usual mathematics, one avoids this kind of problem by specifying a domain, which means that one has many singleton functions. However, when establishing foundations of mathematics, one may have to use functions whose domain, codomain or both are not specified, and some authors, often logicians, give precise definition for these weakly specified functions.

These generalized functions may be critical in the development of a formalization of the foundations of mathematics. For example, Von Neumann–Bernays–Gödel set theory, is an extension of the set theory in which the collection of all sets is a class. This theory includes the replacement axiom, which may be stated as: If X is a set and F is a function, then F[X] is a set.

In computer science

Main articles: Function (programming) and Lambda calculus

In computer programming, a function is, in general, a piece of a computer program, which implements the abstract concept of function. That is, it is a program unit that produces an output for each input. However, in many programming languages every subroutine is called a function, even when there is no output, and when the functionality consists simply of modifying some data in the computer memory.

Functional programming is the programming paradigm consisting of building programs by using only subroutines that behave like mathematical functions. For example, if_then_else is a function that takes three functions as arguments, and, depending on the result of the first function (true or false), returns the result of either the second or the third function. An important advantage of functional programming is that it makes easier program proofs, as being based on a well founded theory, the lambda calculus (see below).

Except for computer-language terminology, "function" has the usual mathematical meaning in computer science. In this area, a property of major interest is the computability of a function. For giving a precise meaning to this concept, and to the related concept of algorithm, several models of computation have been introduced, the old ones being general recursive functions, lambda calculus and Turing machine. The fundamental theorem of computability theory is that these three models of computation define the same set of computable functions, and that all the other models of computation that have ever been proposed define the same set of computable functions or a smaller one. The Church–Turing thesis is the claim that every philosophically acceptable definition of a computable function defines also the same functions.

General recursive functions are partial functions from integers to integers that can be defined from

• constant functions,
• successor, and
• projection functions

via the operators

• composition,
• primitive recursion, and
• minimization.

Although defined only for functions from integers to integers, they can model any computable function as a consequence of the following properties:

• a computation is the manipulation of finite sequences of symbols (digits of numbers, formulas, ...),
• every sequence of symbols may be coded as a sequence of bits,
• a bit sequence can be interpreted as the binary representation of an integer.

Lambda calculus is a theory that defines computable functions without using set theory, and is the theoretical background of functional programming. It consists of terms that are either variables, function definitions (𝜆-terms), or applications of functions to terms. Terms are manipulated through some rules, (the α-equivalence, the β-reduction, and the η-conversion), which are the axioms of the theory and may be interpreted as rules of computation.

In its original form, lambda calculus does not include the concepts of domain and codomain of a function. Roughly speaking, they have been introduced in the theory under the name of type in typed lambda calculus. Most kinds of typed lambda calculi can define fewer functions than untyped lambda calculus.

Franck–Condon principle

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Franck-Condon_principle

Figure 1. Franck–Condon principle energy diagram. Since electronic transitions are very fast compared with nuclear motions, the vibrational states to and from which absorption and emission occur are those that correspond to a minimal change in the nuclear coordinates. As a result, both absorption and emission produce molecules in vibrationally excited states. The potential wells are shown favoring transitions with changes in ν.

The Franck–Condon principle is a rule in spectroscopy and quantum chemistry that explains the intensity of vibronic transitions. Vibronic transitions are the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon of the appropriate energy. The principle states that during an electronic transition, a change from one vibrational energy level to another will be more likely to happen if the two vibrational wave functions overlap more significantly.

Overview

Figure 2. Schematic representation of the absorption and fluorescence spectra corresponding to the energy diagram in Figure 1. The symmetry is due to the equal shape of the ground and excited state potential wells. The narrow lines can usually only be observed in the spectra of dilute gases. The darker curves represent the inhomogeneous broadening of the same transitions as occurs in liquids and solids. Electronic transitions between the lowest vibrational levels of the electronic states (the 0–0 transition) have the same energy in both absorption and fluorescence.

 

Figure 3. Semiclassical pendulum analogy of the Franck–Condon principle. Vibronic transitions are allowed at the classical turning points because both the momentum and the nuclear coordinates correspond in the two represented energy levels. In this illustration, the 0–2 vibrational transitions are favored.

The Franck–Condon principle has a well-established semiclassical interpretation based on the original contributions of James Franck. Electronic transitions are relatively instantaneous compared with the time scale of nuclear motions, therefore if the molecule is to move to a new vibrational level during the electronic transition, this new vibrational level must be instantaneously compatible with the nuclear positions and momenta of the vibrational level of the molecule in the originating electronic state. In the semiclassical picture of vibrations (oscillations) of a simple harmonic oscillator, the necessary conditions can occur at the turning points, where the momentum is zero.

Classically, the Franck–Condon principle is the approximation that an electronic transition is most likely to occur without changes in the positions of the nuclei in the molecular entity and its environment. The resulting state is called a Franck–Condon state, and the transition involved, a vertical transition. The quantum mechanical formulation of this principle is that the intensity of a vibronic transition is proportional to the square of the overlap integral between the vibrational wavefunctions of the two states that are involved in the transition.

— IUPAC Compendium of Chemical Terminology, 2nd Edition (1997)

In the quantum mechanical picture, the vibrational levels and vibrational wavefunctions are those of quantum harmonic oscillators, or of more complex approximations to the potential energy of molecules, such as the Morse potential. Figure 1 illustrates the Franck–Condon principle for vibronic transitions in a molecule with Morse-like potential energy functions in both the ground and excited electronic states. In the low temperature approximation, the molecule starts out in the v = 0 vibrational level of the ground electronic state and upon absorbing a photon of the necessary energy, makes a transition to the excited electronic state. The electron configuration of the new state may result in a shift of the equilibrium position of the nuclei constituting the molecule. In the figure this shift in nuclear coordinates between the ground and the first excited state is labeled as q ₀₁. In the simplest case of a diatomic molecule the nuclear coordinates axis refers to the internuclear separation. The vibronic transition is indicated by a vertical arrow due to the assumption of constant nuclear coordinates during the transition. The probability that the molecule can end up in any particular vibrational level is proportional to the square of the (vertical) overlap of the vibrational wavefunctions of the original and final state (see Quantum mechanical formulation section below). In the electronic excited state molecules quickly relax to the lowest vibrational level of the lowest electronic excitation state (Kasha's rule), and from there can decay to the electronic ground state via photon emission. The Franck–Condon principle is applied equally to absorption and to fluorescence.

The applicability of the Franck–Condon principle in both absorption and fluorescence, along with Kasha's rule leads to an approximate mirror symmetry shown in Figure 2. The vibrational structure of molecules in a cold, sparse gas is most clearly visible due to the absence of inhomogeneous broadening of the individual transitions. Vibronic transitions are drawn in Figure 2 as narrow, equally spaced Lorentzian lineshapes. Equal spacing between vibrational levels is only the case for the parabolic potential of simple harmonic oscillators, in more realistic potentials, such as those shown in Figure 1, energy spacing decreases with increasing vibrational energy. Electronic transitions to and from the lowest vibrational states are often referred to as 0–0 (zero zero) transitions and have the same energy in both absorption and fluorescence.

Development of the principle

In a report published in 1926 in Transactions of the Faraday Society, James Franck was concerned with the mechanisms of photon-induced chemical reactions. The presumed mechanism was the excitation of a molecule by a photon, followed by a collision with another molecule during the short period of excitation. The question was whether it was possible for a molecule to break into photoproducts in a single step, the absorption of a photon, and without a collision. In order for a molecule to break apart, it must acquire from the photon a vibrational energy exceeding the dissociation energy, that is, the energy to break a chemical bond. However, as was known at the time, molecules will only absorb energy corresponding to allowed quantum transitions, and there are no vibrational levels above the dissociation energy level of the potential well. High-energy photon absorption leads to a transition to a higher electronic state instead of dissociation. In examining how much vibrational energy a molecule could acquire when it is excited to a higher electronic level, and whether this vibrational energy could be enough to immediately break apart the molecule, he drew three diagrams representing the possible changes in binding energy between the lowest electronic state and higher electronic states.

Diagram I. shows a great weakening of the binding on a transition from the normal state n to the excited states a and a'. Here we have D > D' and D' > D". At the same time the equilibrium position of the nuclei moves with the excitation to greater values of r. If we go from the equilibrium position (the minimum of potential energy) of the n curve vertically [emphasis added] upwards to the a curves in Diagram I. the particles will have a potential energy greater than D' and will fly apart. In this case we have a very great change in the oscillation energy on excitation by light...

— James Franck, 1926

James Franck recognized that changes in vibrational levels could be a consequence of the instantaneous nature of excitation to higher electronic energy levels and a new equilibrium position for the nuclear interaction potential. Edward Condon extended this insight beyond photoreactions in a 1926 Physical Review article titled "A Theory of Intensity Distribution in Band Systems". Here he formulates the semiclassical formulation in a manner quite similar to its modern form. The first joint reference to both Franck and Condon in regards to the new principle appears in the same 1926 issue of Physical Review in an article on the band structure of carbon monoxide by Raymond Birge.

Figure 5. Figure 1 in Edward Condon's first publication on what is now the Franck–Condon principle [Condon 1926]. Condon chose to superimpose the potential curves to illustrate the method of estimating vibrational transitions.

Quantum mechanical formulation

Consider an electrical dipole transition from the initial vibrational state (υ) of the ground electronic level (ε), ${\displaystyle |\epsilon v\rangle }$, to some vibrational state (υ′) of an excited electronic state (ε′), ${\displaystyle |\epsilon 'v'\rangle }$ (see bra–ket notation). The molecular dipole operator μ is determined by the charge (−e) and locations (r_i) of the electrons as well as the charges (+Z_je) and locations (R_j) of the nuclei:

${\displaystyle {\boldsymbol {\mu }}={\boldsymbol {\mu }}_{e}+{\boldsymbol {\mu }}_{N}=-e\sum \limits _{i}{\boldsymbol {r}}_{i}+e\sum \limits _{j}Z_{j}{\boldsymbol {R}}_{j}.}$

The probability amplitude P for the transition between these two states is given by

${\displaystyle P=\left\langle \psi '\right|{\boldsymbol {\mu }}\left|\psi \right\rangle =\int {\psi '^{*}}{\boldsymbol {\mu }}\psi \,d\tau ,}$

where ${\displaystyle \psi }$ and ${\displaystyle \psi '}$ are, respectively, the overall wavefunctions of the initial and final state. The overall wavefunctions are the product of the individual vibrational (depending on spatial coordinates of the nuclei) and electronic space and spin wavefunctions:

${\displaystyle \psi =\psi _{e}\psi _{v}\psi _{s}.}$

This separation of the electronic and vibrational wavefunctions is an expression of the Born–Oppenheimer approximation and is the fundamental assumption of the Franck–Condon principle. Combining these equations leads to an expression for the probability amplitude in terms of separate electronic space, spin and vibrational contributions:

${\displaystyle P=\left\langle \psi _{e}'\psi _{v}'\psi _{s}'\right|{\boldsymbol {\mu }}\left|\psi _{e}\psi _{v}\psi _{s}\right\rangle =\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}({\boldsymbol {\mu }}_{e}+{\boldsymbol {\mu }}_{N})\psi _{e}\psi _{v}\psi _{s}\,d\tau }$

${\displaystyle =\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\psi _{v}\psi _{s}\,d\tau +\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}{\boldsymbol {\mu }}_{N}\psi _{e}\psi _{v}\psi _{s}\,d\tau }$

${\displaystyle =\underbrace {\int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}} _{\displaystyle {{\text{Franck–Condon}} \atop {\text{factor}}}}\underbrace {\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}} _{\displaystyle {{\text{orbital}} \atop {\text{selection rule}}}}\underbrace {\int \psi _{s}'^{*}\psi _{s}\,d\tau _{s}} _{\displaystyle {{\text{spin}} \atop {\text{selection rule}}}}+\underbrace {\int \psi _{e}'^{*}\psi _{e}\,d\tau _{e}} _{\displaystyle 0}\int \psi _{v}'^{*}{\boldsymbol {\mu }}_{N}\psi _{v}\,d\tau _{v}\int \psi _{s}'^{*}\psi _{s}\,d\tau _{s}.}$

The spin-independent part of the initial integral is here approximated as a product of two integrals:

${\displaystyle \iint \psi _{v}'^{*}\psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\psi _{v}\,d\tau _{e}d\tau _{n}\approx \int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}.}$

This factorization would be exact if the integral ${\displaystyle \int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}}$ over the spatial coordinates of the electrons would not depend on the nuclear coordinates. However, in the Born–Oppenheimer approximation ${\displaystyle \psi _{e}}$ and ${\displaystyle \psi '_{e}}$ do depend (parametrically) on the nuclear coordinates, so that the integral (a so-called transition dipole surface) is a function of nuclear coordinates. Since the dependence is usually rather smooth it is neglected (i.e., the assumption that the transition dipole surface is independent of nuclear coordinates, called the Condon approximation is often allowed).

The first integral after the plus sign is equal to zero because electronic wavefunctions of different states are orthogonal. Remaining is the product of three integrals. The first integral is the vibrational overlap integral, also called the Franck–Condon factor. The remaining two integrals contributing to the probability amplitude determine the electronic spatial and spin selection rules.

The Franck–Condon principle is a statement on allowed vibrational transitions between two different electronic states; other quantum mechanical selection rules may lower the probability of a transition or prohibit it altogether. Rotational selection rules have been neglected in the above derivation. Rotational contributions can be observed in the spectra of gases but are strongly suppressed in liquids and solids.

It should be clear that the quantum mechanical formulation of the Franck–Condon principle is the result of a series of approximations, principally the electrical dipole transition assumption and the Born–Oppenheimer approximation. Weaker magnetic dipole and electric quadrupole electronic transitions along with the incomplete validity of the factorization of the total wavefunction into nuclear, electronic spatial and spin wavefunctions means that the selection rules, including the Franck–Condon factor, are not strictly observed. For any given transition, the value of P is determined by all of the selection rules, however spin selection is the largest contributor, followed by electronic selection rules. The Franck–Condon factor only weakly modulates the intensity of transitions, i.e., it contributes with a factor on the order of 1 to the intensity of bands whose order of magnitude is determined by the other selection rules. The table below gives the range of extinction coefficients for the possible combinations of allowed and forbidden spin and orbital selection rules.

Intensities of electronic transitions

	Range of extinction coefficient (ε) values (mol−1 cm−1)
Spin and orbitally allowed	103 to 105
Spin allowed but orbitally forbidden	100 to 103
Spin forbidden but orbitally allowed	10−5 to 100

Franck–Condon metaphors in spectroscopy

The Franck–Condon principle, in its canonical form, applies only to changes in the vibrational levels of a molecule in the course of a change in electronic levels by either absorption or emission of a photon. The physical intuition of this principle is anchored by the idea that the nuclear coordinates of the atoms constituting the molecule do not have time to change during the very brief amount of time involved in an electronic transition. However, this physical intuition can be, and is indeed, routinely extended to interactions between light-absorbing or emitting molecules (chromophores) and their environment. Franck–Condon metaphors are appropriate because molecules often interact strongly with surrounding molecules, particularly in liquids and solids, and these interactions modify the nuclear coordinates of the chromophore in ways closely analogous to the molecular vibrations considered by the Franck–Condon principle.

Figure 6. Energy diagram of an electronic transition with phonon coupling along the configurational coordinate q _i, a normal mode of the lattice. The upwards arrows represent absorption without phonons and with three phonons. The downwards arrows represent the symmetric process in emission.

Franck–Condon principle for phonons

The closest Franck–Condon analogy is due to the interaction of phonons (quanta of lattice vibrations) with the electronic transitions of chromophores embedded as impurities in the lattice. In this situation, transitions to higher electronic levels can take place when the energy of the photon corresponds to the purely electronic transition energy or to the purely electronic transition energy plus the energy of one or more lattice phonons. In the low-temperature approximation, emission is from the zero-phonon level of the excited state to the zero-phonon level of the ground state or to higher phonon levels of the ground state. Just like in the Franck–Condon principle, the probability of transitions involving phonons is determined by the overlap of the phonon wavefunctions at the initial and final energy levels. For the Franck–Condon principle applied to phonon transitions, the label of the horizontal axis of Figure 1 is replaced in Figure 6 with the configurational coordinate for a normal mode. The lattice mode ${\displaystyle q_{i}}$ potential energy in Figure 6 is represented as that of a harmonic oscillator, and the spacing between phonon levels (${\displaystyle \hbar \Omega _{i}}$) is determined by lattice parameters. Because the energy of single phonons is generally quite small, zero- or few-phonon transitions can only be observed at temperatures below about 40 kelvins.

See Zero-phonon line and phonon sideband for further details and references.

Franck–Condon principle in solvation

Figure 7. Energy diagram illustrating the Franck–Condon principle applied to the solvation of chromophores. The parabolic potential curves symbolize the interaction energy between the chromophores and the solvent. The Gaussian curves represent the distribution of this interaction energy.

Franck–Condon considerations can also be applied to the electronic transitions of chromophores dissolved in liquids. In this use of the Franck–Condon metaphor, the vibrational levels of the chromophores, as well as interactions of the chromophores with phonons in the liquid, continue to contribute to the structure of the absorption and emission spectra, but these effects are considered separately and independently.

Consider chromophores surrounded by solvent molecules. These surrounding molecules may interact with the chromophores, particularly if the solvent molecules are polar. This association between solvent and solute is referred to as solvation and is a stabilizing interaction, that is, the solvent molecules can move and rotate until the energy of the interaction is minimized. The interaction itself involves electrostatic and van der Waals forces and can also include hydrogen bonds. Franck–Condon principles can be applied when the interactions between the chromophore and the surrounding solvent molecules are different in the ground and in the excited electronic state. This change in interaction can originate, for example, due to different dipole moments in these two states. If the chromophore starts in its ground state and is close to equilibrium with the surrounding solvent molecules and then absorbs a photon that takes it to the excited state, its interaction with the solvent will be far from equilibrium in the excited state. This effect is analogous to the original Franck–Condon principle: the electronic transition is very fast compared with the motion of nuclei—the rearrangement of solvent molecules in the case of solvation. We now speak of a vertical transition, but now the horizontal coordinate is solvent-solute interaction space. This coordinate axis is often labeled as "Solvation Coordinate" and represents, somewhat abstractly, all of the relevant dimensions of motion of all of the interacting solvent molecules.

In the original Franck–Condon principle, after the electronic transition, the molecules which end up in higher vibrational states immediately begin to relax to the lowest vibrational state. In the case of solvation, the solvent molecules will immediately try to rearrange themselves in order to minimize the interaction energy. The rate of solvent relaxation depends on the viscosity of the solvent. Assuming the solvent relaxation time is short compared with the lifetime of the electronic excited state, emission will be from the lowest solvent energy state of the excited electronic state. For small-molecule solvents such as water or methanol at ambient temperature, solvent relaxation time is on the order of some tens of picoseconds whereas chromophore excited state lifetimes range from a few picoseconds to a few nanoseconds. Immediately after the transition to the ground electronic state, the solvent molecules must also rearrange themselves to accommodate the new electronic configuration of the chromophore. Figure 7 illustrates the Franck–Condon principle applied to solvation. When the solution is illuminated by light corresponding to the electronic transition energy, some of the chromophores will move to the excited state. Within this group of chromophores there will be a statistical distribution of solvent-chromophore interaction energies, represented in the figure by a Gaussian distribution function. The solvent-chromophore interaction is drawn as a parabolic potential in both electronic states. Since the electronic transition is essentially instantaneous on the time scale of solvent motion (vertical arrow), the collection of excited state chromophores is immediately far from equilibrium. The rearrangement of the solvent molecules according to the new potential energy curve is represented by the curved arrows in Figure 7. Note that while the electronic transitions are quantized, the chromophore-solvent interaction energy is treated as a classical continuum due to the large number of molecules involved. Although emission is depicted as taking place from the minimum of the excited state chromophore-solvent interaction potential, significant emission can take place before equilibrium is reached when the viscosity of the solvent is high or the lifetime of the excited state is short. The energy difference between absorbed and emitted photons depicted in Figure 7 is the solvation contribution to the Stokes shift.