Geometry (from Ancient Greek γεωμετρία (geōmetría) 'land measurement'; from γῆ (gê) 'earth, land', and μέτρον (métron) 'a measure') is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a geometer. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts.
Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, a problem that was stated in terms of elementary arithmetic, and remained unsolved for several centuries.
During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' Theorema Egregium ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied intrinsically, that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries without the parallel postulate (non-Euclidean geometries) can be developed without introducing any contradiction. The geometry that underlies general relativity is a famous application of non-Euclidean geometry.
Since the late 19th century, the scope of geometry has been greatly expanded, and the field has been split in many subfields that depend on the underlying methods—differential geometry, algebraic geometry, computational geometry, algebraic topology, discrete geometry (also known as combinatorial geometry), etc.—or on the properties of Euclidean spaces that are disregarded—projective geometry that consider only alignment of points but not distance and parallelism, affine geometry that omits the concept of angle and distance, finite geometry that omits continuity, and others. This enlargement of the scope of geometry led to a change of meaning of the word "space", which originally referred to the three-dimensional space of the physical world and its model provided by Euclidean geometry; presently a geometric space, or simply a space is a mathematical structure on which some geometry is defined.
History

The earliest recorded beginnings of geometry can be traced to ancient Mesopotamia and Egypt in the 2nd millennium BC. Early geometry was a collection of empirically discovered principles concerning lengths, angles, areas, and volumes, which were developed to meet some practical need in surveying, construction, astronomy, and various crafts. The earliest known texts on geometry are the Egyptian Rhind Papyrus (2000–1800 BC) and Moscow Papyrus (c. 1890 BC), and the Babylonian clay tablets, such as Plimpton 322 (1900 BC). For example, the Moscow Papyrus gives a formula for calculating the volume of a truncated pyramid, or frustum. Later clay tablets (350–50 BC) demonstrate that Babylonian astronomers implemented trapezoid procedures for computing Jupiter's position and motion within time-velocity space. These geometric procedures anticipated the Oxford Calculators, including the mean speed theorem, by 14 centuries. South of Egypt the ancient Nubians established a system of geometry including early versions of sun clocks.
In the 7th century BC, the Greek mathematician Thales of Miletus used geometry to solve problems such as calculating the height of pyramids and the distance of ships from the shore. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales's theorem. Pythagoras established the Pythagorean School, which is credited with the first proof of the Pythagorean theorem, though the statement of the theorem has a long history. Eudoxus (408–c. 355 BC) developed the method of exhaustion, which allowed the calculation of areas and volumes of curvilinear figures, as well as a theory of ratios that avoided the problem of incommensurable magnitudes, which enabled subsequent geometers to make significant advances. Around 300 BC, geometry was revolutionized by Euclid, whose Elements, widely considered the most successful and influential textbook of all time, introduced mathematical rigor through the axiomatic method and is the earliest example of the format still used in mathematics today, that of definition, axiom, theorem, and proof. Although most of the contents of the Elements were already known, Euclid arranged them into a single, coherent logical framework. The Elements was known to all educated people in the West until the middle of the 20th century and its contents are still taught in geometry classes today. Archimedes (c. 287–212 BC) of Syracuse, Italy used the method of exhaustion to calculate the area under the arc of a parabola with the summation of an infinite series, and gave remarkably accurate approximations of pi. He also studied the spiral bearing his name and obtained formulas for the volumes of surfaces of revolution.

Indian mathematicians also made many important contributions in geometry. The Shatapatha Brahmana (3rd century BC) contains rules for ritual geometric constructions that are similar to the Sulba Sutras. According to (Hayashi 2005, p. 363), the Śulba Sūtras contain "the earliest extant verbal expression of the Pythagorean Theorem in the world, although it had already been known to the Old Babylonians. They contain lists of Pythagorean triples, which are particular cases of Diophantine equations. In the Bakhshali manuscript, there are a handful of geometric problems (including problems about volumes of irregular solids). The Bakhshali manuscript also "employs a decimal place value system with a dot for zero." Aryabhata's Aryabhatiya (499) includes the computation of areas and volumes. Brahmagupta wrote his astronomical work Brāhmasphuṭasiddhānta in 628. Chapter 12, containing 66 Sanskrit verses, was divided into two sections: "basic operations" (including cube roots, fractions, ratio and proportion, and barter) and "practical mathematics" (including mixture, mathematical series, plane figures, stacking bricks, sawing of timber, and piling of grain). In the latter section, he stated his famous theorem on the diagonals of a cyclic quadrilateral. Chapter 12 also included a formula for the area of a cyclic quadrilateral (a generalization of Heron's formula), as well as a complete description of rational triangles (i.e. triangles with rational sides and rational areas).
In the Middle Ages, mathematics in medieval Islam contributed to the development of geometry, especially algebraic geometry. Al-Mahani (b. 853) conceived the idea of reducing geometrical problems such as duplicating the cube to problems in algebra. Thābit ibn Qurra (known as Thebit in Latin) (836–901) dealt with arithmetic operations applied to ratios of geometrical quantities, and contributed to the development of analytic geometry. Omar Khayyam (1048–1131) found geometric solutions to cubic equations. The theorems of Ibn al-Haytham (Alhazen), Omar Khayyam and Nasir al-Din al-Tusi on quadrilaterals, including the Lambert quadrilateral and Saccheri quadrilateral, were early results in hyperbolic geometry, and along with their alternative postulates, such as Playfair's axiom, these works had a considerable influence on the development of non-Euclidean geometry among later European geometers, including Vitello (c. 1230 – c. 1314), Gersonides (1288–1344), Alfonso, John Wallis, and Giovanni Girolamo Saccheri.
In the early 17th century, there were two important developments in geometry. The first was the creation of analytic geometry, or geometry with coordinates and equations, by René Descartes (1596–1650) and Pierre de Fermat (1601–1665). This was a necessary precursor to the development of calculus and a precise quantitative science of physics. The second geometric development of this period was the systematic study of projective geometry by Girard Desargues (1591–1661). Projective geometry studies properties of shapes which are unchanged under projections and sections, especially as they relate to artistic perspective.
Two developments in geometry in the 19th century changed the way it had been studied previously. These were the discovery of non-Euclidean geometries by Nikolai Ivanovich Lobachevsky, János Bolyai and Carl Friedrich Gauss and of the formulation of symmetry as the central consideration in the Erlangen programme of Felix Klein (which generalized the Euclidean and non-Euclidean geometries). Two of the master geometers of the time were Bernhard Riemann (1826–1866), working primarily with tools from mathematical analysis, and introducing the Riemann surface, and Henri Poincaré, the founder of algebraic topology and the geometric theory of dynamical systems. As a consequence of these major changes in the conception of geometry, the concept of "space" became something rich and varied, and the natural background for theories as different as complex analysis and classical mechanics.
Main concepts
The following are some of the most important concepts in geometry.
Axioms
Euclid took an abstract approach to geometry in his Elements, one of the most influential books ever written. Euclid introduced certain axioms, or postulates, expressing primary or self-evident properties of points, lines, and planes. He proceeded to rigorously deduce other properties by mathematical reasoning. The characteristic feature of Euclid's approach to geometry was its rigor, and it has come to be known as axiomatic or synthetic geometry. At the start of the 19th century, the discovery of non-Euclidean geometries by Nikolai Ivanovich Lobachevsky (1792–1856), János Bolyai (1802–1860), Carl Friedrich Gauss (1777–1855) and others led to a revival of interest in this discipline, and in the 20th century, David Hilbert (1862–1943) employed axiomatic reasoning in an attempt to provide a modern foundation of geometry.
Objects
Points
Points are generally considered fundamental objects for building geometry. They may be defined by the properties that they must have, as in Euclid's definition as "that which has no part", or in synthetic geometry. In modern mathematics, they are generally defined as elements of a set called space, which is itself axiomatically defined.
With these modern definitions, every geometric shape is defined as a set of points; this is not the case in synthetic geometry, where a line is another fundamental object that is not viewed as the set of the points through which it passes.
However, there are modern geometries in which points are not primitive objects, or even without points. One of the oldest such geometries is Whitehead's point-free geometry, formulated by Alfred North Whitehead in 1919–1920.
Lines
Euclid described a line as "breadthless length" which "lies equally with respect to the points on itself". In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation, but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it. In differential geometry, a geodesic is a generalization of the notion of a line to curved spaces.
Planes
In Euclidean geometry a plane is a flat, two-dimensional surface that extends infinitely; the definitions for other types of geometries are generalizations of that. Planes are used in many areas of geometry. For instance, planes can be studied as a topological surface without reference to distances or angles; it can be studied as an affine space, where collinearity and ratios can be studied but not distances; it can be studied as the complex plane using techniques of complex analysis; and so on.
Angles
Euclid defines a plane angle as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other. In modern terms, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
In Euclidean geometry, angles are used to study polygons and triangles, as well as forming an object of study in their own right. The study of the angles of a triangle or of angles in a unit circle forms the basis of trigonometry.
In differential geometry and calculus, the angles between plane curves or space curves or surfaces can be calculated using the derivative.
Curves
A curve is a 1-dimensional object that may be straight (like a line) or not; curves in 2-dimensional space are called plane curves and those in 3-dimensional space are called space curves.
In topology, a curve is defined by a function from an interval of the real numbers to another space. In differential geometry, the same definition is used, but the defining function is required to be differentiable Algebraic geometry studies algebraic curves, which are defined as algebraic varieties of dimension one.
Surfaces

A surface is a two-dimensional object, such as a sphere or paraboloid. In differential geometry and topology, surfaces are described by two-dimensional 'patches' (or neighborhoods) that are assembled by diffeomorphisms or homeomorphisms, respectively. In algebraic geometry, surfaces are described by polynomial equations.
Solids

A solid is a three-dimensional object bounded by a closed surface; for example, a ball is the volume bounded by a sphere.
Manifolds
A manifold is a generalization of the concepts of curve and surface. In topology, a manifold is a topological space where every point has a neighborhood that is homeomorphic to Euclidean space. In differential geometry, a differentiable manifold is a space where each neighborhood is diffeomorphic to Euclidean space.
Manifolds are used extensively in physics, including in general relativity and string theory.
Measures: length, area, and volume
Length, area, and volume describe the size or extent of an object in one dimension, two dimension, and three dimensions respectively.
In Euclidean geometry and analytic geometry, the length of a line segment can often be calculated by the Pythagorean theorem.
Area and volume can be defined as fundamental quantities separate from length, or they can be described and calculated in terms of lengths in a plane or 3-dimensional space. Mathematicians have found many explicit formulas for area and formulas for volume of various geometric objects. In calculus, area and volume can be defined in terms of integrals, such as the Riemann integral or the Lebesgue integral.
Other geometrical measures include the angular measure, curvature, compactness measures.
Metrics and measures
The concept of length or distance can be generalized, leading to the idea of metrics. For instance, the Euclidean metric measures the distance between points in the Euclidean plane, while the hyperbolic metric measures the distance in the hyperbolic plane. Other important examples of metrics include the Lorentz metric of special relativity and the semi-Riemannian metrics of general relativity.
In a different direction, the concepts of length, area and volume are extended by measure theory, which studies methods of assigning a size or measure to sets, where the measures follow rules similar to those of classical area and volume.
Congruence and similarity
Congruence and similarity are concepts that describe when two shapes have similar characteristics. In Euclidean geometry, similarity is used to describe objects that have the same shape, while congruence is used to describe objects that are the same in both size and shape. Hilbert, in his work on creating a more rigorous foundation for geometry, treated congruence as an undefined term whose properties are defined by axioms.
Congruence and similarity are generalized in transformation geometry, which studies the properties of geometric objects that are preserved by different kinds of transformations.
Compass and straightedge constructions
Classical geometers paid special attention to constructing geometric objects that had been described in some other way. Classically, the only instruments used in most geometric constructions are the compass and straightedge. Also, every construction had to be complete in a finite number of steps. However, some problems turned out to be difficult or impossible to solve by these means alone, and ingenious constructions using neusis, parabolas and other curves, or mechanical devices, were found.
Rotation and orientation
The geometrical concepts of rotation and orientation define part of the placement of objects embedded in the plane or in space.
Dimension

Where the traditional geometry allowed dimensions 1 (a line), 2 (a plane) and 3 (our ambient world conceived of as three-dimensional space), mathematicians and physicists have used higher dimensions for nearly two centuries. One example of a mathematical use for higher dimensions is the configuration space of a physical system, which has a dimension equal to the system's degrees of freedom. For instance, the configuration of a screw can be described by five coordinates.
In general topology, the concept of dimension has been extended from natural numbers, to infinite dimension (Hilbert spaces, for example) and positive real numbers (in fractal geometry). In algebraic geometry, the dimension of an algebraic variety has received a number of apparently different definitions, which are all equivalent in the most common cases.
Symmetry

The theme of symmetry in geometry is nearly as old as the science of geometry itself. Symmetric shapes such as the circle, regular polygons and platonic solids held deep significance for many ancient philosophers and were investigated in detail before the time of Euclid. Symmetric patterns occur in nature and were artistically rendered in a multitude of forms, including the graphics of Leonardo da Vinci, M. C. Escher, and others. In the second half of the 19th century, the relationship between symmetry and geometry came under intense scrutiny. Felix Klein's Erlangen program proclaimed that, in a very precise sense, symmetry, expressed via the notion of a transformation group, determines what geometry is. Symmetry in classical Euclidean geometry is represented by congruences and rigid motions, whereas in projective geometry an analogous role is played by collineations, geometric transformations that take straight lines into straight lines. However it was in the new geometries of Bolyai and Lobachevsky, Riemann, Clifford and Klein, and Sophus Lie that Klein's idea to 'define a geometry via its symmetry group' found its inspiration. Both discrete and continuous symmetries play prominent roles in geometry, the former in topology and geometric group theory, the latter in Lie theory and Riemannian geometry.
A different type of symmetry is the principle of duality in projective geometry, among other fields. This meta-phenomenon can roughly be described as follows: in any theorem, exchange point with plane, join with meet, lies in with contains, and the result is an equally true theorem. A similar and closely related form of duality exists between a vector space and its dual space.
Contemporary geometry
Euclidean geometry
Euclidean geometry is geometry in its classical sense. As it models the space of the physical world, it is used in many scientific areas, such as mechanics, astronomy, crystallography, and many technical fields, such as engineering, architecture, geodesy, aerodynamics, and navigation. The mandatory educational curriculum of the majority of nations includes the study of Euclidean concepts such as points, lines, planes, angles, triangles, congruence, similarity, solid figures, circles, and analytic geometry.
Euclidean vectors
Euclidean vectors are used for a myriad of applications in physics and engineering, such as position, displacement, deformation, velocity, acceleration, force, etc.
Differential geometry
Differential geometry uses techniques of calculus and linear algebra to study problems in geometry. It has applications in physics, econometrics, and bioinformatics, among others.
In particular, differential geometry is of importance to mathematical physics due to Albert Einstein's general relativity postulation that the universe is curved. Differential geometry can either be intrinsic (meaning that the spaces it considers are smooth manifolds whose geometric structure is governed by a Riemannian metric, which determines how distances are measured near each point) or extrinsic (where the object under study is a part of some ambient flat Euclidean space).
Non-Euclidean geometry
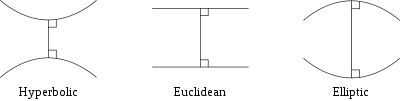
Topology

Topology is the field concerned with the properties of continuous mappings, and can be considered a generalization of Euclidean geometry. In practice, topology often means dealing with large-scale properties of spaces, such as connectedness and compactness.
The field of topology, which saw massive development in the 20th century, is in a technical sense a type of transformation geometry, in which transformations are homeomorphisms. This has often been expressed in the form of the saying 'topology is rubber-sheet geometry'. Subfields of topology include geometric topology, differential topology, algebraic topology and general topology.
Algebraic geometry

Algebraic geometry is fundamentally the study by means of algebraic methods of some geometrical shapes, called algebraic sets, and defined as common zeros of multivariate polynomials. Algebraic geometry became an autonomous subfield of geometry c. 1900, with a theorem called Hilbert's Nullstellensatz that establishes a strong correspondence between algebraic sets and ideals of polynomial rings. This led to a parallel development of algebraic geometry, and its algebraic counterpart, called commutative algebra. From the late 1950s through the mid-1970s algebraic geometry had undergone major foundational development, with the introduction by Alexander Grothendieck of scheme theory, which allows using topological methods, including cohomology theories in a purely algebraic context. Scheme theory allowed to solve many difficult problems not only in geometry, but also in number theory. Wiles' proof of Fermat's Last Theorem is a famous example of a long-standing problem of number theory whose solution uses scheme theory and its extensions such as stack theory. One of seven Millennium Prize problems, the Hodge conjecture, is a question in algebraic geometry.
Algebraic geometry has applications in many areas, including cryptography and string theory.
Complex geometry
Complex geometry studies the nature of geometric structures modelled on, or arising out of, the complex plane. Complex geometry lies at the intersection of differential geometry, algebraic geometry, and analysis of several complex variables, and has found applications to string theory and mirror symmetry.
Complex geometry first appeared as a distinct area of study in the work of Bernhard Riemann in his study of Riemann surfaces. Work in the spirit of Riemann was carried out by the Italian school of algebraic geometry in the early 1900s. Contemporary treatment of complex geometry began with the work of Jean-Pierre Serre, who introduced the concept of sheaves to the subject, and illuminated the relations between complex geometry and algebraic geometry. The primary objects of study in complex geometry are complex manifolds, complex algebraic varieties, and complex analytic varieties, and holomorphic vector bundles and coherent sheaves over these spaces. Special examples of spaces studied in complex geometry include Riemann surfaces, and Calabi–Yau manifolds, and these spaces find uses in string theory. In particular, worldsheets of strings are modelled by Riemann surfaces, and superstring theory predicts that the extra 6 dimensions of 10 dimensional spacetime may be modelled by Calabi–Yau manifolds.
Discrete geometry
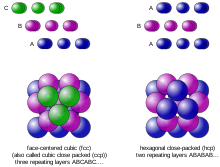
Discrete geometry is a subject that has close connections with convex geometry. It is concerned mainly with questions of relative position of simple geometric objects, such as points, lines and circles. Examples include the study of sphere packings, triangulations, the Kneser-Poulsen conjecture, etc. It shares many methods and principles with combinatorics.
Computational geometry
Computational geometry deals with algorithms and their implementations for manipulating geometrical objects. Important problems historically have included the travelling salesman problem, minimum spanning trees, hidden-line removal, and linear programming.
Although being a young area of geometry, it has many applications in computer vision, image processing, computer-aided design, medical imaging, etc.
Geometric group theory

Geometric group theory uses large-scale geometric techniques to study finitely generated groups. It is closely connected to low-dimensional topology, such as in Grigori Perelman's proof of the Geometrization conjecture, which included the proof of the Poincaré conjecture, a Millennium Prize Problem.
Geometric group theory often revolves around the Cayley graph, which is a geometric representation of a group. Other important topics include quasi-isometries, Gromov-hyperbolic groups, and right angled Artin groups.
Convex geometry
Convex geometry investigates convex shapes in the Euclidean space and its more abstract analogues, often using techniques of real analysis and discrete mathematics. It has close connections to convex analysis, optimization and functional analysis and important applications in number theory.
Convex geometry dates back to antiquity. Archimedes gave the first known precise definition of convexity. The isoperimetric problem, a recurring concept in convex geometry, was studied by the Greeks as well, including Zenodorus. Archimedes, Plato, Euclid, and later Kepler and Coxeter all studied convex polytopes and their properties. From the 19th century on, mathematicians have studied other areas of convex mathematics, including higher-dimensional polytopes, volume and surface area of convex bodies, Gaussian curvature, algorithms, tilings and lattices.
Applications
Geometry has found applications in many fields, some of which are described below.
Art

Mathematics and art are related in a variety of ways. For instance, the theory of perspective showed that there is more to geometry than just the metric properties of figures: perspective is the origin of projective geometry.
Artists have long used concepts of proportion in design. Vitruvius developed a complicated theory of ideal proportions for the human figure. These concepts have been used and adapted by artists from Michelangelo to modern comic book artists.
The golden ratio is a particular proportion that has had a controversial role in art. Often claimed to be the most aesthetically pleasing ratio of lengths, it is frequently stated to be incorporated into famous works of art, though the most reliable and unambiguous examples were made deliberately by artists aware of this legend.
Tilings, or tessellations, have been used in art throughout history. Islamic art makes frequent use of tessellations, as did the art of M. C. Escher. Escher's work also made use of hyperbolic geometry.
Cézanne advanced the theory that all images can be built up from the sphere, the cone, and the cylinder. This is still used in art theory today, although the exact list of shapes varies from author to author.
Architecture
Geometry has many applications in architecture. In fact, it has been said that geometry lies at the core of architectural design. Applications of geometry to architecture include the use of projective geometry to create forced perspective, the use of conic sections in constructing domes and similar objects, the use of tessellations, and the use of symmetry.
Physics
The field of astronomy, especially as it relates to mapping the positions of stars and planets on the celestial sphere and describing the relationship between movements of celestial bodies, have served as an important source of geometric problems throughout history.
Riemannian geometry and pseudo-Riemannian geometry are used in general relativity. String theory makes use of several variants of geometry, as does quantum information theory.
Other fields of mathematics
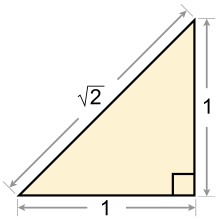
Calculus was strongly influenced by geometry. For instance, the introduction of coordinates by René Descartes and the concurrent developments of algebra marked a new stage for geometry, since geometric figures such as plane curves could now be represented analytically in the form of functions and equations. This played a key role in the emergence of infinitesimal calculus in the 17th century. Analytic geometry continues to be a mainstay of pre-calculus and calculus curriculum.
Another important area of application is number theory. In ancient Greece the Pythagoreans considered the role of numbers in geometry. However, the discovery of incommensurable lengths contradicted their philosophical views. Since the 19th century, geometry has been used for solving problems in number theory, for example through the geometry of numbers or, more recently, scheme theory, which is used in Wiles's proof of Fermat's Last Theorem.









